Cosmological Constraints on Non-flat Exponential $f(R)$ Gravity

We consider the spatially non-flat Friedmann-Lemaitre-Robertson-Walker (FLRW) spacetime, given by

$$ds^{2}=-dt^{2}+a^{2}(t)\bigg{(}\frac{dr^{2}}{1-Kr^{2}}+r^{2}d\theta^{2}+r^{2}sin^{2}\theta d\phi^{2}\bigg{)},$$

(6)

where $a(t)$ is the scale factor, and $K=-1,0,1$ represent the spatially open, flat and closed universe, respectively. Applying the metric (6) into (3), we obtain the modified Friedmann equations, given by

	$\displaystyle 3FH^{2}+\frac{3KF}{a^{2}}=\frac{1}{2}(FR-f)-3H\dot{F}+\kappa^{2}\rho_{M},$		(7)
	$\displaystyle\ddot{F}=H\dot{F}-2F\dot{H}+\frac{2KF}{a^{2}}-\kappa^{2}(\rho_{M}+P_{M}),$		(8)

where $H=\dot{a}/a$ is the Hubble parameter, the dot “$\cdot$” denotes the derivative w.r.t the cosmic time $t$, and the Ricci scalar $R$ takes the form

$\displaystyle R=12H^{2}+6\dot{H}+\frac{6K}{a^{2}}.$

(9)

In order to study the behavior of dark energy and the effects of spatial curvature, we rewrite the modified Friedmann equations in (7) and (8) as

	$\displaystyle H^{2}$	$\displaystyle=\frac{\kappa^{2}}{3}(\rho_{M}+\rho_{de}+\rho_{K}),$		(10)
	$\displaystyle\dot{H}$	$\displaystyle=-\frac{\kappa^{2}}{2}(\rho_{M}+\rho_{de}+\rho_{K}+P_{M}+P_{de}+P_{K}),$		(11)

where $\rho_{M}=\rho_{m}+\rho_{r}$ is the density of non-relativistic matter and radiation, while the dark energy density and pressure are given by

	$\displaystyle\rho_{de}$	$\displaystyle=\frac{3}{\kappa^{2}}\bigg{(}H^{2}(1-F)-\frac{1}{6}(f-FR)-H\dot{F}+\frac{K}{a^{2}}(1-F)\bigg{)},$		(12)
	$\displaystyle P_{de}$	$\displaystyle=\frac{1}{\kappa^{2}}\bigg{(}\ddot{F}+2H\dot{F}+\frac{1}{2}(f-FR)-(1-F)\big{(}3H^{2}+2\dot{H}+\frac{K}{a^{2}}\big{)}\bigg{)},$		(13)

respectively. Here, the effects of spatial curvature in the modified Friedmann equations can be described by the effective energy density and pressure, written as

	$\displaystyle\rho_{K}$	$\displaystyle=-\frac{3K}{\kappa^{2}a^{2}},$		(14)
	$\displaystyle P_{K}$	$\displaystyle=\frac{K}{\kappa^{2}a^{2}}$		(15)

respectively. Note that the energy density and pressure for non-relativistic matter, radiation, dark energy and spatial curvature satisfy the continuity equation

$\displaystyle\frac{d\rho_{i}}{dt}+3H(1+w_{i})P_{i}=0$

(16)

where $w_{i}$ with $i=(m,r,de,K)$ represent the corresponding equations of state, defined by

$\displaystyle w_{i}\equiv\frac{P_{i}}{\rho_{i}}\,,$

(17)

respectively. By rewriting the Friedmann equation of (10) in terms of observational parameters, we have

$\displaystyle 1=\Omega_{m}+\Omega_{r}+\Omega_{de}+\Omega_{K}\,,$

(18)

where $\Omega_{i}$ are the corresponding density parameters, defined by

$\displaystyle\Omega_{i}=\frac{\kappa^{2}\rho_{i}}{3H^{2}}.$

(19)

From (14), we have that $\Omega_{K}=-K/(aH)^{2}$ with $\Omega_{K}>0,=0$ and $<0$ for open, flat and closed universe, respectively.

In order to solve the modified Friedmann equations numerically, we define the dimensionless parameters $y_{H}$ and $y_{R}$ to be

	$\displaystyle y_{H}$	$\displaystyle\equiv\frac{\rho_{de}}{\rho_{m}^{(0)}}=\frac{H^{2}}{m^{2}}-a^{-3}-\chi a^{-4}-\beta a^{-2},$		(20)
	$\displaystyle y_{R}$	$\displaystyle=\frac{R}{m^{2}}-3a^{-3},$		(21)

where $m^{2}=\kappa^{2}\rho_{m}^{(0)}/3$, $\chi=\rho_{r}^{(0)}/\rho_{m}^{(0)}$, and $\beta=\rho_{K}^{(0)}/\rho_{m}^{(0)}$ with $\rho_{i}^{(0)}\equiv\rho_{i}(z=0)$. It can be found from (7) that these two parameters obey the equations

	$\displaystyle\frac{dy_{H}}{d\text{ln}a}$	$\displaystyle=\frac{y_{R}}{3}-4y_{H},$		(22)
	$\displaystyle\frac{dy_{R}}{d\text{ln}a}$	$\displaystyle=\frac{1}{m^{2}}\frac{dR}{d\text{ln}a}+9a^{-3}.$		(23)

As a result, one is able to combine these two first order differential equations into a single second order equation

$\displaystyle y_{H}^{\prime\prime}+J_{1}y_{H}^{\prime}+J_{2}y_{H}+J_{3}=0,$

(24)

where the prime “$\prime$” denotes the derivative w.r.t $\text{ln}a$, and

	$\displaystyle J_{1}$	$\displaystyle=4+\frac{1}{y_{H}+a^{-3}+\chi a^{-4}+\beta a^{-2}}\frac{1-F}{6m^{2}F,_{R}},$		(25)
	$\displaystyle J_{2}$	$\displaystyle=\frac{1}{y_{H}+a^{-3}+\chi a^{-4}+\beta a^{-2}}\frac{2-F}{3m^{2}F,_{R}},$		(26)
	$\displaystyle J_{3}$	$\displaystyle=-3a^{-3}-\frac{(1-F)(a^{-3}+2\chi a^{-4})+(R-f)/3m^{2}}{y_{H}+a^{-3}+\chi a^{-4}+\beta a^{-2}}\frac{1}{6m^{2}F,_{R}}.$		(27)

With the differential equation in (24), the cosmological evolution can be calculated through the various existing programs in the literature.

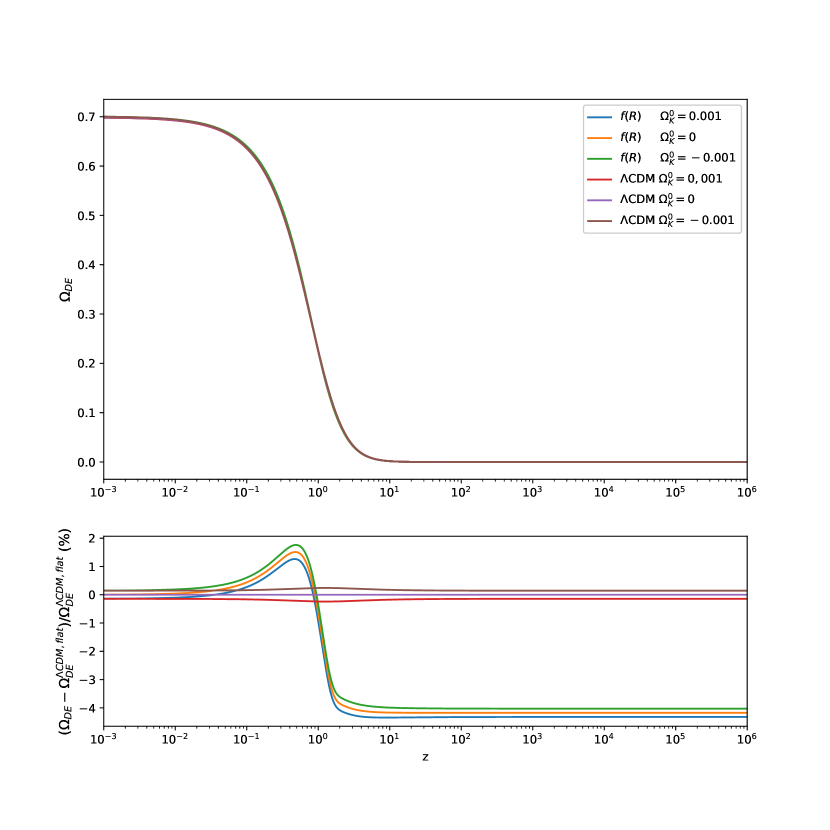
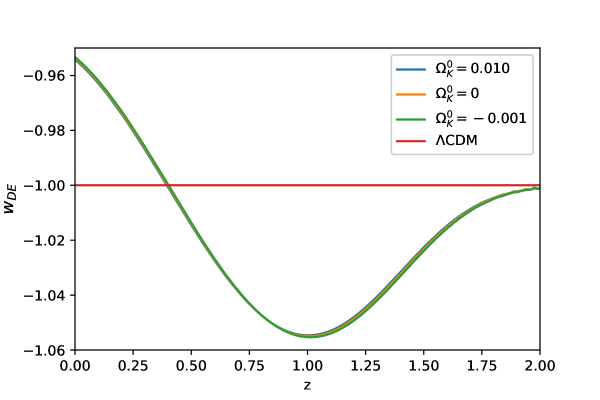
To examine the cosmological evolution of dark energy for the viable exponential gravity model, we plot the density parameter $\Omega_{DE}$, and equation of state $w_{DE}$ of the model in Figs. 1 and 2, respectively. From the previous studies of the exponential $f(R)$ gravity model, the model and spatial curvature density parameters are constrained to be $0.392<\lambda^{-1}<0.851$ Chen:2019uci and $-0.0011<\Omega_{K}^{0}<0.0027$ at 68$\%$ C.L. Vagnozzi:2020rcz , respectively. In this work, we choose $\lambda^{-1}=0.5$ and $\Omega_{K}^{0}=\pm 0.001$ to see the behavior of exponential $f(R)$ gravity. The initial conditions are set to be ($\Omega_{m}^{0}$, $\Omega_{r}^{0}$) = $(0.2998,1.5\times 10^{-3})$, $\Omega_{K}^{0}=(0.001,0,-0.001)$ for the (open, flat, closed) universe, and $H_{0}=67$ km/s/Mpc.

Fig. 1 shows the evolutions of dark energy for exponential $f(R)$ gravity with $\lambda^{-1}=0.5$ and $\Lambda$CDM with $\Omega_{K}^{0}=(0.001,0,-0.001)$. From the figures, we see that the dark energy density parameter for exponential $f(R)$ gravity is slightly larger (smaller) than that of $\Lambda$CDM when $10^{-1}\lesssim z\lesssim 10^{0}$ ($z\gtrsim 10^{0}$). It approaches the cosmological constant in the high redshift region as a characteristic of the viable $f(R)$ gravity models. It is clear that the deviation for $f(R)$ gravity from flat $\Lambda$CDM is small, with $|(\Omega_{DE}-\Omega_{DE}^{\Lambda CDM,flat})/\Omega_{DE}^{\Lambda CDM,flat}|<5\%$. Note that $\Omega_{DE}$ for $f(R)$ gravity in the closed universe has a larger value in comparison with the other cases. Fig. 2 illustrates equation of state $w_{DE}$ for dark energy as a function of $z$. We can see that $w_{DE}$ evolves from the phantom phase ($w_{DE}<-1$) to the non-phantom phase ($w_{DE}>-1$) for a fixed value of $\Omega_{K}^{0}$.

With the initial conditions and

$\displaystyle t_{age}=\frac{1}{H_{0}}\int_{0}^{1}\frac{da}{a\sqrt{\Omega_{m}a^{-3}+\Omega_{r}a^{-4}+\Omega_{K}a^{-2}+\Omega_{de}(a)}},$

(28)

we can calculate the age of the universe. Consequently, we obtain that

	$\displaystyle t_{age}^{open}$	$\displaystyle=\quad 14.021\;,\ 14.045\quad Gyr\qquad(\Omega_{K}^{0}=0.001)$		(29)
	$\displaystyle t_{age}^{flat}$	$\displaystyle=\quad 14.025\;,\ 14.049\quad Gyr\qquad(\Omega_{K}^{0}=0)$		(30)
	$\displaystyle t_{age}^{closed}$	$\displaystyle=\quad 14.028\;,\ 14.054\quad Gyr\qquad(\Omega_{K}^{0}=-0.001),$		(31)

for the exponential $f(R)$ and $\Lambda$CDM models in the open, flat and closed universe, respectively. From (29), (30) and (31), we see that the age of the universe for exponential $f(R)$ gravity is shorter than the corresponding one for $\Lambda$CDM. Note that the bigger value of $t_{age}$ is related to the longer growth time of the large scale structure (LSS) and larger matter density fluctuations.

In this subsection, we present constraints on the cosmological parameters in the exponential $f(R)$ model without the spatial flatness assumption . With the modifications of CAMB at the background level and the CosmoMC package, we perform the MCMC analysis.

To break the geometrical degeneracy Efstathiou:1998xx ; Howlett:2012mh , we fit the model with the combinations of the observational data, including CMB temperature and polarization angular power spectra from Planck 2018 with high-$l$ TT, TE, EE , low-$l$ TT, EE, CMB lensing from SMICA Planck:2018vyg ; Planck:2018lbu ; Planck:2019kim ; Planck:2019nip , BAO observations from 6-degree Field Galaxy Survey (6dF) Beutler:2011gb , SDSS DR7 Main Galaxy Sample (MGS) Ross:2014qpa and BOSS Data Release 12 (DR12) BOSS:2016wmc , and supernova (SN) data from the Pantheon compilation Pan-STARRS1:2017jku . As we set the density parameter of curvature and the neutrino mass sum to be free, our fitting for the exponential $f(R)$ model contains nine free parameters, where the priors are listed in Table 1.

To find the best-fit results, we minimize the $\chi^{2}$ function, which is given by

$\displaystyle\chi^{2}=\chi_{CMB}^{2}+\chi_{BAO}^{2}+\chi_{Pan}^{2}\,.$

(32)

Explicitly, we take

$\displaystyle\chi_{CMB}^{2}=\sum_{ll^{\prime}}(C^{obs}_{l}-C^{th}_{l})\mathcal{M}^{-1}_{ll^{\prime}}(C^{obs}_{l^{\prime}}-C^{th}_{l^{\prime}})$

(33)

where $C^{obs(th)}_{l}$ corresponds to the observational (theoretical) value of the related power spectrum, and $\mathcal{M}$ is the covariance matrix for the CMB data Planck:2018vyg ; Planck:2018lbu .

For the BAO data, we adopt the dataset from 6-degree Field Galaxy Survey (6dF) at $z_{eff}=0.106$ Beutler:2011gb , SDSS DR7 Main Galaxy Sample (MGS) at $z_{eff}=0.15$ Ross:2014qpa and BOSS Data Release 12 (DR12) at $z_{eff}=(0.38,0.51,0.61)$  BOSS:2016wmc . As a result, we have

$\displaystyle\chi_{BAO}^{2}=\chi_{6dF}^{2}+\chi_{MGS}^{2}+\chi_{DR12}^{2}.$

(34)

For the uncorrelated data points, such as 6dF and MGS, $\chi^{2}$ is given by

$\displaystyle\chi^{2}(p)=\sum^{N}_{i=1}\frac{[A_{th}(z_{i})-A_{obs}(z_{i})]^{2}}{\sigma^{2}_{i}},$

(35)

where $A_{th}(z_{i})$ is the predicted value computed in the model under consideration, and $A_{obs}(z_{i})$ denotes the measured value at $z_{i}$ with the standard deviation $\sigma_{i}$. Note that in our study, we adopted 6dF and MGS, whose standard deviations are given by $\sigma_{6dF}=0.015$ and $\sigma_{MGS}=0.168$, respectively. The data points from DR12 are correlated. In this case, $\chi^{2}$ is given by

$\displaystyle\chi_{DR12}^{2}=\bigg{[}\textbf{A}_{th}-\textbf{A}_{obs}\bigg{]}^{T}\cdot\textbf{C}^{-1}\cdot\bigg{[}\textbf{A}_{th}-\textbf{A}_{obs}\bigg{]},$

(36)

where $\textbf{C}^{-1}$ is the inverse of the covariance matrix, which is an $6\times 6$ matrix given in Eq. (20) of Ref. Ryan:2019uor .

For the Pantheon SN Ia samples, there are 1048 data points scattering between $0.01\leq z\leq 2.3$, with the observable to be the distance modulus $\mu$ defined in Ref. Pan-STARRS1:2017jku . We have that

$\displaystyle\chi_{Pan}^{2}=\bigg{[}\bm{\mu}_{obs}-\bm{\mu}_{th}\bigg{]}^{T}\cdot\textbf{Cov}^{-1}\cdot\bigg{[}\bm{\mu}_{obs}-\bm{\mu}_{th}\bigg{]},$

(37)

where $\textbf{Cov}^{-1}$ is the inverse covariance matrix Pan-STARRS1:2017jku of the sample including the contributions from both the statistical and systematic errors. The covariance matrix of Pantheon samples can also be found in the website ¹¹1http://supernova.lbl.gov/Union/.

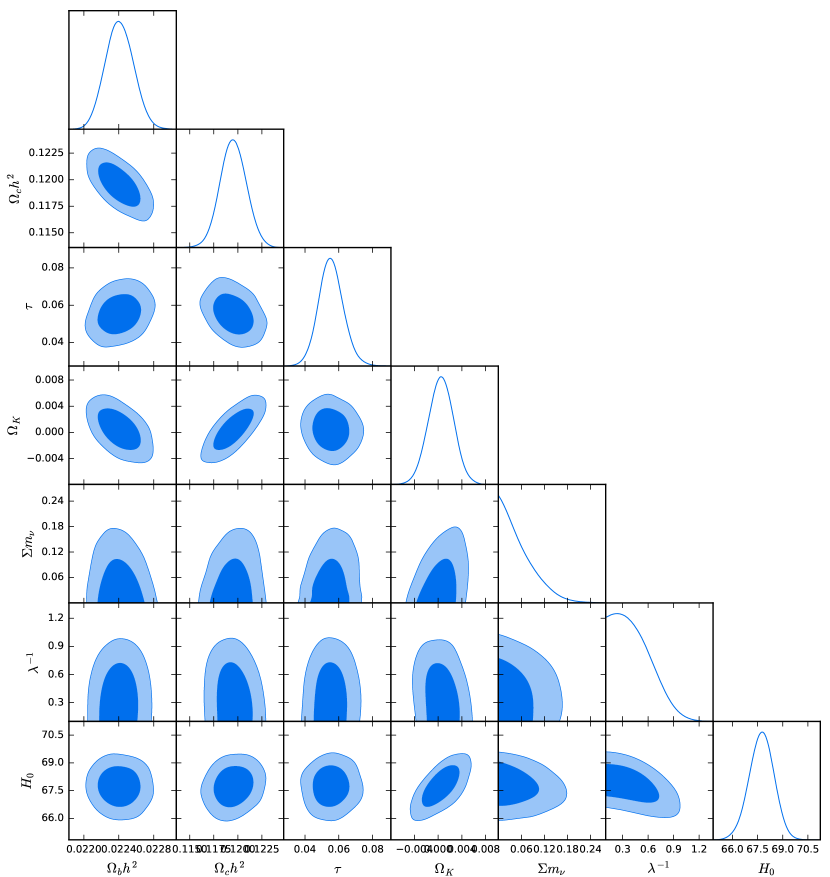
The global fitting results of the exponential $f(R)$ model without the spatial flatness assumption with CMB+BAO+SN data sets are shown in Fig. 3 and listed in Table 2. We note that the exponential $f(R)$ model is barely distinguishable from $\Lambda$CDM. This statement is in agreement with the previous work in the flat universe Geng:2014yoa . FromTable 2, we see that the model and curvature density parameters are constrained to be $\lambda^{-1}=0.42927^{+0.39921}_{-0.32927}$ at 68$\%$ C.L and $\Omega_{K}=-0.00050^{+0.00420}_{-0.00414}$ at 95$\%$ C.L for the exponential $f(R)$ model, respectively. Note that the flat $\Lambda$CDM model is recovered when $\lambda^{-1}=0$ and $\Omega_{K}=0$. We also obtain that $\chi^{2}=3821.50~{}(3821.84)$ for $f(R)$ ($\Lambda$CDM) with $\chi^{2}_{f(R)}\lesssim\chi^{2}_{\Lambda CDM}$, indicating that exponential $f(R)$ is consistent with $\Lambda$CDM. The neutrino mass sum is evaluated to be $\Sigma m_{\nu}<0.06816~{}(0.06121)$ for $f(R)$ ($\Lambda$CDM) at 68$\%$ C.L., which is relaxed at 11 $\%$ comparing with $\Lambda$CDM. This phenomenon is caused by the shortened age of the universe in the exponential $f(R)$ model, in which the matter density fluctuation is suppressed as discussed in Chen:2019uci and Sec. III.1.

To compare exponential $f(R)$ gravity with $\Lambda$CDM, we introduce the Akaike Information Criterion (AIC) Akaike:1974 , Bayesian Information Criterion (BIC) Schwarz:1978tpv , and Deviance Information Criterion (DIC) Spiegelhalter:2002yvw . The AIC is defined through the maximum likelihood $\mathcal{L}_{max}$ (satisfying $-2\,{\rm ln}\,{\mathcal{L}}_{max}\propto\chi^{2}_{min}$ under the Gaussian likelihood assumption) and the number of model parameters, $d$:

$\displaystyle AIC=-2\,{\rm ln}\,{\mathcal{L}}_{max}+2d=\chi^{2}_{min}+2d.$

(38)

The BIC is defined as

$\displaystyle BIC=-2\,{\rm ln}\,{\mathcal{L}}_{max}+d{\rm ln}N=\chi^{2}_{min}+d{\rm ln}N,$

(39)

where $N$ is the number of data points.

The DIC is determined by the quantities obtained from posterior distributions, given by

$\displaystyle DIC=D(\bar{\theta})+2\,p_{D},$

(40)

where $D(\theta)=-2\,{\rm ln}\,{\mathcal{L}}(\theta)+C,p_{D}=\overline{D(\theta)}-D(\overline{\theta}),C$ is a constant, and $p_{D}$ represents the effective number of parameters in the model.

We now compute the AIC, BIC, and DIC values from CMB+BAO+SN samples described above for both models, with the difference given by $\Delta AIC=AIC_{f(R)}-AIC_{\Lambda CDM}=1.66$, $\Delta BIC=BIC_{f(R)}-BIC_{\Lambda CDM}=7.85$, and $\Delta DIC=DIC_{f(R)}-DIC_{\Lambda CDM}=1.49$, respectively. The results are summarized in Table 3, where the differences are residuals with respect to the $\Lambda$CDM model. Since $\Delta AIC,\,\Delta DIC)<2$, being small, there is no strong preference between the exponential $f(R)$ and $\Lambda$CDM models in terms of AIC and DIC Rezaei:2021qpq . However, as $6<\Delta BIC<10$, there is a strong evidence against the exponential $f(R)$ model Liddle:2007fy .