Could TDE outflows produce the PeV neutrino events?
Abstract
A tidal disruption event (TDE), AT2019dsg, was observed to be associated with a PeV neutrino event, IceCube-191001A, lagging the optical outburst by a half year. It is known that TDEs may generate ultrafast outflows. If the TDE occurs in a cloudy environment, the outflow-cloud interactions may form shock waves which generate accelerated protons and hence delayed neutrinos from hadronic interactions in clouds. Here we investigate the neutrino production in AT2019dsg by examining the TDE outflow-cloud interaction model. We find that, for an outflow with a velocity of 0.07c and a kinetic luminosity of , protons may be accelerated up to 60 PeV by the bow shocks, and generate PeV neutrinos by interactions with clouds. The predicted neutrino number in this model depends on the uncertainties of model parameters and in order to match the observations, some challenging values of parameters have been involved. The PeV neutrino event number can be for a hard proton index .
keywords:
Gamma-Rays: ISM – neutrinos – galaxies: active – (galaxies:) quasars: supermassive black holes – radiation mechanisms: non-thermal1 Introduction
On 22 September 2017, IceCube reported a neutrino event with energy , which was shown to be associated with the blazar TXS 0506+056 (Telescope et al., 2018). This opened a window of high energy neutrino astrophysics. The origin of high energy neutrinos is not clear yet, and TDEs are the other possible sources.
Recently, Stein et al. (2021) reported a correlation between a neutrino event with energy 0.2 PeV detected by IceCube on 1 October 2019 (IceCube-191001A) and a TDE (AT2019dsg) discovered by Zwicky Transient Facility (ZTF), and the neutrino event lags the onset of TDE by 6 months. AT2019dsg’s redshift is , i.e., the luminosity distance is Mpc. The optical luminosity was observed to decrease from to (van Velzen et al., 2021) on a timescale of a half year. AT2019dsg is among the top 10% of the 40 known optical TDEs in luminosities. The peak radiation is well described by a -sized blackbody photosphere of temperature K. AT2019dsg is an unusual TDE (Hayasaki, 2021); it belongs to neither the typical soft-X-ray TDEs nor the typical optical/UV TDEs because it emits optical/UV radiations as well as X-ray and radio radiations. Fermi Large Area Telescope (Fermi-LAT) provides an upper limit of flux in 0.1-800 GeV range. HAWC observatory also set an upper limit for the period from 30 September to 2 October, for 300 GeV-100 TeV (van Velzen et al., 2021).
In the previous literatures (e.g., Wang & Liu 2016; Liu et al. 2020), a jet from the TDE is assumed to accelerate protons and generate neutrinos via p interactions, dominating over pp interactions since the density of photons is extremely high. Moreover, in the TDE model by Murase et al. (2020) high-energy neutrinos and soft gamma-rays may be produced via hadronic interactions in the corona, the radiatively inefficient accretion flows and the hidden sub-relativistic wind.
It is known that, in addition to the radiative outburst, TDE is also expected to launch ultra-fast and energetic outflows. First, due to the relativistic apsidal precession, after passing the pericenter, the stream collides with the still falling debris, leading to a collision-induced outflow (Lu & Bonnerot, 2020). Second, after debris settling into an accretion disk, the high accretion mode will launch energetic outflows (Curd & Narayan, 2019). Since the duration of both processes above are of the order of months, the duration of launching energetic TDE outflows is also roughly in months. For AT2019dsg, the physics of the outflow is estimated via radio emission. The velocity inferred in different models are similar: 0.07 c in outflow–circumnuclear medium (CNM) interaction model Cendes et al. (2021), or 0.06–0.1c in outflow–cloud interaction model (Mou et al., 2022)). However, the outflow energy or kinetic luminosity of outflows ranges a lot in different models. Cendes et al. (2021) estimated an energy of erg, which is much smaller than the energy budget of the TDE system ( erg). Mou et al. (2022) inferred that the outflow power should be around erg s-1 which is consistent with numerical simulations (Curd & Narayan, 2019), and the total energy should be in the order of erg if the outflow continues for months.
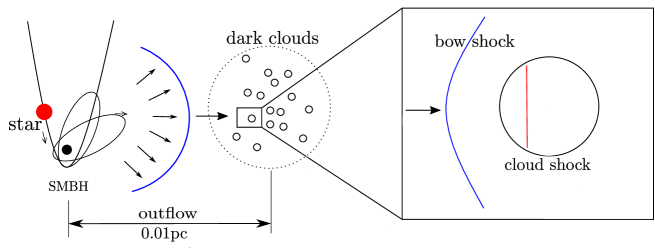
When the outflow impacts a cloud, the bow shock (BS) can be produced outside the cloud, and could effectively accelerate particles via diffusive shock acceleration (DSA) processes. The electrons accelerated at BSs give rise to synchrotron emission, which can be detected in GHz radio band (Mou et al., 2022). The accelerated high energy protons may be the precursor of the neutrinos, especially considering the high-density cloud near the BS which is favorable for pp collisions (Mou et al., 2021). A basic premise is whether there are clouds around the black hole, especially at the distance of pc as inferred from the delay of the neutrino event and the possible outflow speed. It is well known that for active galactic nuclei (AGN), there exists a so-called broad line region (BLR) around the supper massive black hole (SMBH) (Antonucci, 1993), which is frequently referred to as “clouds”. However, for quiescent SMBH or low-luminosity AGN (the case for AT2019dsg), due to the lack of ionizing radiation irradiating the clouds, the existence of the clouds becomes difficult to verify, and the physics of such clouds remains largely unknown.
To distinguish from the BLR cloud concept in AGN, we hereby call the possibly existing clouds around quiescent or low-luminosity SMBH at similar position of the BLR as “dark clouds”. Transient events may help reveal the physics of dark clouds. For AT2019dsg, in addition to the indirect speculation of the existence of dark clouds via radio emission (Mou et al., 2022), direct evidences arise from the dusty echo, and broad emission line components. First, van Velzen et al. (2021) reported that AT2019dsg was detected with remarkable infrared echo about 30 days after the optical onset, suggesting that clouds should exist at a distance of 0.02 pc to the SMBH (note that there may exist clouds in more inward regions but not surveyed by WISE/neoWISE). Second, it is reported that there exist the broad emission line components (line widths 70 Å) of H, H, and HeII (Cannizzaro et al., 2021), implying the existence of materials of the velocity over several thousand kilometers per second, although their nature is unclear. In our TDE outflow-cloud interaction model, we assume that there exist dark clouds at pc to the BH, and we simply set up the parameters (covering factor, cloud size and density) of dark clouds similar referring to those of classical BLR clouds.
This paper is organized as follows. We introduce the general physics picture of the model in Sec. 2; The products (GeV-TeV gamma-rays and PeV neutrinos) from hadronic emission are described in Sec. 3; In Sec. 4, we compare the calculations with the present observations; The conclusions and discussion are presented in the last section.
2 Physical picture of outflow-cloud interactions
As shown in Fig. 1, consider that there are dark clouds surrounding the SMBH.The TDE outflows released from the SMBH collide with the dark clouds, forming two shock waves (McKee & Cowie, 1975), i.e., a bow shock (BS) outside the cloud and a cloud shock (CS) sweeping through the cloud. Following Celli et al. (2020), protons may be accelerated to very high energy with a power-law distribution. The high-energy protons may partly propagate into the cloud and interact with matter therein.
2.1 Dynamics
We consider a simplified spherically symmetric outflow, with kinetic luminosity and velocity . We take as the fiducial value (Curd & Narayan, 2019), which is also close to the constraint given by Mou et al. (2022). Following the interpretation of the radio observation (Stein et al., 2021) by synchrotron radiation from non-thermal electrons in the outflow-CNM model, we take the outflow velocity derived from the model, (Cendes et al., 2021). The duration of the outflow launching is assumed to be months.
Define the density of outflow material, then we write the kinetic luminosity as , with the mass flowing rate. Since the time delay of the neutrino event and the TDE is month (van Velzen et al., 2021), we assume the typical distance of the dark clouds from the central SMBH is pc. Thus the number density of the outflow is .
The interaction between outflows and clouds drives a CS that sweeps across the cloud. The velocity of CS is related to the outflow velocity by (McKee & Cowie, 1975; Mou & Wang, 2021), where , with the particle density in the cloud. According to the photoionization models in BLRs of AGN, we assume the cloud particle density to be (Osterbrock & Ferland, 2006). So, here .
Let us assume the size of the clouds is typically cm111This can be obtained from the column density () and the cloud density (Osterbrock & Ferland, 2006).. The CS crosses the cloud in a timescale of
| (1) |
i.e., month. Note, the cloud could be devastated by the outflow, and the survival timescale of the clouds after the CS crossing is comparable to (Klein et al., 1994), so can also be regarded as the survival timescale of the cloud.
2.2 Particle acceleration and propagation
Both BS and CS may accelerate particles. According to DSA mechanism, the acceleration timescale in the BS for a particle with energy and charge number is (Drury, 1983)
| (2) |
where is the magnetic field strength in the outflow. For the CS, the acceleration timescale is
| (3) |
where is the magnetic field in the cloud. We will assume in the nearby region of the outflow–cloud interaction, and we take G.
The particle acceleration suffers from several factors. The first is the particle energy loss due to hadronic interactions, namely the pp interactions. In the BS, the timescale is
| (4) |
whereas in the CS,
| (5) |
Here mb is the pp cross section. The other suppression factor is the lifetime of the relevant shocks. As the cloud survival timescale is comparable to the CS crossing time, and after the cloud is destroyed, both BS and CS end. So the acceleration in either BS or CS is only available within a time period of (Klein et al., 1994). Finally, the maximum energy of the accelerated particles is determined by equating the acceleration time to the shortest one between the pp interaction time and the CS crossing time of the cloud.
All the timescales are plotted in Fig. 2. For the BS, month is the main constraint than the pp energy loss time, due to the low density in the outflow, yr. By equating we obtain the maximum energy of particles accelerated in the BS, PeV. For the CS, due to the dense cloud, the pp collision time is short, day, and is more important in suppressing acceleration. By , one obtains the maximum energy TeV. Thus only the BS can accelerate particles up to PeV scale.
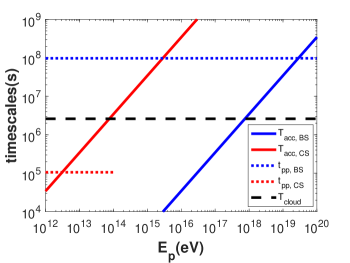
Note that we neglect the effect of energy loss due to p interactions between the high-energy particles and the TDE photons. Given the cross section mb on average, and the TDE photon number density at , (see Sec. 3.2), the timescale of interactions is relatively large, . In the previous works (e.g., Liu et al. 2020), reaction is important because a site closer to the center is considered, so the photon density is high, (with being the TDE luminosity, see below) and reaction is important. In our case, neither p nor pp reactions in the BS consume significant energy of the accelerated particles.
After acceleration in the BS, the high-energy particles may diffuse away from the BS (Bultinck et al., 2010; Taylor, 1961; Kaufman, 1990). As suggested by some literatures (Dar & Laor, 1997; Barkov et al., 2010, 2012; Wang et al., 2018), we assume that a significant fraction of the accelerated particles can effectively reach and enter the cloud, whereas the other propagate away bypassing the cloud. Basically, the relatively low-energy protons are likely to be advected with the shocked material, while the relatively energetic particles () tend to diffuse up to the cloud. Besides, these high-energy particles entering the cloud could be more important by suppressing the possible advection escape under the certain magnetic configuration (Bosch-Ramon, 2012). The detailed treatment of the particle propagation is beyond the scope of this paper. To evaluate this uncertainty, is invoked in our calculations. For the other high-energy particles that do not propagate into the cloud, no hadronic interactions are expected, given the low density of cold particles outside the cloud.
After entering the cloud, the particles may propagate in the cloud by diffusion. The residence time in the cloud before escaping can be estimated by
| (6) |
where is the Bohm diffusion coefficient. and is a correction factor that accounts for the difference between the actual diffusion coefficient and the Bohm diffusion. We take . The Bohm diffusion coefficient of protons is given by (Kaufman, 1990) , where is the cyclotron radius, and is the cyclotron frequency. Thus we get day, a value similar to for PeV.
3 Hadronic emission
In the outflow–cloud interaction, the kinetic energy of the outflow will be converted into the BS and CS. The energy ratio between the CS and BS is , so the energy dissipation in the CS can be neglected compared to the BS (see appendix A in Mou & Wang 2021).
The covering factor of the clouds is , and the shock acceleration efficiency, i.e., the fraction of the shock energy converted to accelerated particles, is . Given the kinetic energy of the outflow, the average luminosity of the accelerated particles is, in the BS,
| (7) |
and in the CS,
| (8) |
Plugging the numbers, , and for . The luminosity of CSs is so small, which allow us to neglect their contribution in emission.
We assume the accelerated relativistic particles distribute as a power-law spectrum with spectral index and an exponential cut-off at the high energy:
| (9) |
The normalization factor can be determined by the normalization of the particle luminosity . Since neglecting contribution from the CS, we have . We will consider a range of value, from 2 to 1.5 (Celli et al., 2020).
The pp collision produce neutral and charged pions,
| (10) | |||
| (11) |
where . The pions decay and generate -rays and leptons:
| (12) | |||
| (13) | |||
| (14) |
The final product particles produced by pp collisions in the clouds per unit time on average can be given by (e.g. Kamae et al., 2006; Aartsen et al., 2014):
| (15) |
where f, etc., represents the type of final particles, is the inclusive cross section as function of final particles and proton’s energy, and is the background number density of protons. The coefficient 1.5 is a correction factor accounting for the contribution of Helium (we assume that the Helium abundance in the BS is similar to Galactic cosmic rays (Mori, 1997)). Here the integration is calculated using the cparamlib package222https://github.com/niklask/cparamlib. If the particle escape from the cloud is fast, the calculated spectrum above should be multiplied by a factor to take into account the reduction of secondary products by escape.
| Parameters | Descriptions | Fiducial Values |
|---|---|---|
| the kinetic luminosity of outflow | ||
| the velocity of outflow | 0.07c | |
| outflow launching duration | 6 months | |
| the typical distance of clouds from the SMBH | ||
| the particle density of cloud | ||
| the typical size of clouds | ||
| magnetic field strength around outflow-cloud interaction region | 1G | |
| covering factor of clouds | 0.1 | |
| the fraction of shock energy converted to accelerated particles | 0.1 | |
| the fraction of accelerated particles propagate into the cloud | 0.5 | |
| the correction factor of diffusion coefficient relative to Bohm limit | 0.75 |
3.1 Neutrino
Given the neutrino luminosity and spectrum, we calculate the neutrino event number expected to be detected by IceCube in a time period of ,
| (16) |
The detected event IceCube-191001A has a neutrino energy of PeV, thus we only calculate the sub-PeV neutrino events in PeV range. The real time effective area of IceCube is described by (Blaufuss et al., 2021)
| (17) |
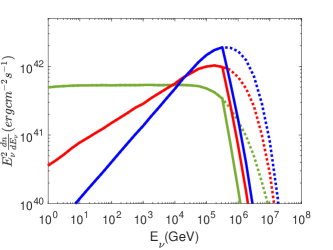
The number of neutrino events is calculated to be for , considering particle escape from cloud (see details in Fig. 3).
3.2 -ray
The intrinsic -ray spectrum accompanying the neutrino emission can also be calculated with equation 15, but high-energy -ray photons may be attenuated by interacting with low-energy background photons via . The background photons may come from the TDE, host galaxy, extragalactic background light (EBL), cosmic microwave background (CMB), and even radiation in the cloud, etc.
Consider the TDE photons first. At a distance from the SMBH, the number density of TDE photons around typical energy eV is estimated by
| (18) |
where is the TDE radiation luminosity, which is given by Stein et al. (2021) for AT2019dsg. The TDE luminosity may evolve with time, approximately estimated as following the accretion rate evolution, i.e., , where yr is the minimum orbit period of the disrupted material (Evans & Kochanek, 1989) depending on the radius and the mass of the star . The TDE luminosity decreases to about of the peak luminosity after months, i.e., . Thus, the TDE photon density is estimated as .
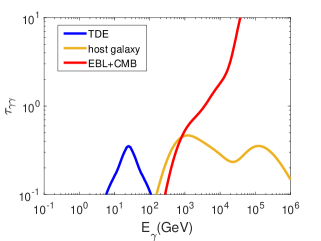
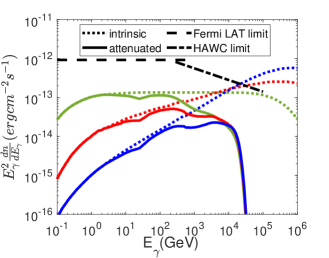
The -rays are emitted from clouds pc away from the SMBH, so the absorption due to the TDE photon field relies on the emergent angle. We calculated the angle-averaged optical depth for the -rays (see the appendix J of Mou & Wang 2021). The optical depth due to TDE photons is found to be moderate for -rays of tens of GeV, as presented in Fig. 4.
Next, the absorption of the host galaxy’s background light is considered. The photons are assumed to be isotropic, and we calculate absorption as Aharonian (2004). For host galaxy background photon fields, there was no more observation of the host galaxy 2MASS J20570298+1412165, except the infrared observation (Skrutskie et al., 2006), namely J (), H (), and K (). Thus we get the mean luminosity in J, H, K bands to be about . For the spectral profile we adopt the model in Finke et al. (2010) (the black line for redshift in Fig. 5 therein), and normalized to the infrared luminosity. The size of the host galaxy is typically of kpc scale. we find only mild absorption beyond TeV (see Fig. 4). Furthermore, there would be significant absorption by the EBL and CMB. Considering the spectrum of EBL as model C in Finke et al. (2010) our calculation result for the EBL and CMB absorption is presented in Fig. 4. Both intrinsic and attenuated spectra are plotted for comparison. The absorption significantly changes the emergent spectrum, mainly due to the EBL and CMB absorption.
Notice that we have considered also the absorption in the cloud since the high-energy -rays are produced in the cloud, but we find the attenuation in the cloud is negligible. Firstly, the shocked cloud is optically thin to the high-energy gamma-rays for the electron-photon scattering between the thermal electron and high-energy photon, the optical depth for the GeV photon with and the Bethe-Heitler process for the parameters adopted in our model, i.e., cloud density and cloud radius . In addition to e- scattering and Bethe-Heitler process for the high-energy gamma-rays, we evaluate the absorption due to thermal radiations of clouds next. The shocked cloud emits through free-free radiation with a temperature , and a luminosity for a single cloud , where is the cooling timescale of free-free radiation and is the CS crossing timescale. The optical depth for the high-energy gamma-rays can be estimated as
| (19) |
with the most optimistic cross section, where the number density can be written as since the cloud is optically moderately thin to its own radiations with the optical depth (contributions of other clouds to number density can be easily neglected). Therefore, the opacity () caused by the cloud to the high-energy gamma-rays can be neglected. In addition, considering the superposition of the free-free emission of clouds (total luminosity ), the corresponding total flux is quite low with a value at the keV energy band so that it is much lower than the observational upper limit of X-rays, even for the deep upper limit of (0.3-10 keV) given by XMM observations in Stein et al. (2021).
3.3 Other radiation
The BS accelerates both electrons and protons. The leptonic process of accelerated electrons also produces radiations. However, the ratio between the energy budgets of electrons and protons could be around (Mou & Wang, 2021), leading to a radiation luminosity by electrons is at most for the fast cooling case, and the corresponding flux is quite low, and can be neglected.
Moreover, the secondary electrons from absorption may generate photons again via Inverse Compton scatterings, leading to the electromagnetic cascades. As shown in Fig. 4, only the EBL and CMB absorption is significant, and may results in electromagnetic cascades in the intergalactic medium. The deflection of electrons by the intergalactic magnetic field is expected to spread out the cascade emission, and contribute little to the observed flux.
4 Results compared with observations
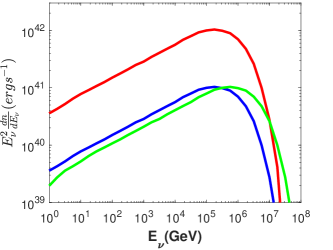
We summarize in Table 1 the fiducial values for the model parameters used in the calculation. The neutrino luminosity is presented in Fig. 3. According to equation 16, we get the expected event number of 0.1-1PeV neutrinos detected by IceCube. Without considering the partile escape from cloud, the expected number is , , , and for , 1.7, 1.9 and 2, respectively. However, if consider particle escape, as described by equation 6, the numbers change to , , , and , respectively. Thus, for the fiducial model parameters, the expected neutrino event number is somewhat lower than the expected neutrino number of for AT2019dsg (Stein et al., 2021).
The interactions produce -rays from GeV to TeV energy bands. Considering the host galaxy distance of 230 Mpc, the photons above TeV cannot arrive at the Earth due to the absorptions by CMB and EBL. In addition, the strong absorption by the host galaxy photon field based on the infrared observations (Skrutskie et al., 2006) is moderate. Finally, the processes produce the maximum -ray flux up to for in the bands of 0.1 GeV - 1 TeV, which is lower than the present gamma-ray observational limits by Fermi/LAT and HAWC (see Fig. 4).
5 Conclusion and discussion
In this work, we considered the high-speed TDE outflows colliding with the clouds to produce the high-energy neutrinos and gamma-rays, which can explain the sub-PeV neutrino event in AT2019dsg. The assumed outflow velocity is and the kinetic luminosity is . The outflow-cloud interactions will produce the BS ahead clouds. Particle acceleration is efficient in the BS and the pp process would contribute to the observational high energy neutrinos and gamma-rays. We assumed an escaping parameter of , which means half of the accelerated protons escape from the BS region while the rest enter the dense cloud participating in pp collisions. Here we should point out that the escaping parameter of cannot be constrained well, leading to the values being quite uncertain, and the factor may be taken as a much smaller value in the more realistic cosmic-ray escape models.
For the fiducial model parameters, the expected neutrino event number would be relatively low compared to observations. In order to reach the observational neutrino number, one has to invoke some challenging model parameters. For instance, (1) considering a higher cloud density or a larger cloud size, inducing the escaping time will be much higher than (see equation 6) and the interactions of protons which produce 0.1-1 PeV neutrinos becomes more efficient, the expected number of neutrinos would increase by a factor of (see Fig. 3); (2) the converting fraction of energy from the outflow to protons relies on the covering factor of BS , and shock acceleration efficiency , so the expected number of neutrinos could increase by a factor of by taking a larger and a larger than the fiducial values listed in Table. 1. For sure, on the contrary, the expected neutrino number could be reduced if a lower cloud column density, smaller and , or a softer proton index is adopted. As a result, the predicted neutrino number in our model depends on the uncertainties of model parameters and in order to match the observations, some challenging values of parameters have been involved.
In above calculations, we anchored two parameters of the outflows, the kinetic luminosity and the velocity of outflows . Numberical simulations indicate that TDE can launch powerful wind with a kinetic luminosity of erg s-1 (Curd & Narayan, 2019), or even higher (Dai et al., 2018). AT2019dsg also exhibits radio flares, arising fifty days post burst and lasting for more than one year (Stein et al., 2021; Cendes et al., 2021). Modeling the radio flare by the outflow-CNM (circumnuclear medium) model suggests that the averaged kinetic luminosity is erg s-1 (Stein et al., 2021) or even lower (Cendes et al., 2021). However, if the radio flare originates from outflow-cloud interaction which is the same scenario as our current model, the inferred kinetic luminosity may be in the order of erg s-1 (Mou et al., 2022). Radio outflow and delayed neutrino may be explained by the same physical process. The detected neutrino number is linearly proportional to the kinetic luminosity. For the case of , the modeling neutrino luminosity is presented in Fig. 5. The expected neutrino number will be about one order of magnitude lower than the above values in the case of .
The velocity of the outflow is taken as , but this value is still uncertain, the radio observations suggested the outflow velocity in AT2019dsg is (Stein et al., 2021), 0.07c (Cendes et al., 2021) or around 0.1c (Mou et al., 2022). If the outflow velocity is higher, the maximum energy of accelerated protons in the BS will be also higher accordingly. Then the peak neutrino luminosity will move to the higher energy ranges. If we integrate the neutrino number from PeV, the detected neutrino number would be different. For a comparison, we also plotted the neutrino luminosity versus energy in the case of , in Fig. 5. Since we only integrate the neutrino number in the range of PeV, if is about 0.04c, and PeV, the neutrino SED will peak at PeV, and the expected number of neutrinos will increase by .
After the submission of this work, we notice recent reports on more neutrino events associated with the time-variable emission from accreting SMBHs (van Velzen et al., 2021; Reusch et al., 2021), among which AT2019fdr is a TDE candidate in a Narrow-Line Seyfert 1 AGN in which the BLR clouds should exist. Moreover, the neutrino events lag the optical outbursts by half year to one year (van Velzen et al. 2021), consistent with the assumption that clouds exist at the distance of pc from the central BH if the outflow velocity is in the order of cm s-1. The outflow–cloud interaction may also contribute to the high energy neutrino background (Abbasi et al., 2021).
Acknowledgments
We are grateful to the referee for the useful suggestions to improve the manuscript. This work is supported by the National Key Research and Development Program of China (Grants No. 2021YFA0718500, 2021YFA0718503), the NSFC (12133007, U1838103, 11622326, 11773008, 11833007, 11703022, 12003007, 11773003, and U1931201), the Fundamental Research Funds for the Central Universities (No. 2020kfyXJJS039, 2042021kf0224), and the China Manned Space Project (CMS-CSST-2021-B11).
Data Availability
The data used in this paper were collected from the previous literatures. These data X-ray, gamma-ray and neutrino observations are public for all researchers.
References
- Aartsen et al. (2014) Aartsen M. e., Ackermann M., Adams J., Aguilar J., Ahlers M., Ahrens M., Altmann D., Anderson T., Arguelles C., Arlen T., et al., 2014, Physical review letters, 113, 101101
- Abbasi et al. (2021) Abbasi R., Ackermann M., Adams J., Aguilar J., Ahlers M., Ahrens M., Alispach C., Alves Jr A., Amin N., Andeen K., et al., 2021, Physical Review D, 104, 022002
- Aharonian (2004) Aharonian F. A., 2004, Very high energy cosmic gamma radiation: a crucial window on the extreme Universe. World Scientific
- Antonucci (1993) Antonucci R., 1993, Annual review of astronomy and astrophysics, 31, 473
- Barkov et al. (2010) Barkov M. V., Aharonian F. A., Bosch-Ramon V., 2010, ApJ, 724, 1517
- Barkov et al. (2012) Barkov M. V., Bosch-Ramon V., Aharonian F. A., 2012, ApJ, 755, 170
- Blaufuss et al. (2021) Blaufuss E., Kintscher T., Lu L., Tung C. F., 2021, in 36th International Cosmic Ray Conference Vol. 358, The next generation of icecube real-time neutrino alerts. p. 1021
- Bosch-Ramon (2012) Bosch-Ramon V., 2012, Astronomy & Astrophysics, 542, A125
- Bultinck et al. (2010) Bultinck E., Mahieu S., Depla D., Bogaerts A., 2010, Journal of Physics D: Applied Physics, 43, 292001
- Cannizzaro et al. (2021) Cannizzaro G., Wevers T., Jonker P., Pérez-Torres M. A., Moldon J., Mata-Sánchez D., Leloudas G., Pasham D., Mattila S., Arcavi I., et al., 2021, Monthly Notices of the Royal Astronomical Society, 504, 792
- Celli et al. (2020) Celli S., Aharonian F., Gabici S., 2020, The Astrophysical Journal, 903, 61
- Cendes et al. (2021) Cendes Y., Alexander K., Berger E., Eftekhari T., Williams P., Chornock R., 2021, The Astrophysical Journal, 919, 127
- Curd & Narayan (2019) Curd B., Narayan R., 2019, Monthly Notices of the Royal Astronomical Society, 483, 565
- Dai et al. (2018) Dai L., McKinney J. C., Roth N., Ramirez-Ruiz E., Miller M. C., 2018, The Astrophysical Journal Letters, 859, L20
- Dar & Laor (1997) Dar A., Laor A., 1997, ApJ, 478, L5
- Drury (1983) Drury L. O., 1983, Reports on Progress in Physics, 46, 973
- Evans & Kochanek (1989) Evans C. R., Kochanek C. S., 1989, The Astrophysical Journal, 346, L13
- Finke et al. (2010) Finke J. D., Razzaque S., Dermer C. D., 2010, The Astrophysical Journal, 712, 238
- Hayasaki (2021) Hayasaki K., 2021, Nature Astronomy, 5, 436
- Kamae et al. (2006) Kamae T., Karlsson N., Mizuno T., Abe T., Koi T., 2006, The Astrophysical Journal, 647, 692
- Kaufman (1990) Kaufman H. R., 1990, Journal of Vacuum Science & Technology B: Microelectronics Processing and Phenomena, 8, 107
- Klein et al. (1994) Klein R. I., McKee C. F., Colella P., 1994, The Astrophysical Journal, 420, 213
- Liu et al. (2020) Liu R.-Y., Xi S.-Q., Wang X.-Y., 2020, Physical Review D, 102, 083028
- Lu & Bonnerot (2020) Lu W., Bonnerot C., 2020, Monthly Notices of the Royal Astronomical Society, 492, 686
- McKee & Cowie (1975) McKee C., Cowie L., 1975, The Astrophysical Journal, 195, 715
- Mori (1997) Mori M., 1997, The Astrophysical Journal, 478, 225
- Mou et al. (2021) Mou G., Dou L., Jiang N., Wang T., Guo F., Wang W., Wang H., Shu X., He Z., Zhang R., et al., 2021, The Astrophysical Journal, 908, 197
- Mou et al. (2022) Mou G., Wang T., Wang W., Yang J., 2022, Monthly Notices of the Royal Astronomical Society, 510, 3650
- Mou & Wang (2021) Mou G., Wang W., 2021, Monthly Notices of the Royal Astronomical Society, 507, 1684
- Murase et al. (2020) Murase K., Kimura S. S., Zhang B. T., Oikonomou F., Petropoulou M., 2020, The Astrophysical Journal, 902, 108
- Osterbrock & Ferland (2006) Osterbrock D. E., Ferland G. J., 2006, Astrophysics Of Gas Nebulae and Active Galactic Nuclei. University science books
- Reusch et al. (2021) Reusch S., Stein R., Kowalski M., van Velzen S., Franckowiak A., Lunardini C., Murase K., Winter W., Miller-Jones J. C., Kasliwal M. M., et al., 2021, arXiv preprint arXiv:2111.09390
- Skrutskie et al. (2006) Skrutskie M., Cutri R., Stiening R., Weinberg M., Schneider S., Carpenter J., Beichman C., Capps R., Chester T., Elias J., et al., 2006, The Astronomical Journal, 131, 1163
- Stein et al. (2021) Stein R., van Velzen S., Kowalski M., Franckowiak A., Gezari S., Miller-Jones J. C., Frederick S., Sfaradi I., Bietenholz M. F., Horesh A., et al., 2021, Nature Astronomy, 5, 510
- Taylor (1961) Taylor J., 1961, Physical Review Letters, 6, 262
- Telescope et al. (2018) Telescope L., Aartsen M., Ackermann M., Adams J., Aguilar J. A., Ahlers M., Ahrens M., Al Samarai I., Altmann D., Andeen K., et al., 2018, Science, 361
- van Velzen et al. (2021) van Velzen S., Gezari S., Hammerstein E., Roth N., Frederick S., Ward C., Hung T., Cenko S. B., Stein R., Perley D. A., et al., 2021, The Astrophysical Journal, 908, 4
- van Velzen et al. (2021) van Velzen S., Stein R., Gilfanov M., Kowalski M., Hayasaki K., Reusch S., Yao Y., Garrappa S., Franckowiak A., Gezari S., et al., 2021, arXiv preprint arXiv:2111.09391
- Wang et al. (2018) Wang K., Liu R.-Y., Li Z., Wang X.-Y., Dai Z.-G., 2018, arXiv e-prints, p. arXiv:1809.00601
- Wang & Liu (2016) Wang X.-Y., Liu R.-Y., 2016, Physical Review D, 93, 083005