Counting Hypergraphs with Large Girth

Let $\mathcal{F}$ be a family of $r$-uniform hypergraphs, or $r$-graphs for short. Define $\mbox{\rm N}^{r}(n,\mathcal{F})$ to be the number of $\mathcal{F}$-free $r$-graphs on $[n]:=\{1,\ldots,n\}$, and define $\mbox{\rm N}_{m}^{r}(n,\mathcal{F})$ to be the number of $\mathcal{F}$-free $r$-graphs on $[n]$ with exactly $m$ hyperedges. If $\mathrm{ex}(n,\mathcal{F})$ denotes the maximum number of hyperedges in an $\mathcal{F}$-free $r$-graph on $[n]$, then it is not difficult to see that for $1\leq m\leq\mathrm{ex}(n,\mathcal{F})$,

$\displaystyle\left(\frac{\mathrm{ex}(n,\mathcal{F})}{m}\right)^{m}\leq{\mathrm{ex}(n,\mathcal{F})\choose m}\leq$

$\displaystyle\;\;\mbox{\rm N}_{m}^{r}(n,\mathcal{F})\leq{{n\choose r}\choose m}\leq\left(\frac{en^{r}}{m}\right)^{m},$

and summing over $m$ one obtains $2^{\Omega(\mathrm{ex}(n,\mathcal{F}))}=\mbox{\rm N}^{r}(n,\mathcal{F})=2^{O(\mathrm{ex}(n,\mathcal{F})\log n)}$. The state of the art for bounding $\mbox{\rm N}^{r}(n,\mathcal{F})$ is the work of Ferber, McKinley, and Samotij [9] which shows that if $F$ is an $r$-uniform hypergraph with $\mathrm{ex}(n,F)=O(n^{\alpha})$ and $\alpha$ not too small, then

$$\mbox{\rm N}^{r}(n,F)=2^{O(n^{\alpha})},$$

and this result encompasses many of the earlier results in the area [3, 4, 6, 17].

In the appendix we give a formal proof of this result. Theorem 1.1 generalizes earlier results of Füredi [11] when $\ell=4$ and of Kohayakawa, Kreuter, and Steger [15]. Erdős and Simonovits [8] conjectured for $\ell\geq 3$ and $k=\lfloor\ell/2\rfloor$,

$$\mathrm{ex}(n,\mathcal{C}_{[\ell]})=\Omega(n^{1+1/k})$$

(1)

which is only known to hold for $\ell\in\{3,4,5,6,7,10,11\}$ – see Füredi and Simonovits [12] and also [24] for details. The truth of this conjecture would imply that the upper bound in Theorem 1.1 is tight up to the exponent of $(\log n)^{m}$.

In this paper we extend Theorem 1.1 to $r$-graphs. For $\ell\geq 2$, an $r$-graph $F$ is a Berge $\ell$-cycle if there exist distinct vertices $v_{1},\ldots,v_{\ell}$ and distinct hyperedges $e_{1},\ldots,e_{\ell}$ with $v_{i},v_{i+1}\in e_{i}$ for all $1\leq i\leq\ell$. In particular, a hypergraph $H$ is said to be linear if it contains no Berge 2-cycle. We denote by $\mathcal{C}_{\ell}^{r}$ the family of all $r$-uniform Berge $\ell$-cycles. If $H$ is an $r$-graph containing a Berge cycle, then the girth of $H$ is the smallest $\ell\geq 2$ such that $H$ contains a Berge $\ell$-cycle. Let $\mathcal{C}_{[\ell]}^{r}=\mathcal{C}_{2}^{r}\cup\mathcal{C}_{3}^{r}\cup\dots\cup\mathcal{C}_{\ell}^{r}$ denote the family of all $r$-uniform Berge cycles of length at most $\ell$. With this $\mathcal{C}_{[\ell]}^{2}=\mathcal{C}_{[\ell]}$, and an $r$-graph has girth larger than $\ell$ if and only if it is $\mathcal{C}_{[\ell]}^{r}$-free. We again emphasize that hypergraphs with girth $\ell\geq 2$ are all linear. We write $\mbox{\rm N}_{m}^{r}(n,\ell):=\mbox{\rm N}_{m}^{r}(n,\mathcal{C}_{[\ell]}^{r})$ for the number of $n$-vertex $r$-graphs with $m$ edges and girth larger than $\ell$ and $\mbox{\rm N}^{r}(n,\ell):=\mbox{\rm N}^{r}(n,\mathcal{C}_{[\ell]}^{r})$ for the number of $n$-vertex $r$-graphs with girth larger than $\ell$.

Balogh and Li [2] proved for all $\ell,r\geq 3$ and $k=\lfloor\ell/2\rfloor$,

$$\mbox{\rm N}^{r}(n,\ell)=2^{O(n^{1+1/k})}.$$

This upper bound would be tight up to a $n^{o(1)}$ term in the exponent if the following is true:

Conjecture I holds for $\ell=3,4$ and $r\geq 3$ – see [7, 16, 22, 23] – but is open and evidently difficult for $\ell\geq 5$ and $r\geq 3$. Györi and Lemons [13] proved $\mathrm{ex}(n,\mathcal{C}_{\ell}^{r})=O(n^{1+1/k})$ with $k=\left\lfloor\ell/2\right\rfloor$, so the conjecture concerns constructions of dense $r$-graphs of girth more than $\ell$. The conjecture for $r=2$ without the $o(1)$ is (1), and for each $r\geq 3$ is stronger than (1), as can be seen by forming a graph from an extremal $n$-vertex $r$-graph of girth more than $\ell$ whose edge set consists of an arbitrary pair of vertices from each hyperedge. We emphasize that the $o(1)$ term in Conjecture I is necessary for $\ell=3$, due to the Ruzsa-Szemerédi Theorem [7, 22], and for $\ell=5$, due to work of Conlon, Fox, Sudakov and Zhao [5].

In this work we simplify and refine the arguments of Balogh and Li [2] to prove effective and almost tight bounds on $\mbox{\rm N}_{m}^{r}(n,\ell)$ relative to $\mbox{\rm N}_{m}^{2}(n,\ell)$.

We note that (2) corrects a bound¹¹1Theorem 20 of [20] claims a stronger upper bound for $\mbox{\rm N}_{m}^{r}(n,4)$ than what we prove in Theorem 1.2, but we have confirmed with the authors that there was a subtle error in their proof. which appears in [20]. The inequality (2) is essentially tight when $\ell-2$ divides $r-2$, due to standard probabilistic arguments (see for instance Janson, Łuczak and Rucinski [14]): it is possible to show that when $m\leq n^{1+1/(\ell-1)}$, the uniform model of random $n$-vertex $r$-graphs with $m$ edges has girth larger than $\ell$ with probability at least $a^{-m}$ for some constant $a>1$ depending only on $\ell$ and $r$. In particular, there exists some constants $b,c>1$ such that for $m\leq n^{1+1/(\ell-1)}$ we have

$$\mbox{\rm N}_{m}^{r}(n,\ell)\geq a^{-m}{{n\choose r}\choose m}\geq b^{-m}(n^{r}/m)^{m}\geq b^{-m}(n^{2}/m)^{(r-1+\frac{r-2}{\ell-2})m}\geq c^{-m}\cdot\mbox{\rm N}_{m}^{2}(n,\ell)^{r-1+\frac{r-2}{\ell-2}},$$

(3)

where the third inequality used $m\leq n^{1+1/(\ell-1)}$ and the last inequality used the trivial bound $\mbox{\rm N}_{m}^{2}(n,\ell)\leq(en^{2}/m)^{m}$. This shows that the bound of Theorem 1.2 is best possible when $\ell-2$ divides $r-2$ up to a multiplicative error of $c^{-m}$ for some constant $c>1$. We believe that (3) should define the optimal exponent, and propose the following conjecture:

Theorem 1.2 shows that this conjecture is true when $\ell-2$ divides $r-2$, so the first open case of Conjecture II is when $\ell=4$ and $r=3$.

In the case that Berge $\ell$-cycles are forbidden instead of all Berge cycles of length at most $\ell$, we can prove an analog of Theorem 1.2 with weaker quantitative bounds. To this end, let $\mbox{\rm N}_{[m]}^{r}(n,\mathcal{F})$ denote the number of $n$-vertex $\mathcal{F}$-free $r$-graphs on at most $m$ hyperedges.

We suspect that this result continues to hold with $\mbox{\rm N}_{[m]}^{2}(n,C_{\ell})$ replaced by $\mbox{\rm N}_{m}^{2}(n,C_{\ell})$.

Denote by $H_{n,p}^{r}$ the $r$-graph obtained by including each hyperedge of $K_{n}^{r}$ independently and with probability $p$. Given a family of $r$-graphs $\mathcal{F}$, let $\mathrm{ex}(H_{n,p}^{r},\mathcal{F})$ denote the size of a largest $\mathcal{F}$-free subgraph of $H_{n,p}^{r}$. Recall that a statement depending on $n$ holds asymptotically almost surely or a.a.s. if it holds with probability tending to 1 as $n\rightarrow\infty$. A hypergraph of girth at least three is a linear hypergraph, and it is not hard to show by a simple first moment calculation that if $p\geq n^{-r}\log n$, then a.a.s

$$\mathrm{ex}(H_{n,p}^{r},\mathcal{C}_{[2]}^{r})=\Theta(\min\{pn^{r},n^{2}\}).$$

Our first result essentially determines the a.a.s behavior of the number of edges in an extremal subgraph of $H_{n,p}^{r}$ of girth four. In this theorem we omit the case $p<n^{-r+\frac{3}{2}}$, as it is straightforward to show that a.a.s $\mathrm{ex}(H_{n,p}^{r},\mathcal{C}_{[3]}^{r})=\Theta(pn^{r})$ when $p\geq n^{-r}\log n$ in this range.

Due to Theorems 1.2 and 1.4, the number of linear triangle-free $r$-graphs with $n$ vertices and $m$ edges where $n^{3/2+o(1)}\leq m\leq\mathrm{ex}(n,\mathcal{C}_{[3]}^{r})=o(n^{2})$ and $r\geq 3$ is:

$$\mbox{\rm N}_{m}^{r}(n,3)=\mbox{\rm N}_{m}^{2}(n,3)^{2r-3+o(1)}=\Bigl{(}\frac{n^{2}}{m}\Bigr{)}^{(2r-3)m+o(m)}.$$

The authors and Nie [19] obtained bounds for $r$-uniform loose triangles²²2The loose triangle is the Berge triangle whose edges pairwise intersect in exactly one vertex., where for $r=3$ the same essentially tight bounds as in Theorem 1.4 were obtained, but for $r>3$ there remains a significant gap. In the case of subgraphs of girth larger than four, Theorem 1.2 allows us to generalize results of Morris and Saxton [17] and earlier results of Kohayakawa, Kreuter and Steger [15] giving subgraphs of large girth in random graphs in the following way:

We emphasize that there is a significant gap in the bounds of Theorem 1.5 due to the presence of $\lambda$ in the exponent of $p$ in the upper bound and its absence in the lower bound, and this gap is closed by Theorem 1.4 when $\ell=3$ by an improvement to the lower bound. A similar phenomenon appears in recent work of Mubayi and Yepremyan [18], who determined the a.a.s value of the extremal function for loose even cycles in $H_{n,p}^{r}$ for all but a small range of $p$. It seems likely that the following conjecture is true:

Conjecture II suggests the possible value $\gamma(\ell,r)=r-1+(r-2)/(\ell-2)$, which is the correct value for $\ell=3$ by Theorem 1.4. We are not certain that this is the right value of $\gamma$ in general, even when $r=3$ and $\ell=4$, and more generally, Conjecture I is an obstacle for $r\geq 3$ and $\ell\geq 5$. Theorem 1.5 shows that if $\gamma$ exists, then $(r-1)k\leq\gamma\leq(r-1+\lambda)k$ provided Conjecture I holds.

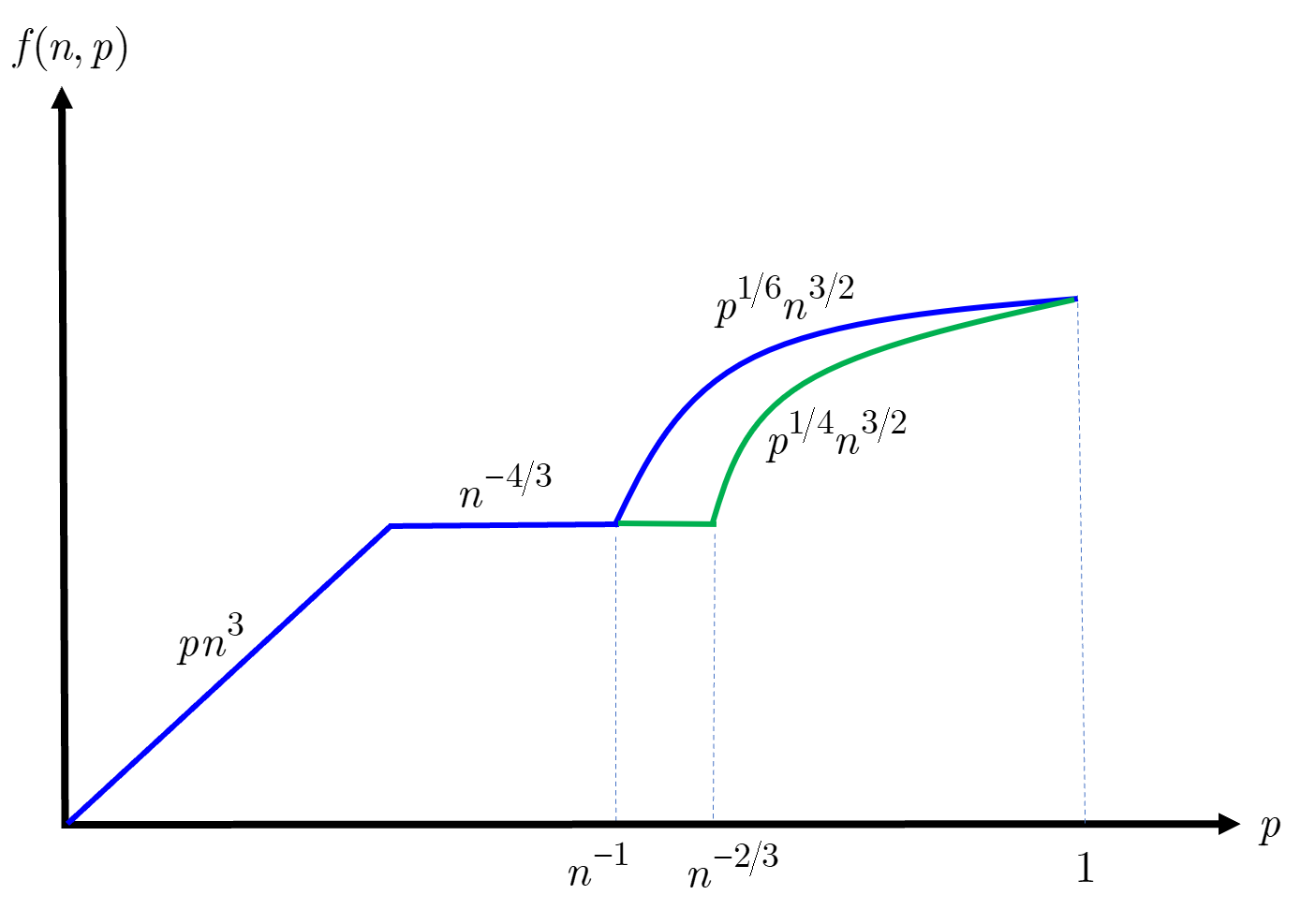
Letting $f(n,p)=\mathrm{ex}(H_{n,p}^{3},\mathcal{C}_{[4]}^{3})$, we plot the bounds of Theorem 1.5 in Figure 1, where the upper bound is in blue and the lower bound is in green. The truth of Conjecture II for $\ell=4$ would imply the slightly better upper bound $f(n,p)\leq p^{1/5}n^{3/2+o(1)}$.

Notation. A set of size $k$ will be called a $k$-set. As much as possible, when working with a $k$-graph $G$ and an $r$-graph $H$ with $k<r$, we will refer to elements of $E(G)$ as edges and elements of $E(H)$ as hyperedges. Given a hypergraph $H$ on $[n]$, we define the $k$-shadow $\partial^{k}H$ to be the $k$-graph on $[n]$ consisting of all $k$-sets $e$ which lie in a hyperedge of $E(H)$. If $G_{1},\ldots,G_{q}$ are $k$-graphs on $[n]$, then $\bigcup G_{i}$ denotes the $k$-graph $G$ on $[n]$ which has edge set $\bigcup E(G_{i})$.

As Balogh and Li [2] observed, if $\ell\geq 3$ and $H$ has girth larger than $\ell$, then $H$ is uniquely determined by $\partial^{2}H$, which we can view as the graph obtained by replacing each hyperedge of $H$ by a clique. A key insight in proving Theorem 1.2 is that we can replace each hyperedge of $H$ with a sparser graph $B$ and still uniquely recover $H$ from this graph. To this end, we say that a graph $B$ is a book if there exist cycles $F_{1},\ldots,F_{k}$ and an edge $xy$ such that $B=\bigcup F_{i}$ and $E(F_{i})\cap E(F_{j})=\{xy\}$ for all $i\neq j$. In this case we call the cycles $F_{i}$ the pages of $B$ and we call the common edge $xy$ the spine of $B$. The following lemma shows that if we replace each hyperedge in $H$ by a book on $r$ vertices which has small pages, then the vertex sets of books in the resulting graph are exactly the hyperedges of $H$.

• Proof.

  Let $F$ be a cycle in $\partial^{2}H$ with $V(F)=\{v_{1},\ldots,v_{p}\}$ such that $v_{i}v_{i+1}\in E(\partial^{2}H)$ for $i<p$ and $v_{1}v_{p}\in E(\partial^{2}H)$. If $p\leq\ell$ we claim that there exists an $e\in E(H)$ such that $V(F)\subseteq e$. Indeed, by definition of $\partial^{2}H$ there exists some hyperedge $e_{i}\in E(H)$ with $v_{i},v_{i+1}\in e_{i}$ for all $i<p$ and some hyperedge $e_{p}$ with $v_{1},v_{p}\in e_{p}$. If all of these $e_{i}$ hyperedges are equal then we are done, so we may assume $e_{1}\neq e_{p}$. Define $i_{1}$ to be the largest index such that $e_{i}=e_{1}$ for all $i\leq i_{1}$, define $i_{2}$ to be the largest index so that $e_{i}=e_{i_{1}+1}$ for all $i_{1}<i\leq i_{2}$, and so on up to $i_{q}=p$, and note that $2\leq q\leq p$ since $e_{1}\neq e_{p}$. If all the $e_{i_{j}}$ hyperedges are distinct, then they form a Berge $q$-cycle in $H$ since $v_{1+i_{j}}\in e_{i_{j}}\cap e_{1+i_{j}}=e_{i_{j}}\cap e_{i_{j+1}}$ for all $j$, a contradiction. Thus we can assume $e_{i_{j}}=e_{i_{j^{\prime}}}$ for some $j<j^{\prime}$. We can further assume that $e_{i_{s}}\neq e_{i_{s^{\prime}}}$ for any $j\leq s<s^{\prime}<j^{\prime}$, as otherwise we could replace $j,j^{\prime}$ with $s,s^{\prime}$. Finally note that $j<j^{\prime}-1$, as otherwise we would have $e_{i_{j}}=e_{i_{j^{\prime}}}=e_{i_{j}+1}$, contradicting the maximality of $i_{j}$. We conclude that the distinct hyperedges $e_{i_{j}},e_{i_{j+1}},\ldots,e_{i_{j^{\prime}-1}}$ form a Berge $(j^{\prime}-j)$-cycle with $2\leq j^{\prime}-j\leq\ell$ in $H$, a contradiction. This proves the claim.

  Now let $B$ be a book with spine $xy$ and pages $F_{1},\ldots,F_{k}$ of length at most $\ell$. By the claim there exist hyperedges $e_{1},\ldots,e_{k}\in E(H)$ such that $V(F_{i})\subseteq e_{i}$ for all $i$, and in particular $x,y\in e_{i}$ for all $i$. Because $H$ is linear, this implies that all of these hyperedges are equal and we have $V(B)\subseteq e_{1}$. If $B$ has $r$ vertices, then we further have $V(B)=e_{1}$. ∎

We now complete the proof of Theorem 1.2. With $\lambda:=\left\lceil(r-2)/(\ell-2)\right\rceil$ we observe for all $\ell,r\geq 3$ that there exists a book graph $B$ on $r$ vertices $\{x_{1},\ldots,x_{r}\}$ with $r-1+\lambda$ edges $f_{1},\ldots,f_{r-1+\lambda}$. Indeed if $\ell-2$ divides $r-2$ one can take $\lambda$ copies of $C_{\ell}$ which share a common edge, and otherwise one can take $\lambda-1$ copies of $C_{\ell}$ and a copy of $C_{p}$ with $p=r-(\lambda-1)(\ell-2)\geq 3$. From now on we let $B$ denote this book graph. If $f_{i}=\{x_{j},x_{j^{\prime}}\}\in E(B)$ and $e=\{v_{1},\ldots,v_{r}\}\subseteq[n]$ is any $r$-set with $v_{1}<\cdots<v_{r}$, define $\phi_{i}(e)=\{v_{j},v_{j^{\prime}}\}$. If $H$ is an $r$-graph on $[n]$, define $\phi_{i}(H)$ to be the graph on $[n]$ which has all edges of the form $\phi_{i}(e)$ for $e\in E(H)$; so in particular $\bigcup\phi_{i}(H)$ is the graph obtained by replacing each hyperedge of $H$ with a copy of $B$.

Let $\mathcal{H}_{m,n}$ denote the set of $r$-graphs on $[n]$ with $m$ hyperedges and girth more than $\ell$, and let $\mathcal{G}_{m,n}$ be the set of graphs on $[n]$ with $m$ edges and girth more than $\ell$. We claim that $\phi_{i}$ maps $\mathcal{H}_{m,n}$ to $\mathcal{G}_{m,n}$. Indeed, if $H\in\mathcal{H}_{m,n}$ then each hyperedge of $H$ contributes a distinct edge to $\phi_{i}(H)$ since $H$ is linear, so $e(\phi_{i}(H))=e(H)=m$. One can show that if $\phi_{i}(e_{1}),\ldots,\phi_{i}(e_{p})$ form a $p$-cycle in $\phi_{i}(H)$, then $e_{1},\ldots,e_{p}$ form a Berge $p$-cycle in $H$; so $H\in\mathcal{H}_{m,n}$ implies $\phi_{i}(H)$ does not contain a cycle of length at most $\ell$.

Let $\mathcal{G}_{m,n}^{t}=\{(G_{1},G_{2},\dots,G_{t}):G_{i}\in\mathcal{G}_{m,n}\}$. Then we define a map $\phi:\mathcal{H}_{m,n}\to\mathcal{G}_{m,n}^{r-1+\lambda}$ by

$$\phi(H)=(\phi_{1}(H),\ldots,\phi_{r-1+\lambda}(H)).$$

We claim that this map is injective. Indeed, fix some $H\in\mathcal{H}_{m,n}$ and let $\mathcal{B}(G)$ denote the set of books $B$ in the graph $G:=\bigcup\phi_{i}(H)\subseteq\partial^{2}H$. By definition of $\phi$ we have $E(H)\subseteq\mathcal{B}(G)$ for all $H$. Moreover, if $H\in\mathcal{H}_{m,n}$ then Lemma 2.1 implies $\mathcal{B}(G)\subseteq E(H)$. Thus $E(H)$ (and hence $H$) is uniquely determined by $G$, which is itself determined by $\phi(H)$, so the map is injective. In total we conclude

$$\mbox{\rm N}_{m}^{r}(n,\ell)=|\mathcal{H}_{m,n}|\leq|\mathcal{G}_{m,n}^{r-1+\lambda}|=\mbox{\rm N}_{m}^{2}(n,\ell)^{r-1+\lambda},$$

proving Theorem 1.2. $\blacksquare$

For arbitrary hypergraphs $H$, the map $\phi(H)=\partial^{r-1}H$ (let alone the map to $\partial^{2}H$) is not injective. However, we will show that this map is “almost” injective when considering $H$ which are $\mathcal{C}_{\ell}^{r}$-free. To this end, we say that a set of vertices $\{v_{1},\ldots,v_{r}\}$ is a core set of an $r$-graph $H$ if there exist distinct hyperedges $e_{1},\ldots,e_{r}$ with $\{v_{1},\ldots,v_{r}\}\setminus\{v_{i}\}\subseteq e_{i}$ for all $i$. The following observation shows that core sets are the only obstruction to $\phi(H)=\partial^{r-1}H$ being injective.

• Proof.

  By assumption of $\{v_{1},\ldots,v_{r}\}$ inducing a $K_{r}^{r-1}$ in $\partial^{r-1}H$, for all $i$ there exist $e^{\prime}_{i}\in E(\partial^{r-1}H)$ with $e^{\prime}_{i}=\{v_{1},\ldots,v_{r}\}\setminus\{v_{i}\}$. By definition of $\partial^{r-1}H$, this means there exist (not necessarily distinct) $e_{i}\in E(H)$ with $e_{i}\supseteq e_{i}^{\prime}=\{v_{1},\ldots,v_{r}\}\setminus\{v_{i}\}$. Given this, either $e_{i}=\{v_{1},\ldots,v_{r}\}$ for some $i$, or all of the $e_{i}$ distinct, in which case $\{v_{1},\ldots,v_{r}\}$ is a core set of $H$. In either case we conclude the result.

  ∎

• Proof.

  If $e=\{v_{1},v_{2},\ldots,v_{r}\}\subseteq[n]$ is any $r$-set with $v_{1}<v_{2}<\cdots<v_{r}$, let $\phi_{i}(e)=\{v_{1},\ldots,v_{r}\}\setminus\{v_{i}\}$. Given an $r$-graph $H$ on $[n]$, let $\phi_{i}(H)$ be the $(r-1)$-graph on $[n]$ with edge set $\{\phi_{i}(e):e\in E(H)\}$, and define $\phi(H)=(\phi_{1}(H),\phi_{2}(H),\ldots,\phi_{r}(H))$ and $\psi(H)=(\phi(H),E(H))$. Observe that $\bigcup\phi_{i}(H)=\partial^{r-1}H$. Let $\mathcal{H}_{[m],n}$ denote the set of all $r$-graphs on $[n]$ with at most $m$ hyperedges which are $\mathcal{C}_{\ell}^{r}$-free, and let $\phi(\mathcal{H}_{[m],n}),\psi(\mathcal{H}_{[m],n})$ denote the image sets of $\mathcal{H}_{[m],n}$ under these respective maps. Observe that $\psi$ is injective since it records $E(H)$, so it suffices to bound how large $\psi(\mathcal{H}_{[m],n})$ can be.

  Let $\mathcal{G}_{[m],n}$ denote the set of $(r-1)$-graphs on $[n]$ which have at most $m$ edges and which are $\mathcal{C}_{\ell}^{r-1}$-free. It is not difficult to see that $\phi(\mathcal{H}_{[m],n})\subseteq\mathcal{G}_{[m],n}^{r}$. We observe by Lemmas 3.1 and 3.2 that for any $(G_{1},G_{2},\ldots,G_{r})\in\phi(\mathcal{H}_{[m],n})$, say with $\phi(H)=(G_{1},\ldots,G_{r})$, there are at most $(1+\ell^{2}r^{2})m$ copies of $K_{r}^{r-1}$ in $\bigcup G_{i}=\partial^{r-1}H$. We also observe that if $((G_{1},G_{2},\ldots,G_{r}),E)\in\psi(\mathcal{H}_{[m],n})$, then $E$ is a set of at most $m$ copies of $K_{r}^{r-1}$ in $\bigcup G_{i}$. Thus given any $(G_{1},\ldots,G_{r})\in\phi(\mathcal{H}_{[m],n})\subseteq\mathcal{G}_{[m],n}^{r}$, there are at most $2^{(1+\ell^{2}r^{2})m}$ choices of $E$ such that $((G_{1},\ldots,G_{r}),E)\in\psi(\mathcal{H}_{[m],n})$. We conclude that

  $$\mbox{\rm N}_{[m]}(n,\mathcal{C}_{\ell}^{r})=|\mathcal{H}_{[m],n}|\leq|\mathcal{G}_{[m],n}|^{r}\cdot 2^{(1+\ell^{2}r^{2})m}=\mbox{\rm N}_{[m]}^{r}(n,\mathcal{C}_{\ell}^{r-1})^{r}\cdot 2^{(1+\ell^{2}r^{2})m},$$

  proving the result. ∎

Applying this proposition repeatedly gives $\mbox{\rm N}_{[m]}^{r}(n,\mathcal{C}_{\ell}^{r})\leq 2^{cm}\mbox{\rm N}_{[m]}^{2}(n,C_{\ell})^{r!/2}$. Combining this with the trivial inequality $\mbox{\rm N}_{m}^{r}(n,\mathcal{C}_{\ell}^{r})\leq\mbox{\rm N}_{[m]}^{r}(n,\mathcal{C}_{\ell}^{r})$ gives Theorem 1.3. $\blacksquare$