Couplings between Photons and Ensemble of Emitters in a High- Cavity at Mesoscopic Excitation Levels
Abstract
We investigate the coupling between an ensemble of individual emitters and multiple photons in a high- cavity at the mesoscopic excitation level. The master equation theory is used to calculate the emission spectrum of the cavity QED system. The increasing excitation level not only pumps the system to the high-energy multi-emitter-photon states, but also introduces the pump-induced dephasing that suppresses the coherent energy exchange (coupling) between photons and emitters. When the emitter lifetime exceeds a threshold, we observe the mesoscopic excitation level i.e., the system is pumped to high energy states whilst the coherent couplings between these states are not yet suppressed. The mesoscopic excitation enables the couplings between multi-emitter-photon states, and thereby, paves the way to building quantum photonic devices based on multiple photons and nonlinear effects.
I Introduction
The cavity QED system consisting of embedded emitters and confined photons provides a quantum interface between light and matter degrees of freedom [1, 2]. Such nanosystem is the basic building block of the processing and storage of quantum information in the network [3, 4, 5, 6, 7] and is also widely applied in other fields including sensor, energy and biology [8, 9, 10]. In the limit of weak excitation, the system is at lowest energy states with either a single photon or an excited two-level emitter. The coherent energy exchange (coupling) between them has been investigated and applied in quantum photonic devices [11, 12, 13, 14]. In addition, the coupling strength between high energy states increases with the number of involved photons and emitters [15, 16, 17, 18]. Such high order coupling allows the emission and quantum information processing involving multiple photons, thereby is attracting increasing interest in recent years [19, 20, 21, 22, 23, 24, 25, 26].
The high order coupling requires the cavity QED system pumped to high energy multi-emitter-photon states. However, as the excitation level increases, the incoherent pump introduces the dephasing which suppresses the coherent emitter-photon coupling [27, 28, 29, 30]. At strong excitation levels, the pump-induced dephasing suppresses the coherent energy exchange, thus all emissions are merged to the bare cavity mode [27]. As such, a mesoscopic excitation level, i.e., the system is pumped to high energy states while the coherent energy exchange between them is not yet suppressed, is required to observe the high order coupling.
Here we investigate the high order couplings between a high- cavity mode and an ensemble of individual emitters using the master equation theory [31]. Pump dependent emission spectra with emitters and maximum photons are calculated. When , the system will be pumped to high energy states as the pump increases. For narrow-linewidth emitters, the high order couplings at mesoscopic excitation levels are clearly observed from the nonmonotonic energy shift of emission peaks. In contrast, for broad-linewidth emitters with the lifetime below the threshold, only the monotonic energy shift is observed, indicating the pump-induced dephasing dominates throughout.
We verify the calculation in a high- nanobeam cavity embedded with a monolayer MoS2 [32]. The localized excitons (LXs) are a good case of individual emitters, since their wavefunctions are strongly localized at defects [33, 34, 35, 36]. We record PL spectra of the cavity-LXs system. As expected, the emission peak exhibits the nonmonotonic power-dependent energy shift that indicates the high order couplings, which is in contrast not observed in control experiments recorded from MoS2 outside cavities.
II Theory and Calculation
II.1 Multi-Emitter-Photon System
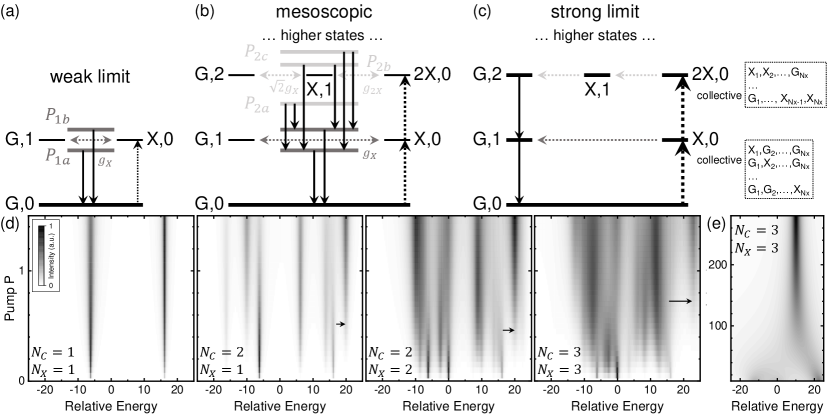
We consider a single cavity mode with energy and linewidth , coupled to an ensemble of individual two-level emitters. Each emitter has the same energy , linewidth , and coupling strength to the cavity mode. The state of cavity QED system consists of the state of emitters and the number of photons in the cavity. As depicted in Fig. 1(a)-(c), the emitter state is collectively described by the number of excited emitters, e.g., means all emitters are at the ground level, means one emitter is excited, and means two emitters are excited. Following is the number of photons in the cavity mode. is thereby the ground state of the whole system. In the framework of the rotating wave approximation, the coupling between photons and emitters is described by the Jaynes-Cummings or Tavis-Cummings model [37, 15, 16]. The system Hamiltonian is given by
| H | (1) | ||||
where () is the Dirac operator for emitter and / is the ladder operators for photons. This model is valid when the cavity mode volume is small i.e., the free spectral range is much larger than the coupling strength [38, 39].
The simple case is the first order coupling in the weak excitation limit, as depicted in Fig. 1(a). This is the focus of usual investigations. In this case, the energy symmetrically and coherently exchanges between the and state. Since the transition is a collective of transitions, the coupling strength between these two states is [15, 16]. This coupling results in the two first-order polariton eigenstates denoted by and . The corresponding two eigenfrequencies can be calculated by solving the Hamiltonian matrix
| (4) |
and results are
where and . The well-known Rabi splitting at resonance occurs when the coupling strength is larger than the decay rate as [40, 41].
In addition, the cavity QED system also supports high energy states e.g., the , and states depicted in Fig. 1(b). The coupling strength between and is , where the arises from the ladder operator for two photons. The transition is a collective of transitions, thus the coupling strength between and is [15, 16]. The couplings between these three states result in three second-order polariton eigenstates denoted by , , and . The eigenfrequency of polaritons can be calculated by solving the Hamiltonian matrix
| (8) |
As such, when the excitation is enough to pump the system to these three states, 6 emission peaks representing the transition from second-order to first-order polaritons would be observed as depicted by the downward arrows in Fig. 1(b). Similar couplings can be expected between higher energy states involving more excited emitters and photons.
However, the Hamiltonian matrix in Eqs. 4 and 8 are only valid with a relative weak excitation, which means the pump has little impact on the energy exchange between emitters and photons. As the excitation level increases, the pump-induced dephasing will suppress the coherent energy exchange [27, 28, 29, 30]. In the limit of strong excitation, emitters are approximately forced at the excited state, with only the unidirectional energy transfer from emitters to photons as depicted in Fig. 1(c). In this case, the spectral emission degenerates to the bare cavity mode, which includes the transitions , , etc., no matter the number of photons and emitters in the system.
II.2 Spectra Calculated from Master Equation
As discussed above, the increasing excitation level has two effects: pump the system to high energy states and suppress the coherent energy exchange. To further investigate the dominance of the two effects, we use Quantum Optics Toolbox [31] to solve the maser equation of the coupling system. The master equation is given by
| (9) |
where is the density matrix including all allowed states with maximum photons, is the Hamiltonian defined in Eq. 1, and the Liouvillian superoperator
| (10) | |||
describes Markovian processes corresponding to the decay of photons, the decay of emitters, and the pump of emitters with rate , respectively. The pump in Eq. 10 is incoherent thereby introduces the pump-induced dephasing [27, 28, 29, 30]. For brevity, we use energy unit for all the parameters , , and (e.g. is actually ) and omit the unit meV. The emission spectrum is calculated from the steady state of Eq. 9.
In Fig. 1(d) we present typical emission spectra calculated for narrow-linewidth emitters with various . The parameters are set as , , , and . The coupling strength of the cavity mode to a single emitter is set to , to keep a same value of the first-order coupling strength between the cases with different . We emphasize that the collective coupling strength e.g., , , and in Eq. 4 and 8, is not a precondition of master equation Eq. 9 (only is), but is a result which can be achieved by solving the master equation.
is the simplest case having four states of the system as , , , and . With the relative small pump , the coherent energy exchange between and results in two polariton eigenstates with the eigenfrequencies as
Due to the degeneration of transitions and (energy of ), as well as and (energy of ), only two emission peaks are observed in the spectra. In contrast, with the maximum photon number , the system has two additional states and . The coherent energy exchange between and results in two second-order polariton eigenstates with the eigenfrequencies
As shown in Fig. 1(d), with increasing pump , emission peaks of the first-order transitions at and at quickly suppress when . Emission peaks from the second-order transitions at , at , and at are firstly enhanced when and then suppressed. The other second-order transition at (out of plot range) behaviors similar to these three. The emission peaks from highest order transitions at and at are continuously enhanced in the calculation range of . As the pump increases, the converting of dominated emission peak is consistent with the coupling pumped from low to high orders.
When more photons and emitters are involved in the system, the coupling becomes complex, and more transitions appear in the emission spectra [21, 42] e.g., the results with and presented in Fig. 1(d). Despite the complex details, we clearly observe the central result i.e., the increasing pumps the system from low to high order couplings, as denoted by the black arrows in Fig. 1(d). In addition, although the first-order coupling strength is set to same, the high order coupling strength increases with [15, 16]. Thereby, larger energy shift between low and high order transitions are observed, e.g., by comparing the spectra with and . In contrast to the relative small in Fig. 1(d), we present the case with but with a much larger in Fig. 1(e). As approaches the strong limit , all emission peaks degenerate to the bare cavity energy at , in accordance to the pump-induced dephasing depicted in Fig. 1(c).
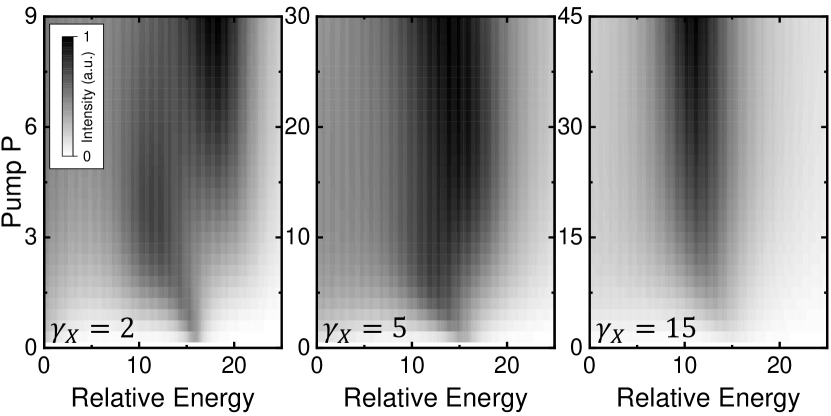
For the system with narrow-linewidth emitters () presented in Fig. 1, the mesoscopic excitation level is clearly observed in the emission peaks. Next, we investigate the dependence of this phenomenon on the emitter decay rate (linewidth) . In Fig. 2, we present the emission spectra calculated with various . Other parameters , , , are same to those used in Fig. 1. The number of photons (emitters) is fixed at . We focus on the spectral emission around the bare cavity energy . As shown in Fig. 2, for , two distinguishable peaks from the low (bottom) and high (top) order coupling are clearly observed, along with the converting of dominated emission peak at . For , although only one emission peak is distinguishable, the nonmonotonic energy shift clearly reveals that the coupling is pumped to high orders before suppressed by the pump-induced dephasing. In contrast, for , only one emission peak with monotonic energy shift is observed, indicating the dephasing effect dominates throughout. These results reveal that the nonmonotonic peak energy shift as the feature of high order couplings is only observed for below a threshold (lifetime above a threshold).
II.3 Ensemble of Emitters in Real Cavities
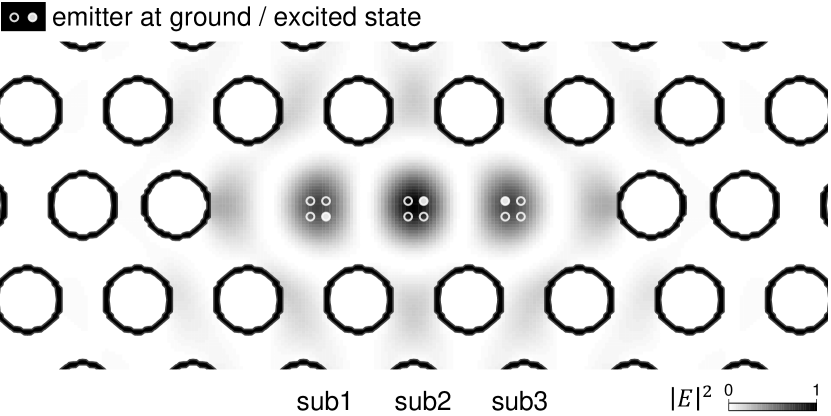
To bridge our theoretical calculation with the experiment, we start by discussing a cavity mode that couples to totally number of emitters, with the same coupling strength to each emitter. As an example, Fig. 3 shows a typical L3 photonic crystal cavity that couples to totally 12 emitters at the antinodes [40, 43]. Usually, not all emitters can be at the excited state simultaneously [44], since the emitter-emitter interaction will be significant when two excited emitters are close to each other in spatial. The emitter-emitter interaction will result in complex effects [45, 46, 47] thus dephase the coupling to the cavity [48, 49]. Therefore, the cavity equally couples to subcollective emitters. Each subcollective emitter has emitters which are close to each other in spatial, and among the at most one excitation is allowed to exclude the emitter-emitter interaction. E.g., in Fig. 3 the 12 emitters are subgrouped into three subcollective emitters. Thus, each subcollective emitter has a coupling strength to the cavity mode [39, 50]. The first-order coupling strength between the cavity mode and subcollective emitters is . Meanwhile, the system also supports high energy states since the subcollective emitters can be simultaneously excited. As shown, this case is exactly described by the calculation with emitters in Sec. II.2. Meanwhile, the limited number of photons in the calculation is allowed to exclude the dephasing effects such as the photon-phonon interaction [51]. Therefore, our model is a good approximation of the cavity QED system involving multiple excitations in experiment.
III Experimental Verification
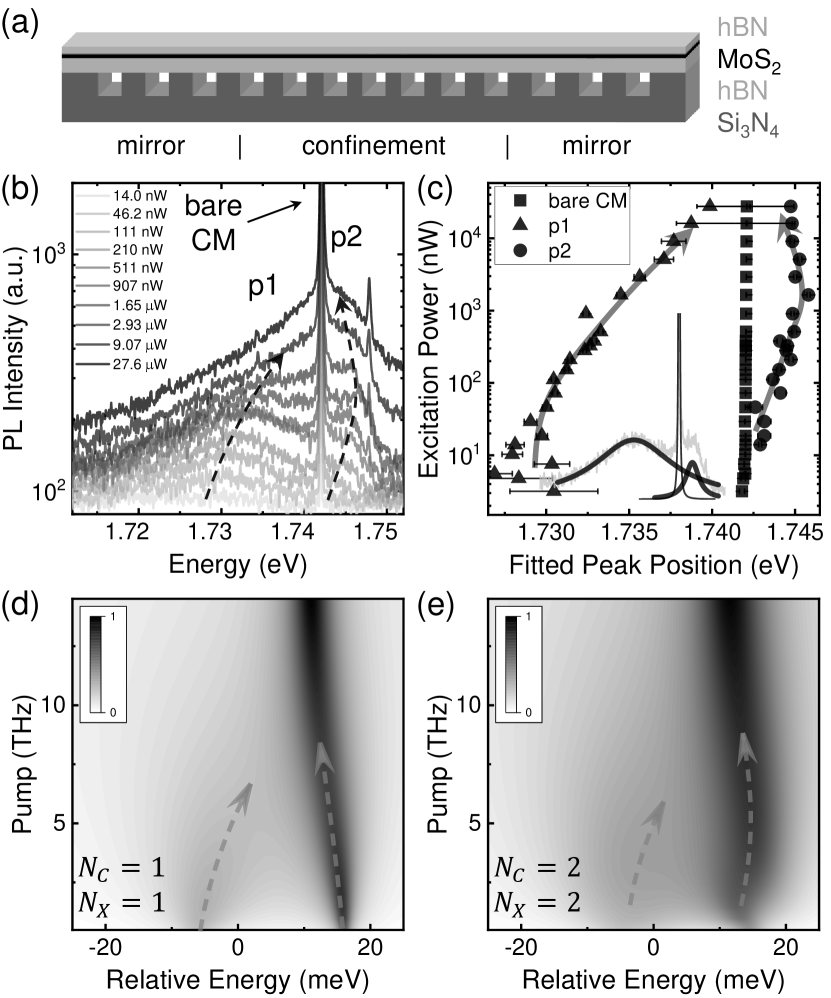
The localized excitons (LXs) in monolayer MoS2 with emissions around 1.75 eV are a good example of individual emitters, since their wavefunctions are strongly localized at defects [33, 34, 35]. The emission energy of each LX is not exactly same, and the emission peak is asymmetric due to phonon sidebands [33]. Nonetheless, recent work shows that an inhomogeneously broadened ensemble of emitters also collectively couples to high-Q cavity mode [52]. We fabricate high-Q nanobeam cavities with monolayer MoS2 embedded as schematically presented in Fig. 4(a) and investigate the cavity-LXs coupling using PL spectroscopy. The cavity is based on the hBN/MoS2/hBN/Si3N4 heterostructure, and details of fabrication methods have been reported in previous literature [32, 53]. The sample is excited by a 532-nm cw-laser with a spot size . The power-dependent PL spectra recorded at low temperature (11 K) are presented in Fig. 4(b). At this temperature, an individual localized exciton has the linewidth at the magnitude around 1 meV [54]. The strong sharp peak at 1.742 eV with the linewidth of 0.16 meV arises from the bare cavity mode, corresponding to a Q-factor of . This bare cavity peak is a widely observed phenomenon in cavity QED experiments, due to fluctuations of the system [55, 56, 57] and background emissions which supply to the cavity mode [58, 59]. The minor sharp peak at 1.748 eV is just noise arising from the bare cavity mode of a neighbor cavity. That neighbor cavity is ( double photon wavelength) away in spatial, thus, has little impact here [32]. Besides the two sharp peaks, we observe two polariton peaks as denoted by p1 and p2 in Fig. 4(b), arising from the cavity-LXs coupling. Considering the typical defect density of 10 [60] and the mode profile [32], we estimate the number of LXs within the cavity mode volume to be .
Peak energies extracted by multi-Lorentz fittings are presented in Fig. 4(c), and one example of fitting is presented in the inset. The fitting accuracy is limited by the factors that LXs are not homogeneously broadened, and their lineshape is not exactly Lorentzian [33]. In addition, at high excitation powers such as , the two polariton peaks merge to the bare cavity energy as predicted in Fig. 1(c), thus only one maximum of the broad polariton emission is observed. For such broad polariton emission, the difference of peak energies between single and double peak fitting is included in the error bar in Fig. 4(c). Nonetheless, the nonmonotonic energy shift of the right emission peak p2 is clearly observed both from the raw data in Fig. 4(a) and the fitted peak energies in Fig. 4(c). In contrast, little power-dependent energy shift is observed in the control experiments recorded from MoS2 outside cavities as presented in Appendix B. This distinct feature indicates that the cavity-LXs coupling is pumped to high orders as discussed in Sec. II.2.
We use the parameters , , , , and to reproduce the cavity-LXs coupling, and typical results are plotted in Fig. 4(d)(e). As expected, with in Fig. 4(d), both two peaks shift monotonically. In contrast, with in Fig. 4(e), the right branch around the bare cavity energy exhibits the nonmonotonic energy shift as the pump increases, consistent with our experimental observation for p2. We note that, the central result here is the high order couplings in the case of . The specific value of for the best fitting of experiment is not our focus, and is out of scope due to the limits in fitting accuracy. In addition, the LXs in experiment are consistent to the ensemble of individual emitters discussed in our theoretical calculations, due to they are localized at defects in the monolayer MoS2. In contrast, free excitons in semiconductors can transport in the material [32], and even formulate the state of exciton gases with many-body interactions [61, 62, 63, 64]. Thus, the coupling between the cavity and free excitons cannot be described by the model here.
IV Conclusion
In summary, we investigate the cavity QED system with the high- cavity mode and the ensemble of emitters using the master equation theory. The increasing excitation of emitters has two effects: pump the system to high energy states and suppress the coherent coupling. We observe the high order coupling between high energy states at mesoscopic excitation levels, when the emitter linewidth is smaller than the threshold. Our model and calculation well describe the coupling between a high- cavity and an ensemble of LXs in monolayer MoS2, and is also expected to apply to other kinds of defect emitters such as defects in hBN, color centers in diamond, and rare-earth ions in silicon. Such mesoscopic excitation levels have great potentials in the multi-photon based quantum information processing and nonlinear quantum photonic devices.
Acknowledgements.
All authors gratefully acknowledge the German Science Foundation (DFG) for financial support via grants FI 947/8-1, DI 2013/5-1 and SPP-2244, as well as the clusters of excellence MCQST (EXS-2111) and e-conversion (EXS-2089). C. Q. gratefully acknowledges support from the Chinese Academy of Sciences Project for Young Scientists in Basic Research (Grant No. YSBR-112) and the National Natural Science Foundation of China (Grants No. 12474426). C. Q and V. V gratefully acknowledge the Alexander v. Humboldt foundation for financial support in the framework of their fellowship programme.Appendix A Threshold of Emitter Linewidth
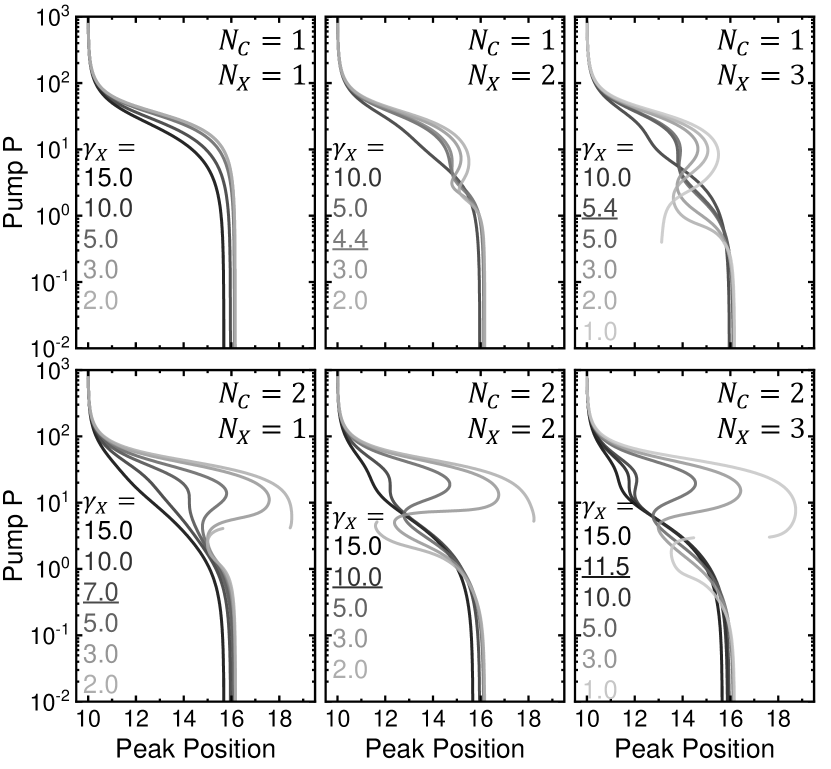
The threshold of emitter linewidth is calculated in more cases with various , and the results are presented in Fig. 5. With , as expected, the nonmonotonic shift never occurs, due to no high order coupling is allowed. In other cases, the nonmonotonic shift occurs for emitter linewidth smaller than a threshold as denoted in Fig. 5(a). The threshold value increases with due to the increasing high order coupling strengths [15, 16]. In the calculation, could further increase, and the nonmonotonic shift would become more significant. However, the number of photons and emitters involved in the coupling cannot increase infinitely. As further increases, the system will become non-Markovian and the rotating wave approximation becomes invalid [38, 39, 65]. The emitter-emitter interaction, photon-phonon coupling [51], experimental fluctuations [55, 56, 57] and other complex effects will also dephase the coupling. Moreover, as discussed in the context of Fig. 4, the specific value of for the best fitting is not the scope of this work. Therefore, we do not present the calculations with more here.
Appendix B Control Experiments
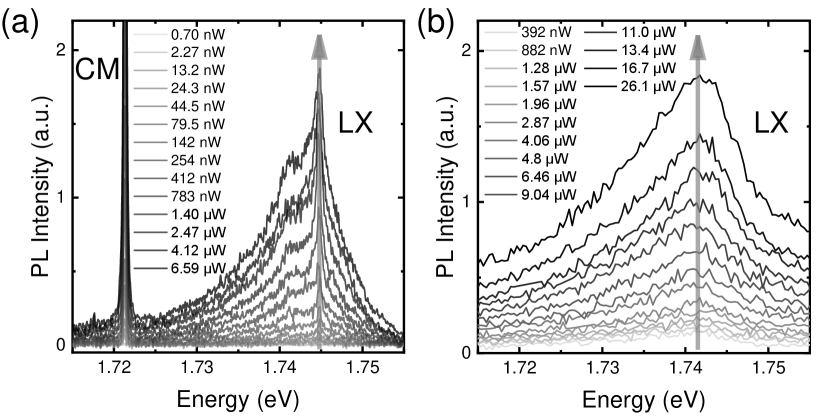
For the experimental results in Fig. 4, one might wonder that, rather than the cavity-LXs coupling, the nonmonotonic shift arise from some intrinsic features of LX or the laser-induced heating [66, 67]. Hereby, we present the control experiments in Fig. 6 to exclude these possibilities. In Fig. 6(a) we present the PL spectra recorded in another cavity on the same sample, where the cavity mode at 1.721 eV is strongly detuned from the LX emissions. In Fig. 6(b) we present the PL spectra recorded from MoS2 on planar substrate without any nanostructures [53]. In both cases, little power-dependent energy shift is observed when the excitation laser power is 30 , as denoted by the gray arrow in Fig. 6. Similar stable emission energy has also been reported for He ion generated LXs, even with the excitation laser power up to [34]. These experiments further support that the nonmonotonic energy shift observed in Fig. 4 arises from the high order cavity-LXs couplings.
References
- Mabuchi and Doherty [2002] H. Mabuchi and A. C. Doherty, Cavity quantum electrodynamics: Coherence in context, Science 298, 1372 (2002).
- Walther et al. [2006] H. Walther, B. T. H. Varcoe, B.-G. Englert, and T. Becker, Cavity quantum electrodynamics, Rep. Prog. Phys. 69, 1325 (2006).
- Kimble [2008] H. J. Kimble, The quantum internet, Nature 453, 1023 (2008).
- O’Brien et al. [2009] J. L. O’Brien, A. Furusawa, and J. Vučković, Photonic quantum technologies, Nat. Photonics 3, 687 (2009).
- Ritter et al. [2012] S. Ritter, C. Nölleke, C. Hahn, A. Reiserer, A. Neuzner, M. Uphoff, M. Mücke, E. Figueroa, J. Bochmann, and G. Rempe, An elementary quantum network of single atoms in optical cavities, Nature 484, 195 (2012).
- Lodahl et al. [2015] P. Lodahl, S. Mahmoodian, and S. Stobbe, Interfacing single photons and single quantum dots with photonic nanostructures, Rev. Mod. Phys. 87, 347 (2015).
- Reiserer and Rempe [2015] A. Reiserer and G. Rempe, Cavity-based quantum networks with single atoms and optical photons, Rev. Mod. Phys. 87, 1379 (2015).
- Alivisatos [2004] P. Alivisatos, The use of nanocrystals in biological detection, Nat. Biotechnol. 22, 47 (2004).
- Martínez-Martínez et al. [2018] L. A. Martínez-Martínez, M. Du, R. F. Ribeiro, S. Kéna-Cohen, and J. Yuen-Zhou, Polariton-assisted singlet fission in acene aggregates, J. Phys. Chem. Lett. 9, 1951 (2018).
- Yu et al. [2021] D. Yu, M. Humar, K. Meserve, R. C. Bailey, S. N. Chormaic, and F. Vollmer, Whispering-gallery-mode sensors for biological and physical sensing, Nat. Rev. Methods Primers 1, 83 (2021).
- Reithmaier et al. [2004] J. P. Reithmaier, G. Sęk, A. Löffler, C. Hofmann, S. Kuhn, S. Reitzenstein, L. V. Keldysh, V. D. Kulakovskii, T. L. Reinecke, and A. Forchel, Strong coupling in a single quantum dot–semiconductor microcavity system, Nature 432, 197 (2004).
- Yoshie et al. [2004] T. Yoshie, A. Scherer, J. Hendrickson, G. Khitrova, H. M. Gibbs, G. Rupper, C. Ell, O. B. Shchekin, and D. G. Deppe, Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity, Nature 432, 200 (2004).
- Bose et al. [2012] R. Bose, D. Sridharan, H. Kim, G. S. Solomon, and E. Waks, Low-photon-number optical switching with a single quantum dot coupled to a photonic crystal cavity, Phys. Rev. Lett. 108, 227402 (2012).
- Kim et al. [2013] H. Kim, R. Bose, T. C. Shen, G. S. Solomon, and E. Waks, A quantum logic gate between a solid-state quantum bit and a photon, Nat. Photonics 7, 373 (2013).
- Tavis and Cummings [1968] M. Tavis and F. W. Cummings, Exact solution for an -molecule—radiation-field hamiltonian, Phys. Rev. 170, 379 (1968).
- TAVIS and CUMMINGS [1969] M. TAVIS and F. W. CUMMINGS, Approximate solutions for an -molecule-radiation-field hamiltonian, Phys. Rev. 188, 692 (1969).
- Amico et al. [2008] L. Amico, R. Fazio, A. Osterloh, and V. Vedral, Entanglement in many-body systems, Rev. Mod. Phys. 80, 517 (2008).
- Wickenbrock et al. [2013] A. Wickenbrock, M. Hemmerling, G. R. M. Robb, C. Emary, and F. Renzoni, Collective strong coupling in multimode cavity QED, Phys. Rev. A 87, 043817 (2013).
- Ota et al. [2011] Y. Ota, S. Iwamoto, N. Kumagai, and Y. Arakawa, Spontaneous two-photon emission from a single quantum dot, Phys. Rev. Lett. 107, 233602 (2011).
- Muñoz et al. [2014] C. S. Muñoz, E. del Valle, A. G. Tudela, K. Müller, S. Lichtmannecker, M. Kaniber, C. Tejedor, J. J. Finley, and F. P. Laussy, Emitters of N-photon bundles, Nat. Photonics 8, 550 (2014).
- Qian et al. [2018] C. Qian, S. Wu, F. Song, K. Peng, X. Xie, J. Yang, S. Xiao, M. J. Steer, I. G. Thayne, C. Tang, Z. Zuo, K. Jin, C. Gu, and X. Xu, Two-photon Rabi splitting in a coupled system of a nanocavity and exciton complexes, Phys. Rev. Lett. 120, 213901 (2018).
- Tang et al. [2019] J. Tang, Y. Deng, and C. Lee, Strong photon blockade mediated by optical stark shift in a single-atom–cavity system, Phys. Rev. Applied 12, 044065 (2019).
- Qian et al. [2019] C. Qian, X. Xie, J. Yang, K. Peng, S. Wu, F. Song, S. Sun, J. Dang, Y. Yu, M. J. Steer, I. G. Thayne, K. Jin, C. Gu, and X. Xu, Enhanced strong interaction between nanocavities and -shell excitons beyond the dipole approximation, Phys. Rev. Lett. 122, 087401 (2019).
- You et al. [2020] J.-B. You, X. Xiong, P. Bai, Z.-K. Zhou, R.-M. Ma, W.-L. Yang, Y.-K. Lu, Y.-F. Xiao, C. E. Png, F. J. Garcia-Vidal, C.-W. Qiu, and L. Wu, Reconfigurable photon sources based on quantum plexcitonic systems, Nano Lett. 20, 4645 (2020).
- Lo [2021] C. F. Lo, Spectral collapse in multiqubit two-photon Rabi model, Scientific Reports 11, 5409 (2021).
- Yamaguchi et al. [2022] M. Yamaguchi, A. Lyasota, T. Yuge, and Y. Ota, Time-resolved physical spectrum in cavity quantum electrodynamics, Phys. Rev. Research 4, 023052 (2022).
- Laucht et al. [2009] A. Laucht, N. Hauke, J. M. Villas-Bôas, F. Hofbauer, G. Böhm, M. Kaniber, and J. J. Finley, Dephasing of exciton polaritons in photoexcited InGaAs quantum dots in GaAs nanocavities, Phys. Rev. Lett. 103, 087405 (2009).
- Ridolfo et al. [2009] A. Ridolfo, O. D. Stefano, S. Portolan, and S. Savasta, Photoluminescence from microcavities strongly coupled to single quantum dots (2009), arXiv:0906.1455 .
- Yao et al. [2010] P. Yao, P. K. Pathak, E. Illes, S. Hughes, S. Münch, S. Reitzenstein, P. Franeck, A. Löffler, T. Heindel, S. Höfling, L. Worschech, and A. Forchel, Nonlinear photoluminescence spectra from a quantum-dot–cavity system: Interplay of pump-induced stimulated emission and anharmonic cavity QED, Phys. Rev. B 81, 033309 (2010).
- Nomura et al. [2010] M. Nomura, N. Kumagai, S. Iwamoto, Y. Ota, and Y. Arakawa, Laser oscillation in a strongly coupled single-quantum-dot–nanocavity system, Nat. Phys. 6, 279 (2010).
- Tan [1999] S. M. Tan, A computational toolbox for quantum and atomic optics, J. Opt. B: Quantum Semiclassical Opt. 1, 424 (1999).
- Qian et al. [2022] C. Qian, V. Villafañe, P. Soubelet, A. Hötger, T. Taniguchi, K. Watanabe, N. P. Wilson, A. V. Stier, A. W. Holleitner, and J. J. Finley, Nonlocal exciton-photon interactions in hybrid high- beam nanocavities with encapsulated monolayers, Phys. Rev. Lett. 128, 237403 (2022).
- Klein et al. [2019] J. Klein, M. Lorke, M. Florian, F. Sigger, L. Sigl, S. Rey, J. Wierzbowski, J. Cerne, K. Müller, E. Mitterreiter, P. Zimmermann, T. Taniguchi, K. Watanabe, U. Wurstbauer, M. Kaniber, M. Knap, R. Schmidt, J. J. Finley, and A. W. Holleitner, Site-selectively generated photon emitters in monolayer MoS2 via local helium ion irradiation, Nat. Commun. 10, 2755 (2019).
- Mitterreiter et al. [2021] E. Mitterreiter, B. Schuler, A. Micevic, D. Hernangómez-Pérez, K. Barthelmi, K. A. Cochrane, J. Kiemle, F. Sigger, J. Klein, E. Wong, E. S. Barnard, K. Watanabe, T. Taniguchi, M. Lorke, F. Jahnke, J. J. Finley, A. M. Schwartzberg, D. Y. Qiu, S. Refaely-Abramson, A. W. Holleitner, A. Weber-Bargioni, and C. Kastl, The role of chalcogen vacancies for atomic defect emission in MoS2, Nat. Commun. 12, 3822 (2021).
- Trainer et al. [2022] D. J. Trainer, J. Nieminen, F. Bobba, B. Wang, X. Xi, A. Bansil, and M. Iavarone, Visualization of defect induced in-gap states in monolayer MoS2, npj 2D Mater. Appl. 6, 13 (2022).
- Qian et al. [2024a] C. Qian, M. Troue, J. Figueiredo, P. Soubelet, V. Villafañe, J. Beierlein, S. Klembt, A. V. Stier, S. Höfling, A. W. Holleitner, and J. J. Finley, Lasing of moiré trapped MoSe2/WSe2 interlayer excitons coupled to a nanocavity, Sci. Adv. 10, eadk6359 (2024a).
- Jaynes and Cummings [1963] E. Jaynes and F. Cummings, Comparison of quantum and semiclassical radiation theories with application to the beam maser, Proc. IEEE 51, 89 (1963).
- Johnson et al. [2019] A. Johnson, M. Blaha, A. E. Ulanov, A. Rauschenbeutel, P. Schneeweiss, and J. Volz, Observation of collective superstrong coupling of cold atoms to a 30-m long optical resonator, Phys. Rev. Lett. 123, 243602 (2019).
- Blaha et al. [2022] M. Blaha, A. Johnson, A. Rauschenbeutel, and J. Volz, Beyond the Tavis-Cummings model: Revisiting cavity QED with ensembles of quantum emitters, Phys. Rev. A 105, 013719 (2022).
- Andreani et al. [1999] L. C. Andreani, G. Panzarini, and J.-M. Gérard, Strong-coupling regime for quantum boxes in pillar microcavities: Theory, Phys. Rev. B 60, 13276 (1999).
- Khitrova et al. [2006] G. Khitrova, H. M. Gibbs, M. Kira, S. W. Koch, and A. Scherer, Vacuum Rabi splitting in semiconductors, Nat. Phys. 2, 81 (2006).
- Qian et al. [2024b] C. Qian, V. Villafañe, P. Soubelet, P. Ji, A. V. Stier, and J. J. Finley, Probing dark excitons in monolayer by nonlinear two-photon spectroscopy, Phys. Rev. Lett. 133, 086902 (2024b).
- Kuruma et al. [2016] K. Kuruma, Y. Ota, M. Kakuda, D. Takamiya, S. Iwamoto, and Y. Arakawa, Position dependent optical coupling between single quantum dots and photonic crystal nanocavities, Appl. Phys. Lett. 109, 071110 (2016).
- Brotons-Gisbert et al. [2021] M. Brotons-Gisbert, H. Baek, A. Campbell, K. Watanabe, T. Taniguchi, and B. D. Gerardot, Moiré-trapped interlayer trions in a charge-tunable heterobilayer, Phys. Rev. X 11, 031033 (2021).
- Erkensten et al. [2021] D. Erkensten, S. Brem, and E. Malic, Exciton-exciton interaction in transition metal dichalcogenide monolayers and van der waals heterostructures, Phys. Rev. B 103, 045426 (2021).
- Kremser et al. [2020] M. Kremser, M. Brotons-Gisbert, J. Knörzer, J. Gückelhorn, M. Meyer, M. Barbone, A. V. Stier, B. D. Gerardot, K. Müller, and J. J. Finley, Discrete interactions between a few interlayer excitons trapped at a MoSe2–WSe2 heterointerface, npj 2D Mater. Appl. 4, 8 (2020).
- Regan et al. [2022] E. C. Regan, D. Wang, E. Y. Paik, Y. Zeng, L. Zhang, J. Zhu, A. H. MacDonald, H. Deng, and F. Wang, Emerging exciton physics in transition metal dichalcogenide heterobilayers, Nat. Rev. Mater. 7, 778 (2022).
- Akselrod et al. [2010] G. M. Akselrod, Y. R. Tischler, E. R. Young, D. G. Nocera, and V. Bulovic, Exciton-exciton annihilation in organic polariton microcavities, Phys. Rev. B 82, 113106 (2010).
- Wu et al. [2019] J. Wu, X. Shi, H. Long, L. Chen, L. Ying, Z. Zheng, and B. Zhang, Large Rabi splitting in InGaN quantum wells microcavity at room temperature, Mater. Res. Express 6, 076204 (2019).
- Dong et al. [2022] Z. Dong, G. Zhang, A.-G. Wu, and R.-B. Wu, On the dynamics of the Tavis-Cummings model, IEEE Trans. Autom. Control , 1 (2022).
- Aspelmeyer et al. [2014] M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, Cavity optomechanics, Rev. Mod. Phys. 86, 1391 (2014).
- Debnath et al. [2019] K. Debnath, Y. Zhang, and K. Mølmer, Collective dynamics of inhomogeneously broadened emitters coupled to an optical cavity with narrow linewidth, Phys. Rev. A 100, 053821 (2019).
- Qian et al. [2023] C. Qian, V. Villafañe, M. M. Petrić, P. Soubelet, A. V. Stier, and J. J. Finley, Coupling of excitons with lattice phonons and cavity vibrational phonons in hybrid nanobeam cavities, Phys. Rev. Lett. 130, 126901 (2023).
- Klein et al. [2021] J. Klein, L. Sigl, S. Gyger, K. Barthelmi, M. Florian, S. Rey, T. Taniguchi, K. Watanabe, F. Jahnke, C. Kastl, V. Zwiller, K. D. Jöns, K. Müller, U. Wurstbauer, J. J. Finley, and A. W. Holleitner, Engineering the luminescence and generation of individual defect emitters in atomically thin MoS2, ACS Photonics 8, 669 (2021).
- Childs et al. [1996] J. J. Childs, K. An, M. S. Otteson, R. R. Dasari, and M. S. Feld, Normal-mode line shapes for atoms in standing-wave optical resonators, Phys. Rev. Lett. 77, 2901 (1996).
- Hennessy et al. [2007] K. Hennessy, A. Badolato, M. Winger, D. Gerace, M. Atatüre, S. Gulde, S. Fält, E. L. Hu, and A. Imamoğlu, Quantum nature of a strongly coupled single quantum dot–cavity system, Nature 445, 896 (2007).
- Yamaguchi et al. [2012] M. Yamaguchi, T. Asano, and S. Noda, Third emission mechanism in solid-state nanocavity quantum electrodynamics, Rep. Prog. Phys. 75, 096401 (2012).
- Ota et al. [2009] Y. Ota, N. Kumagai, S. Ohkouchi, M. Shirane, M. Nomura, S. Ishida, S. Iwamoto, S. Yorozu, and Y. Arakawa, Investigation of the spectral triplet in strongly coupled quantum dot–nanocavity system, Appl. Phys. Express 2, 122301 (2009).
- Ota et al. [2018] Y. Ota, D. Takamiya, R. Ohta, H. Takagi, N. Kumagai, S. Iwamoto, and Y. Arakawa, Large vacuum Rabi splitting between a single quantum dot and an H0 photonic crystal nanocavity, Appl. Phys. Lett. 112, 093101 (2018).
- Vancsó et al. [2016] P. Vancsó, G. Z. Magda, J. Pető, J.-Y. Noh, Y.-S. Kim, C. Hwang, L. P. Biró, and L. Tapasztó, The intrinsic defect structure of exfoliated MoS2 single layers revealed by scanning tunneling microscopy, Sci. Rep. 6, 29726 (2016).
- Pei et al. [2019] J. Pei, J. Yang, T. Yildirim, H. Zhang, and Y. Lu, Many-body complexes in 2D semiconductors, Adv. Mater. 31, 1706945 (2019).
- Jiang et al. [2021] Y. Jiang, S. Chen, W. Zheng, B. Zheng, and A. Pan, Interlayer exciton formation, relaxation, and transport in TMD van der waals heterostructures, Light: Sci. Appl. 10, 72 (2021).
- Wilson et al. [2021] N. P. Wilson, W. Yao, J. Shan, and X. Xu, Excitons and emergent quantum phenomena in stacked 2D semiconductors, Nature 599, 383 (2021).
- Mivehvar et al. [2021] F. Mivehvar, F. Piazza, T. Donner, and H. Ritsch, Cavity QED with quantum gases: new paradigms in many-body physics, Adv. Phys. 70, 1 (2021).
- Meiser and Meystre [2006] D. Meiser and P. Meystre, Superstrong coupling regime of cavity quantum electrodynamics, Phys. Rev. A 74, 065801 (2006).
- Wang et al. [2009] J. Wang, Y. Hernandez, M. Lotya, J. N. Coleman, and W. J. Blau, Broadband nonlinear optical response of graphene dispersions, Adv. Mater. 21, 2430 (2009).
- Scuri et al. [2018] G. Scuri, Y. Zhou, A. A. High, D. S. Wild, C. Shu, K. De Greve, L. A. Jauregui, T. Taniguchi, K. Watanabe, P. Kim, M. D. Lukin, and H. Park, Large excitonic reflectivity of monolayer encapsulated in hexagonal boron nitride, Phys. Rev. Lett. 120, 037402 (2018).