Critical behavior of two-choice rules,
a class of Achlioptas processes
Abstract
Achlioptas processes are a class of dynamically grown random graphs where on each step several edges are chosen at random but only one is added. The sum rule, product rule, and bounded size rules have been extensively studied. Here we introduce a new collection of rules called two-choice rules. In these systems one first pick vertices at random from the graph and chooses a vertex according to some rule based on their cluster sizes. The procedure is then repeated with a second independent sample to pick a vertex and we add an edge from and . These systems are tractable because the cluster size distribution satisfies an analog of the Smoluchowski equation. We study the critical exponents associated with the phase transitions in five of these models. In contrast to the situation for -dimensional percolation we show that all of the critical exponents can be computed if we know , the exponent associated with the size of the giant component. When all the critical exponents are the same as for the Erdös-Rényi graph.
1 Summary of results
We study the phase transitions of a class of dynamically grown graphs that we call two-choice rules. We start with a graph with vertices and no edges. In general, on each step we first pick vertices at random and choose one, , according to some rule. We then pick a second set of vertices , choose one of them, , according to the same rule, and then add to the graph.
The Erdös-Rényi graph is the degenerate case of our system: on each step we pick an edge at random and add it to the graph. To be able to take the limit as we say that graph with edges occurs at time , so that in the limit as the mean degree of vertices at time is . In the case of Erdös-Rényi this means the threshold for the existence of a giant component is . In many papers the graph with edges occurs at time so in the case of Erdös-Rényi this means the threshold for the existence of a giant component is .
If we let be the size of the cluster containing then in three of the rules we consider we choose a vertex (i) with the smallest , (ii) with the largest , or (iii)with the median (assuming is odd). In our fourth system called the Bohman-Frieze vertex rule, we choose an isolated vertex (i.e., ) if there is one in the set, otherwise choose at random from the set. In our fifth example, the alternative edge rule [11], a vertex is chosen at random and then a secon vertex is chosen accroding to the min rule.
As explained in Section 2 these systems are instances of Achlioptas processes. We now introduce two famous examples. In the sum rule one chooses four vertices and connect if and only if . In the product rule we connect if and only if . Achlioptas, D’Souza and Spencer [1] claimed based on simulation that the sum and the product rule had discontinuous phase transitions, but Riordan and Warnkje [22] proved mathematically that the transition was continuous for a very general class of rules. Their proof involved two arguments by contradiction, and hence did not yield much quantitative information about the phase transitions. Here we will study the standard percolation critical exponents for the phase transition of two-choice rules.
1.1 Critical exponents
Let be the probability that a randomly chosen vertex belongs to a cluster of size at time (in the limit ). Let , and (the value is excluded from each of the sums). The exponents , , and are defined by
In the physics literature the meaning of is not precisely defined. It could be something as weak as
In order to derive relations between exponents we will suppose where means . Our final two exponents concern the behavior near the critical value
| (1) |
where is a scaling function.
In Section 5 we will compute the critical exponents for the Erdös-Rényi model,
| (2) |
and show that the scaling relationship (1) holds. These results are well-known. We include them for completeness.
The most significant difference between our critical exponents and those for -dimensional percolation is that we do not have a correlation length that gives the spatial size of a typical finite cluster. Thi squantity is often defined in terms of the exponential decay of probability 0 and are in the same finite cluster
For example, if is the first unit vector
A simpler approach taken by Kesten [18] is to define the correlation length by
and the critical exponent by . Finally on a -dimensional graph we have another exponent called the anomalous dimension
The percolation critical exponents satisfy the following scaling relationships
| (3) |
Kesten [18] established provided that the exponents and exist.
1.2 Models and ODEs
In the Erdös-Rényi model satisfies
| (4) |
In words if the new edge joins a cluster of size and with we now have new vertices that are part of clusters of size , while if a cluster of size is one of the two that merge then the vertices in that cluster are no longer part of a cluster of size . If we let be the number of clusters of size s and then (4) becomes the Smoluchowski equation
| (5) |
For probabilists the best known reference is Aldous [3], but the survey by Leyvraz [19] is more extensive. In addition to results about existence, uniqueness, and asymptotic behavior, there are exact results for (Kingman’s coalescent) and (the additive case).
Example 1. Min(m) rule. da Costa et al, [8, 9, 10], considered a system in which each choice is made as follows: pick vertices with cluster sizes . Let and pick a vertex at random from those with cluster size . To write the differential equation for this and other two-choice rules, let be the probability of choosing a vertex with cluster size at time .
| (6) |
In the case of the min rule if we let be the tail of the distribution, we have
| (7) |
When is large it is unlikely that two vertices achieve the minimum so
| (8) |
Example 2. Median(2m-1) rule. Pick vertices with cluster sizes . Let be the median value. Since is odd the value of the median is unique but it may be achieved by several . In this case we pick one of the vertices with the median cluster size at random. Since the median may occur many times in the sample, it is hard to write an exact formula for . However if we let then for large
| (9) |
where . Thus despite picking from the center of the distribution the asymptotic behavior of will be the same as the Min(m) rule. One can obviously generalize this example to other order statistics, which will then have the same behavior as an apropriate Min rule.
Example 3. Max(m) rule. If picking the vertices of minimum degree slows percolation then it is natural to guess that picking vertices of maximum degree speeds it up, and ask how this affects the phase transtion. As far as we can tell, this version has not been considered. We pick vertices with cluster sizes . Let and pick a vertex at random from those with cluster size . Using , we have
| (10) |
As we have
| (11) |
Since it is natural (but somewhat naive) to guess based on the similaritiy of (6) to (4) that the exponents will be the same as for Erdös-Rényi . The next system also has and we know that it has the same behavior a Erdös-Rényi
Example 4. BF vertex rule Here BF stands for Bohman-Frieze [6]. For a discussion of their work see Section 2. In our version which we call the BF vertex rule, we pick vertices . If any of the first vertices is isolated () then we pick one at random (or pick the first on the list). If not we pick . Though this is not the same as their model, it is a bounded size rule, so it has the same critical exponents as Erdös-Rényi , see Riordan and Warnke [24]. The BF vertex rule has choice distribution
| (12) |
In words, we will choose a vertex in a cluster of size 1, if at least one of the first vertices is isolated, or if all of them are not isolated and is, we end up with an isolated vertex. If none of the first vertices are isolated and has a cluster of size then the size of the chosen cluster is .
1.3 Results
It has long been known for percolation (see Stauffer [27]) that (1) implies
| (13) | ||||
| (14) | ||||
| (15) |
In Section 4.1 we give the proofs, and state the assumptions on and the scaling function in (1) that are needed for these results to be theorems.
Let , , , and be the values of the critical exponents when is replaced by . Since is computed from , we assume that has the scaling property
| (16) |
Here and . As we explain in Section 4.1 (13)–(15) hold for the exponents with subscript , Using (8), (9), (11), and (12) we see that
Lemma 1.
For the Min(m) and Median(2m-1) rules we have and
| (17) |
For the Max(m) and BF vertex rules and .
Using (6) we can show, see Lemma 4 and 6 that if then
| (18) | ||||
| (19) |
From this it follows that
| (20) | ||||
| (21) | ||||
| (22) |
On the second and third lines the two formulas come from and in (19).
Finally using a calculation from Appendix E of da Costa et al [10] we have the remarkable result which relates the two variable in the scaling relation
| (23) |
The proof begins by letting , and in order to rewrite the scaling formulas as
in order to more easily differentiate with respect to . One then substitutes in (6) of so that all of the terms have the large time in them. When the smoke clears after all of the change of variables, every term on the right0hand side is of order and equating this to the order of the left-hand side gives the result.
Using our scaling relationships we can analyze our examples
Theorem 1.
For the Min(m) and Median(2m-1) rules we have
The first two relationships are immediate consequences of (20) and (21). The other two equations require more algebra so the proof is delayed to Section 3.1. Note that using the four equations in Theorem 1, all of the critical exponents can be computed if is known. In contrast, jn ordinary percolation one needs to know the two exponents that appear in the basic scaling relationship to do this. The reduction from two to one is due to (23).
Example 1. Min(m) rule. In this case our result was first proved by daCosta et al [10]. The results in the first three rows of the table below are based on their simulations. They follow the convention that the th graph occurs at time so we have multiplying their estimates of by 2:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 1.8464 | 1.9636 | 1.9898 | |
| 1 | 0.0555 | 0.0104 | 0.0024 | |
| 5/2 | 2.0476 | 2.0099 | 2.0024 | |
| 2 | 1.1665 | 1.0520 | 1.0168 | |
| 1 | 1.1110 | 1.0416 | 1.0144 | |
| 1 | 1.0555 | 1.0208 | 1.0072 |
The results in this table suggest that as
| (24) |
It is clear from the table that but the question is: how fast? Figure 1 suggests that exponentially fast. If so then and the conjectures about critical exponents in (24) follow
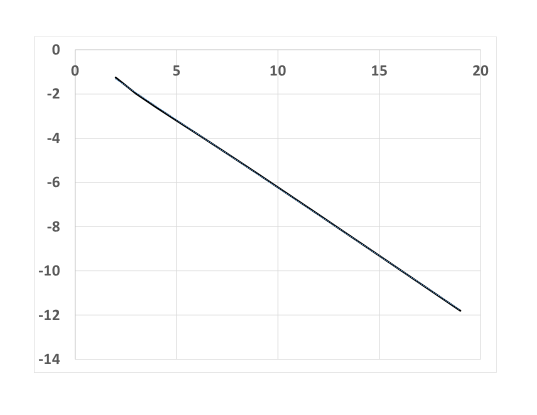
Example 2. Median(2m-1) rule. It would be interesting to know if this models and Min(m) have the same value of and hence all the critical exponents are the same. This conjecture is based on the notion of a universality class of models. For example if one considers bond or site percolation on different two-dimensional lattices (rectangular, triangular, hexagonal, etc) then the critical values for the existence of an infinite component are different but the critical exponents are expected to be the same. Likewise the -dimensional contact process ie expected to have exponents that are do not depend on the neighborhood used to define the model and will have the same cirtical exponents as oriented percolation in dimensions.
Theorem 1 implies that the Min(m) models are in different universlaity classes (if the values of are the same for and then the values of must be different). Sabbir and Hassam [25] claim that the sum and the product rule defined in the next section have the same critical exponents, but otherwise it seems that within this class of models, the universality classes are small.
The next result treats our other two models.
Theorem 2.
In the case of the Max(m) and BF vertex rules we have
Again if we know we can calculate all of the exponents, but this time we want to do more. As explained in the next section, the BF vertex rule is a bounded size rule, so it follows from work of Riordan and Warnke [24] that all the critical exponents are the same Erdös-Rényi We think it might be possible to use the proof of Theorem 6 to prove for the Max(m) rule or any other system in which .
While in principle we can study two-edge rules in which the choice functions are different, in practice we can only analyze the case in which the first choice is a randomly chosen vertex,
Example 5. Adjacent edge rule. D’Souza and MItzenmacher [11] considered the case where the first vertex is chosen at random and the second according the min rule. They restricted their attention to the case but here we consider the general situation.
Generalizing the proofs of Lemmas 4 and 6 in Section 4.2
From this it follows that
| (25) | ||||
| (26) |
where in the second equation we have only used the limit . Generalizing the proof of (23) we can conclude that
| (27) |
Combining our results we have
Theorem 3.
In the case of the alternative edge rules we have
At the moment we are only able to prove the second result under the assumption that . In support of this belief we refer the reader to the sketch of the proof of (23).
2 Achlioptas processes
In this section we review previous work.
2.1 Bounded size rules
Bohman and Frieze [6] were the first to describe a rule that made percolation come later than in the Erdös-Rényi case. Again and edges are chosen at random from the set of all possible edges. If on the th step connects two isolated vertices it is added to the graph, otherwise is added. Using our convention that the graph after choices is the sate at time to time then as They showed that
Theorem 4.
There is a constant so that the largest component at time has size bounded by
This is an example of a bounded size rule. In these systems the decisions about which edge to add is based on the sizes of the components of the vertices chosen, with all of the components of size being treated the same. Spencer and Wormald [26] developed a number of important results for the bounded-size case. To state their “main result let
be the susceptibility, which in percolation terminology is just the mean cluster size. They showed, among other things, that
Theorem 5.
The critical value for the emergence of a giant cmponents can be defined by .
As in ordinary percxolation, when there is a giant component containing a positive fraction of the sites, while for the cluster size distribution has where and depend on .
In 2013, Bhamidi, Budhirja and Wang [5] showed that the behavior of the Bohman-Frieze process near the critical values is the same as in the Erdös-Rényi case. To be precise if we consider the behavior at with then as the system converges to the multiplicative coalecsent in which a cluster of size and a cluster of size merge at rate . See Aldous [2] for the corresponding result for Erdös-Rényi graphs.
Theorem 6.
There are constants the Bohman-Frieze process at time and let be the clusters writtein in order of decreasing size then then the vector of component sizes
viewed as a function of converges to multiplicative coalescent.
Riordan and Warnke [24] have show that “bounded-size rules share (in a strong sense) all the features of the Erdös-Rényi phase transiiton.” Let be the size of the th largest component and let
where the first sum is over all components and is the number of vertices that belong to components of size . Writing whp (with high probability) for with probaility tending to 1 as they established (see their Theorem 1.1):
Theorem 7.
Let be a bounded-size rule with critical time . There are rule dependent positive constants and , so that for any with as
1. (Subcritical phase) For any fixed and
2. (Subcritical phase) For any fixed and
3. (Critical regime) Suppose that and satisfy , , , and
2.2 Explosive percolation
In 2009 Achliptas, D’Souza, and Spencer [1] shouted from the pages of Science that they had found “Explosive percolation in networks.” To quote from their paper:
Here we provide conclusive numerical evidence that unbounded size rules can give rise to discontinuous transitions. For concreteness, we present results for the so-called product rule.
To be precise, and changing notation to avoid conflict with ours, let be the size of the largest cluster when there are edges, let be the last time , and let be the first time it is . Then for large we have .
In 2011 Riordan and Warnke wrote their own Science paper declaring that “Explosive percolation is continuous.” Here we will follow the version published the next year in the Annals of Applied Probability. [22]. The continuity of the phase transition is proved for a very general set of models
-vertex rule. Let be an i.i.d. sequence of vectors in . and is obtained from by adding a possibly empty set of edges . if the are in distinct components.
Theorem 1 in [22]. Let be an vertex rule with . Given any functions and that are and any constant the probability there are and with and and tends to 0 as .
To obtain more detailed results they reduced the collection of models. An -vertex rule is said to be merging if whenever and are distinct components with then in the next step we have probability of joining to .
Theorem 7 in [22]. Let be a merging -vertex rule. Given constant and any function the probability that there are and with and and tends to 0 as .
This result gives a proof of Spencer’s “no two giants” conjecture. If at some time there is a component of size in addition to the giant component then when they merge the size will increase by at least contradicting the last result
The results in [22] are very general and their proofs are ingenious. However, the proof of their Theorem 1 given on page 1457 is based on an argument by contradiction, and it does not seem possible to extract quantitative result. Our goal here is to prove results about the critical behavior of some of these processes, specifically about the values of critical exponents defined in the next section.
3 Proofs of the Theorems
3.1 Proof of Theorem 1
3.2 Proof of Theorem 2
3.3 Proof of Theorem 3
4 Proofs of scaling relations
4.1 Results that follow from (1)
To have rigorous result we state explicitly what we assume about and about the scaling function. Throughout we only use the scaling relationship
Since the versions of the scaling relationships follow immediately.
Lemma 2.
If and is bounded, and is Lipschitz continuous at 0.
Proof.
Using (1) and replacing sum by integration.
Changing variables , the above
Since is bounded and the integral over is finite. Since is Lipschitz continuous the integrand is near 0. Since , the integral over is finite, and it follows that . ∎
Lemma 3.
If and for all then for all
It follows that for all integers ,
Proof.
| (29) |
Changing variables , the above
The assumption for all implies that the integral over is finite. Since and the integral over is finite ∎
4.2 Proofs of ODE consequences
We will now derive two consequences of the ODE for two-choice rules (LABEL:genODE). Let be the fraction of vertices in giant components. The first result establishes (20)
Lemma 4.
Let and
Proof.
so we have
which proves the desired result. ∎
While the proof is fresh on the readers mind we will prove the result for the alternate edge rule.
Lemma 5.
Proof.
Computing as above using the alterantive edge ODE
which proves the desired result. ∎
We now prove the second result
Lemma 6.
Proof.
Multiplying by and then summing
which gives the desired result. ∎
Again our next step is to extend to the alternative edge rule.
Lemma 7.
Proof.
Multiplying by and then summing
which gives the desired result. ∎
4.3 A computation from Appendix E of [10]
Their argument is for the 2 choice min rule. To generalize we suppose
It is convenient to let , and in order to rewrite the scaling formulas as
| (30) | ||||
| (31) |
To eliminate the contribution from small values of and we substitute and in (LABEL:genODE) to get
where we have dropped the dependence on to simplify the formulas.
4.4 Proof for adjacent edge rule
To eliminate the contribution from small values of and in (LABEL:genODE) we again substitute and to get
Rearranging gives
Canceling and writing in integral form
| (36) |
The formula for the left hand side given in (33) remains the same. Using the right-hand side is
Using ,
5 Erdös-Rényi model
5.1 Survival probability
Let be a randomly chosen vertex and let be the number of vertices at distance from . When the cluster containing is whp a tree and is a branching process in which each individual in generation has a Poisson() number of offespring.
Consider a branching process with offspring distribution with mean and finite second moment. Let be the generating function. If is Poisson() then
| (38) |
Let be probability the system dies out. Breaking things down according to the number of children in the first generation
is a trivial solution. is the unique solution of in .
If is close to 1 then will be close to 1. Ignoring a few details, if is close to 1 expanding in power series around 1 gives
so for a fixed point we want
or . If we let which is the same as the fraction of vertices in the giant component
| (39) |
so the critical exponent .
5.2 Mean cluster size.
Let be the cluster containing . If
| (40) |
so . In the supercritical regime we consider
The cluster size is the same as the total progeny in a supercritical branching process conditioned to die out.
Theorem 8.
A supercritical branching process conditioned to become extinct is a subcritical branching process. If the original offspring distribution is Poisson() with then the conditioned one is Poisson() where is the extinction probability.
Proof.
Let and consider . To check the Markov property for note that the Markov property for implies:
To compute the transition probability for , observe that if is the extinction probability then . Let be the transition probability for . Note that the Markov property implies
Taking and computing the generating function
| (41) |
where is the offspring distribution.
is the distribution of the size of the family of an individual, conditioned on the branching process dying out. If we start with individuals then in each gives rise to an independent family. In each family must die out, so is a branching process with offspring distribution . To prove this formally observe that
Writing as shorthand for the sum in the last display
In the case of the Poisson() distribution so if , so using (41)
which completes the proof that the conditioned process is a Poisson() branching process ∎
5.3 Higher moments
Although the connection with clusters in Erdös-Rényi random graps and branching processes is intuitive, it is more convenient technically to expose the cluster one site at a time to obtain something that can be approximated by a random walk. Let if there is an edge between and . Let be the set of removed sites, be the unexplored sites and is the set of active sites. Initially , , and . If , pick at random from let
| (42) | ||||
| (43) | ||||
| (44) |
At time we have found all the sites in the cluster and the process stops. for all , so the cluster size is . If and the number of rermoved sites is small
To have the process defined for all time let be i.i.d. and .
We begin by computing the moment generating function of
| (45) |
is a nonnegative martingale, so using the optional stopping theorem for the nonnegative supermartingale , see e.g., (7.6) in Chapter 4 of Durrett (2004)
| (46) |
so if then when is small. To optimize we note that the derivative
when . At this point and
Since , using Chebyshev’s inequality with (46)
One particle dies on each time step so and we have
| (47) |
There are several other martingale associated with a random walk. Perhaps the simplest is . Using the domination in (47) we can conclude that
so the expected cluster size is .
If is a random walk in which steps have mean 0 and variance then is a martingale. Applying this result to and recalling that ) has variance we see that
is a martingale. Using the domination we can stop at time and conclude
Rearranging we have
| (48) |
Since the critical exponent .
5.4 Cluster size at criticality.
Lemma 2.7.1 in [13] states the following
Theorem 9.
Let . If and then the expected number of tree components of size
| (49) | ||||
| (50) |
Proof.
Cayley showed in 1889 that there are trees with labeled vertices. is the number of ways of choosing the vertices from the in the graph. For the tree to be there in the ER graph the edges must be present in the graph, there can be no connection between the vertices and the other vertices, and the other connections between the vertices must be missing. This proves (49).
To simplify to get the version in (50) we start by noting that
Using the expansion we see that if then
while if we have
Combining the last three calculations gives the desired formula. ∎
Taking , Lemma 2.7.1 implies that the expected number of components of size in Erdös-Rényi() is
This says that the largest components are of size . The critical exponent defined in (LABEL:tau)
has the value
References
- [1] Achlipotas, D., D’Souza, R.M., and Spencer, J. (2009) Explosive percolation in networks. Science. 323, 1453–1455
- [2] Aldous, D. (1999) Brownian excursions, critical random graphs, and multiplicative coalescent. Ann. Probab. 25, 812–854
- [3] Aldous, D. (1999) Determinisitc and stochastic models for coalescence (aggregation and coagulation): a review of the mean-file theory for probabilists. Bernoulli 5, 3–45
- [4] Bastas, N., Giazitzidis, P., Maragakis, M., and Komidis, K. (2014) Explosive percolation: unusual transition in a simple model. Physica A. 407, 54–65
- [5] Bhamidi, S., Budhiraja, A., and Wang, X. (2013) Aggregation models with limited choice and the multiplicative coalescent. Prob. Theory Rel. Fields. 160, 733–796
- [6] Bohman, T., and Frieze, A. (2001) Avoiding a giant component. Rand. Struct. Alg. 19, 75–85
- [7] Bohman, T., and Kravitz, D. (2006) Creating a giant component. Comb. Prob., Comp. 15, 489–511
- [8] da Costa, R.A., Dorogovtsev, S.N., Goltsev, A.V., and Mendes, J.F.F. (2010) Explosive percolation transition is actually continuous. Physical Review Letters. 105, paper 255701
- [9] da Costa, R.A., Dorogovtsev, S.N., Goltsev, A.V., and Mendes, J.F.F. (2014) Critical exponents of the explosive percolation transition. arXiv:1402.4450
- [10] da Costa, R.A., Dorogovtsev, S.N., Goltsev, A.V., and Mendes, J.F.F. (2014) Solution of the explosive percolation quest: Scaling functions and critical exponents. arXiv:1405.1037
- [11] D’Souza, R.M., and Mitzenmacher, M. (2010) Local cluster aggregation models of explosive percolation. Physical Review Letters. 104, paper 195702
- [12] D’Souza, R.M., and Nagler, J. (2016) Anomalous critical and supercritical phenomena in supercritical percolation. nature Physics. 11, 531–538
- [13] Durrett, R. (2007) Random Graph Dynamics. Cambridge U. Press
- [14] Erdös, P., and Rényi A. (1960) Publ. Math. Inst. Hungar. Acad. Sci. 5, 17
- [15] Grimmett, G. (1999) Percolation. Second edition Springer-Verlag
- [16] Janson, S., and Spencer, J. (2012) Phase transitions for modified Erdös-Rényi processes. Ark. Mat. 50, 305–329
- [17] Kang, M., Perkins, W., and Spencer, J. (2013) The Bohman-Frieze process near criticality. Comb. Prob. Comp. 43, 221-250
- [18] Kesten, H. (1987) Scaling relations for 2D-percolation Commun. Math. Phys. 109, 109-156
- [19] Leyvraz, F. (2003) Scaling theory and exactly solved models in the kinets of irreversible aggregation. Physics Report. 383, 95–212
- [20] Raddicchi, F., and Fortunato, S. (2010) Explosive percolation: a numerical analysis. Physical Review E. 81, paper 036110
- [21] Riordan, R., and Warnke, L. (2011) Explosive percolation is continuous. Science. 333, 322–324
- [22] Riordan, R., and Warnke, L. (2012) Achlioptas process phase transitions are continuous. Ann. Appl. Probab. 22, 1450–1464
- [23] Riordan, R., and Warnke, L. (2016) Convergence of Achlioptas processes via differential equations with unique solutions. Combinatorics, probability, and Computing. 25, 154–171
- [24] Riordan, R., and Warnke, L. (2017) The phase transition in bounded-size Achlioptas processes. arXiv:1704.08714
- [25] Sabbir, M.M.H., and Hassan, M.K. (2018) Product-sum universiality and Rushbrooke inequlaity for explosive percolation. Physical Review E. 97, paper 050102(R)
- [26] Spencer, J., and Wormald, N. (2007) Birth control for giants. Combinatorica. 37, 587–638
- [27] Stauffer, D. (1979) Scaling theory for percolation clusters. Physics Reports. 54, 1–79