Critical superfluid velocity in a trapped dipolar gas

Liquid ${}^{4}\mathrm{He}$ was the first experimentally accessible system to exhibit dissipationless flow at low temperature, i.e., to demonstrate the existence of superfluidity in a quantum system. Landau famously explained this phenomenon by identifying a critical velocity $v_{L}$ below which elementary excitations in the fluid could not be excited while conserving energy and momentum Landau (1941). Because of this connection to the spectrum of elementary excitations, the Landau critical velocity can be expressed in terms of the fluid’s dispersion relation $\omega(k)$ as

Remarkably, the Landau critical velocity $v_{L}$ does not coincide with the speed of sound in liquid helium, but is smaller due to the existence of an anomalously low-energy roton mode at wave vector $k\sim\AA ^{-1}$. This critical velocity was ultimately verified in experiments of ion drift velocity in liquid ⁴He Allum et al. (1977).

More recently, a new class of superfluids has been produced in the form of Bose-Einstein condensates (BECs) of ultracold atomic gases. These gases have a distinct advantage over liquid helium in that they are dilute and hence easily characterized in terms of microscopic interactions. In particular, their critical velocity is nominally given by the speed of sound in the center of the gas, which can be easily calculated from the density and the s-wave scattering length of the constituent atoms. Early experiments at MIT sought to measure $v_{L}$ in a BEC of sodium atoms by stirring the condensate with a blue-detuned laser Raman et al. (1999); Onofrio et al. (2000). However, these experiments measured a critical velocity for spinning off vortices rather than the true Landau critical velocity. This is a generic feature of such experiments in which the size of the object (in this case, the blue-detuned laser) is large compared to the healing length of the gas Frisch et al. (1992); Winiecki et al. (2000); Stießberger and Zwerger (2000); Jackson et al. (2000).

Still more recently, atomic BECs have been created whose constituent atoms possess magnetic dipole moments large enough to influence the condensate Griesmaier et al. (2005); Werner et al. (2005). These gases present a middle ground between atomic BECs and dense superfluid helium. Namely, the dipolar BEC (DBEC) is dilute enough to be understood in detail, yet its spectrum may exhibit roton features in prolate traps, like those of liquid He Santos et al. (2003). The characteristic momentum of such a roton is set by the geometry of the trap in which it is held, whereas its energy is controlled by the density of dipoles, as well as the magnitude of the dipole moment Lahaye et al. (2009). Thus, by Eq. (1), the Landau critical velocity is completely under the control of the experimentalist. In contrast, $v_{L}$ in ⁴He can be only weakly modified by changing the pressure of the liquid Dietrich et al. (1972). Thus, the DBEC provides an unprecedented opportunity to explore the fundamental relationship between the roton dispersion and superfluidity.

In this Letter we model an experiment on a DBEC similar to the MIT experiments. We consider a blue-detuned laser sweeping through a DBEC at a constant velocity, then compute the resulting condensate depletion due to the excitation of quasiparticles. We find an onset of depletion at a critical velocity that is near the Landau critical velocity at low densities. At higher densities, where the roton determines $v_{L}$, the critical velocity is a decreasing function of density, a behavior unique to a DBEC. Moreover, the simulations show a critical velocity that is somewhat smaller than $v_{L}$ at higher densities. We attribute this to the role that the roton plays in the mechanical stability of a DBEC.

An ultracold, dilute DBEC containing $N$ atoms is well-modeled within mean-field theory by the time-dependent non-local Gross-Pitaevskii equation (GPE),

where $\Psi(\mathbf{r},t)$ is the condensate wave function, normalized to unity; $\mathbf{r}$ is the distance from the trap center; and $U(\mathbf{r})=\frac{1}{2}M\omega_{\rho}^{2}(\rho^{2}+\lambda^{2}z^{2})$ is the cylindrically symmetric harmonic trap potential with aspect ratio $\lambda=\omega_{z}/\omega_{\rho}$ where $\omega_{z}$ and $\omega_{\rho}$ are the axial and radial trap frequencies, respectively. The two-body interaction potential for polarized dipoles with dipole moment $d$ and zero scattering length is Yi and You (2000)

where $\theta$ is the angle between $\mathbf{r}-\mathbf{r}^{\prime}$ and the polarization axis. We choose the polarization axis to be the trap axis, $\hat{z}$, so that the system is cylindrically symmetric. To characterize the strength of the dipole-dipole interaction (ddi) in a DBEC, we define the dimensionless quantity $D=(N-1)\frac{Md^{2}}{\hbar^{2}a_{\rho}}$ where $a_{\rho}=\sqrt{\hbar/M\omega_{\rho}}$ is the radial harmonic oscillator length of the trap. The quantity $D$ then characterizes either the density of the gas or the dipole moments of the atoms in the gas.

We perturb this DBEC with a blue-detuned laser moving at constant velocity $v$, which amounts to adding a potential

where $\sigma=1+(z/z_{0})^{2}$, $z_{0}=\pi\tilde{w}_{0}^{2}/\lambda_{\mathrm{las}}$ is the Raleigh length, $\tilde{w}_{0}$ is the beam waist of the laser, $\lambda_{\mathrm{las}}$ is the wavelength of the laser, $y_{\mathrm{ob}}(t)=\Theta(t-t_{0})[v(t-t_{0})]$ describes the motion of the laser in the $y$-direction and $\Theta(t)$ is the Heaviside step function. This potential describes a laser that is stationary until $t=t_{0}$, at which time it moves to the edge with velocity $\vec{v}=v\hat{y}$.

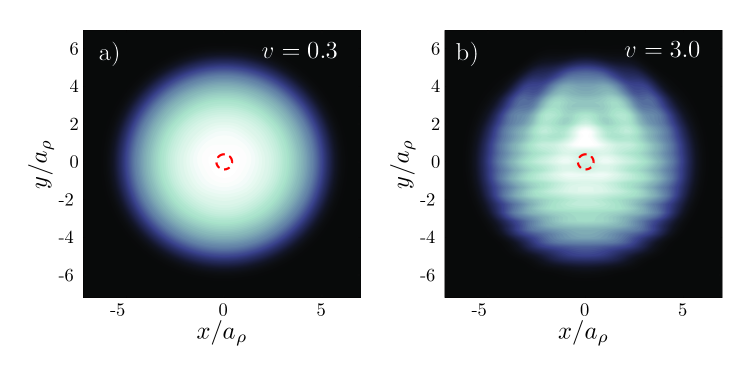
The effect of this blue-detuned laser on a DBEC is shown in Figure 1 for a DBEC with aspect ratio $\lambda=20$, $D=124$, and a laser with $\tilde{w}_{0}=0.4a_{\rho}$ and $U_{0}=2\hbar\omega_{\rho}$ where the chemical potential of the unperturbed condensate is $\mu=26.3\hbar\omega_{\rho}$. We estimate the Landau critical velocity for this system to be $v_{L}\sim 1.5$ $a_{\rho}\omega_{\rho}$. For a laser velocity less than this (Fig. 1a), the condensate is completely unaffected whereas for a velocity larger than this (Fig. 1b), quasiparticles are excited and the fluid would produce a net force on the moving laser.

To determine the Landau critical velocity $v_{L}$, we calculate the condensate’s quasiparticle spectrum by solving the Bogoliubov de Gennes (BdG) equations Ronen et al. (2006). Due to cylindrical symmetry of the system, the condensate plus BdG quasiparticles can be written as

where $\omega_{j}$ is the quasiparticle energy, $m$ is the projection of the quasiparticle momentum onto the $z$-axis and $\mu$ is the chemical potential of the ground state. Here, $\psi_{0}(\rho,z)$ is the stationary condensate wave function, i.e., the solution of Eq. (Critical superfluid velocity in a trapped dipolar gas) with time-dependence $e^{-i\mu t}$, and is normalized to unity. The coefficients $c_{j}(t)$ must be sufficiently small so that the BdG equations can be derived by linearizing the GPE about them. Their time dependence describes slowly varying quasiparticle occupations (compared to $\omega_{j}^{-1}$) in out-of-equilibrium states.

In this formalism, the quasiparticles are characterized by their energies $\omega_{j}$ and $m$ quantum numbers. However, in order to apply the Landau criterion to this system, the quasiparticles must be characterized by a momentum, as well. To do this, we calculate the expectation value of the momentum, or $\langle k_{\rho}\rangle\equiv\sqrt{\langle k_{\rho}^{2}\rangle}$, of the quasiparticles. Using a Fourier-Hankel transform Ronen et al. (2006), we transform the modes into momentum-space and compute the expectation value of the linear momentum of the $j^{\mathrm{th}}$ quasiparticle in momentum-space representation,

where we have time-averaged cross terms $\propto\cos{2\omega_{j}t}$ that oscillate on fast time scales Morgan et al. (1998). By associating these momenta to the excitation energies $\omega_{j}$, we determine a discrete dispersion relation for this system. The Landau criteria for superfluid critical velocity is derived by applying conservation laws to translationally invariant fluids. Since the fully trapped system that we consider here is translationally variant, we apply the Landau criteria both to provide a hint as to where a critical velocity for quasiparticle excitations might be, and to test the application of this criterion to discrete systems.

Figure 2 shows the discrete dispersion relations of a DBEC for various values of $D$. For $D=0$ (not shown), the dispersion is given by the well known harmonic oscillator spectrum $\omega=n_{\rho}\omega_{\rho}$ with $\langle k_{\rho}\rangle=\sqrt{n_{\rho}+1}/a_{\rho}$ and $n_{\rho}=0,1,2,..$. However, as $D$ is increased, the spectrum changes to develop a phonon character at low-momenta and a roton character at intermediate momenta. Indeed, for $D=175.2$, and more so for $D=230.0$, there are some quasiparticles that branch off from the dispersion towards lower energies and approach a momentum $\langle k_{\rho}\rangle\sim\sqrt{20}/a_{\rho}$, corresponding to the characteristic roton wavelength $\lambda_{\mathrm{roton}}\simeq 2\pi a_{z}$, where $a_{z}=\sqrt{\hbar/M\omega_{z}}$ is the axial harmonic oscillator length Santos et al. (2003); Wilson et al. (2008). The modes with similar momenta but larger energy, on the upper branch of the dispersion, exist in lower-density regions of the condensate while the quasiparticles on the roton branch exist in the high density center of the condensate. Note that Figure 2 includes only quasiparticles with $m=0,1,2$.

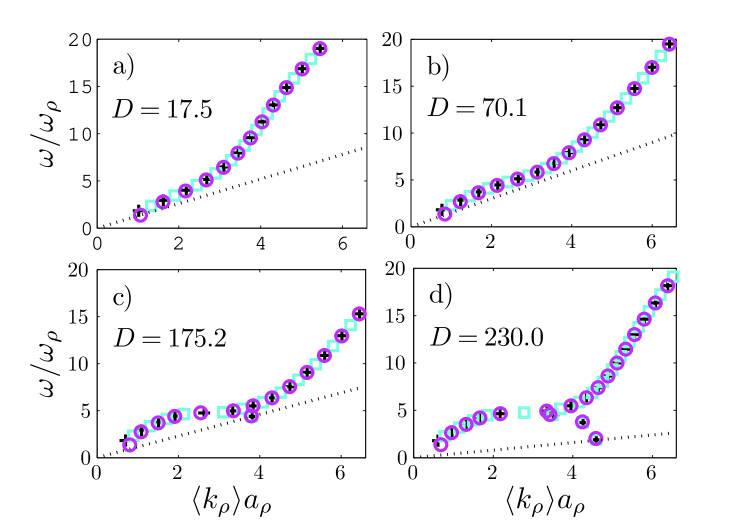
In each case, the Landau critical velocity $v_{L}$ is determined according to Eq. (1) as the slope of the shallowest line through the origin that intersects a point on the dispersion curve; these lines are indicated in the figure. For smaller $D$, $v_{L}$ is determined by the low-momentum phonon-like modes where $\omega$ is linear in $\langle k_{\rho}\rangle$. By contrast, for larger $D$, $v_{L}$ is determined by the low-lying roton mode and becomes a decreasing function of interaction strength in contrast to a BEC with only contact interactions, where $v_{L}$ grows as the square root of scattering length.

In evaluating $v_{L}$ from the discrete dispersion relation, we have ignored two excitations. One is the unphysical $m=0$ Goldstone mode. A second is the $m=1$ Kohn mode, which has eigenvalue $\omega_{1}=\hbar\omega_{\rho}$ independent of interactions, and which corresponds to transverse sloshing of the condensate Kohn (1961). The Kohn mode moves the condensate’s center of mass rather than exciting quasiparticles relative to the center of mass, which would imply the breaking of superfluidity in a translationally invariant system. We therefore ignore it here. In any event, we find that the occupation of the Kohn mode is very small compared to the total condensate depletion.

We now compare $v_{L}$ as determined from the discrete dispersion relation with the onset of condensate depletion due to the laser having been moved through the DBEC. To quantify the breaking of superfluidity in the simulations, we calculate the depletion of the condensate by finding the quasiparticle occupations, or the number of particles that are excited out of the condensed state. In practice, this is achieved by calculating the amplitudes $c_{j}(t)$ in Eq. (Critical superfluid velocity in a trapped dipolar gas) Ianeselli et al. (2006) via the orthogonality relations of the BdG modes Morgan et al. (1998), including their normalization $\int d\mathbf{r}\left[u^{\star}_{j}(\mathbf{r}^{\prime})u_{j^{\prime}}(\mathbf{r}^{\prime})-v^{\star}_{j}(\mathbf{r}^{\prime})v_{j^{\prime}}(\mathbf{r}^{\prime})\right]=\delta_{jj^{\prime}}$, to give

where $\Psi(\mathbf{r},t)$ is the numerical solution of the time-dependent GPE with the blue-detuned laser potential. The quasiparticle occupations are then given by $n_{j}(t)=|c_{j}(t)|^{2}\int d\mathbf{r}^{\prime}(|u_{j}(\mathbf{r}^{\prime})|^{2}+|v_{j}(\mathbf{r}^{\prime})|^{2})$. In the simulations, the system evolves for a time $T$ after the laser has completely left the system. We average the quasiparticle occupations for a time $T$ after this, giving the average excited state occupations $\bar{n}_{j}=\frac{1}{T}\int_{0}^{T}dt^{\prime}n_{j}(t^{\prime})$. We find that $T=5\,\omega_{\rho}^{-1}$ is sufficient to converge these averages.

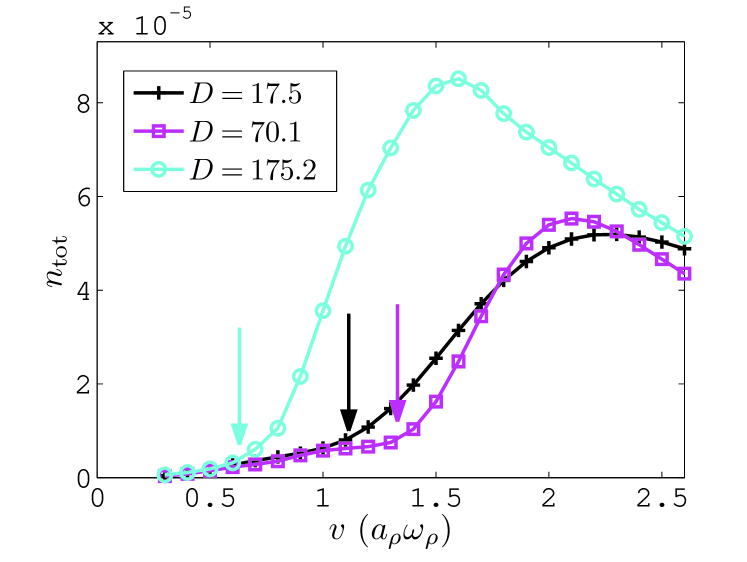
Figure 3 illustrates the total quasiparticle occupation $n_{\mathrm{tot}}=\sum_{j}\bar{n}_{j}$ as a function of laser velocity for various values of $D$ using the laser parameters $\tilde{w}_{0}=0.3a_{\rho}$, $z_{0}=0.7a_{\rho}$ and $U_{0}=0.4\hbar\omega_{\rho}$. For each $D$, $n_{\mathrm{tot}}$ stays very small until, at a certain critical velocity $v_{\mathrm{crit}}$, it begins to increase significantly. Operationally, $v_{\mathrm{crit}}$ is determined by the intersection of linear fits below and above $v_{\mathrm{crit}}$. Well above $v_{\mathrm{crit}}$, the occupations decrease with velocity since the laser spends proportionally less time in the system as its velocity is increased.

Notice that the overall depletion remains small with our weak laser. We have deliberately remained in the perturbative limit with our simulations to uncover the basic physics without the complications of large laser size. Additionally, we have checked that these lasers are not sufficient to excite vortex states in the DBEC. In practice, larger condensate depletion would be obtained from a repeated back-and-forth stirring, as was done in the MIT experiments, or from a wider, stronger laser. While such a laser may spin off vortices in the condensate, thus defining a critical velocity smaller than $v_{L}$, the roton, for large enough $D$, would still determine the critical velocity.

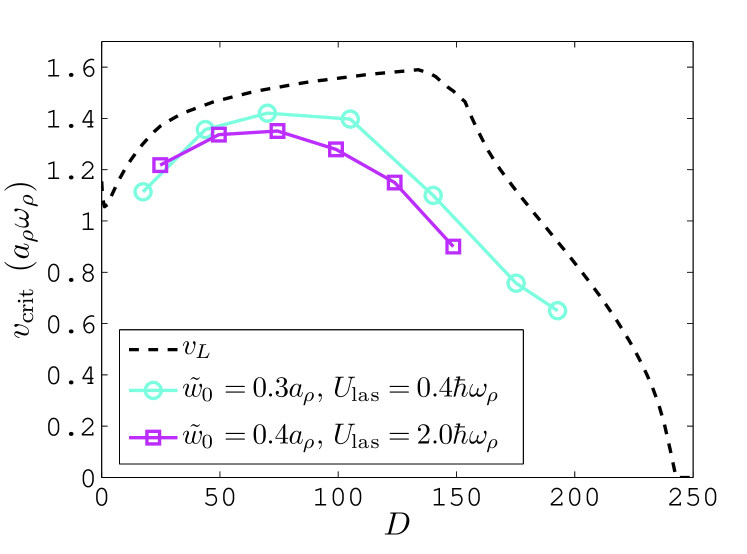
Critical velocities determined from numerical simulations are presented in Figure 4 as a function of $D$. Results are shown for the comparatively weak ($U_{0}=0.4\hbar\omega_{\rho}$) and strong ($U_{0}=2\hbar\omega_{\rho}$) lasers. Also shown for comparison is $v_{L}$ (dashed line) as determined from the discrete dispersion relations. At small $D$, the critical velocity grows slightly as the phonon modes stiffen and the speed of sound increases. This behavior is much like that of a BEC with purely contact interactions.

At higher density, the critical velocity instead decreases, due to the decreasing energy of the roton, and this is seen in both simulation and $v_{L}$. The agreement is less perfect than in the phonon regime, however, with the simulated result coming in lower. This is because the roton, being the collapse mechanism for DBECs in traps with larger aspect ratios, softens with increasing condensate density. The presence of the laser in the DBEC serves to increase the density of the system, softening the roton and thus decreasing the critical velocity of the condensate, just as a stationary laser leads a DBEC to instability uz Zaman and Blume . For vanishingly small lasers, the critical velocities extracted from numerical simulation show increasingly better agreement with $v_{L}$.

Finally, it is worthwhile to consider measurements of critical velocities in experimentally accessible DBECs, such as the ${}^{52}\mathrm{Cr}$ system in Stuttgart Griesmaier et al. (2005). Consider ${}^{52}\mathrm{Cr}$ atoms whose scattering lengths have been tuned to zero in a trap with radial and axial frequencies $\omega_{\rho}=2\pi\times 100$ Hz and $\omega_{z}=2\pi\times 2000$ Hz, respectively. This corresponds to a radial harmonic oscillator length of $a_{\rho}=1.391\,\mu\mathrm{m}$, particle numbers of $N\sim 570D$ and critical velocities in the range of 0.11 cm/s. These circumstances suggest that it may be plausible to observe the decline of the superfluid velocity with $D$ for $N\gtrsim 8.5\times 10^{4}$ ${}^{52}\mathrm{Cr}$ atoms, and hence to exhibit directly the roton’s influence on superfluidity. This atom number corresponds to a maximum condensate density of $n_{\mathrm{max}}\simeq 9.5\times 10^{14}$ cm^-3, which, given the measured 3-body loss coefficient $L_{3}=2\times 10^{-28}$ cm⁶/s Lahaye et al. (2009), should not produce significant losses over the time scales considered here. Additionally, we have checked that, for sufficiently large $D$, the roton serves to determine $v_{L}$ for ${}^{52}\mathrm{Cr}$ DBECs with non-zero $s$-wave scattering lengths within the experimental uncertainty for ${}^{52}\mathrm{Cr}$, $-3a_{0}\leq a_{s}\leq 3a_{0}$ Lahaye et al. (2008), which is expected because these scattering lengths are sufficiently less than ${}^{52}\mathrm{Cr}$’s dipole length $a_{dd}\simeq 15a_{0}$ Lahaye et al. (2009).

The authors would like to acknowledge the financial support of the DOE and the NSF, and useful discussions with C. Raman.