Criticisms of modelling packet traffic using long-range dependence

Since the seminal paper of Leland et al [6] it has been considered important that a statistical model of Internet traffic captures the phenomenon of Long-Range Dependence (LRD). In particular it has often been suggested that a model of Internet traffic must capture the Hurst parameter $H\in(1/2,1)$ of real traffic. LRD is characterised by the unsummability of the autocorrelation function (ACF). It is often stated that this is an important characteristic for the queuing performance of the traffic.

A related topic is that of heavy-tailed distributions. A commonly suggested origin for the LRD in Internet traffic is the heavy-tailed distribution of traffic on periods .

A specific functional form is usually assumed (and will be throughout this paper)

where $C>0$ is a constant and $2>\beta>0$. The symbol $\sim$ means asymptotically equal to. If $\beta<1$ then $\mathrm{E}\left[X\right]$ is infinite and therefore most models use $\beta\in(1,2)$.

Suggested models for Internet traffic which generate LRD include fractional Gaussian noise and the related fractional Brownian motion (fGn, fBm) [7], chaotic maps [4], wavelets [9, 8] and Markov modulated processes [1, 3]. Some of these models output a “traffic level” which represents the mean arrival rate in some notional time period but others are packet based models, that is they produce a model of packets and inter-arrival times. It is the latter class of models (including [4, 1, 3] which are covered by theorem 1 in this paper.

This paper criticises the notion that the long-range correlations in traffic are important to queuing in two ways. In section 2 it is shown that a class of models used to simulate traffic with LRD arising from heavy tails gives an infinite result when queued in infinite buffers. It is demonstrated in section 4 that this is at odds with the behaviour of real traffic. In section 5 real traffic traces are analysed again and reordered to break up correlations beyond a certain level. It is shown that this reordering does not affect the queueing behaviour of the traffic beyond a certain time-scale except when unrealistically high loads are used. The behaviour of the long-range dependent models (and in particular a certain class based on heavy-tails) is theoretically undesirable and fundamentally different to that of real traffic.

Let $\{A_{t}:t\geq 0\}$ be an arrival process to a queue drained by a deterministic server which serves at a constant rate assumed w.l.o.g. to be one. The mean arrival rate $\lambda$ is given by $\lambda=\lim_{T\rightarrow\infty}\int_{0}^{T}A(t)dt/T$ and it is assumed throughout that $A_{t}$ is such that this limit exists and $\lambda\in(0,1)$. Since the server rate is one then $\lambda$ is equal to the utilisation $\rho$ (the ratio of the rate at which work enters to the maximum rate at which it can be served). Let $\{Q_{t}:t\geq 0\}$ be the queue process where it is assumed that $Q_{0}=0$. Assume that the queue evolves according to

Let $\mathrm{E}\left[Q(s,t)\right]=\int_{s}^{t}\mathrm{E}\left[Q_{u}\right]du/(t-s)$ where $t>s$ and $\mathrm{E}\left[\cdot\right]$ denotes expectation. Let $\mathrm{E}\left[Q\right]=\lim_{t\rightarrow\infty}\mathrm{E}\left[Q(0,t)\right]$ and note that this is limit is not guaranteed to exist (and may tend to infinity). The mean arrival rate at time $t$ is $\lambda_{t}=\mathrm{E}\left[A_{t}\right]$ and the overall mean arrival rate $\lambda=\lim_{T\rightarrow\infty}\int_{0}^{T}\lambda_{t}/Tdt$. If $\lambda>1$ then $\rho>1$ and the queue must eventually grow to infinity regardless of the details of the arrival process.

This theorem can be restated as: if an infinite buffer queuing model is driven by a a single on/off source with i.i.d. heavy-tailed on periods then the expected queue length is either zero (if $a\leq 1$) or infinite. This remains true even if the utilisation – $\rho\in(0,1)$ defined as the proportion of the time the server is busy, is much less than one (the queue is empty for an arbitrarily high proportion of the time). It may seem paradoxical that a queue which is empty arbitrarily often can have an infinite expected length. However, this has parallels with the classical Pollaczek–Khinchine formula for an M/G/1 queue [5] where a server with an infinite variance in the service time has an infinite expected queue length even if the mean service time is arbitrarily small and the queue empty an arbitrarily large proportion of the time.

Note that for $\alpha<1$ the mean length of an on period will not converge and such processes will not, in general, be useful for a queuing system. However, for $1<\alpha<2$ the mean length of an on period will be finite and such a process could be used to produce a time series with a known Hurst parameter.

A similar result holds for discrete time on-off arrival processes $\{A_{n}:n\in\mathbb{N}\}$ with heavy-tailed on periods . However, the result is not true, for example, if the queue is driven by two or more heavy-tailed sources each of which has an arrival rate less than one but together having an arrival rate over one. Processes such as fractional Gaussian noise exhibit LRD but have a finite expected queue length in an infinite buffer. In fact the theorem has an obvious corollary.

It should be noted that heavy-tailed arrival processes of the type from Theorem 1 which give rise to a finite value of $\mathrm{E}\left[Q\right]$ are possible but paradoxically these have an arrival rate $\lambda=0$. For example, let $q>0$ and let every on period of length $X_{i}$ (at rate $a$) be followed by an off period of length $\max((a-1)X_{i},(a-1)aX_{i}^{2}/2q-X_{i})$. The queue drains completely in every off period and the mean queue size for that on period and off period is at most $q$ (with equality attained when $((a-1)aX_{i}^{2}/2q-X_{i})\geq(a-1)X_{i}$) and therefore $\mathrm{E}\left[Q\right]\leq q$. However, in the heavy-tailed case, $\mathrm{E}\left[X_{i}^{2}\right]$ does not converge and hence neither does the expected length of an off period . This implies a proportion of time in the off period tending to one and a mean arrival rate $\lambda$ of zero.

It might still be argued that real traffic traces have this property but the outcome of infinite queue size is not seen in real life because they are fed to a finite sized array. This possibility will be investigated in section 4.

CAIDA data: This data set is taken from a trace approximately an hour long. It is referred to on the CAIDA website ¹¹1See http://www.caida.org/data/passive/ for more information about this trace. as
20030424-000000-0-anon.pcap.gz and was captured on the 24th April 2003. It was captured on an OC48 link with a rate of 2.45 Gb/s. The first 550,000 packets are used in the analysis here. This trace has a relatively low Hurst parameter $H=0.6$ (see [2]).

Bellcore data: This is a much studied data set and, while certainly not representative of modern traffic, it is included as one of the original traces from [6]. The data here is taken from an August 1989 measurement referred to as BC-pAug89.TL. The data was collected on an Ethernet link²²2See http://ita.ee.lbl.gov/html/contrib/BC.html for more information about this traffic. The first 1,000,000 packets are studied here. This trace has a relatively high Hurst parameter $H=0.8$ (see [2]).

The simulations used in this paper are all based upon an extremely simple queuing model. Packets arrive in a FIFO buffer which never drops packets. The buffer has a given bandwidth $b$ (in bytes/second) – which can be adjusted to give a specific level of utilisation. While the absolute level of the queue changes, the results presented here are not very sensitive to this parameter. A packet of length $l$ bytes takes $l/b$ seconds to depart the queue. If $Q_{t}$ is the queue length in packets at time $t$ and the simulation runs until time $T$ then the mean queue $\overline{Q}$ is evaluated as $\overline{Q}=\int_{0}^{T}Q_{t}/Tdt$ (this integral can be evaluated exactly since $Q_{t}$ is a constant between arrivals and departures from the queue).

This simple model has been used by the first author to assess several the queuing performance of several models which attempt to replicate the statistical nature of Internet traffic. This work is reported in [2]. None of the long-range dependence based models replicated the queuing performance of the real traffic traces they were tuned to match. Such a simple model is, of course, open to much criticism. It does not account for TCP feedback mechanisms. However, if the question being addressed is about an “open loop” model of traffic and whether it replicates the characteristics of real traffic then we should expect both to have the same behaviour at a queue.

The first simulations here consider the theoretical results presents in section 2. The first results show how the infinite expected queue size in the model reveals itself in simulation results. Obviously any experiment with a model of the form in Theorem 1 will produce a finite value for $\overline{Q}$ the mean queue size. However, this finite value will increase as the model is run for longer and longer (up to the numerical accuracy of the model). The value of $\overline{Q}$ generated will (in theory at least – in practice the finite accuracy of computers limits this) increase as the runtime increases. The question may be asked if this is true of real data.

The experiment performed here is to take different sized samples of the real data and to queue those samples with the model from the previous section. The behaviour of the mean queue length versus sample size is investigated. Experiments on LRD are notorious for their high (often theoretically infinite) variability. Here ten replications are performed for each size are used and the mean plotted. In addition error bars of the size of the standard deviation (one standard deviation above and below the mean) are added (standard confidence interval techniques are not applicable in the case of LRD data).

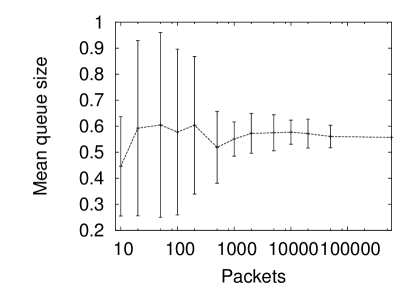
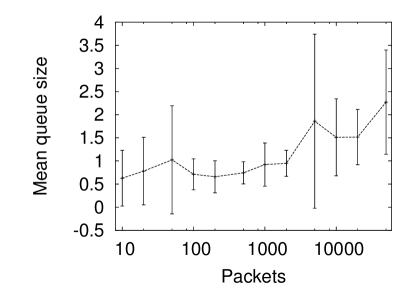
Figure 1 (left) shows the results for the CAIDA data. The x axis shows the number of packets in the sample and the y axis the mean queue size (or rather the mean of the ten means for the ten experiments with that sample size). Since the queue is assumed to start empty then very small sample sizes would naturally have a smaller expected queue. However, beyond this, figure 1 shows no clear influence of the sample size on the expected queue. As the samples get larger the standard deviation bounds from the ten experiments gets smaller. It should be noted that the final (rightmost) point is the whole data set and no error bars can be included.

Figure 1 (right) shows the same experiment but performed on a simulated data set with the same mean arrival rate and the same Hurst parameter using the techniques described in [2] (the Wang model from that paper). The simulation does not well reflect the queuing performance of the trace and this is because of theorem 1 which applies here. In contrast with figure 1 the mean queue size increases with the number of packets in the sample. In addition the error bars (representing one standard deviation either side of the mean) stay as large or become larger.

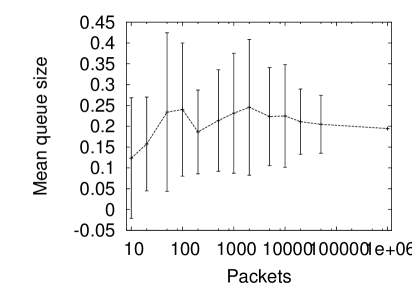
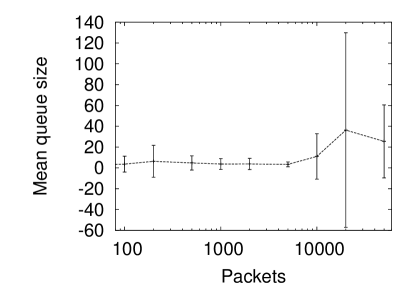
Figure 2 (left) shows the same experiment for the Bellcore data. This data has a higher Hurst parameter and the outcome is less clear. However, remembering that the last point has no error bars (representing the entire data) this figure is not consistent with the idea that the mean queue rises as the length of the sample rises apart from in the early part of the plot. (The rise in the mean and the larger error bars in the center of the plot coincides with a single very large burst of a particular duration).

Figure 2 (right) shows simulated data with the same Hurst parameter and same mean arrival rate as the Bellcore data. As in figure 1 (right) and in accordance with theorem 1 the mean queue size rises with the number of packets simulated (although the connection is certainly not unambiguous). As can be seen, these simulations can be problematic to work with and a researcher looking only at the early part of the graphs could be convinced that they had used sufficiently many packets for the simulation to converge to a good estimation of the mean queue length.

It may be thought that the problem may be connected with the fact that the LRD based methods dramatically overestimated levels of queuing. However, repeating the experiment with lower bandwidth on the real data for both Bellcore and CAIDA traces does not dramatically alter the shape of the graph although obviously the mean queue level increases.

This section takes a different approach by deliberately destroying correlations in the data to see which scales of correlation are important to the queuing properties. It is often stated that LRD is an extremely important property for queuing in real data. If this is the case, then deliberately truncating the correlation beyond a certain scale should have important effect on the queuing.

The experiment performed in this section is to take a certain blocksize $B$ and to split the data into blocks each containing $B$ packets (and associated delays). The order of these blocks is then randomised so no correlation can persist beyond $B$ packets. The entire trace is then queued and the mean queue length recorded. Again ten replications are performed to assess the repeatability.

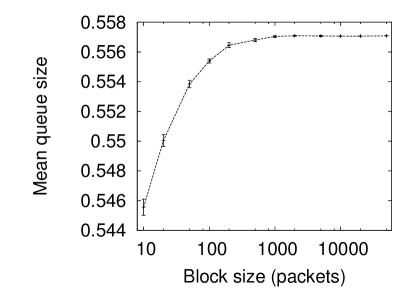
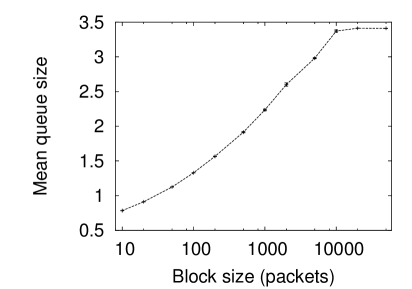
Figure 3 (left) shows this experiment on the CAIDA data. Again there are ten repetitions of each blocksize and the graph shows mean of the means and the standard deviation of the means above and below. Note the small scale on the y axis. Even for very small block sizes the variation in the queuing performance is not great. Beyond a block size of 1,000 the correlation seems unimportant to the queuing performance and the resultant mean queue size is the same to several decimal places.

By contrast, in figure 3 (right) for the LRD simulation all scales of correlation theoretically affect queuing performance (within the bounds implied by the fact that only a finite sample of data is used). Here, the relationship between correlation and queuing is clearly shown. Correlations of block sizes up to 10,000 packets are important to the queuing performance of the simulated data.

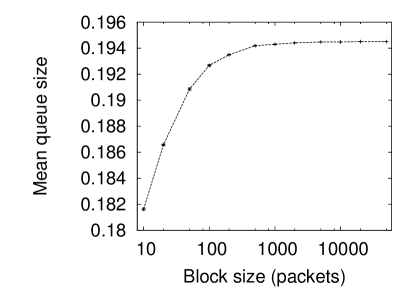
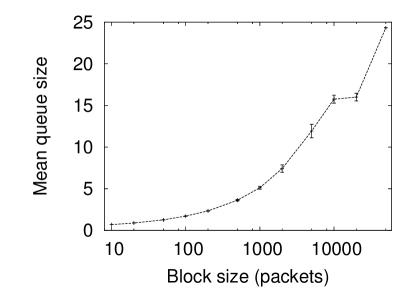
Figure 4 shows the same experiment on the Bellcore data. Again the LRD method used drastically over predicts the level of queuing compared to the real data when the same mean arrival rate and Hurst parameter is used. Again the same result is seen only a small difference in the amount of queuing when the correlations are broken up. The correlations of long time scale are unimportant in the real data but important in the artificial data.

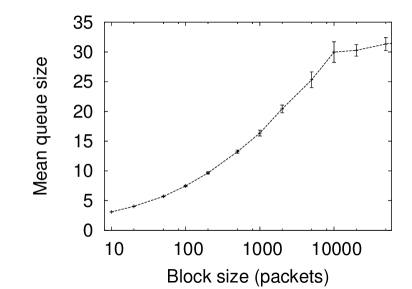
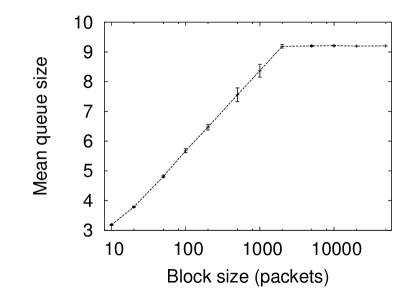
Again the question might be asked would the same conclusion hold true for the real data if the bandwidth used for the experiment were reduced. Figure 5 (left) shows this for the Bellcore data with the bandwidth reduced so the queue occupancy is 5 (right) shows this for the CAIDA data (with an even higher queue occupancy of 0.62). In the CAIDA data there seems to be a very clear transition from important correlation scales (at lengths below 2000 packets) and unimportant correlation scales (above). Indeed this transition is so marked it raises questions about whether something in the data capture process or in the system itself would cause this. In the case of the Bellcore data, more timescales are important but not nearly so many as in the long-range dependent data of figure 4 (right).

The conclusion of this section is clear. The claim that correlations over long scales is important to queuing behaviour is not true of the CAIDA data and arguably true of the Bellcore data only when the system occupancy is extremely high.

This paper criticises long-range dependence as a useful model for packet traffic. Firstly, a theoretical problem with a class of models used to simulate LRD is shown. This class of models predicts either no queuing or an infinite expected queue length when fed into an infinite buffer. At the very least, experimenters should be aware of this problem to ensure that simulations are not affected by it (the answer given by the simulation is a product of the runtime of the simulation rather than a stable reflection of queuing performance). The effect is shown to be different to the queuing performance of real traffic. In the second part of the paper it is shown using simulated queuing on real traffic that for real traffic traces long-range correlations are not important for queuing behaviour except with extremely high traffic. These results should be replicated on more traffic traces to work out how general this conclusion is.