textcompSymbol №not provided \WarningFilterbabelNo Cyrillic
Cross-Lingual Word Embedding Refinement by Norm Optimisation
Аннотация
Cross-Lingual Word Embeddings (CLWEs) encode words from two or more languages in a shared high-dimensional space in which vectors representing words with similar meaning (regardless of language) are closely located. Existing methods for building high-quality CLWEs learn mappings that minimise the norm loss function. However, this optimisation objective has been demonstrated to be sensitive to outliers. Based on the more robust Manhattan norm (aka. norm) goodness-of-fit criterion, this paper proposes a simple post-processing step to improve CLWEs. An advantage of this approach is that it is fully agnostic to the training process of the original CLWEs and can therefore be applied widely. Extensive experiments are performed involving ten diverse languages and embeddings trained on different corpora. Evaluation results based on bilingual lexicon induction and cross-lingual transfer for natural language inference tasks show that the refinement substantially outperforms four state-of-the-art baselines in both supervised and unsupervised settings. It is therefore recommended that this strategy be adopted as a standard for CLWE methods.
1 Introduction
Cross-Lingual Word Embedding (CLWE) techniques have recently received significant attention as an effective means to support Natural Language Processing applications for low-resource languages, e.g., machine translation (Artetxe et al., 2018b) and transfer learning (Peng et al., 2021).
The most successful CLWE models are the so-called projection-based methods, which learn mappings between monolingual word vectors with very little, or even zero, cross-lingual supervision (Lample et al., 2018; Artetxe et al., 2018a; Glavaš et al., 2019). Mainstream projection-based CLWE models typically identify orthogonal mappings by minimising the topological dissimilarity between source and target embeddings based on loss (aka. Frobenius loss or squared error) Glavaš et al. (2019); Ruder et al. (2019). This learning strategy has two advantages. First, adding the orthogonality constraint to the mapping function has been demonstrated to significantly enhance the quality of CLWEs (Xing et al., 2015). Second, the existence of a closed-form solution to the optima (Schönemann, 1966) greatly simplifies the computation required (Artetxe et al., 2016; Smith et al., 2017).
Despite its popularity, work in various application domains has noted that loss is not robust to noise and outliers. It is widely known in computer vision that -loss-based solutions can severely exaggerate noise, leading to inaccurate estimates (Aanaes et al., 2002; De La Torre and Black, 2003). In data mining, Principal Component Analysis (PCA) using loss has been shown to be sensitive to the presence of outliers in the input data, degrading the quality of the feature space produced (Kwak, 2008). Previous studies have demonstrated that the processes used to construct monolingual and cross-lingual embeddings may introduce noise (e.g. via reconstruction error (Allen and Hospedales, 2019) and structural variance (Ruder et al., 2019)), making the presence of outliers more likely. Empirical analysis of CLWEs also demonstrates that more distant word pairs (which are more likely to be outliers) have more influence on the behaviour of loss than closer pairs. This raises the question of the appropriateness of loss functions for CLWEs.
Compared to the conventional loss, loss (aka. Manhattan distance) has been mathematically demonstrated to be less affected by outliers (Rousseeuw and Leroy, 1987) and empirically proven useful in computer vision and data mining (Aanaes et al., 2002; De La Torre and Black, 2003; Kwak, 2008). Motivated by this insight, our paper proposes a simple yet effective post-processing technique to improve the quality of CLWEs: adjust the alignment of any cross-lingual vector space to minimise the loss without violating the orthogonality constraint. Specifically, given existing CLWEs, we bidirectionally retrieve bilingual vectors and optimise their Manhattan distance using a numerical solver. The approach can be applied to any CLWEs, making the post-hoc refinement technique generic and applicable to a wide range of scenarios. We believe this to be the first application of loss to the CLWE problem.
To demonstrate the effectiveness of our method, we select four state-of-the-art baselines and conduct comprehensive evaluations in both supervised and unsupervised settings. Our experiments involve ten languages from diverse branches/families and embeddings trained on corpora of different domains. In addition to the standard Bilingual Lexicon Induction (BLI) benchmark, we also investigate a downstream task, namely cross-lingual transfer for Natural Language Inference (NLI). In all setups tested, our algorithm significantly improves the performance of strong baselines. Finally, we provide an intuitive visualisation illustrating why loss is more robust than it counterpart when refining CLWEs (see Fig. 1). Our code is available at https://github.com/Pzoom522/L1-Refinement.
Our contribution is three-fold: (1) we propose a robust refinement technique based on the norm training objective, which can effectively enhance CLWEs; (2) our approach is generic and can be directly coupled with both supervised and unsupervised CLWE models; (3) our refinement algorithm achieves state-of-the-art performance for both BLI and cross-lingual transfer for NLI tasks.
2 Related Work
CLWE methods.
One approach to generating CLWEs is to train shared semantic representations using multilingual texts aligned at sentence or document level (Vulić and Korhonen, 2016; Upadhyay et al., 2016). Although this research direction has been well studied, the parallel setup requirement for model training is expensive, and hence impractical for low-resource languages.
Recent years have seen an increase in interest in projection-based methods, which train CLWEs by finding mappings between pretrained word vectors of different languages Mikolov et al. (2013); Lample et al. (2018); Peng et al. (2020). Since the input embeddings can be generated independently using monolingual corpora only, projection-based methods reduce the supervision required for training and offer a viable solution for low-resource scenarios.
Xing et al. (2015) showed that the precision of the learned CLWEs can be improved by constraining the mapping function to be orthogonal, which is formalised as the so-called Orthogonal Procrustes Analysis (OPA):
| (1) |
where is the CLWE mapping, denotes the orthogonal manifold (aka. the Stiefel manifold (Chu and Trendafilov, 2001)), and and are matrices composed using vectors from source and target embedding spaces.
While Xing et al. (2015) exploited an approximate and relatively slow gradient-based solver, more recent approaches such as Artetxe et al. (2016) and Smith et al. (2017) introduced an exact closed-form solution for Eq. (1). Originally proposed by Schönemann (1966), it utilises Singular Value Decomposition (SVD):
| (2) |
where denotes the -optimal mapping matrix. The efficiency and effectiveness of Eq. (2) have led to its application within many other approaches, e.g., Ruder et al. (2018), Joulin et al. (2018) and Glavaš et al. (2019). In particular, Proc-B (Glavaš et al., 2019), a supervised CLWE framework that simply applies multiple iterations of OPA, has been demonstrated to produce very competitive performance on various benchmark tasks including BLI as well as cross-lingual transfer for NLI and information retrieval.
While the aforementioned approaches still require some weak supervision (i.e., seed dictionaries), there have also been some successful attempts to train CLWEs in a completely unsupervised fashion. For instance, Lample et al. (2018) proposed a system called Muse, which bootstraps CLWEs without any bilingual signal through adversarial learning. VecMap (Artetxe et al., 2018a) applied a self-learning strategy to iteratively compute the optimal mapping and then retrieve bilingual dictionary. Comparing Muse and VecMap, the latter tends to be more robust as its similarity-matrix-based heuristic initialisation is more stable in most cases (Glavaš et al., 2019; Ruder et al., 2019). Very recently, some studies bootstrapped unsupervised CLWEs by jointly training word embeddings on concatenated corpora of different languages and achieved good performance Wang et al. (2020).
The refinement algorithm.
CLWE models often apply refinement, a post-processing step shown to improve the quality of the initial alignment (see Ruder et al. (2019) for survey). Given existing CLWEs , for languages and , bidirectionally one can use approaches such as the classic nearest-neighbour algorithm, the inverted softmax (Smith et al., 2017) and the cross-domain similarity local scaling (CSLS) (Lample et al., 2018) to retrieve two bilingual dictionaries and . Note that word pairs in are highly reliable, as they form ‘‘mutual translations’’. Next, one can compose bilingual embedding matrices and by aligning word vectors (rows) using the above word pairs. Finally, a new orthogonal mapping is learned to fit and based on least-square regressions, i.e., perform OPA described in Eq. (1).
Early applications of refinement applied a single iteration, e.g. Vulić and Korhonen (2016). Due to the wide adoption of the closed-form OPA solution (cf. Eq. (2)), recent methods perform multiple iterations. The iterative refinement strategy is an important component of approaches that bootstrap from small or null training lexicons (Artetxe et al., 2018a). However, a single step of refinement is often sufficient to create suitable CLWEs (Lample et al., 2018; Glavaš et al., 2019).
3 Methodology
A common characteristic of CLWE methods that apply the orthogonality constraint is that they optimise using loss (see § 2). However, outliers have disproportionate influence in since the penalty increases quadratically and this can be particularly problematic with noisy data since the solution can ‘‘shift’’ towards them (Rousseeuw and Leroy, 1987). The noise and outliers present in real-world word embeddings may affect the performance of -loss-based CLWEs.
The norm cost function is more robust than loss as it is less affected by outliers (Rousseeuw and Leroy, 1987). Therefore, we propose a refinement algorithm for improving the quality of CLWEs based on loss. This novel method, which we refer to as refinement, is generic and can be applied post-hoc to improve the output of existing CLWE models. To our knowledge, the use of alternatives to -loss-based optimisation has never been explored by the CLWE community.
To begin with, analogous to OPA (cf. Eq. (1)), OPA can be formally defined and rewritten as
| (3) |
where returns the matrix trace, is the signum function, and denotes that is subject to the orthogonal constraint. Compared to OPA which has a closed-form solution, solving Eq. (3) is much more challenging due to the discontinuity of . This issue can be addressed by replacing with , a smoothing function parameterised by , such that
| (4) |
Larger values for lead to closer approximations to but reduce the smoothing effect. This approach has been used in many applications, such as the activation function of long short-term memory networks (Hochreiter and Schmidhuber, 1997).
However, in practice, we find that Eq. (4) remains unsolvable in our case with standard gradient-based frameworks for two reasons. First, has to be sufficiently large in order to achieve a good approximation of . Otherwise, relatively small residuals will be down-weighted during fitting and the objective will become biased towards outliers, just similar to loss. However, satisfying this requirement (i.e., large ) will lead to the activation function becoming easily saturated, resulting in an optimisation process that becomes trapped during the early stages. In other words, the optimisation can only reach an unsatisfactory local optimum. Second, the orthogonality constraint (i.e., ) also makes the optimisation more problematic for these methods.
We address these challenges by adopting the approaches proposed by Trendafilov (2003). This method explicitly encourages the solver to only explore the desired manifold thereby reducing the solver’s search space and difficulty of the optimisation problem. We begin by calculating the gradient w.r.t. the objective in Eq. (4) through matrix differentiation:
| (5) |
where and is the Hadamard product. Next, to find the steepest descent direction while ensuring that any produced is orthogonal, we project onto , yielding111See Chu and Trendafilov (2001) for derivation details.
| (6) |
Here is an identity matrix with the shape of . With Eq. (6) defining the optimisation flow, our loss minimisation problem reduces to an integration problem, as
| (7) |
where is a proper initial solution of Eq. (3) (e.g., -optimal mapping obtained via Eq. (2)).
Empirically, unlike the aforementioned standard gradient-based methods, by following the established policy of Eq. (6), the optimisation process of Eq. (7) will not violate the orthogonality restriction or get trapped during early stages. However, this OPA solver requires extremely small step size to generate reliable solutions (Trendafilov, 2003), making it computationally expensive222It takes averagely 3 hours and up to 12 hours to perform Eq. (7) on an Intel Core i9-9900K CPU. In comparison, the time required to solve Eq. (2) in each training loop is less than 1 second and the iterative -norm-based training takes 1 to 5 hours in total.. Therefore, it is impractical to perform refinement in an iterative fashion like refinement without significant computational resources.
Previous work has demonstrated that applying the -loss-based algorithms from a good initial state can speed up the optimisation. For instance, Kwak (2008) found that feature spaces created by PCA were severely affected by noise. Replacing the cost function with loss significantly reduced this problem, but required expensive linear programming. To reduce the convergence time, Brooks and Jot (2013) exploited the first principal component from the solution as an initial guess. Similarly, when reconstructing corrupted pixel matrices, -loss-based results are far from satisfactory; using norm estimators can improve the quality, but are too slow to handle large-scale datasets Aanaes et al. (2002). However, taking the optima as the starting point allowed less biased reconstructions to be learned in an acceptable time De La Torre and Black (2003).
Inspired by these works, we make use of refinement to carry out post-hoc enhancement of existing CLWEs. Our full pipeline is described in Algorithm 1 (see § 4.3 for implemented configurations). In common with refinement (cf. § 2), steps 1-4 bootstrap a synthetic dictionary and compose bilingual word vector matrices and which have reliable row-wise correspondence. Taking them as the starting state, in step 5 an identity matrix naturally serves as our initial solution .
During the execution of Eq. (7), we record loss per iteration and see if either of the following two stopping criteria have been satisfied: (1) the updated loss exceeds that of the previous iteration; (2) on-the-fly has non-negligibly departed from the orthogonal manifold, which can be indicated by the maximum value of the disparity matrix as
| (8) |
where is a sufficiently small threshold. The resulting can be used to adjust the word vectors of and output refined CLWEs.
A significant advantage of our algorithm is its generality: it is fully independent of the method used for creating the original CLWEs and can therefore be used to enhance a wide range of models, both in supervised and unsupervised settings.
4 Experimental Setup
4.1 Datasets
In order to demonstrate the generality of our proposed method, we conduct experiments using two groups of monolingual word embeddings trained on very different corpora:
Wiki-Embs (Grave et al., 2018): embeddings developed using Wikipedia dumps for a range of ten diverse languages: two Germanic (Englishen, Germande), two Slavic (Croatianhr, Russianru), three Romance (Frenchfr, Italianit, Spanishes) and three non-Indo-European (Finnishfi from the Uralic family, Turkishtr from the Turkic family and Chinesezh from the Sino-Tibetan family).
News-Embs (Artetxe et al., 2018a): embeddings trained on a multilingual News text collection, i.e., the WaCKy Crawl of , the Common Crawl of fi, and the WMT News Crawl of es.
News-Embs are considered to be more challenging for building good quality CLWEs due to the heterogeneous nature of the data, while a considerable portion of the multilingual training corpora for Wiki-Embs are roughly parallel. Following previous studies (Lample et al., 2018; Artetxe et al., 2018a; Zhou et al., 2019; Glavaš et al., 2019), only the first 200K vocabulary entries are preserved.
4.2 Baselines
Glavaš et al. (2019) provided a systematic evaluation for projection-based CLWE models, demonstrating that three methods (i.e., Muse, VecMap, and Proc-B) achieve the most competitive performance. A recent algorithm (JA) by Wang et al. (2020) also reported state-of-the-art results. For comprehensive comparison, we therefore use all these four methods as the main baselines for both supervised and unsupervised settings:
Muse (Lample et al., 2018): an unsupervised CLWE model based on adversarial learning and iterative refinement;
VecMap (Artetxe et al., 2018a): a robust unsupervised framework using a self-learning strategy;
Proc-B (Glavaš et al., 2019): a simple but effective supervised approach to creating CLWEs;
JA-Muse and JA-RCSLS Wang et al. (2020): a recently proposed Joint-Align (JA) Framework, which first initialises CLWEs using joint embedding training, followed by vocabularies reallocation. It then utilises off-the-shelf CLWE methods to improve the alignment in both unsupervised (JA-Muse) and supervised (JA-RCSLS) settings.
In the original implementations, Muse, Proc-B and JA were only trained on Wiki-Embs while VecMap additionally used News-Embs. Although all baselines reported performance for BLI, they used various versions of evaluation sets, hence previous results are not directly comparable with the ones reposted here. More concretely, the testsets for Muse/JA and VecMap are two different batches of en-centric dictionaries, while the testset for Proc-B also supports non-en translations.
4.3 Implementation Details of Algorithm 1
The CSLS scheme with a neighbourhood size of 10 (CSLS-10) is adopted to build synthetic dictionaries via the input CLWEs. A variable-coefficient ordinary differential equation (VODE) solver333http://www.netlib.org/ode/vode.f was implemented for the system described in Eq. (7). Suggested by Trendafilov (2003), we set the maximum order at 15, the smoothness coefficient in Eq. (5) at 1e8, the threshold in Eq. (8) at 1e-5, and performed the integration with a fixed time interval of 1e-6. An early-stopping design was adopted to ensure computation completed in a reasonable time: in addition to the two default stopping criteria in § 3, integration is terminated if reaches 5e-3 ( is the differentiation term in Eq. (7)).
In terms of the tolerance of the VODE solver, we set the absolute tolerance at 1e-7 and the relative tolerance at 1e-5, following the established approach of Kulikov (2013). These tolerance settings show good generality empirically and were used for all tested language pairs, datasets, and models in our experiments.
| en–de | en–es | en–fr | en–ru | en–zh | |
|---|---|---|---|---|---|
| Muse \ETX | 74.0 | 81.7 | 82.3 | 44.0 | 32.5 |
| Muse- | 74.0 | 82.1 | 82.6 | *43.8* | *31.9* |
| \hdashlineMuse- | 75.2 | 82.6 | 82.9 | *45.6* | *33.8* |
| JA-Muse \EOT | 74.2 | 81.4 | 82.8 | 45.0 | 36.1 |
| JA-Muse- | 74.1 | 81.6 | 82.7 | 45.1 | 36.2 |
| \hdashlineJA-Muse- | 75.4 | 82.0 | 83.1 | 46.3 | 38.1 |
| VecMap \ENQ | 75.1 | 82.3 | 80.0 | 49.2 | 00.0 |
| VecMap- | 74.8 | 82.3 | 79.4 | 48.9 | 00.0 |
| \hdashlineVecMap- | 75.4 | 82.9 | 80.2 | 49.9 | 00.0 |
| en–de | en–es | en–fi | en–it | |
|---|---|---|---|---|
| Muse \ETX | 00.0 | 07.1 | 00.0 | 09.1 |
| Muse- | 00.0 | 00.0 | 00.0 | 00.0 |
| \hdashlineMuse- | 00.0 | 00.0 | 00.0 | 00.0 |
| JA-Muse | 47.9 | 48.4 | 33.0 | 37.2 |
| JA-Muse- | 47.9 | 48.6 | 32.9 | 37.3 |
| \hdashlineJA-Muse- | 48.8 | 49.7 | 35.2 | 37.7 |
| VecMap \ETX | 48.2 | 48.1 | 32.6 | 37.3 |
| VecMap- | 48.1 | 47.9 | 32.9 | 37.1 |
| \hdashlineVecMap- | 49.0 | 48.9 | 34.4 | 37.8 |
| en–de | en–fi | en–fr | en–hr | en–it | en–ru | en–tr | |
|---|---|---|---|---|---|---|---|
| JA-RCSLS | 50.9 | 33.9 | 63.0 | 29.1 | 58.3 | 41.3 | 29.4 |
| JA-RCSLS- | 50.7 | 33.8 | 63.0 | 29.1 | 58.2 | 41.3 | 29.5 |
| \hdashlineJA-RCSLS- | 51.6 | 34.5 | 63.4 | 30.4 | 59.0 | 41.9 | 30.2 |
| Proc-B \ETX | 52.1 | 36.0 | 63.3 | 29.6 | 60.5 | 41.9 | 30.1 |
| Proc-B- | 51.8 | 34.4 | 63.1 | 28.2 | 60.5 | 39.8 | 28.0 |
| \hdashlineProc-B- | 52.6 | 36.3 | 63.7 | 30.5 | 60.5 | 42.3 | 30.9 |
| en–de | en–fi | en–it | |
|---|---|---|---|
| JA-RCSLS | 46.8 | 42.0 | 37.4 |
| JA-RCSLS- | 46.9 | 42.2 | 37.5 |
| \hdashlineJA-RCSLS- | 48.3 | 44.6 | 39.0 |
| Proc-B | 47.5 | 41.4 | 37.3 |
| Proc-B- | 47.1 | 41.7 | 37.4 |
| \hdashlineProc-B- | 52.6 | 43.3 | 41.1 |
5 Results
We evaluate the effectiveness of the proposed refinement technique on two benchmarks: Bilingual Lexicon Induction (BLI), the de facto standard for measuring the quality of CLWEs, and a downstream natural language inference task based on cross-lingual transfer. In addition to comparison against state-of-the-art CLWE models, we also report the performance of the single-iteration refinement method which follows steps 1-4 of Algorithm 1 then minimises loss in the final step.
To reduce randomness, we executed each model in each setup three times and the average accuracy (ACC, aka. precision at rank 1) is reported. Following Glavaš et al. (2019), by comparing scores achieved before and after refinement, statistical significance is indicated via the -value of two-tailed t-tests with Bonferroni correction (Dror et al., 2018) (note that -values are not recorded for Tab. 2(b) given the small number of runs).
5.1 Bilingual Lexicon Induction
Refining unsupervised baselines.
Tab. 1(a) follows the main setup of Lample et al. (2018), who tested six language pairs using Wiki-Embs444Note that we are unable to report the result of English to Esperanto as the corresponding dictionary is missing, see https://git.io/en-eo-dict-issue.. After refinement, Muse-, JA-Muse-, and VecMap- all significantly () outperform their corresponding base algorithms, with an average 1.1% performance gain over Muse, 1.1% over JA-Muse, and 0.5% over VecMap. To put these improvements in context, Heyman et al. (2019) reported an improvement of 0.4% for VecMap on same dataset and language pairs.
Our method tends to work better on the more distant language pairs. For instance, for the distant pairs en–, the increments achieved by Muse- are 1.6% and 1.3%, respectively; whereas for the close pairs en– the average gain is a maximum of 0.9%. A similar trend can be observed for JA-Muse- and VecMap-. (As the VecMap algorithm always collapses for en–zh, no result is reported for this language pair).
Another set of experiments were conducted to evaluate the robustness of our algorithm following the main setup of Artetxe et al. (2018a), who tested four language pairs based on the more homogeneous News-Embs. Tab. 1(b) shows that JA-Muse- and VecMap- consistently improves the original VecMap with an average gain of 1.2% and 1.0% (<0.01). Obtaining such substantial improvements over the state-of-the-art is nontrivial. For example, even a very recent weakly supervised method by Wang et al. (2019) is inferior to VecMap by 1.0% average ACC. On the other hand, Muse fails to produce any analysable result as it always collapses on the more challenging News-Embs. Improvement with refinement is also larger when language pairs are more distant, e.g., for VecMap- the ACC gain on en-fi is 1.8%, more than double of the gain (0.7%) on the close pairs en– (cf. Tab. 1(a) and above).
We also conduct an ablation study by reporting the performance of refinement scheme (-). This observation is in accordance with that of Lample et al. (2018), who reported that after performing refinement in the first loop, applying further iterations only produces marginal precision gain, if any.
Overall, the refinement consistently and significantly improve the CLWEs produced by base algorithms, regardless of the embeddings and setups used, thereby demonstrating the effectiveness and robustness of the proposed algorithm.
| Unsupervised | de–it | de–tr | fi–hr | fi–it | hr–ru | it–fr | tr–it |
| ICP\ETX | 44.7 | 21.5 | 20.8 | 26.3 | 30.9 | 62.9 | 24.3 |
| GWA\ETX | 44.0 | 10.1 | 00.9 | 17.3 | 00.1 | 65.5 | 14.2 |
| Muse \ETX | 49.6 | 23.7 | 22.8 | 32.7 | 00.0 | 66.2 | 30.6 |
| Muse- | 50.3 | 23.9 | 23.1 | 32.7 | 34.9 | 67.1 | *30.5* |
| \hdashlineMuse- | 50.7 | 26.5 | 25.4 | 35.0 | 37.9 | 67.6 | *33.3* |
| JA-Muse | 50.9 | 25.6 | 23.4 | 34.9 | 36.9 | 68.3 | 34.7 |
| JA-Muse- | 50.9 | 25.5 | 23.4 | 34.7 | 36.9 | 68.4 | 34.7 |
| \hdashlineJA-Muse- | 51.5 | 28.4 | 26.1 | 36.0 | 37.6 | 68.7 | 36.1 |
| VecMap \ETX | 49.3 | 25.3 | 28.0 | 35.5 | 37.6 | 66.7 | 33.2 |
| VecMap- | 48.8 | 25.7 | 28.5 | 35.8 | 38.4 | 67.0 | 33.5 |
| \hdashlineVecMap- | 50.1 | 28.2 | 30.3 | 37.1 | 40.1 | 67.6 | 35.9 |
| Supervised | |||||||
| DLV\ETX | 42.0 | 16.7 | 18.4 | 24.4 | 26.4 | 58.5 | 20.9 |
| RCSLS\ETX | 45.3 | 20.1 | 21.4 | 27.2 | 29.1 | 63.7 | 24.6 |
| JA-RSCLS | 46.6 | 20.9 | 22.1 | 29.0 | 29.9 | 65.2 | 25.3 |
| JA-RSCLS- | 46.4 | 20.8 | 22.3 | 29.0 | 29.8 | 65.2 | 25.3 |
| \hdashlineJA-RSCLS- | 47.3 | 22.2 | 23.8 | 30.1 | 31.2 | 65.9 | 26.6 |
| Proc-B \ETX | 50.7 | 25.0 | 26.3 | 32.8 | 34.8 | 66.5 | 29.8 |
| Proc-B- | 50.0 | 24.1 | 25.6 | 31.8 | 34.3 | 66.4 | 29.6 |
| \hdashlineProc-B- | 51.1 | 25.6 | 26.9 | 33.6 | 35.0 | 67.4 | 30.5 |
Refining supervised baselines.
To test the generalisability of our method, we also applied it on state-of-the-art supervised CLWE models: Proc-B Glavaš et al. (2019) and JA-RCSLS Wang et al. (2020). Following the setup of Glavaš et al. (2019), we learn mappings using Wiki-Embs and 1K training splits of their dataset.
Their evaluation code retrieves bilingual word pairs using the classic nearest-neighbour algorithm and outputs the Mean Reciprocal Rank (MRR). As shown in Tab. 2(a), both JA-RCSLS- and Proc-B- outperform the baseline algorithms for all language pairs (with the exception of en–it where the score of Proc-B is unchanged) with an average improvement of 0.9% and 0.5%, respectively (<0.01).
JA-RCSLS- and Proc-B- were also tested using News-Embs with results shown in Tab. 2(b)555Note that results for en–es is not included, as no en–es dictionary is provided in Glavaš et al. (2019)’s dataset.. refinement achieves an impressive improvement for both close (en–) and distant (en–fi) language pairs: average gain of 1.9% and 3.9% respectively and over 5% for en–de (Proc-B-) in particular. The refinement does not benefit the supervised baseline, similar to the lack of improvement observed in the unsupervised setups.
Comparison of unsupervised and supervised settings.
This part provides a comparison of the effectiveness of refinement in unsupervised and supervised scenarios. Unlike previous experiments where only alignments involving English were investigated, these tests focus on non-en setups. Glavaš et al. (2019)’s dataset is used to construct seven representative pairs which cover every category of etymological combination, i.e., intra-language-branch –ru, it–, inter-language-branch –, and inter-language-family –tr, fi–hr, fi–it, tr–. The 1K training splits are used as seed lexicons in supervised runs. Apart from our main baselines, we further report the results of several other competitive CLWE models: Iterative Closest Point Model (ICP, Hoshen and Wolf, 2018), Gromov-Wasserstein Alignment Model (GWA, Alvarez-Melis and Jaakkola, 2018), Discriminative Latent-Variable Model (DLV, Ruder et al., 2018) and Relaxed CSLS Model (RCSLS, Joulin et al., 2018).
Results shown in Tab. 3 demonstrate that the main baselines (Muse, JA-Muse, VecMap, JA-RCSLS, and Proc-B) outperform these other models by a large margin. For all these main baselines, post applying refinement improves the mapping quality for all language pairs (), with average improvements of 1.7%, 1.4%, 1.8%, 1.1%, and 0.8%, respectively. Consistent with findings in the previous experiments, refinement does not enhance performance. Improvement with refinement is higher when language pairs are more distant, e.g., for all inter-language-family pairs such as fi–hr and tr–it, even the minimum improvement of Muse- over Muse is 2.3%.
Comparing unsupervised and supervised approaches, it can be observed that Muse, JA-Muse and VecMap achieve higher overall gain with refinement than JA-RCSLS and Proc-B, where JA-Muse- and VecMap- give the best overall performance. One possible explanation to this phenomenon is that there is only a single source of possible noise in unsupervised models (i.e. the embedding topology) but for supervised methods noise can also be introduced via the seed lexicons. Consequently unsupervised approaches drive more benefit from refinement, which reduces the influence of topological outliers in CLWEs.
Topological behaviours of and refinement.
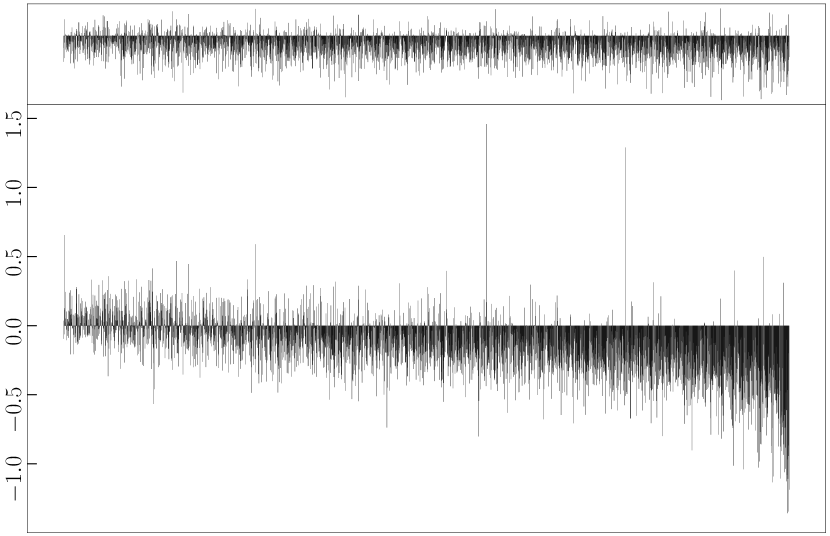
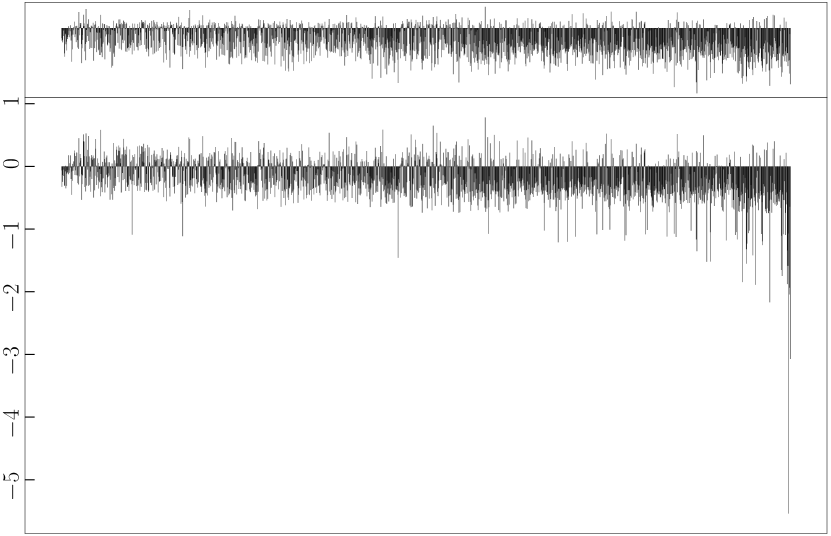
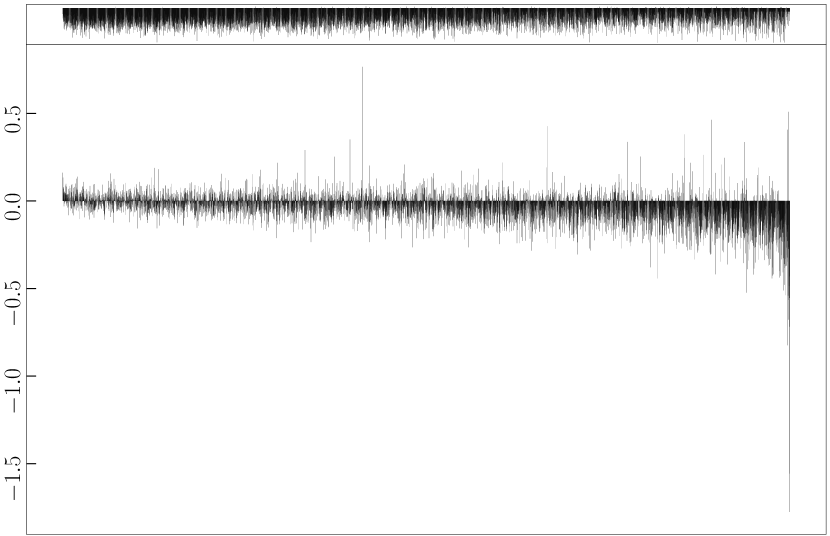
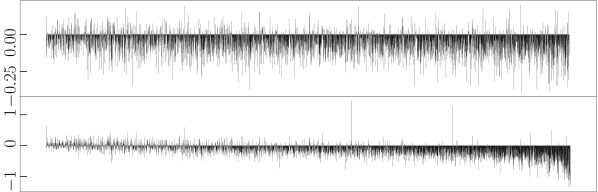
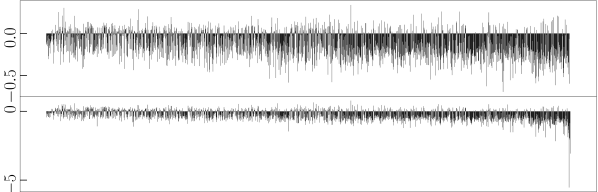
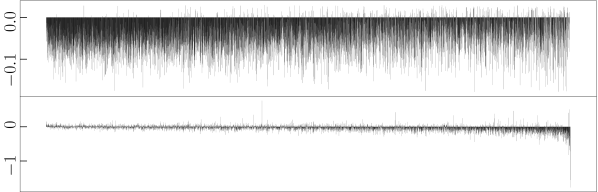
To validate our assumption that refinement is more sensitive to outliers while its counterpart is more robust, we analyse how each refinement strategy changes the distance between bilingual word vector pairs in the synthetic dictionary (cf. Algorithm 1) constructed from trained CLWE models. Specifically, for each word vector pair we subtract its post-refinement distance from the original distance (i.e., without applying additional or refinement step). Fig. 1 shows visualisation examples for three algorithms and language pairs, where each bar represents one word pair. It can be observed that refinement effectively reduces the distance for most word pairs, regardless of their original distance (i.e., indicated by bars with negative values in the figures). The conventional refinement strategy, in contrast, exhibits very different behaviour and tends to be overly influenced by word pairs with large distance (i.e. by outliers). The reason for this is that the -norm penalty increases quadratically, causing the solution to put much more weight on optimising distant word pairs (i.e., word pairs on the right end of the X-axis show sharp distance decrements). This observation is in line with Rousseeuw and Leroy (1987) and explains why loss performs substantially stronger than loss in the refinement.
Case study.
After aligning en-ru embeddings with unsupervised Muse, we measured the distance between vectors corresponding to the ground-truth dictionary of Lample et al. (2018) (cf. Fig. 1(a)). We then detected large outliers by finding vector pairs whose distance falls above , where and respectively denote the lower and upper quartile based on the popular Inter-Quartile Range Hoaglin et al. (1986). We found that many of the outliers correspond to polysemous entries, such as {state (2 noun meanings and 1 verb meaning), состояние (only means status)}, {type (2 nominal meanings and 1 verb meaning), тип (only means kind)}, and {film (5 noun meanings), фильм (only means movie)}. We then re-perform -based mapping after removing these vector pairs, observing that the accuracy jumps to 45.9% (cf. the original -norm alignment it is 43.8% and after refinement it is 45.6%, cf. Tab. 1). This indicates that although all baselines already make use of preprocessing steps including vector normalization, outlier issues still exist and harms the norm CLWEs. However, they can be alleviated by the proposed refinement technique.
5.2 Natural Language Inference
| Unsupervised | en–de | en–fr | en–ru | en–tr |
| ICP\ETX | 58.0 | 51.0 | 57.2 | 40.0 |
| GWA\ETX | 42.7 | 38.3 | 37.6 | 35.9 |
| Muse \ETX | 61.1 | 53.6 | 36.3 | 35.9 |
| Muse- | 61.1 | 53.0 | *57.3* | *48.9* |
| \hdashlineMuse- | 63.5 | 55.3 | *58.9* | *52.3* |
| JA-Muse | 61.3 | 55.2 | 58.1 | 55.0 |
| JA-Muse- | 61.2 | 55.2 | 57.6 | 55.1 |
| \hdashlineJA-Muse- | 62.9 | 57.9 | 59.4 | 57.5 |
| VecMap \ETX | 60.4 | 61.3 | 58.1 | 53.4 |
| VecMap- | 60.3 | 60.6 | 57.7 | 53.5 |
| \hdashlineVecMap- | 61.5 | 63.7 | 60.1 | 56.4 |
| Supervised | ||||
| RCSLS\ETX | 37.6 | 35.7 | 37.8 | 38.7 |
| JA-RSCLS | 50.2 | 48.9 | 51.0 | 51.7 |
| JA-RSCLS- | 50.4 | 48.6 | 50.9 | 51.5 |
| \hdashlineJA-RSCLS- | 51.3 | 50.1 | 53.2 | 52.6 |
| Proc-B \ETX | 61.3 | 54.3 | 59.3 | 56.8 |
| Proc-B- | 61.0 | 54.8 | 58.9 | 55.1 |
| \hdashlineProc-B- | 62.1 | 54.8 | 60.7 | 58.2 |
Finally, we experimented with a downstream NLI task in which the aim is to determine whether a ‘‘hypothesis’’ is true (entailment), false (contradiction) or undetermined (neutral), given a ‘‘premise’’. Higher ACC indicates better encoding of semantics in the tested embeddings. The CLWEs used are those trained with Wiki-Embs for BLI. For Muse, JA-Muse and VecMap, we also obtain CLWEs for en–tr pair with the same configuration.
Following Glavaš et al. (2019), we first train the Enhanced Sequential Inference Model (Chen et al., 2017) based on the large-scale English MultiNLI corpus (Williams et al., 2018) using vectors of language (en) from an aligned bilingual embedding space (e.g., en–de). Next, we replace the vectors with the vectors of language (e.g., de), and directly test the trained model on the language portion of the XNLI corpus (Conneau et al., 2018).
Results in Tab. 4 show that the CLWEs refined by our algorithm yield the highest ACC for all language pairs in both supervised and unsupervised settings. The refinement, on the contrary, is not beneficial overall. Improvements in cross-lingual transfer for NLI exhibit similar trends to those in the BLI experiments, i.e. greater performance gain for unsupervised methods and more distant language pairs, consistent with previous observations Glavaš et al. (2019). For instance, Muse- JA-Muse- and VecMap- outperform their baselines by at least 2% in ACC on average (), whereas the improvements of JA-RSCLS- and Proc-B- over their corresponding base methods are 2% and 2.1% respectively (). For both unsupervised and supervised methods, refinement demonstrates stronger effect for more distant language pairs, e.g., Muse- surpasses Muse by 1.2% for en–fr, whereas a more impressive 2.7% gain is achieved for en–tr.
In summary, in addition to improving BLI performance, our refinement method also produces a significant improvement for a downsteam task (NLI), demonstrating its effectiveness in improving the CLWE quality.
6 Conclusion and Future Work
This paper proposes a generic post-processing technique to enhance CLWE performance based on optimising loss. This algorithm is motivated by successful applications in other research fields (e.g. computer vision and data mining) which exploit the norm cost function since it has been shown to be more robust to noisy data than the commonly-adopted loss. The approach was evaluated using ten diverse languages and word embeddings from different domains on the popular BLI benchmark, as well as a downstream task of cross-lingual transfer for NLI. Results demonstrated that our algorithm can significantly improve the quality of CLWEs in both supervised and unsupervised setups. It is therefore recommended that this straightforward technique be applied to improve performance of CLWEs.
The convergence speed of the optimiser prevented us from performing loss optimisation over multiple iterations. Future work will focus on improving the efficiency of our OPA solver, as well as exploring the application of other robust loss functions within CLWE training strategies.
Ethics Statement
This work provides an effective post-hoc method to improve CLWEs, advancing the state-of-the-art in both supervised and unsupervised settings. Our comprehensive empirical studies demonstrate that the proposed algorithm can facilitate researches in machine translation, cross-lingual transfer learning, etc, which have deep societal impact of bridging cultural gaps across the world.
Besides, this paper introduces and solves an optimisation problem based on an under-explored robust cost function, namely loss. We believe it could be of interest for the wider community as outlier is a long-standing issue in many artificial intelligence applications.
One caveat with our method, as is the case for all word-embedding-based systems, is that various biases may exist in vector spaces. We suggest this problem should always be looked at critically. In addition, our implemented solver can be computationally expensive, leading to increased electricity consumption and the associated negative environmental repercussions.
Acknowledgements
This work is supported by the award made by the UK Engineering and Physical Sciences Research Council (Grant number: EP/P011829/1) and Baidu, Inc. We would also like to express our sincerest gratitude to Guanyi Chen, Ruizhe Li, Xiao Li, Shun Wang, and the anonymous reviewers for their insightful and helpful comments.
Список литературы
- Aanaes et al. (2002) H. Aanaes, R. Fisker, K. Astrom, and J. M. Carstensen. 2002. Robust factorization. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Allen and Hospedales (2019) Carl Allen and Timothy M. Hospedales. 2019. Analogies explained: Towards understanding word embeddings. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA, volume 97 of Proceedings of Machine Learning Research, pages 223–231. PMLR.
- Alvarez-Melis and Jaakkola (2018) David Alvarez-Melis and Tommi Jaakkola. 2018. Gromov-Wasserstein alignment of word embedding spaces. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 1881–1890, Brussels, Belgium. Association for Computational Linguistics.
- Artetxe et al. (2016) Mikel Artetxe, Gorka Labaka, and Eneko Agirre. 2016. Learning principled bilingual mappings of word embeddings while preserving monolingual invariance. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pages 2289–2294, Austin, Texas. Association for Computational Linguistics.
- Artetxe et al. (2018a) Mikel Artetxe, Gorka Labaka, and Eneko Agirre. 2018a. A robust self-learning method for fully unsupervised cross-lingual mappings of word embeddings. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 789–798, Melbourne, Australia. Association for Computational Linguistics.
- Artetxe et al. (2018b) Mikel Artetxe, Gorka Labaka, Eneko Agirre, and Kyunghyun Cho. 2018b. Unsupervised neural machine translation. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net.
- Brooks and Jot (2013) J. Paul Brooks and Sapan Jot. 2013. pcal1 : An implementation in r of three methods for -norm principal component analysis. In Optimization Online preprint.
- Chen et al. (2017) Qian Chen, Xiaodan Zhu, Zhen-Hua Ling, Si Wei, Hui Jiang, and Diana Inkpen. 2017. Enhanced LSTM for natural language inference. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1657–1668, Vancouver, Canada. Association for Computational Linguistics.
- Chu and Trendafilov (2001) Moody T Chu and Nickolay T Trendafilov. 2001. The orthogonally constrained regression revisited. Journal of Computational and Graphical Statistics, pages 746–771.
- Conneau et al. (2018) Alexis Conneau, Ruty Rinott, Guillaume Lample, Adina Williams, Samuel Bowman, Holger Schwenk, and Veselin Stoyanov. 2018. XNLI: Evaluating cross-lingual sentence representations. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 2475–2485, Brussels, Belgium. Association for Computational Linguistics.
- De La Torre and Black (2003) Fernando De La Torre and Michael J Black. 2003. A framework for robust subspace learning. International Journal of Computer Vision.
- Dror et al. (2018) Rotem Dror, Gili Baumer, Segev Shlomov, and Roi Reichart. 2018. The hitchhiker’s guide to testing statistical significance in natural language processing. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1383–1392, Melbourne, Australia. Association for Computational Linguistics.
- Glavaš et al. (2019) Goran Glavaš, Robert Litschko, Sebastian Ruder, and Ivan Vulić. 2019. How to (properly) evaluate cross-lingual word embeddings: On strong baselines, comparative analyses, and some misconceptions. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 710–721, Florence, Italy. Association for Computational Linguistics.
- Grave et al. (2018) Edouard Grave, Piotr Bojanowski, Prakhar Gupta, Armand Joulin, and Tomas Mikolov. 2018. Learning word vectors for 157 languages. In Proceedings of the Eleventh International Conference on Language Resources and Evaluation (LREC 2018), Miyazaki, Japan. European Language Resources Association (ELRA).
- Heyman et al. (2019) Geert Heyman, Bregt Verreet, Ivan Vulić, and Marie-Francine Moens. 2019. Learning unsupervised multilingual word embeddings with incremental multilingual hubs. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 1890–1902, Minneapolis, Minnesota. Association for Computational Linguistics.
- Hoaglin et al. (1986) David C Hoaglin, Boris Iglewicz, and John W Tukey. 1986. Performance of some resistant rules for outlier labeling. Journal of the American Statistical Association.
- Hochreiter and Schmidhuber (1997) Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long short-term memory. Neural computation.
- Hoshen and Wolf (2018) Yedid Hoshen and Lior Wolf. 2018. Non-adversarial unsupervised word translation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 469–478, Brussels, Belgium. Association for Computational Linguistics.
- Joulin et al. (2018) Armand Joulin, Piotr Bojanowski, Tomas Mikolov, Hervé Jégou, and Edouard Grave. 2018. Loss in translation: Learning bilingual word mapping with a retrieval criterion. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 2979–2984, Brussels, Belgium. Association for Computational Linguistics.
- Kulikov (2013) Gennady Yu Kulikov. 2013. Cheap global error estimation in some runge–kutta pairs. IMA Journal of Numerical Analysis.
- Kwak (2008) N. Kwak. 2008. Principal component analysis based on l1-norm maximization. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Lample et al. (2018) Guillaume Lample, Alexis Conneau, Marc’Aurelio Ranzato, Ludovic Denoyer, and Hervé Jégou. 2018. Word translation without parallel data. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net.
- Mikolov et al. (2013) Tomas Mikolov, Quoc V. Le, and Ilya Sutskever. 2013. Exploiting similarities among languages for machine translation. CoRR.
- Peng et al. (2020) Xutan Peng, Chenghua Lin, Mark Stevenson, and Chen Li. 2020. Revisiting the linearity in cross-lingual embedding mappings: from a perspective of word analogies.
- Peng et al. (2021) Xutan Peng, Yi Zheng, Chenghua Lin, and Advaith Siddharthan. 2021. Summarising historical text in modern languages. In Proceedings of the 16th Conference of the European Chapter of the Association for Computational Linguistics, Online. Association for Computational Linguistics.
- Rousseeuw and Leroy (1987) P. J. Rousseeuw and A. M. Leroy. 1987. Robust Regression and Outlier Detection. John Wiley & Sons, Inc., USA.
- Ruder et al. (2018) Sebastian Ruder, Ryan Cotterell, Yova Kementchedjhieva, and Anders Søgaard. 2018. A discriminative latent-variable model for bilingual lexicon induction. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 458–468, Brussels, Belgium. Association for Computational Linguistics.
- Ruder et al. (2019) Sebastian Ruder, Ivan Vulić, and Anders Søgaard. 2019. A survey of cross-lingual word embedding models. J. Artif. Int. Res., 65(1).
- Schönemann (1966) Peter Schönemann. 1966. A generalized solution of the orthogonal procrustes problem. Psychometrika.
- Smith et al. (2017) Samuel L. Smith, David H. P. Turban, Steven Hamblin, and Nils Y. Hammerla. 2017. Offline bilingual word vectors, orthogonal transformations and the inverted softmax. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net.
- Trendafilov (2003) Nickolay T. Trendafilov. 2003. On the procrustes problem. Future Generation Computer Systems. Selected papers on Theoretical and Computational Aspects of Structural Dynamical Systems in Linear Algebra and Control.
- Upadhyay et al. (2016) Shyam Upadhyay, Manaal Faruqui, Chris Dyer, and Dan Roth. 2016. Cross-lingual models of word embeddings: An empirical comparison. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1661–1670, Berlin, Germany. Association for Computational Linguistics.
- Vulić and Korhonen (2016) Ivan Vulić and Anna Korhonen. 2016. On the role of seed lexicons in learning bilingual word embeddings. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 247–257, Berlin, Germany. Association for Computational Linguistics.
- Wang et al. (2019) Haozhou Wang, James Henderson, and Paola Merlo. 2019. Weakly-supervised concept-based adversarial learning for cross-lingual word embeddings. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 4419–4430, Hong Kong, China. Association for Computational Linguistics.
- Wang et al. (2020) Zirui Wang, Jiateng Xie, Ruochen Xu, Yiming Yang, Graham Neubig, and Jaime G. Carbonell. 2020. Cross-lingual alignment vs joint training: A comparative study and A simple unified framework. In 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020. OpenReview.net.
- Williams et al. (2018) Adina Williams, Nikita Nangia, and Samuel Bowman. 2018. A broad-coverage challenge corpus for sentence understanding through inference. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 1112–1122, New Orleans, Louisiana. Association for Computational Linguistics.
- Xing et al. (2015) Chao Xing, Dong Wang, Chao Liu, and Yiye Lin. 2015. Normalized word embedding and orthogonal transform for bilingual word translation. In Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 1006–1011, Denver, Colorado. Association for Computational Linguistics.
- Zhou et al. (2019) Chunting Zhou, Xuezhe Ma, Di Wang, and Graham Neubig. 2019. Density matching for bilingual word embedding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 1588–1598, Minneapolis, Minnesota. Association for Computational Linguistics.