Cross Ratio Geometry
Advances for Four Co-Linear Points in the
Desargues Affine Plane-Skew Field
Abstract.
This paper introduces advances in the geometry of the cross ratio of four co-linear points in in the Desargues affine plane. The cross-ratio of co-linear points of a skew field in the Desargues affine plane. The results given here have a clean rendition, based on Desargues affine plane axiomatics, skew field properties and the addition and multiplication of planar co-linear points.
Key words and phrases:
Co-Linear Points, Cross Ratio, Skew Field, Desargues Affine Plane2010 Mathematics Subject Classification:
51-XX; 51Axx; 51A30; 51E15, 51N25, 30C20, 30F401. Introduction and Preliminaries
In the advancement of our research in the connections of axiomatic geometry and algebraic structures, we have achieved some results which we have presented in this paper. More recently, results are given about the association of algebraic structures in affine planes and in Desargues affine plane, and vice versa in [21, 22, 6, 19, 20, 18, 27, 28, 26, 25, 23]. The foundations for the study of the connections between axiomatic geometry and algebraic structures were set forth by D. Hilbert [9]. And some classic research results in this context are given, for example, by E. Artin [1], D.R. Huges and F.C. Piper [10], H. S. M Coxeter [5]. Marcel Berger in [3], Robin Hartshorne in [7].
In this paper, we advance in study regarding the cross ratio of 4-points, in a line of the Desargues affine plane. We study and discuses the properties and results related to the cross ratio for four points, also we see the points of line as a elements of a skew field which constructed over this line on Desargues affine plane.
We use skew field properties for the proof of our results, since the cross-ratio sketch is very confusing (even with the Euclidean interpretation).
Earlier, we study the ratio of 2 and 3 points in a line on Desargues affine plane (see [23], [24], [24]), also we have shown that on each line on Desargues affine plane, we can construct a skew-field simply and constructively, using simple elements of elementary geometry, and only the basic axioms of Desargues affine plane (see [22], [6], [18], [27] ).
In this paper, we utilize a method that is naive and direct, without requiring the concept of coordinates. We bases only in Desargues affine plane axiomatic and in skew field properties (the points in a line on Desargues affine plane, we think of them as elements of skew fields, which is a construct over this line).
1.1. Desargues Affine Plane
Let be a nonempty space, a nonempty subset of . The elements of are points and an element of is a line.
Definition 1.
The incidence structure , called affine plane, where satisfies the above axioms:
-
1o
For each points , there is exactly one line such that .
- 2o
-
3o
There is a 3-subset of points , which is not a subset of any in the plane. Put another way, there exist three non-collinear points [15].
Desargues’ Axiom, circa 1630 [11, §3.9, pp. 60-61] [17]. Let and let pairwise distinct lines such that
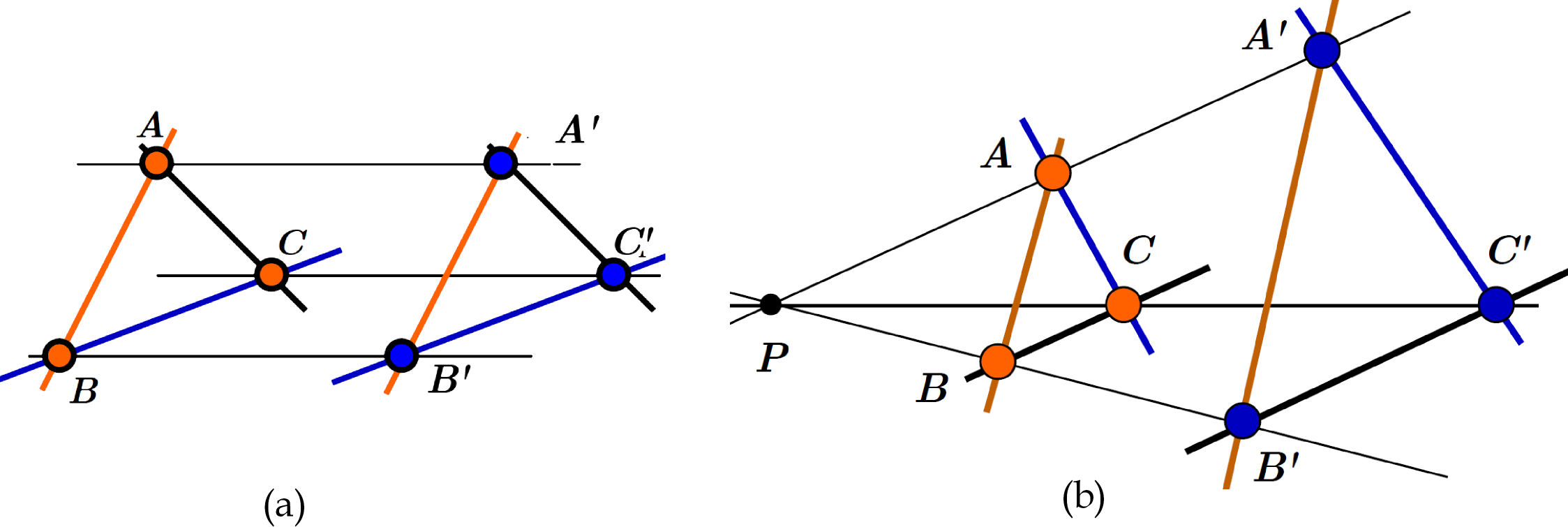
Then .
Example 1.
In Euclidean plane, three vertexes and , are similar (in (a) are equivalent-triangle and in (b) are homothetical-triangle) the parallel lines, in Desargues’ Axiom are represented in Fig. 1. In other words, the side of the triangle of is parallel with the side of the triangle , provided the restrictions on the points and lines in Desargues’ Axiom are satisfied.
A Desargues affine plane is an affine plane that satisfies Desargues’ Axiom.
Notation 1.
Three vertexes and , which, fulfilling the conditions of the Desargues Axiom, we call ’Desarguesian’.
1.2. Addition and Multiplication of points in a line of Desargues affine plane
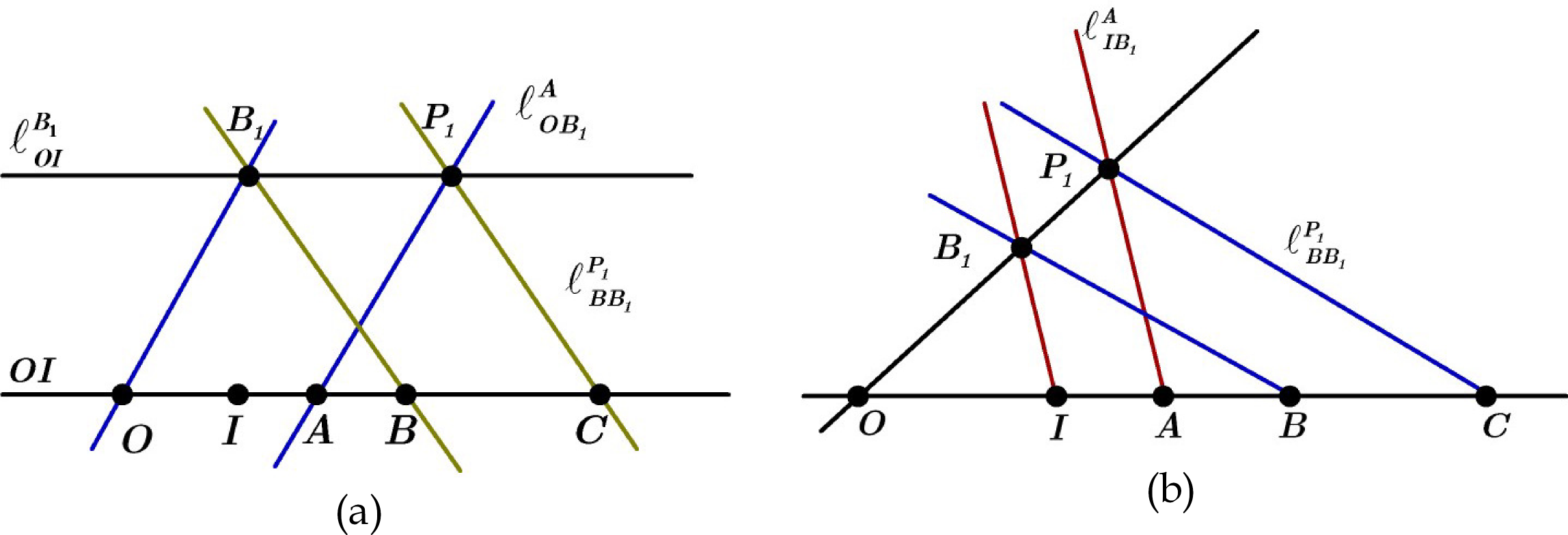
Addition of points in a line of affine plane: In an Desargues affine plane we fix two different points which, according to Axiom 1, determine a line Let and be two arbitrary points of a line . In plane we choose a point not incident with : (we call the auxiliary point). Construct line which is only according to the Axiom 2. Then construct line which also is the only according to the Axiom 2. Marking their intersection Finally construct line For as much as cuts the line in point , then this line, parallel with , cuts the line in a single point , this point we called the addition of points with point (Figure 2 (a)).
Multiplication of points in a line in affine plane. Choose in the plane one point not incident with lines and construct the line . Construct the line which is the only accoding to the Axiom 2 and cutting the line . Marking their intersection with Finally, construct the line Since cuts the line in a single point , then this line, parallel with , cuts the line in one single point , this point we called the multiplication of points with point (Figure 2 (b)).
The process of construct the points for adition and multiplication of points in line in affine plane, is presented in the tow algorithm form
Addition Algorithm
- Step.1:
-
- Step.2:
-
- Step.3:
-
Multiplication Algorithm
- Step.1:
-
- Step.2:
-
- Step.3:
-
1.3. Some algebraic properties of Skew Fields
I n this section will denote a skew field [8] and its center, where is the set such that
Proposition 1.
is a commutative subfield of a skew field .
Let now be a fixed element of the skew field . We will denote the centralizer in of the element , where is the set,
is sub skew field of K, but, in general, it is not commutative.
Let be a skew field, , and let us denote by the conjugacy class of :
If, , for all we have that
1.4. Ratio of two and three points
In the paper [23], we have done a detailed study, related to the ratio of two and three points in a line of Desargues affine plane. Below we are listing some of the results for ratio of two and three points.
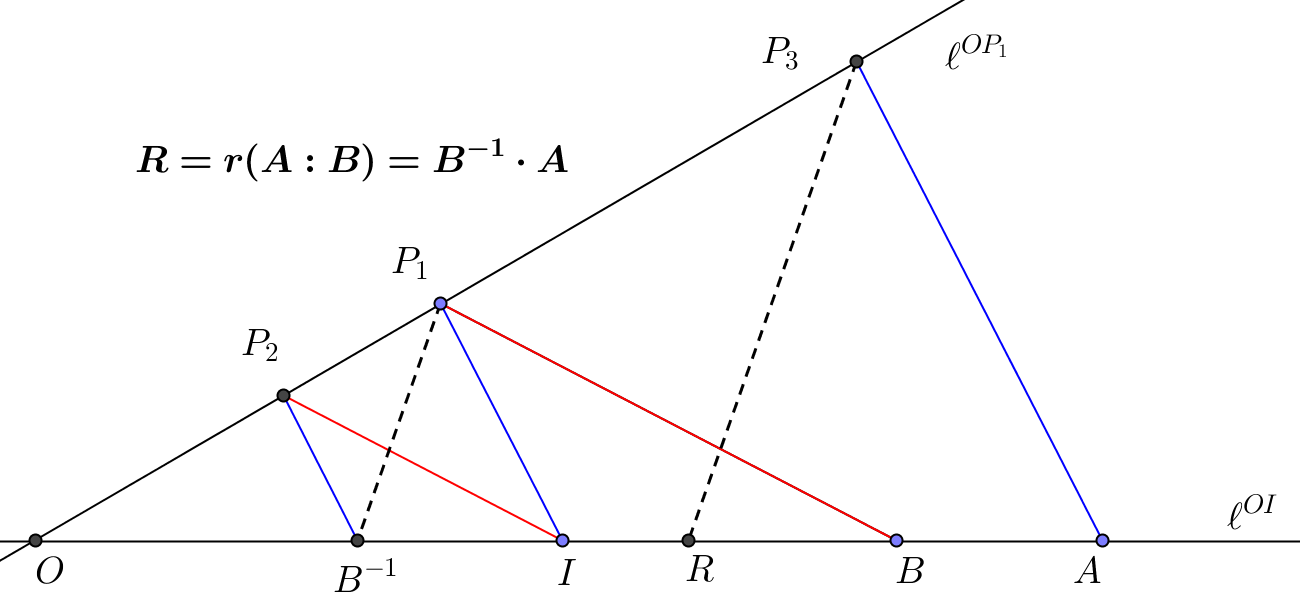
Definition 2.
[23] Lets have two different points line, and , in Desargues affine plane. We define as ratio of this tow points, a point , such that,
For a ’ratio-point’ , and for point in line , is a unique defined point, , such that .
Some results for Ratio of 2-points in Desargues affine plane (see [23]).
-
•
If have two different points line, and , in Desargues affine plane, then, .
-
•
For three collinear point and , in line, have,
-
•
For three collinear point and , in line, have,
-
(1)
-
(2)
-
(1)
-
•
Let’s have the points line where . Then have that,
-
•
This ratio-map, is a bijection in line in Desargues affine plane.
-
•
The ratio-maps-set , for a fixed point in line, forms a skew-field with ’addition and multiplication’ of points. This, skew field is sub-skew field of the skew field .
Ratio of three points in a line on Desargues affine plane. (see [23])
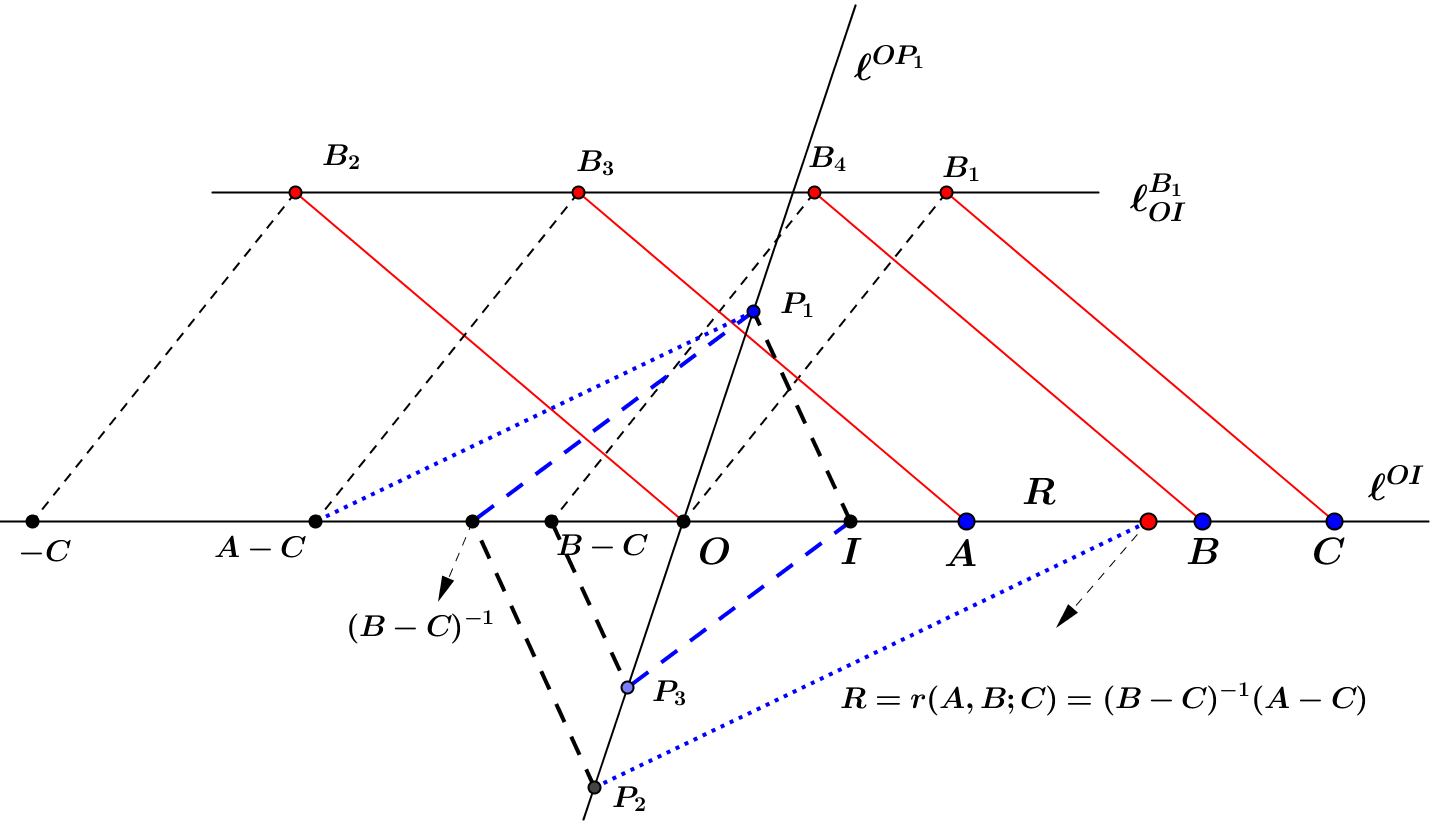
Definition 3.
If are three points on a line (collinear) in Desargues affine plane, then we define their ratio to be a point , such that:
and we mark this with .
Some Results for Ratio of 3-points in Desargues affine plane ([23]).
-
•
For 3-points in a line of Desargues affine plane, we have that,
-
•
For 3-points in a line in the Desargues affine plane, have
-
•
If , are three different points, and different from point , in a line on Desargues affine plane, then
-
•
In the Pappus affine plane, for three point different from point , in line, we have
-
•
This ratio-map, is a bijection in line in Desargues affine plane.
-
•
The ratio-maps-set , for a different fixed points in line, forms a skew-field with ’addition and multiplication’ of points in line. This, skew field is sub-skew field of the skew field .
2. Cross-Ratio for Fuor points in a line of Desargues affine plane
This section culminates in a main result in this paper. We consider the cross-ratio of co-linear points in Desargues affine planes, utilizing a method that is naive and direct without requiring planar coordinates. We define the cross-ratio of four co-linear points in a line on Desargues affine plane as a point in this line. This work carries forward earlier results that reveal the close connection between lines in the Desargues affine planes and corresponding skew fields. Skew fields properties in our proofs. Mainly, we rely on our results regarding the addition and multiplication of co-linear points in the Desargues affine plane, and the fact that a line (set of points), with addition and multiplication, forms a skew field (for more about this, see [18], [22], [6], [20], [19], [21], [27], [28], [24]).
The classical definition of the cross-ratio (see [13, 9, 2, 3]) for 4-points, is given as a product of tow ratio of lengths. So, for example, for four co-linear points ,
where are the lengths of segments , respectively.
Since we will not use coordinates and metrics, our definitions are rely solely on the algebra and axiomatics for the Desargues affine plane.
Let us have the line in Desargues affine plane , and four points,
Definition 4.
If are four points on a line in Desarges affine plane , no three of them equal, then we define their cross ratio to be a point:
Remark 1.
Similar to ’ratio’, we can define it, the cross-ratio, also as
or
(or all combination of product of this 4-factors) the results would be similar, but the obtained point will always be different for each case. In line, in Desargues affine planes, these are a different point from that of our definition, since:
and
also for the other cases, we would have a difference for each pair, found for the cross ratio, according to any definition we take. We are keeping our definition.
Definition 5.
If the line in Desargues affine plane, is a infinite line (number of points in this line is ), we define as follows:
From this definition and from ratio definition 3 we have that,
-
•
, so
-
•
, so,
-
•
, so,
-
•
, so
-
•
, so,
Some simple properties of Cross-Ratios, which derive directly from the definition, related to the position of the points in line in Desargues affine plane.
-
•
If , then
-
•
If , then
-
•
If , then
(think that (point in infinity)) -
•
If , then
(think that (point in infinity)) -
•
If , then
-
•
If , then
Theorem 1.
Let , such that and . If are three different points, then exist a single point , such that
Proof.
Suppose that exist tow different points an in line, such that
We rewrite them, cross ratios, as products of ’ratios’, and we have,
and
So, have,
we mark , remember that these are points of the line , so they are elements of the skew-fields , and have
Thus, for it, we have
But the points, , are points of line in Desargues affine plane, therefore, they are elements of skew-fields . We also know the fact that ’a skew field does not have a divisor of zero’ (more on skew fields, see [4], [8], [16], [12])
so,
and from the uniqueness of the definition for ’ratio’, we have,
∎
Theorem 2.
If are distinct points in a line, in Desargues affine plane, then
Proof.
From cross-ratio definition 4, we have
From skew fields properties we have that and , , and ∎
Theorem 3.
If are distinct points in a line, in Desargues affine plane, then
Proof.
Theorem 4.
For 4 co-linear points in a line in the Desargues affine plane, the cross-ratio satisfies the equation,
Proof.
From the definition 4 we have , and the points of this line forms a skew-field, therefore, we have association property:
| (since this factor are elements of skew field, so have the associative property) | |||
So, the point , is,
multiply in the right side by side with , and have
now multiply in the right side by side with , and have
multiply side by side with , and have,
Transform the left side of this equation as
rewrite it, and have
So, have
In the same way as above, (always bearing in mind that the points of a line of Desargues affine planes form a skew-field related to the addition and multiplication of the points, on this line, and the properties that satisfy a skew-field) we do the following transformations.
First we have the associative property for the multiplication of points on a line,
Now we transform the expression
So, have
Hence
so,
∎
Theorem 5.
If are distinct points in a line, in Desargues affine plane and is unital point for multiplications of points in same line, then
Proof.
Let’s start the calculations, using the result of the theorem
write,
so,
from skew-field properties, we have and ∎
Theorem 6.
If are distinct points in a line, in Desargues affine plane and is unitary point for multiplications of points in same line, then,
- (a):
-
- (b):
-
- (c):
-
Proof.
(c) At this point we will prove that: .
From point (a), we prove that and from theorem 3 have that . So, we have that
Mark the cross-ratios point , and rewrite. So we have to prove that the equation holds,
remember that the points are points of line, in Desargues affine planes, and can also be thought of as elements of skew-fields , therefore, we can make algebraic transformations, allowed for skew-fields, and we have
| (multiply from the | right with ) | ||
| (from skew field property | have that ) | ||
∎
Theorem 7.
If are distinct points, and different from zero-point , in a line, in Desargues affine plane and is unitary point for multiplications of points in same line, have,
Proof.
From cross-ratio definition 4, we have,
Points and , are points of line in Desargues affine plane, so are and elements of the skew field . First we prove that, for tow elements in a skew field , we have that . Indeed
We use this result in the calculation of , and have
| (from skew field properties ) | |||
| (from associative properties for multiplication) | |||
therefore, we can say that the points, and are conjugatet-points in a line of Desargues affine plane. ∎
Corollary 1.
If the point (center of skew field ), then,
Proof.
If then, , so . So, for , we have that,
Hence
∎
Corollary 2.
In Papus affine plane, .
Theorem 8.
If are distinct points in a line, in Desargues affine plane and is unitary point for multiplications of points in same line, have,
so, is different point from .
Proof.
From Definition of Cross-Ratio we have,
and
We mark the points, like below
so
This points are in line in Desargues affine plane, so are elements of the skew fields , which are constructet over this line, so . So we have,
∎
Corollary 3.
If are distinct points in a line, in Pappus affine plane and is unital point for multiplications, then
Proof.
If affine plane is Pappian plane, then the skew-field is commutative, then is a Field. ∎
We marked with the skew field over line in Desargues affine plane, we know that the center of the skew field , is a sub-skew field of , moreover, it is also commutative.
Theorem 9.
If are distinct points in a line, in Desargues affine plane and is unital point for multiplications of points in same line, then equation
it’s true, if
- (a):
-
points are in ’center of skew-field’ ;
- (b):
-
ratio-points are in ’center of skew-field’;
- (c):
-
ratio-point are in ’center of skew-field’;
- (d):
-
ratio-point is in centaralizer of point , or vice versa.
Proof.
(a) If points , we have that,
and
also the production is commutative. Hence,
so,
(b) If ratio-points are in ’center of skew-field’, we have that,
so the equation is also true for the ratio-point , and have,
(c) in the same way, as in case (b).
(d) The Centralizer , and we have that, , so we have,
so,
in the same way, it is proved that if , then ∎
References
- [1] Emil Artin, Geometric algebra, Intersci. Tracts Pure Appl. Math., vol. 3, Interscience Publishers, New York, NY, 1957 (English).
- [2] M. Berger, Geometry revealed, Springer, Heidelberg, 2010, xvi+831 pp., ISBN: 978-3-540-70996-1, MR2724440.
- [3] Marcel Berger, Geometry. I, II. Transl. from the French by M. Cole and S. Levy, corrected 4th printing ed., Universitext, Berlin: Springer, 2009 (English).
- [4] P. M. Cohn, Skew fields. Theory of general division rings., paperback reprint of the hardback edition 1995 ed., Encycl. Math. Appl., vol. 57, Cambridge: Cambridge University Press, 2008.
- [5] H. S. M. Coxeter, Introduction to geometry, 2nd ed., John Wiley & Sons, Inc., New York-London-Sydney, 1969, xvii+469 pp., MR0123930, MR0346644.
- [6] K. Filipi, O. Zaka, and A. Jusufi, The construction of a corp in the set of points in a line of desargues affine plane, Matematicki Bilten 43 (2019), no. 01, 1–23, ISSN 0351-336X (print), ISSN 1857–9914 (online).
- [7] R. Hartshorne, Foundations of projective geometry, New York: W.A. Benjamin, Inc. 1967. VII, 167 p. (1967)., 1967.
- [8] I.N. Herstein, Topics in algebra, 2nd ed., Xerox College Publishing, Lexington, Mass., 1975, xi+388 pp., MR0356988; first edition in 1964, MR0171801 (detailed review).
- [9] D. Hilbert, The foundations of geometry, The Open Court Publishing Co., La Salle, Ill., 1959, vii+143 pp., MR0116216.
- [10] D.R. Hughes and F.C. Piper, Projective planes, graduate texts in mathematics, vol. 6, Spnnger-Verlag, Berlin, New York, 1973, x+291 pp., MR0333959.
- [11] A. Kryftis, A constructive approach to affine and projective planes, Ph.D. thesis, University of Cambridge, Trinity College and Department of Pure Mathematics and Mathematical Statistics, 2015, supervisor: M. Hyland, v+170pp.,arXiv 1601.04998v1 19 Jan. 2016.
- [12] T. Y. Lam, A first course in noncommutative rings., 2nd ed. ed., Grad. Texts Math., vol. 131, New York, NY: Springer, 2001 (English).
- [13] J. J. Milne, An elementary treatise on cross-ratio geometry, with historical notes., Cambridge: University Press. XXII u. 288 S. (1911)., 1911 (English).
- [14] G. Pickert, Affine planes: An example of research on geometric structures, The Mathematical Gazette 57 (2004), no. 402, 278–291, MR0474017.
- [15] M. Prażmowska, A proof of the projective Desargues axiom in the Desarguesian affine plane, Demonstratio Mathematica 37 (2004), no. 4, 921–924, MR2103894.
- [16] Joseph J. Rotman, Advanced modern algebra. Part 1, 3rd edition ed., Grad. Stud. Math., vol. 165, Providence, RI: American Mathematical Society (AMS), 2015 (English).
- [17] W. Szmielew, Od geometrii afinicznej do euklidesowej (polish) [from affine geometry to euclidean geometry] rozwa?ania nad aksjomatyk? [an approach through axiomatics], Biblioteka Matematyczna [Mathematics Library], Warsaw, 1981, 172 pp., ISBN: 83-01-01374-5, MR0664205.
- [18] O. Zaka, Contribution to reports of some algebraic structures with affine plane geometry and applications, Ph.D. thesis, Polytechnic University of Tirana,Tirana, Albania, Department of Mathematical Engineering, 2016, supervisor: K. Filipi, vii+113pp.
- [19] by same author, A description of collineations-groups of an affine plane, Libertas Mathematica (N.S.) 37 (2017), no. 2, 81–96, ISSN print: 0278 – 5307, ISSN online: 2182 – 567X, MR3828328.
- [20] by same author, Three vertex and parallelograms in the affine plane: Similarity and addition abelian groups of similarly -vertexes in the Desargues affine plane, Mathematical Modelling and Applications 3 (2018), no. 1, 9–15, http://doi:10.11648/j.mma.20180301.12.
- [21] by same author, Dilations of line in itself as the automorphism of the skew-field constructed over in the same line in desargues affine plane, Applied Mathematical Sciences 13 (2019), no. 5, 231–237.
- [22] O. Zaka and K. Filipi, The transform of a line of Desargues affine plane in an additive group of its points, Int. J. of Current Research 8 (2016), no. 07, 34983–34990.
- [23] O. Zaka and J.F. Peters, Advances in the geometry of the ratio of linear points in the Desargues affine plane skew field, corr abs/2208.12745 (2022), arXiv:2208.12745.
- [24] by same author, Progress in invariant and preserving transforms for the ratio of co-linear points in the desargues affine plane skew field, corr abs/2209.02636 (2022), arXiv:2209.02636.
- [25] Orgest Zaka and Mohanad A. Mohammed, The endomorphisms algebra of translations group and associative unitary ring of trace-preserving endomorphisms in affine plane, Proyecciones 39 (2020), no. 4, 821–834 (English).
- [26] by same author, Skew-field of trace-preserving endomorphisms, of translation group in affine plane, Proyecciones 39 (2020), no. 4, 835–850 (English).
- [27] Orgest Zaka and James F. Peters, Isomorphic-dilations of the skew-fields constructed over parallel lines in the Desargues affine plane, Balkan J. Geom. Appl. 25 (2020), no. 1, 141–157 (English).
- [28] Orgest Zaka and James Francis Peters, Ordered line and skew-fields in the Desargues affine plane, Balkan J. Geom. Appl. 26 (2021), no. 1, 141–156 (English).