Current address:] University of Virginia, Charlottesville, Virginia 22901 Current address:] Osaka University, 567-0047 Ibarakishi, Japan Current address:] INFN, Sezione di Genova, 16146 Genova, Italy Current address:]University of Connecticut, Storrs, Connecticut 06269 Current address:] Skobeltsyn Nuclear Physics Institute, 119899 Moscow, Russia Current address:] Institut de Physique Nucléaire ORSAY, Orsay, France Current address:] Old Dominion University, Norfolk, Virginia 23529 Current address:] Universita’ di Roma Tor Vergata, 00133 Rome Italy
The CLAS Collaboration
Cross sections for the and reactions measured at CLAS
Abstract
The first high-statistics cross sections for the reactions and were measured using the CLAS detector at photon energies between threshold and 3.9 GeV at the Thomas Jefferson National Accelerator Facility. Differential cross sections are presented over the full range of the center-of-mass angles, , and then fitted to Legendre polynomials to extract the total cross section. Results for the final state are compared with two different calculations in an isobar and a Regge model, respectively. Theoretical calculations significantly underestimate the total cross sections between 2.1 and 2.6 GeV, but are in better agreement with present data at higher photon energies.
I Introduction
One motivation for the study of photoproduction is to investigate the role of the meson (also called the ) through -channel exchange. The is expected to be in the same scalar meson nonet as the meson (also called the ). Neither of these mesons have been directly observed because of their large widths, which are nearly as big as their respective masses. Such a large width is expected for scalar mesons, which have quantum numbers . In many quark models, there is virtually no angular momentum barrier to prevent these mesons from falling apart into two mesons, such as or . Because the and mesons cannot be observed directly, indirect production mechanisms provide better evidence of their existence.
The meson is rather well established pdg as a resonance, which is an important component of models of the nucleon-nucleon (-) interaction such as the Bonn potential cdbonn . The meson, however, is less easily established due to its strange quark content. Data for hyperon-nucleon (-) interactions are sparse and hence models have a range of parameter space that may or may not include exchange. Perhaps the best current evidence for the is from the decay angular distributions of the -meson into final states belle .
Here, in photoproduction of the , the enters into the -channel exchange diagrams oh2 . cannot contribute to kaon photoproduction because the photon cannot couple to the - vertex due to G-parity conservation. Theoretical calculations have been done oh2 showing the effect of the on photoproduction of and final states. Several years ago, two reports of photoproduction were published hleiqawi ; cbelsa but only preliminary results on were available guo .
We present the first results of and photoproduction with high statistics. Together, the and photoproduction results could put significant constraints on the role of the meson in -channel exchange. Here, for the first time, we make the ratio of total cross sections for the reactions and and compare with the same ratio calculated from a theoretical model for large and small contributions from exchange. Other evidence for the comes from recently published data on the linear beam asymmetry in photoproduction of the reaction hwang which shows a significant positive value at forward angles that is the signature of exchange oh2 .
A secondary motivation for this study is to understand if theoretical models using Regge trajectories plus known baryon resonances can explain the photoproduction data. If not, then there may be higher-mass baryon resonances that could couple strongly to decay. In a classic paper on the quark model, Capstick and Roberts calculated capstick many nucleon resonances that were predicted, but not observed in existing partial wave analyses of pion-nucleon scattering. They also observed that some of the higher-mass resonances may couple weakly to pion decay channels and more strongly to and decays. Indeed, studies of photoproduction bradford2 have shown that hadronic model calculations cannot explain the data without the addition of a new nucleon resonance near 1.9 GeV. We can look for other ”missing resonance states at higher mass, such as those identified in the Bonn-Gatchina analysis gatchina largely through precise hyperon photoproduction data from CLAS, by comparing photoproduction data to model calculations.
This paper is organized into the following sections. First, the experiment is described. Next, the data analysis is presented in some detail. Then we compare the results with theoretical calculations. Finally, we discuss the significance of the comparison and provide some conclusions.
II Experimental Setup
The data used in this analysis are from part of the g11a experiment,
which was taken from May 17 to July 29, 2004, using the CEBAF Large
Acceptance Spectrometer (CLAS) located in Hall-B at the Thomas
Jefferson National Accelerator Facility (TJNAF) in Newport News, Virginia.
Real photons were produced by bremsstrahlung from a 4.0186 GeV
electron beam incident on a 1 10-4 radiation length gold foil.
The electron beam was delivered by the Continuous Electron Beam
Accelerator Facility (CEBAF).
The Hall-B Tagging System sober was used to determine the
photon energies by measuring the energies of the recoil electrons
using a dipole magnetic field and a scintillator hodoscope.
The associated photon energies were then calculated by the difference
between the incident electron energies and the recoil electron energies
with an energy resolution of about 2-3 MeV.
The Hall-B Tagging System tags photons in the range from 20% to 95% of the
incident electron energy.
A liquid hydrogen target was used in the g11a experiment. The
target was contained in a cylindrical Kapton chamber of 2 cm radius and 40 cm length. The target density was determined by the temperature and pressure, which were monitored once per hour during the g11a experiment running.
The CLAS apparatus was used to detect particles generated from the
interaction of the incident photons with the target.
The CLAS detector was able to track charged particles that have momenta
larger than 200 MeV, and the detection area covered polar angles
from 8∘ to 142∘ and 80% of the azimuthal region.
It was composed of several sub-systems, arranged with
a six-fold azimuthal symmetry.
A plastic scintillator Start Counter, placed just outside of the target,
was used to measure the vertex time of particles in coincidence with
the incoming photon.
The Start Counter was made of 24 scintillator strips
with a time resolution of 350 ps sharabian .
The superconducting coils of the CLAS detector generated a toroidal
magnetic field that bent the path of outgoing charged particles.
Those particles traveled through 3 regions of drift chambers mestayer
that measured the curved paths to give the particle momenta
with a typical resolution of 1.0%.
For the g11a experiment, the current in the superconducting coils was
set at 1920 A, which gave a maximum magnetic field of 1.8 T.
The time of flight (TOF) system was located beyond the outermost drift
chambers at a radius of 4 m from the target and was used to measure the time and position of each charged
particle that hit the TOF scintillators.
The TOF information, along with the particle momentum, was used for
the particle identification in the analysis.
The time resolution of the TOF system was about 80 ps to 160 ps,
depending on the length of the scintillators smith .
A more detailed description of the CLAS detector is given in
Ref. mecking .
The event trigger for the g11a experiment required that at least
two tracks were detected in different sectors of CLAS.
Once the event satisfied this condition, it was written to tape for
future analysis.
The data acquisition system for the g11a experiment was able to run
at 5 kHz with a typical livetime of 90%.
III Data Analysis
As one of the largest photoproduction datasets at CLAS, the g11a experiment has 20 billion triggers. The calibration of each CLAS sub-system followed the same procedures as described in Ref. mike . Additional details can be found in Ref. Tang .
III.1 Channels of Interest
Because the is an unstable particle, it will quickly decay to (see Table 1) by the strong interaction. By applying energy and momentum conservation, the momentum is reconstructed from its decay particles, . The is a mixture of 50% and 50% , but only the decay is detected by the CLAS detector. The is reconstructed from the decay to with a decay branching fraction of 69.2%. The same branching fractions are reproduced by the Monte Carlo detector simulations (see section 3.6), and hence are implicit in the detector acceptance values.
| Mass(GeV) | 0.89166 | 1.11568 | 1.19264 |
|---|---|---|---|
| Decay products | , | , | |
| Branching fraction | 66.7%, 33.3% | 63.9%, 35.8% | 100% |
To summarize, we report on the differential and total cross sections of the photoproduction channel(s):
| (1) |
followed by
| (2) |
and
| (3) |
The and are reconstructed directly from their decay products, while the and are reconstructed using the missing mass technique.
III.2 Particle Identification
The Time of Flight (TOF) difference method was used to identify events with three pions (two positive and one negative charge) in the final state. Explicitly,
| (4) |
where is the measured TOF of the particle and is the calculated TOF with the measured momentum and the mass of a pion. In more detail,
| (5) |
where is the time when the particle hits the TOF scintillators and is the time when the photon hits the target. This information is determined by the CLAS Start Counter. In comparison, is given by:
| (6) |
where
| (7) |
Thus
| (8) |
where is the path length from the target to the TOF scintillators, is the speed of light, is the particle’s momentum, and is the mass of a pion. The pion candidates are required to have ns. Fig. 1 shows the TOF difference spectrum. The solid lines define the region of the cut, the small peaks on the both side of the cuts are due to photons coming from other beam bunches, showing evidence of the 2 ns beam bunch structure of CEBAF.
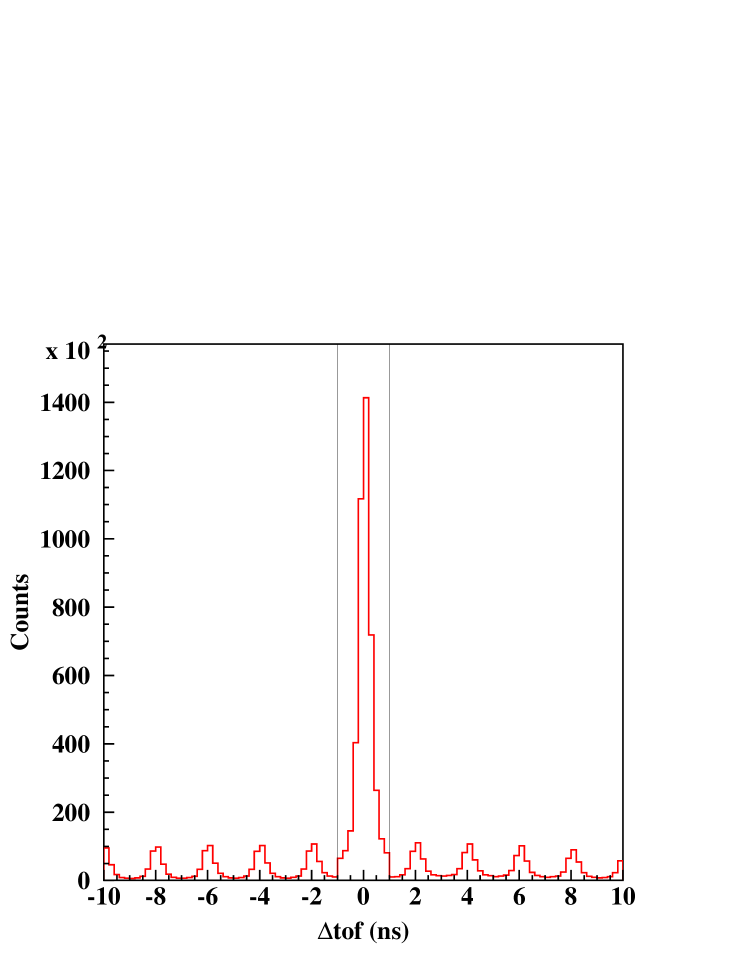
III.3 Photon Selection
After applying the 1.0 ns cut, particles that came from different RF beam buckets were removed naturally. Of the photons measured by the photon tagger, we want those that come within 1.0 ns of the particle vertex time, which are called “good” photons. However, there might still be more than one “good” photon in each event. To select the correct photon, all “good” photons were scanned to find the one that gave the three-pion missing mass closest to the known mass of the (), where
| (9) |
is the missing mass summed over all three pions in the event, while and are the energy and momentum vector of the photon. The two-pion missing mass is similarly defined.
III.4 Cuts applied
Several cuts were applied to the data to reduce the background and to remove events below threshold for the reaction of interest. In general, the strategy is to use geometric and kinematic constraints to eliminate backgrounds while ensuring that the signal remains robust. The efficiency of various cuts was tested with Monte Carlo simulations (see section III.7).
The geometric and kinematic constraints used here are listed below:
-
•
Fiducial cuts were applied to remove events that were detected in regions of the CLAS detector where the calibration of the detector is not well understood.
-
•
A cut on the vertex position along the beam axis (the -axis) to be within the target position was applied. All pions were required to be generated from the same vertex position within the experimental position uncertainty.
-
•
The missing mass from the was required to satisfy the relation GeV to include all hyperon mass peaks, for pion pairs with an invariant mass inside the mass window (see next section). Similarly, the missing mass from the was required to be greater than the nucleon mass, GeV.
After this step, the and reaction channels were treated differently, since different backgrounds are present for each final state. For instance, the large background from
(10) present for the reaction channel makes the the extraction of yields by simply fitting the peak impossible. On the other hand, there are only very small portions of the (1385) that contribute to the background, which can be easily removed based on Monte Carlo studies (see following section). Thus we could fit directly the peak in the three-pion missing mass for channel, whereas a different approach (given below) is necessary to extract the yield separately from background due to (1385) production. The following lists the extra cuts applied for each reaction channel.
-
•
For the analysis, a cut was placed on the peak in the three-pion missing mass: 1.08 GeV 1.15 GeV. This ensures that a was present in the final state.
-
•
For the analysis, a cut was placed on the peak of the three-pion invariant mass: 0.812 GeV 0.972 GeV. This ensures that a was produced.
III.5 Sideband Subtraction
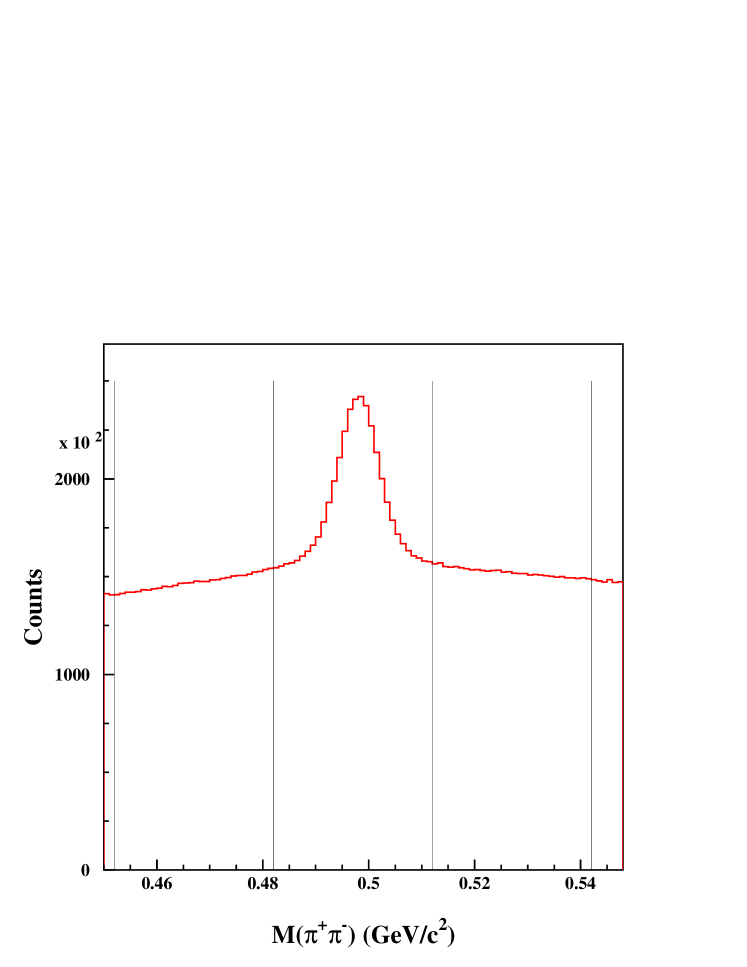
Because reactions other than photoproduction are present, background is still mixed in with the channels of interest. Fig. 2 shows the two-pion invariant mass plot after the first three cuts in the previous section, integrated over all photon energies. A clear peak centered near 0.497 GeV sits on top of a smooth background. The invariant mass is calculated using the momentum vector of one in the event, along with the momentum. Since there are two s, both pairs are tested, but typically only one combination will satisfy all kinematic constraints. To avoid double-counting, in rare cases where both satisfy all constraints, this combinatoric background is removed, for both data analysis and Monte Carlo acceptances.
To reduce the background, a Sideband Subtraction Method (SSM) was applied. The concept of the SSM is to assume that the background in the signal region can be approximated by a combination of the left and the right regions, which are adjacent to the signal region. In our analysis, the two-pion mass of the is used as the criteria to select the signal and sideband regions. Fig. 2 shows the regions used in our analysis. The middle band is the signal region, centered at the mass of with a width of 0.03 GeV. The other two bands, with the same band sizes, are the combinatorial background.
Fig. 3 shows the sideband subtraction applied to the reconstructed three-pion invariant mass and to the three-pion missing mass. The SSM reduces the background, giving cleaner signal peaks.
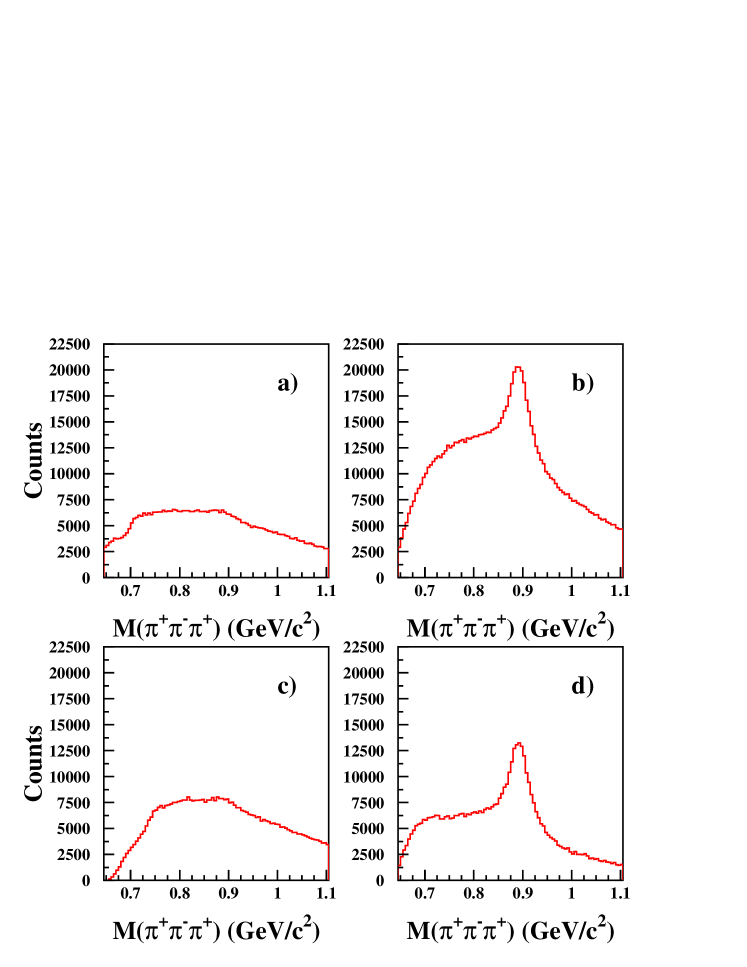
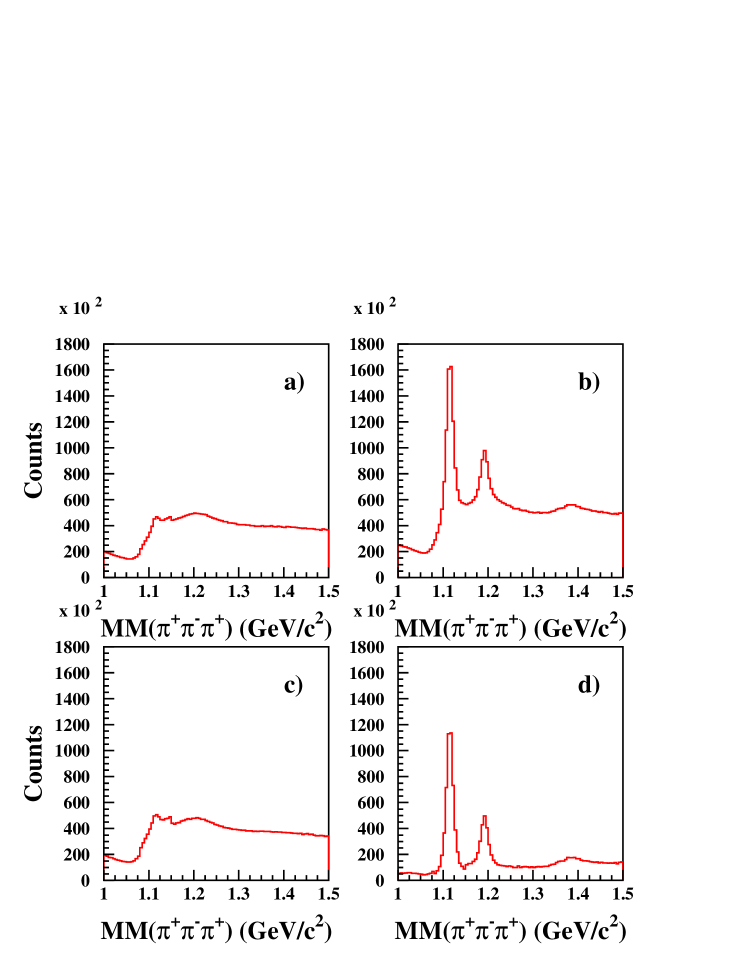
III.6 Peak Fitting
After applying the SSM to each invariant mass plot, corresponding to different incident photon energy and different production angle ranges, the peak becomes clearer, but it is still not free of background. The main contribution to the background comes from the reaction channel (1385), which passed through all the cuts. In addition, the 3-body phase space reaction is also present, and will contribute to the background as well.
In order to extract the correct peak yield, instead of fitting the peaks directly with a Breit-Wigner plus background functions, we applied a template fit. The precondition for this template fitting is that we assume there is negligible interference between the and (1385) channels; in other words, we assume that the and (1385) add incoherently. If we remove all other sources of background, then the mass plot should have background only from the (1385) peak. Similarly, the background in the (1385) plot comes only from events in the peak. Because the three-body channel is also a possible background, we assume it will add incoherently as well in both mass projections.
To justify these assumptions, we explored the effect of various levels of interference between these two final states in the simulations. The result is that the template fits correctly reproduced the generated events to within a 5% uncertainty for assumptions of maximal constructive or destructive interference.
Fig. 4 shows an example of the template fitting, where the solid dots with error bars are from the data, while the curve is from the fit, which contains contributions from both the , and channels. The peak is seen in the left plots and the peak is seen in the right plots. The template shape for each contribution comes from the simulation for that channel, and the magnitude of each channel is a free parameter to optimize the fit, with the result for each component of the fit shown in the bottom plots of Fig. 4. Both mass projections of Fig. 4 are fit simultaneously to minimize the overall .
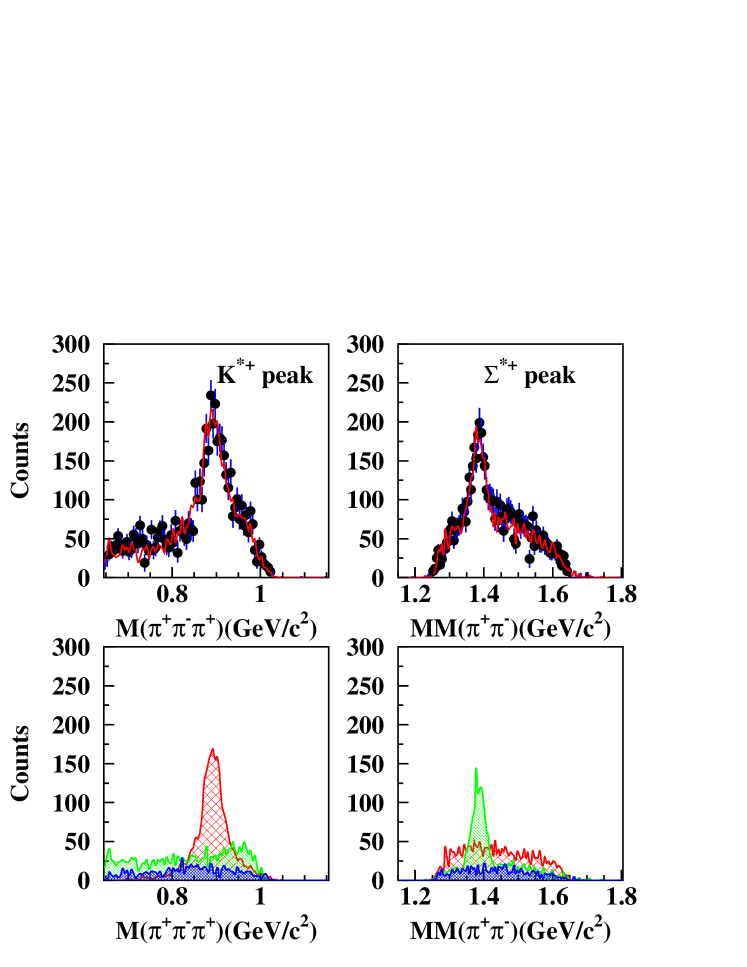
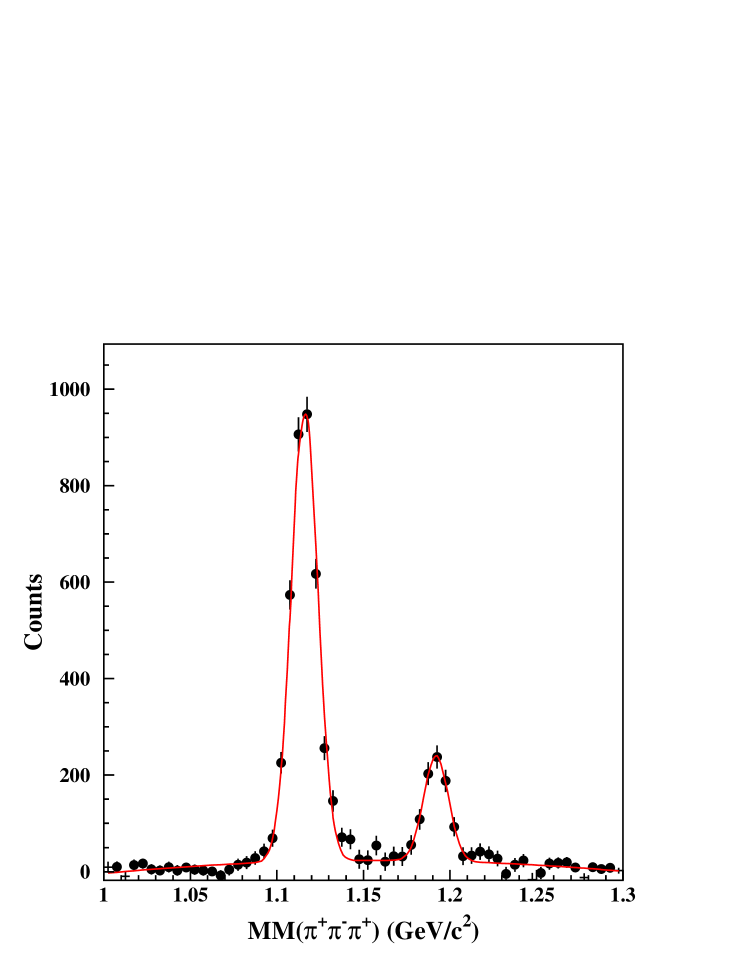
For the reaction, the counts from the were extracted by using a Gaussian fit, then the yields were corrected bin by bin based on a Monte Carlo study of how much (1385) leakage there is to reaction channel. The correction was studied and found to be less than 0.1%, which was included in our cross section calculation. Fig. 5 shows an example of the fitting. There are two peaks in the three-pion missing mass plot, one corresponding to the and the other to the . The fitting function used two Gaussians plus a second order polynomial, for the peak, peak and background, respectively.
III.7 Detector Acceptance
A computational simulation package, the CLAS GEANT Simulation (GSIM), was used for the Monte Carlo modeling of the detector acceptance. GSIM is based on the CERN GEANT simulation code with the CLAS detector geometry. Thirty million events were randomly generated, with all possible decay channels of the final state particles (, , …). The Monte Carlo files were generated with a Bremsstrahlung photon energy distribution and a tunable angular distribution that best fit the data. The energy bin size was 0.1 GeV and the total cross section was assumed constant across the bin. This assumption is reasonable based on the slowly-varying total cross sections shown below. Because the simulations have a better resolution than the real CLAS data, the output from GSIM are put through a software program to smear the particle momentum, timing, etc. to better match the real data.
An extensive study of the g11a trigger mike showed a small inefficiency for the experimental trigger. To account for the trigger inefficiency, an empirical correction was mapped into the Monte Carlo. The trigger corrections applied here is the same as used for other CLAS analyses of this same dataset mike .
The detector acceptance is calculated by:
| (11) |
where represents the detector acceptance, is the number of simulated events after processing and is the number of generated events.
The same software used for the experimental data was applied directly to the Monte Carlo data. Simulated events are extracted by fitting each reconstructed peak for a given photon energy and production angle. In our analysis, a non-relativistic Breit-Wigner function
| (12) |
was used to extract the counts of the peaks for channel. Here, is the full width at half maximum of the resonance peak, is the scattering energy and is the center of the resonance.
As described in section III.4, different methods were used for the and channels due to the presence of resonance contributions in the former. For the channel, where there is no kinematic overlap from hyperon states, the counts under the peak were fitted directly using a Gaussian function. Fitting the three-pion missing mass of the has less uncertainty than fitting the peak, since the peak is relatively narrow on top of a nearly flat background. This method was used for both simulated and experimental data.
IV Normalization and Cross Section Results
The differential cross sections are calculated by the formula:
| (13) |
where is the differential cross section in the angle center-of-mass (CM) frame, is the experimental yield, is the area density of protons in the target, is the incident photon beam flux, is the detector acceptance, is the bin size in the angle in the CM frame and is the DAQ live time for the experiment.
The detector acceptance and experimental yields for the and reactions are described in the previous sections.
For each incident photon beam energy range ( GeV), nine angular regions were measured, uniformly distributed between . Hence, is .
The livetime for the g11a experiment was carefully studied as a function of beam intensity, and found to be 0.82 0.01 for this measurement battag .
In our analysis, photon flux was extracted in photon energy steps of 0.05 GeV. In the final analysis, we used photon energy bins of 0.1 GeV, and the fluxes added appropriately.
The proton density is calculated using the formula:
| (14) |
where , and are the target density, target length and the atomic weight of hydrogen, respectively. is Avogadro’s number. For the g11a experiment, an unpolarized liquid hydrogen target was used. The target density was measured using:
| (15) |
where , are the target temperature and pressure (measured at the beginning of each CLAS run), while , , are the fitting parameters. The mean value of the target density for the g11a data was obtained by taking the average mike :
| (16) |
where is the number of runs. Using the target length of 40 cm, this gives .
V Results
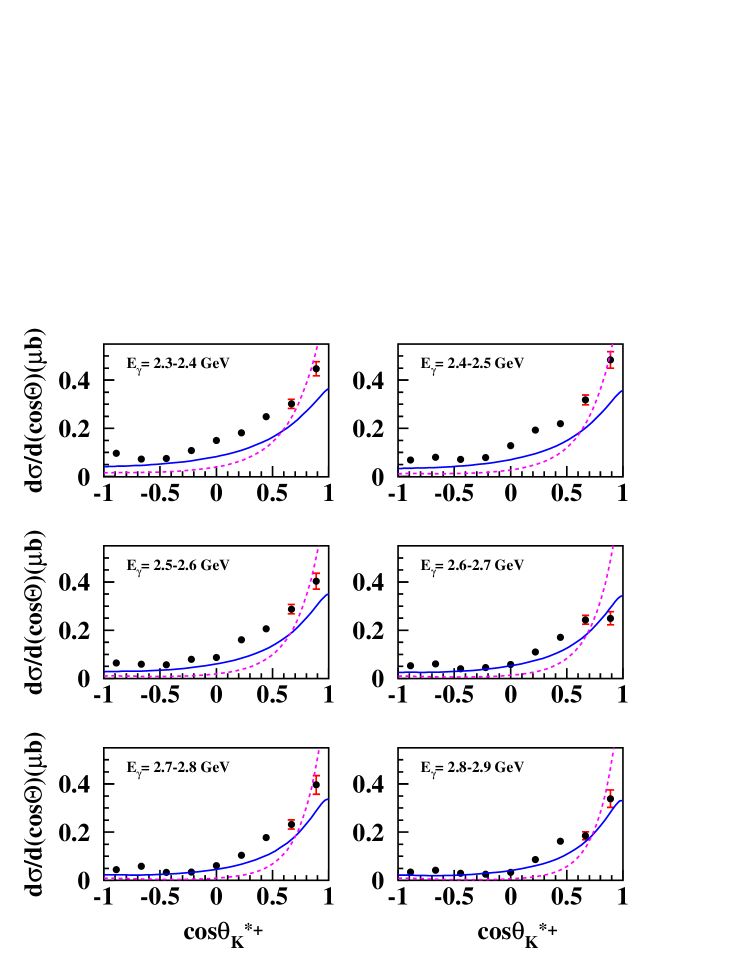
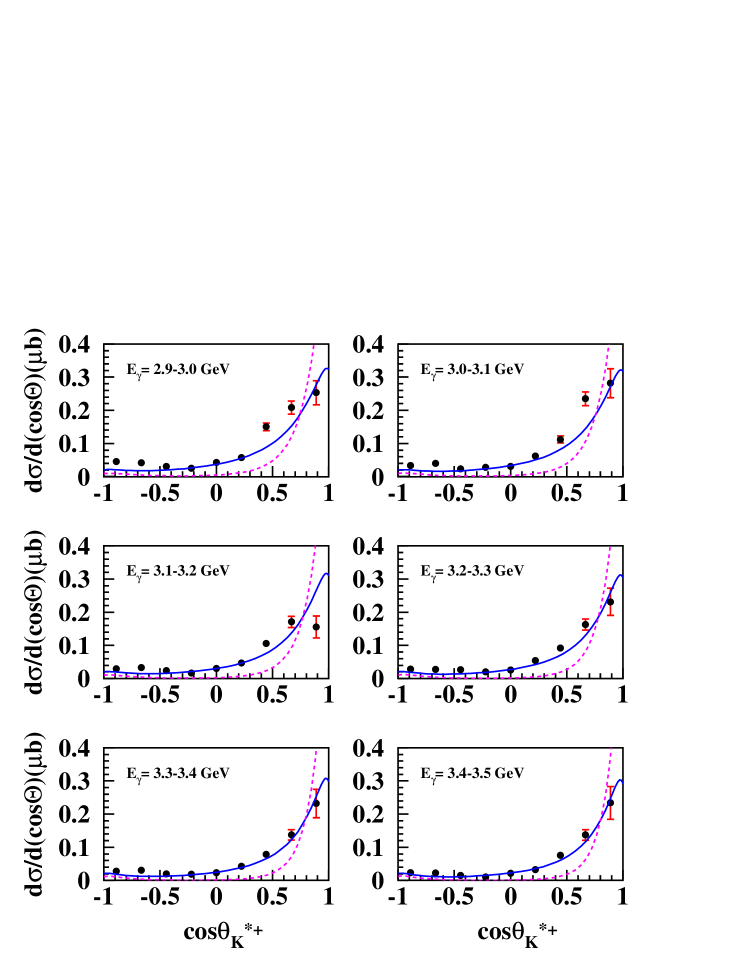
Fig. 6 shows the differential cross sections for the photoproduction reaction , where there are 22 plots, for bins ranging from 1.70 to 3.90 GeV. There are nine angular measurements in each plot, uniformly distributed in between -1.0 and 1.0. In general, the differential cross sections shows dominantly a -channel behavior, with an increase at forward-angles. Similarly, Fig. 7 shows the differential cross sections for photoproduction over the same photon energy range. Comparison with theoretical calculations are given below in section V.2.
The differential cross sections can be decomposed into Legendre polynomials as bradford2 :
| (17) |
where is the total cross section. By fitting the differential cross sections up to 4th order Legendre polynomials
| (18) |
the total cross section was extracted by integrating over from -1 to 1. Using the properties of the Legendre polynomials, after the integration, only the term is left. Hence the total cross section is given by
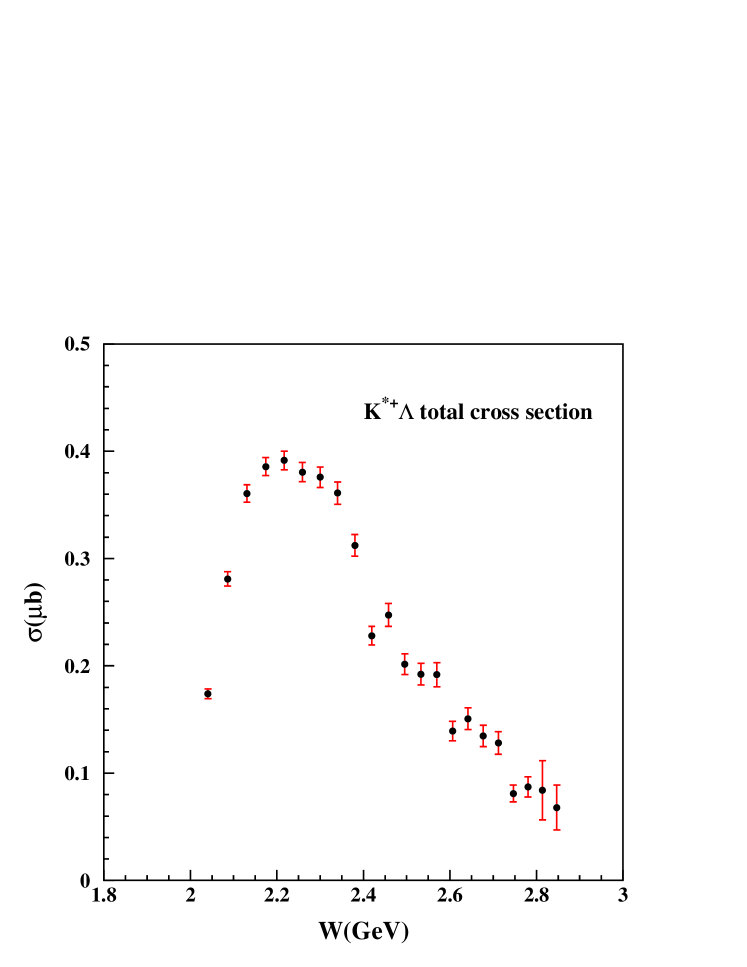
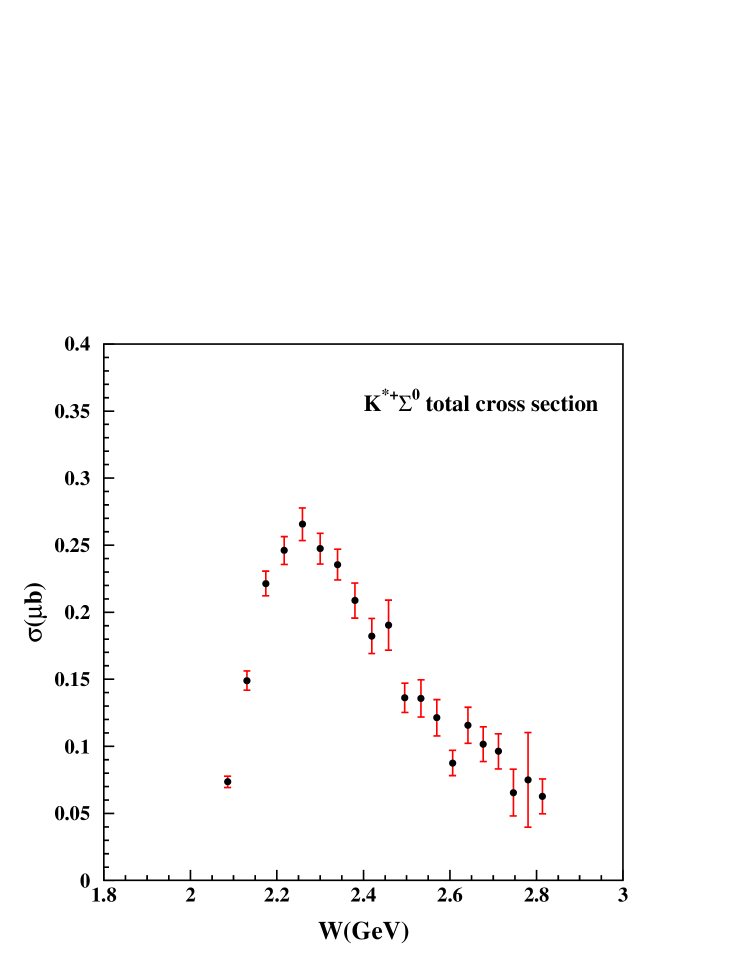
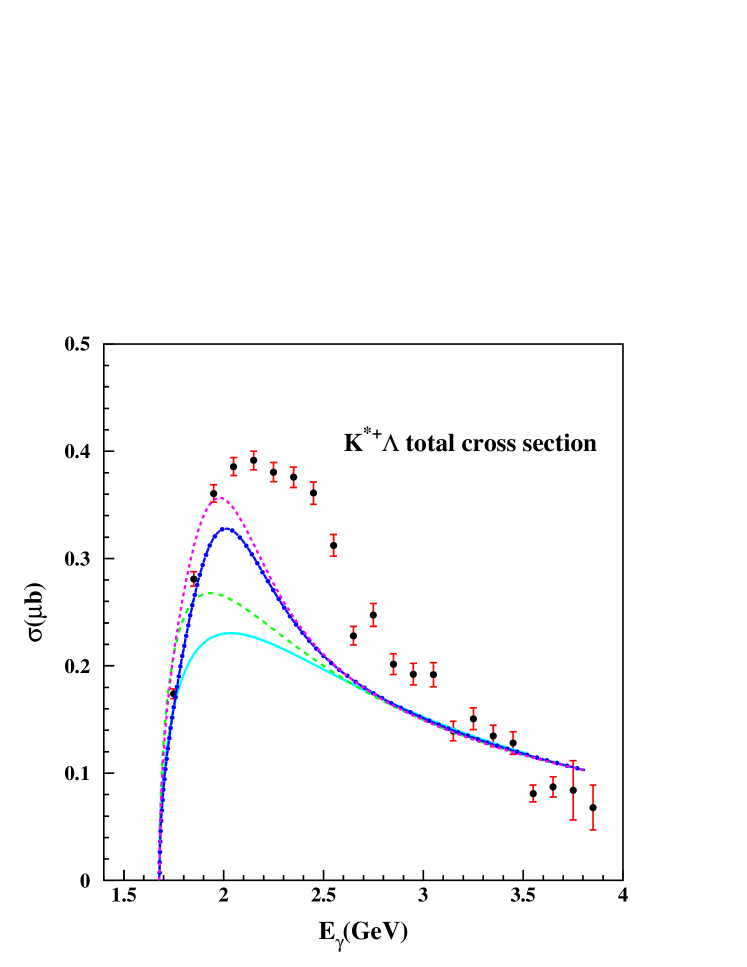
Fig. 6 shows the fitting for the channel, and Fig. 7 shows the fits for the final state. The fitting parameters through for each channel are plotted versus the incident photon energy in Fig. 8. The extracted total cross sections are shown in Fig. 9 for the and final states along with some theoretical curves explained below. The error bars show only the statistical uncertainty.










V.1 Systematic Uncertainties
Systematic uncertainties come from several sources: the applied cut parameters, the choice of fitting functions, the Monte Carlo used for the detector acceptance and so on.
Systematic uncertainties were estimated for each cut by varying the cut intervals and then recalculating the differential cross sections. The changes to cut parameters were applied to both the experimental data and the simulated output. The relative difference between the new cross sections and the original cross sections was calculated bin by bin using:
| (19) |
and then the resulting values were histogrammed. This histogram was fitted with a Gaussian function, and the width from the Gaussian fit was taken as the systematic uncertainty for each variation. The cut intervals were varied to both larger and smaller values, and we chose the larger of the systematic uncertainties calculated from each variation.
Similar estimation were done for the detector acceptance, by varying the inputs to the Monte Carlo. Also, different fitting functions and background shapes were used to determine the systematic uncertainties associated with the peak yields. The total systematical uncertainty is then given by
| (20) |
which assumes no correlated uncertainties.
The total systematic uncertainty from all sources, added in quadrature, is shown in Table 2, where the other sources include the target length, density and so on. For the final state the overall systematic uncertainty is 14% and for the systematic uncertainty is 12%.
| channel | channel | |
|---|---|---|
| Event Selections | 2.9% | 4.5% |
| Peak Fitting | 7.4% | 5.8% |
| Detector Acceptance | 9.2% | 5.7% |
| Beam Flux | 7.0% | 7.0% |
| Other Sources | 2.5% | 2.5% |
| Total | 14% | 12% |
V.2 Theoretical Calculations
The models that are currently available for photoproduction are based on effective Lagrangians, which fall into two groups: isobar models and Reggeized meson exchange models. Isobar models evaluate tree-level Feynman diagrams, which include resonant and nonresonant exchanges of baryons and mesons. The reggeized models, on the other hand, emphasize the -channel meson exchange, which is expected to dominate the reaction at energies above the resonance region. The standard propagators in the Lagrangian are replaced by Regge propagators, which take into account an entire family of exchanged particles with the same quantum numbers instead of just one meson exchange. In this section, the cross section results will be compared with calculations from these two theoretical models.
One model we use is by Oh and Kim (O-K Model) oh2 , which is an isobar model. This model starts with Born terms, which include -channel (with , and exchanges), -channel ground state nucleon exchanges and -channel , and exchanges. Additional -channel nucleon resonance exchanges were added to the model using the known resonances from the PDG in Ref. KNOK , referred to here as the K-N-O-K model. One attractive point of these models is the inclusion of diagrams with a light meson exchange in the -channel. As mentioned in the introduction, the meson has not yet been firmly established, and these models allows us to study the effect of possible exchange.
The other model shown here is the Ozaki, Nagahiro and Hosaka (O-N-H) Model ONH , which is a reggeized model. This model takes into account all possible hadron exchanges with the same quantum numbers (except for the spin). The coupling constants and exchange parameters are the same as those used in O-K Model oh2 .
Fig. 10 shows those calculations compared with our differential cross sections, where the solid curves represent the theoretical calculations from the K-N-O-K Model and the dashed curves represent the O-N-H Model. The corresponding curves are shown in Fig. 11 for the total cross sections, where the curves are explaind in the figure caption. The O-K model includes -channel diagrams with most well-established nucleon resonances below 2 GeV pdg , whereas the K-N-O-K model includes two additional -channel resonances up to 2.2 GeV. Interpretation of these results are discussed in section VI.
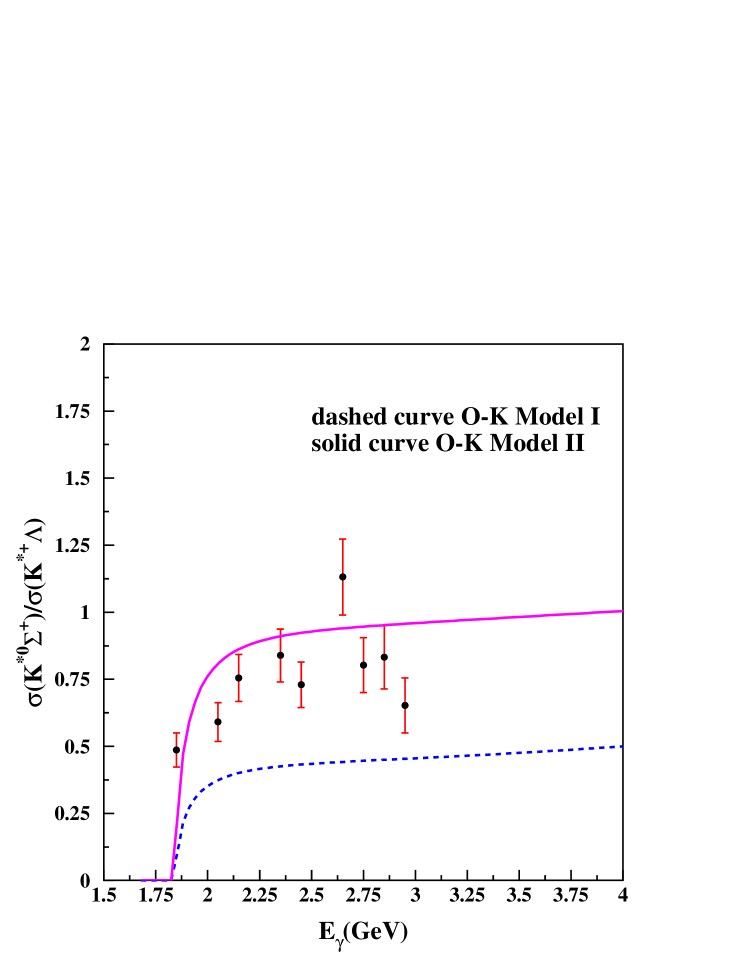
Fig. 12 shows the total cross section ratio of the reactions to . The data alone are not very sensitive to the exchange due to the unknown strength of the coupling constant, . However, the coupling constants of these two reactions is related in the effective Lagrangian models, and so the ratio is sensitive to the effects of exchange. The dots with error bars in Fig. 12 use the present data along with the previously published CLAS data for hleiqawi . We note that another data set exists for the reaction from CBELSAcbelsa , but we have chosen to use CLAS data in both numerator and denominator to reduce systematics. The two curves are the theoretical predictions from O-K Model I and II oh2 , where Model I includes minimal -channel exchange, while Model II has a significant contribution from exchange.
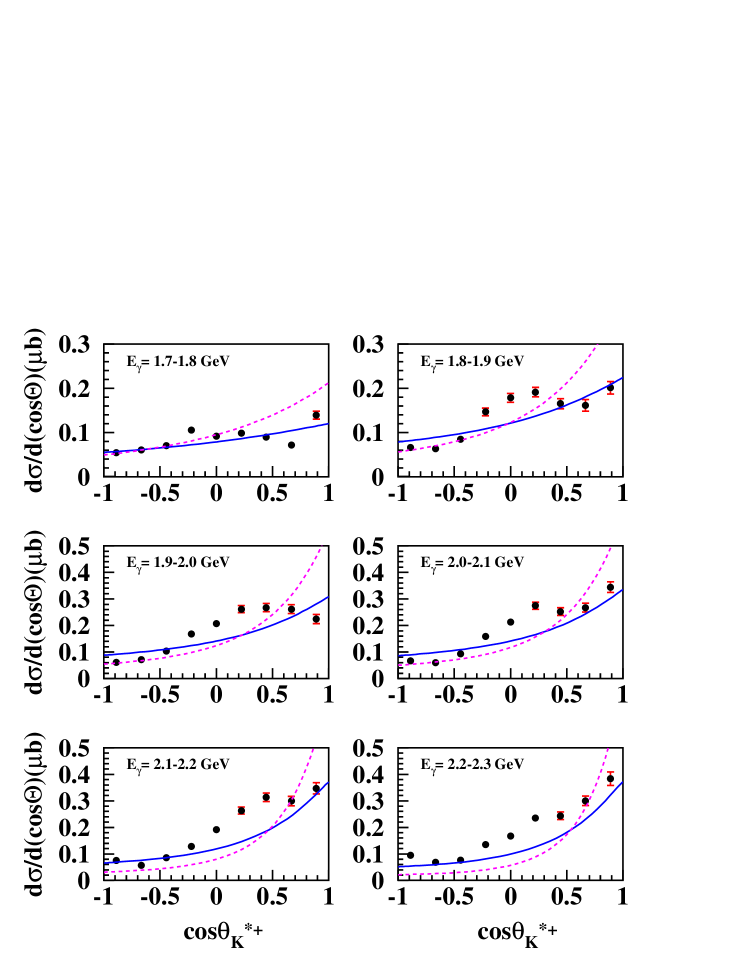
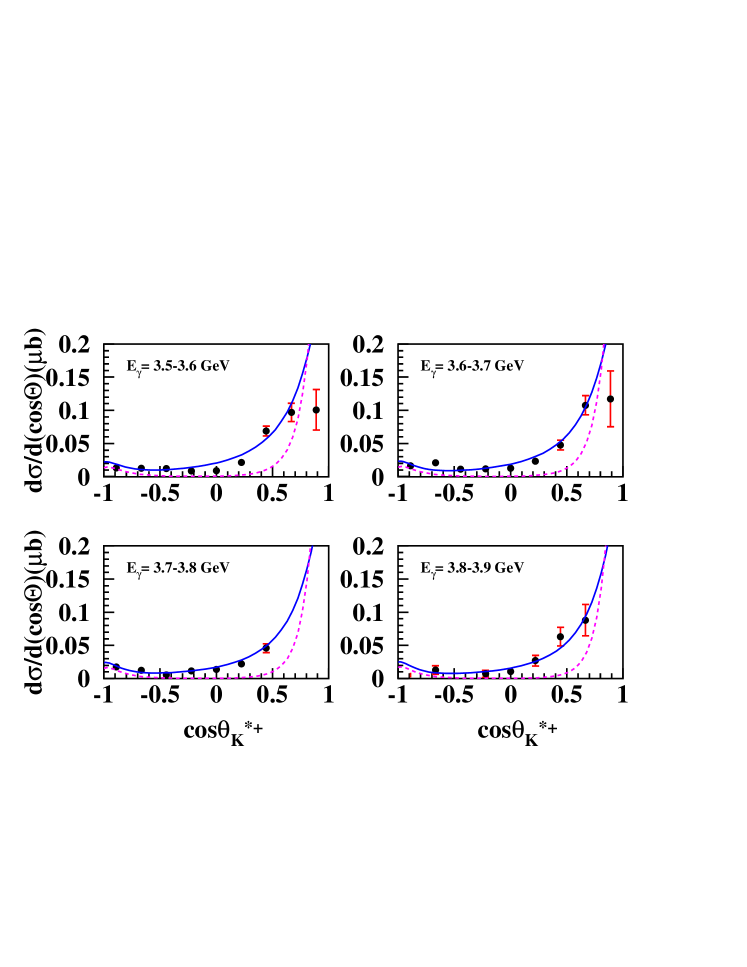
VI Discussion and Conclusions
We presented here the first high-statistics measurement of the reactions and . The data are from the g11a experiment using the CLAS detector at Thomas Jefferson National Accelerator Facility. Differential cross sections are presented for nine equal-spaced bins in for each photon energy bin of 0.1 GeV width from threshold (1.7 or 1.8 GeV, respectively) up to 3.9 GeV. Total cross sections, based on fits to the differential cross sections are also presented for both reactions.
The cross sections for the final state are compared with calculations from two effective Lagrangian models, one based on an isobar model and the other based on the Regge model. Neither calculation matches the data over the broad kinematic range measured here, but the isobar model compares more favorably, especially at higher photon energies. However, both models significantly underpredict the total cross sections in the range GeV. Inclusion of all well-known nucleon resonances improves agreement with the data in the region of GeV, but has only a small contribution above GeV, and cannot explain this excess cross sections in the new data.
It remains an open question whether the excess strength of the final state in this photon energy region is due to additional couplings to yet-unidentified nucleon resonances at higher mass, or whether it is due to other effects such as channel-coupling through final-state interactions or interference at the amplitude level with other physics processes such as photoproduction of the final state. The latter effect was studied using a simplified Monte Carlo generator and showed little or no effect due to interference with the final state, but more sophisticated theoretical calculations should be done to study interference effects.
In comparison, the final state has a sharper peak in the total cross section at GeV, and falls off more quickly with increasing photon energy than for the final state. This suggests whatever mechanism that causes the excess cross section for the latter final state is not present in the photoproduction. However, theoretical calculations are not yet available for this final state, and we must wait for more theoretical development before any such conclusion can be reached.
One of the goals of this measurement was to understand the role of the meson exchange, which can contribute to photoproduction but not to photoproduction. Although no definite conclusion can be reached from the present data, the ratio of total cross sections for the and the final state compared with a similar ratio calculated in the model of Oh and Kim suggests that the model with significant exchange is in better agreement with the data ratio. This agrees with the conclusion from a recent study of the beam asymmetry measurement hwang of the final state using a linearly polarized photon beam at forward angles. However, we must be careful in making any firm conclusion regarding the role of the exchange until the theoretical models have better agreement with the total cross sections above GeV. The excess strength of the new data above 2.1 GeV may change the effects of exchange in the ratio. However, the general idea of comparing the and cross sections, which are affected differently by exchange, is something that can be studied now that these new data are available.
VII Acknowledgment
The authors thank the staff of the Thomas Jefferson National Accelerator Facility who made this experiment possible. This work was supported in part by the Chilean Comisión Nacional de Investigación Científica y Tecnológica (CONICYT), the Italian Istituto Nazionale di Fisica Nucleare, the French Centre National de la Recherche Scientifique, the French Commissariat à l’Energie Atomique, the U.S. Department of Energy, the National Science Foundation, the UK Science and Technology Facilities Council (STFC), the Scottish Universities Physics Alliance (SUPA), and the National Research Foundation of Korea.
The Southeastern Universities Research Association (SURA) operates the Thomas Jefferson National Accelerator Facility for the United States Department of Energy under contract DE-AC05-84ER40150.
References
- (1) J. Beringer et al. (Particle Data Group), Phys. Rev. D 86, 010001 (2012).
- (2) R. Machleidt, Phys. Rev. C 63, 024001 (2001); R. Machleidt, et al., Phys. Rept. 140, 1 (1987).
- (3) M. Ablikim et al., Phys. Lett. B 633, 681 (2006); E.M. Aitala et al., Phys. Rev. Lett. 89, 121801 (2002).
- (4) Yongseok Oh and Hungchong Kim, Phys. Rev. C 74 015208 (2006).
- (5) I. Hleiqawi, et al. (The CLAS Collaboration), Phys. Rev. C 75 042201(R) (2007).
- (6) M. Nanova, et al., Eur. Phys. J. A 35 333-342 (2008).
- (7) L. Guo and D. P. Weygand, arXiv:hep-ex/0601010v1.
- (8) S. H. Hwang et al. (The LEPS Collaboration), Phys. Rev. Lett. 108, 092001 (2012).
- (9) Simon Capstick, W. Roberts, Phys. Rev. D 58 074011 (1998).
- (10) R. Bradford, et al. (The CLAS Collaboration), Phys. Rev. C 73, 035202 (2006).
- (11) A.V. Anisovich et al., Eur. Phys. J. A 48 15, (2012); A.V. Anisovich et al., Phys. Lett. B 711, 167 (2012).
- (12) D. I. Sober, et al., Nucl. Inst. Meth. A 440, 263 (2000).
- (13) Y. G. Sharabian, et al., Nucl. Inst. Meth. A 556, 246 (2006).
- (14) M. D. Mestayer, et al., Nucl. Inst. Meth. A 449, 81, 2000.
- (15) E.S. Smith, et al., Nucl. Inst. Meth. A 432, 265, 1999.
- (16) B.A. Mecking et al., Nucl. Inst. Meth. A 503, 513, 2003.
- (17) Michael Williams, PhD Thesis, Carnegie Melon University, 2007. http://www-meg.phys.cmu.edu/williams/pdfs/thesis.pdf
- (18) Wei Tang, PhD Thesis, Ohio University, 2012. https://userweb.jlab.org/tangwei/WeiTang_Thesis.pdf
- (19) R. De Vita et al. (The CLAS Collaboration), Phys. Rev. D 74 032001 (2006).
- (20) S.-H. Kim, S.-I. Nam, Y. Oh and H.-Ch. Kim, Phys. Rev. D 84, 114023 (2011).
- (21) Sho Ozaki, Hideko Nagahiro and Atsushi Hosaka, Phys. Rev. C 81 035206 (2010).