Cutting and Pasting in the Torelli subgroup of
Abstract
Using ideas from 3-manifolds, Hatcher–Wahl defined a notion of automorphism groups of free groups with boundary. We study their Torelli subgroups, adapting ideas introduced by Putman for surface mapping class groups. Our main results show that these groups are finitely generated, and also that they satisfy an appropriate version of the Birman exact sequence.
1 Introduction
Let be the free group on letters, and let be the group of outer automorphisms of . In many ways, behaves very similarly to , the mapping class group of the surface of genus with boundary components. For an overview of some of these similarities, see [7].
One such connection is that they both contain a Torelli subgroup. In the mapping class group, the Torelli subgroup is defined to be the kernel of the action on for . In , we define a similar subgroup222It is also common to see this group denoted by , but we wish to reserve this notation for the analogous subgroup of , denoted , as the kernel of the action of on .
On surfaces with multiple boundary components, there are many possible definitions one might use to define a Torelli subgroup of . In [22], Putman defines a Torelli subgroup for requiring the additional data of a partition of the boundary components. The goal of the current paper is to mirror Putman’s procedure to define an “ with boundary.”
Let . For simplicity, we will write if . A key property of is that it has fundamental group . Fix such an identification. The mapping class group is the group of orientation-preserving diffeomorphisms of fixing the boundary pointwise modulo isotopies fixing the boundary pointwise. Letting be the topological group of diffeomorphisms fixing the boundary pointwise, we can also write . By a theorem of Laudenbach [19], there is an exact sequence
| (1) |
where the map is given by the action (up to conjugation) on , and the is generated by sphere twists about disjointly embedded -spheres (see Section 2 for the definition and relevant properties of sphere twists). Recent work of Brendle, Broaddus, and Putman [6] shows that this sequence actually splits as a semidirect product. This exact sequence implies that, modulo a finite group, acts on up to isotopy. Therefore, plays almost the same role for that plays for .
Adding boundary components.
From Laudenbach’s sequence (1), we see that , where is the subgroup of generated by sphere twists. Now that we have related to a geometrically defined group, we can start introducing boundary components. Extending the relationship given by Laudenbach’s sequence, we define “ with boundary” as
When , Laudenbach [19] also shows that . Hatcher-Wahl [14] introduced a more general version of , which they denoted by . The original definition of has to do with classes of self-homotopy equivalences of a certain graph. However, in [14] the authors give an equivalent definition, which says that is the mapping class group of with spherical and toroidal boundary components, modulo sphere twists. With this definition, we see that . Similar groups have been examined in the work of Jensen-Wahl [16] and Wahl [26]. Their versions, however, involve only toroidal boundary components, and thus are distinct from .
Torelli subgroups.
An important feature of sphere twists (discussed in Section 2) is that they act trivially on homotopy classes of embedded loops, and thus act trivially on . Therefore, the action of on induces an action of on . We can then define the Torelli subgroup to be the kernel of this action. However, this definition does not capture all homological information when , especially when is being embedded in . To see why, consider the scenario depicted in Figure 1, in which has been embedded into . This embedding induces a homomorphism obtained by extending by the identity. This map sends sphere twists to sphere twists, and so we get an induced map . However, this does not restrict to a map under this definition of since elements of are not required to fix the homology class of the subarc of lying inside . To address this issue, we will use a slightly modified homology group.
Definition.
Fix a partition of the boundary components of .
-
(a)
Two boundary components of are -adjacent if there is some such that .
-
(b)
Let be the subgroup of spanned by
either is a simple closed curve or is a properly embedded arc with endpoints -
(c)
There is a natural action of on , and we define the Torelli subgroup to be the kernel of this action.
Returning to Figure 1, let be the trivial partition of the boundary components of with a single -adjacency class. With this choice of partition, we see that . If , then it follows that preserves the homology class of . Therefore, , and so restricts to a map .
2pt
\pinlabel at 210 125
\pinlabel at 360 125
\pinlabel at 130 125
\pinlabel at 445 125
\endlabellist
Restriction.
As we discussed in the last paragraph, given an embedding , we can extend by the identity to get a map . In general, may not be injective. However, it is injective if no connected component of is diffeomorphic to (see Appendix A). Moreover, such an embedding induces a natural partition of the boundary components of as follows.
Definition.
Fix an embedding . Let be a connected component of , and let be the set of boundary components of shared with . Then the partition of the boundary components of induced by is defined to be
With this definition, one might guess that . This turns out to be the case, and this is our first main theorem, which we prove in Section 3.
Theorem A (Restriction Theorem).
Let be an embedding, the induced map, and the induced partition of the boundary components of . Then .
Birman exact sequence.
From here, we move on to exploring the parallels between these Torelli subgroups and those of mapping class groups. There is a well-known relationship between the mapping class groups of surfaces with a different number of boundary components called the Birman exact sequence (see [12]):
Here, is the unit tangent bundle of , the map is given by pushing a boundary component around a loop, and the map is given by attaching a disk onto this boundary component. In Section 4, we will prove versions of the Birman exact sequence for and , all culminating in the following sequence for .
Theorem B (Birman exact sequence).
Fix such that , and let be an embedding obtained by gluing a ball to the boundary component . Fix . Let be a partition of the boundary components of , let be the induced partition of the boundary components of , and let be the set containing . We then have an exact sequence
where is equal to:
-
(a)
if .
-
(b)
if .
Moreover, this sequence splits if .
Finite generation.
Once we have established this version of the Birman exact sequence, in Section 5, we will define a generating set for . This generating set will be inspired by the generating set for found by Magnus [21] in 1935.
Theorem 1.1 (Magnus).
Let . The group is generated by the -classes of the automorphisms
for all distinct with . Here, the automorphisms are understood to fix for .
Throughout this paper, we will use the convention . Since we defined to be a subgroup of , our generators will be defined geometrically rather than algebraically. However, in the case of , they will reduce directly to Magnus’s generators. In Section 6, we will show that these elements do indeed generate .
Theorem C.
The group is finitely generated for , .
This is rather striking because the analogous result for Torelli subgroups of mapping class groups with multiple boundary components is still open. We will prove this theorem by using the Birman exact sequence to reduce to and applying Magnus’s theorem. Unfortunately, the tools we have constructed do not seem strong enough to give a novel proof of Magnus’s theorem. We will, however, prove a weaker version in Section 7. The original proof of Magnus’s Theorem 1.1 comes in two steps: showing that the given automorphisms -normally generate , and then showing that the subgroup they generate is normal in . We will give a proof of the first step in our setting. For alternative proofs of the first step, as well as more information on the second step in this context, see [5] and [10].
Theorem D.
The group is -normally generated by the automorphisms and , where and .
Abelianization.
Once we have a finite generating set for , a natural question arises: how does the cardinality of this generating set compare to the rank of ? For , this question is answered by a result of Andreadakis [1] and Bachmuth [3].
Theorem 1.2 (Andreadakis, Bachmuth).
The abelianization of is torsion-free of rank if , and rank if .
This theorem was proved using a version of the Johnson homomorphism
where . We will recall the definition of this homomorphism in Section 8, along with the proof of Theorem 1.2. We then move on to computing the rank of for . To do this, we choose an embedding , which induces an injection . Composing this map with gives a map . We then compute the image of our generators under , and use this to count the rank of .
Theorem E.
The abelianization of is torsion-free of rank
Acknowledgements.
I would like to thank my advisor Andy Putman for directing me to and its Torelli subgroup, and for his input during the revision process. I would also like to thank Patrick Heslin and Aaron Tyrrell for helpful conversations regarding diffeomorphism groups, as well as Dan Margalit for an enlightening question which resulted in the addition of Section 8.
Outline.
In section 2, we will give a short overview of sphere twists. We then move on to proving Theorem A in Section 3. We will establish all of our versions of the Birman exact sequence (including Theorem B) in Section 4. In Section 5, we will define our candidate generators for , and we will prove that they generate (Theorem C) in Section 6 using the Birman exact sequence and Magnus’s Theorem 1.1. In Section 7, we will prove Theorem D. We then move on to Section 8, in which we recall the definition of the Johnson homomorphism for , and use it to compute the rank of the abelianization of , proving Theorem E. Finally, we conclude with two appendices. In Appendix A, we provide conditions for a map induced by an inclusion to be injective, and in Appendix B we prove a lemma which allows us to realize bases of as collections of disjoint oriented spheres.
Figure conventions.
We will frequently direct the reader to figures which are intended to give some geometric intuition for the manifold . In order to assemble , we begin with one or more copies of , remove a collection of open balls, and then glue the resulting boundary components together in pairs. These gluings will be indicated by double-sided arrows connecting the boundary spheres being glued. As an example, see Figure 2.
2pt
\pinlabel at 88 88
\pinlabel at 290 88
\pinlabel at 500 88
\endlabellist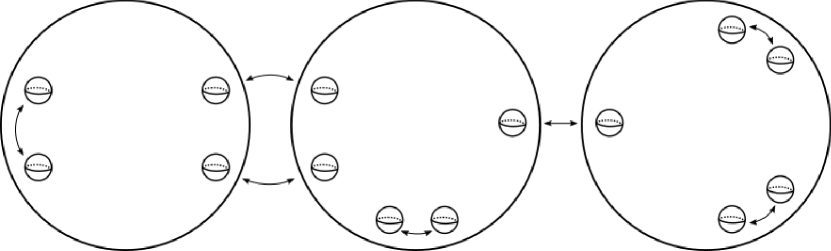
2 Preliminaries
Since sphere twists play a fundamental role throughout the remainder of the paper, we will give a brief overview of them here.
Sphere twists.
Fix a smoothly embedded 2-sphere , and let be a tubular neighborhood of . Recall that , and the nontrivial element is given by rotating one full revolution about any fixed axis through the origin. Fix an identification . Then, we define the sphere twist about , denoted , to be the class of the diffeomorphism which is the identity on and is given by on . The isotopy class of depends only on the isotopy class of . In fact, more is true: Laudenbach [19] showed that the class of depends only on the homotopy class of .
Action on curves and surfaces.
Since , we see that sphere twists have order at most two. However, it is tricky to show that sphere twists are actually nontrivial because they act trivially on homotopy classes of embedded arcs and surfaces. To see why this is true, let be an embedded 2-sphere, and let be a tubular neighborhood of . Suppose that is an arc or surface embedded in . We can homotope such that it is either disjoint from or intersects transversely. Let be one of points in which lies on the axis of rotation used to construct . We can homotope such that collapses into . Note that this process is not an isotopy, and is no longer embedded in . This is not an issue because a result of Laudenbach [19] shows that if is fixed up to homotopy, then it is fixed up to isotopy. Since fixes pointwise, it follows that fixes up to homotopy. The upshot of this is that a more sophisticated invariant must be constructed to detect the nontriviality of . In [18, 19], Laudenbach uses framed cobordisms to show that for , the sphere twist is trivial if and only if is separating. In the case of no boundary components, Brendle, Broaddus, and Putman [6] give another proof of this fact by showing that sphere twists act nontrivially on a trivialization of the tangent bundle of up to isotopy.
Sphere twist subgroup.
Let be the subgroup generated by sphere twists. Given and a sphere twists , we have the “change of coordinates” formula
This shows that is a normal subgroup of . In fact, even more is true. Letting in the above formula and using the fact that sphere twists act trivially on embedded surfaces up to isotopy, we find that
which implies is actually abelian. Since nontrivial sphere twists have order two, it follows that is isomorphic to a product of copies of . For , another result of Laudenbach shows that and is generated by the sphere twists about the core spheres in each summand. For , one can show that . The in the exponent reflects the fact that the product of all the sphere twists about boundary components is trivial. Since we will need this fact later, we include a proof here.
2pt
\pinlabel at 310 680
\pinlabel at 60 395
\pinlabel at 350 490
\pinlabel at 350 300
\pinlabel at 350 110
\endlabellist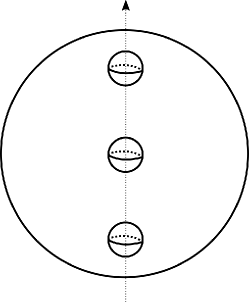
Lemma 2.1.
If be spheres parallel to the boundary components of , then the element is trivial in .
Proof.
We will prove this by induction on . As the base case, consider . The argument in this case follows a proof of Hatcher and Wahl [15, Pg. 214-215], but we include the proof here as well for completeness. If , then the statement is trivial. If , then we can embed in as the unit ball with smaller balls removed along the -axis (see Figure 3). We may then use the -axis as the axis of rotation for the sphere twists about all the boundary components. Taking to be the unit sphere, we then see that the product is isotopic to . Since sphere twists have order two, this gives the desired relation, and so we have completed the base case.
Next, consider for . Since , there exists a nonseparating sphere which is disjoint from . Splitting along yields a submanifold diffeomorphic to . Let be the map induced by inclusion. Let be the sphere twists about the boundary components of , and order them such that for . With this ordering, notice that . Since sphere twists have order two,
By our induction hypothesis, is trivial in , and so we are done. ∎
If , this shows that the sphere twist about the boundary component is trivial. However, if , then the sphere twists about boundary components are nontrivial. We will also need this fact, so we prove it here.
Lemma 2.2.
Let , and let be a boundary component of . Then is nontrivial.
Proof.
Let be a boundary component of different from . Then we get an embedding by attaching and with a copy of , and capping off all the remainding boundary components. Let be the map induced by . Then is a sphere twist about about a nonseparating sphere. Earlier in this section, we saw that such sphere twists are nontrivial, and so we conclude that is nontrivial as well. ∎
3 Restriction Theorem
Fix , and let be a partition of the boundary components of . Recall that we have defined to be the submodule of generated by
| either is a simple closed curve or | |||
| is a properly embedded arc with endpoints | |||
and is the kernel of the action of on induced by the action of .
Remark.
This version of homology is simpler than the one used in [22]. There are two reasons for this.
-
•
In our case, we can take homology relative to the entire boundary, whereas in [22], homology is taken relative to a set consisting of a single point from each boundary component. This is because in surfaces, the boundary components give nontrivial elements of , and the arcs considered in can get “wrapped around” those boundary components. This is not a problem in our setting because loops in boundary components of are trivial in .
-
•
Next, suppose we have an embedding of surfaces. It is possible for a nontrivial element to become trivial in (for instance, if a boundary component is capped off). So, there could be elements of which act trivially on , but not fix . In other words, the Torelli group would not be closed under restrictions. To fix this, the author in [22] must mod out by the submodules of spanned by the (with proper orientation chosen). This is not a problem in the 3-dimensional case however, since an inclusion induces an injection on homology.
We can now move on to the proof of Theorem A.
Proof of Theorem A.
Let be an embedding, and let be the induced map. Recall that we must show that , where is the partition of the boundary components induced by as described in the introduction.
This proof will follow the proof of [22, Theorem 3.3]. Define the following subsets of (we use to denote concatenation of arcs):
| is a properly embedded arc in with | |||
| endpoints in distinct -adjacent boundary | |||
| components and is a properly embedded arc | |||
We claim that the homology group is spanned by . To see why, let be the class of a loop . If can be homotoped to lie entirely inside or , then we are done. On the other hand, suppose that crosses the boundary of . Without loss of generality, we may assume that crosses the boundary of exactly twice since any loop can be surgered into a collection of such loops (see Figure 4). It follows that has the form , where is an arc connecting boundary components of , and is a arc with the same endpoints as . Recall that under the partition induced by the inclusion , two boundary components are -adjacent if they lie on the same component of . Therefore, the existence of implies that the boundary components intersected by are -adjacent, and thus . This completes the proof of the claim.
2pt
\pinlabel at 88 70
\pinlabel at 320 70
\pinlabel at 88 240
\endlabellist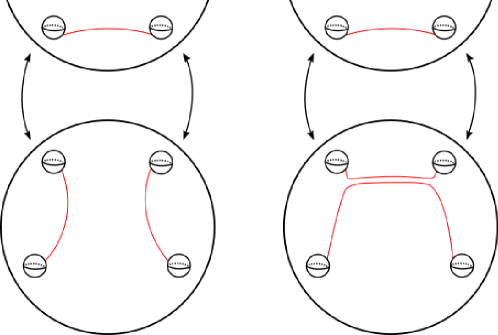
Let . By the definition of , the element acts trivially on . Moreover, acts trivially on by the definition of . Lastly, suppose that . Then fixes the homology class of since , and fixes pointwise by the definition of . Therefore, .
Next, suppose that . By definition, acts trivially on , and thus on as well since the map induced by is injective. This implies that acts trivially on homology classes of simple closed curves in . So, we only need to check that preserves the homology classes of arcs in connecting distinct -adjacent boundary components. Suppose there is a class of arcs . Since is the partition of the boundary components induced by , can be completed to a homology class , where is an arc in connecting the endpoints of . Then since and fixes pointwise, we have
This shows that acts trivially on . Therefore, . ∎
4 Birman exact sequence
In this section, we give a version of the Birman exact sequence for the groups . We will start by giving a Birman exact sequence on the level of mapping class groups. We note that Banks has proved a version of the Birman exact sequence for 3-manifolds (see [4]). However, this version involves forgetting a puncture rather than capping a boundary component, so we will prove our own version here. Once we have the sequence for mapping class groups, we will mod out by sphere twists to get a corresponding sequence for , and finally restrict to get a sequence for .
Remark.
In the following theorems, we exclude the case . This is because boundary drags in are trivial (see the proof of Theorem 4.1 for the definition of boundary drags). In this case, we have isomorphisms
-
•
,
-
•
,
-
•
,
where one of the generators of is a sphere twist about the sphere and the other is the antipodal map in both coordinates.
Theorem 4.1.
Fix such that . Glue a ball to a boundary component of , and let be the resulting embedding. Fix .
-
(a)
If , choose a lift of , where is the oriented frame bundle of . We then have an exact sequence
-
(b)
If and , then we have an exact sequence
Proof.
Let denote the space of orientation-preserving diffeomorphisms of which restrict to the identity on , and let be the subspace of consisting of diffeomorphisms which fix the framing . It is standard that there is a fiber bundle
| (2) |
where the map is given by . Passing to the long exact sequence of homotopy group associated to this fiber bundle, we find the segment
Since is the oriented frame bundle, it is connected, and so is trivial. Moreover, is isomorphic to . For a proof of this fact in the surface case, see [12, p. 102]; the proof goes exactly the same way in our setting. Therefore, the above sequence becomes
| (3) |
To get a short exact sequence, we must understand the kernel of the map . We remark here that the map is given by pushing and rotating a small ball containing about a loop based at . This is in analogy with the “disk pushing maps” seen in the case of surfaces. Since is parallelizable, we have
Consider the map , where the basepoint is on the boundary component being capped off. As is shown in Figure 5, the composition
is given by conjugation about the loop being pushed around. Since is centerless for , the entire kernel of must be contained in . However, the image of the generator of this subgroup in is the sphere twist . By Theorems 2.1 and 2.2, this sphere twist is nontrivial if and only if . If , this shows that is injective, and (3) gives us the desired exact sequence. On the other hand, if , then . Therefore, the image of in is isomorphic to
as desired. ∎
2pt
\pinlabel at 150 165
\pinlabel at 150 85
\pinlabel at 480 145
\pinlabel at 245 142
\endlabellist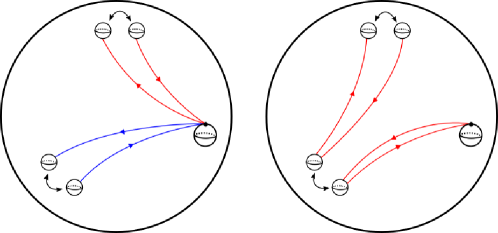
Modding out by sphere twists.
Now that we have a Birman exact sequence for , we can mod out by sphere twists to get a Birman exact sequence for . Consider the map given by capping off a boundary component . Since takes sphere twists to sphere twists, this map descends to a map . Since is surjective, is as well. Let be the kernel of , and let be the quotient map. If , then the kernel of is by Theorem 4.1. Let be the map defined in the proof of Theorem 4.1, and fix an identification . Since
for all , the image of under is contained in . In other words, we have the following commutative diagram:
where . Next, we claim that the map is surjective. To see this, let , and choose a lift of . Since , the image is a product of sphere twists . For each , choose a preimage which is also a sphere twist. Then
which implies that for some . Moreover, , which verifies our claim that is surjective.
Now, we wish to identify the kernel of . Let , and fix a basepoint on the boundary component being capped off. At the end of the proof of Theorem 4.1, we saw that acts nontrivially on if and only if is trivial. Since sphere twists act trivially on homotopy classes of curves, it follows that is nontrivial if is nontrivial. Therefore, the kernel of must lie inside . However, the generator of gets mapped to under , which is killed in . Therefore, , and so it follows that .
On the other hand, if and , then the kernel of the map is by Theorem 4.1. Almost exactly the same argument used above shows that the quotient map restricts to a surjective map . However, in this case, is injective since the sphere twist has already been killed off. Thus, we find that in this case as well.
From now on, we will identify the kernel of the map with . The map will play a significant role throughout the remainder of the paper, and so we give a formal definition here.
Definition.
The map is defined as , where is arbitrary. Since sphere twists become trivial in , this element depends only on .
The upshot of this is that we have proven the Birman exact sequence for .
Theorem 4.2.
Fix such that , and let be an embedding obtained by gluing a ball to a boundary component. Fix . Then the following sequence is exact:
Restrict to Torelli.
We now move on to proving Theorem B, which gives a Birman exact sequence for . We start by recalling its statement. Let be a partition of the boundary components of , and fix a boundary component . Let be the set containing , and let be the inclusion obtained by capping off . The partition induces a partition of the boundary components of by removing from . With this definition of , the map restricts to a map , which we will also call . The sequence from Theorem 4.2 then restricts to
Theorem B asserts that is surjective, and identifies its kernel . We start with surjectivity.
Lemma 4.3.
The induced map is surjective for any embedding .
Proof.
Consider an element . Our goal is to find some such that . There are two cases.
First, suppose that . Then the inclusion induces an isomorphism which is equivariant with respect to the actions of and . In other words, for any and , we have
| (4) |
By Theorem 4.2, there exists some such that . We claim that . To see this, let . Then, by Equation (4), we see that
Since is an isomorphism, this implies that , and so , as desired.
Next, suppose that . Again, choose such that . In this case, there is no longer a well-defined map . However, there is a subgroup of which projects isomorphically onto . Let be the subgroup generated by
| either is a simple closed curve | |||
| or is a properly embedded arc with | |||
It is clear that .
Let be the class of an arc which has an endpoint on . We claim that is generated by and . To establish this claim, it suffices to show that , where is the class of any arc with an endpoint on and the other elsewhere. Such an exists since . Fix such a class , and let be an arc connecting the endpoints of and on . Orient , , and such that the curve is well-defined.
If the endpoints of and which are not on lie on distinct boundary components, then is an arc connecting -adjacent boundary components. Therefore, . Since in , it follows that . On the other hand, if the endpoints of and which are not on lie on the same boundary component , then we can complete to a loop , where is an arc connecting the endpoints of and . Then
and so . This completes the proof of the claim that is generated by and .
Since projects isomorphically onto , and this projection is equivariant with respect to the actions of and , we have . It follows that acts trivially on . Therefore, if fixes , then by the discussion in the preceding paragraph, and so we are done. On the other hand, if does not fix , then is a nontrivial loop based at a point on . So, the element fixes . Moreover, acts trivially on , and so does as well. Thus, . Finally, since , we have that , and so we are done. ∎
We now move on to the proof of Theorem B.
Proof of Theorem B.
Recall that we want to show that we have an exact sequence
where is equal to:
-
(a)
if .
-
(b)
if .
By Lemma 4.3 and the discussion preceding it, all that is left to show is that agrees with the subgroups given above.
We begin with the case . Recall that acts on by pushing the boundary component about a given loop. Since is not -adjacent to any other boundary components, it follows that acts trivially on . Therefore, , and so . This completes this case.
Next, suppose that . In this case, not all elements of are contained in . This is because dragging about loops may change the homology class of arcs connected to . In particular, if and is the class of arc with an endpoint in and the other elsewhere, then acts on via
See Figure 6 for an illustration. This implies that an element is in if and only if in . Thus,
which is what we wanted to show. ∎
2pt
\pinlabel at 205 150
\pinlabel at 145 190
\pinlabel at 235 170
\endlabellist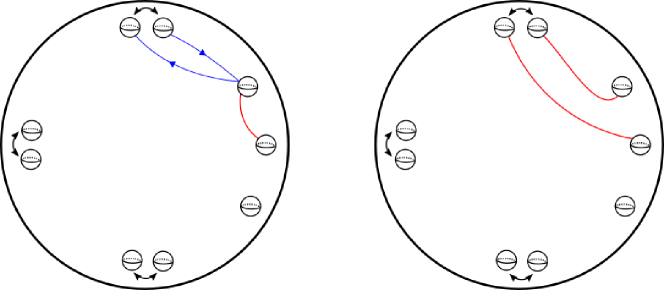
5 Generators
In this section, we will define our generators of . The definition of these generators will involve splitting and dragging boundary components, so we will discuss these processes in more detail first, then move on to the definitions.
Splitting along spheres.
Let be an embedded 2-sphere. By splitting along , we mean removing an open tubular neighborhood of from . If is nonseparating, the resulting manifold will be diffeomorphic to and if is separating, the result will be diffeomorphic to , where and . Notice that the resulting manifold is a submanifold of , and so we get a corresponding map if is nonseparating, or if is separating. In either case, this map sends sphere twists to sphere twists, and thus induces a map or , depending on whether or not separates .
Dragging boundary components.
Let be a boundary component of , and let be the embedding obtained by capping off . By Theorem 4.2, we have an exact sequence
where . Given , recall that the element is given by pushing about the loop . In the remainder of this section, we will be dragging multiple boundary components at a time. So, from now on we will write in order to keep track of which boundary component is being pushed.
Magnus generators.
We now move on to defining our generators for . In the case, we have that , where is the subgroup of acting trivially on homology. In [21], Magnus found the following generating set for .
Theorem 5.1 (Magnus).
Let . The group is generated by the -classes of the automorphisms
for all distinct with . Here, the automorphisms are understood to fix for .
2pt
\pinlabel at 332 280
\pinlabel at 262 385
\pinlabel at 175 271
\pinlabel at 262 175
\pinlabel at 140 420
\pinlabel at 311 481
\pinlabel at 66 345
\pinlabel at 66 184
\pinlabel at 122 87
\pinlabel at 296 49
\pinlabel at 446 420
\pinlabel at 490 324
\pinlabel at 490 213
\pinlabel at 437 131
\endlabellist
Our generating set will be inspired by Magnus’s, and will indeed reduce to it when . In order to choose a concrete collection of elements, we will need to make some choices. First, fix a basepoint and a set of oriented simple closed curves intersecting only at whose homotopy classes form a free basis for . We will call such a set a geometric free basis for . In addition, choose a corresponding sphere basis; that is, a collection of disjointly embedded oriented 2-spheres such that each intersects exactly once with a positive orientation and is disjoint from the other . Notice that splitting along the reduces it to a 3-sphere with boundary components. The submanifold will play a significant role throughout the remainder of this section because it will allow all of our choices made in the definitions to be unique. For each , let and be the boundary components of arising from the split along , where (resp. ) is the component lying on the positive (resp. negative) side of . We will also choose an ordering and an ordering for each . See Figure 7.
The following lemma will be helpful in showing that our generators lie in .
2pt
\pinlabel at 105 95
\pinlabel at 435 95
\pinlabel at 520 105
\pinlabel at 500 180
\pinlabel at 462 141
\endlabellist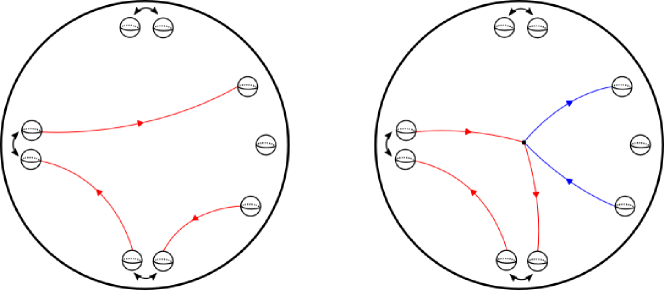
Lemma 5.2.
Let be as above, and suppose that is a properly embedded oriented arc connecting -adjacent boundary components of . Then the homology class of has the form
where is a loop based at , and is the unique arc (up to isotopy) in which has the same endpoints as .
Proof.
We may homotope such that it has the form , where (see Figure 8):
-
•
is the unique arc (up to isotopy) from the initial point of to the basepoint of ,
-
•
is the unique arc from to the endpoint of ,
-
•
.
Then,
as desired. ∎
Handle drags.
Let , and let be the unique (up to isotopy) properly embedded arc in connecting and which is disjoint from the . Choose a tubular neighborhood of that does not intersect any for . Let be the boundary component of which is not isotopic to or (notice that is diffeomorphic to a 2-sphere). Splitting along yields . Let be the boundary component coming from this split, and fix a basepoint . Fix an oriented arc from to which only intersects at . Since is a 3-sphere with spherical boundary components, is unique up to isotopy. The arc induces an isomorphism given by . Define . Then we define the handle drag for , where is the map induced by splitting along .
2pt
\pinlabel at 200 275
\pinlabel at 170 215
\pinlabel at 135 230
\pinlabel at 100 150
\pinlabel at 560 210
\endlabellist
To see that , notice that acts trivially on for , and acts on via . See Figure 9. This shows that acts trivially on homology classes of simple closed curves. Additionally, this shows that reduces to of the Magnus generators if .
Next, suppose that is an arc connecting -adjacent boundary components. By Lemma 5.2, we may write , where is a loop based at , and is the unique arc (up to isotopy) in which has the same endpoints as . We have seen that fixes the homology class of . Moreover, we may homotope such that it fixes the arc . Thus, fixes the homology class of , and we conclude that .
Commutator drags.
Let be distinct with . Split along to get , where . Fix basepoint and , and choose oriented arcs connecting and to , respectively. Just as in the construction of handle drags, and are unique up to isotopy. Let and for . Then, we define the commutator drags as and , respectively, where is the map induced by splitting along . See Figure 10.
Again, we see that acts trivially on for , the commutator drag sends to , and sends to . This shows that reduces to of the Magnus generators when .
Now, suppose that is an arc connecting -adjacent boundary components of . By Lemma 5.2, we may express in the form . We just saw that fixes . We may also homotope such that it fixes . Thus, fixes , and so .
2pt
\pinlabel at 109 225
\pinlabel at 155 205
\pinlabel at 100 150
\pinlabel at 150 100
\pinlabel at 60 240
\endlabellist
Boundary commutator drags.
Let and . Fix such that . Choose a basepoint . Let be the unique arc (up to isotopy) from to . Let for . Then, we define the boundary commutator drags .
It is clear from the definition that acts trivially on and arcs that do not have an endpoint on . Suppose that is an oriented arc with an endpoint on . Without loss of generality, suppose the terminal endpoint of lies on . Applying lemma 5.2, we may write , where is a loop based at and is the unique arc (up to isotopy) which shares endpoints with . We just saw that fixes the , and thus fixes the homology class . Therefore,
So, it follows that as well.
-drags.
The final type of elements we will define are called -drags, where is a partition of the boundary components of . Let and . Let be the unique 2-sphere (up to isotopy) which separates the boundary components of from the remaining boundary components and the . Splitting along gives , where is the number of boundary components in . Let be the boundary component coming from this splitting. Just as in the construction of the other drags, fix a basepoint and an oriented arc from to to get a basis of . See Figure 11. Then, we define the -drag , where is the map induced by splitting along .
To see why , first notice that we can isotope to fix all the . Next, if is an arc connecting -adjacent boundary components, we write as in Lemma 5.2. As we just noted, fixes , so it suffices to show that fixes the homology class of . If the endpoints of lie on boundary components in , then we may homotope such that it never crosses . Then, fixes . On the other hand, if the endpoints of lie on boundary components which are not in , then again we can homotope such that it does not cross , and then homotope such that it fixes . In either case, fixes the homology class of of , and so we conclude that .
2pt
\pinlabel at 210 192
\pinlabel at 100 150
\pinlabel at 282 197
\pinlabel at 298 222
\pinlabel at 235 240
\endlabellist
Images under capping.
Suppose we have an embedding given by capping off the boundary component . Let be the induced map, where is the partition of the boundary components of induced by . Using the geometric free basis and corresponding sphere basis for , we get a corresponding geometric free basis and sphere basis for . Moreover, the ordering on (and each ) induces an ordering on . We can repeat the process described throughout this section to define handle drags, commutator drags, boundary commutator drag, and -drags in , which we will denote by , , , and , respectively. With this setup, we find that:
-
•
-
•
-
•
if and if
-
•
if and if .
6 Finite Generation
Now that we have defined our collection of candidate generators for , we now move on to proving that they do in fact generate. The first step in this proof will be an induction on to reduce to the case of . This induction will rely on the following theorem of Tomaszewski [25] (see [24] for a geometric proof).
Theorem 6.1 (Tomaszewski).
Let be the free group on letters . The commutator subgroup of is freely generated by the set
where the superscript denotes conjugation.
We will also need the following lemma from group theory.
Lemma 6.2.
Consider an exact sequence of groups
Let be a generating set for . Moreover, assume that there are sets and such that is contained in the subgroup of generated by and . Then is generated by the set , where is a set consisting of one lift for every element .
Proof of lemma.
Let be the subgroup generated by , and let . Then the following diagram commutes and has exact rows:
The vertical maps are all inclusions, and hence injective. Also, by assumption, the map is surjective. Therefore, by the five lemma, all of the vertical maps are isomorphisms, and so we are done. ∎
We now prove Theorem C by proving the following stronger result.
Theorem 6.3.
The group is generated by handle, commutator, boundary commutator, and -drags for , .
Proof.
As mentioned above, we will prove this by induction on . The base case follows directly from Magnus’s Theorem 1.1.
If , fix a boundary component of and let be the partition containing . Let be an embedding obtained by capping off , and choose a basepoint . By Theorem B, there is an exact sequence
where if and otherwise. As we saw in the discussion at the end of Section 5, we can define the drags of and in a consistent way; that is, we can define our drags in such a way that takes handle drags to handle drags, commutator drags to commutator drags, and so on. By induction, is generated by the desired drags. Therefore, it suffices to show that is generated by our drags as well. If , then is precisely the subgroup of generated by the -drags, and so we are done in this case.
The case of is less straightforward since the commutator subgroup of a free group is not finitely generated when . However, this is not necessary for to be finitely generated by our collection of drags. We will appeal to Lemma 6.2. Suppose that . Then, by Theorem 6.1, the kernel of the Birman exact sequence is generated by elements of the form . First, notice that is the boundary commutator drag , where is the boundary component of being capped off. Moreover, we have seen that the handle drag acts on by . It follows that . Continuing this pattern, we see that
where is taken to be trivial. Therefore,
This shows that is contained in the subgroup of generated by boundary commutator and handle drags. Applying Lemma 6.2 (taking and ), we conclude that is generated by the desired drags. ∎
7 Partial Proof of Magnus’s Theorem
In this section, we will give a partial proof of Magnus’s Theorem 1.1, which constituted the base case in the proof of Theorem 6.3. As stated in the introduction, the original proof of Magnus’s Theorem involved two steps: showing that the elements and normally generate , and then showing that the subgroup generated by these elements is normal. We will give a proof of the first step here (Theorem D).
In order to establish this fact, we will examine the action of on a certain simplicial complex, and apply the following theorem of Armstrong [2]. We say that a group acts on a simplicial complex without rotations if every simplex is fixed pointwise by every element of its stabilizer, which we will denote by .
Theorem 7.1 (Armstrong).
Suppose the group acts on a simply-connected simplicial complex without rotations. If is simply-connected, then is generated by the set
Here is the 0-skeleton of .
Remark.
The nonseparating sphere complex.
The complex to which we will apply Theorem 7.1 will be the nonseparating sphere complex . Vertices of are isotopy classes of smoothly embedded non-nullhomotopic 2-spheres in , and has a -simplex if the spheres can be realized pairwise disjointly and their union does not separate . This is a subcomplex of the more ubiquitous sphere complex, which was introduced by Hatcher in [13] as a tool to explore the homological stability of and . In [13, Proposition 3.1], Hatcher proves the following connectivity result about .
Proposition 7.2 (Hatcher).
The complex is -connected.
In particular, is simply connected for . Recall that sphere twists act trivially on isotopy classes of embedded surfaces, and so we get an action of on . Notice that spheres in a simplex of necessarily represent distinct -classes. By Poincaré duality, elements of act trivially on , and so this implies that acts on without rotations. Thus, in order to apply Theorem 7.1, we must show that is simply-connected.
To do this, we will give a description of in terms of linear algebra. Fix an identification . Let be the simplicial complex whose vertices are rank 1 summands of , and there is a -simplex if is a rank summand of . There is a map defined as follows. Let be a vertex, and choose a sphere which represents . As noted above, elements of act trivially on . Therefore, the homology class does not depend on the choice of representative . We then define to be the span of in . It is clear that extends to simplices.
Lemma 7.3.
The map is an isomorphism of simplicial complexes.
Proof.
Let be an -simplex of . We must show that, up to the action of , there exists a unique -simplex of which projects to .
Let be a primitive element generating for , and extend this to a basis for . In Appendix B, we will prove Lemma B.2, which says that there exists a collection of disjoint embedded 2-spheres such that for . Then the simplex of maps to the under the composition
We will now show that is unique up to the action of . Suppose that is another simplex of which projects to . Since and bother project to , we may order and orient the spheres such that for . Again by Lemma B.2, we can extend and to collections of spheres and such that for . Notice that splitting along either of these collections reduces to a sphere with boundary components. Therefore, there exists some such that for all . Let be the image of . By construction, . Furthermore, fixes a basis for homology, and so . This completes the proof. ∎
This description of is advantageous because is known to be -connected, and hence simply connected for . The first proof of this fact is due to Maazen [20] in his unpublished thesis (see [8, Theorem E] for a published proof). Thus, we have shown that is sufficiently connected.
Corollary 7.4 (Maazen).
The complex is simply connected for .
As indicated in Theorem 7.1, the stabilizers of spheres play an important role in the proof of Theorem D, and so we introduce notation for them here. If is an isotopy class of embedded sphere in , we denote by the stabilizer of in , and define . We now move on to the proof of Theorem D.
Proof of Theorem D.
We will induct on . The base cases are easy; and are both trivial. Suppose now that is -normally generated by handle and commutator drags. We must now show that is -normally generated by handle and commutator drags as well. By Theorem 7.1, Proposition 7.2, and Corollary 7.4, it suffices to show that is generated by -conjugates of these drags for all . Let be the geometric free basis of identified with our fixed generating set of , and let be a corresponding sphere basis. Use these bases to construct the handle and commutator drags as in Section 5. Recall that handle drags correspond to the automorphisms of Magnus’s generators, and commutator drags correspond to . We will first show that is -normally generated by handle and commutator drags.
Splitting along yields a copy of . Let be the tubular neighborhood of removed in this splitting, and let and be the boundary components of . Then this splitting induces a surjective map , which restricts to a map , where . This map is also surjective.
Use the bases and to construct the handle, commutator, boundary commutator, and -drags in . By our induction hypothesis combined with the proof of Theorem 6.3, these drags -normally generate . Notice that with these choices of drags, the map takes handle and commutator drags to handle and commutator drags. Moreover, takes boundary commutator drags in to commutator drags in , and takes the -drag to the handle drag . Thus, is -normally generated by handle and commutator drags.
Finally, let be an arbitrary vertex of . Since is nonseparating, there exists some such that . It follows that
Since is -normally generated by handle and commutator drags, it follows that is generated by -conjugates of handle and commutator drags, which is what we wanted to show. ∎
8 Computing the abelianization
In this section, we compute the abelianization of the group , proving Theorem E. For the Torelli subgroup of the mapping class group of a surface, this was done by Johnson [17]. Some key tools used in this computation are the Johnson homomorphisms
where . Johnson showed that these homomorphisms are the abelianization maps modulo torsion if . For , Andreadakis [1] and Bachmuth [3] used an analogous homomorphism (where now ) to show that
We will begin by recalling the definition of , along with the computation of the ranks of and , and then proceed to the case of multiple boundary components.
The Johnson homomorphism.
Recall that , and the subgroup is precisely those automorphisms which act trivially on . The goal is to construct a homomorphism , where .
First, we claim that the group is isomorphic to , where denotes the commutator subgroup of . To see this, consider the short exact sequence
Passing to the five-term exact sequence in homology, we get the sequence
where denotes the group of co-invariants of with respect to the action of (induced by the conjugation action of on ). The map is clearly an isomorphism, and so it follows that the map is an isomorphism as well. This proves our claim because . Let be the projection. Following the definitions above, we see that is defined by
where and denote the classes of and in , respectively.
Next, let . Then is nullhomologous for all , and therefore lies in . We define the map via
We now check that is a homomorphism. Let . Applying the relation , we get
since . This shows that is indeed a homomorphism. Furthermore, since is abelian, the map factors through the abelianization, inducing a map . Therefore, we have a map
sending to . We now check that is a homomorphism. Let . Then
since fixes . Thus, is the desired homomorphism.
We now move on to computing the image of our generators under . Since we are dealing with the case of one boundary component, boundary commutator drags are unnecessary since they are products of -drags. Fix a basepoint , and choose a basis of . Construct the handle, commutator, and -drags with respect to this basis.
Handle drags.
Recall that the handle drag acts on by sending to , and fixing the remaining basis elements. Therefore,
Thus, is the homomorphism (and all other generators are sent to ).
Commutator drags.
Notice that the product of commutator drags is equal to a commutator of handle drags. Therefore, only the are needed in our generating set, and we can disregard the from now on. Recall that acts on by sending to . Therefore,
It follows that is the map .
-drags.
Next, we note that the product
| (5) |
is trivial in . For a justification of this fact, see the proof of the claim at the end of Theorem A.2. It follows that the -drags are also redundant in our generating set for , and can be removed.
Abelianization of .
To compute the rank of the abelianization of , we use the following lemma.
Lemma 8.1.
Let be a group and a finite generating set for . Suppose that is a surjective homomorphism. Then .
Proof.
Let denote the free group on the set . Since is abelian, the homomorphism factors through the abelianization to give a map , which is also surjective. Additionally, by the universal property of free groups, we have a map . Passing to the abelianizations induces a map . Since is a generating set for , this map is also surjective. It follows that is a surjective map between free abelian groups of equal rank, and is hence an isomorphism. Thus, is an isomorphism as well. ∎
From the discussion in the preceeding paragraphs, we have a generating set for of size
(since -drags can be written as a product of handle drags), and the image of this generating set spans , which also has dimension . Therefore, by Lemma 8.1, the group has rank .
To compute the rank of , consider the quotient map , whose kernel is the subgroup of inner automorphisms (or -drags under our geometric interpretation of ). We compute the image of a -drag under :
Since is nontrivial, does not descend to a map . However, the images span a subgroup of isomorphic to (where the isomorphism is given by ). So, induces a map . Just as the element given in Equation (5) is trivial in , the product is trivial in for all . Thus, we may throw out handle drags from our generating set to obtain a generating set for of size . Since has rank , Lemma 8.1 implies that has rank as well. This verifies Theorem 1.2 from the introduction.
Multiple boundary components.
We now move on to the case of multiple boundary components. Just as we did when constructing our drags in Section 5, fix an ordering and an ordering for each . We cap off the boundary components of each as follows:
-
•
If , we attach a copy of to the single boundary component of .
-
•
If , we attach a copy of to these boundary components.
-
•
If , we follow the same rules as above, except we introduce an additional boundary component in the piece glued to .
Capping off the boundary components in this way gives an embedding
where the boundary component of lies in the piece attached to . This embedding induces a map . We obtain a similar map by attaching a disk to the boundary component of . In Appendix A, we will prove Theorem A.2, which says that the composition
is injective. It follows that is injective as well. Therefore, to compute the rank of the abelianization of , it suffices to compute the rank of the abelianization of its image in . Let , and let denote the composition
Our goal now becomes computing the images of handle, commutator, boundary commutator, and -drags under .
Choosing a basis.
To carry out this computation, it will be helpful to choose bases for and carefully. For simplicity, we will assume that . The case of is more straightforward. Fix a basepoint and a basis for . Choose a corresponding sphere basis . We define our drags in with respect to these bases.
Next, choose a basepoint , and an oriented arc from to (this is possible since the boundary component of lies on the piece attached to ). For , let . Then is a partial basis for . We wish to extend this to a full basis. Throughout the definition of this extended basis, we encourage the reader to follow along in Figure 12.
For each boundary component of , fix a point (leaving as before). For each , let be the unique oriented arc (up to isotopy) in from to . For , define . In Figure 12, the loops and are of this form.
Next, let . If , let be an oriented loop based at which generates the fundamental group of the copy of attached to . Then we define . In Figure 12, the curve is an example of such a loop.
On the other hand, suppose . For , let be the unique (up to isotopy) oriented curve in from to . Then, define
The curve is an example of this type of loop in Figure 12.
2pt \pinlabel at 95 280
at 280 105 \pinlabel at 370 100 \pinlabel at 430 143
at 85 200 \pinlabel at 65 160
at 320 393
at 550 360
at 530 70
\endlabellist
Let . For , let if , and otherwise. Then the collection
forms a free basis for .
Computations and relations.
We now move on to the computation of the images of our collection of drags under . These computations are straightforward, and are summarized in Figure 13. We see from these computations that there is a relation between the images of -drags and Handle Drags. Namely,
| (6) |
for all . As we saw in the case of one boundary component, this is because
| (7) |
in . Additionally, we see a relation between the image of boundary commutator drags:
| (8) |
for all and with . This relation holds because
| (9) |
in .
| Drag | Action on | Image under | |||
| () | |||||
| () | () | () | |||
| () | |||||
| () | () | ||||
| () | () | ||||
| () | () | () | |||
| () | () |
Contributions to abelianization.
From the computations and relations above, we see that the handle drags and commutator drags together still contribute dimensions to the abelianization of . There are boundary commutator drags, but the relations given in Equation (8) kill off of these in the abelianization (though we can also remove this many elements from our generating set by using Equation (9)). Finally, the number of -drags is , but of them are killed in the abelianization by Equation (6) (and again, we may remove elements from our generating set by Equation (7)). Adding these all together, we find that the image of has rank
Moreover, we can reduce our generating set (using Equations (7) and (9)) to a set of size as well. Thus, by Lemma 8.1, the group has rank , which proves Theorem E.
Appendix A Injectivity of the inclusion map
We end this paper with a proof of the following facts, which are surely known to experts, but for which we do not know a reference. They are significant because they allow us to realize the groups (and hence ) as subgroups of . We will begin with a low-genus case.
Lemma A.1.
The induced map is injective for any embedding .
Proof.
By Laudenbach [18], the group , where the nontrivial element acts on by inverting the generator. Therefore, is the class of the automorphism
This automorphism is not an inner automorphism for any , so is injective. ∎
Theorem A.2.
Fix such that , and let be an embedding. The induced map is injective if and only if no component of is diffeomorphic to a 3-disk.
Proof.
Suppose first that some component of is diffeomorphic to a disk, and let be the boundary component of capped off by this disk. By the Birman exact sequence (Theorem 4.2), dragging this boundary component along any nontrivial loop will give a nontrivial element in the kernel of .
Suppose now that no component of is a disk. We will first prove the theorem in the case , and then move on to the general result.
Case 1: Suppose we have an embedding . Since no component of is a disk, . If , then we are done by Lemma A.1, so we may assume that . Fix a basepoint on the boundary of , and choose a free basis of . The embedding induces an injection which identifies with a free summand of . This allows us to extend to a free basis of . Given , the image is the class of the automorphism generated by
Suppose that is an inner automorphism. If , then fixes at least two generators of , and thus must be trivial. It follows that is trivial as well. On the other hand, if , then fixes . Since is inner, must conjugate by a power of . However, if conjugates by a nontrivial power of , then would not act as an automorphism on , which is a contradiction. Thus, is trivial, and so is trivial as well.
In summary, we have shown that is an inner automorphism if and only if is trivial, which implies that is injective.
2pt \pinlabel at 214 240
at 330 155 \pinlabel at 345 205 \pinlabel at 330 300
at 490 112 \pinlabel at 467 320 \pinlabel at 480 408
at 245 100
\pinlabel at 140 230
\endlabellist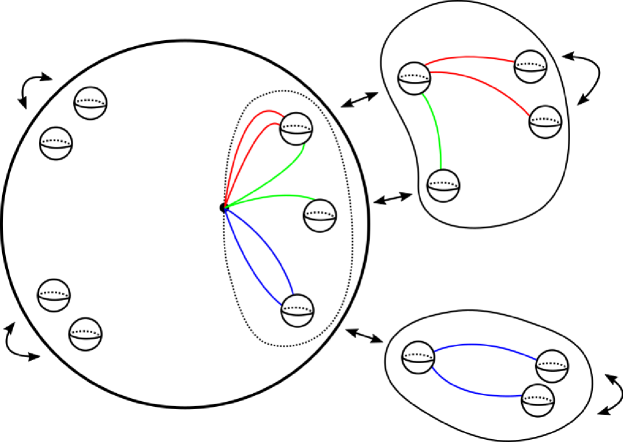
Case 2: Next, suppose that is an embedding, where . Let be the boundary components of . Let be a 2-sphere which separates into and (see Figure 14). Then we have a composition of inclusions
Let be the map induced by inclusion. By the preceding case, is injective. Let , and suppose that . By repeated applications of the Birman exact sequence (Theorem 4.2), has the form , where and is a boundary drag of along a loop . Fix a basepoint , and let be representative of the free homotopy class of . Choose a free basis for . Extend this to a free basis for such that for each , the loop intersects the set exactly twice: once when exiting , and once when re-entering (see Figure 14). For , let be the boundary component through which leaves , and let be the boundary component through which it returns. Then is the class of the automorphism given by
By assumption, this automorphism is an inner automorphism. Suppose that conjugates by a reduced word in the . Since is an automorphism of , it follows that . We will show that this implies that is trivial by induction on the reduced word length of .
For the base case, suppose that the word length of is 0. Then and are both trivial. Since is injective, is trivial as well. Suppose now that some is non-nullhomotopic. Since no component of is a disk, there exists some which passes through , where . In other words, either or . This is a contradiction because then . Thus, all are nullhomotopic, and so is trivial. This completes the base case.
Next, suppose that has positive word length, and let be the last letter in the reduced form of . Then, , where the length of is less than that of . To avoid notational complexity, we will assume that , but the same argument works for any other . Consider the element
where is the handle drag of the -th handle about the first handle (see Section 5) and is obtained by dragging about a loop in the free homotopy class of . By construction, is the class of the automorphism which conjugates by . Therefore, is the class of the automorphism which conjugates by . By our induction hypothesis, this implies that is trivial.
Claim.
The element is trivial.
Proof.
Let be a 2-sphere which separates into and , where the is the handle containing . Let be the map induced by this inclusion. Notice that , where drags the boundary component of about the nontrivial loop in the positive direction. We saw in the proof of Lemma A.1 that , and the nontrivial element acts on by inversion. However, the element acts trivially on , and is thus trivial itself. It follows that is trivial as well. ∎
Combining the claim with the fact that is trivial, we find that is trivial. This completes the induction, and so we conclude that is injective.
∎
Appendix B Realizing homology classes as spheres
In this section, we prove a result used in the proof of Lemma 7.3 which involves realizing bases of as collections of 2-spheres. Recall that . This identification induces a homomorphism which takes a mapping class to its action on homology.
Lemma B.1.
The map is surjective.
Proof.
First, notice that . This identification also induces a homomorphism which is well-known to be surjective. Indeed, this map factors as
where is the quotient map, and sends an automorphism class to its action on . Therefore, if we choose our identifications and to agree with Poincaré duality, then and are the same map. Thus, is surjective. ∎
Lemma B.2.
Let be a basis for , and let be a collection of disjoint embedded oriented 2-spheres in which satisfy for . Then can be extended to a collection of disjoint embedded oriented 2-spheres such that for .
Proof.
We will induct on . The base case is trivial. So assume , and let and be as stated. There are two cases.
First, suppose that . If we identity with , then by Lemma B.1 the resulting map is surjective. Choose any collection of disjoint non-nullhomotopic embedded 2-spheres. Then is a basis for . Since acts transitively on ordered bases of and the map is surjectve (Lemma B.1), there exists some such that for all . In other words, , and so is the desired collection of spheres.
Next, suppose that . Splitting along gives an embedding . Notice that the induced map is an isomorphism. Let for , and let and be the boundary components of . Capping the two boundary components of with disks and , we get another embedding . This embedding induces a surjective map whose kernel is generated by . Let for , and let for . By our induction hypothesis, we can extend the collection to a collection of disjoint embedded oriented 2-spheres in such that for . Moreover, since the disks and used to cap the boundary components of are contractible, we may isotope such that they are disjoint from and . Let for . If for all , then is the desired collection, and we are done. However, since the kernel of is generated by , we have
where . Note that for . To fix this, we may surger parallel copies of or onto such that it has the correct homology class. The process is as follows (see Figure 15):
-
(i)
If , take parallel copies of , which we denote by . If instead , take to be parallel copies of . Order the such that is furthest from its respective boundary component, then , and so on.
-
(ii)
Let be a properly embedded arc connecting the positive side of to which does not intersect any of the other or .
-
(iii)
Surger and together via a tube running along .
-
(iv)
Repeat steps (ii) and (iii) for the remaining .
Once we have carried out this process for all the , we will have obtained a collection collection of spheres whose homology classes are exactly . Thus, is the desired collection of 2-spheres. ∎
2pt \pinlabel at 135 110 \pinlabel at 125 70 \pinlabel at 100 45
at 330 120 \pinlabel at 330 80
at 530 80
\endlabellist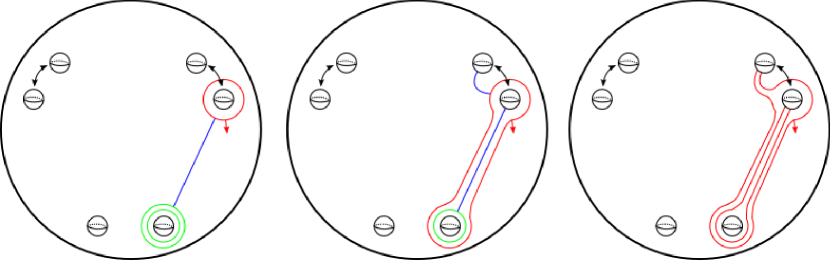
References
- [1] S. Andreadakis. On the automorphisms of free groups and free nilpotent groups. Proc. London Math. Soc. (3), 15:239–268, 1965.
- [2] M. A. Armstrong. On the fundamental group of an orbit space. Proc. Cambridge Philos. Soc., 61:639–646, 1965.
- [3] S. Bachmuth. Induced automorphisms of free groups and free metabelian groups. Trans. Amer. Math. Soc., 122:1–17, 1966.
- [4] Jessica E. Banks. The Birman exact sequence for 3-manifolds. Bull. Lond. Math. Soc., 49(4):604–629, 2017.
- [5] Mladen Bestvina, Kai-Uwe Bux, and Dan Margalit. Dimension of the Torelli group for . Invent. Math., 170(1):1–32, 2007.
- [6] Tara Brendle, Nathan Broaddus, and Andrew Putman. The mapping class group of connect sums of . Preprint, 2020.
- [7] Martin R. Bridson and Karen Vogtmann. Automorphism groups of free groups, surface groups and free abelian groups. In Problems on mapping class groups and related topics, volume 74 of Proc. Sympos. Pure Math., pages 301–316. Amer. Math. Soc., Providence, RI, 2006.
- [8] Thomas Church, Benson Farb, and Andrew Putman. Integrality in the Steinberg module and the top-dimensional cohomology of . Amer. J. Math., 141(5):1375–1419, 2019.
- [9] Matthew Day and Andrew Putman. A Birman exact sequence for . Adv. Math., 231(1):243–275, 2012.
- [10] Matthew Day and Andrew Putman. The complex of partial bases for and finite generation of the Torelli subgroup of . Geom. Dedicata, 164:139–153, 2013.
- [11] Matthew Day and Andrew Putman. A Birman exact sequence for the Torelli subgroup of . Internat. J. Algebra Comput., 26(3):585–617, 2016.
- [12] Benson Farb and Dan Margalit. A primer on mapping class groups, volume 49 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 2012.
- [13] Allen Hatcher. Homological stability for automorphism groups of free groups. Comment. Math. Helv., 70(1):39–62, 1995.
- [14] Allen Hatcher and Nathalie Wahl. Stabilization for the automorphisms of free groups with boundaries. Geom. Topol., 9:1295–1336, 2005.
- [15] Allen Hatcher and Nathalie Wahl. Stabilization for mapping class groups of 3-manifolds. Duke Math. J., 155(2):205–269, 2010.
- [16] Craig A. Jensen and Nathalie Wahl. Automorphisms of free groups with boundaries. Algebr. Geom. Topol., 4:543–569, 2004.
- [17] Dennis Johnson. The structure of the Torelli group. III. The abelianization of . Topology, 24(2):127–144, 1985.
- [18] F. Laudenbach. Sur les -sphères d’une variété de dimension . Ann. of Math. (2), 97:57–81, 1973.
- [19] François Laudenbach. Topologie de la dimension trois: homotopie et isotopie. Société Mathématique de France, Paris, 1974. With an English summary and table of contents, Astérisque, No. 12.
- [20] Hendrik Maazen. Homology stability for the general linear group. thesis, 1951.
- [21] Wilhelm Magnus. Über -dimensionale Gittertransformationen. Acta Math., 64(1):353–367, 1935.
- [22] Andrew Putman. Cutting and pasting in the Torelli group. Geom. Topol., 11:829–865, 2007.
- [23] Andrew Putman. Obtaining presentations from group actions without making choices. Algebr. Geom. Topol., 11(3):1737–1766, 2011.
- [24] Andrew Putman. The commutator subgroups of free groups and surface groups. Preprint, 2021.
- [25] Witold Tomaszewski. A basis of Bachmuth type in the commutator subgroup of a free group. Canad. Math. Bull., 46(2):299–303, 2003.
- [26] Nathalie Wahl. From mapping class groups to automorphism groups of free groups. J. London Math. Soc. (2), 72(2):510–524, 2005.