DACT-BERT: Differentiable Adaptive Computation Time for an Efficient BERT Inference
Abstract
Large-scale pre-trained language models have shown remarkable results in diverse NLP applications. Unfortunately, these performance gains have been accompanied by a significant increase in computation time and model size, stressing the need to develop new or complementary strategies to increase the efficiency of these models. In this paper we propose DACT-BERT, a differentiable adaptive computation time strategy for BERT-like models. DACT-BERT adds an adaptive computational mechanism to BERT’s regular processing pipeline, which controls the number of Transformer blocks that need to be executed at inference time. By doing this, the model learns to combine the most appropriate intermediate representations for the task at hand. Our experiments demonstrate that our approach, when compared to the baselines, excels on a reduced computational regime and is competitive in other less restrictive ones.
1 Introduction
The use of pre-trained language models based on large-scale Transformers (Vaswani et al., 2017) has gained popularity after the release of BERT (Devlin et al., 2019). The usual pipeline consists of finetuning BERT by adapting and retraining its classification head to meet the requirements of a specific NLP task. Unfortunately, the benefits of using a powerful model are also accompanied by a highly demanding computational load. In effect, current pre-trained language models such as BERT have millions of parameters, making them computationally intensive both during training and inference.
While high accuracy is usually the ultimate goal, computational efficiency is also desirable. The use of a demanding model not only causes longer processing times and limits applicability to low-end devices, but it also has major implications in terms of the environmental impact of AI technologies (Schwartz et al., 2019). As an example, Strubell et al. (2019) provides an estimation of the carbon footprint of several large NLP models, including BERT, concluding that they are becoming unfriendly to the environment.
Fortunately, recent works have shown that behind BERT’s immense capacity, there is considerable redundancy and over-parametrization (Kovaleva et al., 2019; Rogers et al., 2020). Consequently, others works have explored strategies to develop efficient and compact versions of BERT. One such strategy known as dynamic Transformers consists of providing BERT with an adaptive mechanism to control how many Transformers blocks are used (Xin et al., 2020; Liu et al., 2020; Zhou et al., 2020).
In this paper, we present DACT-BERT, an alternative to current dynamic Transformers that uses an Adaptive Computation Time mechanism (Graves, 2016) to control the complexity of the processing pipeline of BERT. This mechanism controls the number of Transformer blocks executed at inference time by using additional classifiers. This allows resulting models to take advantage of the information already encoded in intermediate layers without the need to run all layers. Specifically, our model integrates DACT, a fully differentiable variant of the adaptive computation module (Eyzaguirre and Soto, 2020) that allows us to train a halting neuron after each Transformer block. This neuron indicates the confidence the model has on returning the correct answer after executing said block. We use the DACT algorithm to determine when the answer stabilizes in a given output using the halting neuron, and halt once we are sure running more blocks cannot change the output.
2 Related Work
Several architectures have been designed to avoid overcomputing in Transformer-based models. According to Zhou et al. (2020), there are two groups.
2.1 Static Efficient Transformers
The first strategy is to distill the knowledge of pretrained models into more efficient "students". Models such as PKD-BERT (Sun et al., 2019), TinyBERT (Jiao et al., 2020), and DistilBERT (Sanh et al., 2020) compress the knowledge of large models (teachers) into more compact or efficient ones to obtain similar performance at a reduced computation or memory cost. While these approaches effectively reduce the total calculation needed to execute the model, they are limited in the same way as BERT, they do not take into account that some examples could be less complicated than others and always use the same amount of computation.
2.2 Dynamic Transformers
Recently, a series of algorithms have been proposed to reduce computation in Transformer language models based on early exiting (Kaya et al., 2019). Models such as DeeBERT (Xin et al., 2020), FastBert (Liu et al., 2020), and PABEE (Zhou et al., 2020) introduce intermediate classifiers after each Transformer block. These classifiers are then trained independently from these blocks (not end-to-end). At inference, a “halting criterion” is used to dynamically determine the number of blocks needed to perform a specific prediction. Instead of using a brittle confidence approach (Guo et al., 2017) to determine when to stop, recent approaches rely on computing the Shannon’s entropy of the output probabilities (Xin et al., 2020; Liu et al., 2020), an agreement between intermediate classifiers (Zhou et al., 2020), or a trained confidence predictor (Xin et al., 2021).
Unlike previous works that use heuristic proxies of models confidence to decide when to halt, DACT-BERT is based on a learning scheme that induces the model to halt when it predicts that its current answer will not change with further processing. As an illustrative example consider a difficult input. Here, our model could “understand” that further processing steps are superfluous and decide to stop early, even if its current answer has a low confidence. On the other hand, existing early stopping models would keep wasting computation because the confidence is low.
3 DACT-BERT: Differentiable Adaptive Computation Time for BERT
Dynamic early stopping methods use a proxy of model confidence to decide when it is safe to cut computation. In this work our signaling module, DACT, approximates this gating mechanism with a soft variant that allows our model to independently learn the confidence function. This mechanism can then be used to detect when stable results are obtained, allowing for the reduction of the total number of steps necessary for a given prediction. The original formulation of DACT (Eyzaguirre and Soto, 2020) applies this module to recurrent models. In our case, we adapt the formulation to the case of Transformer based architectures, namely BERT.
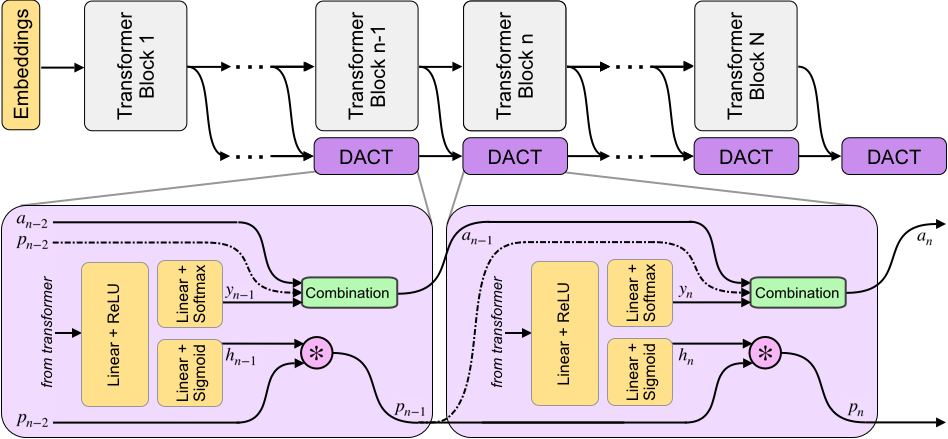
As shown in Figure 1, DACT-BERT introduces additional linear layers after each computational unit, similar to the off-ramps in DeeBERT (Xin et al., 2020) or the student classifiers in the work of Liu et al. (2020). However, differently from previous approaches, each -th DACT module also computes an scalar confidence score (or halting value) in addition to the output vector . Following Devlin et al. (2019), both, and , are estimated by using the classification token () that is included in BERT as part of the output representation of each layer. During training all the output vectors and halting values are combined to obtain and the final predicted probabilities following an expression that can be rewritten as the weighted average of all intermediate outputs multiplied by a function of the confidences of earlier blocks. Then, during inference, the confidence scores can be used to reduce computation.
The model output is built inductively by using a monotonically decreasing function of the model confidence to interpolate between the current step’s answer and the result of the same operation from the previous step. We then train the model to reduce the classification loss of the final output with a regularizer that induces a bias towards reduced computation. Unlike the regularizer used by Eyzaguirre and Soto (2020), we use the following:
| (1) |
where is a hyper-parameter used to moderate the trade-off between complexity and error. We find empirically that our changes help convergence and further binarize the halting probabilities.
Notably, the formulation is end-to-end differentiable. This allows to fine-tune the weights of the underlying backbone (i.e. the Transformer and embedding layers) using a joint optimization with the process that trains the intermediate classifiers.
3.1 Dynamic Computation at Inference
By construction, the DACT algorithm allows us to calculate upper and lower bounds of each of the output classes after any computation step (i.e. Transformer block). At inference, execution halts once the predicted probabilities for the topmost class are shown to remain higher than that of the runner-up class (and by extension, of any other class). That is, the model stops executing additional blocks once it finds that doing so will not change the class with maximum probability in the output because the difference between the top class and the rest is insurmountable. Therefore, the halting condition remains the same as the original DACT formulation (Eyzaguirre and Soto, 2020). More details of the method can be find at Appendix A.
3.2 Training
The training of the module follows a two step process. First, the underlying Transformer model must be tuned to the objective task. This ensures a good starting point onto which the DACT module can then be adapted to and speeds up convergence. This is followed by a second fine-tuning phase where the complete model is jointly trained for the task. This differs slightly from existing dynamic Transformer methods, which first pre-train the backbone and then freeze it to modify only the classifier weights.
4 Results
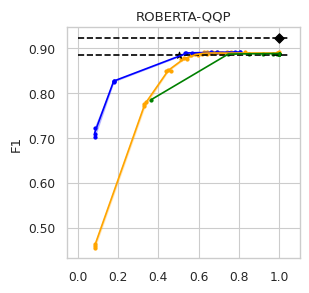
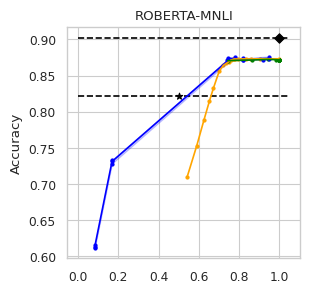
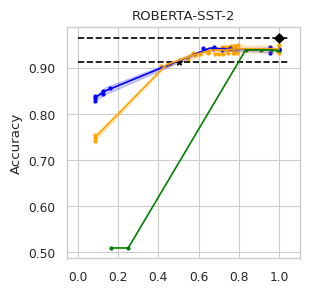
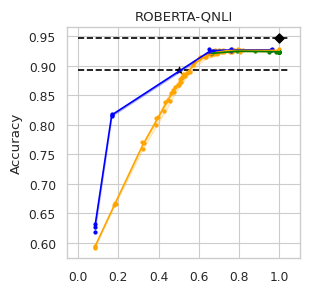
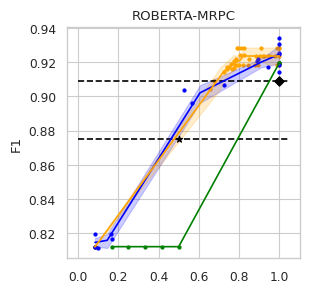
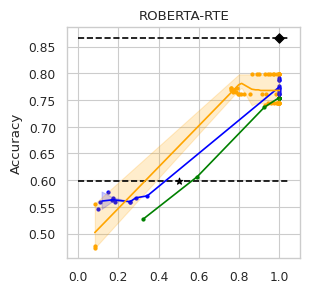
4.1 Experimental Setup
We tested our method using both BERT and RoBERTa backbones, evaluating both models on six different tasks from the GLUE benchmark (Wang et al., 2018). We use DeeBERT (Xin et al., 2020) and PABEE (Zhou et al., 2020) as our dynamic baselines, using the same backbones for a fair comparison, and the respective non-adaptive backbones along with DistilBERT (Sanh et al., 2020) as static baselines. More details are presented at the Appendix B.
4.2 Computational Efficiency
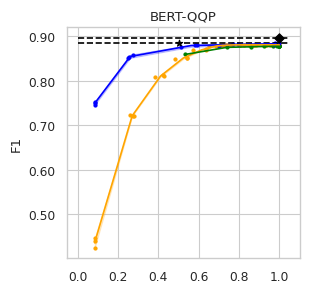
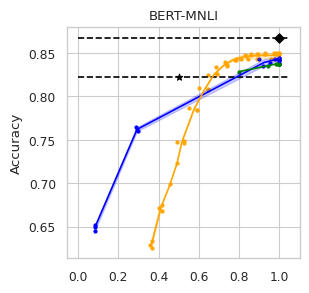
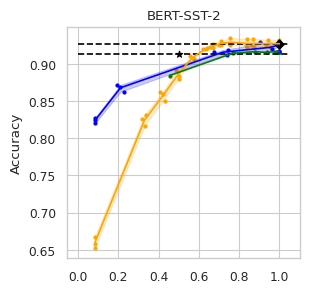
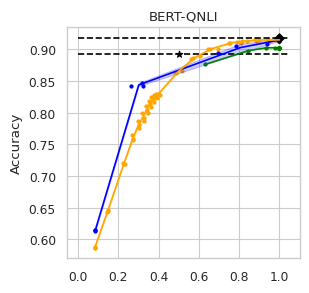
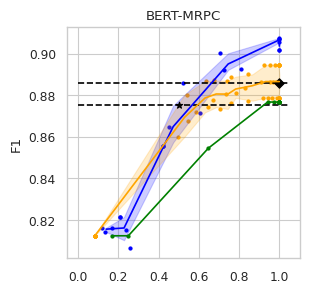
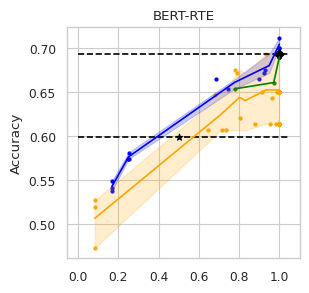
To compare the trade-off that exists between computation efficiency and the performances obtained with it, we computed efficiency-performance diagrams for the validation set. Efficiency was measured as the proportion of Transformer layers used compared to the total number of layers in their static counterparts. The specific metrics for performance are those suggested in the GLUE paper (Wang et al., 2018) for each task.
In our experiments we fine-tune the backbone model for the GLUE tasks using the default values of the hyper-parameters. For the second stage we vary the value of in Equation (1) to compute our computation-performance diagram curves, selecting from a set of fixed values for all the experiments: . By modifying this hyperparameter in DACT we can manage the amount of computation the model will perform and record the performance it managed to achieve at this level.
Similarly, using DeeBERT to create the computation-performance diagrams the entropy threshold was varied continuously in increments of . For PaBEE we fluctuate the patience value between 1 and 12, effectively trying out the full range. The results for the unmodified static backbones are also included as a reference, as are the results obtained by the half-depth DistilBERT pre-trained model.
The area under the curve (AUC) in the Performance vs. Efficiency plot shown in Figure 2 shows our approach improves the trade-off between precision and computation. As was to be expected, all models perform similarly when saving little computation as they replicate the results achieved by the non-adaptive BERT backbone that performs a similar number of steps. On the other hand, when using limited amounts of computation our model outperforms the alternatives in almost every task, especially in tasks for with more training data available. We attribute this advantage in trading off computation and performance to fine-tuning of the backbone weights for reduced computation. Intuitively, as we move away from the 12 step regime for which the underlying static model was trained, more modification of the weights is required. Recall that of all the Dynamic Transformer algorithms only DACT-BERT can modify the Transformer weights because of its full-differentiability.
Importantly, because our model learns to regulate itself, it shows remarkable stability in the amount of calculation saved. As the same values of ponder penalties give rise to similar efficiency outputs. By contrast, DeeBERT proves to be highly sensitive to the chosen value for the entropy hyperparameter. The robustness of our model appears to come from learning the efficiency mechanism rather than relying on a somewhat arbitrary heuristic for its control.
5 Conclusions
This work explored the value of using the DACT algorithm with pre-trained Transformer architectures. This results in a fully differentiable model that explicitly learns how many Transformers blocks it needs to perform a specific task. Our results show that our approach, DACT-BERT, outperforms the current dynamic Transformer architectures in several tasks when significantly reducing computation.
References
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Computational Linguistics.
- Eyzaguirre and Soto (2020) Cristobal Eyzaguirre and Alvaro Soto. 2020. Differentiable adaptive computation time for visual reasoning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 12817–12825.
- Graves (2016) A. Graves. 2016. Adaptive computation time for recurrent neural networks. ArXiv, abs/1603.08983.
- Guo et al. (2017) Chuan Guo, Geoff Pleiss, Yu Sun, and Kilian Q. Weinberger. 2017. On calibration of modern neural networks.
- Jiao et al. (2020) Xiaoqi Jiao, Yichun Yin, Lifeng Shang, Xin Jiang, Xiao Chen, Linlin Li, Fang Wang, and Qun Liu. 2020. Tiny{bert}: Distilling {bert} for natural language understanding.
- Kaya et al. (2019) Yigitcan Kaya, Sanghyun Hong, and Tudor Dumitras. 2019. Shallow-deep networks: Understanding and mitigating network overthinking. In International Conference on Machine Learning, pages 3301–3310. PMLR.
- Kovaleva et al. (2019) Olga Kovaleva, Alexey Romanov, Anna Rogers, and Anna Rumshisky. 2019. Revealing the dark secrets of BERT. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 4365–4374, Hong Kong, China. Association for Computational Linguistics.
- Liu et al. (2020) Weijie Liu, Peng Zhou, Zhiruo Wang, Zhe Zhao, Haotang Deng, and Qi Ju. 2020. FastBERT: a self-distilling BERT with adaptive inference time. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 6035–6044, Online. Association for Computational Linguistics.
- Paszke et al. (2017) Adam Paszke, Sam Gross, Soumith Chintala, Gregory Chanan, Edward Yang, Zachary DeVito, Zeming Lin, Alban Desmaison, Luca Antiga, and Adam Lerer. 2017. Automatic differentiation in pytorch.
- Rogers et al. (2020) A. Rogers, O. Kovaleva, and A. Rumshisky. 2020. A primer in BERTology: What we know about how BERT works. ArXiv, abs/2002.12327.
- Sanh et al. (2020) Victor Sanh, Lysandre Debut, Julien Chaumond, and Thomas Wolf. 2020. Distilbert, a distilled version of bert: smaller, faster, cheaper and lighter.
- Schwartz et al. (2019) R. Schwartz, J. Dodge, N.A. Smith, and O. Etzioni. 2019. Green ai. ArXiv, abs/1907.10597.
- Strubell et al. (2019) E. Strubell, A. Ganesh, and A. McCallum. 2019. Energy and policy considerations for deep learning in NLP. ArXiv, abs/1906.02243.
- Sun et al. (2019) Siqi Sun, Yu Cheng, Zhe Gan, and Jingjing Liu. 2019. Patient knowledge distillation for BERT model compression. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 4323–4332, Hong Kong, China. Association for Computational Linguistics.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in neural information processing systems, pages 5998–6008.
- Wang et al. (2018) Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel Bowman. 2018. GLUE: A multi-task benchmark and analysis platform for natural language understanding. In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, pages 353–355, Brussels, Belgium. Association for Computational Linguistics.
- Wolf et al. (2019) Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Rémi Louf, Morgan Funtowicz, Joe Davison, Sam Shleifer, Patrick von Platen, Clara Ma, Yacine Jernite, Julien Plu, Canwen Xu, Teven Le Scao, Sylvain Gugger, Mariama Drame, Quentin Lhoest, and Alexander M. Rush. 2019. Huggingface’s transformers: State-of-the-art natural language processing. ArXiv, abs/1910.03771.
- Xin et al. (2020) Ji Xin, Raphael Tang, Jaejun Lee, Yaoliang Yu, and Jimmy Lin. 2020. DeeBERT: Dynamic early exiting for accelerating BERT inference. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 2246–2251, Online. Association for Computational Linguistics.
- Xin et al. (2021) Ji Xin, Raphael Tang, Yaoliang Yu, and Jimmy Lin. 2021. BERxiT: Early exiting for BERT with better fine-tuning and extension to regression. In Proceedings of the 16th Conference of the European Chapter of the Association for Computational Linguistics: Main Volume, pages 91–104, Online. Association for Computational Linguistics.
- Zhou et al. (2020) Wangchunshu Zhou, Canwen Xu, Tao Ge, Julian McAuley, Ke Xu, and Furu Wei. 2020. Bert loses patience: Fast and robust inference with early exit.
Appendix A Method Description
As illustrated in Figure 1 and shown in Algorithm 1, we define the discrete unit of computation to be a single BERT Transformer block, i.e. our gating mechanism will trade precision for additional complexity in discrete units of full additional Transformer blocks. In addition to the output vector with the predicted class probabilities, each -th DACT module computes an accompanying scalar confidence score (or halting value) .
Line 8 shows how the output vectors are combined using a function of the halting values () to obtain the final predicted probabilities. The intermediate results, accumulated in auxiliary variables , encode the models best guess after unrolling Transformer layers. Then, during inference, the confidence scores are used to effectively reduce computation by avoiding running all the layers using the appropriate halting criterion. Because no non-differentiable functions are used during training the algorithm is end to end differentiable.
The inductive formulation of lends itself to calculating upper and lower bounds on the probabilities of the output classes. If, during inference, it can be determined that the lowest possible value for the top-class in after running all remaining steps is still higher than the highest value for the runner-up class , then halting doesn’t change the output:
| (2) |
Appendix B Implementation Details
Our model was developed using PyTorch (Paszke et al., 2017) on top of the implementations released by Xin et al. (2020) and Zhou et al. (2020), as well as the HuggingFace Transformers library (Wolf et al., 2019). Because the focus of this paper was to introduce an alternative architecture of dynamic Transformers and not achieve state of the art results we use the default parameters and architectures from the Transformers library.
Both DeeBERT and DACT-BERT experiments were repeated three times to obtain the confidence intervals (95% confidence) shown in Figure 2, each time using a different random initialization for the weights in the auxiliary classifiers 111The random seeds were saved and will be published along with the code to facilitate replicating the results.. Results for FastBERT (Liu et al., 2020) are not reported since both DeeBERT and FastBERT use the same entropy-threshold halting criterion.
Each experiment was run using a single 11GB NVIDIA graphics accelerator, which allows for training on the complete batch using 32-bit precision and without needing gradient accumulation.
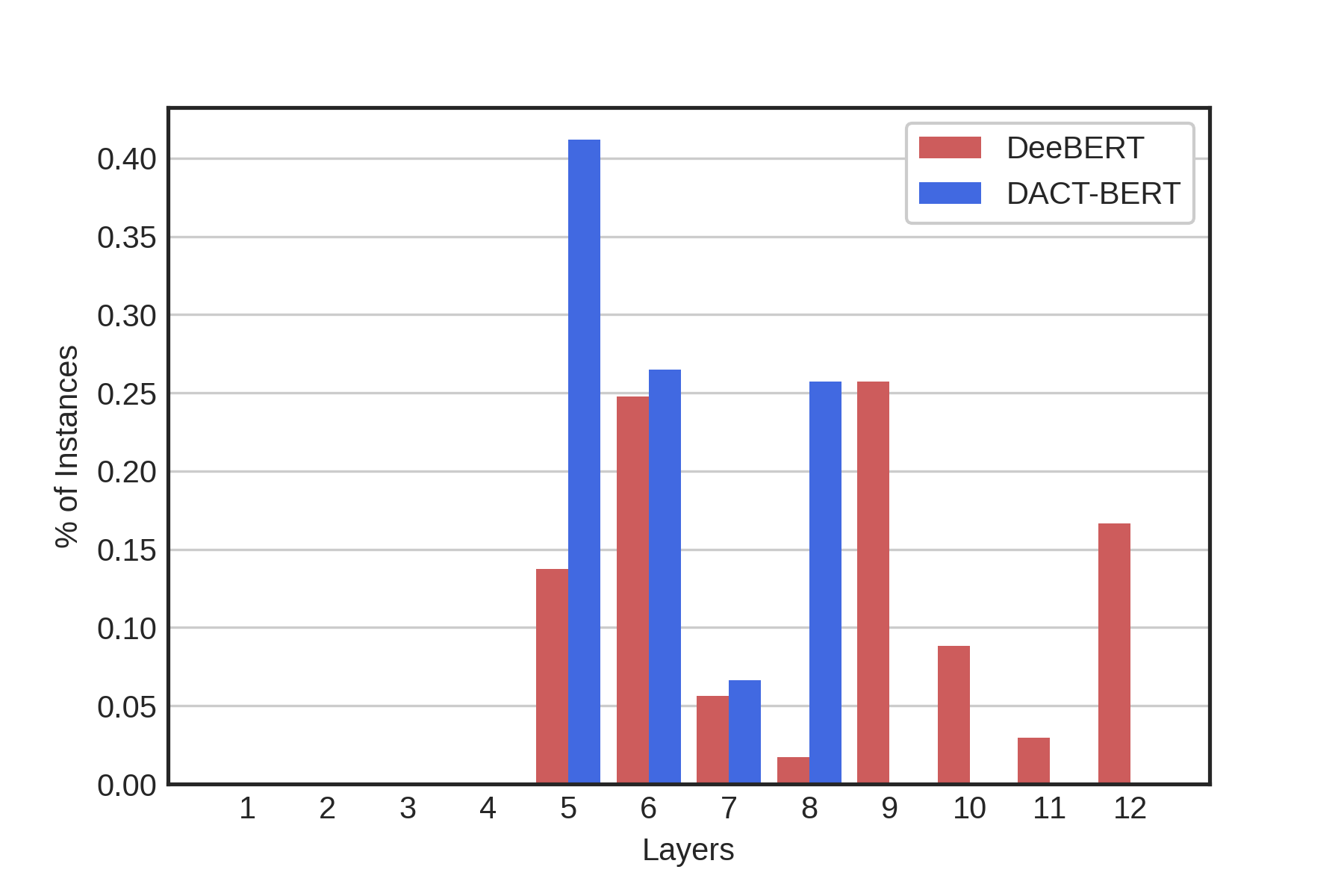
Appendix C Compressibility
We find our model uses less layers compared to DeeBERT (see example at Fig. 3), allowing us to prune the final layers. We explain this difference by noting that the entropy will remain high throughout the whole model for the case of difficult questions as it will be uncertain about the answer. On the other hand, any layer in DACT-BERT is capable of quitting computation if it believes future layers cannot answer with more certainty than its own (regardless of how certain the model actually is).