Data-aided Sensing for Distributed Detection

In wireless sensor networks (WSNs), a set of sensors are deployed to perform environmental monitoring and send observations or measurements to a fusion center (FC) [1]. The FC is responsible for making a final decision on the physical phenomenon from the reported information. WSNs can be part of the Internet of Things (IoT) [2] [3] to provide data sets collected from sensors to various IoT applications.

In conventional WSNs, various approaches are studied to perform distributed detection with decision fusion rules at the FC [4]. The optimal decision fusion rules in various channel models have been intensively studied in the literature (see references in [5] [6]). In [7], efficient transmissions from sensors to the FC studied using the channel state information (CSI). Furthermore, in [8], cross-layer optimization is considered to maximize the life time of WSN when sensors’ measurements are correlated. In [9], the notion of massive multiple input multiple output (MIMO) [10] is exploited for distributed detection when the FC is equipped with a large number of antennas.

In a number of IoT applications, as in WSNs, devices’ sensing to acquire local measurements or data and uploading to a server in cloud are required. In cellular IoT, sensors are to send their local measurements to an access point (AP). While sensing and uploading can be considered separately, they can also be integrated, which leads to data-aided sensing (DAS) [11] [12]. In general, DAS can be seen as iterative intelligent data collection scheme where an AP is to collect data sets from devices or sensor nodes through multiple rounds. In DAS, the AP chooses a set of nodes at each round based on the data sets that are already available at the AP from previous rounds for efficient data collection. As a result, the AP (actually a server that is connected to the AP) is able to efficiently provide an answer to a given query with a small number of measurements compared to random polling.

In this paper, we apply DAS to distributed detection in WSNs. Due to the nature of DAS where sensor nodes sequentially send their measurements according to a certain order, distributed detection can be seen as sequential detection [13]. Clearly, if sensors’ measurements are independent and identically distributed (iid), the performance of distributed detection is independent of the uploading order. However, for correlated measurements, a certain order can allow an early decision or a reliable decision with a smaller number of sensors’ measurements. Thus, based on DAS, we can provide an efficient way to decide the order of sensor nodes for uploading, which can lead to a reliable decision with a smaller number of measurements. In particular, we derive an objective function based on the J-divergence [14] to decide the next sensor node in DAS for distributed detection.

The paper is organized as follows. The system model is presented in Section II. The notion of DAS is briefly explained and applied to ditributed detection in Sections III and IV. We present simulation results and conclude the paper with some remarks in Sections V and VI.

In this section, we present the system model for a WSN that consists of a number of sensor nodes and one AP that is also an FC for distributed detection [4]. Thus, throughout the paper, we assume that AP and FC are interchangeable.

Suppose that there are $K$ sensor nodes and denote by $z_{k}$ the local measurement of node $k$ as illustrated in Fig. 1. Each sensor is to send its local measurement to the AP. The AP is to choose one of $Q$ hypotheses, which are denoted by $\{\theta_{1},\ldots,\theta_{Q}\}$, based on the received local measurements. Provided that all $K$ measurements are available, the AP can make a decision based on the maximum likelihood (ML) principle as follows:

$\displaystyle q^{*}=\operatorname*{\arg\!\max}_{q}f(z_{1},\ldots,z_{K}\,|\,\theta_{q}),$

(1)

where $f(z_{1},\ldots,z_{K}\,|\,\theta_{q})$ represents the likelihood function of $\theta_{q}$ for given $\{z_{1},\ldots,z_{K}\}$.

For example, suppose that the $z_{k}$’s follow a Gaussian distribution with mean vector ${\bf m}_{q}$ and covariance matrix ${\bf R}_{q}$ under hypothesis $\theta_{q}$. In this case, (1) can be re-written as

	$\displaystyle q^{*}$	$\displaystyle=\operatorname*{\arg\!\max}_{q}\ln f({\bf z}\,|\,\theta_{q})$		(2)
		$\displaystyle=\operatorname*{\arg\!\min}_{q}({\bf z}-{\bf m}_{q})^{\rm T}{\bf R}_{q}^{-1}({\bf z}-{\bf m}_{q})+\ln\det({\bf R}_{q}),$		(3)

where ${\bf z}=[z_{1}\ \ldots z_{K}]^{\rm T}$ that is referred to as the complete information.

For a large number of sensor nodes, $K$, while a reliable decision can be made if all the measurements are uploaded to the AP, the time to receive all the measurements can be long due to a limited bandwidth, which results in a long decision delay. In particular, if only one sensor node is allowed to transmit at a slot time (in time division multiple access (TDMA)), the time to make a decision is equivalent to that to receive all the measurements, i.e., $K$-slot time (under the assumption that the processing time to choose a hypothesis according to (3) is negligible). As a result, in order to shorten the decision delay, a fraction of measurements can be used at the cost of degraded decision performance.

In this section, we briefly present the notion of DAS for joint sensing and communication to efficiently upload measurements of nodes [12] [15].

Suppose that only one node can upload its measurement at each round. Denote by ${\cal Z}(l)$ the set of local measurements that are available at the AP after iteration $l$. Then, for a certain objective function, denoted by $\Theta(\cdot)$, the AP can decide the next node to upload its local information as follows:

$$k(l+1)=\operatorname*{\arg\!\min}_{k\in{\cal K}^{c}(l)}\Theta(z_{k},{\cal Z}(l)),$$

(4)

where $k(l)$ is the index of the node that is to upload its local measurement at round $l$, ${\cal K}(l)$ represents the index set of the nodes associated with ${\cal Z}(l)$, and ${\cal K}^{c}(l)$ denotes the complement of ${\cal K}(l)$. Clearly, it can be shown that ${\cal K}(l)=\{k(1),\ldots,k(l)\}$. In (4), we can see that the selected node, say $k(l+1)$, at each round depends on the accumulated measurements from the previous rounds, ${\cal Z}(l)$, which shows the key idea of DAS.

The objective function in (4) varies depending on the application. As an example, let us consider an entropy-based DAS where the AP is to choose the uploading order based on the entropy of measurements. Since ${\cal Z}(l)$ is available at the AP after iteration $l$, the entropy or information of the remained measurements becomes ${\sf H}({\cal Z}^{c}(l)\,|\,{\cal Z}(l))$, where ${\sf H}(X|Y)$ represents the conditional entropy of $X$ for given $Y$. Thus, as in [15], the following objective function can be used for the node selection:

$$\Theta(z_{k},{\cal Z}(l))=\underbrace{{\sf H}({\cal Z}^{c}(l)\,|\,{\cal Z}(l))}_{\rm Remained\ Information}-\underbrace{{\sf H}(z_{k}\,|\,{\cal Z}(l))}_{\rm Updated\ Information},$$

(5)

which is the entropy gap, where ${\sf H}(z_{k}\,|\,{\cal Z}(l))$ is the amount of information by uploading the measurement from node $k$. Clearly, for fast data collection (or data collection with a small number of nodes), we want to choose the next nodes to minimize the entropy gap.

Note that ${\sf H}({\cal Z}^{c}(l)\,|\,{\cal Z}(l))$ is independent of $k$. Thus, the next node is to be chosen according to the maximization of conditional entropy is given by

$$k(l+1)=\operatorname*{\arg\!\max}_{k\in{\cal K}^{c}(l)}{\sf H}(z_{k}\,|\,{\cal Z}(l)).$$

(6)

That is, the next node should have the maximum amount of information (in terms of the conditional entropy) given that ${\cal Z}(l)$ is already available at the AP.

In [12], the mean squared error (MSE) between the total measurement ${\bf z}$ and its estimate is to be minimized in choosing the node at round $l+1$, i.e.,

$$\Theta(z_{k},{\cal Z}(l))={\mathbb{E}}\left[||{\bf z}-\hat{\bf z}(z_{k},{\cal Z}(l))||^{2}\,|\,{\cal Z}(l)\right],$$

(7)

where $\hat{\bf z}(z_{k},{\cal Z}(l))$ is the minimum MSE estimator of ${\bf z}$ for given $\{z_{k},{\cal Z}(l)\}$ and the expectation is carried out over ${\cal Z}^{c}(l)$, which is the subset of measurements that are not available before round $l$. Since the measurements are assumed to be Gaussian in [12], second order statistics can be used for DAS, which is called Gaussian DAS. After some manipulations, it can also be shown that

$$\Theta(z_{k},{\cal Z}(l))=-{\mathbb{E}}\left[|z_{k}-\hat{z}_{k}|^{2}\,\bigl{|}\,{\cal Z}(l)\right]+C,$$

(8)

where $C$ is constant and $\hat{z}_{k}={\mathbb{E}}[z_{k}\,|\,{\cal Z}(l)]$ is the conditional mean of $z_{k}$ for given ${\cal Z}(l)$. Thus, the next node can be selected as follows:

$$k(l+1)=\operatorname*{\arg\!\max}_{k\in{\cal K}^{c}(l)}{\mathbb{E}}\left[|z_{k}-\hat{z}_{k}|^{2}\,\bigl{|}\,{\cal Z}(l)\right].$$

(9)

For Gaussian measurements, the MSE, ${\mathbb{E}}\left[|z_{k}-\hat{z}_{k}|^{2}\,\bigl{|}\,{\cal Z}(l)\right]$, is proportional to the conditional entropy, ${\sf H}(z_{k}\,|\,{\cal Z}(l))$. Thus, Gaussian DAS is also to minimize the entropy gap in selecting nodes, i.e., Gaussian DAS is also the entropy-based DAS.

In this section, we apply DAS to distributed detection. We first consider the entropy-based DAS to decide the next node in distributed detection. Then, another approach is proposed, which has the objective function based on the J-divergence.

In this section, we present simulation results with LLRs. For each average LLR, the results of 500 independent runs are used. In simulations, we assume that the $z_{k}$’s are jointly Gaussian with $K=50$ and $Q=2$. For comparisons, we consider the three node selection criteria: J-DAS (i.e., (18)), entropy-based DAS (i.e., (10)), and random selection.

For the first simulation, we assume that

$\displaystyle\bar{z}_{k;1}=A\cos\left(\frac{\pi}{10}(k-1)\right),\ \bar{z}_{k;2}=A\sin\left(\frac{\pi}{10}(k-1)\right),$

(26)

where $A>0$ is the amplitude of the mean signal. In addition, the covariance matrix of ${\bf z}$ under $\theta_{q}$ is given by

$$[{\bf R}_{q}]_{k,t}=\sigma^{2}(\rho_{q})^{|k-t|},\ k,t=1,\ldots,K,$$

(27)

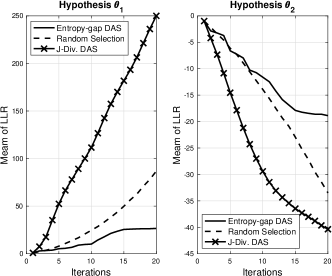
where $\rho_{1}=\frac{3}{4}$ and $\rho_{2}=-\frac{3}{4}$, and $\sigma^{2}$ represents the noise variance. The signal-to-noise ratio (SNR) is defined as ${\sf SNR}=\frac{A^{2}}{2\sigma^{2}}$. In Fig. 2, the average LLR is shown as a function of iterations. When $\theta_{1}$ is correct, it is shown that the LLR increases with the number of samples or iterations. Clearly, the performance of J-DAS outperforms those of entropy-based DAS and random selection. In other words, when a decision is made with a small number of iterations or samples in distributed detection, J-DAS can help provide reliable outcomes compared to the others.

It is interesting to see that the entropy-based DAS does not provide a good performance in distributed detection as shown in Fig. 2. The entropy-based DAS is to choose the node that has the most uncorrelated measurement as shown in (10). In fact, such a measurement needs not contribute to maximizing the difference between the hypotheses.

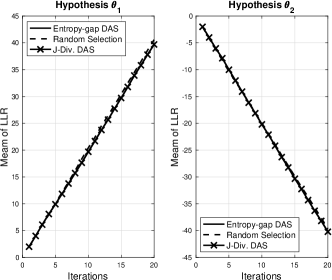
For the next simulation, we consider the case of iid measurements. That is, ${\bf R}_{q}=\sigma^{2}{\bf I}$ for all $q\in\{1,2\}$. In addition, it is assumed that $\bar{z}_{k;1}=A$ and $\bar{z}_{k;2}=-A$ for all $k$. As mentioned earlier, in this case, the performance is independent of the uploading order, which can be confirmed by the results in Fig. 3.

In this paper, the notion of DAS has been exploited to provide a good performance of distributed detection in WSN with a smaller number of sensors that upload their measurements. In particular, a J-divergence based node selection criterion was proposed for DAS, which was referred to as J-DAS, so that the measurement from the next node can maximize LLR. From simulation results, it was shown that LLR increased rapidly as the number of iterations increased when J-DAS was employed.

There would be a number of further research topics. Among those, as in [17], the application of J-DAS to distributed machine learning for classification is interesting. The performance analysis of J-DAS would also be another topic to be studied in the future.