DCPT/21/86,
DESY-21-174,
IPPP/21/43,
MCNET-21-14,
SAGEX-21-33
HEJ 2.1: High-energy Resummation with Vector Bosons and Next-to-Leading Logarithms
University of Durham, Durham, DH1 3LE, UK
b School of Physics and Astronomy, Monash University, Clayton, VIC 3800, Australia
c Higgs Centre for Theoretical Physics, University of Edinburgh,
Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK
d Deutsches Elektronen-Synchrotron DESY,
Platanenallee 6, 15738 Zeuthen, Germany)
Abstract
We present version 2.1 of the High Energy Jets (HEJ) event generator for hadron colliders. HEJ is a Monte Carlo generator for processes at high energies with multiple well-separated jets in the final state. To achieve accurate predictions, conventional fixed-order perturbative QCD is supplemented with an all-order resummation of large high-energy logarithms. The new version 2.1 now supports processes with final-state leptons originating from a charged or neutral vector boson together with multiple jets, in addition to processes available in earlier versions. Furthermore, the all-order resummation is extended to include an additional gauge-invariant class of subdominant logarithmic corrections. HEJ 2.1 can be obtained from https://hej.hepforge.org.
1 Introduction
High Energy Jets (HEJ) is a Monte Carlo event generator for processes involving two or more jets. It implements the eponymous formalism for the all-order summation of high-energy logarithms in developed in [1, 2, 3]. This summation is necessary to obtain a good description of events with large invariant masses or large rapidity separations between the outgoing particles. Extensive reviews of the formalism can be found in [4, 5].
HEJ has been validated against data in numerous studies on pure multijet production [6, 7, 8, 9], production of a leptonically decaying W boson together with two or more jets [10, 11, 12], and the production of multiple jets together with two charged leptons, created from an intermediate photon or Z boson [13]. A further particularly interesting channel is the gluon-fusion production of a Higgs boson together with two or more jets. It constitutes the dominant background in measurements of Higgs boson production in weak boson fusion (VBF), and the application of typical VBF cuts projects out a region of phase space where the summation of high-energy logarithms yields significant corrections [14]. For this process, as well as for pure multijet production, the original leading-logarithmic (LL) summation was supplemented with a numerically important gauge-invariant subset of the next-to-leading-logarithmic (NLL) corrections to achieve a better description away from the asymptotic high-energy limit [4].
A complete redesign allowed to extend the matching between resummation and fixed-order predictions to the highest multiplicities [15], taking into account at the same time quark mass corrections in the gluon-fusion production of a Higgs boson together with jets [16]. This revised matching procedure, initially implemented for pure multijet and Higgs boson plus jets production, is the foundation of HEJ 2 [17].
Here, we present HEJ 2.1. This new version elevates the fixed-order matching for the aforementioned processes involving an intermediate W or Z boson or photon to the superior HEJ 2 procedure. Furthermore, it includes a new subset of NLL corrections for pure multijet production and the production of a W boson together with jets. With these additions, HEJ 2.1 supersedes all earlier HEJ versions. We briefly describe the addition of the processes involving intermediate vector bosons and the new NLL corrections associated with the emission of additional quark-antiquark pairs in section 2. In section 3, we give an explicit example demonstrating how HEJ 2.1 can be used to supplement leading-order descriptions of the production of two leptons with jets with high-energy resummation. We conclude in section 4.
2 Improvements over previous versions
The most significant improvements over previous versions of HEJ are the addition of high-energy resummation for the production of two leptons together with two or more jets and the inclusion of NLL corrections involving the production of an additional quark-antiquark pair. In the following, we briefly summarise how these new processes are described in the High Energy Jets formalism. A more detailed description of both the underlying formalism and the improvements discussed here is given in [5]. The changes are summarised in table 1.
| Process | LL | NLL unordered gluon | NLL quark-antiquark |
|---|---|---|---|
| 2 jets | HEJ 2.0 | HEJ 2.0 | HEJ 2.1 |
| H + 2 jets | HEJ 2.0 | HEJ 2.0 | — |
| W + 2 jets | HEJ 2.1 | HEJ 2.1 | HEJ 2.1 |
| Z/ + 2 jets | HEJ 2.1 | HEJ 2.1 | — |
2.1 Leading-logarithmic resummation in HEJ 2
In HEJ 2, fixed-order predictions are supplemented with high-energy resummation in the following way. First, a number of leading-order events are generated. Then, for each event, it is determined whether the corresponding matrix element contributes at a logarithmic accuracy that is included in the current state-of-the art HEJ resummation. While HEJ currently includes partial NLL resummation, we restrict the following discussion to LL resummation for the sake of clarity.
To identify event configurations contributing at LL accuracy, we order incoming and outgoing particles according to rapidity, see figure 1. We then draw a leading-order auxiliary diagram with as many -channel gluons as possible. It should be stressed that this diagram only serves to determine the logarithmic order and is never used to compute the actual matrix element. A configuration contributes at LL accuracy iff the number of -channel gluons is maximal, i.e. if no other rapidity ordering of an equivalent set of final-state particles allows a diagram with a larger number of -channel gluon exchanges. By “equivalent” we mean that we do not distinguish between parton flavours, such that all final states shown in figure 1 are treated on the same footing.
 |
 |
 |
 |
If the matrix element of the currently considered event contributes at a logarithmic order that is covered by the resummation, we replace the original event with a number of newly generated events. These new events add further gluon emissions, while preserving the rapidities of the original jets and non-parton particles. Details of the procedure are given in [15]. In order to obtain an all-order resummed prediction, while at the same time retaining leading-order accuracy, the newly generated events are reweighted by a factor
| (1) |
where is the all-order resummed matrix element in the high-energy limit and its leading-order truncation. The bar denotes the sum (average) over outgoing (incoming) helicities and colours.
The HEJ matrix elements are the only process-specific ingredient in the resummation procedure. In the following, we recall their general structure and give results for the new processes included in HEJ 2.1.
2.2 Leading-logarithmic matrix elements
We are interested in the LL HEJ matrix elements for processes , where denotes any number of additional colourless outgoing particles. With the exception of , particles are ordered according to rapidity. is therefore the incoming parton in the backward direction, with flavour , and the parton in the forward direction. The most backward outgoing parton is with rapidity , followed by gluons with rapidities and the most forward outgoing parton with rapidity .
In the absence of , the outgoing flavours match the incoming ones, i.e. . This is still the case if a charged lepton-antilepton pair is produced. However, for this process we require a virtual photon or Z boson, which implies that at least one of and has to be a quark or antiquark. When producing a pair of charged lepton and a neutrino, or , a quark or antiquark couples to a virtual W boson. This means that the respective flavour is changed, so that either or .
2.2.1 Matrix element without interference
The square of the LL HEJ matrix element in the absence of interference has the following structure, illustrated also in figure 2:
| (2) |
and are the momenta of and , with the outgoing momenta ordered by ascending rapidity, and the -channel momenta related by . The first -channel momentum is process-dependent; if there are no additional particles it is given by . represents the local momenta associated with the production of .
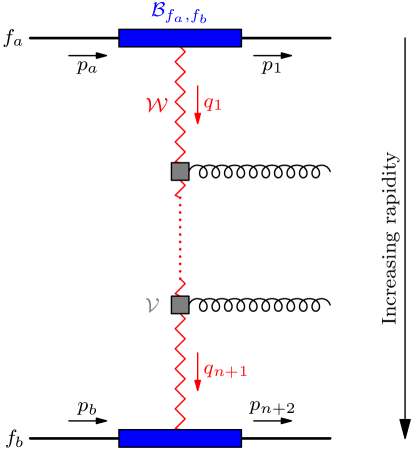
is the square of the Born-level matrix element for the process without any additional gluon emissions, . describes the real gluon emission corrections to this process, whereas accounts for the virtual corrections. Both are process-independent and given by
| (3) | ||||
| (4) |
where is the component of the -channel momentum that is perpendicular to the beam axis. Using a short-hand notation, we have suppressed the dependence of the Lipatov vertex function on the incoming and outgoing momenta:
| (5) |
Explicit expressions for and the regularised Regge trajectory are derived in [1, 18].
The only process-dependent part is the Born function . It is derived via matching to full QCD, i.e. by requiring that is equivalent to the corresponding QCD amplitude in the high-energy limit. In the High Energy Jets formalism, exact gauge invariance and superior numerical agreement with full QCD over the whole phase space are achieved by only neglecting a gauge-invariant subset of the terms that are supressed in the high-energy limit. Specifically, only those terms that would break the following -channel factorised form are discarded.
| (6) |
and are colour factors depending on the incoming partons. For an (anti-)quark the corresponding factor is simply . Gluons lead to more complex factors involving also their kinematics [2]. Finally, is the contraction of two (generalised) currents, with double bars indicating the sum over helicities. In pure QCD, is absent and the current contraction is simply
| (7) |
where is the current
| (8) |
for helicity .
A pair consisting of a lepton111We do not distinguish between charged leptons and neutrinos here. with momentum and an antilepton with momentum is produced via a virtual vector boson coupling to either of the partons or . We can account for this process by modifying the corresponding current. Assuming without loss of generality a coupling to , we obtain
| (9) |
with the generalised current [5]
| (10) |
is the vector boson momentum, its coupling to the fermion , its mass and the width. Note that the emission of a virtual vector boson off implies that the first -channel momentum is now given by .
2.2.2 Interference
So far, we have not considered interference between different channels. For charged lepton plus neutrino production interference can arise between emission of the virtual W boson off parton and emission off parton if both are (anti-)quarks of the same flavour. This contribution is numerically small as it requires a crossing of the quark line and is therefore neglected in HEJ 2.1. Crossing is not required in the production of a charged lepton-antilepton as the quark line does not change flavour and same-flavour initial states are no longer required making it numerically more significant. What is more, there is an additional interference between production via a photon and production via a Z boson. Since both effects are non-negligible, we consider the squared LL matrix element with full interference for this process. Here, we have to distinguish between -channel momenta for emission of the vector boson off parton and for emission off . They are given by
| (11) | ||||||
| (12) |
The square of the matrix element then reads [13]
| (13) |
where we have introduced the combined current and the notation (cf. equation (9))
| (14) |
The equation (13) for the square of the matrix element with interference assumes that both and are (anti-)quarks. If, for instance, is a gluon instead, terms involving do not contribute and the expression simplifies to equation (2) with the current contraction in equation (9) and .
2.3 Next-to-leading logarithmic corrections
There are two sources of NLL contributions. First, the matrix elements for LL configurations, discussed in section 2.2, receive NLL corrections. These types of corrections will be considered in future HEJ versions. Second, configurations that do not allow the maximal number of gluonic -channel exchanges according to the discussion in section 2.1 only contribute at higher logarithmic orders. For instance, this is the case for configurations where a gluon is produced outside the rapidity order mandated for LL configurations. Ordering all particles apart from according to their rapidity, these processes are denoted by , where is an (anti-)quark and with an (anti-)quark . These “unordered gluon” NLL configurations were considered in [4] and are already accounted for in HEJ 2.0.
Studying the production of a W boson together with jets, it is found that further numerically important NLL configurations arise through the production of additional pairs of a quark and an antiquark . Note that in general the flavours and can be different if there is a W boson coupling. We distinguish between “central” production,
| (15) |
and “extremal” production
| (16) | ||||
| (17) |
In either case, the description is independent of the relative rapidity ordering between and . In fact, the squares of the matrix elements for these configurations have the same structure as at LL accuracy, see equation (2). Differences only arise in the Born function and in the expressions for the -channel momenta . HEJ 2.1 supports resummation of these configurations for pure multijet production ( is absent) and the production of a leptonically decaying W boson together with multiple jets ( or ).
2.3.1 Pure multijet production
We first consider multijet production with an extremal quark-antiquark pair. For this, we assume the (same-flavour) quark-antiquark pair to be emitted in the backward direction; forward emission is completely analogous. The configurations in question are of the form
| (18) |
In the High Energy Jets formalism the production of the pair from an incoming gluon is described by an effective current , where is a colour index in the adjoint representation, the helicity of the incoming gluon, and () the momentum and helicity of the outgoing (anti-)quark. An explicit expression for is derived in [5]. The structure of the matrix element is illustrated in figure 3(a). Note that due to the emission of the pair the first -channel momentum is now given by . In summary, the Born function contributing to the matrix element with extremal production reads
| (19) |
where
| (20) |
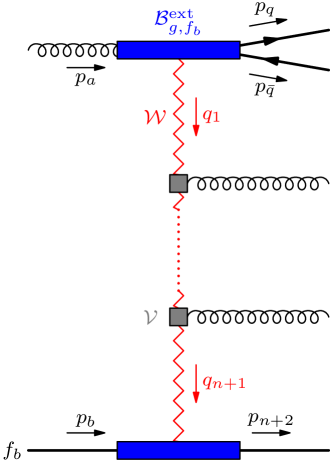
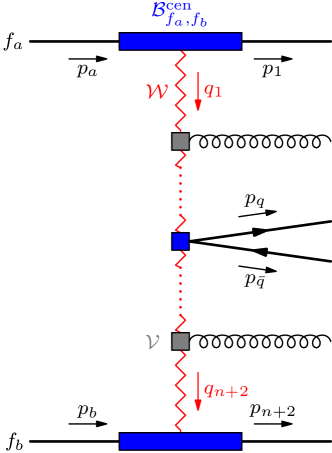
Central production is depicted in figure 3(b) and corresponds to the configuration
| (21) |
The central production is described by an effective vertex that can be absorbed into the current contraction. The Born function then reads
| (22) |
with the current contraction
| (23) |
where is derived in [5]. The -channel momenta are given by
| (24) |
2.3.2 W + jets production
If an additional leptonically decaying W boson is produced we have to distinguish between two cases. Similarly to the LL configurations, the W boson may couple to a fermion line associated with an incoming quark or antiquark. This causes a flavour change or . Assuming without loss of generality the latter possibility the corresponding configurations read
| (25) | |||||
| (26) |
where or .
The Born functions for both configurations are obtained from the corresponding pure-jets Born functions in equations (19) and (22) by replacing the standard current with the generalisation for the emission of a vector boson , see equation (10).
The second possibility is a coupling of the W boson to the fermion line of the produced , where now . For extremal production, the Born function is obtained from equations (19) and (20) by replacing the current with a new effective current . In complete analogy the central production is described by replacing with a new effective vertex in equations (22), (23). Explicit results for and were obtained in [5].
3 Application: W + jets production
In order to demonstrate the recent additions to HEJ we now show in detail how to obtain a prediction for the production of a W boson with multiple jets. Specifically, we consider the process jets. The parameters are listed in table 2.
| Collider energy | TeV | |
| Scales | ||
| PDF set | CT18NLO | |
| Electroweak input parameters | ||
| GeV | ||
| GeV | ||
| GeV | ||
| GeV | ||
| Jet definition | anti- [19] | |
| GeV |
3.1 Fixed-order input
In order to run , we have to generate leading-order input events. Any generator producing event files in the Les Houches Event File (LHEF) [20] format can be used to this end. Here, we use Sherpa [21] with the following run card. The entries are explained in detail in the Sherpa documentation.
Note that we have chosen a minimum jet transverse momentum of GeV instead of the GeV listed in table 2. The reason for this is that the HEJ resummation can change the transverse momenta of the jets slightly compared to the input leading-order events. It is therefore recommended to choose a minimum transverse momentum that is at least smaller in the fixed-order generation. It is also prudent to ensure that the final predictions do not change when choosing an even smaller value.
The contribution from events containing such “soft” jets with transverse momenta below the value required in the final analysis is numerically small. This means that a significant amount of computing time can be saved by generating two separate input event samples: one sample with low statistics in which each event contains at least one soft jet, and one large sample without any soft jets. We then apply resummation separately to each of the samples. Since the two samples cover distinct regions of the fixed-order phase space, the final prediction is simply the set of all generated events. For simplicity, we do not consider this optimisation in the following.
With the above Run.dat run card, an event file events_W2j.lhe can be generated by running
in the same directory. The generated events will contain exactly two jets, but it is straightforward to generate higher-multiplicity samples by increasing the required number of jets in FastjetFinder, adding the corresponding number of 93 entries to the Process final state, and adjusting the name of the output file in the EVENT_OUTPUT. HEJ can then be used to merge samples with different multiplicities. Typically, the contribution of higher jet multiplicities in the analysis will be decreasing, and it is often enough to consider at most four or five jets. One can save computing time at the price of sacrificing leading-order accuracy by using the HEJ fixed-order generator (HEJFOG) for high multiplicities. An example is shown in appendix A.
3.2 Resummation with HEJ
In addition to the fixed-order input, HEJ also requires a configuration file. A template config.yml is included in the HEJ source code. Adopting the current set of parameters from table 2 and enabling resummation for all supported NLL configurations we get
We can now generate HEJ events and calculate the total resummed cross section. If HEJ is not installed, it can still be run using the Docker virtualisation software [22] and the following command.
If a HEJ installation is available, we can instead run
If HEJ was compiled with support for Rivet [23],222The HEJ Docker container includes all optional dependencies. the generated events can be forwarded directly to the MC_WJETS analysis by adding the following lines to config_Wjets.yml before running HEJ:
Another possibility is to create an output event file for manual analysis. After compiling HEJ with support for the HepMC 2 [24] format, we can add the following entry to config_Wjets.yml:
We can then run HEJ as before and feed the generated events into the MC_WJETS analysis with
Results for higher jet multiplicities are obtained in the same way after adjusting the file names in the configuration files and run commands. To guarantee statistical independence it is also recommended to change the seed in config_Wjets.yml. To obtain a prediction that is inclusive in jet multiplicity, we combine the Rivet output with333In older Rivet versions yodamerge –add can be used instead of yodastack.
Finally,
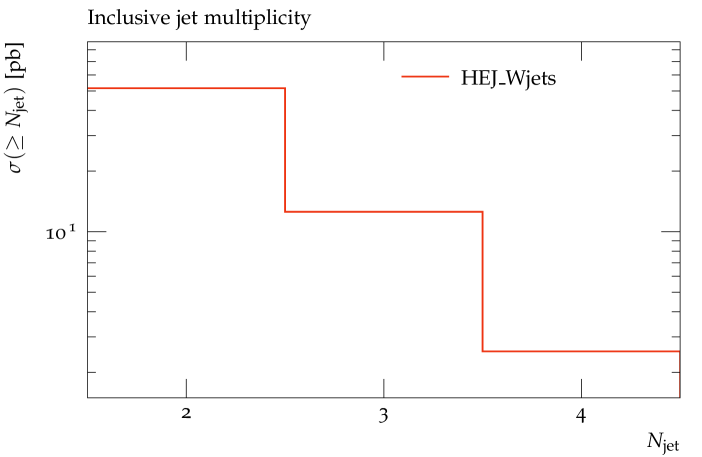
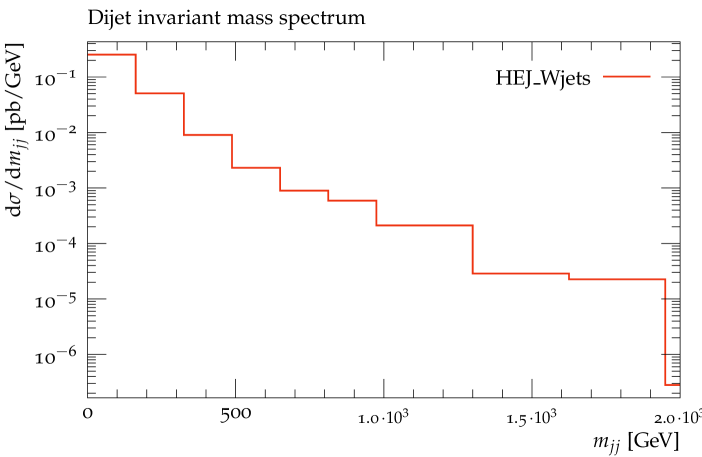
produces analysis plots. As examples, we show the inclusive -jet cross sections and the invariant mass distribution of the two hardest jets obtained from fixed-order input events with up to four jets in figure 4.
4 Conclusions
This article accompanies the release of the event generator, HEJ 2.1 which provides predictions for hadronic colliders which contain contributions at all orders in to achieve leading-logarithmic accuracy in . The output is given as exclusive events meaning that predictions can be obtained for arbitrary experimental cuts and analyses.
Here, after a brief outline of the general HEJ formalism, we have described the new extensions which have broadened the scope of the all-order predictions. Specifically, new matrix elements which allow for interference between channels with different assignments of effective -channel momenta have been developed to give an accurate description of jets (section 2.2.2). Secondly, the full set of NLL contributions corresponding to processes which have no LL component have been incorporated through the derivation of necessary additional Born processes (section 2.3). These form a well-defined, gauge-invariant subset of the full NLL corrections.
Finally, we have provided a worked example explicitly showing all the steps necessary to generate predictions for jets.
Acknowledgements
We are pleased to acknowledge funding from the UK Science and Technology Facilities Council, the Royal Society, the ERC Starting Grant 715049 “QCDforfuture”, the Marie Skłodowska-Curie Innovative Training Network MCnetITN3 (grant agreement no. 722104), and the EU TMR network SAGEX agreement No. 764850 (Marie Skłodowska-Curie).
Appendix A W + jets production with the HEJ fixed-order generator
The generation of fixed-order events with high jet multiplicities can become prohibitively expensive in computing time. In such cases the HEJ fixed-order generator (HEJFOG) can be used to quickly obtain results in the high-energy approximation. A typical use case is to produce HEJ input files with exact leading-order accuracy up to a given jet multiplicity as discussed in section 3.1 and supplement them with high-multiplicity event files produced with the HEJFOG.
As an example, we slightly modify the configuration file configFO.yml included in the HEJ source code to produce events for the process jets.
References
- [1] J. R. Andersen and J. M. Smillie, Constructing All-Order Corrections to Multi-Jet Rates, JHEP 1001 (2010) 039, [0908.2786].
- [2] J. R. Andersen and J. M. Smillie, The Factorisation of the t-channel Pole in Quark-Gluon Scattering, Phys.Rev. D81 (2010) 114021, [0910.5113].
- [3] J. R. Andersen and J. M. Smillie, Multiple Jets at the LHC with High Energy Jets, JHEP 1106 (2011) 010, [1101.5394].
- [4] J. R. Andersen, T. Hapola, A. Maier and J. M. Smillie, Higgs Boson Plus Dijets: Higher Order Corrections, JHEP 09 (2017) 065, [1706.01002].
- [5] J. R. Andersen, J. A. Black, H. M. Brooks, E. P. Byrne, A. Maier and J. M. Smillie, Combined subleading high-energy logarithms and NLO accuracy for W production in association with multiple jets, JHEP 04 (2021) 105, [2012.10310].
- [6] ATLAS collaboration, G. Aad et al., Measurement of dijet production with a veto on additional central jet activity in collisions at TeV using the ATLAS detector, JHEP 09 (2011) 053, [1107.1641].
- [7] CMS collaboration, S. Chatrchyan et al., Measurement of the inclusive production cross sections for forward jets and for dijet events with one forward and one central jet in collisions at TeV, JHEP 06 (2012) 036, [1202.0704].
- [8] CMS collaboration, S. Chatrchyan et al., Ratios of dijet production cross sections as a function of the absolute difference in rapidity between jets in proton-proton collisions at TeV, Eur. Phys. J. C 72 (2012) 2216, [1204.0696].
- [9] ATLAS collaboration, G. Aad et al., Measurements of jet vetoes and azimuthal decorrelations in dijet events produced in collisions at using the ATLAS detector, Eur. Phys. J. C 74 (2014) 3117, [1407.5756].
- [10] J. R. Andersen, T. Hapola and J. M. Smillie, W Plus Multiple Jets at the LHC with High Energy Jets, JHEP 1209 (2012) 047, [1206.6763].
- [11] D0 collaboration, V. M. Abazov et al., Studies of W boson plus jets production in collisions at TeV, Phys. Rev. D 88 (2013) 092001, [1302.6508].
- [12] ATLAS collaboration, G. Aad et al., Measurements of the W production cross sections in association with jets with the ATLAS detector, Eur. Phys. J. C 75 (2015) 82, [1409.8639].
- [13] J. R. Andersen, J. J. Medley and J. M. Smillie, plus multiple hard jets in high energy collisions, JHEP 05 (2016) 136, [1603.05460].
- [14] J. R. Andersen, V. Del Duca and C. D. White, Higgs Boson Production in Association with Multiple Hard Jets, JHEP 02 (2009) 015, [0808.3696].
- [15] J. R. Andersen, T. Hapola, M. Heil, A. Maier and J. M. Smillie, Higgs-boson plus Dijets: Higher-Order Matching for High-Energy Predictions, JHEP 08 (2018) 090, [1805.04446].
- [16] J. R. Andersen, J. D. Cockburn, M. Heil, A. Maier and J. M. Smillie, Finite Quark-Mass Effects in Higgs Boson Production with Dijets at Large Energies, JHEP 04 (2019) 127, [1812.08072].
- [17] J. R. Andersen, T. Hapola, M. Heil, A. Maier and J. Smillie, HEJ 2: High Energy Resummation for Hadron Colliders, Comput.Phys.Commun. 245 (2019) , [1902.08430].
- [18] L. N. Lipatov, Reggeization of the Vector Meson and the Vacuum Singularity in Nonabelian Gauge Theories, Sov. J. Nucl. Phys. 23 (1976) 338–345.
- [19] M. Cacciari, G. P. Salam and G. Soyez, The anti- jet clustering algorithm, JHEP 04 (2008) 063, [0802.1189].
- [20] J. Alwall et al., A Standard format for Les Houches event files, Comput. Phys. Commun. 176 (2007) 300–304, [hep-ph/0609017].
- [21] Sherpa collaboration, E. Bothmann et al., Event Generation with Sherpa 2.2, SciPost Phys. 7 (2019) 034, [1905.09127].
- [22] “Docker.”
- [23] C. Bierlich et al., Robust Independent Validation of Experiment and Theory: Rivet version 3, SciPost Phys. 8 (2020) 026, [1912.05451].
- [24] M. Dobbs and J. B. Hansen, The HepMC C++ Monte Carlo event record for High Energy Physics, Comput. Phys. Commun. 134 (2001) 41–46.
- [25] M. Cacciari, G. P. Salam and G. Soyez, FastJet User Manual, Eur. Phys. J. C 72 (2012) 1896, [1111.6097].
- [26] A. Buckley, J. Ferrando, S. Lloyd, K. Nordström, B. Page, M. Rüfenacht et al., LHAPDF6: parton density access in the LHC precision era, Eur. Phys. J. C 75 (2015) 132, [1412.7420].
- [27] J. A. M. Vermaseren, New features of FORM, math-ph/0010025.