Decision trees for regular factorial languages
Abstract
In this paper, we study arbitrary regular factorial languages over a finite alphabet . For the set of words of the length belonging to a regular factorial language , we investigate the depth of decision trees solving the recognition and the membership problems deterministically and nondeterministically. In the case of recognition problem, for a given word from , we should recognize it using queries each of which, for some , returns the th letter of the word. In the case of membership problem, for a given word over the alphabet of the length , we should recognize if it belongs to the set using the same queries. For a given problem and type of trees, instead of the minimum depth of a decision tree of the considered type solving the problem for , we study the smoothed minimum depth . With the growth of , the smoothed minimum depth of decision trees solving the problem of recognition deterministically is either bounded from above by a constant, or grows as a logarithm, or linearly. For other cases (decision trees solving the problem of recognition nondeterministically, and decision trees solving the membership problem deterministically and nondeterministically), with the growth of , the smoothed minimum depth of decision trees is either bounded from above by a constant or grows linearly. As corollaries of the obtained results, we study joint behavior of smoothed minimum depths of decision trees for the considered four cases and describe five complexity classes of regular factorial languages. We also investigate the class of regular factorial languages over the alphabet each of which is given by one forbidden word.
Keywords: regular factorial language, recognition problem, membership problem, deterministic decision tree, nondeterministic decision tree.
1 Introduction
In this paper, we study arbitrary regular factorial languages over a finite alphabet . For the set of words of the length belonging to a regular factorial language , we investigate the depth of decision trees solving the recognition and the membership problems deterministically and nondeterministically. In the case of recognition problem, for a given word from , we should recognize it using queries each of which, for some , returns the th letter of the word. In the case of membership problem, for a given word over the alphabet of the length , we should recognize if it belongs to using the same queries.
For a given problem (problem of recognition or membership problem) and type of trees (solving the problem deterministically or nondeterministically), instead of the minimum depth of a decision tree of the considered type solving the problem for , we study the smoothed minimum depth . The reason is that the graph of the function may have sawtooth form.
For an arbitrary regular factorial language, with the growth of , the smoothed minimum depth of decision trees solving the problem of recognition deterministically is either bounded from above by a constant, or grows as a logarithm, or linearly. These results follow immediately from more general, obtained in [5] for arbitrary regular languages.
For other cases (decision trees solving the problem of recognition nondeterministically, and decision trees solving the membership problem deterministically and nondeterministically), with the growth of , the smoothed minimum depth of decision trees is either bounded from above by a constant, or grows linearly. In the conference paper [4], a classification of arbitrary regular languages depending on the smoothed minimum depth of decision trees solving the problem of recognition nondeterministically was announced without proofs. In the present paper, we consider simpler classification for regular factorial languages with full proof. Results related to the decision trees solving the membership problem are new.
As corollaries of the obtained results, we study joint behavior of smoothed minimum depths of decision trees for the considered four cases and describe five complexity classes of regular factorial languages. We also investigate the class of regular factorial languages over the alphabet each of which is given by one forbidden word.
We should mention a recent paper [6] in which similar results were obtained for subword-closed languages over the alphabet , where by subword we mean subsequence. It is clear that each subword-closed language is a factorial language. Moreover, each subword-closed language over a finite alphabet is a regular language [2]. One can show that the language over the alphabet given by one forbidden word is a regular factorial language, which is not subword-closed. Therefore the class of subword-closed languages over the alphabet is a proper subclass of the class of regular factorial languages over the alphabet .
The main difference between the present paper and [6] is that, in the latter paper, we do not assume that the subword-closed languages are given by sources (partial deterministic finite automata). Instead of this, we describe simple criteria (based on the presence in the language of words of special types) for the behavior of the minimum depths of decision trees solving the problem of recognition deterministically and nondeterministically. Differently formulated criteria for the behavior of the minimum depth of decision trees solving the recognition problem require very different proofs. One more difference is that in [6] we directly consider the minimum depth of decision trees since it is a fairly smooth function for subword-closed languages.
2 Main Notions
In this section, we discuss the notions related to regular factorial languages and decision trees solving problems of recognition and membership for these languages.
2.1 Regular Factorial Languages
Let be the set of nonnegative integers and be a finite alphabet with at least two letters. By , we denote the set of all finite words over the alphabet , including the empty word . A word is called a factor of a word if and . A language is called factorial if it contains all factors of its words. A word is called a minimal forbidden word for if and all proper factors of belong to . We denote by the language of minimal forbidden words for . It is known [1] that a factorial language is regular if and only if the language is regular. In particular, a factorial language with a finite set of minimal forbidden words is regular. In this paper, we study arbitrary nonempty regular factorial languages.
A source over the alphabet is a triple , where is a finite directed graph, possibly with multiple edges and loops, in which each edge is labeled with a letter from and edges leaving each node are labeled with pairwise different letters, is a node of called initial, and is a nonempty set of the graph nodes called terminal. Note that the source can be interpreted as a partial deterministic finite automaton.
A path of the source is an arbitrary sequence of nodes and edges of such that the edge leaves the node and enters the node for . We now define a word from in the following way: if , then . Let and let be the letter attached to the edge , . Then . We say that the path generates the word . Note that different paths which start in the same node generate different words.
We denote by the set of all paths of the source each of which starts in the node and finishes in a node from . Let
We say that the source generates the language . It is well known that is a regular language.
The source is called everywhere defined over the alphabet if exactly edges leave each node of . Note that these edges are labeled with pairwise different letters from . The source is called reduced if, for each node of , there exists a path from , which contains this node. It is known [3] that, for each regular language over the alphabet , there exists an everywhere defined over the alphabet source, which generates this language. Therefore, for each nonempty regular language, there exists a reduced source, which generates this language.
Let be a regular factorial language and be a reduced source that generates the language . Since the language is factorial, we can assume additionally that each node of the graph is terminal – it will not change the language generated by . The source will be called t-reduced if it is reduced and each node of the graph is terminal. Further we will assume that a considered regular factorial language is nonempty and it is given by a t-reduced source, which generates this language.
2.2 Decision Trees for Recognition and Membership Problems
Let be a regular factorial language over the alphabet . For any natural , denote , where is the set of words over the alphabet , which length is equal to . We consider two problems related to the set . The problem of recognition: for a given word from , we should recognize it using attributes (queries) , where , , is a function from to such that for any word . The problem of membership: for a given word from , we should recognize if this word belongs to the set using the same attributes. To solve these problems, we use decision trees over .
A decision tree over is a marked finite directed tree with root, which has the following properties:
-
•
The root and the edges leaving the root are not labeled.
-
•
Each node, which is not the root nor terminal node, is labeled with an attribute from the set .
-
•
Each edge leaving a node, which is not a root, is labeled with a letter from the alphabet .
A decision tree over is called deterministic if it satisfies the following conditions:
-
•
Exactly one edge leaves the root.
-
•
For any node, which is not the root nor terminal node, the edges leaving this node are labeled with pairwise different letters.
Let be a decision tree over . A complete path in is any sequence of nodes and edges of such that is the root, is a terminal node, and is the initial and is the terminal node of the edge for . We define a subset of the set in the following way: if , then . Let , the attribute be attached to the node , and be the letter attached to the edge , . Then
Let . We say that a decision tree over solves the problem of recognition for nondeterministically if satisfies the following conditions:
-
•
Each terminal node of is labeled with a word from .
-
•
For any word , there exists a complete path in the tree such that .
-
•
For any word and for any complete path in the tree such that , the terminal node of the path is labeled with the word .
We say that a decision tree over solves the problem of recognition for deterministically if is a deterministic decision tree, which solves the problem of recognition for nondeterministically.
We say that a decision tree over solves the problem of membership for nondeterministically if satisfies the following conditions:
-
•
Each terminal node of is labeled with a number from the set .
-
•
For any word , there exists a complete path in the tree such that .
-
•
For any word and for any complete path in the tree such that , the terminal node of the path is labeled with the number if and with the number , otherwise.
We say that a decision tree over solves the problem of membership for deterministically if is a deterministic decision tree which solves the problem of membership for nondeterministically.
Let be a decision tree over . We denote by the maximum number of nodes in a complete path in that are not the root nor terminal node. The value is called the depth of the decision tree .
We denote by () the minimum depth of a decision tree over , which solves the problem of recognition for nondeterministically (deterministically). If , then .
We denote by () the minimum depth of a decision tree over , which solves the problem of membership for nondeterministically (deterministically). If , then .
3 Bounds on Decision Tree Depth
Let be a nonempty factorial regular language. In this section, we consider the behavior of four functions , , , and defined on the set and with values from . For any natural ,
For any pair , the function is a smoothed analog of the function .
3.1 Decision Trees Solving Recognition Problem Deterministically
Let be a t-reduced source over the alphabet . A path of the source is called a cycle of the source if there is at least one edge in this path, and the first node of this path is equal to the last node of this path. A cycle of the source is called elementary if nodes of this cycle, with the exception of the last node, are pairwise different.
The source is called simple if every two different elementary cycles of the source do not have common nodes. Let be a simple source and be a path of the source . The number of different elementary cycles of the source , which have common nodes with , is denoted by and is called the cyclic length of the path . The value
is called the cyclic length of the source .
Let be a simple source, be an elementary cycle of the source , and be a node of the cycle . Beginning with the node , the cycle generates an infinite periodic word over the alphabet . This word will be denoted by . We denote by the minimum period of the word . The source is called dependent if there exist two different elementary cycles and of the source , nodes and of the cycles and , respectively, and a path of the source from to , which satisfy the following conditions: and the length of the path is a number divisible by . If the source is not dependent, then it is called independent. Next theorem follows immediately from Theorem 2.1 [5].
Theorem 1.
Let be a nonempty regular factorial language over the alphabet and be a t-reduced source, which generates the language . Then the following statements hold:
(a) If is an independent simple source and , then .
(b) If is an independent simple source and , then .
(c) If is not independent simple source, then .
3.2 Decision Trees Solving Recognition Problem Nondeterministically
Let be a nonempty regular factorial language over the alphabet . For any natural , we define a parameter of the language . If , then . Let , , and . Denote (if , then ) and . Then
Note that, for any word , is the minimum number of letters of the word , which allow us to distinguish it from all other words belonging to . One can show that .
Theorem 2.
Let be a nonempty regular factorial language over the alphabet and be a t-reduced source, which generates the language . Then the following statements hold:
(a) If is an independent simple source, then .
(b) If is not independent simple source, then .
Proof.
(a) Let be an independent simple source and . By Theorem 1, . It is clear that . Therefore .
Let be an independent simple source and . Let be a natural number. If , then . Let . Denote by the number of nodes in the graph . In the proof of Lemma 4.5 [5], it was proved that for any word . Therefore . Thus, for any natural and .
(b) Let be not simple source and be different elementary cycles of the source , which have a common node . Since is a t-reduced source, it contains a path from the node to the node , and is a terminal node. Let the length of the path be equal to , the length of the cycle be equal to , and the length of the cycle be equal to . Let be the word generated by the path , be the word generated by a path from to obtained by the passage times along the cycle , and be the word generated by a path from to obtained by the passage times along the cycle . The words and are different and they have the same length .
Consider the sequence of numbers , . Let . The set contains the word and the words for . It is easy to show that : to distinguish the word from the words , , we need to use at least one letter from each of words appearing in . Therefore and . Let and let be the maximum natural number such that . Evidently, . Hence . Therefore for large enough . The inequality is obvious. Thus, .
Let be a dependent simple source. Then there exist two different elementary cycles and of the source , nodes and of the cycles and , respectively, and a path of the source from to , which satisfy the following conditions: and the length of the path is a number divisible by . Let us remind that, for , is the infinite periodic word over the alphabet generated by the cycle beginning with the node , and is the minimum period of the word . Since is a t-reduced source, it contains a path from the node to the node , and all nodes of the graph are terminal. Let the path generate the word of the length . Denote . Let the length of the cycle be equal to , the length of the path be equal to , and the path generate the word . Denote by the prefix of the length of the word . We now define two words of the length : and . It is clear that .
Consider the sequence of numbers , . Let . The set contains the word and the words for . It is easy to show that : to distinguish the word from the words , , we need to use at least one letter from each of words appearing in . Therefore and . Let and let be the maximum natural number such that . Evidently, . Hence . Therefore for large enough . The inequality is obvious. Thus, . ∎
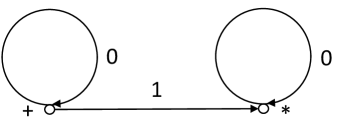
Note that in general case (when we consider not only factorial languages) the classification of reduced sources depending on the minimum depth of decision trees solving the problem of recognition nondeterministically is more complicated [4]. In particular, there exists a dependent simple reduced source (see Fig. 1) with the initial node labeled with the symbol and the unique terminal node labeled with the symbol that generates the regular language over the alphabet , which is not factorial and for which .
3.3 Decision Trees Solving Membership Problem
For a regular factorial language over the alphabet , we denote by its complementary language . The notation means that is an infinite language, and the notation means that is a finite language.
Theorem 3.
Let be a regular factorial language over the alphabet .
(a) If and , then and .
(b) If or , then and .
Proof.
It is clear that for any natural .
(a) Let , , and be a word with the minimum length from . Denote by the length of . Since , for any natural . Let be a natural number such that and be a decision tree over that solves the problem of membership for nondeterministically and has the minimum depth. Let and be a complete path in such that . Then the terminal node of is labeled with the number . Beginning with the first letter, we divide the word into blocks with letters in each and the suffix of the length . Let us assume that the number of nodes labeled with attributes in is less than . Then there is a block such that queries (attributes) attached to nodes of does not ask about letters from the block. We replace this block in the word with the word and denote by the obtained word. It is clear that and , but this is impossible since the terminal node of the path is labeled with the number 1. Therefore the depth of is greater than or equal to . Thus, . It is easy to construct a decision tree over that solves the problem of membership for deterministically and has the depth equals to . Therefore . Thus, and .
(b) Let . Then there exists natural such that for any natural . Therefore, for each natural , and . Thus, and .
Let , be a natural number, and be a decision tree over , which consists of the root, a terminal node labeled with and an edge that leaves the root and enters the terminal node. One can show that solves the problem of membership for deterministically and has the depth equals to . Therefore and . Thus, and . ∎
4 Corollaries
4.1 Joint Behavior of Functions , , , and
In this section, we assume that each regular factorial language over the alphabet is given by a t-reduced source , which generates the considered language denoted by . To study all possible types of joint behavior of functions , , , and , we consider five classes of regular factorial languages described in the columns 2–4 of Table 1. In particular, consists of all regular factorial languages for which the source is an independent simple source and . It is easy to show that the complexity classes are pairwise disjoint, and each regular factorial language belongs to one of these classes. The behavior of functions , , , and for languages from these classes is described in the last four columns of Table 1. For each class, the results considered in Table 1 for the functions and follow directly from Theorems 1 and 2.
| is independent | |||||||
|---|---|---|---|---|---|---|---|
| simple source | |||||||
| Yes | |||||||
| Yes | |||||||
| Yes | |||||||
| No | |||||||
| No |
We now consider the behavior of the functions and for each of the classes . Let be a t-reduced source over the alphabet , which generates a regular factorial language.
Let . Since , is a directed acyclic graph, and the language is finite. Using Theorem 3 we obtain and .
Let . Since , is a graph containing a cycle, and the language is infinite. By Lemma 4.2 [5], . Therefore . Using Theorem 3 we obtain and .
Let . Since , is a graph containing a cycle, and the language is infinite. By Lemma 4.2 [5], . Therefore . Using Theorem 3 we obtain and .
Let . Since is not an independent simple source, is a graph containing a cycle, and the language is infinite. We know that . Using Theorem 3 we obtain and .
Let . Then . Using Theorem 3 we obtain and .
We now show that the classes are nonempty. For simplicity, we assume that , where . It is easy to generalize the considered examples to the case of an arbitrary finite alphabet with at least two letters. In the examples of sources, the initial node is labeled with the symbol , and all nodes are terminal.
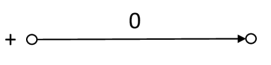
Denote by the source over the alphabet depicted in Fig. 2. One can show that is an independent simple t-reduced source and . This source generates the language , which is factorial. Therefore .
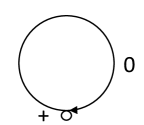
Denote by the source over the alphabet depicted in Fig. 3. One can show that is an independent simple t-reduced source and . This source generates the language , which is factorial. Therefore .
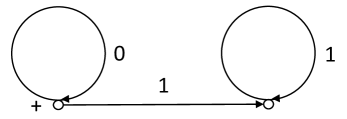
Denote by the source over the alphabet depicted in Fig. 4. One can show that is an independent simple t-reduced source and . This source generates the language , which is factorial. Therefore .
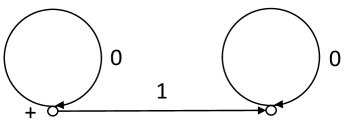
Denote by the source over the alphabet depicted in Fig. 5. One can show that is a dependent simple t-reduced source generating the language , which is factorial. It is clear that . Therefore .
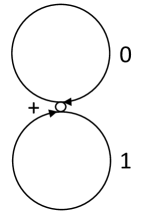
Denote by the source over the alphabet depicted in Fig. 6. One can show that is a t-reduced source that is not simple. This source generates the language , which is factorial. It is clear that . Therefore .
A regular factorial language can have different t-reduced sources, which generate it. However, for each of such sources , the language will belong to the same complexity class. Let us assume the contrary: there exist a regular factorial language and two t-reduced sources and , which generate it and for which languages and belong to different complexity classes. Then, for some pair , the functions and have different behavior, but this is impossible since for any natural .
4.2 Languages Over Alphabet Given by One Forbidden Word
Let , , and . We denote by the language over the alphabet , which consists of all words from that does not contain as a factor. This is a regular factorial language with . The following theorem indicates for each nonempty word the complexity class to which the language belongs.
Theorem 4.
Let and .
(a) If , then .
(b) If , then .
(c) If , then .
We now describe a t-reduced source that generates the language for a nonempty word . Let , , and for . The set is the set of all proper prefixes of the word . Then , where the set of nodes of the graph is equal to , , and . For , an edge leaves the node and enters the node . This edge is labeled with the letter . For , an edge leaves the node and enters the node such that is the longest suffix of the word , where if and if . This edge is labeled with the letter . It is easy to show that is a t-reduced source over the alphabet . From Theorem 10 [1] it follows that the source generates the language .
Let and . We denote by the word . It is easy to prove the following statement.
Lemma 1.
Let and . Then for any pair and any natural .
Lemma 2.
Let , , and . Then .
Proof.
Since , and . One can show that . Using this fact it is not difficult to prove that and for any natural . From here and from Theorems 1 and 2 it follows that and .
Since , . The source contains at least one circle formed by the edge that leaves and enters the node and is labeled with the letter , where is the first letter of the word . Therefore the language is infinite. By Theorem 3, and . Thus, . ∎
of Theorem 4.
In each figure depicting a source , , we label each node with a corresponding prefix of the word .

(a) The source is depicted in Fig. 7. This is an independent simple t-reduced source with . Therefore . By Lemma 1, .
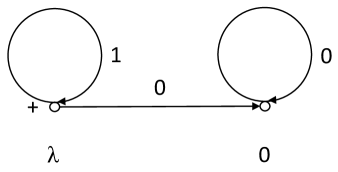
(b) The source is depicted in Fig. 8. This is an independent simple t-reduced source with . Therefore . By Lemma 1, .

(c) The source is depicted in Fig. 9. This is not a simple source. It is clear that . Therefore . By Lemma 1, . Using Lemma 2 we obtain .
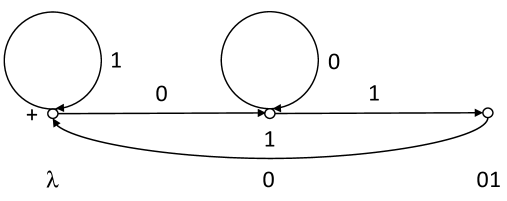
The source is depicted in Fig. 10. This is not a simple source. It is clear that . Therefore . By Lemma 1, .
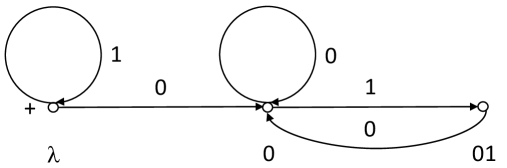
The source is depicted in Fig. 11. This is not a simple source. It is clear that . Therefore . By Lemma 1, .
We proved that, for any word of the length three, . Using Lemma 2 we obtain that, for any word of the length greater than or equal to four, . ∎
Acknowledgments
Research reported in this publication was supported by King Abdullah University of Science and Technology (KAUST).
References
- [1] Crochemore, M., Mignosi, F., Restivo, A.: Automata and forbidden words. Inf. Process. Lett. 67(3), 111–117 (1998)
- [2] Haines, L.H.: On free monoids partially ordered by embedding. J. Comb. Theory 6, 94–98 (1969)
- [3] Markov, A.A.: Introduction into Coding Theory (in Russian). Nauka, Moscow (1982)
- [4] Moshkov, M.: Complexity of deterministic and nondeterministic decision trees for regular language word recognition. In: S. Bozapalidis (ed.) Proceedings of the 3rd International Conference Developments in Language Theory, DLT 1997, Thessaloniki, Greece, July 20–23, 1997, pp. 343–349. Aristotle University of Thessaloniki (1997)
- [5] Moshkov, M.: Decision trees for regular language word recognition. Fundam. Inform. 41(4), 449–461 (2000)
- [6] Moshkov, M.: Decision trees for binary subword-closed languages. CoRR abs/2201.01493 (2022). URL https://arxiv.org/abs/2201.01493