This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Decoding algorithms of monotone codes and azinv codes and their unified view

Hokuto Takahashi Graduate School of Science and Engineering,
Chiba University
1-33 Yayoi-cho, Inage-ku, Chiba-city, Chiba, Japan
263-0022
Email: ayca5495@chiba-u.jp    Manabu Hagiwara Graduate School of Science,
Chiba University
1-33 Yayoi-cho, Inage-ku, Chiba-city, Chiba, Japan
263-0022
Email: hagiwara@math.s.chiba-u.ac.jp
Abstract

This paper investigates linear-time decoding algorithms for two classes of error-correcting codes. One of the classes is monotone codes which are known as single deletion codes. The other is azinv codes which are known as single balanced adjacent deletion codes. As results, this paper proposes generalizations of Levenshtein’s decoding algorithm for Levenshtein’s single deletion codes. This paper points out that it is possible to unify our new two decoding algorithms.

I Introduction

Insertion errors and deletion errors are considered to be synchronization errors over communication channels and storage channels such as DNA-data based storages [1, 2], racetrack memories[3, 4], or Bit Patterned Media[5, 6]. The study of deletion error-correcting codes started with Levenshtein’s work[7], where he proved that Varshamov-Tenengolts (VT) codes are capable of correcting single insertions or deletions. In Levenshtein’s proof, he showed beautiful decoding algorithm to correct single deletions. This paper provides two generalizations of Levenshtein’s decoding algorithms. One corrects single deletions and reversals for monotone codes, the other corrects single balanced adjacent deletions and single balanced adjacent reversals for azinv codes. A single Balanced Adjacent Deletion (BAD) error is a double deletion error that deletes two different consecutive binary symbols, i.e., 01 or 10. A single Balanced Adjacent Reversal (BAR) error is a swap error that reverses two different consecutive binary symbols.

For applications, the computational cost of decoding algorithms is preferable to be polynomial. One of remarkable aspects of our algorithms is the computational cost. The costs are only linear to their input, i.e., the length of received word. Another remarkable aspect is the following. While these classes and their correctable error are different, our algorithms can be allowed to be unified.

This paper is organized as follows. In Section II, we first introduce monotone codes and provide a single deletion/reveral error-correcting algorithm of the monotone codes. In Section III, we first introduce azinv codes and provide a single BAD/BAR error-correcting algorithm of the azinv codes. In Section IV, we provide a unified view of the algorithms of the monotone codes and the azinv codes.

II Monotone Code and its Decoding Algorithm

Throughout this paper, 𝔹\mathbb{B} denotes the binary set {0,1}\{0,1\}. For a positive integer nn, [n][n] denotes {1,2,⋯,n}\left\{1,2,\cdots,n\right\}.

In this section, we introduce monotone codes and provide an algorithm to make the monotone codes single deletion/reversal error-correctable (Algorithm 1). Errors treated in this section are deletion errors and reversal errors, which are defined below.

Definition II.1 (Deletion and Reversal).

Let nn be a positive integer and i∈[n]i\in[n]. Define a map deli:𝔹n→𝔹n−1\mathrm{del}_{i}:\mathbb{B}^{n}\rightarrow\mathbb{B}^{n-1} as

deli​(x1​x2​⋯​xn)≔x1​⋯​xi−1​xi+1​⋯​xn.\mathrm{del}_{i}(x_{1}x_{2}\cdots x_{n})\coloneqq x_{1}\cdots x_{i-1}x_{i+1}\cdots x_{n}.

We call the map deli\mathrm{del}_{i} deletion. Note that 𝔹0:={ε}\mathbb{B}^{0}:=\{\varepsilon\}, where ε\varepsilon is the empty word.

Define a map revi:𝔹n→𝔹n\mathrm{rev}_{i}:\mathbb{B}^{n}\rightarrow\mathbb{B}^{n} as

revi​(x1​x2​⋯​xn)≔x1​⋯​xi−1​x¯i​xi+1​⋯​xn\mathrm{rev}_{i}(x_{1}x_{2}\cdots x_{n})\coloneqq x_{1}\cdots x_{i-1}\overline{x}_{i}x_{i+1}\cdots x_{n}

with 0¯=1\overline{0}=1 and 1¯=0\overline{1}=0. We call the map revi\mathrm{rev}_{i} reversal.

The following codes, monotone codes, are known as single deletion error-correcting codes [8]. However, no decoding algorithm has been studied.

Definition II.2 (Monotone code[8]).

Let nn and mm be positive integers, aa an integer, and 𝐤=(k1,k2,⋯,kn){\bf k}=(k_{1},k_{2},\cdots,k_{n}) a positive monotonic increasing integer sequence with m>knm>k_{n}. Define a set Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n) as

Ma,m,𝐤​(n)≔{𝐱∈𝔹n∣ρ𝐤​(𝐱)≡a(modm)},M_{a,m,{\bf k}}(n)\coloneqq\left\{{\bf x}\in\mathbb{B}^{n}\mid\rho_{{\bf k}}({\bf x})\equiv a\pmod{m}\right\},

where

ρ𝐤​(𝐱)≔∑i=1|𝐱|ki​xi\rho_{{\bf k}}({\bf x})\coloneqq\sum_{i=1}^{|{\bf x}|}k_{i}x_{i}

and |𝐱||{\bf x}| denotes the length of 𝐱{\bf x}. ρ𝐤​(𝐱)\rho_{{\bf k}}({\bf x}) is defined only for k with |𝐤|≥|𝐱||{\bf k}|\geq|{\bf x}|. We call Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n) a monotone code.

Remark II.3.

If 𝐤=(1,2,⋯,n){\bf k}=(1,2,\cdots,n), the monotone code is called a Levenshtein code. If 𝐤=(1,2,⋯,n){\bf k}=(1,2,\cdots,n) and m=n+1m=n+1, the monotone code is called a VT code. Levenshtein [7] proved that Levenshtein codes are single deletion error-correcting codes with m>nm>n. He also proved that Levenshtein codes are single deletion/reversal error-correcting codes with m≥2​nm\geq 2n.

The following is one of the main contributions of this paper.

Theorem II.4.

Let Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n) be a monotone code and 𝐱{\bf x} be a codeword of Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n). Let DecM\mathrm{Dec}_{M} denote Algorithm 1.

1. DecM​(𝐱)=𝐱\mathrm{Dec}_{M}({\bf x})={\bf x}.

2. Assume kn<mk_{n}<m. For any single deletion del\mathrm{del}, DecM∘del​(𝐱)=𝐱\mathrm{Dec}_{M}\circ\mathrm{del}({\bf x})={\bf x}.

3. If kn<mk_{n}<m, any monotone code Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n) is a single deletion error-correcting code with Algorithm 1 as a decoding algorithm.

4. Assume 2​kn≤m2k_{n}\leq m. For any single reversal rev\mathrm{rev}, DecM∘rev​(𝐱)=𝐱\mathrm{Dec}_{M}\circ\mathrm{rev}({\bf x})={\bf x}.

5. If 2​kn≤m2k_{n}\leq m, any monotone code Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n) is a single deletion/reversal error-correcting code with Algorithm 1 as a decoding algorithm. Here ∘\circ denotes the map composition.

Proof.

1. It is trivial from the steps 3 and 4 of Algorithm 1. 2. A proof is provided in subsection II-B. 3. It is a corollary of 1. and 2. 4. A proof is provided in subsection II-C. 5. It is a corollary of 3. and 4. ∎

II-A Decoding algorithm for single deletion/reversal errors

In this subsection, we provide notation in Algorithm 1 and the details of Algorithm 1.

For an integer n≥1n\geq 1, a positive integer i∈[n]i\in[n], a positive monotonic increasing integer sequence 𝐤=(k1,k2,⋯,kn){\bf k}=(k_{1},k_{2},\cdots,k_{n}), and a binary sequence 𝐲=y1​y2​⋯​yn−1∈𝔹n−1{\bf y}=y_{1}y_{2}\cdots y_{n-1}\in\mathbb{B}^{n-1}, define maps as

L𝐤(0)​(i,𝐲)≔{∑j=1i−1y¯j​(kj+1−kj)(i≠1),0(i=1).\displaystyle L^{(0)}_{\bf k}(i,{\bf y})\coloneqq\begin{cases}\displaystyle\sum_{j=1}^{i-1}\overline{y}_{j}(k_{j+1}-k_{j})\quad&(i\neq 1),\\ 0&(i=1).\end{cases}
L𝐤(1)​(i,𝐲)≔{∑j=1i−1yj​(kj+1−kj)(i≠1),0(i=1).\displaystyle L^{(1)}_{\bf k}(i,{\bf y})\coloneqq\begin{cases}\displaystyle\sum_{j=1}^{i-1}y_{j}(k_{j+1}-k_{j})\quad&(i\neq 1),\\ 0&(i=1).\end{cases}
R𝐤(0)​(i,𝐲)≔{∑j=in−1y¯j​(kj+1−kj)(i≠n),0(i=n).\displaystyle R^{(0)}_{\bf k}(i,{\bf y})\coloneqq\begin{cases}\displaystyle\sum_{j=i}^{n-1}\overline{y}_{j}(k_{j+1}-k_{j})\quad&(i\neq n),\\ 0&(i=n).\end{cases}
R𝐤(1)​(i,𝐲)≔{∑j=in−1yj​(kj+1−kj)(i≠n),0(i=n).\displaystyle R^{(1)}_{\bf k}(i,{\bf y})\coloneqq\begin{cases}\displaystyle\sum_{j=i}^{n-1}y_{j}(k_{j+1}-k_{j})\quad&(i\neq n),\\ 0&(i=n).\end{cases}

We denote R𝐤(1)​(1,𝐲)R^{(1)}_{\bf k}(1,{\bf y}) by wt𝐤​(𝐲)\mathrm{wt}_{\bf k}({\bf y}). Note that wt𝐤​(𝐲)\mathrm{wt}_{\bf k}({\bf y}) is coincided with the Hamming weight of y if 𝐤=(1,2,⋯,n).{\bf k}=(1,2,\cdots,n). We omit 𝐤{\bf k} from the notations, if 𝐤=(1,2,⋯,n){\bf k}=(1,2,\cdots,n).

For 𝐛∈𝔹{\bf b}\in\mathbb{B}, i∈[n]i\in[n], and insi,𝐛​(𝐲)\mathrm{ins}_{i,{\bf b}}({\bf y}), L(0)​(i,𝐲)L^{(0)}(i,{\bf y}) (resp. L(1)​(i,𝐲)L^{(1)}(i,{\bf y})) equals to the number of 0 (resp. 11) to the left of inserted position ii, R(0)​(i,𝐲)R^{(0)}(i,{\bf y}) (resp. R(1)​(i,𝐲)R^{(1)}(i,{\bf y})) equals to the number of 0 (resp. 11) to the right of inserted position ii.

The map defined below is known as an inverse operation of deletion and is used in Algorithm 1.

Definition II.5.

For a positive integer i∈[n+1]i\in[n+1] and a non-empty binary sequence 𝐛{\bf b}, define a map insi,𝐛:𝔹n→𝔹n+|𝐛|\mathrm{ins}_{i,{\bf b}}:\mathbb{B}^{n}\rightarrow\mathbb{B}^{n+|{\bf b}|} as

insi,𝐛​(x1​x2​⋯​xn)≔x1​⋯​xi−1​b​xi​⋯​xn.\mathrm{ins}_{i,{\bf b}}(x_{1}x_{2}\cdots x_{n})\coloneqq\\ x_{1}\cdots x_{i-1}bx_{i}\cdots x_{n}.

We call the map insi,𝐛\mathrm{ins}_{i,{\bf b}} insertion.

Algorithm 1 Decoding algorithm for single deletion/reversal errors
1:  Input: a∈ℤ≥0a\in\mathbb{Z}_{\geq 0}, nn and m∈ℤ≥1m\in\mathbb{Z}_{\geq 1}, 𝐲∈⋃t≥0𝔹t{\bf y}\in\bigcup_{t\geq 0}\mathbb{B}^{t}, and 𝐤=(k1,k2,⋯,kn)∈ℤn{\bf k}=(k_{1},k_{2},\cdots,k_{n})\in\mathbb{Z}^{n}. Output: 𝐳∈𝔹n{\bf z}\in\mathbb{B}^{n} or a symbol ?.
2:  Compute the length of 𝐲{\bf y}, say |𝐲||{\bf y}|.
3:  if |𝐲|=n|{\bf y}|=n then
4:     go to 10.
5:  else if |𝐲|=n−1|{\bf y}|=n-1 then
6:     go to 21.
7:  else
8:     𝐳≔?{\bf z}\coloneqq?. Go to 35.
9:  end if
10:  Compute r≔min⁡{s∈ℤ≥0∣s≡a−ρ𝐤​(𝐲)(modm)}r\coloneqq\min\{s\in\mathbb{Z}_{\geq 0}\mid s\equiv a-\rho_{\bf k}({\bf y})\pmod{m}\}.
11:  if r=0r=0 then
12:     𝐳≔𝐲{\bf z}\coloneqq{\bf y}. Go to 35.
13:  else
14:     Compute p≔min⁡{j∈[n]∣kj=min⁡{r,m−r}}p\coloneqq\min\{j\in[n]\mid k_{j}=\min\{r,m-r\}\}.
15:     if revp​(𝐲)∈Ma,m,𝐤​(n)\mathrm{rev}_{p}({\bf y})\in M_{a,m,{\bf k}}(n) then
16:        𝐳≔revp​(𝐲){\bf z}\coloneqq\mathrm{rev}_{p}({\bf y}). Go to 35.
17:     else
18:        𝐳≔?{\bf z}\coloneqq?. Go to 35.
19:     end if
20:  end if
21:  Compute r≔min⁡{s∈ℤ≥0∣s≡a−ρ𝐤​(𝐲)(modm)}r\coloneqq\min\{s\in\mathbb{Z}_{\geq 0}\mid s\equiv a-\rho_{\bf k}({\bf y})\pmod{m}\}.
22:  Compute w≔wt𝐤​(𝐲)w\coloneqq\mathrm{wt}_{\bf k}({\bf y}).
23:  if r≤wr\leq w then
24:     Compute p≔max⁡{j∈[n]∣R𝐤(1)​(j,𝐲)=r}p\coloneqq\max\{j\in[n]\mid R^{(1)}_{\bf k}(j,{\bf y})=r\}.
25:     b≔0b\coloneqq 0.
26:  else
27:     Compute p≔min⁡{j∈[n]∣L𝐤(0)​(j,𝐲)=r−w−k1}.p\coloneqq\min\{j\in[n]\mid L^{(0)}_{\bf k}(j,{\bf y})=r-w-k_{1}\}.
28:     b≔1b\coloneqq 1.
29:  end if
30:  if insp,𝐛​(𝐲)∈Ma,m,𝐤​(n)\mathrm{ins}_{p,{\bf b}}({\bf y})\in M_{a,m,{\bf k}}(n) then
31:     𝐳≔insp,𝐛​(𝐲){\bf z}\coloneqq\mathrm{ins}_{p,{\bf b}}({\bf y}).
32:  else
33:     𝐳≔?{\bf z}\coloneqq?.
34:  end if
35:  Output 𝐳{\bf z}.

Note that the steps 21st - 34th of Algorithm 1 are coincided with Levenshtein’s decoding algorithm for single deletion errors if 𝐤=(1,2,⋯,n){\bf k}=(1,2,\cdots,n) [7].

Before we move to proofs for Theorem II.4, we provide examples of Algorithm 1 for each error.

Example II.6 (Decoding for a single deletion error).

Let n=4,a=0,m=9,𝐤=(1,3,6,8),n=4,a=0,m=9,{\bf k}=(1,3,6,8), and 𝐲=101{\bf y}=101. Note that the monotone code has four words,

M0,9,𝐤​(4)={0000,1001,0110,1111}.M_{0,9,{\bf k}}(4)=\{0000,1001,0110,1111\}.
  • •

    Since |𝐲|=3|{\bf y}|=3, we go to step 6 and then to step 21.

  • •

    Algorithm 1 computes rr and ww. We obtain r=2r=2 and w=4.w=4.

  • •

    Since r≤wr\leq w,

    p\displaystyle p =max{j∈[4]∣R(1)(j,𝐲)=2)}\displaystyle=\max\{j\in[4]\mid R^{(1)}(j,{\bf y})=2)\}
    =3,\displaystyle=3,
    b\displaystyle b =0.\displaystyle=0.
  • •

    The output DecM​(𝐲)=insp,b​(𝐲)\mathrm{Dec}_{M}({\bf y})=\mathrm{ins}_{p,b}({\bf y}) is

    ins3,0​(101)=1001.\mathrm{ins}_{3,0}(101)=1001.
Example II.7 (Decoding for a single reversal error).

Let n=6,a=0,m=20,𝐤=(1,2,3,8,9,10),n=6,a=0,m=20,{\bf k}=(1,2,3,8,9,10), and 𝐲=111110{\bf y}=111110. Note that the monotone code has five words,

M0,20,𝐤​(6)={000000,110110,001110,100011,010101}.M_{0,20,{\bf k}}(6)=\{000000,110110,001110,100011,010101\}.
  • •

    Since |𝐲|=6|{\bf y}|=6, we go to step 4 and then to step 10.

  • •

    Algorithm 1 computes rr, then we obtain r=17r=17.

  • •

    Since r≠0r\neq 0,

    p\displaystyle p =min⁡{3,17}\displaystyle=\min\{3,17\}
    =3.\displaystyle=3.
  • •

    The output DecM​(𝐲)=revp​(𝐲)\mathrm{Dec}_{M}({\bf y})=\mathrm{rev}_{p}({\bf y}) is

    rev3​(111110)=110110.\mathrm{rev}_{3}(111110)=110110.

II-B Proof for single deletion error-correction

To prove 2 of Theorem II.4, we introduce the following four Lemmas II.9, II.10, II.11, and II.12. From now on, till the end of this subsection, we assume the following.

Hypothesis II.8.

A binary sequence 𝐱{\bf x} is a codeword of Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n). Set 𝐲≔deli​(𝐱){\bf y}\coloneqq\mathrm{del}_{i}({\bf x}) for a fixed ii. rr is the value at the step 21 of Algorithm 1.

Lemma II.9.
ki=k1+L𝐤(0)​(i,𝐲)+L𝐤(1)​(i,𝐲).k_{i}=k_{1}+L^{(0)}_{\bf k}(i,{\bf y})+L^{(1)}_{\bf k}(i,{\bf y}).
Proof.

It follows from the definitions of L𝐤(0)​(i,𝐲)L^{(0)}_{\bf k}(i,{\bf y}) and L𝐤(1)​(i,𝐲)L^{(1)}_{\bf k}(i,{\bf y}).

(R.H.S.)\displaystyle(\text{R.H.S.}) =k1+∑j=1i−1y¯j​(kj+1−kj)+∑j=1i−1yj​(kj+1−kj)\displaystyle=k_{1}+\sum_{j=1}^{i-1}\overline{y}_{j}(k_{j+1}-k_{j})+\sum_{j=1}^{i-1}y_{j}(k_{j+1}-k_{j})
=k1+∑j=1i−1(y¯j+yj)​(kj+1−kj)\displaystyle=k_{1}+\sum_{j=1}^{i-1}(\overline{y}_{j}+y_{j})(k_{j+1}-k_{j})
=k1+∑j=1i−1(kj+1−kj)\displaystyle=k_{1}+\sum_{j=1}^{i-1}(k_{j+1}-k_{j})
=ki.\displaystyle=k_{i}.

∎

Lemma II.10.

wt𝐤​(𝐲)=L𝐤(1)​(i,𝐲)+R𝐤(1)​(i,𝐲)\mathrm{wt}_{\bf k}({\bf y})=L^{(1)}_{\bf k}(i,{\bf y})+R^{(1)}_{\bf k}(i,{\bf y}).

Proof.

It follows from the definitions of wt𝐤​(𝐲),L𝐤(1)​(i,𝐲),\mathrm{wt}_{\bf k}({\bf y}),L^{(1)}_{\bf k}(i,{\bf y}), and R𝐤(1)​(i,𝐲)R^{(1)}_{\bf k}(i,{\bf y}).

(R.H.S.)\displaystyle(\text{R.H.S.}) =∑j=1i−1yj​(kj+1−kj)+∑j=in−1yj​(kj+1−kj)\displaystyle=\sum_{j=1}^{i-1}y_{j}(k_{j+1}-k_{j})+\sum_{j=i}^{n-1}y_{j}(k_{j+1}-k_{j})
=∑j=1n−1yj​(kj+1−kj)\displaystyle=\sum_{j=1}^{n-1}y_{j}(k_{j+1}-k_{j})
=wt𝐤​(𝐲).\displaystyle=\mathrm{wt}_{\bf k}({\bf y}).

∎

Lemma II.11.

The following four inequalities hold.

0\displaystyle 0 ≤R𝐤(1)​(i,𝐲)\displaystyle\leq R^{(1)}_{\bf k}(i,{\bf y}) (1)
≤wt𝐤​(𝐲)\displaystyle\leq\mathrm{wt}_{\bf k}({\bf y}) (2)
<k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)\displaystyle<k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y}) (3)
≤kn.\displaystyle\leq k_{n}. (4)
Proof.

The inequality (1) follows from that 𝐤{\bf k} is a positive monotonic increasing integer sequence. The inequality (2) follows from Lemma II.10 and L𝐤(1)​(i,𝐲)≥0L^{(1)}_{\bf k}(i,{\bf y})\geq 0. The inequality (3) follows from k1>0k_{1}>0 and L𝐤(0)​(i,𝐲)≥0L^{(0)}_{\bf k}(i,{\bf y})\geq 0.

We show the inequality (4). From Lemma II.9 and Lemma II.10, the equation on the first line below follows.

k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)\displaystyle k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y}) =ki+R𝐤(1)​(i,𝐲)\displaystyle=k_{i}+R^{(1)}_{\bf k}(i,{\bf y})
=ki+∑j=in−1yj​(kj+1−kj)\displaystyle=k_{i}+\sum_{j=i}^{n-1}y_{j}(k_{j+1}-k_{j})
≤ki+∑j=in−1(kj+1−kj)\displaystyle\leq k_{i}+\sum_{j=i}^{n-1}(k_{j+1}-k_{j})
=kn.\displaystyle=k_{n}.

∎

Lemma II.12.
r={R𝐤(1)​(i,𝐲)(xi=0),k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)(xi=1).r=\begin{cases}R^{(1)}_{\bf k}(i,{\bf y})&(x_{i}=0),\\ k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y})&(x_{i}=1).\end{cases}
Proof.

The value of rr is obtained by using Lemma II.9, Lemma II.10 and Lemma II.11. It follows from the definitions of rr and aa.

r\displaystyle r ≡a−ρ𝐤​(𝐲)(modm)\displaystyle\equiv a-\rho_{{\bf k}}({\bf y})\pmod{m}
=a−∑i=1n−1ki​yi\displaystyle=a-\sum_{i=1}^{n-1}k_{i}y_{i}
≡∑i=1nki​xi−∑i=1n−1ki​yi(modm).\displaystyle\equiv\sum_{i=1}^{n}k_{i}x_{i}-\sum_{i=1}^{n-1}k_{i}y_{i}\pmod{m}.

By the assumption 𝐲=deli​(𝐱){\bf y}=\mathrm{del}_{i}({\bf x}), the following holds.

𝐱=insi,xi​(𝐲)=y1​⋯​yi−1​xi​yi​⋯​yn−1.{\bf x}=\mathrm{ins}_{i,x_{i}}({\bf y})=y_{1}\cdots y_{i-1}x_{i}y_{i}\cdots y_{n-1}.

Therefore,

∑i=1nki​xi−∑i=1n−1ki​yi\displaystyle\sum_{i=1}^{n}k_{i}x_{i}-\sum_{i=1}^{n-1}k_{i}y_{i}
=k1​y1+⋯+ki−1​yi−1+ki​xi+ki+1​yi​⋯+kn​yn−1\displaystyle=k_{1}y_{1}+\cdots+k_{i-1}y_{i-1}+k_{i}x_{i}+k_{i+1}y_{i}\cdots+k_{n}y_{n-1}
−k1​y1+⋯+ki−1​yi−1+ki​yi​⋯+kn−1​yn−1\displaystyle-k_{1}y_{1}+\cdots+k_{i-1}y_{i-1}~{}~{}~{}~{}~{}~{}~{}~{}~{}+k_{i}y_{i}\cdots+k_{n-1}y_{n-1}
=ki​xi+∑j=in−1yj​(kj+1−kj)\displaystyle=k_{i}x_{i}+\sum_{j=i}^{n-1}y_{j}(k_{j+1}-k_{j})
=ki​xi+R𝐤(1)​(i,𝐲)\displaystyle=k_{i}x_{i}+R^{(1)}_{\bf k}(i,{\bf y})
={R𝐤(1)​(i,𝐲)(xi=0),ki+R𝐤(1)​(i,𝐲)(xi=1)\displaystyle=\begin{cases}R^{(1)}_{\bf k}(i,{\bf y})&(x_{i}=0),\\ k_{i}+R^{(1)}_{\bf k}(i,{\bf y})&(x_{i}=1)\\ \end{cases}
={R𝐤(1)​(i,𝐲)(xi=0),k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)(xi=1).\displaystyle=\begin{cases}R^{(1)}_{\bf k}(i,{\bf y})&(x_{i}=0),\\ k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y})&(x_{i}=1).\end{cases}

The last follows from Lemma II.9 and Lemma II.10. We show that the equality holds in the cases of xi=0x_{i}=0 and xi=1x_{i}=1.

Case xi=0x_{i}=0: we have shown

r≡R𝐤(1)​(i,𝐲)(modm).r\equiv R^{(1)}_{\bf k}(i,{\bf y})\pmod{m}.

On the other hand, the following inequalities hold by Lemma II.11.

0≤R𝐤(1)​(i,𝐲)<kn<m.0\leq R^{(1)}_{\bf k}(i,{\bf y})<k_{n}<m.

By the definition of rr,

0≤r<m.0\leq r<m.

This implies r=R𝐤(1)​(i,𝐲)r=R^{(1)}_{\bf k}(i,{\bf y}).

Case xi=1x_{i}=1: We have shown

r≡k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)(modm).r\equiv k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y})\pmod{m}.

On the other hand, the following inequalities hold by Lemma II.11.

0≤k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)≤kn<m.0\leq k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y})\leq k_{n}<m.

By the definition of rr,

0≤r<m.0\leq r<m.

This implies r=k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)r=k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y}).

Therefore, Lemma II.12 holds. ∎

proof of 2 of Theorem II.4.

Let us focus on the step 23 of Algorithm 1. The case of r≤wr\leq w and the case of r>wr>w are shown separately.

In the case of r≤wr\leq w, we have DecM​(𝐲)=insp,0​(𝐲)\mathrm{Dec}_{M}({\bf y})=\mathrm{ins}_{p,0}({\bf y}). We show insp,0​(𝐲)=𝐱\mathrm{ins}_{p,0}({\bf y})={\bf x}. First, we show that r=R𝐤(1)​(i,𝐲)r=R^{(1)}_{\bf k}(i,{\bf y}) holds. This is shown by contradiction. From Lemma II.12, either

r=R𝐤(1)​(i,𝐲)orr=R^{(1)}_{\bf k}(i,{\bf y})\quad\text{or}
r=k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)r=k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y})

holds. Assume that r=k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲)r=k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y}) holds. Lemma II.11 implies r>w=wt𝐤​(𝐲)r>w=\mathrm{wt}_{\bf k}({\bf y}), which contradicts to r≤wr\leq w. Thus, r=R𝐤(1)​(i,𝐲)r=R^{(1)}_{\bf k}(i,{\bf y}) holds.

Next, we show that the deleted symbol xix_{i} is equal to 0. This is also shown by contradiction. Since xi∈𝔹x_{i}\in\mathbb{B}, either xi=0x_{i}=0 or xi=1x_{i}=1 holds. If xi=1x_{i}=1 holds, Lemma II.12 implies

r=k1+wt𝐤​(𝐲)+L𝐤(0)​(i,𝐲),r=k_{1}+\mathrm{wt}_{\bf k}({\bf y})+L^{(0)}_{\bf k}(i,{\bf y}),

which contradicts to

r=R𝐤(1)​(i,𝐲).r=R^{(1)}_{\bf k}(i,{\bf y}).

Therefore, xi=0x_{i}=0.

Finally, we show that insp,0​(𝐲)=𝐱\mathrm{ins}_{p,0}({\bf y})={\bf x}. We showed the deleted symbol xix_{i} is equal to 0. Since xi=0x_{i}=0 and 𝐲=deli​(𝐱){\bf y}=\mathrm{del}_{i}({\bf x}), 𝐱=insi,0​(𝐲){\bf x}=\mathrm{ins}_{i,0}({\bf y}) holds. Therefore, it suffices to prove that insp,0​(𝐲)=insi,0​(𝐲)\mathrm{ins}_{p,0}({\bf y})=\mathrm{ins}_{i,0}({\bf y}). Furthermore, we will show

0=yi=yi+1=⋯=yp−1.0=y_{i}=y_{i+1}=\cdots=y_{p-1}.

Since r=R𝐤(1)​(i,𝐲)r=R^{(1)}_{\bf k}(i,{\bf y}), then

i∈{j∈[n]∣R𝐤(1)​(j,𝐲)=r}i\in\{j\in[n]\mid R^{(1)}_{\bf k}(j,{\bf y})=r\}

holds. Since

p∈{j∈[n]∣R𝐤(1)​(j,𝐲)=r},p\in\{j\in[n]\mid R^{(1)}_{\bf k}(j,{\bf y})=r\},

then

r=R𝐤(1)​(i,𝐲)=R𝐤(1)​(p,𝐲)\displaystyle r=R^{(1)}_{\bf k}(i,{\bf y})=R^{(1)}_{\bf k}(p,{\bf y})

holds. Therefore,

∑j=in−1yj​(kj+1−kj)=∑j=pn−1yj​(kj+1−kj)\displaystyle\sum_{j=i}^{n-1}y_{j}(k_{j+1}-k_{j})=\sum_{j=p}^{n-1}y_{j}(k_{j+1}-k_{j})

holds. In the case of r≤wr\leq w, i≤pi\leq p follows from the definition of pp. Since i≤pi\leq p, we have

0\displaystyle 0 =∑j=in−1yj​(kj+1−kj)−∑j=pn−1yj​(kj+1−kj)\displaystyle=\sum_{j=i}^{n-1}y_{j}(k_{j+1}-k_{j})-\sum_{j=p}^{n-1}y_{j}(k_{j+1}-k_{j})
=∑j=ip−1yj​(kj+1−kj).\displaystyle=\sum_{j=i}^{p-1}y_{j}(k_{j+1}-k_{j}).

Since (kj+1−kj)>0(k_{j+1}-k_{j})>0, we have

0=yi=yi+1=⋯=yp−1.0=y_{i}=y_{i+1}=\cdots=y_{p-1}.

By a similar argument, we can prove in the remaining case r>wr>w. ∎

II-C Proof for single reversal error-correction

To prove 4 of Theorem II.4, we introduce the following Lemma II.14. From now on, till the end of this subsection, we assume the following.

Hypothesis II.13.

A binary sequence 𝐱{\bf x} is a codeword of Ma,m,𝐤​(n)M_{a,m,{\bf k}}(n) with m≥2​knm\geq 2k_{n}. Set 𝐲≔revi​(𝐱){\bf y}\coloneqq\mathrm{rev}_{i}({\bf x}) for a fixed ii. rr is the value at the step 10 of Algorithm 1.

Lemma II.14.
r={ki(yi=0),m−ki(yi=1)r=\begin{cases}k_{i}&(y_{i}=0),\\ m-k_{i}&(y_{i}=1)\end{cases}

and r≠0r\neq 0.

Proof.

It follows from the definitions of rr and aa.

r\displaystyle r ≡a−ρ𝐤​(𝐲)(modm)\displaystyle\equiv a-\rho_{{\bf k}}({\bf y})\pmod{m}
=a−∑i=1nki​yi\displaystyle=a-\sum_{i=1}^{n}k_{i}y_{i}
≡∑i=1nki​xi−∑i=1nki​yi(modm).\displaystyle\equiv\sum_{i=1}^{n}k_{i}x_{i}-\sum_{i=1}^{n}k_{i}y_{i}\pmod{m}.

By the assumption 𝐲=revi​(𝐱){\bf y}=\mathrm{rev}_{i}({\bf x}), the following holds.

𝐱=revi​(𝐲)=y1​⋯​yi−1​y¯i​yi+1​⋯​yn.{\bf x}=\mathrm{rev}_{i}({\bf y})=y_{1}\cdots y_{i-1}\overline{y}_{i}y_{i+1}\cdots y_{n}.

Therefore, we have

∑i=1nki​xi−∑i=1nki​yi\displaystyle\sum_{i=1}^{n}k_{i}x_{i}-\sum_{i=1}^{n}k_{i}y_{i}
=k1​y1+⋯+ki−1​yi−1+ki​y¯i+ki+1​yi+1​⋯+kn​yn\displaystyle=k_{1}y_{1}+\cdots+k_{i-1}y_{i-1}+k_{i}\overline{y}_{i}+k_{i+1}y_{i+1}\cdots+k_{n}y_{n}
−k1​y1+⋯+ki−1​yi−1+ki​yi+ki+1​yi+1​⋯+kn​yn\displaystyle-k_{1}y_{1}+\cdots+k_{i-1}y_{i-1}+k_{i}y_{i}+k_{i+1}y_{i+1}\cdots+k_{n}y_{n}
=ki​(y¯i−yi)\displaystyle=k_{i}(\overline{y}_{i}-y_{i})
={ki(yi=0),−ki(yi=1)\displaystyle=\begin{cases}k_{i}&(y_{i}=0),\\ -k_{i}&(y_{i}=1)\\ \end{cases}
≡{ki(yi=0),m−ki(yi=1).\displaystyle\equiv\begin{cases}k_{i}&(y_{i}=0),\\ m-k_{i}&(y_{i}=1).\\ \end{cases}

We show that the equality holds in the cases of yi=0y_{i}=0 and yi=1y_{i}=1. Since the sequence k is a positive monotonic increasing integer sequence with m≥2​knm\geq 2k_{n}, we have 0<ki≤kn<m0<k_{i}\leq k_{n}<m and 0<m−kn≤m−ki<m0<m-k_{n}\leq m-k_{i}<m. Therefore,

r={ki(yi=0),m−ki(yi=1)r=\begin{cases}k_{i}&(y_{i}=0),\\ m-k_{i}&(y_{i}=1)\\ \end{cases}\\

and r≠0r\neq 0. ∎

proof of of 4 of Theorem II.4.

Lemma II.14 implies r≠0r\neq 0. Therefore, DecM​(𝐲)≠𝐲\mathrm{Dec}_{M}({\bf y})\neq{\bf y}. Let us focus on the step 14 of Algorithm 1. Lemma II.14 implies r=kir=k_{i} or r=m−kir=m-k_{i}. Whichever r=kir=k_{i} or r=m−kir=m-k_{i},

min⁡{r,m−r}\displaystyle\min\{r,m-r\} =min⁡{ki,m−ki}\displaystyle=\min\{k_{i},m-k_{i}\}
=ki\displaystyle=k_{i}

holds, since m ≥2​ki\geq 2k_{i}. Furthermore, for distinct indices j1j_{1} and j2∈[n]j_{2}\in[n], kj1≠kj2k_{j_{1}}\neq k_{j_{2}} holds, since 𝐤{\bf k} is a positive monotonic increasing integer sequence. Therefore, we have

p\displaystyle p =min⁡{j∈[n]∣kj=min⁡{r,m−r}}\displaystyle=\min\{j\in[n]\mid k_{j}=\min\{r,m-r\}\}
=i\displaystyle=i

holds. Thus,

revp​(𝐲)\displaystyle\mathrm{rev}_{p}({\bf y}) =revi​(𝐲)\displaystyle=\mathrm{rev}_{i}({\bf y})
=𝐱\displaystyle={\bf x}
∈Ma,m,𝐤​(n).\displaystyle\in M_{a,m,{\bf k}}(n).

Therefore, DecM​(𝐲)=revp​(𝐲)=𝐱\mathrm{Dec}_{M}({\bf y})=\mathrm{rev}_{p}({\bf y})={\bf x}. ∎

III Azinv Code and its Decoding Algorithm

In this section, we provide an algorithm to make azinv codes single BAD/BAR error-correctable (Algorithm 2). Errors treated in this section are BAD errors and BAR errors, which are defined below.

Definition III.1 (BAD and BAR).

For an integer n≥2n\geq 2 and i∈[n−1]i\in[n-1], define a partial map BDi:𝔹n→𝔹n−2\mathrm{BD}_{i}:\mathbb{B}^{n}\rightarrow\mathbb{B}^{n-2} as

BDi​(x1​x2​⋯​xn)≔x1​⋯​xi−1​xi+2​⋯​xn\mathrm{BD}_{i}(x_{1}x_{2}\cdots x_{n})\coloneqq x_{1}\cdots x_{i-1}x_{i+2}\cdots x_{n}

only for 𝐱{\bf x} with xi≠xi+1x_{i}\neq x_{i+1}. We call the partial map BDi\mathrm{BD}_{i} balanced adjacent deletion (BAD).

Define a partial map BRi:𝔹n→𝔹n\mathrm{BR}_{i}:\mathbb{B}^{n}\rightarrow\mathbb{B}^{n} as

BRi​(x1​x2​⋯​xn)≔x1​⋯​xi−1​x¯i​x¯i+1​⋯​xn\mathrm{BR}_{i}(x_{1}x_{2}\cdots x_{n})\coloneqq x_{1}\cdots x_{i-1}\overline{x}_{i}\overline{x}_{i+1}\cdots x_{n}

only for 𝐱{\bf x} with xi≠xi+1x_{i}\neq x_{i+1}. We call the partial map BRi\mathrm{BR}_{i} balanced adjacent reversal (BAR).

The following codes, azinv codes, are known as single BAD error-correcting codes [9]. However, no decoding algorithm has been studied.

Definition III.2 (Azinv code [9]).

For integers n≥2n\geq 2 and m≥2m\geq 2 and an integer aa, define a set Aa,m​(n)A_{a,m}(n) as

Aa,m​(n)≔{𝐱∈𝔹n∣τ​(𝐱)≡a(modm),𝐱≠𝟎,𝟏}\displaystyle A_{a,m}(n)\coloneqq\{{\bf x}\in\mathbb{B}^{n}\mid\tau({\bf x})\equiv a\pmod{m},{\bf x}\neq{\bf 0},{\bf 1}\}

with m≥nm\geq n, where 𝟎{\bf 0} (resp. 𝟏{\bf 1}) is the all zero (resp. one) word, the function τ\tau is the composition of the function inv\mathrm{inv} below and the permutation σ−1\sigma^{-1} below i.e., τ≔inv∘σ−1\tau\coloneqq\mathrm{inv}\circ\sigma^{-1}.

The function inv\mathrm{inv} is a map from a binary word to a non-negative integer and is defined as

inv​(x1​x2​⋯​xn)≔#​{(i,j)∣1≤i<j≤n,xi>xj}.\mathrm{inv}(x_{1}x_{2}\cdots x_{n})\coloneqq\#\{(i,j)\mid 1\leq i<j\leq n,x_{i}>x_{j}\}.

The value inv​(𝐱)\mathrm{inv}({\bf x}) is called the inversion number of 𝐱{\bf x}.

The permutation σ\sigma is defined as

σ​(x1​x2​⋯​xn)≔\sigma(x_{1}x_{2}\cdots x_{n})\coloneqq

{x1​xn​x2​xn−1​x3​⋯​xn+42​xn2​xn+22(n:even),x1​xn​x2​xn−1​x3​⋯​xn−12​xn+32​xn+12(otherwise).\begin{cases}x_{1}x_{n}x_{2}x_{n-1}x_{3}\cdots x_{\frac{n+4}{2}}x_{\frac{n}{2}}x_{\frac{n+2}{2}}&(n:\text{even}),\\ x_{1}x_{n}x_{2}x_{n-1}x_{3}\cdots x_{\frac{n-1}{2}}x_{\frac{n+3}{2}}x_{\frac{n+1}{2}}&(\text{otherwise}).\end{cases}

We call Aa,m​(n)A_{a,m}(n) an azinv code.

The following is one of the main contributions of this paper.

Theorem III.3.

Let Aa,m​(n)A_{a,m}(n) be an azinv code and 𝐱{\bf x} be a codeword of Aa,m​(n)A_{a,m}(n). Let DecA\mathrm{Dec}_{A} denote Algorithm 2.

1. DecA​(𝐱)=𝐱\mathrm{Dec}_{A}({\bf x})={\bf x}.

2. Assume n≤mn\leq m. For any single BAD delBA\mathrm{del_{BA}}, DecA∘delBA​(𝐱)=𝐱\mathrm{Dec}_{A}\circ\mathrm{del_{BA}}({\bf x})={\bf x}.

3. If n≤mn\leq m, any azinv code Aa,m​(n)A_{a,m}(n) is a single BAD error-correcting code with Algorithm 2 as a decoding algorithm.

4. Assume 2​(n−1)≤m2(n-1)\leq m. For any single BAR revBA\mathrm{rev_{BA}}, DecA∘revBA​(𝐱)=𝐱\mathrm{Dec}_{A}\circ\mathrm{rev_{BA}}({\bf x})={\bf x}.

5. If 2​(n−1)≤m2(n-1)\leq m, any monotone code Aa,m​(n)A_{a,m}(n) is a single BAD/BAR error-correcting code with Algorithm 2 as a decoding algorithm. Here ∘\circ denotes the map composition.

Proof.

1. It is trivial from the steps 3 and 4 of Algorithm 2. 2. A proof is provided in subsection III-B. 3. It is a corollary of 1. and 2. 4. A proof is provided in subsection III-C. 5. It is a corollary of 3. and 4. ∎

III-A Decoding algorithm for single BAD errors

In this subsection, we provide the details of Algorithm 2. Curiously, Algorithm 2 is similar to Algorithm 1 for correcting single deletion/reversal errors for monotone codes.

We introduce the following notation. For a positive integer nn and a binary sequence 𝐲=y1​y2​⋯​yn{\bf y}=y_{1}y_{2}\cdots y_{n}, define 𝐲~{\bf\tilde{y}} as

𝐲~≔{y1​y¯2​y3​⋯​yn−1​y¯n(n:even),y1​y¯2​y3​⋯​y¯n−1​yn(otherwise).{\bf\tilde{y}}\coloneqq\begin{cases}y_{1}\overline{y}_{2}y_{3}\cdots y_{n-1}\overline{y}_{n}&(n:\text{even}),\\ y_{1}\overline{y}_{2}y_{3}\cdots\overline{y}_{n-1}y_{n}&(\text{otherwise}).\end{cases}

For the iith entry of 𝐲{\bf y}, say yiy_{i}, define y~i\tilde{y}_{i} as

y~i≔{y¯i(i:even),yi(otherwise).\tilde{y}_{i}\coloneqq\begin{cases}\overline{y}_{i}&(i:\text{even}),\\ y_{i}&(\text{otherwise}).\end{cases}

For integers ii and jj, define [i,j][i,j] as [i,j]≔{k∈ℤ|i≤k≤j}[i,j]\coloneqq\{k\in\mathbb{Z}|i\leq k\leq j\}. We denote the subsequence of 𝐲{\bf y} in the range [i,j][i,j], by 𝐲[i,j]{\bf y}_{[i,j]}, i.e., 𝐲[i,j]≔yi​yi+1​⋯​yj{\bf y}_{[i,j]}\coloneqq y_{i}y_{i+1}\cdots y_{j}. By using the range notation, the permutation σ−1\sigma^{-1} can be written in the following form.

Remark III.4.

σ−1​(y1​y2​⋯​yn)=y1​σ−1​(𝐲[3,n])​y2\sigma^{-1}(y_{1}y_{2}\cdots y_{n})=y_{1}\sigma^{-1}({\bf y}_{[3,n]})y_{2}.

Algorithm 2 Decoding algorithm for single BAD/BAR errors
1:  Input: a∈ℤ≥0,na\in\mathbb{Z}_{\geq 0},n and m∈ℤ≥2m\in\mathbb{Z}_{\geq 2}, and 𝐲∈⋃t≥0𝔹t{\bf y}\in\bigcup_{t\geq 0}\mathbb{B}^{t}. Output: 𝐳∈𝔹n{\bf z}\in\mathbb{B}^{n} or a symbol ?.
2:  Compute the length of 𝐲{\bf y}, say |𝐲||{\bf y}|.
3:  if |𝐲|=n|{\bf y}|=n then
4:     Go to 10.
5:  else if |𝐲|=n−2|{\bf y}|=n-2 then
6:     go to 21.
7:  else
8:     𝐳≔?{\bf z}\coloneqq?. Go to 43.
9:  end if
10:  Compute r≔min⁡{s∈ℤ≥0∣s≡a−τ​(𝐲)(modm)}r\coloneqq\min\{s\in\mathbb{Z}_{\geq 0}\mid s\equiv a-\tau({\bf y})\pmod{m}\}.
11:  if r=0r=0 then
12:     𝐳≔𝐲{\bf z}\coloneqq{\bf y}. Go to 43.
13:  else
14:     Compute p≔n−min⁡{r,m−r}p\coloneqq n-\min\{r,m-r\}.
15:     if revBAp​(𝐲)∈Aa,m​(n)\mathrm{rev_{BA}}_{p}({\bf y})\in A_{a,m}(n) then
16:        𝐳≔revBAp​(𝐲){\bf z}\coloneqq\mathrm{rev_{BA}}_{p}({\bf y}). Go to 43.
17:     else
18:        𝐳≔?{\bf z}\coloneqq?. Go to 43.
19:     end if
20:  end if
21:  Compute r≔min⁡{s∈ℤ≥0∣s≡a−τ​(𝐲)(modm)}r\coloneqq\min\{s\in\mathbb{Z}_{\geq 0}\mid s\equiv a-\tau({\bf y})\pmod{m}\}.
22:  Compute w≔wt​(𝐲~)w\coloneqq\mathrm{wt}({\bf\tilde{y}}).
23:  if r≤wr\leq w then
24:     Compute p≔max{j∈[n−1]∣L(1)(j,𝐲~)=r)}p\coloneqq\max\{j\in[n-1]\mid L^{(1)}(j,{\bf\tilde{y}})=r)\}.
25:     if pp: even then
26:        b≔10b\coloneqq 10.
27:     else
28:        b≔01b\coloneqq 01.
29:     end if
30:  else
31:     Compute p≔min{j∈[n−1]∣R(0)(j,𝐲~)=r−w−1)}p\coloneqq\min\{j\in[n-1]\mid R^{(0)}(j,{\bf\tilde{y}})=r-w-1)\}.
32:     if pp: even then
33:        b≔01b\coloneqq 01.
34:     else
35:        b≔10b\coloneqq 10.
36:     end if
37:  end if
38:  if insp,𝐛​(𝐲)∈Aa,m​(n)\mathrm{ins}_{p,{\bf b}}({\bf y})\in A_{a,m}(n) then
39:     𝐳≔insp,𝐛​(𝐲){\bf z}\coloneqq\mathrm{ins}_{p,{\bf b}}({\bf y}).
40:  else
41:     𝐳≔?{\bf z}\coloneqq?.
42:  end if
43:  Output z.

Before we move to proofs for Theorem III.3, we provide examples of Algorithm 2 for each error.

Example III.5 (Decoding for a single BAD error).

Let n=5,a=0,m=5,n=5,a=0,m=5, and 𝐲=101{\bf y}=101. Note that the azinv code has six words,

C0,5​(5)={01000,01010,01010,01011,01111,10110,10001}.C_{0,5}(5)=\{01000,01010,01010,01011,01111,10110,10001\}.
  • •

    Since |𝐲|=3|{\bf y}|=3, we go to step 6 and then to step 21.

  • •

    Algorithm 2 computes rr and ww, then we obtain r=3r=3 and w=3.w=3.

  • •

    Since r≤wr\leq w, then

    p\displaystyle p =max{j∈[4]∣L(1)(j,𝐲~)=3)}\displaystyle=\max\{j\in[4]\mid L^{(1)}(j,{\bf\tilde{y}})=3)\}
    =4.\displaystyle=4.
  • •

    Since p=4p=4 is even, then b=10b=10.

  • •

    The output DecA​(𝐲)=insp,b​(𝐲)\mathrm{Dec}_{A}({\bf y})=\mathrm{ins}_{p,b}({\bf y}) is

    ins4,10​(101)=10110.\mathrm{ins}_{4,10}(101)=10110.
Example III.6 (Decoding for a single BAR error).

Let n=6,a=0,m=10,n=6,a=0,m=10, and 𝐲=100000{\bf y}=100000. Note that the azinv code has five words,

C0,10​(6)={010000,010100,010101,010111,011111}.C_{0,10}(6)=\{010000,010100,010101,010111,011111\}.
  • •

    Since |𝐲|=6|{\bf y}|=6, we go to step 4 and then to step 10.

  • •

    Algorithm 2 computes rr, then r=5r=5.

  • •

    Since r≠0r\neq 0,

    p\displaystyle p =6−min⁡{5,5}\displaystyle=6-\min\{5,5\}
    =1.\displaystyle=1.
  • •

    The output DecA​(𝐲)=revBAp​(𝐲)\mathrm{Dec}_{A}({\bf y})=\mathrm{rev_{BA}}_{p}({\bf y}) is

    BR1​(100000)=010000.\mathrm{BR}_{1}(100000)=010000.

III-B Proof for single BAD error-correction

To prove 2 of Theorem III.3, we introduce the following three Lemmas III.8, III.9 and III.10 From now on, till the end of this subsection, we assume the following.

Hypothesis III.7.

A binary sequence 𝐱{\bf x} is a codeword of Aa,m​(n)A_{a,m}(n). Set 𝐲≔delBAi​(𝐱){\bf y}\coloneqq\mathrm{del_{BA}}_{i}({\bf x}) for a fixed ii. rr is the value at the step 21 of Algorithm 2.

Lemma III.8.

The following four inequalities hold.

0\displaystyle 0 ≤L(1)​(i,𝐲)\displaystyle\leq L^{(1)}(i,{\bf y}) (1)
≤wt​(𝐲)\displaystyle\leq\mathrm{wt}({\bf y}) (2)
<1+wt​(𝐲)+R(0)​(i,𝐲)\displaystyle<1+\mathrm{wt}({\bf y})+R^{(0)}(i,{\bf y}) (3)
<n.\displaystyle<n. (4)
Proof.

The inequality (1) follows from the definition of L(1)​(i,𝐲)L^{(1)}(i,{\bf y}). The inequality (2) follows from Lemma II.10 and R(1)​(i,𝐲)≥0R^{(1)}(i,{\bf y})\geq 0. The inequality (3) follows from R(0)​(i,𝐲)≥0R^{(0)}(i,{\bf y})\geq 0. We show the inequality (4).

1+wt​(𝐲)+R(0)​(i,𝐲)\displaystyle 1+\mathrm{wt}({\bf y})+R^{(0)}(i,{\bf y}) =1+R(1)​(1,𝐲)+R(0)​(i,𝐲)\displaystyle=1+R^{(1)}(1,{\bf y})+R^{(0)}(i,{\bf y})
≤1+R(1)​(1,𝐲)+R(0)​(1,𝐲)\displaystyle\leq 1+R^{(1)}(1,{\bf y})+R^{(0)}(1,{\bf y})
=n−1\displaystyle=n-1
<n.\displaystyle<n.

∎

Lemma III.9.

Either x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00 or x~i​x~i+1=11\tilde{x}_{i}\tilde{x}_{i+1}=11 holds.

Proof.

By the assumption 𝐲=delBAi​(𝐱){\bf y}=\mathrm{del_{BA}}_{i}({\bf x}), xi≠xi+1x_{i}\neq x_{i+1} holds. Thus, either xi​xi+1=01x_{i}x_{i+1}=01 or xi​xi+1=10x_{i}x_{i+1}=10 holds. Therefofre, whichever ii is odd or even, either x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00 or x~i​x~i+1=11\tilde{x}_{i}\tilde{x}_{i+1}=11 holds. ∎

Lemma III.10.
r={L(1)​(i,𝐲~)(x~i​x~i+1=00),1+wt​(𝐲~)+R(0)​(i,𝐲~)(x~i​x~i+1=11).r=\begin{cases}L^{(1)}(i,{\bf\tilde{y}})&(\tilde{x}_{i}\tilde{x}_{i+1}=00),\\ 1+\mathrm{wt}({\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}})&(\tilde{x}_{i}\tilde{x}_{i+1}=11).\end{cases}
Proof.

It follows from the definitions of rr and aa.

r\displaystyle r ≡a−τ​(𝐲)(modm)\displaystyle\equiv a-\tau({\bf y})\pmod{m}
=a−inv​(σ−1​(𝐲))\displaystyle=a-\mathrm{inv}(\sigma^{-1}({\bf y}))
≡inv​(σ−1​(𝐱))−inv​(σ−1​(𝐲))(modm)\displaystyle\equiv\mathrm{inv}(\sigma^{-1}({\bf x}))-\mathrm{inv}(\sigma^{-1}({\bf y}))\pmod{m}

By the assumption 𝐲=BADi​(𝐱){\bf y}=\mathrm{BAD}_{i}({\bf x}), the following holds.

𝐱=insi,xi​xi+1​(𝐲)=y1​y2​⋯​yi−1​xi​xi+1​yi​yi+1​⋯​yn−2.{\bf x}=\mathrm{ins}_{i,x_{i}x_{i+1}}({\bf y})=y_{1}y_{2}\cdots y_{i-1}x_{i}x_{i+1}y_{i}y_{i+1}\cdots y_{n-2}.

Therefore, we have

inv​(σ−1​(𝐱))−inv​(σ−1​(𝐲))\displaystyle\mathrm{inv}(\sigma^{-1}({\bf x}))-\mathrm{inv}(\sigma^{-1}({\bf y}))
=inv​(σ−1​(insi,xi​xi+1​(𝐲)))−inv​(σ−1​(𝐲))\displaystyle=\mathrm{inv}(\sigma^{-1}(\mathrm{ins}_{i,x_{i}x_{i+1}}({\bf y})))-\mathrm{inv}(\sigma^{-1}({\bf y}))
=inv​(σ−1​(y1​y2​⋯​yi−1​xi​xi+1​yi​yi+1​⋯​yn−2))\displaystyle=\mathrm{inv}(\sigma^{-1}(y_{1}y_{2}\cdots y_{i-1}x_{i}x_{i+1}y_{i}y_{i+1}\cdots y_{n-2}))
−inv​(σ−1​(y1​y2​⋯​yi−1yi​yi+1​⋯​yn−2))\displaystyle-\mathrm{inv}(\sigma^{-1}(y_{1}y_{2}\cdots y_{i-1}\quad\quad\quad y_{i}y_{i+1}\cdots y_{n-2}))
={inv​(y1​y3​⋯​yi−2​xi​σ−1​(𝐲[i,n−2])​xi+1​yi−1​⋯​y4​y2)−inv​(y1​y3​⋯​yi−2σ−1​(𝐲[i,n−2])yi−1​⋯​y4​y2)(i:odd),inv​(y1​y3​⋯​yi−1​xi+1​σ−1​(𝐲[i+1,n−2])​yi​xi​⋯​y4​y2)−inv​(y1​y3​⋯​yi−1σ−1​(𝐲[i+1,n−2])​yi⋯​y4​y2)(i:even)\displaystyle=\left\{\begin{array}[]{cc}\mathrm{inv}(y_{1}y_{3}\cdots y_{i-2}x_{i}\sigma^{-1}({\bf y}_{[i,n-2]})x_{i+1}y_{i-1}\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i-2}\quad\sigma^{-1}({\bf y}_{[i,n-2]})\quad y_{i-1}\cdots y_{4}y_{2})\\ (i:\text{odd}),\\ \\ \\ \mathrm{inv}(y_{1}y_{3}\cdots y_{i-1}x_{i+1}\sigma^{-1}({\bf y}_{[i+1,n-2]})y_{i}x_{i}\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i-1}\quad\sigma^{-1}({\bf y}_{[i+1,n-2]})y_{i}\quad\cdots y_{4}y_{2})\\ (i:\text{even})\end{array}\right.
={inv​(y1​y3​⋯​yi−20​σ−1​(𝐲[i,n−2])​1yi−1​⋯​y4​y2)−inv​(y1​y3​⋯​yi−2σ−1​(𝐲[i,n−2])yi−1​⋯​y4​y2)(i:odd,xi​xi+1=01),inv​(y1​y3​⋯​yi−10​σ−1​(𝐲[i+1,n−2])​yi​1⋯​y4​y2)−inv​(y1​y3​⋯​yi−1σ−1​(𝐲[i+1,n−2])​yi⋯​y4​y2)(i:even,xi​xi+1=10),inv​(y1​y3​⋯​yi−21​σ−1​(𝐲[i,n−2])​0yi−1​⋯​y4​y2)−inv​(y1​y3​⋯​yi−2σ−1​(𝐲[i,n−2])yi−1​⋯​y4​y2)(i:odd,xi​xi+1=10),inv​(y1​y3​⋯​yi−11​σ−1​(𝐲[i+1,n−2])​yi​0⋯​y4​y2)−inv​(y1​y3​⋯​yi−1σ−1​(𝐲[i+1,n−2])​yi⋯​y4​y2)(i:even,xi​xi+1=01)\displaystyle=\left\{\begin{array}[]{cc}\mathrm{inv}(y_{1}y_{3}\cdots y_{i-2}\quad 0\sigma^{-1}({\bf y}_{[i,n-2]})1\quad y_{i-1}\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i-2}\quad\sigma^{-1}({\bf y}_{[i,n-2]})\quad y_{i-1}\cdots y_{4}y_{2})\\ (i:\text{odd},x_{i}x_{i+1}=01),\\ \\ \\ \mathrm{inv}(y_{1}y_{3}\cdots y_{i-1}\quad 0\sigma^{-1}({\bf y}_{[i+1,n-2]})y_{i}1\quad\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i-1}\quad\sigma^{-1}({\bf y}_{[i+1,n-2]})y_{i}\quad\cdots y_{4}y_{2})\\ (i:\text{even},x_{i}x_{i+1}=10),\\ \\ \\ \mathrm{inv}(y_{1}y_{3}\cdots y_{i-2}\quad 1\sigma^{-1}({\bf y}_{[i,n-2]})0\quad y_{i-1}\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i-2}\quad\sigma^{-1}({\bf y}_{[i,n-2]})\quad y_{i-1}\cdots y_{4}y_{2})\\ (i:\text{odd},x_{i}x_{i+1}=10),\\ \\ \\ \mathrm{inv}(y_{1}y_{3}\cdots y_{i-1}\quad 1\sigma^{-1}({\bf y}_{[i+1,n-2]})y_{i}0\quad\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i-1}\quad\sigma^{-1}({\bf y}_{[i+1,n-2]})y_{i}\quad\cdots y_{4}y_{2})\\ (i:\text{even},x_{i}x_{i+1}=01)\end{array}\right.
={∑j=1,j:oddi−2yj+∑j=2,j:eveni−1y¯j(i:odd,xi​xi+1=01),∑j=1,j:oddi−1yj+∑j=2,j:eveni−2y¯j(i:even,xi​xi+1=10),∑j=1,j:oddi−2yj+∑j=2,j:eveni−1y¯j+(n−2−(i−1))+1(i:odd,xi​xi+1=10),∑j=1,j:oddi−1yj+∑j=2,j:eveni−2y¯j+(n−2−(i−1))+1(i:even,xi​xi+1=01)\displaystyle=\left\{\begin{array}[]{ll}\displaystyle\sum_{j=1,j:\text{odd}}^{i-2}y_{j}+\sum_{j=2,j:\text{even}}^{i-1}\overline{y}_{j}\\ (i:\text{odd},x_{i}x_{i+1}=01),\\ \\ \displaystyle\sum_{j=1,j:\text{odd}}^{i-1}y_{j}+\sum_{j=2,j:\text{even}}^{i-2}\overline{y}_{j}\\ (i:\text{even},x_{i}x_{i+1}=10),\\ \\ \displaystyle\sum_{j=1,j:\text{odd}}^{i-2}y_{j}+\sum_{j=2,j:\text{even}}^{i-1}\overline{y}_{j}+(n-2-(i-1))+1\\ (i:\text{odd},x_{i}x_{i+1}=10),\\ \\ \displaystyle\sum_{j=1,j:\text{odd}}^{i-1}y_{j}+\sum_{j=2,j:\text{even}}^{i-2}\overline{y}_{j}+(n-2-(i-1))+1\\ (i:\text{even},x_{i}x_{i+1}=01)\\ \end{array}\right.
={∑j=1i−1y~j(i:odd,xixi+1=01ori:even,xixi+1=10),∑j=1i−1y~j+∑j=in−2(y~j+y~¯j)+1(i:odd,xixi+1=10ori:even,xixi+1=01)\displaystyle=\left\{\begin{array}[]{cc}\displaystyle\sum_{j=1}^{i-1}\tilde{y}_{j}\\ (i:\text{odd},x_{i}x_{i+1}=01\quad\text{or}\quad i:\text{even},x_{i}x_{i+1}=10),\\ \\ \displaystyle\sum_{j=1}^{i-1}\tilde{y}_{j}+\sum_{j=i}^{n-2}(\tilde{y}_{j}+\overline{\tilde{y}}_{j})+1\\ (i:\text{odd},x_{i}x_{i+1}=10\quad\text{or}\quad i:\text{even},x_{i}x_{i+1}=01)\end{array}\right.
={L(1)​(i,𝐲~)(x~i​x~i+1=00),L(1)​(i,𝐲~)+R(1)​(i,𝐲~)+R(0)​(i,𝐲~)+1(x~i​x~i+1=11)\displaystyle=\left\{\begin{array}[]{cc}L^{(1)}(i,{\bf\tilde{y}})\\ (\tilde{x}_{i}\tilde{x}_{i+1}=00),\\ \\ L^{(1)}(i,{\bf\tilde{y}})+R^{(1)}(i,{\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}})+1\\ (\tilde{x}_{i}\tilde{x}_{i+1}=11)\end{array}\right.
={L(1)​(i,𝐲~)(x~i​x~i+1=00),1+wt​(𝐲~)+R(0)​(i,𝐲~)(x~i​x~i+1=11).\displaystyle=\left\{\begin{array}[]{cc}L^{(1)}(i,{\bf\tilde{y}})&(\tilde{x}_{i}\tilde{x}_{i+1}=00),\\ 1+\mathrm{wt}({\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}})&(\tilde{x}_{i}\tilde{x}_{i+1}=11).\end{array}\right.

The last follows from Lemma II.10. We show that the equality holds in the cases of x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00 and x~i​x~i+1=11\tilde{x}_{i}\tilde{x}_{i+1}=11.

Case x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00: we have shown

r≡L(1)​(i,𝐲~)(modm).r\equiv L^{(1)}(i,{\bf\tilde{y}})\pmod{m}.

On the other hand, the following inequalities hold by Lemma III.8.

0≤L(1)​(i,𝐲~)<n<m.0\leq L^{(1)}(i,{\bf\tilde{y}})<n<m.

By the definition of rr,

0≤r<m.0\leq r<m.

This implies r=L(1)​(i,𝐲~)r=L^{(1)}(i,{\bf\tilde{y}}).

Case x~i​x~i+1=11\tilde{x}_{i}\tilde{x}_{i+1}=11: We have shown

r≡1+wt​(𝐲~)+R(0)​(i,𝐲~)(modm).r\equiv 1+\mathrm{wt}({\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}})\pmod{m}.

On the other hand, the following inequalities hold by Lemma III.8.

0≤1+wt​(𝐲~)+R(0)​(i,𝐲~)≤n<m.0\leq 1+\mathrm{wt}({\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}})\leq n<m.

By the definition of rr,

0≤r<m.0\leq r<m.

This implies r=1+wt​(𝐲~)+R(0)​(i,𝐲~)r=1+\mathrm{wt}({\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}}). Therefore, Lemma III.10 holds. ∎

proof of 2 of Theorem III.3.

Let us focus on the step 23 of Algorithm 2. The case of r≤wr\leq w and the case of r>wr>w are shown separately.

In the case of r≤wr\leq w, we have DecA​(𝐲)=insp,b​(𝐲)\mathrm{Dec}_{A}({\bf y})=\mathrm{ins}_{p,b}({\bf y}). We show insp,b​(𝐲)=𝐱\mathrm{ins}_{p,b}({\bf y})={\bf x}. First, we can show that r=L(1)​(i,𝐲~)r=L^{(1)}(i,{\bf\tilde{y}}) holds, similarly to the case of Monotone codes.

Next, we show that the deleted symbols xi​xi+1x_{i}x_{i+1} satisfy x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00. This is shown by contradiction. Since xi​xi+1∈{01,10}x_{i}x_{i+1}\in\{01,10\}, either x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00 or x~i​x~i+1=11\tilde{x}_{i}\tilde{x}_{i+1}=11 holds. Assume that x~i​x~i+1=11\tilde{x}_{i}\tilde{x}_{i+1}=11 holds. Lemma III.10 implies

r=1+wt​(𝐲~)+R(0)​(i,𝐲~),r=1+\mathrm{wt}({\bf\tilde{y}})+R^{(0)}(i,{\bf\tilde{y}}),

which contradicts to

r=L(1)​(i,𝐲~).r=L^{(1)}(i,{\bf\tilde{y}}).

Therefore, x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00.

Finally, we show that insp,b​(𝐲)=𝐱\mathrm{ins}_{p,b}({\bf y})={\bf x}. We showed that the deleted symbols xi​xi+1x_{i}x_{i+1} satisfy x~i​x~i+1=00\tilde{x}_{i}\tilde{x}_{i+1}=00. By the assumption 𝐲=delBAi​(𝐱){\bf y}=\mathrm{del_{BA}}_{i}({\bf x}), we have 𝐱=insi,xi​xi+1​(𝐲){\bf x}=\mathrm{ins}_{i,x_{i}x_{i+1}}({\bf y}). Therefore, it suffices to prove that insp,b​(𝐲)=insi,xi​xi+1​(𝐲)\mathrm{ins}_{p,b}({\bf y})=\mathrm{ins}_{i,x_{i}x_{i+1}}({\bf y}). Furthermore we will show

0=y~i=y~i+1=⋯=y~p−1.0=\tilde{y}_{i}=\tilde{y}_{i+1}=\cdots=\tilde{y}_{p-1}.

Since r=L(1)​(i,𝐲~)r=L^{(1)}(i,{\bf\tilde{y}}), then

i∈{j∈[n−1]∣L(1)(j,𝐲~)=r)}i\in\{j\in[n-1]\mid L^{(1)}(j,{\bf\tilde{y}})=r)\}

holds. Since

p∈{j∈[n−1]∣L(1)(j,𝐲~)=r)},p\in\{j\in[n-1]\mid L^{(1)}(j,{\bf\tilde{y}})=r)\},

then

r=L(1)​(i,𝐲~)=L(1)​(p,𝐲~)\displaystyle r=L^{(1)}(i,{\bf\tilde{y}})=L^{(1)}(p,{\bf\tilde{y}})

holds. Therefore,

∑j=1i−1y~j=∑j=1p−1y~j\displaystyle\sum_{j=1}^{i-1}\tilde{y}_{j}=\sum_{j=1}^{p-1}\tilde{y}_{j}

holds. In the case of r≤wr\leq w, i≤pi\leq p follows from the definition of pp. Since i≤pi\leq p, then

0\displaystyle 0 =∑j=1p−1y~j−∑j=1i−1y~j\displaystyle=\sum_{j=1}^{p-1}\tilde{y}_{j}-\sum_{j=1}^{i-1}\tilde{y}_{j}
=∑j=ip−1y~j\displaystyle=\sum_{j=i}^{p-1}\tilde{y}_{j}

holds. Therefore, we have

0=y~i=y~i+1=⋯=y~p−1.0=\tilde{y}_{i}=\tilde{y}_{i+1}=\cdots=\tilde{y}_{p-1}.

By a similar argument, we can prove in the remaining case r>wr>w. ∎

III-C Proof for single BAR error-correction

To prove 4 of Theorem III.3, we introduce the following two Lemmas III.12 and III.13. From now on, till the end of this subsection, we assume the following.

Hypothesis III.11.

A binary sequence 𝐱{\bf x} is a codeword of Aa,m​(n)A_{a,m}(n) with m≥2​(n−1)m\geq 2(n-1). Set 𝐲≔revBAi​(𝐱){\bf y}\coloneqq\mathrm{rev_{BA}}_{i}({\bf x}) for a fixed ii. rr is the value at the step 10 of Algorithm 2.

Lemma III.12.

Either y~i​y~i+1=00\tilde{y}_{i}\tilde{y}_{i+1}=00 or y~i​y~i+1=11\tilde{y}_{i}\tilde{y}_{i+1}=11 holds.

Proof.

By the assumption 𝐲=revBAi​(𝐱){\bf y}=\mathrm{rev_{BA}}_{i}({\bf x}), xi≠xi+1x_{i}\neq x_{i+1} holds. Hence, yi≠yi+1y_{i}\neq y_{i+1} holds. Thus, either yi​yi+1=01y_{i}y_{i+1}=01 or yi​yi+1=10y_{i}y_{i+1}=10 holds. Therefofre, whichever ii is odd or even, either y~i​y~i+1=00\tilde{y}_{i}\tilde{y}_{i+1}=00 or y~i​y~i+1=11\tilde{y}_{i}\tilde{y}_{i+1}=11 holds. ∎

Lemma III.13.
r={n−i(y~i​y~i+1=00),m−(n−i)(y~i​y~i+1=11)r=\begin{cases}n-i&(\tilde{y}_{i}\tilde{y}_{i+1}=00),\\ m-(n-i)&(\tilde{y}_{i}\tilde{y}_{i+1}=11)\end{cases}

and r≠0r\neq 0.

Proof.

It follows from the definitions of rr and aa.

r\displaystyle r ≡a−τ​(𝐲)(modm)\displaystyle\equiv a-\tau({\bf y})\pmod{m}
=a−inv​(σ−1​(𝐲))\displaystyle=a-\mathrm{inv}(\sigma^{-1}({\bf y}))
≡inv​(σ−1​(𝐱))−inv​(σ−1​(𝐲))(modm)\displaystyle\equiv\mathrm{inv}(\sigma^{-1}({\bf x}))-\mathrm{inv}(\sigma^{-1}({\bf y}))\pmod{m}

By the assumption 𝐲=revBAi​(𝐱){\bf y}=\mathrm{rev_{BA}}_{i}({\bf x}), the following holds.

𝐱=revBAi​(𝐲)=y1​y2​⋯​yi−1​yi+1​yi​⋯​yn.{\bf x}=\mathrm{rev_{BA}}_{i}({\bf y})=y_{1}y_{2}\cdots y_{i-1}{y}_{i+1}y_{i}\cdots y_{n}.

Therefore, we have

inv​(σ−1​(𝐱))−inv​(σ−1​(𝐲))\displaystyle\mathrm{inv}(\sigma^{-1}({\bf x}))-\mathrm{inv}(\sigma^{-1}({\bf y}))
=inv​(σ−1​(revBAi​(𝐲)))−inv​(σ−1​(𝐲))\displaystyle=\mathrm{inv}(\sigma^{-1}(\mathrm{rev_{BA}}_{i}({\bf y})))-\mathrm{inv}(\sigma^{-1}({\bf y}))
=inv​(σ−1​(y1​y2​⋯​yi−1​yi+1​yi​⋯​yn))\displaystyle=\mathrm{inv}(\sigma^{-1}(y_{1}y_{2}\cdots y_{i-1}y_{i+1}y_{i}\cdots y_{n}))
−inv​(σ−1​(y1​y2​⋯​yi−1​yi​yi+1​⋯​yn))\displaystyle-\mathrm{inv}(\sigma^{-1}(y_{1}y_{2}\cdots y_{i-1}y_{i}y_{i+1}\cdots y_{n}))
={inv​(y1​y3​⋯​yi+1​σ−1​(𝐲[i+2,n])​yi​yi−1​⋯​y4​y2)−inv​(y1​y3​⋯​yiσ−1​(𝐲[i+2,n])​yi+1​yi−1​⋯​y4​y2)(i:odd),inv​(y1​y3​⋯​yi​σ−1​(𝐲[i+3,n])​yi+2​yi+1​⋯​y4​y2)−inv​(y1​y3​⋯​yi+1​σ−1​(𝐲[i+3,n])​yi+2​yi​⋯​y4​y2)(i:even)\displaystyle=\left\{\begin{array}[]{cc}\mathrm{inv}(y_{1}y_{3}\cdots y_{i+1}\sigma^{-1}({\bf y}_{[i+2,n]})y_{i}y_{i-1}\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i}\quad\sigma^{-1}({\bf y}_{[i+2,n]})y_{i+1}y_{i-1}\cdots y_{4}y_{2})\\ (i:\text{odd}),\\ \\ \\ \mathrm{inv}(y_{1}y_{3}\cdots y_{i}\sigma^{-1}({\bf y}_{[i+3,n]})y_{i+2}y_{i+1}\cdots y_{4}y_{2})\\ \\ -\mathrm{inv}(y_{1}y_{3}\cdots y_{i+1}\sigma^{-1}({\bf y}_{[i+3,n]})y_{i+2}y_{i}\cdots y_{4}y_{2})\\ (i:\text{even})\end{array}\right.
={n−i(i:odd,yiyi+1=01ori:even,yiyi+1=10),−(n−i)(i:odd,yiyi+1=10ori:even,yiyi+1=01)\displaystyle=\left\{\begin{array}[]{cc}n-i\\ (i:\text{odd},y_{i}y_{i+1}=01\quad\text{or}\quad i:\text{even},y_{i}y_{i+1}=10),\\ \\ -(n-i)\\ (i:\text{odd},y_{i}y_{i+1}=10\quad\text{or}\quad i:\text{even},y_{i}y_{i+1}=01)\end{array}\right.
≡{n−i(y~i​y~i+1=00),m−(n−i)(y~i​y~i+1=11).\displaystyle\equiv\left\{\begin{array}[]{cc}n-i&(\tilde{y}_{i}\tilde{y}_{i+1}=00),\\ m-(n-i)&(\tilde{y}_{i}\tilde{y}_{i+1}=11).\end{array}\right.

We show that the equality holds in the case of y~i​y~i+1=00\tilde{y}_{i}\tilde{y}_{i+1}=00 and y~i​y~i+1=11\tilde{y}_{i}\tilde{y}_{i+1}=11. Since i∈[n−1]i\in[n-1], we have 1≤n−i≤n−1<m1\leq n-i\leq n-1<m. Then, 0<m−(n−i)≤m−1<m0<m-(n-i)\leq m-1<m. Therefore,

r={n−i(y~i​y~i+1=00),m−(n−i)(y~i​y~i+1=11)r=\begin{cases}n-i&(\tilde{y}_{i}\tilde{y}_{i+1}=00),\\ m-(n-i)&(\tilde{y}_{i}\tilde{y}_{i+1}=11)\end{cases}

and r≠0r\neq 0. ∎

proof 4 of Theorem III.3.

Lemma III.13 implies r≠0r\neq 0. Therefore, Dec​(𝐲)≠𝐲\mathrm{Dec}({\bf y})\neq{\bf y}. Let us focus on the step 14 of Algorithm 2. Lemma III.13 implies r=n−ir=n-i or r=m−(n−i)r=m-(n-i). Whichever r=n−ir=n-i or r=m−(n−i)r=m-(n-i),

min⁡{r,m−r}\displaystyle\min\{r,m-r\} =min⁡{n−i,m−(n−i)}\displaystyle=\min\{n-i,m-(n-i)\}
=n−i\displaystyle=n-i

holds, since m≥2​nm\geq 2n. Then,

p\displaystyle p =n−min⁡{r,m−r}\displaystyle=n-\min\{r,m-r\}
=n−(n−i)\displaystyle=n-(n-i)
=i\displaystyle=i

holds. Thus,

revBAp​(𝐲)\displaystyle\mathrm{rev_{BA}}_{p}({\bf y}) =revBAi​(𝐲)\displaystyle=\mathrm{rev_{BA}}_{i}({\bf y})
=𝐱\displaystyle={\bf x}
∈Aa,m​(n).\displaystyle\in A_{a,m}(n).

Therefore, Dec​(𝐲)=revBAp​(𝐲)=𝐱\mathrm{Dec}({\bf y})=\mathrm{rev_{BA}}_{p}({\bf y})={\bf x}. ∎

IV Analysis and unification of the algorithms

In this section, we provide a unified view of our proposed algorithms. After that, we prove that the algorithms can be computed in linear time in the code-length.

Flowchart 1 is the unified representation of the parts of Algorithm 1 and Algorithm 2, that is, the steps 21st - 34th of Algorithm 1 and the steps 21st - 42th of Algorithm 2.

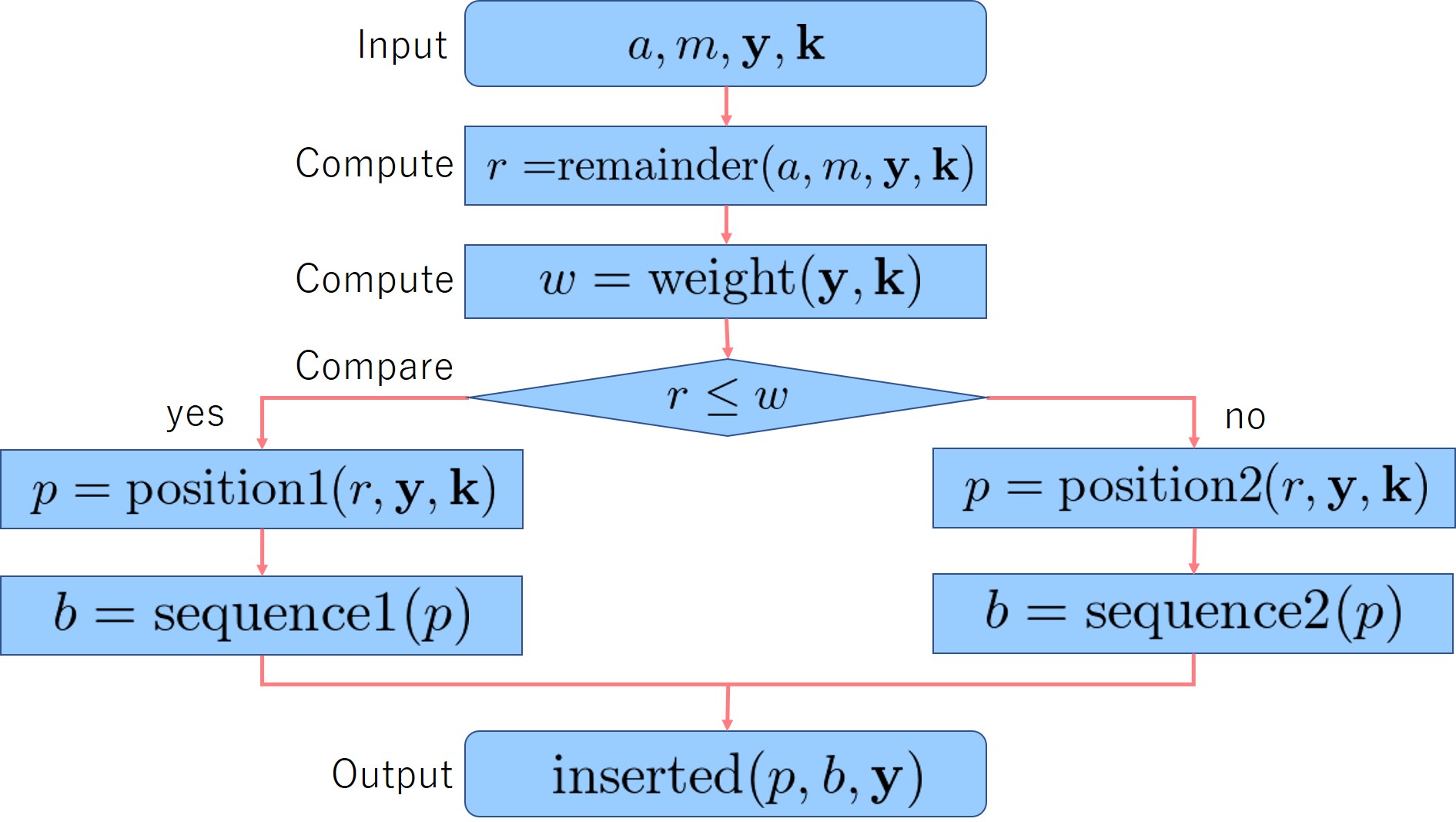
Refer to caption
Figure 1: Flowchart 1 for deletion error-correction

The following table summarizes the variables and the functions in Flowchart 1.

Monotone codes Azinv codes
the condition of aa ∈ℤ≥0\in\mathbb{Z}_{\geq 0} ∈ℤ≥0\in\mathbb{Z}_{\geq 0}
the condition of mm ≥kn+1\geq k_{n}+1 ≥n\geq n
the condition of 𝐲{\bf y} ∈𝔹n−1\in\mathbb{B}^{n-1} ∈𝔹n−2\in\mathbb{B}^{n-2}
the condition of 𝐤{\bf k} (k1,k2,⋯,kn)(k_{1},k_{2},\cdots,k_{n}) (1,2,⋯,n)(1,2,\cdots,n)
remainder​(a,m,𝐲,𝐤)\mathrm{remainder}(a,m,{\bf y},{\bf k}) (a−ρ𝐤​(𝐲))%​m(a-\rho_{\bf k}({\bf y}))\%m (a−τ​(𝐲))%​m(a-\tau({\bf y}))\%m
weight​(𝐲,𝐤)\mathrm{weight}({\bf y},{\bf k}) wt𝐤​(𝐲)\mathrm{wt}_{\bf k}({\bf y}) wt​(𝐲~)\mathrm{wt}({\bf\tilde{y}})
position1​(r,𝐲,𝐤)\mathrm{position1}(r,{\bf y},{\bf k}) max⁡J1,1\max J_{1,1} max⁡J1,2\max J_{1,2}
position2​(r,𝐲,𝐤)\mathrm{position2}(r,{\bf y},{\bf k}) min⁡J2,1\min J_{2,1} min⁡J2,2\min J_{2,2}
sequence1​(p)\mathrm{sequence1}(p) 0 {10(p:even)01(p:odd)\begin{cases}10(p:\text{even})\\ 01(p:\text{odd})\end{cases}
sequence2​(p)\mathrm{sequence2}(p) 11 {01(p:even)10(p:odd)\begin{cases}01(p:\text{even})\\ 10(p:\text{odd})\end{cases}
inserted​(p,b,𝐲)\mathrm{inserted}(p,b,{\bf y}) insp,𝐛​(𝐲)\mathrm{ins}_{p,{\bf b}}({\bf y}) insp,𝐛​(𝐲)\mathrm{ins}_{p,{\bf b}}({\bf y})
TABLE I: Variables and Functions in Flowchart 1

Here, (k1,k2,⋯,kn)(k_{1},k_{2},\cdots,k_{n}) is a positive monotonic increasing integer sequence and J1,1J_{1,1}, J1,2J_{1,2}, J2,1J_{2,1} and J2,2J_{2,2} are defined as follows.

J1,1≔{j∈[n]∣R𝐤(1)​(j,𝐲)=r},\displaystyle J_{1,1}\coloneqq\{j\in[n]\mid R^{(1)}_{{\bf k}}(j,{\bf y})=r\},
J1,2≔{j∈[n−1]∣L(1)​(j,𝐲~)=r},\displaystyle J_{1,2}\coloneqq\{j\in[n-1]\mid L^{(1)}(j,{\bf\tilde{y}})=r\},
J2,1≔{j∈[n]∣L𝐤(0)​(j,𝐲)=r−w−k1},\displaystyle J_{2,1}\coloneqq\{j\in[n]\mid L^{(0)}_{{\bf k}}(j,{\bf y})=r-w-k_{1}\},
J2,2≔{j∈[n−1]∣R(0)​(j,𝐲~)=r−w−1}.\displaystyle J_{2,2}\coloneqq\{j\in[n-1]\mid R^{(0)}(j,{\bf\tilde{y}})=r-w-1\}.

For integers aa and bb, a%​ba\%b denotes the remainder of aa divided by bb.

Flowchart 2 is the unified representation of the parts of Algorithm 1 and Algorithm 2, that is, the steps 10th - 20th of Algorithm 1 and Algorithm 2.

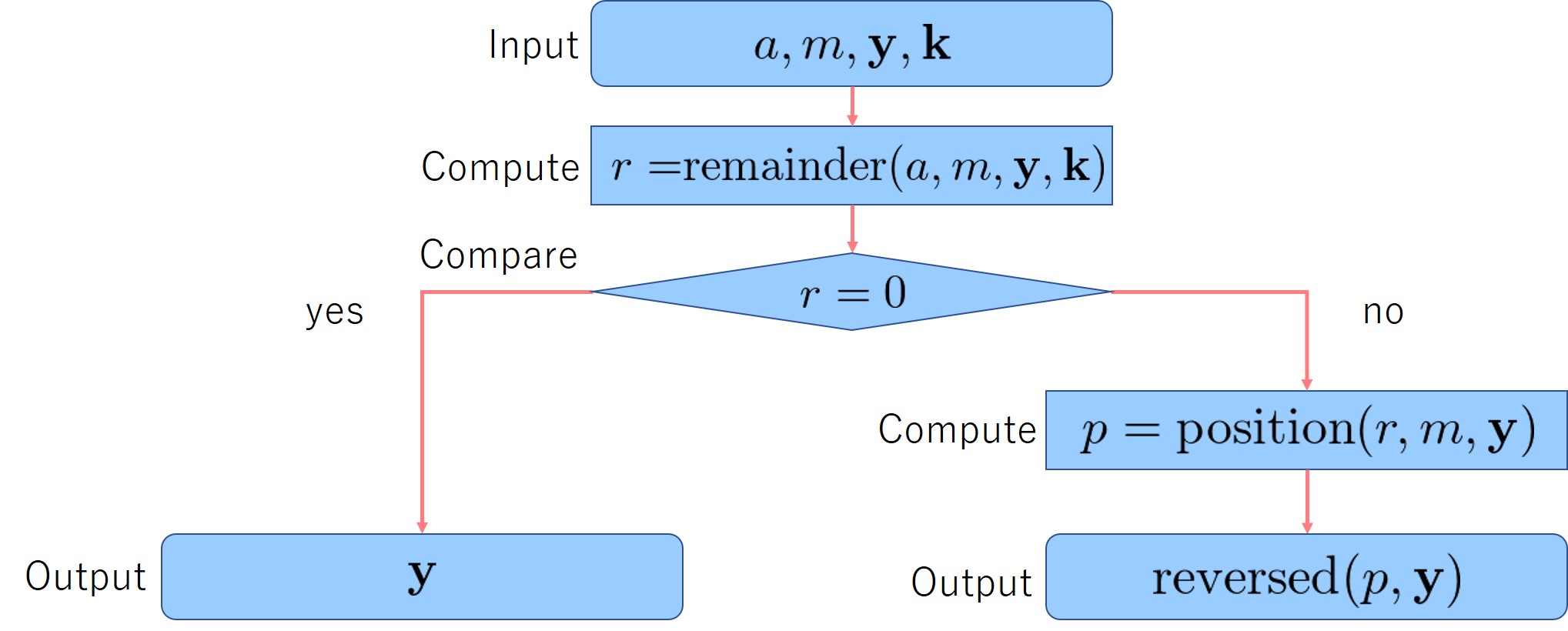
Refer to caption
Figure 2: Flowchart 2 for reversal error-correction

The following table summarizes the variables and the functions in Flowchart 2, where (k1,k2,⋯,kn)(k_{1},k_{2},\cdots,k_{n}) is a positive monotonic increasing integer sequence and JJ is defined as follows.

J≔{j∈[n]∣kj=min⁡{r,m−r}}.\displaystyle J\coloneqq\{j\in[n]\mid k_{j}=\min\{r,m-r\}\}.
Monotone codes Azinv codes
the condition of aa ∈ℤ≥0\in\mathbb{Z}_{\geq 0} ∈ℤ≥0\in\mathbb{Z}_{\geq 0}
the condition of mm ≥2​kn\geq 2k_{n} ≥2​(n−1)\geq 2(n-1)
the condition of 𝐲{\bf y} ∈𝔹n\in\mathbb{B}^{n} ∈𝔹n\in\mathbb{B}^{n}
the condition of 𝐤{\bf k} (k1,k2,⋯,kn)(k_{1},k_{2},\cdots,k_{n}) (1,2,⋯,n)(1,2,\cdots,n)
remainder​(a,m,𝐲,𝐤)\mathrm{remainder}(a,m,{\bf y},{\bf k}) (a−ρ𝐤​(𝐲))%​m(a-\rho_{\bf k}({\bf y}))\%m (a−τ​(𝐲))%​m(a-\tau({\bf y}))\%m
position​(r,𝐲,𝐤)\mathrm{position}(r,{\bf y},{\bf k}) min⁡J\min J n−min⁡{r,m−r}n-\min\{r,m-r\}
reversed​(p,𝐲)\mathrm{reversed}(p,{\bf y}) revp​(𝐲)\mathrm{rev}_{p}({\bf y}) revBAp​(𝐲)\mathrm{rev_{BA}}_{p}({\bf y})
TABLE II: Variables and Functions in Flowchart 2

We can compute inv​(𝐲)\mathrm{inv}({\bf y}) in linear time in the length of 𝐲{\bf y} by using the following Theorem IV.1.

Theorem IV.1.

Set 𝐬≔(n,n−1,⋯,2,1){\bf s}\coloneqq(n,n-1,\cdots,2,1). For 𝐲∈𝔹n{\bf y}\in\mathbb{B}^{n},

inv​(𝐲)=ρ𝐬​(𝐲)−(wt​(𝐲)+12).\displaystyle\mathrm{inv}({\bf y})=\rho_{\bf s}({\bf y})-{{\mathrm{wt}({\bf y})+1}\choose 2}.
Proof.

Since 𝐲∈𝔹n{\bf y}\in\mathbb{B}^{n},

inv​(𝐲)\displaystyle\mathrm{inv}({\bf y}) =#​{(i,j)∣1≤i<j≤n,yi>yj}\displaystyle=\#\{(i,j)\mid 1\leq i<j\leq n,y_{i}>y_{j}\}
=#​{(i,j)∣1≤i<j≤n,(yi,yj)=(1,0)}\displaystyle=\#\{(i,j)\mid 1\leq i<j\leq n,(y_{i},y_{j})=(1,0)\}

holds. Set I≔{i∈[n]∣yi=1}I\coloneqq\{i\in[n]\mid y_{i}=1\}. Then, we have

#​{(i,j)∣1≤i<j≤n,(yi,yj)=(1,0)}\displaystyle\#\{(i,j)\mid 1\leq i<j\leq n,(y_{i},y_{j})=(1,0)\}
=∑i∈I#​{j∈[n]∣i<j,yj=0}\displaystyle=\sum_{i\in I}\#\{j\in[n]\mid i<j,y_{j}=0\}
=∑i∈I((n−i)−#​{j∈[n]∣i<j,yj=1})\displaystyle=\sum_{i\in I}((n-i)-\#\{j\in[n]\mid i<j,y_{j}=1\})
=∑i∈I((n−i+1)−(1+#​{j∈[n]∣i<j,yj=1}))\displaystyle=\sum_{i\in I}((n-i+1)-(1+\#\{j\in[n]\mid i<j,y_{j}=1\}))
=∑i∈I(n−i+1)−∑i∈I#​{j∈[n]∣i≤j,yj=1}\displaystyle=\sum_{i\in I}(n-i+1)-\sum_{i\in I}\#\{j\in[n]\mid i\leq j,y_{j}=1\}
=∑i∈Iyi​(n−i+1)−#​I​(#​I+1)2\displaystyle=\sum_{i\in I}y_{i}(n-i+1)-\frac{\#I(\#I+1)}{2}
=ρ𝐬​(𝐲)−(wt​(𝐲)+12).\displaystyle=\rho_{\bf s}({\bf y})-{{\mathrm{wt}({\bf y})+1}\choose 2}.

∎

Theorem IV.2.

For each function in Flowcharts 1 or 2, its computational cost is O​(|𝐲|)O(|{\bf y}|), where |𝐲||{\bf y}| is the length of 𝐲{\bf y}.

Proof.

Since the definitions of sequence1​(p)\mathrm{sequence1}(p), sequence2​(p)\mathrm{sequence2}(p), and reversed​(p,𝐲)\mathrm{reversed}(p,{\bf y}), they can be computed in constant time.

Since we only need to use ”For loop” once, position1​(r,𝐲,𝐤)\mathrm{position1}(r,{\bf y},{\bf k}), position2​(r,𝐲,𝐤)\mathrm{position2}(r,{\bf y},{\bf k}), position​(r,𝐲,𝐤)\mathrm{position}(r,{\bf y},{\bf k}), inserted​(p,b,𝐲)\mathrm{inserted}(p,b,{\bf y}), and 𝐲~{\bf\tilde{y}} can be computed in linear time in the length of 𝐲{\bf y}.

Since the inner product, inv​(𝐲)\mathrm{inv}({\bf y}), and 𝐲~{\bf\tilde{y}} can be computed in linear time, remainder​(a,m,𝐲,𝐤)\mathrm{remainder}(a,m,{\bf y},{\bf k}) and weight​(𝐲,𝐤)\mathrm{weight}({\bf y},{\bf k}) can be computed in linear time in the length of 𝐲{\bf y}. ∎

The following is a corollary of Theorem IV.2.

Corollary IV.3.

Algorithm 1 and Algorithm 2 are linear time algorithms in the code-length.

V conclusion

In this paper, we provided the single deletion/reversal error-correcting algorithm for monotone codes and the single BAD/BAR error-correcting algorithm for azinv codes. Constructions of these codes are different. However, algorithms for these codes and the proofs of Theorem II.4 and Theorem III.3 correspond to each other.

In Section IV, we provided the unification of these decoding algorithms for monotone codes and azinv codes. The respective deletion error-correcting algorithms for monotone codes and azinv codes are represented by the same flowchart, and the respective reversal error-correcting algorithms for monotone codes and azinv codes are represented by the same flowchart. We also showed that these algorithms are linear-time algorithms.

As a future work, we will consider decoding algorithms for single insertion errors for monotone codes and azinv codes. Furthermore, we will concider decoding algorithms for other deletion/reversal errors. Monotone codes are defined by ρ𝐤​(𝐱)\rho_{\bf k}({\bf x}) and azinv codes are defined by τ​(𝐱)\tau(\bf x). By replacing one of these functions with the other, we will create new codes that are capable of the other deletion error-correcting and the other reversal error-correcting. These error-correcting algorithms are expected to have the same flowcharts as the ones for monotone codes and azinv codes.

Moreover, since monotone codes can freely take a positive monotonic increasing integer sequence 𝐤{\bf k}, it is expected to be able to add the other property to monotone codes in addition to the single deletion/reversal error-correctable property. For example, it is known to be able to add properties of being two-deletion error-correctable[10] and easy to encode [8]. Monotone codes are generalized by introducing parameter 𝐤{\bf k} into Levenshtein codes. In the same way, the generalization with parameter 𝐤{\bf k} in azinv codes can be considered. The function inv​(𝐱)\mathrm{inv}({\bf x}) used to define azinv codes has the property of IV.1. We can generalize azinv codes by taking a positive monotonic decreasing integer sequence as 𝐬{\bf s} in IV.1. The generalized azinv codes are expected to be able to add properties of being two-BAD error-correctable and easy to encode. In addition to these properties, there are some other similar properties in Levenshtein codes and azinv codes, such as optimality and convergence[9]. We would like to discuss these topics in a future work for further development of our research.

VI acknowledgement

This paper is partially supported by KAKENHI 18H01435.

References

  • [1] Tilo Buschmann and Leonid V Bystrykh. Levenshtein error-correcting barcodes for multiplexed dna sequencing. BMC bioinformatics, 14(1):272, 2013.
  • [2] Ryan Gabrys, Eitan Yaakobi, and Olgica Milenkovic. Codes in the damerau distance for deletion and adjacent transposition correction. IEEE Transactions on Information Theory, 64(4):2550–2570, 2017.
  • [3] Yeow Meng Chee, Han Mao Kiah, Alexander Vardy, Eitan Yaakobi, et al. Coding for racetrack memories. IEEE Transactions on Information Theory, 64(11):7094–7112, 2018.
  • [4] Jin Sima and Jehoshua Bruck. Correcting deletions in multiple-heads racetrack memories. In 2019 IEEE International Symposium on Information Theory (ISIT), pages 1367–1371. IEEE, 2019.
  • [5] Masato Inoue and Haruhiko Kaneko. Deletion/insertion/reversal error correcting codes for bit-patterned media recording. In 2011 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems, pages 286–293. IEEE, 2011.
  • [6] Anantha Raman Krishnan and Bane Vasic. Coding for correcting insertions and deletions in bit-patterned media recording. In 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011, pages 1–5. IEEE, 2011.
  • [7] V.I. Levenshtein. Binary codes capable of correcting deletions, insertions, and reversals. Soviet physics doklady, 10(8):707–710, 1966.
  • [8] Manabu Hagiwara. On ordered syndromes for multi insertion/deletion error-correcting codes. In Information Theory (ISIT), 2016 IEEE International Symposium on, pages 625–629. IEEE, 2016.
  • [9] Manabu Hagiwara. Perfect codes for single balanced adjacent deletions. In Information Theory (ISIT), 2017 IEEE International Symposium on, pages 1938–1942. IEEE, 2017.
  • [10] Albertus SJ Helberg and Hendrik C Ferreira. On multiple insertion/deletion correcting codes. IEEE Transactions on Information Theory, 48(1):305–308, 2002.