Deep-Learning-Aided Successive-Cancellation Decoding of Polar Codes

A polar code $\mathcal{P}(N,K)$ of block length $N$ with $K$ information bits is derived as $\bm{x}=\bm{u}\bm{G}^{\otimes n}$, where $\bm{x}=\{x_{0},x_{1},\ldots,x_{N-1}\}$ is the polar codeword, $\bm{u}=\{u_{0},u_{1},\ldots,u_{N-1}\}$ is the message word, $\bm{G}^{\otimes n}$ is the $n$-th Kronecker power of the polarizing matrix $\bm{G}=\bigl{[}\begin{smallmatrix}1&0\\ 1&1\end{smallmatrix}\bigr{]}$, and $n=\log_{2}N$. The vector $\bm{u}$ consists of a set $\mathcal{A}$ of the indices of $K$ information bits and a set $\mathcal{A}^{c}$ of the indices of $N-K$ frozen bits. The positions of frozen bits are known to both the encoder and the decoder, and their values are set to $0$. In this paper, binary phase-shift keying (BPSK) modulation technique is considered. Therefore, the received signals of the transmitted codeword are represented as $\bm{y}=(\mathbf{1}-2\bm{x})+\bm{z}$, where $\mathbf{1}$ is an all-one vector of size $N$, and $\bm{z}\in\mathbb{R}^{N}$ is the additive white Gaussian noise (AWGN) vector with variance $\sigma^{2}$ and zero mean. The LLR vector of the received signal is then given as $\bm{L}_{n}=\frac{2\bm{y}}{\sigma^{2}}$.

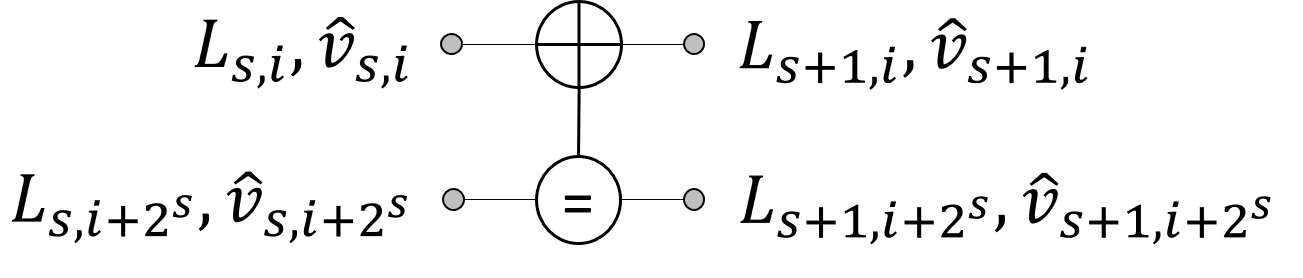
SC decoding can be illustrated on a polar code factor graph representation. Fig. 1(a) shows an example of a factor graph for $\mathcal{P}(8,5)$. To obtain the estimated message word, the LLR values and the hard bit estimations are propagated through all the processing elements (PEs) in the factor graph that are depicted in Fig. 1(b). A PE performs LLR computations as

where $L_{s,i}$ and $\hat{v}_{s,i}$ are the LLR value and the hard bit estimation at the $s$-th stage, $0\leq s\leq n$, and the $i$-th bit, $0\leq i\leq N-1$, respectively. The hard bit values of the PE are computed as

where $\oplus$ denotes the logical XOR operation.

The LLR values at the $n$-th stage are initialized to $\bm{L}_{n}$. In SC decoding, the hard bit estimations at the $0$-th stage are calculated as

In SCL decoding, at the $0$-th stage, each information bit is estimated as either $0$ or $1$ and at each decoding step, only $M$ most likely candidate paths are allowed to survive. After the last bit is estimated in SCL decoding, the path with the highest reliability metric is selected as the decoding result. If a CRC of length $c$ is used to help SCL decoding, after the last bit is estimated, the path that passes the CRC verification is selected as the decoding result.

SCF decoding is used to decode a polar code that is concatenated with a CRC of length $c$ for verification. It starts by performing SC decoding and if the CRC verification fails after the initial SC decoding, it flips the bit estimation of an information bit which has the smallest absolute LLR value [4]. However, this simple bit-flipping metric prevents SCF decoding to obtain a satisfactory error-correction performance [8].

To determine the bit-flipping position, DSCF decoding estimates the probability $P^{*}_{i_{\omega}}$ of the $i_{\omega}$-th bit ($i_{\omega}\in\mathcal{A}$) being the first-order error bit after the initial SC decoding attempt as

where $p^{*}_{i}$ is defined as

with $\bm{\hat{u}}_{0}^{i-1}=\{\hat{u}_{0},\hat{u}_{1},\dots,\hat{u}_{i-1}\}$, $\bm{u}_{0}^{i-1}=\{u_{0},u_{1},\dots,u_{i-1}\}$. Therefore, the bit-flipping position $i^{*}_{\omega}$ that maximizes the probability of $\bm{\hat{u}}$ being correctly decoded after the second SC decoding attempt can be calculated as

Note that $p^{*}_{i}$ cannot be obtained during the course of decoding since the message word $\bm{u}$ is unknown to the decoder [8]. Therefore, DSCF approximates $p^{*}_{i}$ as

It was observed in [8] that the approximation in (7) does not result in a desirable error-correction performance. Therefore, a perturbation parameter $\alpha\in\mathbb{R}^{+}$ is introduced to obtain a better estimation of $p^{*}_{i}$ as

To enable numerically stable computations for a hardware implementation, the bit-flipping metric is defined as [8]

Consequently, the most probable bit-flipping position $i^{*}_{\omega}$ under DSCF decoding can be found as

In this paper, all the presented decoders only target the first-order error bit. However, the bit-flipping selection schemes presented in this paper can be directly extended to cover the cases of high-order error bits [8, 13].

Consider a failure in the SCL decoding with list size $M$ as the SCL decoding attempt in which all the $M$ decoding paths fail the CRC verification. Let $\bm{\hat{u}}[m]$, $0\leq m<M$, be the $m$-th candidate path after the first SCL decoding, $\bm{\hat{u}}[0]$ be the best path after the first SCL decoding attempt, i.e. the path with the smallest path metric [14], and let $i^{*}_{\omega}$ be the estimated first erroneous bit of $\bm{\hat{u}}[0]$. In the proposed scheme, a secondary SCL decoding attempt is performed by keeping only $\bm{\hat{u}}[0]$ and fixing all the information bits before the $i^{*}_{\omega}$-th bit. This is because all the estimated information bits before $i^{*}_{\omega}$-th are believed to be correct, and the $i^{*}_{\omega}$-th bit is flipped to correct the first error bit of $\bm{\hat{u}}[0]$.

The information bits for the second SCL decoding attempt up to the $i^{*}_{\omega}$-th bit are fixed as

for $0\leq m<M$. After the $i^{*}_{\omega}$-th information bit, the conventional SCL decoding procedure is performed by estimating each information bit $i>i^{*}_{\omega},i\in\mathcal{A}$ as both $0$ and $1$ and by keeping the best $M$ paths at each decoding step. The path metrics of all the decoding paths are then given as [14]

where $0\leq i<N$, $\operatorname{PM}[m]_{-1}=0$, and $\Delta\geq 0$ is the path metric penalty at the $i$-th bit that is calculated as

where $L[m]_{0,i}$ is the LLR value of the $i$-th bit at the $m$-th path.

Note that the bit-flipping metric of DSCF can be used to estimate $i^{*}_{\omega}$. However, this approach requires costly logarithmic and exponential functions, hence they are not attractive for an efficient hardware implementation. In the next subsection, a novel bit-flipping metric is proposed that only requires multiplication and addition operations.

Unlike the DSCF decoder which relies on the estimation of the probability $p^{*}_{i},\forall i\in\mathcal{A}$, for the bit-flipping metric computation, a method is proposed to directly estimate the following likelihood ratio

The value $l^{*}_{i_{\omega}}$ indicates how likely the estimated message bit $\hat{u}[0]_{i_{\omega}}$ is correctly decoded given the received signal $\bm{y}$ and the message word $\bm{u}$. The bit index $i^{*}_{\omega}$ which is most likely to be the first-order erroneous bit is then obtained as

Similar to $p^{*}_{i}$, the value of $l^{*}_{i_{\omega}}$ is not available during the decoding process as $\bm{u}$ remains unknown to the decoder. Therefore, the following hypothesis is proposed for the estimation of $l^{*}_{i_{\omega}}$:

where

and $\beta_{i_{\omega},i}\in\mathbb{R}$ are perturbation parameters such that ${\beta_{i_{\omega},i}=\beta_{i,i_{\omega}}}$ and $\beta_{i_{\omega},i_{\omega}}=1$, for $i\in\mathcal{A}$ and $i_{\omega}\in\mathcal{A}$.

To enable numerically stable computations, the bit-flipping metric of the proposed decoder can be obtained by transforming the likelihood ratio $l^{*}_{i_{\omega}}$ to the LLR domain as

The most probable bit-flipping index $i^{*}_{\omega}$ can then be selected as

Note that the bit-flipping metric computation in (18) can be represented in the matrix form as

where $\bm{Q}_{\text{DL-SCL}}$ and $\bm{L}_{0}$ are row vectors of size ${1\times(K+c)}$, and $\bm{\beta}$ is a matrix of size $(K+c)\times(K+c)$. Equivalently, $i^{*}_{\omega}$ is the index of the element in $\bm{Q}_{\text{DL-SCL}}$ that has the smallest value.

With $\beta_{i_{\omega},i_{\omega}}=1$ and $\beta_{i_{\omega},i}=\beta_{i,i_{\omega}}$, $0\leq i,i_{\omega}<K+c$, $\bm{\beta}$ can be seen as a correlation matrix that captures the inherent relations of the absolute LLR values of all the information bits under SCL decoding. For the sake of simplicity, since only the LLR values of information bits are considered, all of the bit indices used in the rest of this paper are referred to as information bit indices, and therefore have the values in the range of $[0,K+c-1]$.

Note that $\beta_{i_{\omega},i_{\omega}}$ is fixed to 1 and is not trainable for all $0\leq i_{\omega}<K+c$. On the other hand, other elements of the matrix $\bm{\beta}$ are trainable with a condition that ${\beta_{i_{\omega},i}=\beta_{i,i_{\omega}}}$, ${0\leq i,i_{\omega}<K+c}$. In the proposed DL-SCL decoding, the number of trainable parameters of the matrix $\bm{\beta}$ is $\frac{(K+c)(K+c-1)}{2}$, which is too large to efficiently apply heuristic methods such as Monte Carlo simulation for parameter optimization. Therefore, the optimization of $\bm{\beta}$ is considered as a learning problem and DL techniques are exploited to optimize $\bm{\beta}$. The bit-flipping metric $\bm{Q}_{\text{DL-SCL}}$ of the proposed decoder does not depend on the values of the message word $\bm{u}$. Thus, all-zero codewords can be used during the training phase. This symmetric property is particularly useful for DL-based decoders of linear block codes, as it simplifies the training process [13, 12, 15].

Let $\bm{\hat{T}}$ be the estimated bit-flipping vector of the information bits with $-1$ indicating a bit-flip and $+1$ indicating no bit-flip. From (19), the elements of the vector $\bm{\hat{T}}$ are defined as

for $0\leq i<K+c$. In this paper, stochastic-gradient-descent (SGD) based techniques are used to update the values of $\bm{\beta}$ during training, thus the computation of $\bm{\hat{T}}$ is modified to enable back-propagation during training [13]. Otherwise, learning is not feasible as the derivative of (21) with respect to $\bm{Q}_{\text{DL-SCL}}[i]$, i.e., the $i$-th element of $\bm{Q}_{\text{DL-SCL}}$, is always 0.

Let the soft estimation of $\hat{T}_{i}$ be

where $\tau=\frac{\tau_{0}+\tau_{1}}{2}$, and $\tau_{0}$ and $\tau_{1}$ are the smallest and the second smallest values of $\bm{Q}_{\text{DL-SCL}}$, respectively. The objective loss function is then defined as

where ${\mathcal{L}(a,b)=-b\log(a)-(1-b)\log(1-a)}$ is the binary cross-entropy function, and $\lambda$ is the scaling factor of the L2 regularization [16].

In this paper, PyTorch [17] is used as the DL framework. Training is done using RMSprop optimizer [18] with a mini-batch size of $128$ and a learning rate of $10^{-4}$. The training set consists of $2^{18}$ samples of the received channel signals, which are not correctly decoded after the first SCL decoding attempt, and the data is collected at ${E_{b}/N_{0}=5}$ dB. The L2 regularization hyperparameter $\lambda$ is set to $0.25$. The initial values of the non-diagonal elements of $\bm{\beta}$ are drawn from an i.i.d distribution within the range of $[-0.2,0.2]$ before training takes place. The matrix $\bm{\beta}$ is trained for list sizes $M\in\{1,2,4,8\}$¹¹1Optimized $\bm{\beta}$ matrices are available at https://github.com/nghiadt05/DLSCL-CorMatrices.

In this section, the performance of the proposed DL-SCL decoder in terms of frame-error-rate (FER) and computational complexity is examined. The polar code $\mathcal{P}(128,64)$ concatenated with a $24$-bit CRC is considered. The selected polar code and the CRC polynomial are used in the eMBB control channel of the 5G standard [2].

Fig. 2 compares the FER performance of various decoders for $\mathcal{P}(128,64)$. In this figure, DL-SCL$M$ denotes the proposed DL-SCL decoding algorithm with list size $M=\{1,2,4,8\}$, and the bit-flipping SCL decoder with the bit-flipping metric proposed in [8] is denoted as SCLF$M$. In addition, the original SCL decoding in [14] is also considered for the comparison. For all the bit-flipping SCL decoders, $8$ additional decoding attempts are considered for the secondary SCL decoding. As observed from Fig. 2, the proposed bit-flipping metric in the proposed DL-SCL decoders results in almost no FER performance loss compared to that of the SCLF decoders.

Fig. 3 visualizes the values of the elements in matrix $\bm{\beta}-\bm{I}$ in the form of a heat map²²2Matrix $\bm{\beta}-\bm{I}$ is shown to exclude the diagonal elements of $\bm{\beta}$ which have a value of $1$., where $\bm{I}$ is the identity matrix with the same size as $\bm{\beta}$. It can be seen that $\bm{\beta}-\bm{I}$ (and thus $\bm{\beta}$) is a sparse matrix with many of its elements having a value close to $0$. This observation is exploited to reduce the computational complexity of computing the proposed bit-flipping metric, which in turn reduces the computational complexity of the proposed DL-SCL decoding algorithm.

Table I reports the computational complexity of the proposed bit-flipping metric of the DL-SCL decoder in comparison with that of the SCLF decoder in terms of the number of different operations performed. Other than the bit-flipping metric, the proposed DL-SCL decoder and the SCLF decoder are identical. In this table, all the elements of $\bm{\beta}$ which have a value in the range $[-10^{-4},10^{-4}]$ are set to $0$, thus removing the need to perform additions or multiplications over those elements, without tangibly degrading the error-correction performance. It can be seen that the bit-flipping metric computation in the proposed DL-SCL decoders require up to $66\%$ fewer multiplications and up to $36\%$ fewer additions in comparison with that of the SCLF decoder. Moreover, unlike SCLF decoder, the proposed bit-flipping metric in the DL-SCL decoders does not require the computation of any transcendental functions.