Deep learning of experimental electrochemistry for battery cathodes across diverse compositions
Abstract
Artificial intelligence (AI) has emerged as a tool for discovering and optimizing novel battery materials. However, the adoption of AI in battery cathode representation and discovery is still limited due to the complexity of optimizing multiple performance properties and the scarcity of high-fidelity data. In this study, we present a machine-learning model (DRXNet) for battery informatics and demonstrate the application in the discovery and optimization of disordered rocksalt (DRX) cathode materials. We have compiled the electrochemistry data of DRX cathodes over the past five years, resulting in a dataset of more than 19,000 discharge voltage profiles on diverse chemistries spanning 14 different metal species. Learning from this extensive dataset, our DRXNet model can automatically capture critical features in the cycling curves of DRX cathodes under various conditions. Illustratively, the model gives rational predictions of the discharge capacity for diverse compositions in the Li–Mn–O–F chemical space as well as for high-entropy systems. As a universal model trained on diverse chemistries, our approach offers a data-driven solution to facilitate the rapid identification of novel cathode materials, accelerating the development of next-generation batteries for carbon neutralization.
pacs:
I Introduction
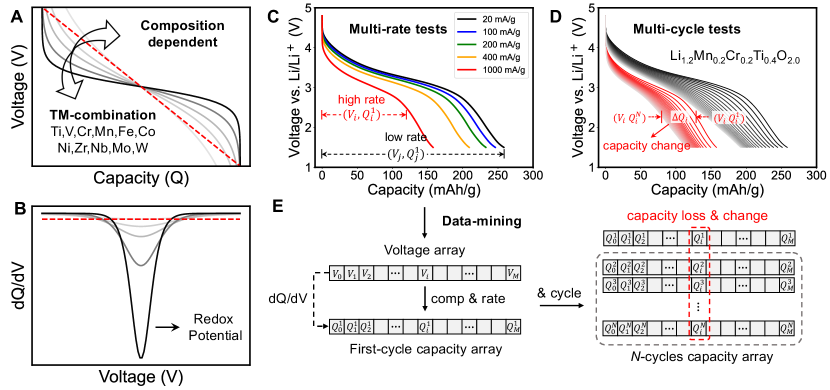
The pursuit of carbon neutrality has become a global imperative in the face of climate change, driving the transition to renewable energy sources and the widespread adoption of electric vehicles [1, 2, 3]. High-performance battery cathode materials with large energy density, high-rate performance, and long cycle life are central to these advancements. The development of new cathode materials is essential to meeting the increasing demand for energy storage and advancing the electrification of transportation systems [4].
Artificial intelligence (AI) has emerged as a potential tool in the discovery and optimization of novel battery materials [5, 6]. By leveraging vast amounts of experimental and computational data, AI-assisted techniques can accelerate the design and synthesis of battery materials by identifying promising candidates within large chemical spaces [7, 8, 9], uncovering hidden structure-property relationships via machine-learned atomistic modeling [10], predicting the remaining lifespan of batteries [11, 12, 13, 14, 15], and optimizing protocols for fast charge/discharge protocol [16]. These efforts significantly reduce the time and cost required for conventional trial-and-error approaches. Most recently, a battery data genome initiative has been proposed to use AI assistance to accelerate the discovery and optimization of battery materials [17].
Despite these advancements, current machine-learning efforts in battery research primarily focus on predicting the lifespan for a simple chemistry or within a limited chemical space, such as NMC (Ni–Mn–Co) or LFP (LiFePO4). The development of exploratory machine learning for representing comprehensive compositional effects in a multi-dimensional chemical space remains underdeveloped due to the challenges associated with simultaneously optimizing multiple electrochemical properties (e.g., rate capability, cyclability, and various test voltage windows) [18]. Moreover, the scarcity of high-fidelity data further hinders the progress of AI in the battery field.
Disordered rocksalt (DRX) materials have emerged as promising cathode materials that make use of earth-abundant precursors to enable scaling of Li-ion energy storage to several TWh/year production [19]. Owing to the nearly unlimited compositional design space and considerably more complex structure-property relationship of DRX cathodes compared with conventional layered cathodes (Figure 1A), their rational design requires the extensive involvement of advanced characterization techniques (e.g., pair-distribution function analysis [20], spherical-aberration-corrected transmission electron microscopy [21], solid-state nuclear magnetic resonance spectroscopy [22]) as well as sophisticated computational tools (e.g., high-dimensional cluster expansion and Monte Carlo simulation [23, 24]). Data-driven methods offer alternative means of compositional design and optimization of materials without having to fully construct their structure-property relationships.
In light of these challenges, we developed DRXNet, an exploratory machine-learning model for the discovery and optimization of battery cathode materials. DRXNet uses composition, test current density, working voltage window, and cycle number as inputs to predict entire discharge voltage profiles. By training and testing over 19,000 experimental discharge voltage profiles of DRX materials comprising various metal species, we show that the model accurately captures the cathode electrochemistry under different test conditions. Notably, DRXNet captures accessible discharge capacity in diverse Li–Mn–O–F compositions and makes rational predictions for several high-entropy systems. As a universal model trained on diverse chemistries, DRXNet offers a data-driven solution to facilitate the rapid identification of novel cathode materials with improved energy-storage capabilities.
II Results
II.1 Parsing discharge profiles
Unlike conventional NMC-based layered cathodes [27, 28], DRX materials exhibit more diverse electrochemical behavior due to the significantly larger chemical space over which they can exist and their more subtle structure involving various forms of cation short-range order [29]. A prototype DRX cathode (Li1+xM’aM”bO2-yFy) is composed of three primary compositional parameters: (1) the redox-active species M’; (2) the inert high-valent transition metal M”, which charge-compensates for the Li excess and stabilizes disordered structures [30]; (3) fluorine, which enhances the cyclability and accommodates more Li excess without losing TM redox by reducing the anion valence [31]. In addition, other compositional modifications are often made to enhance capacity, rate, or cyclability. For instance, Mg doping in Mn-based oxyfluoride DRX can increase the discharge capacity while retaining a similar voltage-profile shape [32]; Cr doping in Li1.2Mn0.4Ti0.4O2.0 results in comparable low-rate capacity but significantly improves the high-rate performance near the top of charge [33]. These non-linear effects arising from compositional changes make both material design and machine-learning modeling challenging, thereby necessitating a comprehensive, high-fidelity dataset to address such issues.
Figure 1A introduces the typical discharge-voltage profile in battery tests. The profile shape is tied to various factors, such as the DRX composition, applied current density rate, and degradation that may have occurred in prior cycles. Figure 1C and D show the multi-rate tests (the first cycle) and multi-cycle tests (of 20 mA/g and 1000 mA/g) of Li1.2Mn0.2Cr0.2Ti0.4O2.0 cathode as an example. The capacity is measured in experiments by determining the cumulative charge transferred in a galvanostatic test. Taking the derivative of with respect to , the value can be evaluated for a given voltage profile, which is a crucial physical quantity for analyzing characteristic redox potentials from different TMs [34].
II.2 DRX Battery Test Dataset
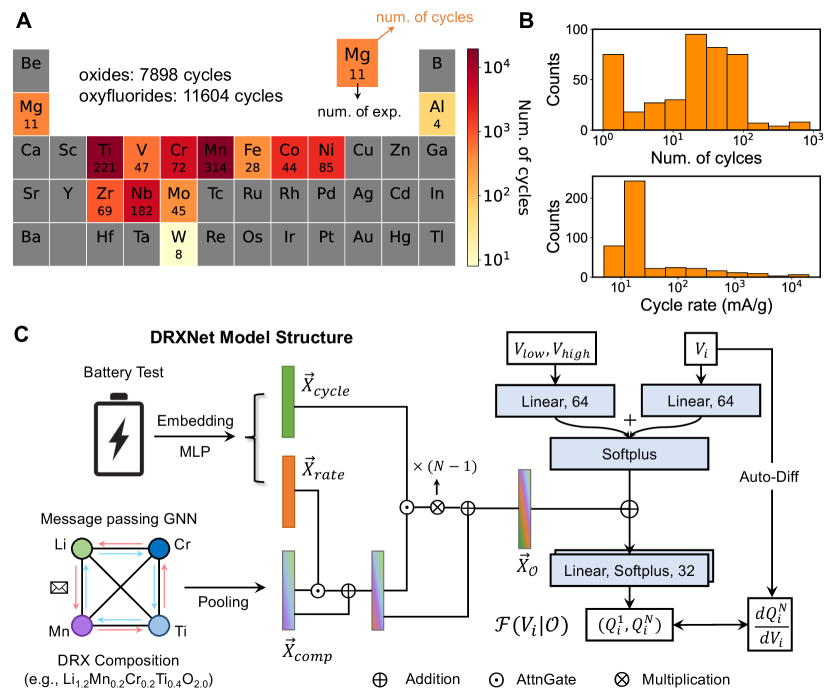
We have compiled the electrochemical test data related to DRX compounds by mining electronic experimental notebooks in our research group over the past five years to construct the DRX Test Dataset (DRX-TD). The dataset contains not only results on successful materials published in several papers [35, 36, 29, 37, 38, 39, 40, 33, 32] but also data on less well-performing DRX compounds. This endeavor yielded a comprehensive dataset containing 19,000 discharge profiles across 16 different elements (14 metal species + O and F) from lab experiments and published literature (see Methods). An individual electrochemical test is defined as a group of discharge profiles with a fixed current density rate, where is the number of cycles conducted in such a test, corresponding to the results obtained from one coin-cell. The distribution of elements in the DRX-TD is shown in Figure 2A, where the number in each element’s box represents the number of compounds with that element present for which an electrochemical test is present. The box’s color indicates the total number of discharge profiles for compounds containing that element. Comprising 7,898 discharge profiles of DRX oxides and 11,604 discharge profiles of oxyfluorides, the dataset offers extensive coverage of major redox-active TMs. Figure 2B displays histograms for the number of cycles, , and the current rates at which experiments were performed. As is typical for exploratory research programs in a research laboratory, most of the electrochemical tests were conducted at a low current rate (20 mA/g) and for 10-100 cycles.
For each discharge profile, 100 points were uniformly sampled from the values of and , resulting in a voltage series and a capacity series . The curve was then calculated by differentiating with . As is a more intrinsic property for battery materials, including this value in the modeling allows for a more representative analysis of the electrochemical performance of DRX compounds under various conditions (see Methods).
II.3 DRXNet architecture
DRXNet aims to draw a connection between chemistry and cathode performance by establishing a mapping between and for arbitrary cathode compositions under various test conditions. This idea can be conceptualized as identifying a function that maps cathode parameters and the voltage state to produce the capacity state as an output. The function is conditionally defined by the parameters , which consider the electrode composition, current rate, and cycle number
| (1) |
We designed DRXNet with two main components, as shown in Figure 2C: (1) An electrochemical condition network that generates a feature vector based on the compound’s composition and electrochemical test information; (2) A state prediction network to approximate the discharge state of the cathode as a function of the voltage state, , given the electrochemical conditional encoding of . For instance, Algorithm 1 demonstrates how DRXNet predicts the first-cycle discharge profile of at a current rate of 20 mA/g between 1.5 and 4.8 V.
Initially, three condition inputs (composition, rate, cycle) are encoded to represent . We use Roost, a graph neural network model proposed by Goodall and Lee [26], for compositional encoding. Roost takes elements as graph nodes and updates the correlation between elements through weighted message passing based on each element’s fractional concentration. The nodes are initialized with elemental embedded vectors (: species) from mat2vec to capture as much prior chemical information as possible through text mining of previously published literature [41]. Moreover, we consider only the cation species as independent nodes in Roost, treating the anion-species information (fluorine) as a mean-field background, i.e., , where is the fractional concentration of fluorine and is the embedded vector of Li/F. Rate and cycle information is encoded using multi-layer perceptrons (MLPs).
Because the rate and cycle properties are intrinsically affected by the composition, we used gated MLPs with soft attention for electrochemical condition encoding via a hierarchical network structure [25]. The is a rate-informed feature vector, where and represent MLPs with different activation functions and denotes the concatenation operation. In addition, the cycle-informed vector is linearly dependent on the cycle number with a trainable weight . As such, the feature vector is used to represent the 1st cycle and is used to represent the -th cycle, respectively.
Lastly, we used several MLPs to construct the state prediction network , as shown in Figure 2C. takes the voltage state and working window as inputs, and the is element-wise added to the hidden layer of to inform of conditions (see Methods). As such, the state prediction network is constructed as a simple function mapping from the voltage state to the capacity . In addition, is obtained by auto-differentiation of .
II.4 Applicability domain
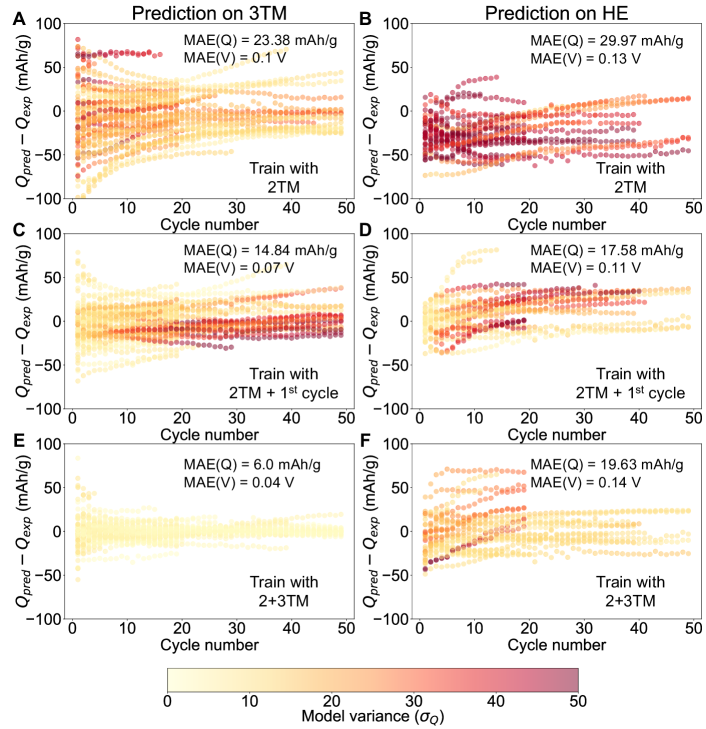
We explore the scope of DRXNet’s applicability in the realm of composition space. Determination of the applicability domain in battery machine-learning models can be challenging due to the unavailability of sufficient test data, as generating new data necessitates the synthesis of new materials or conducting battery cycling tests for weeks to months [18, 42]. Simply separating the sequence of voltage and capacity signals into training and test sets can result in data leakage and a failure to represent the expected error in real applications. To evaluate the expressibility and generalization of DRXNet, we designed several experiments by partitioning the dataset based on compositions. The electrochemical tests with no more than two metal species (2TM, excluding Li) were designated as the training set, whereas the tests with three metal species (3TM) and higher numbers of TM components (high-entropy, HE) were assigned as test sets. For each test, an ensemble of five independent models was trained to enhance the overall prediction accuracy and robustness and to quantify the model variance. The average value is used for the prediction, and the standard deviation of the prediction from the ensemble of five DRXNet models () is used to represent the model variance as an approximation of how uncertain the predictions are.
A rational design of battery cathodes typically focuses on the capacity that can be delivered within a certain voltage window. Therefore, we used DRXNet to compute the voltage profiles with electrochemical test parameters in the test set and compared the delivered capacity between 2.0 – 4.4 V of experiments and predictions within 50 cycles (see Figure 3). The voltage range of 2.0 – 4.4 V (vs. Li+/Li) is reasonable for current electrolytes, and most commercialized cathodes such as LiFePO4, LiCoO2, and NMC operate within this voltage range. Our choice of this voltage range for testing model performance is aligned with these industry norms. The average voltages () between 2.0 – 4.4 V were subsequently computed. As a baseline, the mean absolute deviation (MAD) of average voltage is 0.16/0.21 V for 3TM/HE, and the MAD of discharge capacity is 36.59/38.54 mAh/g for 3TM/HE. Figure 3A and B demonstrate the performance of the DRXNet models trained on the 2TM dataset and tested on the 3TM and HE datasets. Mean absolute errors (MAEs) of 0.1/0.13 V for the average voltage and 23.38/29.97 mAh/g for the capacity were obtained for the 3TM/HE test datasets, respectively. It is found that large prediction errors already occur for the first cycle and propagate into the subsequent cycles. Notably, a systematic underestimation of capacity is observed for the HE compounds (Figure 3B), which can be rationalized by the fact that 2TM compounds cannot capture the improved performance arising from the novel high-entropy physics [40, 43].
For practical applications, new data points can be continuously collected as experiments progress, enabling on-the-fly training with incoming data to improve predictive performance. To evaluate possible improvement with additional information specific to the system being tested, we evaluated the improvement when DRXNet is trained on a dataset containing all 2TM data and is provided with the first cycle data from 3TM/HE materials. The knowledge of just the first cycle data results in a reduction of the mean capacity error from 23.38/29.97 mAh/g to 14.84/17.58 mAh/g for 3TM/HE (Figure 3C and D). The enhanced performance achieved by explicitly training with the first cycle indicates that the model can better generalize cycling performance, even when experiments for a specific composition are not extensively sampled. This capability has the potential to significantly reduce the month-long timeframe typically required for electrochemical testing to identify whether a new cathode material has a desired cyclability or rate capability. Training the model with first-cycle data led to a substantial decrease in both the prediction error and model variance for the initial few cycles, although the model variance increased subsequently with the cycle number for untrained domains (Figures 3C and D).
To examine how data augmentation could improve the performance of DRXNet, we further trained models on the 2+3TM dataset where chemical information in addition to 2TM interactions is included. Figure 3E and F display the predictions on the 3TM (MAE: 6.0 mAh/g) and HE (MAE: 19.63 mAh/g) datasets. It is important to note that the models trained on 2+3TM data show an error reduction of around 10 mAh/g for the HE capacity prediction compared to the results obtained when training the 2TM model (Figures 3B and F), along with a significant reduction on the model variance. This finding suggests that the 2TM dataset is inadequate for extracting relevant information and generalizing it to other compositions. The scaling to electrode material with a high number of components necessitates capturing more than 2TM correlations or interactions in training the graph neural network. Failure to do so may lead to systematic prediction errors, as demonstrated in Figure 3B. When the model is able to acquire sufficient chemical domain knowledge (e.g., 2+3TM-model), it becomes feasible to extrapolate the electrochemical properties of high-component electrodes, which is evidenced in Figure 3F with reduced prediction error as well as model variance, and only a few outlier experiments exhibit large errors.
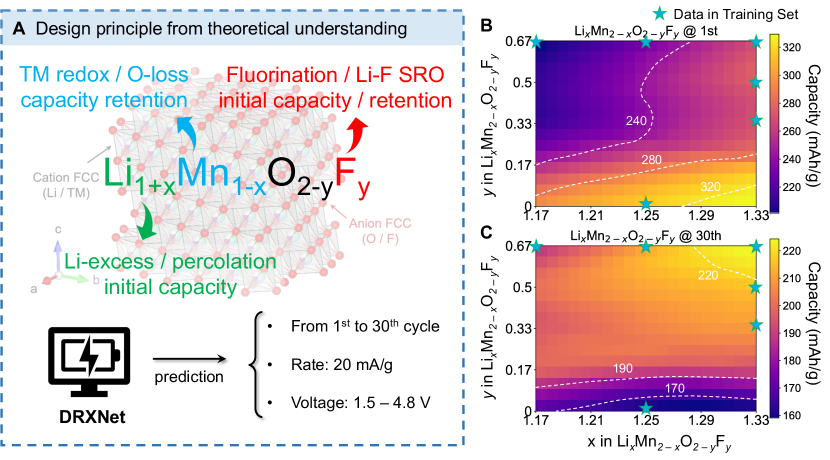
(B, C) Prediction of discharge capacity in the Li–Mn–O–F chemical space for the 1st (B) and 30th (C) cycle between 1.5 – 4.8 V at a current density rate of 20 mA/g. The blue stars indicate the compositions included in the training set.
II.5 Recover design principles in Li–Mn–O–F chemical space
We present several examples to illustrate how DRXNet learns the underlying cathode chemistry and assists in designing new materials, where the models used for these applications are pretrained on all discharge profiles. As an attractive earth-abundant, non-precious TM, Mn is of considerable interest for designing next-generation cathode materials [35]. Lun et al. [39] proposed three primary design degrees of freedom for Mn-based DRX (Figure 4A): (1) the Li-excess content, which controls the presence of a percolating network facilitating Li diffusion; (2) the Mn content, as achieving high capacity with a low amount of Mn requires a large amount of oxygen redox, leading to poor cyclability; and (3) the fluorine content, which lowers the total cation valence and provides greater freedom to optimize the Li and Mn content. Fluorine modifies cation short-range order (SRO) through the strong Li–F attraction and lowers the initial capacity [44, 32], but can increase stability at high voltage charging [21]. These principles are highly correlated and exert non-linear effects on performance.
We used DRXNet to predict the discharge capacity of DRX compounds between 1.5 and 4.8 V at a current rate of 20 mA/g for the 1st and 30th cycles. The results, as a function of Li and F content, are shown in Figures 4B and C. The Mn content and valence follow directly from the Li and F content. The effect of fluorine on performance, extensively characterized experimentally, is well captured by our model: A higher F content ( in O2-yFy) results in a lower discharge capacity for the 1st cycle but a higher capacity for the 30th cycle, consistent with its documented role in promoting surface stability [21]. In particular, cation-disordered Li1.333Mn0.667O2 (bottom right corner of Figure 4C) is predicted to have the highest capacity ( mAh/g) for the first cycle but the lowest capacity for the 30th cycle. In this compound, the valence of Mn is 4+, and all capacity originates from oxygen. Such a large amount of O-redox leads to rapid capacity fade consistent with the experimental observations on disordered Li2MnO3 reported in Ref. [45].
To provide some context for the extrapolation capability of DRXNet, we have illustrated the compositions in the training dataset with blue stars in Figures 4B and C. From this, it can be observed that even with a limited distribution of training points on the composition map, DRXNet offers reasonably consistent predictions that seem to be in line with the experimental observations beyond the training points. As DRXNet is trained on various compositions beyond the Li–Mn–O–F chemical space, the ability to extrapolate to other domains can be attributed to the transfer learning from other F- and non-F-containing compounds. The example in this section demonstrates how practitioners can generalize the design principles from a data-driven perspective purely starting from the data mined from experiments.
II.6 Exploratory search for high-entropy cathodes
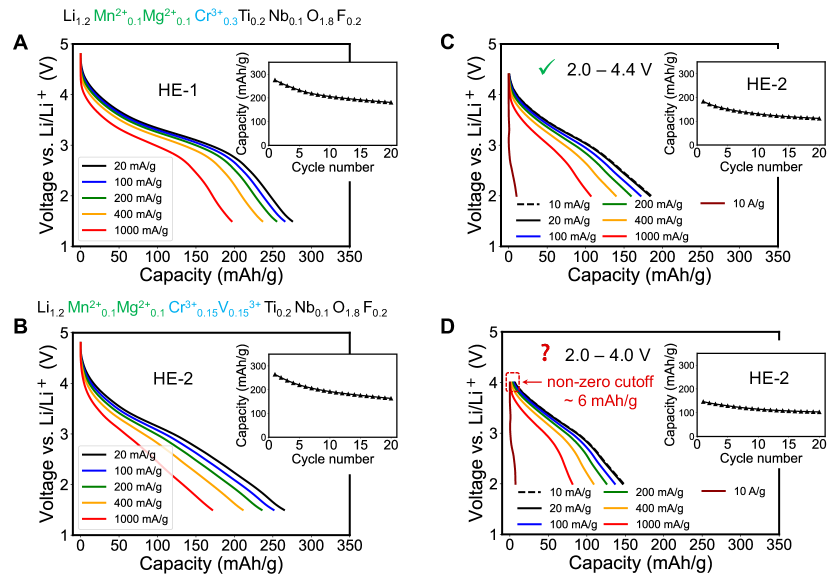
High-entropy DRXs are composed of many species and present a vast chemical space to explore for battery materials discovery. We used DRXNet for virtual high-throughput screening considering redox-compatible species from the bivalent (Mn2+, Fe2+, Ni2+, Mg2+) and trivalent group (Mn3+, Cr3+, V3+, Fe3+). Two case studies of predicted high-entropy DRXs are presented: Li1.2Mn0.1Mg0.1Cr0.3Ti0.2Nb0.1O1.8F0.2 (HE-1) and Li1.2Mn0.1Mg0.1Cr0.15V0.15Ti0.2Nb0.1O1.8F0.2 (HE-2). The discharge profiles predicted with DRXNet under various current densities are shown in Figures 5A and B. A more comprehensive collection of predictions for other compositions is included in Figure S6.
For HE-1, DRXNet predicts a discharge capacity of 276 mAh/g at a current rate of 20 mA/g. The compound delivers its largest discharge capacity near 3V and transitions to a higher voltage slope below 3V, a phenomenon that has been widely observed in Mn redox and/or Cr redox-based DRXs [46, 33, 40]. HE-1 is predicted to have an unusually high rate capability for a DRX compound when discharging. A capacity of 196 mAh/g is estimated at 1000 mA/g, which is of the capacity at 20 mA/g. Previous work has demonstrated that multi-elemental substitution (i.e., high-entropy strategy) frustrates the unfavorable short-range order that leads to poor Li kinetics. In addition, the incorporation of Cr and its migration as Cr6+ at high voltage creates a more extended 0-TM network for Li transport. Both of these features improve the Li diffusion kinetics [33, 40]. DRXNet clearly learns those benefits and extrapolates rationally into electrochemistry prediction of the high-entropy compositions.
As a comparison to HE-1, we formulated HE-2 with partial V3+ to Cr3+ substitution. The change in the shape of the voltage profile due to the low potential of V5+/V3+ reduction is well captured by DRXNet as shown in Figure 5B and curves in SI. It is clearly demonstrated that with V3+ incorporation, a nearly constant slope can be observed down to the low-voltage region, which is characteristic for reported V-based DRX cathodes [47, 48]. Nevertheless, similar to Cr6+, V5+ can migrate into the tetrahedral sites to enhance Li transport, which benefits the rate capability [47]. Consistently, with this concept, HE-2 is predicted to retrain 171 mAh/g capacity at 1000 mA/g ( of the 266 mAh/g capacity at 20 mA/g), which is superior to the majority of the DRX cathodes reported to date.
The inset plots in Figures 5A and B show the predicted discharge capacity of HE-1 and HE-2 for 20 cycles. The capacity drop in the first five cycles is predicted to slow down upon further cycling. This result is in full agreement with experimental findings, which indicate some of the irreversibility in the initial cycles, such as cathode–electrolyte interface formation [49]. These examples illustrate how practitioners can effectively use DRXNet to navigate the extensive chemical space of high-entropy DRXs and identify promising candidates for cathode design and optimization.
II.7 Electrochemical conditions
We further tested the depth and transferability of DRXNet’s predictive capabilities by varying the HE-2 discharge voltage window and cycling rate, which are typical parameters varied in the investigation of a new cathode material. Figure 5C displays the discharge profiles between 2.0 – 4.4 V, with two additional rates tested (10 mA/g for a low rate and 104 mA/g for an extremely high rate). These conditions are infrequently incorporated into our training data. The 10 mA/g exhibits a discharge profile very similar to that obtained at 20 mA/g, which is entirely consistent with typical experimental findings, as the discharge process at such a low rate exhibits a reduced overpotential and is closer to the equilibrium. The 10 A/g rate discharge profile demonstrates a sharp drop in voltage, reasonably indicating poor performance at this extremely high rate. Some unphysical predictions start to appear when the model is tested to predict the discharge profiles between 2.0 – 4.0 V. As Figure 5D shows a small non-zero offset mAh/g for the 20 mA/g rate profile appears at the onset of discharge (4.0 V). Since the start of the capacity curve at the upper level of the voltage cutoff is not formally enforced to zero by the model, but emerges from the linear embeddings of the voltage state with the voltage window , an offset can be created when there is not enough data for that specific voltage window.
Based on the tests, our primary conclusion is that DRXNet exhibits a reasonable ability to learn the cathode material’s chemical information in the latent space and generalize to test conditions that are included in the dataset. However, for test conditions that the model has not or rarely encountered (e.g., experiments with V), discrepancies or unphysical profiles may still arise. This highlights the data scarcity issue, which is typical for human-generated experimental conditions, which are biased toward what is needed to demonstrate performance rather than what is optimal for model training [50].
III Discussion
Most machine learning approaches predicting battery performance have been focused on predictions for a specific chemistry or limited chemical space of commercialized cathodes, typically, the remaining useful life forecasted from the initial cycles [11, 51, 52]. However, the nature of battery cathode material discovery and optimization lies in a broad domain of chemistries, which is more challenging for AI as it needs to capture the direct (e.g., voltage) and indirect effect (e.g., cycle life) of chemical changes [18]. Recent studies have demonstrated the feasibility of building universal models for atomistic modeling by harnessing more than ten years of ab-initio calculations spanning the periodic table [53, 54, 10, 55, 56]. It becomes a logical extension to envision universal models for the experimental discovery of battery materials by leveraging the wealth of both ab-initio calculation and experimental data generated on cathode materials worldwide [17, 57]. In this work, we propose an end-to-end training pipeline to encode and learn the (electro)chemical information of cathode materials from voltage profiles. Focused on DRX cathodes, we data-mined years of lab-generated experimental discharge voltage profiles and trained a universal machine-learning model (DRXNet) to make predictions across diverse compositions. This was achieved through a novel model design consisting of an electrochemical condition network and a state prediction network .
The design of the two networks promotes modularity in the architecture, streamlining the optimization and interpretation of each network individually and their learned features. For instance, composition is an intrinsic property of the synthesized cathode materials, and the encoding of such features is independent of other factors such as current density and cycle status, rationalizing our approach to first extract the composition-only feature via a GNN. Although it remains a challenge that the composition may change as a function of current density and cycle status due to TM dissolution and the irreversible reaction of lithium outside the cathode, DRXNet encompasses these factors into the rate- and cycle-informed feature vector representations. By leveraging a ResNet-inspired architecture using skip connections [58], we achieve a more effective synthesis of the feature vector within the latent space. This design allows for a direct connection between the rate-informed feature, , and the prediction of the first cycle capacity. Such architecture has been proven to boost model training and alleviate the well-known gradient vanishing issues.
Given the inherent sequential nature of battery testing data – where possessing information from the -th cycle implies the availability of data from the first cycle – it becomes crucial to design features that reflect this causality. This insight leads to the formulation of the cycle-informed feature, . This feature accentuates the difference between the first and the -th cycles, guiding the prediction for the -th cycle capacity, as detailed in Eq.(6). Consequently, our loss function is constructed for multi-task learning with both terms for the first and -th cycle capacities, ensuring the causal relationships in cycle-dependent capacity predictions (refer to Eq.(12)). Through an ablation study on whether to include the first cycle term, , in the loss function or not, we found that the model without tends to be underfitted (more details in Figure S8). Our incorporation of loss terms for both the first and -th cycle capacities enhances the model expressibility, which is a crucial factor in the optimization of battery materials.
In addition, the modular design of the electrochemical condition network provides flexibility for the feature representation when expanding the model to include other information. The training dataset, being derived from our own experimental results, does not encompass testing parameters such as particle size, electrolyte type, synthesis variations, etc. Since the battery electrodes were fabricated in our laboratory using standardized recipes and methodologies, these factors have been coarsely integrated into the compositional model and are treated as constants across our dataset. Currently, the model does not include features to capture structural information (crystal structure, short-range order, etc.). In DRX compounds, short-range order is known to influence performance and to the extent that this is not a direct consequence of composition, but modified by synthesis parameters its effects are not accounted for [59]. In principle, researchers can choose to include such factors to design the electrochemical feature vector, depending on the specific problem they are addressing. Given the vast amount and complexity of these properties, a synthetic data collection approach is necessary. Data-mining techniques, such as text mining and figure mining, can automatically retrieve valuable experimental information from decades of published literature [60, 61], though a challenge with aggregating diverse data from literature is the numerous hidden and unspecified variables relevant to materials synthesis and electrochemical testing. Looking forward, automated labs can address both data scarcity and transparency issues by enabling more extensive exploration of the experimental space and even better collect data from ”failed” experiments [62, 63, 64, 65].
In conclusion, DRXNet represents a step forward in developing machine-learning models for battery materials research. By continuously refining the model and incorporating additional data and parameters, we anticipate that such a machine-learning framework will play an increasingly critical role in discovering and optimizing next-generation battery materials.
IV Methods
IV.1 Data collection
We collected coin-cell electrochemical test data from our lab starting in 2016 and converted them into a digital format (.json). Each .json file contains information on one individual electrochemical test, including the electrode composition, electrode mass (g), active mass (g), test current rate (mA/g), low and high voltage value of the working window (V), and charge/discharge profiles of collected cycles. The compositions used for the model training were taken as the targeted composition in experiments. For the fraction of our data set which was previously published, the composition values were typically confirmed by Inductively Coupled Plasma (ICP) analysis. For these compounds, the feature vectors of the targeted compositions and ICP-analyzed composition exhibit in cosine similarity as shown in Supplementary Information, which supports using the targeted composition for the general prediction purpose. Nonetheless, minor variations between the actual composition and the target composition can be a source of noise in the data.
For the in-house battery tests, the CR2032 coin cells were assembled using commercial 1 M LiPF6 in an ethylene carbonate and dimethyl carbonate solution (volume ratio 1:1) as the electrolyte, glass microfiber filters (Whatman) as separators, and Li-metal foil (FMC) as the anode. The coin cells were tested on an Arbin battery cycler at room temperature. The cathode consisted of a mixture of active material (DRX), Super C65 carbon black, and polytetrafluoroethylene (PTFE). The capacity signal, collected in units of Ah from the Arbin battery cycler, was normalized to mAh/g using the mass of the active material (active mass). The data from the failed tests (e.g., Arbin cycler breakdown, electrolyte failure, strong signal fluctuations, etc.) were removed from the dataset (see Figure S1 for examples).
To enhance the generalization and expressibility of DRXNet, we expanded the dataset by figure mining published voltage profiles in related systems not covered by our lab tests (see Table S1), which was accomplished using the WebPlotDigitizer [66]. We used the UnivariateSpline method to denoise and resample the experimental profiles and compute the curves. One hundred points were uniformly sampled to form the voltage series for each discharge profile, and the capacity series and series were calculated accordingly from .
IV.2 Model design
IV.2.1 Preliminaries
A linear layer with trainable weight and bias is defined as
| (2) |
For simplicity of notion, each represents different trainable weights in the following equations.
IV.2.2 Compositional encoding
For elemental information, each element is first embedded into a 200-dimensional vector using mat2vec [41]. The Roost (Representation Learning from Stoichiometry) model is used for compositional encoding [26], which is a graph neural network (GNN) with message passings as follows:
| (3) | ||||
In these equations, represents the -th hidden layer for the -th element; denotes the concatenation operation; and the soft-attention coefficient describes the interaction between elements and , with as the index of multi-head attention. and denote the linear layer for the core and attention layer, respectively. The fractional concentration of element depends on the specific compound (e.g., for Li/Mn/Cr/Ti in Li1.2Mn0.2Cr0.2Ti0.4O2.0). is the SiLu activation function. After graph convolution layers, the encoded composition vector is obtained by average pooling over the elements with weighted attention
| (4) |
IV.2.3 Electrochemical condition encoding
The electrochemical test primarily involves two pieces of information: the current density rate and cycle number. We use MLPs to encode the rate and cycle number:
| (5) |
As the actual rate and cycle performance are strongly correlated with cathode materials, the relationship between the composition, rate, and cycle is synthesized using gated-MLPs with soft attention[25]:
| (6) | ||||
where is an MLP, is the Sigmoid activation function, and is an MLP with SiLu activation function . The BatchNormalization layer is added before the activation function. In this equation, is a feature vector jointly determined by the composition and rate information, which is used to predict the first cycle property. is a feature vector jointly determined by the composition, rate, and cycle information, which is used to predict the -th cycle property. The difference between and is linearly dependent on the number of cycles with a trainable weight , allowing the model to learn cycle performance contrastively.
IV.2.4 State prediction network
The state prediction network () takes the inputs of voltage state () and outputs the discharge-capacity state ()
| (7) |
In practice, the voltage profile is measured within the applied voltage window []. To accommodate the voltage window in the discharge state prediction, the first layer in is encoded via an MLP:
| (8) |
where is the activation function. The test-condition information is element-wise added to the state prediction network [58]
| (9) |
The state of capacity is obtained by
| (10) |
where is the capacity for the -th cycle (including the first cycle). Because the discharge capacity is always positive, is added to constrain the predicted capacity to be positive and accelerate the training process. for the redox potential can be obtained via PyTorch auto-differentiation [67]
| (11) |
IV.3 Model training
The model is trained to minimize the sum of multi-task losses for the capacity of the first cycle, the -th cycle, and :
| (12) |
A MSE loss function is used for and , whereas a MAE loss function is employed for the first cycle as a contrastive term . The weights for , , and are set to = 1, = 1, and = 5. The term represents regularization, which consists of two parts: (1) an -norm regularization of the network’s parameters and (2) a smoothing term to avoid large, unphysical performance fluctuations (c denotes the fractional concentration of elements). The weight of regularization is .
To make predictions, an ensemble of five independent models was trained to make predictions. Each model was trained with a batch size of 1024 within 30 epochs. The Adam optimizer was used with as the initial learning rate. The ExponentialLR scheduler was used to adjust the learning rate with a decay of 0.9 per epoch.
V Acknowledgments
This work was primarily supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC0205CH11231 (Materials Project program KC23MP). The data collection in this work was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Vehicle Technologies Office, under the Advanced Battery Materials Research (BMR) Program of the US Department of Energy (DOE) under contract No. DE-AC0205CH11231. The computational modeling in this work was supported by the computational resources provided by the Extreme Science and Engineering Discovery Environment (XSEDE), supported by National Science Foundation grant number ACI1053575; the National Energy Research Scientific Computing Center (NERSC); and the Lawrencium computational cluster resource provided by the IT Division at the Lawrence Berkeley National Laboratory. The authors thank Huiwen Ji, Jianping Huang, and Zijian Cai for their help in experimental data collection, and Yifan Chen for valuable discussions.
VI Availability
The codes of DRXNet are open-sourced at https://github.com/zhongpc/DRXNet and https://doi.org/10.5281/zenodo.10719829. The open-source dataset is available at https://doi.org/10.6084/m9.figshare.25328578.v1 for public access, which contains 12,688 experimental discharge voltage profiles excluding the Mn-rich and Ti-based DRX. The open-source dataset is not identical to, but rather a part of, the DRX-TD that was used for the pretrained models in the paper.
VII Supplementary Information
Supplemental information can be found online at https://doi.org/10.1016/j.joule.2024.03.010.
VIII Author Contributions
P.Z. and G.C. conceived the initial idea. P.Z. collected the dataset and developed the code base with help from B.D. and T.H.. Z.L. and G.C. offered insight into the project. P.Z. and G.C. prepared the manuscript. All authors contributed to discussions and approved the manuscript.
References
- Olivetti et al. [2017] E. A. Olivetti, G. Ceder, G. G. Gaustad, and X. Fu, Lithium-Ion Battery Supply Chain Considerations: Analysis of Potential Bottlenecks in Critical Metals, Joule 1, 229 (2017).
- Xie et al. [2021] L. Xie, C. Singh, S. K. Mitter, M. A. Dahleh, and S. S. Oren, Toward carbon-neutral electricity and mobility: Is the grid infrastructure ready?, Joule 5, 1908 (2021).
- Tian et al. [2021] Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, et al., Promises and Challenges of Next-Generation “Beyond Li-ion” Batteries for Electric Vehicles and Grid Decarbonization, Chemical Reviews 121, 1623 (2021).
- Goodenough and Kim [2010] J. B. Goodenough and Y. Kim, Challenges for rechargeable Li batteries, Chemistry of Materials 22, 587 (2010).
- Lv et al. [2022] C. Lv, X. Zhou, L. Zhong, C. Yan, M. Srinivasan, Z. W. Seh, C. Liu, H. Pan, S. Li, Y. Wen, and Q. Yan, Machine Learning: An Advanced Platform for Materials Development and State Prediction in Lithium‐Ion Batteries, Advanced Materials 34, 2101474 (2022).
- Wang et al. [2023] H. Wang, T. Fu, Y. Du, W. Gao, K. Huang, Z. Liu, P. Chandak, S. Liu, P. Van Katwyk, et al., Scientific discovery in the age of artificial intelligence, Nature 620, 47 (2023).
- Ahmad et al. [2018] Z. Ahmad, T. Xie, C. Maheshwari, J. C. Grossman, and V. Viswanathan, Machine Learning Enabled Computational Screening of Inorganic Solid Electrolytes for Suppression of Dendrite Formation in Lithium Metal Anodes, ACS Central Science 4, 996 (2018).
- Liow et al. [2022] C. H. Liow, H. Kang, S. Kim, M. Na, Y. Lee, A. Baucour, K. Bang, Y. Shim, J. Choe, et al., Machine learning assisted synthesis of lithium-ion batteries cathode materials, Nano Energy 98, 107214 (2022).
- Chen et al. [2024] C. Chen, D. T. Nguyen, S. J. Lee, N. A. Baker, A. S. Karakoti, L. Lauw, C. Owen, K. T. Mueller, B. A. Bilodeau, V. Murugesan, et al., Accelerating computational materials discovery with artificial intelligence and cloud high-performance computing: from large-scale screening to experimental validation, arXiv preprint arXiv:2401.04070 (2024).
- Deng et al. [2023] B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel, and G. Ceder, CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nature Machine Intelligence 5, 1031 (2023).
- Severson et al. [2019] K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, et al., Data-driven prediction of battery cycle life before capacity degradation, Nature Energy 4, 383 (2019).
- Jones et al. [2022] P. K. Jones, U. Stimming, and A. A. Lee, Impedance-based forecasting of lithium-ion battery performance amid uneven usage, Nature Communications 13, 1 (2022).
- Aykol et al. [2021] M. Aykol, C. B. Gopal, A. Anapolsky, P. K. Herring, B. van Vlijmen, M. D. Berliner, M. Z. Bazant, R. D. Braatz, W. C. Chueh, and B. D. Storey, Perspective—Combining Physics and Machine Learning to Predict Battery Lifetime, Journal of The Electrochemical Society 168, 030525 (2021).
- Hu et al. [2020] X. Hu, L. Xu, X. Lin, and M. Pecht, Battery lifetime prognostics, Joule 4, 310 (2020).
- Sulzer et al. [2021] V. Sulzer, P. Mohtat, A. Aitio, S. Lee, Y. T. Yeh, F. Steinbacher, M. U. Khan, J. W. Lee, J. B. Siegel, et al., The challenge and opportunity of battery lifetime prediction from field data, Joule 5, 1934 (2021).
- Attia et al. [2020] P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins, et al., Closed-loop optimization of fast-charging protocols for batteries with machine learning, Nature 578, 397 (2020).
- Ward et al. [2022] L. Ward, S. Babinec, E. J. Dufek, D. A. Howey, V. Viswanathan, M. Aykol, D. A. Beck, B. Blaiszik, B.-R. Chen, et al., Principles of the Battery Data Genome, Joule 6, 2253 (2022).
- Sendek et al. [2022] A. D. Sendek, B. Ransom, E. D. Cubuk, L. A. Pellouchoud, J. Nanda, and E. J. Reed, Machine Learning Modeling for Accelerated Battery Materials Design in the Small Data Regime, Advanced Energy Materials 12, 2200553 (2022).
- Clément et al. [2020] R. J. Clément, Z. Lun, and G. Ceder, Cation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium-ion cathodes, Energy & Environmental Science 13, 345 (2020).
- Key et al. [2011] B. Key, M. Morcrette, J.-M. Tarascon, and C. P. Grey, Pair Distribution Function Analysis and Solid State NMR Studies of Silicon Electrodes for Lithium Ion Batteries: Understanding the (De)lithiation Mechanisms, Journal of the American Chemical Society 133, 503 (2011).
- Li et al. [2021] L. Li, Z. Lun, D. Chen, Y. Yue, W. Tong, G. Chen, G. Ceder, and C. Wang, Fluorination‐Enhanced Surface Stability of Cation‐Disordered Rocksalt Cathodes for Li‐Ion Batteries, Advanced Functional Materials 31, 2101888 (2021).
- Clément et al. [2018] R. J. Clément, D. Kitchaev, J. Lee, and Gerbrand Ceder, Short-Range Order and Unusual Modes of Nickel Redox in a Fluorine-Substituted Disordered Rocksalt Oxide Lithium-Ion Cathode, Chemistry of Materials 30, 6945 (2018).
- Zhong et al. [2022] P. Zhong, T. Chen, L. Barroso-Luque, F. Xie, and G. Ceder, An -norm regularized regression model for construction of robust cluster expansions in multicomponent systems, Physical Review B 106, 024203 (2022).
- Barroso-Luque et al. [2022] L. Barroso-Luque, P. Zhong, J. H. Yang, F. Xie, T. Chen, B. Ouyang, and G. Ceder, Cluster expansions of multicomponent ionic materials: Formalism and methodology, Physical Review B 106, 144202 (2022).
- Xie and Grossman [2018] T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Physical Review Letters 120, 145301 (2018).
- Goodall and Lee [2020] R. E. A. Goodall and A. A. Lee, Predicting materials properties without crystal structure: deep representation learning from stoichiometry, Nature Communications 11, 6280 (2020).
- Mizushima et al. [1980] K. Mizushima, P. Jones, P. Wiseman, and J. Goodenough, LixCoO2 (): A new cathode material for batteries of high energy density, Materials Research Bulletin 15, 783 (1980).
- Manthiram [2020] A. Manthiram, A reflection on lithium-ion battery cathode chemistry, Nature Communications 11, 1550 (2020).
- Ji et al. [2019a] H. Ji, A. Urban, D. A. Kitchaev, D.-H. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, et al., Hidden structural and chemical order controls lithium transport in cation-disordered oxides for rechargeable batteries, Nature Communications 10, 592 (2019a).
- Urban et al. [2017] A. Urban, A. Abdellahi, S. Dacek, N. Artrith, and G. Ceder, Electronic-Structure Origin of Cation Disorder in Transition-Metal Oxides, Physical Review Letters 119, 1 (2017).
- Lee et al. [2017] J. Lee, J. K. Papp, R. J. Clément, S. Sallis, D.-H. Kwon, T. Shi, W. Yang, B. D. McCloskey, and G. Ceder, Mitigating oxygen loss to improve the cycling performance of high capacity cation-disordered cathode materials, Nature Communications 8, 981 (2017).
- Zhong et al. [2020] P. Zhong, Z. Cai, Y. Zhang, R. Giovine, B. Ouyang, G. Zeng, Y. Chen, R. Clément, Z. Lun, and G. Ceder, Increasing Capacity in Disordered Rocksalt Cathodes by Mg Doping, Chemistry of Materials 32, 10728 (2020).
- Huang et al. [2021] J. Huang, P. Zhong, Y. Ha, D.-h. Kwon, M. J. Crafton, Y. Tian, M. Balasubramanian, B. D. McCloskey, W. Yang, and G. Ceder, Non-topotactic reactions enable high rate capability in Li-rich cathode materials, Nature Energy 6, 706 (2021).
- Newman and Balsara [2021] J. Newman and N. P. Balsara, Electrochemical systems (John Wiley & Sons, 2021).
- Lee et al. [2018] J. Lee, D. A. Kitchaev, D.-h. Kwon, C.-w. Lee, J. K. Papp, Y.-s. Liu, Z. Lun, R. J. Clément, T. Shi, B. D. McCloskey, J. Guo, M. Balasubramanian, and G. Ceder, Reversible Mn2+/Mn4+ double redox in lithium-excess cathode materials, Nature 556, 185 (2018).
- Kitchaev et al. [2018] D. A. Kitchaev, Z. Lun, W. D. Richards, H. Ji, R. J. Clément, M. Balasubramanian, D.-H. Kwon, K. Dai, J. K. Papp, T. Lei, B. D. McCloskey, W. Yang, J. Lee, and G. Ceder, Design principles for high transition metal capacity in disordered rocksalt Li-ion cathodes, Energy & Environmental Science 11, 2159 (2018).
- Lun et al. [2019] Z. Lun, B. Ouyang, D. A. Kitchaev, R. J. Clément, J. K. Papp, M. Balasubramanian, Y. Tian, T. Lei, T. Shi, et al., Improved Cycling Performance of Li-Excess Cation-Disordered Cathode Materials upon Fluorine Substitution, Advanced Energy Materials 9, 1802959 (2019).
- Ji et al. [2019b] H. Ji, D. A. Kitchaev, Z. Lun, H. Kim, E. Foley, D.-H. Kwon, Y. Tian, M. Balasubramanian, M. Bianchini, et al., Computational Investigation and Experimental Realization of Disordered High-Capacity Li-Ion Cathodes Based on Ni Redox, Chemistry of Materials 31, 2431 (2019b).
- Lun et al. [2020] Z. Lun, B. Ouyang, Z. Cai, R. J. Clément, D.-H. Kwon, J. Huang, J. K. Papp, M. Balasubramanian, Y. Tian, et al., Design Principles for High-Capacity Mn-Based Cation-Disordered Rocksalt Cathodes, Chem 6, 153 (2020).
- Lun et al. [2021] Z. Lun, B. Ouyang, D.-h. Kwon, Y. Ha, E. E. Foley, T.-Y. Huang, Z. Cai, H. Kim, M. Balasubramanian, et al., Cation-disordered rocksalt-type high-entropy cathodes for Li-ion batteries, Nature Materials 20, 214 (2021).
- Tshitoyan et al. [2019] V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder, and A. Jain, Unsupervised word embeddings capture latent knowledge from materials science literature, Nature 571, 95 (2019).
- Sutton et al. [2020] C. Sutton, M. Boley, L. M. Ghiringhelli, M. Rupp, J. Vreeken, and M. Scheffler, Identifying domains of applicability of machine learning models for materials science, Nature Communications 11, 4428 (2020).
- Zhou et al. [2023] S. Zhou, Y. Sun, T. Gao, J. Liao, S. Zhao, and G. Cao, Enhanced Li + Diffusion and Lattice oxygen Stability by the High Entropy Effect in Disordered‐Rocksalt Cathodes, Angewandte Chemie International Edition 100084, 10.1002/anie.202311930 (2023).
- Ouyang et al. [2020] B. Ouyang, N. Artrith, Z. Lun, Z. Jadidi, D. A. Kitchaev, H. Ji, A. Urban, and G. Ceder, Effect of Fluorination on Lithium Transport and Short‐Range Order in Disordered‐Rocksalt‐Type Lithium‐Ion Battery Cathodes, Advanced Energy Materials 10, 1903240 (2020).
- Kataoka et al. [2018] R. Kataoka, T. Kojima, and N. Takeichi, Electrochemical Property of Li-Mn Cation Disordered Li-Rich Li 2 MnO 3 with NaCl Type Structure, Journal of The Electrochemical Society 165, A291 (2018).
- Ren et al. [2015] S. Ren, R. Chen, E. Maawad, O. Dolotko, A. A. Guda, V. Shapovalov, D. Wang, H. Hahn, and M. Fichtner, Improved Voltage and Cycling for Li+ Intercalation in High-Capacity Disordered Oxyfluoride Cathodes, Advanced Science 2, 1500128 (2015).
- Nakajima and Yabuuchi [2017] M. Nakajima and N. Yabuuchi, Lithium-Excess Cation-Disordered Rocksalt-Type Oxide with Nanoscale Phase Segregation: Li1.25Nb0.25V0.5O2, Chemistry of Materials 29, 6927 (2017).
- Chen et al. [2015] R. Chen, S. Ren, M. Yavuz, A. A. Guda, V. Shapovalov, R. Witter, M. Fichtner, and H. Hahn, Li+ intercalation in isostructural Li2VO3 and Li2VO2F with O2- and mixed O2-/F- anions, Physical Chemistry Chemical Physics 17, 17288 (2015).
- Edström et al. [2004] K. Edström, T. Gustafsson, and J. Thomas, The cathode–electrolyte interface in the Li-ion battery, Electrochimica Acta 50, 397 (2004).
- Raccuglia et al. [2016] P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier, and A. J. Norquist, Machine-learning-assisted materials discovery using failed experiments, Nature 533, 73 (2016).
- Zhu et al. [2022] J. Zhu, Y. Wang, Y. Huang, R. Bhushan Gopaluni, Y. Cao, M. Heere, M. J. Mühlbauer, L. Mereacre, H. Dai, et al., Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation, Nature Communications 13, 2261 (2022).
- Roman et al. [2021] D. Roman, S. Saxena, V. Robu, M. Pecht, and D. Flynn, Machine learning pipeline for battery state-of-health estimation, Nature Machine Intelligence 3, 447 (2021).
- Jain et al. [2013] A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Materials 1, 011002 (2013).
- Chen and Ong [2022] C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nature Computational Science 2, 718 (2022).
- Merchant et al. [2023] A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon, and E. D. Cubuk, Scaling deep learning for materials discovery, Nature 624, 80 (2023).
- Batatia et al. [2023] I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, W. J. Baldwin, N. Bernstein, et al., A foundation model for atomistic materials chemistry, arXiv preprint arXiv:2401.00096 (2023).
- Hong et al. [2021] S. Hong, C. H. Liow, J. M. Yuk, H. R. Byon, Y. Yang, E. Cho, J. Yeom, G. Park, H. Kang, et al., Reducing Time to Discovery: Materials and Molecular Modeling, Imaging, Informatics, and Integration, ACS Nano 15, 3971 (2021).
- He et al. [2016] K. He, X. Zhang, S. Ren, and J. Sun, Deep Residual Learning for Image Recognition, in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vol. 2016-Decem (IEEE, 2016) pp. 770–778.
- Cai et al. [2022] Z. Cai, Y. Zhang, Z. Lun, B. Ouyang, L. C. Gallington, Y. Sun, H. Hau, Y. Chen, M. C. Scott, and G. Ceder, Thermodynamically Driven Synthetic Optimization for Cation‐Disordered Rock Salt Cathodes, Advanced Energy Materials 12, 2103923 (2022).
- Kononova et al. [2021] O. Kononova, T. He, H. Huo, A. Trewartha, E. A. Olivetti, and G. Ceder, Opportunities and challenges of text mining in materials research, iScience 24, 102155 (2021).
- Baibakova et al. [2022] V. Baibakova, M. Elzouka, S. Lubner, R. Prasher, and A. Jain, Optical emissivity dataset of multi-material heterogeneous designs generated with automated figure extraction, Scientific Data 9, 589 (2022).
- Szymanski et al. [2021] N. J. Szymanski, Y. Zeng, H. Huo, C. J. Bartel, H. Kim, and G. Ceder, Toward autonomous design and synthesis of novel inorganic materials, Materials Horizons 8, 2169 (2021).
- Stach et al. [2021] E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi, et al., Autonomous experimentation systems for materials development: A community perspective, Matter 4, 2702 (2021).
- Szymanski et al. [2023] N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, T. He, D. Milsted, M. J. McDermott, M. Gallant, E. D. Cubuk, et al., An autonomous laboratory for the accelerated synthesis of novel materials, Nature 624, 86 (2023).
- Lunt et al. [2024] A. Lunt, H. Fakhruldeen, G. Pizzuto, L. Longley, A. White, N. Rankin, R. Clowes, B. Alston, L. Gigli, et al., Modular, Multi-Robot Integration of Laboratories: An Autonomous Workflow for Solid-State Chemistry, Chemical Science 10.1039/D3SC06206F (2024).
- Rohatgi [2022] A. Rohatgi, Webplotdigitizer: Version 4.6 (2022).
- Paszke et al. [2019] A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, et al., Pytorch: An imperative style, high-performance deep learning library, Advances in neural information processing systems 32 (2019).