Defending against Reconstruction Attack in Vertical Federated Learning
Abstract
Recently researchers have studied input leakage problems in Federated Learning (FL) where a malicious party can reconstruct sensitive training inputs provided by users from shared gradient (Zhu et al., 2019; Geiping et al., 2020; Yin et al., 2021). It raises concerns about FL since input leakage contradicts the privacy-preserving intention of using FL. Despite relatively rich literature on attacks and defenses of input reconstruction in Horizontal FL, input leakage and protection in vertical FL starts to draw researchers attention recently. In this paper, we study how to defend against input leakage attack in Vertical FL. We design an adversarial training based framework that contains three modules: adversarial reconstruction, noise regularization, and distance correlation minimization. Those modules can not only be employed individually but also applied together since they are independent to each other. Through extensive experiments on a large-scale industrial online advertising dataset, we show our framework is effective in protecting input privacy while retaining the model utility.
1 Introduction
With the increasing concerns on data security and user privacy in machine learning, Federated Learning (FL) (McMahan et al., 2017a) becomes a promising solution to allow multiple parties collaborate without sharing their data completely. Based on how sensitive data are distributed among various parties, FL can be classified into two categories (Yang et al., 2019): Cross-silo or Vertical FL (vFL) and Cross-device or Horizontal FL (hFL). In contrast to hFL where the data are partitioned by samples or entities (i.e. a person), vFL partitions the data by different attributes (i.e. features and labels). In vFL, multiple parties can own different attributes from the same entities.
One typical example of vFL is a collaboration between general and specialized hospitals. They might hold the data for the same patient, but the general hospital owns generic information (i.e. private attributes such as gender and age) of the patient while the specialized hospital owns the specific testing results (i.e. labels) of the same patient. Therefore they can use vFL to jointly train a model that predicts a specific disease examined by the specialized hospital from the features provided by the general hospital.
Under two-party vFL setting, the model is split into two submodels and each submodel is owned by one party. During training, the party without labels (namely passive party) sends the computation results (namely embedding) of the intermediate layer (namely cut layer) rather than the raw data to the party with labels (namely active party). The active party takes the embedding as the input, completes the rest of forward pass, computes backward gradient based on the labels, and performs backward pass up to the cut layer. Then it sends the gradient w.r.t the cut layer back to the passive party. Finally the passive party completes the backpropagation with the gradients of the cut layer using chain rule.
At first glance, vFL seems private because no feature/input or label is shared between the two parties. However, from the viewpoint of passive party, the cut layer embedding still contains rich information which can be exploited by a malicious active party to leak the input information. Recently researchers have identified some input leakage problems under hFL settings. For example, Mahendran et al. showed that an attacker can exploit the intermediate embedding to reconstruct the input images, and hence the people who show up in the input images can be re-identified (Mahendran & Vedaldi, 2015). Furthermore, Zhu et al.; Geiping et al.; Yin et al. showed that in hFL setting, the central server could recover the raw inputs and labels of the clients from the gradient sent from clients.
Despite the relatively well-studied problems of input leakage in hFL, defending against reconstruction attack starts to draw researchers attention recently (Luo et al., 2020). In this paper, we propose an adversarial training based framework that can defend against input reconstruction attack in vFL. The proposed framework simulates the game between an attacker (i.e. the active party) who actively reconstructs raw input from the cut layer embedding and a defender (i.e. the passive party) who aims to prevent the input leakage. Our framework consists of three modules to protect input privacy: adversarial reconstructor, noise regularization, and distance correlation. These modules are designed to make the submodel owned by the passive party more robust against potential attacks that extract sensitive information about the raw input from the cut layer embedding. The adversarial reconstructor is designed to maximize the reconstruction error of the attacker. Noise regularization is designed to reduce information about input in embedding by misleading attacker’s optimization toward a random direction. Distance correlation module is to decrease the correlation between the raw input and the cut layer embedding. We conduct extensive experiments in a large-scale online advertising dataset collected under an industrial setting to demonstrate the effectiveness of our framework in protecting input privacy while retaining model utility.
We summarize our contributions as follows:
-
•
We design an adversarial training based framework with three independent modules to defend against input reconstruction attack in vFL.
-
•
Through extensive experiments on a real-world and industrial-scale online advertising dataset, we show our framework can achieve a good trade-off between preserving input privacy and retaining model performance.
2 Methodology
vFL Background.
We begin by providing some background on how the vanilla vFL works, as shown in the part of Figure 1. A conventional vFL framework splits the model into two parts: feature extractor (owned by passive party) and label predictor (owned by active party). In the forward pass, the passive party feeds the raw input into , and then sends the cut layer embedding to the active party. The active party takes as the input for the label predictor (designed for the intended task), and then computes the gradients based on the ground-truth labels owned by it. Then, in the backward pass, the active party sends the gradient with respect to the cut layer back () to the passive party. Finally, the passive party completes the backpropagation using chain rule and updates .
Threat Model.
We assume the attacker is a malicious active party that attempts to reconstruct input from the cut layer embedding passed by the passive party. The attacker has access to and label . Our goal, as the defender and the passive party, is to prevent the reconstruction by making feature extractor more robust. We have access to , raw input , and ability to modify feature extractor .
Framework Overview.
Figure 1 shows the design of our framework which consists of three modules: Adversary Reconstructor (AR), Noise Regularization (NR), and Distance Correlation (dCor). These modules are designed to hide privacy-sensitive information from that can be exploited by the attacker (i.e. active party) to reconstruct the raw input from . Specifically, AR (Section 2.1) is designed to simulate an attacker that actively attempts to reconstruct the input, and then it maximizes error of the attacker. NR (Section 2.2) is designed to reduce information about in and stabilize AR. dCor (Section 2.3) is designed to decrease the correlation between and . Note that since these three modules are independent to each other, they can be either implemented as separate modules or unified into a single framework. We name this united framework as DRAVL (Defending against Reconstruction Attack in Vertical Federated Learning).
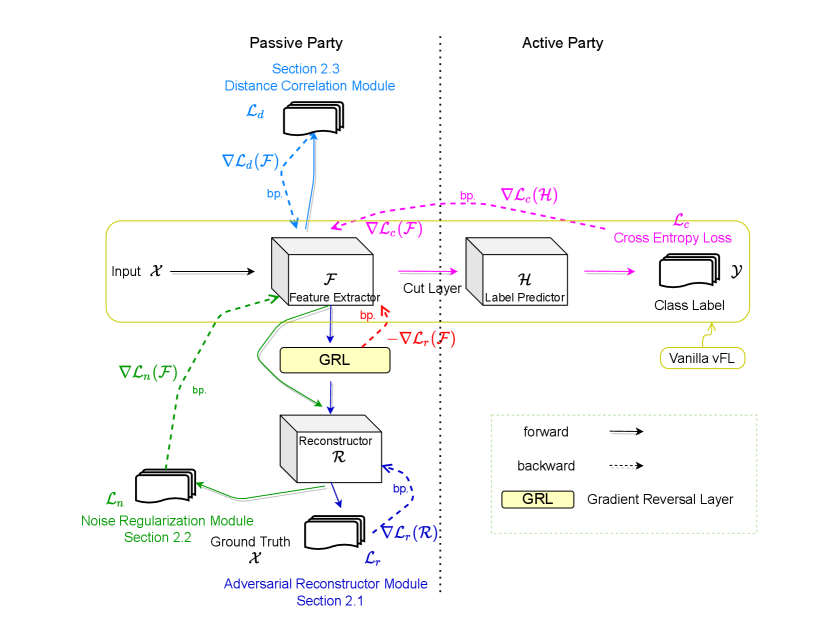
2.1 Adversarial Reconstructor Module
Inspired by prior work (Li et al., 2019; Feutry et al., 2018; Goodfellow et al., 2014), AR simulates an adversarial attacker who aims to train a reconstructor that maps the embedding to the input by minimizing the following reconstruction loss:
| (1) |
where can be any model (e.g. a MLP).
Ideally we can formulate the protection as a max-min problem that maximizes the minimized . However we empirically find that such optimization is unstable and hard to tune. Instead, we use Gradient Reversal Layer (GRL) from prior work (Ganin & Lempitsky, 2015; Feutry et al., 2018) that demonstrated promising results in stabilizing adversarial training. As shown in Figure 1, GRL is inserted between the feature extractor and the adversarial reconstructor . In forward pass, GRL just performs identity transformation. In backward pass, it multiplies the corresponding gradient w.r.t to the cut layer by (, i.e. ) and passes to the preceding layer. Intuitively, GRL leads to the opposite of gradient descent that is performing gradient ascent on the feature extractor with respect to maximize the adversarial reconstruction loss (as an attacker). Therefore it roughly achieves the goal of maximizing the minimized reconstruction loss. After inserting GRL, we just need to minimize as adversarial training. We update both and during training; after training is finished, we discard and save as the more robust feature extractor.
2.2 Noise Regularization Module
Noise Regularization also simulates an adversarial reconstructor but with a different goal. It is designed to reduce information about in by misleading the reconstructed input toward a random direction (and therefore degrading reconstruction quality). During training, we generate random Gaussian noise 111Random noise from other distributions such as Uniform distribution are effective too. and minimize the following noise regularization loss:
| (2) |
Note that if only NR is used, we can train an independent reconstructor (without GRL) as . If AR and NR are used together, we can reuse the AR reconstructor as 222Since the adversarial training is effective, and can achieve similar reconstruction performance. . In our experiments, we use the same reconstructor for both AR and NR. For notation simplicity, we will use to represent both AR and NR reconstructor.
As shown in Figure 1, are fed into the reconstructor directly (without GRL). NR calculates and computes the gradients of the w.r.t. , i.e. , and updates accordingly via backpropogation. Note that only works as a reconstructor and provides the reconstructed result as an input for optimized by NR. NR only has effects on and does not update any parameters of during backpropogation phase.
2.3 Distance Correlation Module
Distance correlation is designed to make input and embedding less dependent, and therefore reduces the likelihood of gaining information of from . Distance correlation measures statistical dependence between two vectors333Two vectors can have different length. (Vepakomma et al., 2018). The distance correlation loss is the following:
| (3) |
where we minimize the (log of) distance correlation loss () during the model training. It can be interpreted as being a good proxy dataset to construct but not as vice versa in terms of reconstructing from (Vepakomma et al., 2018).
Note that dCor computates pairwise distance between samples and requires time complexity where is the batch size. In practice, there are some faster estimators of dCor (Chaudhuri & Hu, 2019; Huang & Huo, 2017). In addition, dCor is sensitive to the and a larger can give a more accurate estimation of the distance correlation.
2.4 A Unified Framework
We can unify all three modules into one framework. The overall loss function is a combination of four losses: adversarial reconstruction loss (), noise regularization loss (), distance correlation loss (), and normal label prediction loss (). In this paper, we focus on classification and use categorical cross entropy as label prediction loss. Optimizing makes sure the model maintain a good utility; optimizing , , and increases model privacy. Uniting them in one framework can help us defend against the reconstruction attack while maintaining the accuracy of the primary learning task. The overall loss function is:
| (4) |
where , and are weights for distance correlation, noise regularization, and adversarial reconstructor module respectively. Note that during training, only the passive party optimizes these three modules while there is no change on the active party’s training optimization.
3 Experimental Study
Dataset and Setting.
We evaluate the proposed framework on a large-scale industrial binary classification dataset for conversion prediction tasks with millions of user click records. The data was collected over a period of three months from one of the largest online media platforms in industry (with hundreds of millions of users) that collaborates with e-commerce advertising. In total, the dataset contains million records of user conversion interactions (samples).
In our setting, the passive party is an online media platform that displays advertisements for an e-commerce company (the active party) to its users. Both parties have different attributes for the same set of users: the passive party has features of user viewing history on the platform and the active party has features of user product browsing history on its website and labels indicating if the user converted or not. Under our threat model, the goal of the passive party is to prevent their raw input features from being reconstructed from cut layer embedding.
Model.
We train a Wide&Deep model (Cheng et al., 2016) where the passive party’s feature extractor consists of the embedding layers for the input features and several layers of ReLU activated MLP (deep part) and the active party’s label predictor consists of the last logit layer of the deep part and the entire wide part of the model. During training, in each batch the passive party sends an embedding matrix with size to the passive party where batch size is 444The batch size is 512 if not specified. and embedding size is .
Evaluation Metrics.
To measure the privacy, we train an independent reconstructor that minimizes eq 1555In practice, the attacker cannot train since as the passive party, he does not have access to the ground truth input . For evaluation purpose, our experiment simulates the most powerful attacker, and therefore the privacy-preserving performance when facing real attacks should only be higher than what we report.. Note that is different from in AR or in NR; it is the simulated attack used for evaluation purpose and agnostic during our defense. The input privacy is measured by ’s reconstruction loss, i.e. the mean squared error (MSE) between its reconstructed input and real input666Different from existing reconstruction attacks on image models, our input is a set of user related features rather than humanly perceptible images. Therefore it is infeasible to show how well the reconstructed inputs look like visually. Instead we use MSE to quantify the reconstruction quality.. A larger MSE means more privacy is preserved. We also measure the privacy with as described in Section 2.3. A lower dCor means less dependency between and and therefore better privacy. To measure the model utility, we use AUC of conversion prediction. We use the online stream training to train the vFL model along with our framework. We average dCor, MSE and AUC in a daily basis and report them on evaluation data from Jan to Feb 2020.
We first show experimental results of optimizing individual NR and dCor module alone. Then we combine them with AR as a united framework (DRAVL) and measure its performance.
3.1 Evaluating Noise Regularization Module
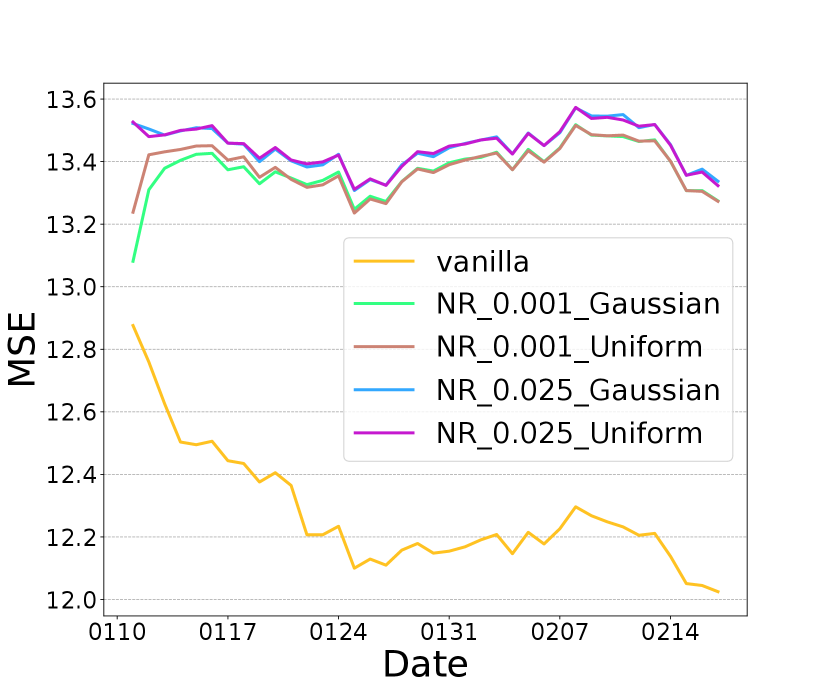
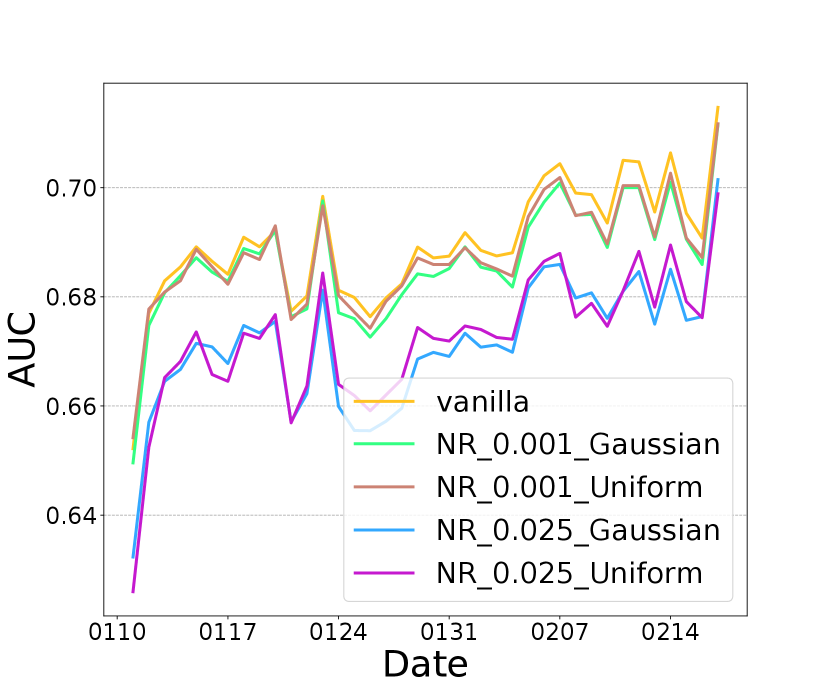
We evaluate the performance of using noise regularization module alone, i.e. minimizing . First, we evaluate the impact of noise choice on model privacy and utility. In Figure 2 (a) and (b), we compare two different types of random noise: Gaussian noise and Uniform noise . With the same , both random noises achieve similar MSE and AUC. Therefore the NR module is not sensitive to the type of the random noise. In addition, we can see the tradeoff between privacy (MSE) and utility (AUC) by varying the value of . A larger leads to a higher MSE (therefore better privacy) but a lower AUC score (therefore worse utility).
3.2 Evaluating Distance Correlation Module
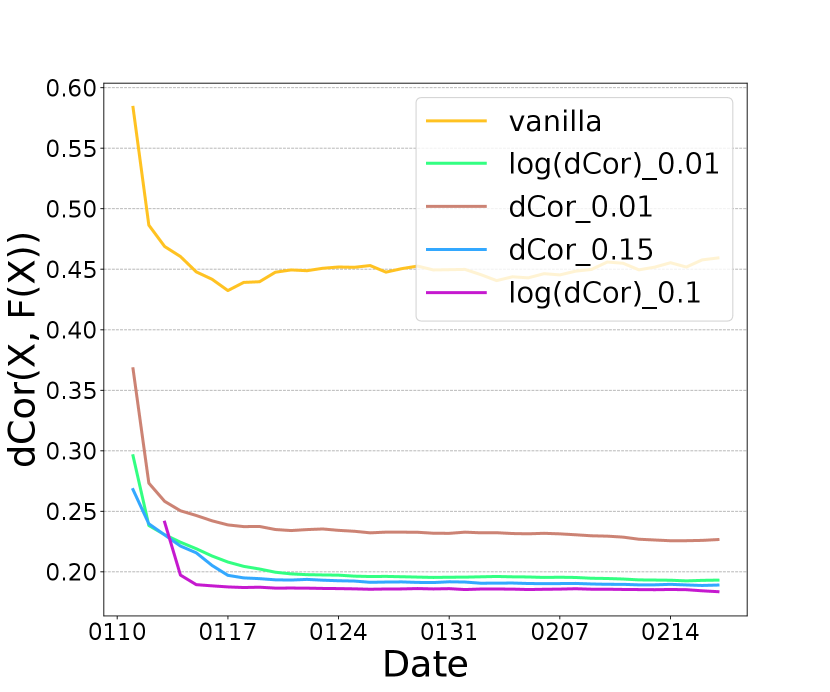
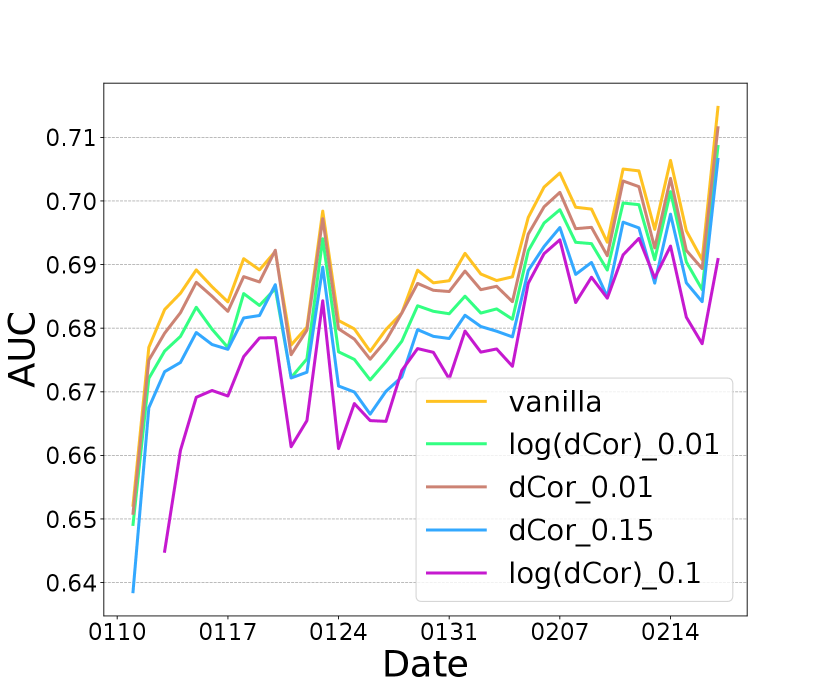
We evaluate the performance of minimizing distance correlation alone, i.e. minimizing . Figure 2 (c) and (d) show the dCor performance with different values of . First, vanilla vFL without any privacy protection, can naturally reduce the during the training (dropping from at the beginning of the training to ). Second, unsurprisingly optimizing dCor can reduce more than vanilla ( for vanilla and for dCor with ) while AUC drops less than . It indicates that dCor module can achieve a reasonable privacy-utility tradeoff with an appropriate . Third, log(dCor) is more robust to than dCor since the gap of log(dCor) between and is much smaller.
3.3 Effectiveness of DRAVL
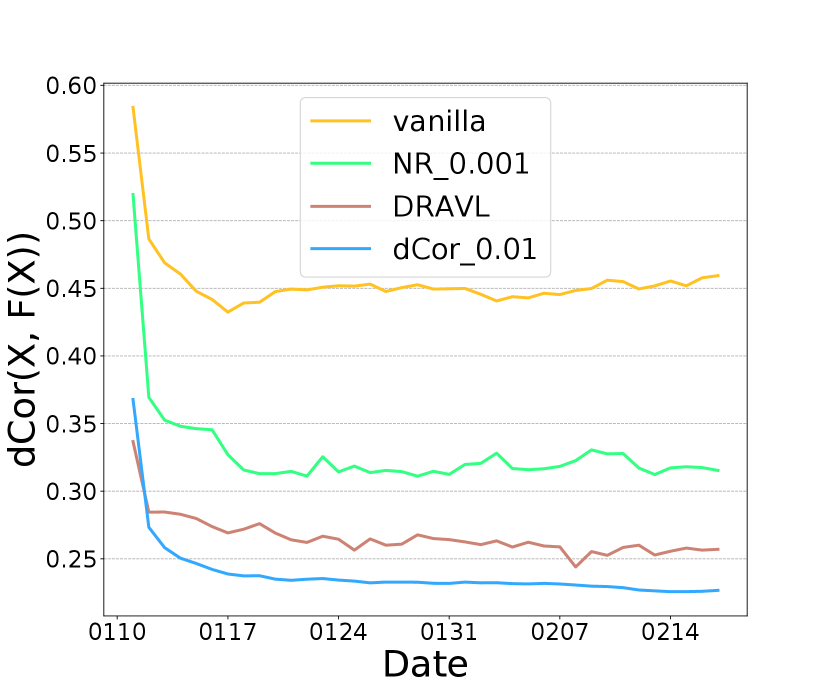
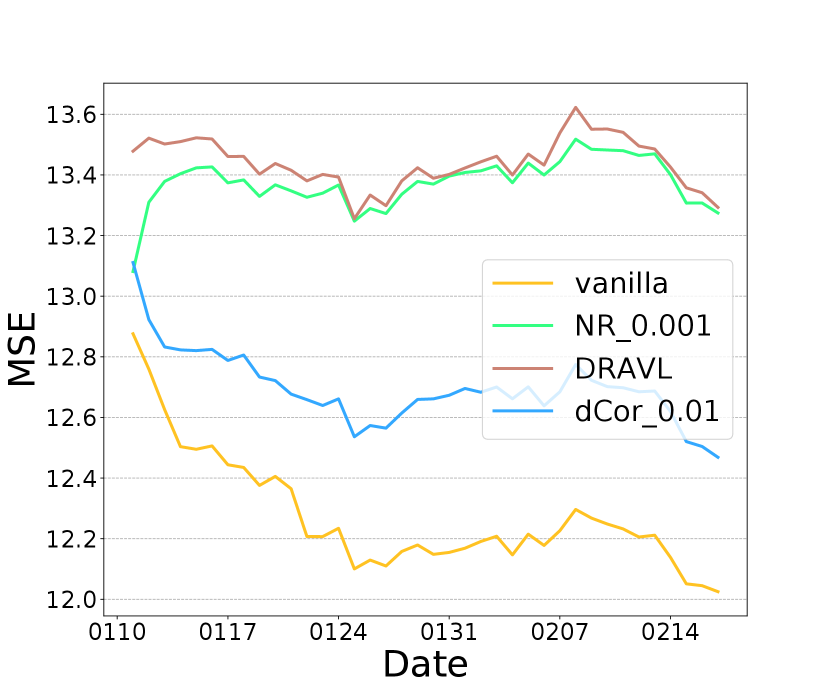
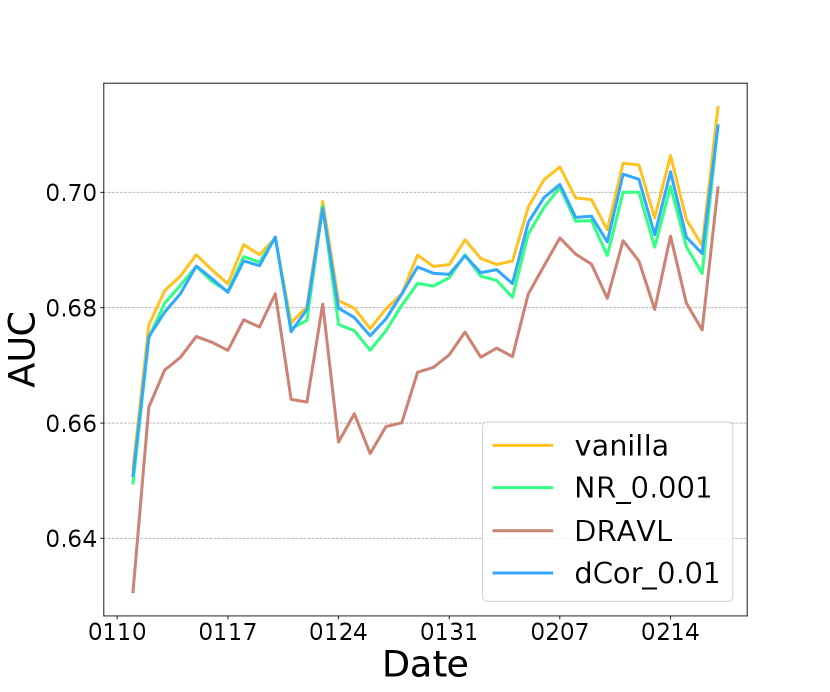
We now demonstrate the effectiveness of optimizing all losses together, i.e. DRAVL, by comparing it with individually optimizing each module. Figure 3 (a) shows that using NR module alone can reduce more than vanilla but its AUC is lower than dCor (Figure 3 (c)). Figure 3 (b) shows that dCor has lower MSE than NR, meaning NR preserves more privacy. This is unsurprising given NR is specifically designed to degrade the reconstruction quality. In addition, DRAVL helps gain the advantages of each module-it can reduce and increase MSE simultaneously. Unfortunately, DRAVL also hurts AUC more than optimizing any of modules alone. However, in terms of finding the best overall tradeoff, DRAVL shows more promising results among all competitors: compared to vanilla, on average DRAVL increases MSE by and decreases the dCor by with a cost of AUC drop by only .
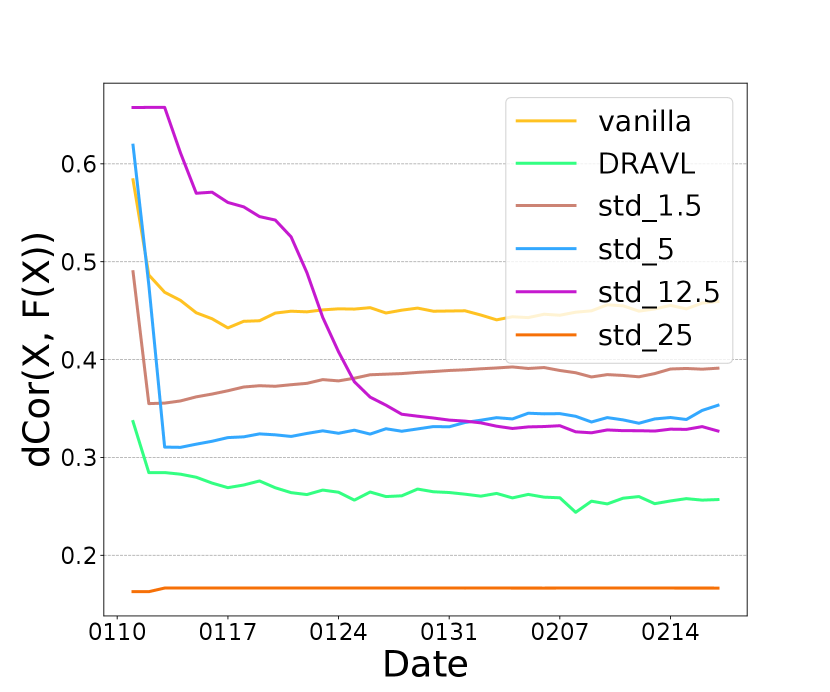
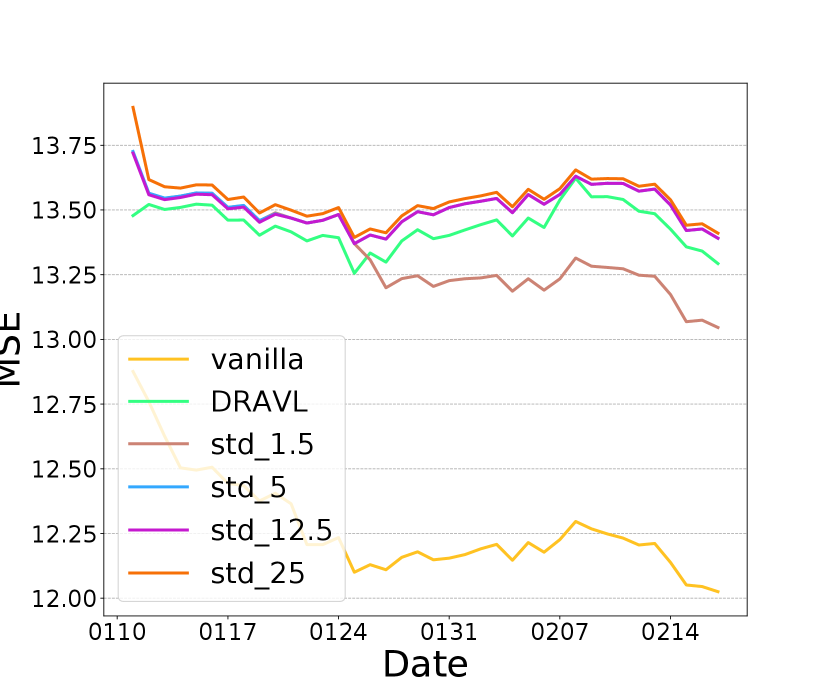
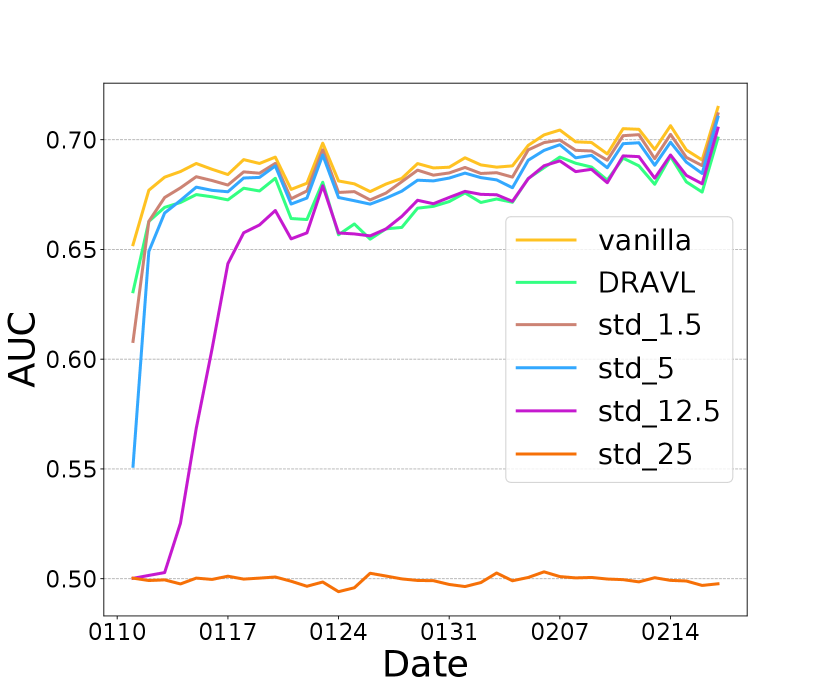
We also compare DRAVL with a straightforward yet effective protection baseline: adding random noise to the cut layer embedding. We generate a random noise from a zero-mean Gaussian and add it to the embedding. We only tune the standard deviation of the Gaussian noise to control the noise strength. As shown in Figure 3 (d), (e), and (f), with increasing the amount of noise added to the embedding, we can get a better privacy protection (lower dCor and higher MSE) but worse model utility (lower AUC). When noise strength is large enough (standard deviation ), the cut layer embedding is covered by the noise . As a result, the AUC drops to , which is equivalent with a random guess. Overall, with a good control of the amount of the random noise added to the cut layer embedding, it might be an effective protection strategy.
We compare this noise perturbation with DRAVL in Figure 3 (d), (e), and (f). DRAVL and noise perturbation method with can achieve similar AUC and MSE, since both models can make the reconstructed input be similar to the mean of the raw input. However, DRAVL reduces dCor more than the noise perturbation. Another drawback of perturbation based is that compared to DRAVL, empirically it is much harder to tune in order to find a good trade-off between model utility and privacy.
4 Related Work
Input Reconstruction Attack in FL.
Most of input reconstruction attacks are designed for Horizontal FL where a malicious server can reconstruct raw input from gradients sent from clients. Zhu et al. showed that an honest-but-curious server can jointly reconstruct raw data and its label from gradient on a 4-layer CNN (Zhu et al., 2019). Geiping et al. extended the attack on deep models with ability to reconstruct high-resolution images (Geiping et al., 2020). Yin et al. proposed the state-of-the-art method that is able to reconstruct high-resolution images in batches (in contrast to single-image optimization) from averaged gradient in a deep model (Yin et al., 2021). We do not include those attacks in our experiments because they are designed for Horizontal FL and cannot be applied to Vertical FL. Luo et al. (Luo et al., 2020) studied the feature inference problem in the settings of vFL. The biggest differences with DRAVL is that they leverage prediction outputs in the prediction/inference stage of vFL to conduct the feature inference attacks. However, when some specific conditions are satisfied, e.g. the number of classes is large or the active party’s features and the passive party’s are highly correlated, their attack methods can infer the passive party’s features well.
Privacy-enhancement in FL.
There are mainly three categories of approaches to enhance privacy within existing FL framework: 1) cryptography methods such as Secure Multi-party Computation (Agrawal et al., 2019; Du et al., 2004; Bonawitz et al., 2017; Nikolaenko et al., 2013) and homomorphic encryption(Aono et al., 2017; Sathya et al., 2018); 2) system-based methods such as Trusted Execution Environments (Subramanyan et al., 2017; Tramer & Boneh, 2018); 3) perturbation methods such as randomly perturbing the communicated message (Abadi et al., 2016; McMahan et al., 2017b), shuffling the messages (Erlingsson et al., 2019; Cheu et al., 2019), reducing message’s data-precision, compressing and sparsifying the message (Zhu et al., 2019).
5 Conclusion
In this paper, we design a defense framework that mitigates input leakage problems in Vertical FL. Our framework contains three modules: adversarial reconstruction, noise regularization, and distance correlation minimization. Those modules can not only be employed individually but also applied together since they are independent to each other. We conduct extensive experiments on a industrial-scale online advertising dataset to show that our framework is effective in protecting input privacy while maintain a reasonable model utility. We urge the community to study more about privacy leakage problems in the context of Vertical FL, and to continue efforts to develop more defenses against input reconstruction attacks and provide robustness against malicious parties.
References
- Abadi et al. (2016) Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B., Mironov, I., Talwar, K., and Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 308–318, 2016.
- Agrawal et al. (2019) Agrawal, N., Shahin Shamsabadi, A., Kusner, M. J., and Gascón, A. Quotient: two-party secure neural network training and prediction. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, pp. 1231–1247, 2019.
- Aono et al. (2017) Aono, Y., Hayashi, T., Wang, L., Moriai, S., et al. Privacy-preserving deep learning via additively homomorphic encryption. IEEE Transactions on Information Forensics and Security, 13(5):1333–1345, 2017.
- Bonawitz et al. (2017) Bonawitz, K., Ivanov, V., Kreuter, B., Marcedone, A., McMahan, H. B., Patel, S., Ramage, D., Segal, A., and Seth, K. Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pp. 1175–1191, 2017.
- Chaudhuri & Hu (2019) Chaudhuri, A. and Hu, W. A fast algorithm for computing distance correlation. Computational Statistics & Data Analysis, 135:15 – 24, 2019. ISSN 0167-9473. doi: https://doi.org/10.1016/j.csda.2019.01.016. URL http://www.sciencedirect.com/science/article/pii/S0167947319300313.
- Cheng et al. (2016) Cheng, H.-T., Koc, L., Harmsen, J., Shaked, T., Chandra, T., Aradhye, H., Anderson, G., Corrado, G., Chai, W., Ispir, M., et al. Wide & deep learning for recommender systems. In Proceedings of the 1st workshop on deep learning for recommender systems, pp. 7–10, 2016.
- Cheu et al. (2019) Cheu, A., Smith, A., Ullman, J., Zeber, D., and Zhilyaev, M. Distributed differential privacy via shuffling. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp. 375–403. Springer, 2019.
- Du et al. (2004) Du, W., Han, Y. S., and Chen, S. Privacy-preserving multivariate statistical analysis: Linear regression and classification. In Proceedings of the 2004 SIAM international conference on data mining, pp. 222–233. SIAM, 2004.
- Erlingsson et al. (2019) Erlingsson, Ú., Feldman, V., Mironov, I., Raghunathan, A., Talwar, K., and Thakurta, A. Amplification by shuffling: From local to central differential privacy via anonymity. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 2468–2479. SIAM, 2019.
- Feutry et al. (2018) Feutry, C., Piantanida, P., Bengio, Y., and Duhamel, P. Learning anonymized representations with adversarial neural networks. 2018.
- Ganin & Lempitsky (2015) Ganin, Y. and Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the 32nd International Conference on International Conference on Machine Learning - Volume 37, ICML’15, pp. 1180–1189. JMLR.org, 2015.
- Geiping et al. (2020) Geiping, J., Bauermeister, H., Dröge, H., and Moeller, M. Inverting gradients–how easy is it to break privacy in federated learning? In Advances in Neural Information Processing Systems, 2020.
- Goodfellow et al. (2014) Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. Generative adversarial networks, 2014.
- Huang & Huo (2017) Huang, C. and Huo, X. A statistically and numerically efficient independence test based on random projections and distance covariance. 2017.
- Li et al. (2019) Li, A., Guo, J., Yang, H., and Chen, Y. Deepobfuscator: Adversarial training framework for privacy-preserving image classification. CoRR, abs/1909.04126, 2019. URL http://arxiv.org/abs/1909.04126.
- Luo et al. (2020) Luo, X., Wu, Y., Xiao, X., and Ooi, B. C. Feature inference attack on model predictions in vertical federated learning. CoRR, abs/2010.10152, 2020. URL https://arxiv.org/abs/2010.10152.
- Mahendran & Vedaldi (2015) Mahendran, A. and Vedaldi, A. Understanding deep image representations by inverting them. In 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5188–5196, 2015. doi: 10.1109/CVPR.2015.7299155.
- McMahan et al. (2017a) McMahan, B., Moore, E., Ramage, D., Hampson, S., and y Arcas, B. A. Communication-efficient learning of deep networks from decentralized data. In Artificial Intelligence and Statistics, pp. 1273–1282. PMLR, 2017a.
- McMahan et al. (2017b) McMahan, H. B., Ramage, D., Talwar, K., and Zhang, L. Learning differentially private recurrent language models. arXiv preprint arXiv:1710.06963, 2017b.
- Nikolaenko et al. (2013) Nikolaenko, V., Weinsberg, U., Ioannidis, S., Joye, M., Boneh, D., and Taft, N. Privacy-preserving ridge regression on hundreds of millions of records. In 2013 IEEE Symposium on Security and Privacy, pp. 334–348. IEEE, 2013.
- Sathya et al. (2018) Sathya, S. S., Vepakomma, P., Raskar, R., Ramachandra, R., and Bhattacharya, S. A review of homomorphic encryption libraries for secure computation. arXiv preprint arXiv:1812.02428, 2018.
- Subramanyan et al. (2017) Subramanyan, P., Sinha, R., Lebedev, I., Devadas, S., and Seshia, S. A. A formal foundation for secure remote execution of enclaves. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pp. 2435–2450, 2017.
- Tramer & Boneh (2018) Tramer, F. and Boneh, D. Slalom: Fast, verifiable and private execution of neural networks in trusted hardware. arXiv preprint arXiv:1806.03287, 2018.
- Vepakomma et al. (2018) Vepakomma, P., Swedish, T., Raskar, R., Gupta, O., and Dubey, A. No peek: A survey of private distributed deep learning. CoRR, abs/1812.03288, 2018. URL http://arxiv.org/abs/1812.03288.
- Yang et al. (2019) Yang, Q., Liu, Y., Chen, T., and Tong, Y. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology (TIST), 10(2):1–19, 2019.
- Yin et al. (2021) Yin, H., Mallya, A., Vahdat, A., Alvarez, J. M., Kautz, J., and Molchanov, P. See through gradients: Image batch recovery via gradinversion. arXiv preprint arXiv:2104.07586, 2021.
- Zhu et al. (2019) Zhu, L., Liu, Z., and Han, S. Deep leakage from gradients. In Advances in Neural Information Processing Systems, pp. 14774–14784, 2019.