Defocusing Hirota equation with fully asymmetric non-zero boundary conditions: the inverse scattering transform

It will be convenient to define some notations:

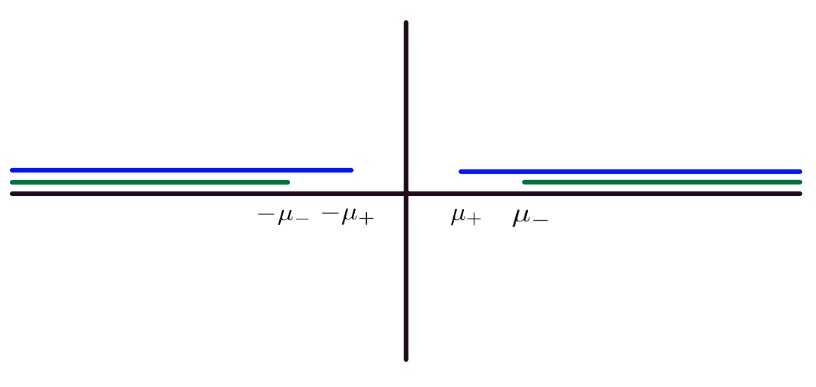
As $x\to\pm\infty$, the branch points are the values of $z$ for which $\lambda_{\pm}=0$, i.e. $z=\pm\mu_{\pm}$. We take the branch cuts on $\Xi_{\pm}$ (see Fig. 1). We define $\lambda_{\pm}$ as analytic functions for all $z\in\mathbb{C}\backslash\Xi_{\pm}$, and these functions remain continuous as $z$ approaches $\Xi_{\pm}$ from above. We see that Im$\lambda_{\pm}\geq 0$ and Im$(\lambda_{\pm}\pm z)\geq 0$ for all $z\in\mathbb{C}$. Clearly, $\Xi_{-}\subset\Xi_{+}$ and $\lambda_{\pm}\in\mathbb{R}$, $\forall$ $z\in\Xi_{-}$. Thus, continuous spectrum of the scattering problem consists of $z\in\Sigma_{-}$.

Similarly to [21], the eigenvector matrices of $U_{\pm}$ can be expressed as follows:

For $z\in\mathring{\Xi}_{\pm}$, we introduce the Jost solutions $\Psi_{\pm}(x,t,z)$ by

Let

where

We introduce the the modified eigenfunctions

It is evident that

One can formally integrate the ODE for $v_{\pm}$ to obtain

where $\hbox{e}^{\alpha\hat{\sigma}_{3}}A:=\hbox{e}^{\alpha\sigma_{3}}A\hbox{e}^{-\alpha\sigma_{3}}$ and $\Delta P_{\pm}(x,t):=P(x,t)-P_{\pm}(t)$.

Let $v_{\pm}=(v_{\pm,1},v_{\pm,2})$. Using the standard Neumann iteration for (2.15), we can prove that if $p(x,t)-p_{\pm}(t)\in L^{1}(\mathbb{R}^{\pm})$, then $v_{-,2}$ is analytic in $\mathbb{C}\backslash\Xi_{-}$, whereas $v_{+,1}$ is analytic in $\mathbb{C}\backslash\Xi_{+}$. In addition, for $t\geq 0$, when $(1+|x|)(p(x,t)-p_{\pm}(t))\in L^{1}(\mathbb{R}^{\pm})$, (2.15) are well-defined when $z\to\pm\mu_{\pm}$. We can see that $v_{-}$ and $v_{+}$ admit the form as $z\to\pm\mu_{-}$ and $z\to\pm\mu_{+}$, respectively,

Using tr$U=0$ and Abel’s formula, we find that $\hbox{det}\Psi_{\pm}$ is independent of $x$. Evaluate $\hbox{det}\Psi_{\pm}$ as $x\to\pm\infty$ to obtain

Since both $\Psi_{\pm}$ solve the scattering problem for $z\in\mathring{\Xi}_{-}$, one has

with

It is mentioned that $S$ is independent of $x$. From (2.19), we have $\hbox{det}S\neq 1$, which is a significant distinction from the case of symmetric NZBCs [21]. Let $S(z,t)=(s_{ij}(z,t))_{1\leq i,j\leq 2}$. Using (2.18), $s_{ij}$ $(i,j=1,2)$ can be expressed as follows:

From (2.20), it is shown that $s_{22}$ is analytic for $z\in\mathbb{C}\backslash\Xi_{+}$. Because $\Psi_{-,2}$ can be extended analytically to $z\in\mathbb{C}\backslash\Xi_{-}$, $\Psi_{+,1}$ and $\Psi_{+,2}$ are defined on $\Xi_{+}$, we may extend the definitions of $s_{12}$ and $s_{22}$ pointwise to $\mathring{\Xi}_{+}$. Since $d_{+}$ has a double zero at $z=\pm\mu_{+}$, $s_{12}$ and $s_{22}$ are singular at $z=\pm\mu_{+}$ .

It will be useful to introduce the reflection coefficients

which will be needed in the following discussions.

Due to the involutions $z\mapsto z^{*}$ and $\lambda_{\pm}(z)\mapsto-\lambda_{\pm}(z)$, we have the two kinds of symmetries.

(i) The first symmetry follows from $z\mapsto z^{*}$. It can be directly verified that $\sigma_{1}\Psi^{*}(x,t,z^{*})\sigma_{1}$ also satisfies the scattering problem and demonstrates identical asymptotic behavior to $\Psi(x,t,z)$ as $x\to\pm\infty$, where

Hence, we have

Combining the (2.18) and (2.22), we have the following symmetry relation

which yields

and

It follows from (2.19) and (2.24) that

From $d_{-}/d_{+}>0$ for $z\in\mathring{\Xi}_{-}$, we see that $s_{22}$ has no zeros on $z\in\mathring{\Xi}_{-}$.

Next, we consider $z\mapsto z^{*}$ for $z\notin\Sigma_{+}$. One can verify that if $\Psi(x,t,z)$ satisfies the scattering problem, then $\sigma_{1}\Psi^{*}(x,t,z^{*})$ also satisfies it. Taking the limit $x\to-\infty$, we have

Similarly, take the limit as $x\to\infty$ to obtain

Using the formula (2.20), we find that

(ii) The second symmetry arises from an alternative selection of $\lambda_{\pm}(z)$, i.e. $\lambda_{\pm}(z)\mapsto-\lambda_{\pm}(z)$. To prevent any confusion caused by notation, we denote

It is worth noting that this choice does not affect the formal independence of the integral equations for the eigenfunctions. If $\Psi_{\pm}(x,t,z,\lambda_{\pm}(z))$ represents the solution to the scattering problem, it follows that $\hat{\Psi}_{\pm}(x,t,z):=\Psi_{\pm}(x,t,z,\hat{\lambda}_{\pm}(z))$ is also a valid solution.

From (2.9) and (2.10), we define the Jost solutions $\hat{\Psi}_{\pm}(x,t,z)$ admit the following asymptotic behavior

Since $\Psi_{\pm}$ and $\hat{\Psi}_{\pm}$ are matrix solutions for the first part of the (2.1) for all $z\in\mathring{\Xi}_{\pm}$, we express

Define $\hat{S}(z,t)$ as the scattering matrix for $\hat{\Psi}_{\pm}$. Following direct calculations, we have

Thus, elements in $S$ are simply related to elements in $\hat{S}$ as

According to the definition of $\lambda_{\pm}$, it is clear that $\lambda_{\pm}$ are defined to be continuous as $z\to\Xi_{\pm}$ from above, i.e.

And, $\lambda_{\pm}^{-}$ as $z\to\Xi_{\pm}$ from below, are given by

Using the definition (2.13) and analytical properties of $v_{-,2}$ and $v_{+,1}$, we see that $\Psi_{-,2}$ is analytic for $z\in\mathbb{C}\backslash\Xi_{-}$ and exhibits continuity towards $\Xi_{-}$ from above, and $\Psi_{+,1}$ is analytic for $z\in\mathbb{C}\backslash\Xi_{+}$ and exhibits continuity towards $\Xi_{+}$ from above. On the other hand, $\Psi_{-,2}$ and $\Psi_{+,1}$ as $z\to\Xi_{\pm}$ from below, are given by

Using the relation (2.32), we have

From above relations, we get the limits of $s_{22}$ as $z\to\Xi_{\pm}$ from below:

Recall that $\Psi_{-}$ is well-defined as $z\to\pm\mu_{-}$ and $\Psi_{+}(x,t,\pm\mu_{-})$ solves the scattering problem, we see immediately that the scattering coefficients $s_{ij}$ are well defined at $z=\pm\mu_{-}$. When $z=\pm\mu_{-}$, $d_{-}(z)=0$. It follows that det$S(\pm\mu_{-},t)=0$ and the columns of $\Psi_{-}(x,t,\pm\mu_{-})$ are linearly dependent. By utilizing the asymptotics of $\Psi_{-}(x,t,\pm\mu_{-})$ as well as Wronskian definitions (2.20), we have

Then in view of the expressions (2.24) and (2.40), we find that

From (2.21), we have

Next, we consider $z\to\pm\mu_{+}$. From the definitions and properties of $\Psi_{\pm}$ as well as the Wronskian relations (2.20), we find that only scattering coefficients $s_{22}$ and $s_{12}$ are defined for $z\in\mathring{\Xi}_{\circ}$. Since $d_{+}$ has a double zero at $z=\pm\mu_{+}$, $s_{22}$ and $s_{12}$ have a double pole as $z\to\pm\mu_{+}$. Specifically, we obtain the limits of $s_{22}$ and $s_{12}$ as $z\to\pm\mu_{+}$:

Notice that

It follows that $|\hat{r}(\pm\mu_{+},t)|=1$.

Following the similar analysis in [33], we conclude that no zeros in the inverse scattering problem for $\mathring{\Xi}_{\circ}$. Specifically,

which shows that $\hat{r}(z,t)$ has no zeros in $\mathring{\Xi}_{\circ}$. In the following, we make the assumption that there exists a finite number of zeros of $s_{22}(z,t)$ lie in $(-\mu_{+},\mu_{+})$. This condition is satisfied if $s_{22}(\pm\mu_{+},t)\neq 0$.

Let $z_{1},\cdots,z_{W}$ represent the zeros of $s_{22}(z,t)$ in $(-\mu_{+},\mu_{+})$. At $z=z_{l}$, we get

where $b_{l}$ is a scalar independent of $x$ and $z$. Now, we define the norming constants

where ^′ indicates the derivative with respect to $z$.

From (2.27), (2.28) and (2.29), one can derive the following relations:

and

which yields