Demonstration of static atomic gravimetry using Kalman filter
Abstract
The measurement precision of the static atomic gravimetry is limited by white Gaussian noise in short term, which costs previous works an inevitable integration to reach the precision demanded. Here, we propose a statistical model based on the quantum projection noise and apply the associated Kalman filter to the waveform estimation in static atomic gravimetry. With the white Gaussian noise significantly removed by the the Kalman-filter formalism, the measurement noise of the gravimetry is reshaped in short term and shows feature that corresponds to random walk. During 200 hours of static measurement of gravity, the atomic gravimeter using Kalman filter demonstrates a sensitivity as good as 0.6 , and highlights a precision of 1.7 at the measuring time of a single sample. The measurement noise achieved is also lower than the quantum projection limit below 30 s.
I INTRODUCTION
Atom interferometry realizes a versatile tool that offers precise and accurate measurement for inertial sensingKasevich ; Geiger , which greatly complements the state of the art classical instrumentsFerier ; Menoret ; Wu ; Bidel1 ; Bidel2 ; McGuirk ; Caldani ; Bertoldi ; Durfee ; Dutta . Among these inertial sensors, gravimetersPeters ; Ferier ; Menoret ; Wu ; Bidel1 ; Bidel2 are of great interest for a wide range of essential applications, from geophysics to fundamental physicsKai .
When measuring the gravity acceleration , the interferometer phase shift to be estimated is time-dependentHu ; Fu ; Gillot ; Ferier ; Menoret , since is a quantity that varies with time due to gravimetric Earth tides, atmospheric and polar motion effects, and other phenomenaNibauer ; Torge ; Rothleitner . Meanwhile, the interferometer phase shift fluctuates due to various measurement noises that comprises vibration noise, phase noise of the Raman lasers, detection noise, and ultimately the quantum projection noiseLegouet . Experimentally, after implementing a combination of vibration compensationHensley ; Merlot ; Legouet , phase lockingSantarelli ; Cacciapuoti , and efficient detection schemeRocco , the residual measurement noise of atomic gravimetry is dominated by white Gaussian noise in short term, and demonstrates characteristic of reduction via integrating in timeHu ; Ferier . For static atomic gravimetry, white Gaussian noise is one of the most challenging obstacles to pursuing boosts in short-term sensitivityLegouet , and costs previous works of precise measurements an integration time scaling from hundreds of secondsHu ; Gillot to hoursFerier ; Fu ; Menoret to reach the precision demanded.
The central statistical problem of estimating the time-varying interferometer phase shift is obviously waveform estimationBrown . And for the waveform estimation problem of the system driven by white Gaussian processes and observed with white Gaussian noise, the Kalman filter (KF) is an optimal estimator with the minimum mean square error, and provides fast and causal estimationKalman1 ; Kalman2 . Its application to atom interferometry promises to benefit applications in inertial sensing. For example, recently, the KF formalism has been experimentally implemented in a hybrid sensor to track and correct the bias drift of a classical accelerometerCheiney . Despite the promising expectations, a completely satisfactory implementation for static atomic gravimetry has not been found yet, since rare works shed light on the statistical model of a quantum sensor.
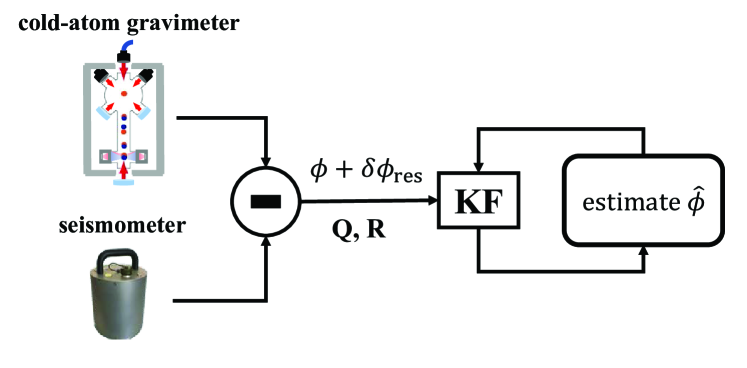
Thus, in this work, we propose a statistical model based on the quantum projection noise and apply the associated KF formalism to the waveform estimation in static atomic gravimetry, obtaining a fast and precise estimation of the time-varying interferometer phase shift. The atomic gravimeter using KF performs the continuous gravity measurement for 200 hours at a seismic station. By comparing the KF estimates to the 725-second integration of the pre-KF signal, the reliability of the KF formalism is confirmed. With the white Gaussian noise significantly removed by the KF, the measurement noise of the gravimetry is reshaped in short term and shows feature that corresponds to random walk. The atomic gravimeter using KF demonstrates a sensitivity as good as 0.6 , and highlights a precision of 1.7 at the measuring time of a single sample. The measurement noise achieved is also lower than the quantum projection limit below 30 s.
II EXPERIMENTAL SETUP
The experimental setup for the atomic gravimeter using KF is presented in Fig. 1. The atomic gravimeter uses a free falling cloud of Rubidium 87 atoms as the test mass. The atoms are initially trapped and cooled by a three dimensional magneto-optical trap to 3.7 K. After state preparation and velocity selection, atoms are selected and participate the interferometry that is composed of a sequence of three Raman pulses separated by two equal time intervals ms. After the interferometer sequence, we acquire transition probabilities from both the top () and each side () of the central interference fringe (3 shots for each phase modulation), and determine the measured interferometer phase shift by the mid-fringe protocolBidel3 . The direction of the momentum transfer of Raman transitions is reversed every 9 shots in order to reject the direction-independent systematic errors. Every 5.7 s, the interferometer cycles 18 shots and outputs one interferometer phase shift that is related to the gravity acceleration via the scale factor
| (1) | |||||
with being the sensitivity function of the interferometerCheinet . After implementing a combination of low phase noise laser system, efficient detection scheme, and seismometer correctionMerlot ; Legouet , the noise on the readout of is limited by the residual measurement noise .
The KF formalism (described below) is then applied to estimate from the readout that fluctuates due to . The KF works in a recursive mode, that is, the previous estimate is used to aid in obtaining the current estimate . In the KF loop shown in Fig. 1, the estimate is obtained by using the th readout to update the prior estimate based on .
As discussed in previous worksLegouet ; Hu ; Ferier , is dominated by white Gaussian noise in short term. The white Gaussian noise in readout limits the short-term sensitivity of atomic gravimetersLegouet , and traditionally costs the gravimetry an integration time scaling from hundreds of secondsHu ; Gillot to hoursFerier ; Fu ; Menoret to retrieve the interferometer phase shift with the precision demanded.
III THE KALMAN FILTER
For the linear system driven by white Gaussian processes and observed with white Gaussian noise, the KF is an optimal estimator with the minimum mean square errorKalman1 ; Kalman2 . The KF formalism provides a fast and causal methodBrown that reshapes the measurement noise in short term and avoids the integration. To achieve the optimal estimate, the KF relies on a statistical model for interferometer phase shift and readout dynamics.
We model the interferometer phase shift with a single-parameter state vector
| (2) |
where is the interferometer phase shift that is related to the gravity acceleration through the scale factor . Though is time-varying due to gravimetric Earth tides, atmospheric and polar motion effects, and other phenomena, the periods of the waveform are much longer than the time interval between two readoutNibauer ; Torge ; Rothleitner . Thus, we reasonably treat the system as cyclostationary.
The discrete-time stochastic equation describing the dynamics of the interferometer phase shift is derived base on the physics fact of the cold-atom interferometry: that is, even in the cyclostationary case, the state vectors at adjacent times are not equal , since the ability of resolving two different quantum phase shifts is ultimately limited by the quantum projection noiseTino . Thus, there is always a phase error between and , and stems from the quantum projection noise, which is the ultimate physical limit to atom interferometry below all the technical noise contributionsLegouet . Here, we straightforwardly describe the state by the discrete-time stochastic equation
| (3) |
where describes the white Gaussian noise contribution to the state, with zero mean and variance . Here, is the variance of the quantum projection noise and is theoretically predicted according to Ref. Tino .
Meanwhile, the readout of the interferometer phase shift is subjected to both the residual technical noises and quantum projection noise. To account for this fact, we describe the readout by the discrete-time stochastic equation
| (4) |
where is the measurement vector describing the readout process, and represents the white Gaussian noise of each readout, with zero mean and variance . The variance is experimentally determined from a 10-minute sample of the pre-KF readout.
The KF works in a recursive mode. In the KF loop, the estimate and the associated error covariance matrix are constructed in two steps. In the propagation step, and are predicted conditioned on the previous posterior estimate and its covariance as follows
| (5) |
where the ”super minus” indicates the prior estimate deduced according to statistical model of the system dynamics. Then, in the update step, the readout is used to improve and , the posterior estimate and its covariance are deduced according to
| (6) |
where the Kalman gain that minimizes the mean square error is computed as
| (7) |
The KF loop is initialized with and , according to our prior knowledge about the system. Here, is experimentally determined by a 10-minute averaging of the pre-KF readout.
IV PERFORMANCE
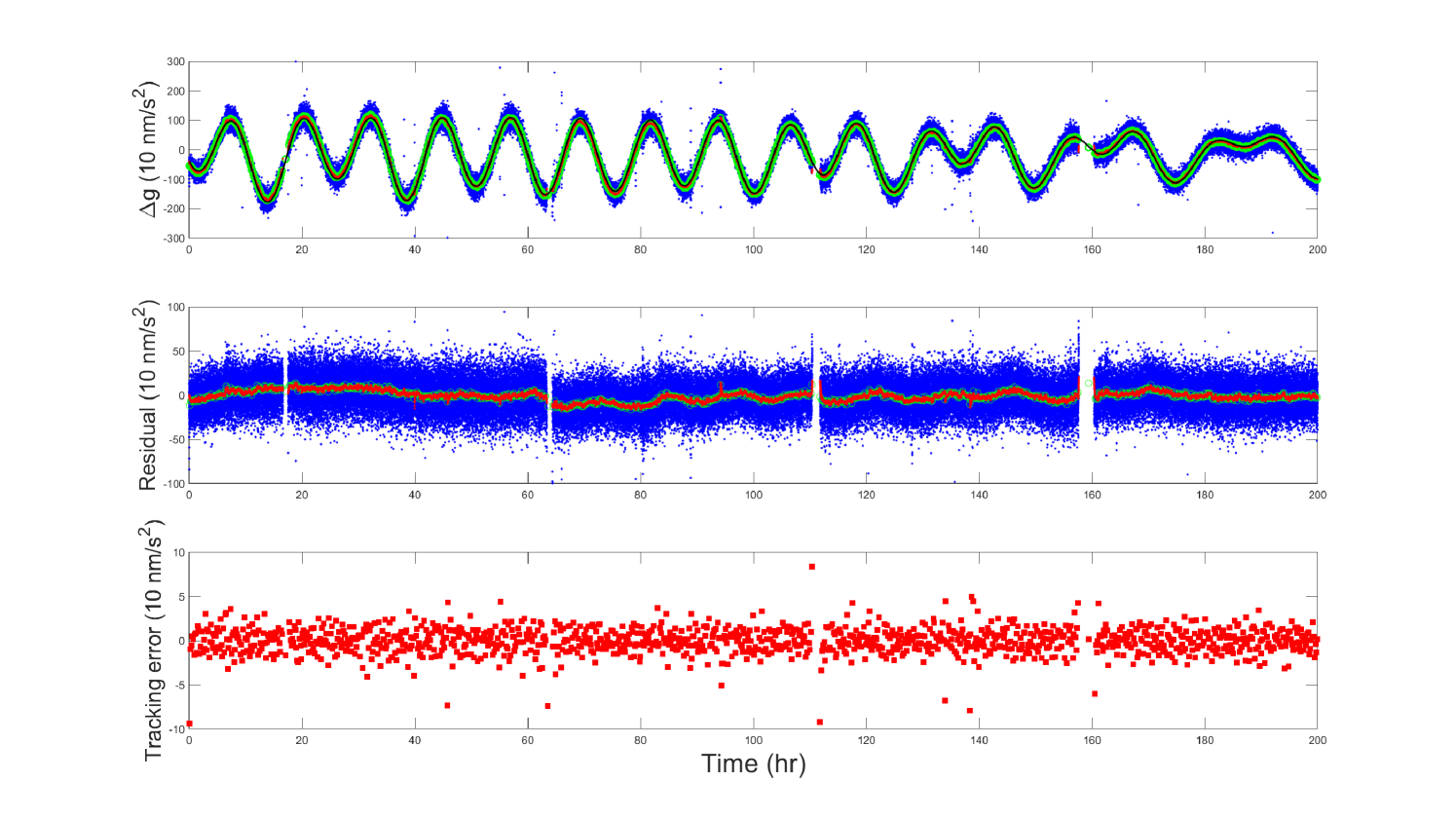
As shown in Fig. 2, at a seismic station, the experimental setup described in Sec. II performed the continuous measurement of the local gravity for 200 hours, and the experiment data of the gravity acceleration were derived from the interferometer phase shift through . These data were chosen since they consisted of a fairly long record with sufficient quality. To test the robustness of the Kalman estimator, no preprocessing was necessary to remove gaps in the time series. The gaps are due to temporary failures of the power supply. These failures did not damage the gravimeter, and a remote restart was possible once electrical power was restored. Both the pre-KF readout (blue) and the KF estimates (red) agree well with the gravimetric Earth tides (black) predicted theoretically with an inelastic non-hydrostatic Earth modelDehant . We also obtain the corresponding residual acceleration by subtracting the gravity signal from the theoretical prediction of the gravimetric Earth tides. The residual acceleration clearly shows that though the gaps exist in the gravimeter readings, their effects on the Kalman estimator are not significant. Note that the true gravity changes measured by the setup are more complicated than the theoretical prediction of the gravimetric Earth tides, and is usually monitored by superconducting gravimeters during the comparisonWuS . Here, without superconducting gravimeters, a 725-second integration (green) of the pre-KF readout serves as the ”true” time-varing gravity signal, as is the precision limit we can reach via the pre-KF gravimetry (see Fig. 3). To evaluate the reliability of the interferometer phase shift tracking, we compare the KF estimates directly to the 725-second integration of the pre-KF readout. The rms value of the tracking error (red square) is , which is in good agreement with the the precision limit of the pre-KF gravimetry . Obviously, the measurement noise of the pre-KF gravimetry plays a dominant role in the tracking error. And the result shows that the precision of the interferometer phase shift tracking using KF is significantly better than the precision limit of the pre-KF gravimetry.
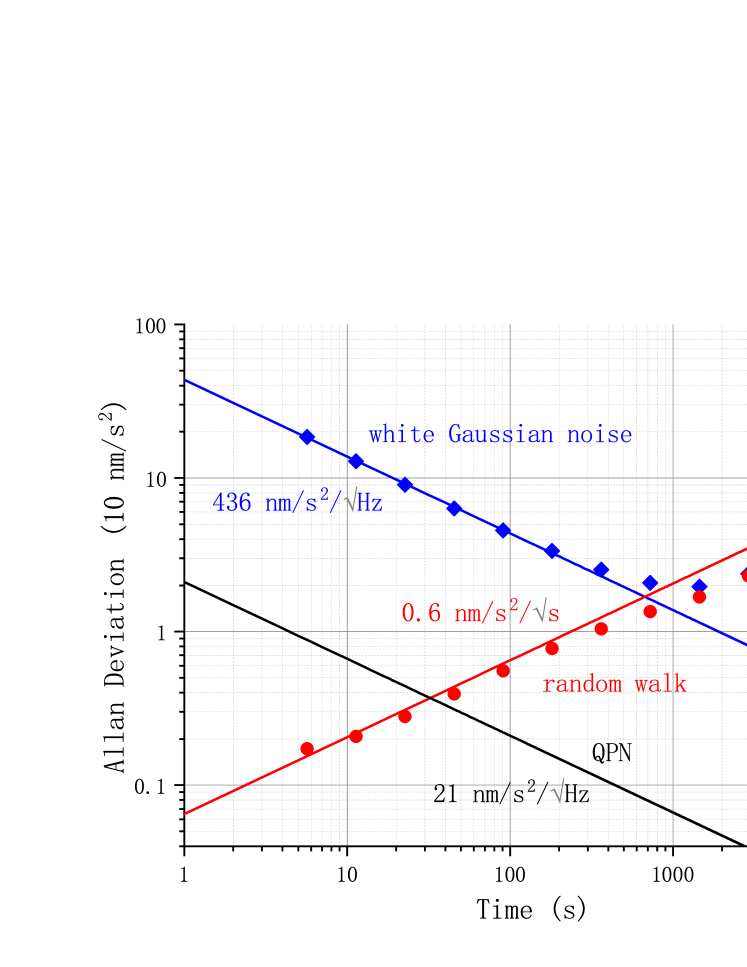
The Allan deviation (ADev) of the residual acceleration is then calculated to characterize the short-term sensitivity and the long-term stability of the pre-KF and post-KF gravimetry. As shown in Fig. 3, the sensitivity of the pre-KF gravimetry (blue) follows 436 for up to 1000 s. The measurement noise is dominated by white Gaussian noise in this regime, and demonstrates characteristic of reduction via integrating in time. Beyond 1000 s, the stability of the pre-KF gravimetry is degraded due to phase errors that accumulate with the random walk. However, we find that the KF significantly reshapes the measurement noise by removing the white Gaussian noise in short term. The measurement noise of the post-KF gravimetry (red) then shows integrating that corresponds to random walk, and the sensitivity follows 0.6 for up to more than s. Though not affecting the long-term stability, the KF does greatly improve the measurement precision in short term and highlights a precision of 1.7 at the measuring time of a single sample (5.7 s). Moreover, the measurement noise of the post-KF gravimetry dives under the quantum projection limit (black) below 30 s, which means that the KF could also be a potential method for approaching or beating the standard quantum limit in short term. Here, the sensitivity limit due to the quantum projection noise is theoretically calculated to be 21 for this setup (with contrast ).
V CONCLUSION
In conclusion, we propose a statistical model based on the quantum projection noise and apply the associated KF formalism to the waveform estimation in static atomic gravimetry, obtaining a fast and precise estimation of the time-varying interferometer phase shift. The atomic gravimeter using KF performs the continuous gravity measurement for 200 hours at a seismic station. By comparing the KF estimates to the 725-second integration of the pre-KF signal, the reliability of the KF formalism is confirmed. With the white Gaussian noise significantly removed by the KF, the measurement noise of the post-KF gravimetry is reshaped in short term and shows integrating that corresponds to random walk. The atomic gravimeter using KF demonstrates a sensitivity as good as 0.6 , and highlights a precision of 1.7 at the measuring time of a single sample, which costs previous works an integration time scaling from hundreds of seconds to hours to reach.
The KF estimation demonstrated here increases the measurement precision of the static atomic gravimetry in short term, and makes the gravimetry ”the faster, the more precise”. The demonstration would be of interest for those applications involving static measurements of gravity, such as fundamental physics, geophysics, or metrologyKai . Moreover, as this work achieves measurement noise lower than the quantum projection limit below 30 s, the KF could also be a potential method for approaching or beating the standard quantum limit in short term.
Acknowledgments
We thanks Prof. Shuai Chen and his team for the work in the early stage. This work is funded by the Youth Program of National Natural Science Foundation of China (Grant No. 11804019), and also partially supported by the National Key R&D Program of China (Grant No. 2016YFA0301601), National Natural Science Foundation of China (Grant No. 11674301), Anhui Initiative in Quantum Information Technologies (Grant No. AHY120000), and Shanghai Municipal Science and Technology Major Project (Grant No. 2019SHZDZX01).
References
- (1) M. Kasevich and S. Chu, Phys. Rev. Lett. 67, 181-184 (1991)
- (2) R. Geiger, A. Landragin, S. Merlet, and F. Pereira Dos Santos, AVS Quantum Sci. 2, 024702 (2020)
- (3) C. Freier, M. Hauth, V. Schkolnik, B. Leykauf, M. Schilling, H. Wziontek, H.-G. Scherneck, J. Müller and A. Peters, J. Phys.: Conf. Ser. 723, 012050 (2016)
- (4) V. Ménoret, P. Vermeulen, N. Le Moigne, S. Bonvalot, P. Bouyer, A. Landragin, and B. Desruelle, Sci. Rep. 8, 12300 (2018)
- (5) X. Wu, Z. Pagel, B. S. Malek, T. H. Nguyen, F. Zi, D. S. Scheirer, and H. Muller, Sci. Adv. 5, 9 (2019)
- (6) Y. Bidel, N. Zahzam, C. Blanchard, A. Bonnin, M. Cadoret, A. Bresson, D. Rouxel, and M. F. Lequentrec-Lalancette, Nat. Commun. 9, 627 (2018)
- (7) Y. Bidel, N. Zahzam, A. Bresson, C. Blanchard, M. Cadoret, A. V. Olesen, and R. Forsberg, J. Geod. 94, 20 (2020)
- (8) J. M. McGuirk, G. T. Foster, J. B. Fixler, M. J. Snadden, and M. A. Kasevich, Phys. Rev. A 65, 033608 (2002)
- (9) R. Caldani, K. X. Weng, S. Merlet, and F. Pereira Dos Santos, Phys. Rev. A 99, 033601 (2019)
- (10) A. Bertoldi, G. Lamporesi, L. Cacciapuoti, M. de Angelis, M. Fattori, T. Petelski, A. Peters, M. Prevedelli, J. Stuhler, and G. M. Tino, Eur. Phys. J. D 40, 271 (2006)
- (11) D. S. Durfee, Y. K. Shaham, and M. A. Kasevich, Phys. Rev. Lett. 97, 240801 (2006)
- (12) I. Dutta, D. Savoie, B. Fang, B. Venon, C. L. Garrido Alzar, R. Geiger, and A. Landragin, Phys. Rev. Lett. 116, 183003 (2016)
- (13) A. Peters, K. Y. Chung, and S. Chu, Metrologia 38, 25 (2001)
- (14) Kai Bongs, M. Holynski, J. Vovrosh, P. Bouyer, G. Condon, E. Rasel, C. Schubert, W. P. Schleich, and A. Roura, Nat. Rev. Phys. 1, 731-739 (2019)
- (15) Z.-K. Hu, B.-L. Sun, X.-C. Duan, M.-K. Zhou, L.-L. Chen, Su Zhan, Q.-Z. Zhang, and Jun Luo, Phys. Rev. A 88, 043610 (2013)
- (16) Z. Fu, B. Wu, B. Cheng, Y. Zhou, K. Weng, D. Zhu, Z. Wang, and Q. Lin, Metrologia 56, 025001 (2019)
- (17) P. Gillot, O. Francis, A. Landragin, F. Pereira Dos Santos, and S Merlet, Metrologia 51, L15-L17 (2014)
- (18) T. Nibauer, G. Sasagawa, J. Faller, R. Hilt, and F. Kopping, Metrologia 32, 159-180 (1995)
- (19) W. Torge, Gravimetry (Walter De Gruyter Inc., New York, 1989)
- (20) C. Rothleitner, Ultra-high Precision, Absolute, Earth Gravity Measurements, PhD Thesis, Friedrich-Alexander-Universität Erlangen-Nünberg, 2008
- (21) J. Le gouët, T. E. Mehlstäubler, J. Kim, et al., Appl Phys B 92, 133-144 (2008)
- (22) J. Hensley, A. Peters, and S. Chu, Rev. Sci. Instrum. 70, 2735 (1999)
- (23) S. Merlet, J. Le gouët, Q. Bodart, A. Clairon, A. Landragin, F. P. D. Santos, and P. Rouchon, Metrologia 46, 87 (2009)
- (24) G. Santarelli, A. Clairon, S. N. Lea, and G. M. Tino, Opt. Commn. 104, 339-344 (1994)
- (25) L. Cacciapuoti, M. de Angelis, M. Fattori, G. Lamporesi, T. Petelski, M. Prevedelli, J. Stuhler, and G. M. Tino, Rev. Sci. Instrum. 76, 053111 (2005)
- (26) E. Rocco, R. Palmer, T. Valenzuela, V. Boyer, A. Freise and K. Bongs, New J. Phys. 16, 093046 (2014)
- (27) R. Brown and P. Hwang, Introduction to Random Signals and Applied Kalman Filtering (John Wiley & Sons, Inc., Hoboken, NJ, 2012)
- (28) R. Kalman, J. Basic Eng. 82, 35 (1960)
- (29) R. Kalman and R. Bucy, J. Basic Eng. 83, 95 (1961)
- (30) P. Cheiney, L. Fouche, S. Templier, F. Napolitano, B. Battelier, P. Bouyer, and B. Barrett, Phys. Rev. Appl. 10, 034030 (2018)
- (31) Y. Bidel, O. Carraz, R. Charrière, M. Cadoret, N. Zahzam, and A. Bresson, Appl. Phys. Lett. 102, 144107 (2013)
- (32) P. Cheinet, B. Canuel, F. Pereira Dos Santos, A. Gauguet, F. Yver-Leduc, and A. Landragin, IEEE Trans on Instrumn and Meas. 57, 1141 (2008)
- (33) W. M. Itano, J. C. Bergquist, J. J. Bollinger, J. M. Gilligan, D. J. Heinzen, F. L. Moore, M. G. Raizen, and D. J. Wineland, Phys. Rev. A 47, 3554-3570 (1993)
- (34) V. Dehant, P. Defraigne, and J. M. Wahr, J. Geophys. Res.: Solid Earth 104, 1035 (1999)
- (35) S. Wu, et al., Metrologia 57, 07002 (2020)