Denoised Self-Augmented Learning for Social Recommendation
Abstract
Social recommendation is gaining increasing attention in various online applications, including e-commerce and online streaming, where social information is leveraged to improve user-item interaction modeling. Recently, Self-Supervised Learning (SSL) has proven to be remarkably effective in addressing data sparsity through augmented learning tasks. Inspired by this, researchers have attempted to incorporate SSL into social recommendation by supplementing the primary supervised task with social-aware self-supervised signals. However, social information can be unavoidably noisy in characterizing user preferences due to the ubiquitous presence of interest-irrelevant social connections, such as colleagues or classmates who do not share many common interests. To address this challenge, we propose a novel social recommender called the Denoised Self-Augmented Learning paradigm (DSL). Our model not only preserves helpful social relations to enhance user-item interaction modeling but also enables personalized cross-view knowledge transfer through adaptive semantic alignment in embedding space. Our experimental results on various recommendation benchmarks confirm the superiority of our DSL over state-of-the-art methods. We release our model implementation at: https://github.com/HKUDS/DSL.
1 Introduction
Social recommendation is a widely-used technique to improve the quality of recommender systems by incorporating social information into user preference learning Yu et al. (2021a). To accomplish this, various neural network techniques have been developed to encode social-aware user preferences for recommendation. Currently, the most advanced social recommendation methods are built using Graph Neural Networks (GNNs) for recursive message passing, which enables the capture of high-order correlations Fan et al. (2019); Wu et al. (2019); Song et al. (2019). In these architectures, user representations are refined by integrating information from both social and interaction neighbors.
While supervised GNN-enhanced models have achieved remarkable performance in social recommendation, they require a large amount of supervised labels to generate accurate user representations. In practical social recommendation scenarios, however, user-item interaction data is often very sparse Wei et al. (2022a); Chen et al. (2023). This label sparsity severely limits the representation power of deep social recommenders and hinders their ability to reach their full potential. Recently, Self-Supervised Learning (SSL) has gained success due to its ability to avoid heavy reliance on observed label data in various domains, e.g., computer vision He et al. (2020a), natural language processing Liu and Liu (2021), and graph representation learning Zhu et al. (2021).
Motivated by the limitations of supervised GNN-enhanced models, recent attempts have adopted the self-supervised learning framework Yu et al. (2021a). These approach introduce an auxiliary learning task to supplement the supervised main task for data augmentation. For example, MHCN Yu et al. (2021b) uses a hypergraph-enhanced self-supervised learning framework to improve global relation learning in social recommender systems. Additionally, SMIN Long et al. (2021) constructs metapath-guided node connections to explore the isomorphic transformation property of graph topology with augmented self-supervision signals.
Despite the decent performance of self-supervised learning, we argue that the SSL-based augmentation is severely hindered by noisy social relations when enhancing the representation learning of complex user preferences. While observed user-user social ties have the potential to capture social influence on user-item interaction behaviors, the model’s performance can significantly degrade when trained on social-aware collaborative graphs with noisy social information. For instance, people may establish social connections with colleagues, classmates, or family members, but they may not share many common interests with each other Liu et al. (2019); Epasto and Perozzi (2019). Therefore, these noisy social influences may not align with user preferences in real-life recommendation scenarios. In most existing solutions, information aggregated from noisy social neighbors may mislead graph message passing and self-supervised learning, resulting in sub-optimal recommendation performance.
To address the limitations mentioned earlier, we propose the Denoised Self-Augmented Learning (DSL) paradigm for social recommender systems. Our approach leverages social information to better characterize user preferences with noise-resistant self-supervised learning, aimed at pursuing cross-view alignment. Firstly, we develop a dual-view graph neural network to encode latent representations over both user social and interaction graphs. Then, to mitigate the bias of social relations for recommendation, we design a denoising module to enhance the integrated social-aware self-supervised learning task. This module identifies unreliable user-wise connections with respect to their interaction patterns. Our DSL is aware of the interaction commonality between users and can automate the social effect denoising process with adaptive user representation alignment. By doing so, the social-aware uniformity is well preserved in the learned user embeddings by alleviating the impact of noisy social information in our recommender.
Key contributions of this work are summarized as follows:
-
•
In this work, we investigate denoised self-augmented learning for social recommendation, effectively reducing the impact of noisy social relations on the representation of socially-aware collaborative signals.
-
•
We propose DSL, which enables denoised cross-view alignment between the encoded embeddings from social and interaction views. The denoising module assigns reliability weights to useful social relations to encode user preference, endowing our DSL with the capability of generating adaptive self-supervised signals.
-
•
We instantiate DSL for social recommendation on three real-world datasets. Experimental results show that our method provides more accurate recommendations and superior performance in dealing with noisy and sparse data, compared with various state-of-the-art solutions.
2 Preliminaries and Related Work
2.1 Social-aware Recommendation
We denote the sets of users and items as and , respectively, where and represent the number of users and items. The user-item interaction data is represented by an interaction graph , where user-item connection edges are generated when user interacts with item . To incorporate social context into the recommender system, we define a user social graph to contain user-wise social connections. Social recommender systems aim to learn a model from both the user-item interaction graph and the user-user social graph , encoding user interests to make accurate recommendations.
In recent years, several neural network techniques have been proposed to solve the social recommendation problem. For instance, attention mechanisms have been used to differentiate social influence among users with learned attentional weights, as seen in EATNN Chen et al. (2019b) and SAMN Chen et al. (2019a). Many GNN-based social recommender systems have been developed to jointly model user-user and user-item graphs via message passing, leveraging the effectiveness of high-order relation encoding with graph neural networks Wang et al. (2019). Examples include GraphRec Fan et al. (2019), DiffNet Wu et al. (2019), and FeSoG Liu et al. (2022). Some recent attempts have leveraged self-supervised learning to enhance social recommendation with auxiliary self-supervision signals, such as MHCN Yu et al. (2021b) and SMIN Long et al. (2021). However, their representation learning abilities are limited by social relation noise, which leads to biased models.
2.2 Self-Supervised Recommender Systems
Self-supervised learning has recently gained attention in various recommendation tasks. Supervised contrastive loss has been shown to benefit graph collaborative filtering with effective data augmentation Wu et al. (2021); Cai et al. (2023). For sequential recommender systems, self-supervised pre-training Zhou et al. (2020) and imitation Yuan et al. (2022) have been introduced to enhance sequence modeling. Researchers have also brought the benefits of self-supervised learning to multi-interest/multi-behavior recommender systems, as seen in Re4 Zhang et al. (2022) and CML Wei et al. (2022b). Our method advances this research by proposing a novel unbiased self-supervised learning paradigm to denoise social relation modeling in social recommender systems.
3 Methodology
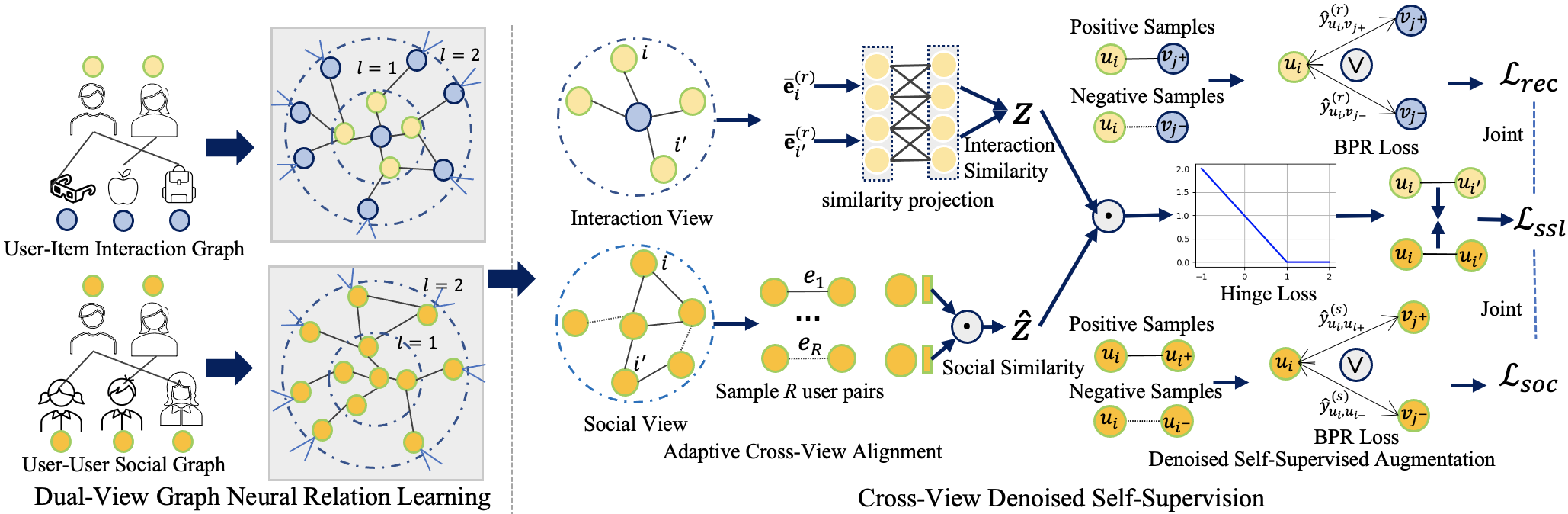
In this section, we present our DSL model with technical details. The model architecture is illustrated in Figure 1.
3.1 Dual-View Graph Neural Relation Learning
With the initialized id-corresponding embeddings, our DSL first employs a dual-view graph neural network to capture high-order collaborative relations for both user-item interactions and user-user social ties. Inspired by the effectiveness of lightweight GCN-enhanced collaborative filtering paradigms He et al. (2020b); Chen et al. (2020), DSL is configured with a simplified graph neural network, which is:
| (1) |
The above equation shows the iterative information propagation scheme of our GCN over the user-item interaction graph. Here, denote the embeddings of users and items after iterations of user-item relation modeling. is initialized by stacking the initial user embedding matrix and the item embedding matrix . denotes the identity matrix for enabling self-loop. denotes the Laplacian matrix of the user-item interaction graph Wang et al. (2019).
| (4) |
denotes the user-item interaction matrix, and 0 refers to all-zero matrices. The bidirectional adjacent matrix of the user-item interaction view is multiplied by its corresponding diagonal degree matrix for normalization.
To encode user-wise social relations in our recommender, we also apply the lightweight GCN to the user social graph . Specifically, our social view GNN takes the initial users’ id-corresponding embeddings as input by setting . The user embeddings are generated by cross-layer passing:
| (5) |
Here, encodes the user-wise social relations, and denote the corresponding diagonal degree matrix and the normalized Laplacian matrix for the social view. are the users’ social embeddings in the -th and -th graph neural iteration, respectively.
Embedding Aggregation.
To aggregate the embeddings encoded from different orders in and , DSL adopts mean-pooling operators for both the interaction and social views.
| (6) |
Here, is the maximum number of graph iterations. With our dual-view GNN, we encode view-specific relations for user interaction and social influence in our model.
3.2 Cross-View Denoised Self-Supervision
In our recommender, the learned user-item relations and user-wise dependencies are complementary to each other. To integrate both relational contextual signals, we design a cross-view denoised self-supervised learning paradigm that can alleviate the noisy effects of transferring social knowledge into user-item interaction modeling. In real-life scenarios, passively-built social relations, such as colleagues or classmates, may not bring much influence to user interaction preference due to their diverse shopping tastes. Blindly relying on such irrelevant social ties to infer users’ interests could damage the performance of social recommendation models. To address this issue, we filter out the noisy social influence between dissimilar users with respect to their interaction preference for unbiased self-supervision.
Adaptive Cross-View Alignment.
In our DSL, we incorporate the cross-view denoising task to supplement the main learning task with auxiliary self-supervision signals. The learned user interaction patterns guide the social relation denoising module to filter out misleading embedding propagation based on observed social connections. Specifically, the interaction similarity between the user pair (, ) is generated by , given the user embeddings (, ) learned from our interaction GNN. Similarly, user social similarity can be obtained by , based on user representations (, ) encoded from our social GNN. To alleviate the semantic gap between interaction view and social view, we design a learnable similarity projection function to map interaction semantics into a latent embedding space for cross-view alignment, as follows:
| (7) |
where and denote the sigmoid and LeakyReLU activation functions, respectively. Our designed parameterized projection function consists of as learnable parameters, enabling adaptive alignment between social and interaction views.
Denoised Self-Supervised Augmentation.
To incorporate denoised social influence to improve recommendation quality, we design a self-supervised learning task for cross-view alignment with augmented embedding regularization. Specifically, the cross-view alignment loss function is:
| (8) |
The user pair () is individually sampled from user set . With the above self-supervised learning objective, the integrated user relation prediction task will be guided based on the self-supervised signals for social influence denoising. Dy doing so, the noisy social connections between users with dissimilar preference, which contradicts with the target recommendation task will result in distinguishable user representations for recommendation enhancement.
3.3 Multi-Task Model Optimization
The learning process of our DSL involves multi-task training for model optimization. The augmented self-supervised learning tasks are integrated with the main recommendation optimized loss to model denoised social-aware user preferences. Given the encoded user and item embeddings, we predict user-item () and user-user () relations as:
| (9) |
where represents the likelihood of user interacting with item from the interaction view, while indicates the probability of and being socially connected. Given these definitions, we minimize the following BPR loss functions Rendle et al. (2009) for optimization:
| (10) |
where and denote the sampled positive and negative item for user . and are sampled from ’s socially-connected and unconnected users, respectively. By integrating self-supervised learning objectives with weight parameter , the joint optimized loss is given as:
| (11) |
3.4 In-Depth Analysis of DSL
In this section, our aim is to answer the question: How does our model enable adaptive and efficient self-supervised learning? We provide analysis to further understand our model.
Adaptive Self-Supervised Learning.
In most existing contrastive learning (CL) approaches, auxiliary SSL signals are generated to address the issue of sparse supervision labels. Following the mutual information maximization (Infomax) principle, these approaches maximize the agreement between positive samples while pushing negative pairs away in the embedding space, as shown below with derived gradients.
| (12) |
The first term in the equation maximizes the similarity between positive pairs ( and ) with the same strength. Negative pairs ( and ) with higher similarity are pushed away with greater strength, while negative pairs with lower similarity are pushed away with lesser strength. For simplicity, we have omitted the vector normalization and the temperature coefficient in the above-presented InfoNCE loss.
In comparison, our cross-view denoising SSL schema aims to maximize the similarity between sampled user pairs adaptively, based on the labels . The non-zero gradients of our denoising SSL over are shown below:
| (13) |
The learnable reflects the common preference between user and , which adaptively controls the strength of our self-supervised regularization. This enables us to filter out noisy signals in the observed social connections, and supercharge our SSL paradigm with adaptive data augmentation by transferring knowledge across different semantic views.
Efficient SSL.
Our DSL model adopts a lightweight graph convolutional network (GCN) as the graph relation encoder, with a complexity of . The cross-view denoised self-supervised learning conducts pairwise node-wise relationships, which takes time complexity, where represents the batch size. In contrast, most existing vanilla InfoNCE-based contrastive learning methods calculate relations between a batch of nodes and all other nodes, resulting in an operation complexity of .
4 Evaluation
| Data | Ciao | Epinions | Yelp |
|---|---|---|---|
| # Users | 6,672 | 11,111 | 161,305 |
| # Items | 98,875 | 190,774 | 114,852 |
| # Interactions | 198,181 | 247,591 | 1,118,645 |
| Interaction Density | 0.0300% | 0.0117% | 0.0060% |
| # Social Ties | 109,503 | 203,989 | 2,142,242 |
We conduct extensive experiments to evaluate the effectiveness of our DSL by answering the following research questions: RQ1: Does DSL outperform state-of-the-art recommender systems? RQ2: How do different components affect the performance of DSL? RQ3: Is DSL robust enough to handle noisy and sparse data in social recommendation? RQ4: How efficient is DSL compared to alternative methods?
4.1 Experimental Settings
Dataset.
We conduct experiments on three benchmark datasets collected from the Ciao, Epinions, and Yelp online platforms, where social connections can be established among users in addition to their observed implicit feedback (e.g., rating, click) over different items. Table 1 lists the detailed statistical information of the experimented datasets.
Metrics.
We use Hit Ratio (HR)@N and Normalized Discounted Cumulative Gain (NDCG)@N as evaluation metrics, where is set to 10 by default. We adopt a leave-one-out strategy, following similar settings as in Long et al. (2021).
| Dataset | Metrics | PMF | TrustMF | DiffNet | DGRec | EATNN | NGCF+ | MHCN | KCGN | SMIN | DSL | %Imp |
| Ciao | HR | 0.4223 | 0.4492 | 0.5544 | 0.4658 | 0.4255 | 0.5629 | 0.5950 | 0.5785 | 0.5852 | 0.6374 | 26.0 |
| NDCG | 0.2464 | 0.2520 | 0.3167 | 0.2401 | 0.2525 | 0.3429 | 0.3805 | 0.3552 | 0.3687 | 0.4065 | 37.2 | |
| Epinions | HR | 0.1686 | 0.1769 | 0.2182 | 0.2055 | 0.1576 | 0.2969 | 0.3507 | 0.3122 | 0.3159 | 0.3983 | 76.9 |
| NDCG | 0.0968 | 0.0842 | 0.1162 | 0.0908 | 0.0794 | 0.1582 | 0.1926 | 0.1721 | 0.1867 | 0.2290 | 96.2 | |
| Yelp | HR | 0.7554 | 0.7791 | 0.8031 | 0.7950 | 0.8031 | 0.8265 | 0.8571 | 0.8484 | 0.8478 | 0.8923 | 10.1 |
| NDCG | 0.5165 | 0.5424 | 0.5670 | 0.5593 | 0.5560 | 0.5854 | 0.6310 | 0.6028 | 0.5993 | 0.6599 | 15.5 |
4.2 Baseline Methods
We evaluate the performance of DSL by comparing it with 10 baselines from different research lines for comprehensive evaluation, including: i) MF-based recommendation approaches (i.e., PMF, TrustMF); ii) attentional social recommenders (i.e., EATNN); iii) GNN-enhanced social recommendation methods (i.e., DiffNet, DGRec, NGCF+); and iv) self-supervised social recommendation models (i.e., MHCN, KCGN, SMIN, DcRec). Details are provided as follows:
-
•
PMF Mnih and Salakhutdinov (2007): is a probabilistic approach that uses matrix factorization technique to factorize users and items into latent vectors for representations.
-
•
TrustMF Yang et al. (2016): This method incorporates trust relations between users into matrix factorization as social information to improve recommendation performance.
-
•
EATNN Chen et al. (2019b): It is an adaptive transfer learning model built upon attention mechanisms to aggregate information from both user interactions and social ties.
-
•
DiffNet Wu et al. (2019): This is a deep influence propagation architecture to recursively update users’ embeddings with social influence diffusion components.
-
•
DGRec Song et al. (2019): This social recommender leverages a graph attention network to jointly model the dynamic behavioral patterns of users and social influence.
-
•
NGCF+ Wang et al. (2019): This GNN-enhanced collaborative filtering approach performs message passing over a social-aware user-item relation graph.
-
•
MHCN Yu et al. (2021b): This model proposes a multi-channel hypergraph convolutional network to enhance social recommendation by considering high-order relations.
-
•
KCGN Huang et al. (2021): It improves social recommendation by integrating item inter-dependent knowledge with social influence through a multi-task learning framework.
-
•
SMIN Long et al. (2021): This model incorporates a metapath-guided heterogeneous graph learning task into social recommendation, utilizing self-supervised signals based on mutual information maximization.
Implementation Details.
We implement our DSL using PyTorch and optimize parameter inference with Adam. During training, we use a learning rate range of and a decay ratio of per epoch. The batch size is selected from and the hidden dimensionality is tuned from . We search for the optimal number of information propagation layers in our graph neural architecture from . The regularization weights and are selected from and , respectively. The weight for weight-decay regularization is tuned from .
4.3 Overall Performance Comparison (RQ1)
Table 2 and Table 4 demonstrate that our DSL framework consistently outperforms all baselines on various datasets, providing evidence of its effectiveness. Based on our results, we make the following observations.
-
•
Our results demonstrate that DSL achieves encouraging improvements on datasets with diverse characteristics, such as varying interaction densities. Specifically, on the Ciao and Epinions datasets, DSL achieves an average improvement of 26.0% and 76.0% over baselines, respectively. This validates the importance of addressing noise issues in social information incorporation, which can effectively debias user representations and boost recommendation performance.
-
•
Methods incorporating self-supervised augmentation consistently outperform other baselines, highlighting the importance of exploring self-supervision signals from unlabeled data to alleviate sparsity issues in social recommendation. Our DSL outperforms other methods, suggesting that denoising social relation modeling in socially-aware recommender systems can benefit the design of more helpful self-supervision information. In MHCN and SMIN, mutual information is maximized to reach agreement between socially-connected users under a self-supervised learning framework. However, blindly generating augmented self-supervision labels from noisy social connections can align embeddings of connected users, diluting their true preferences. In contrast, our DSL can mitigate the effects of false positives for socially-dependent users.
-
•
GNN-enhanced social recommenders, e.g., DiffNet and DGRec, outperform vanilla attentive methods like EATNN, highlighting the effectiveness of modeling high-order connectivity in social-aware collaborative relationships. This observation aligns with the conclusion that incorporating high-hop information fusion is beneficial for embedding learning in CF signals. However, aggregating irrelevant social information via GNNs can lead to unwanted embedding propagation and weaken model representation ability.
| Data | Ciao | Epinions | Yelp | |||
| Metrics | HR | NDCG | HR | NDCG | HR | NDCG |
| DSL-d | 0.615 | 0.399 | 0.354 | 0.207 | 0.887 | 0.658 |
| DSL-s | 0.594 | 0.374 | 0.327 | 0.169 | 0.839 | 0.621 |
| DSL-c | 0.603 | 0.388 | 0.336 | 0.199 | 0.889 | 0.662 |
| DSL | 0.637 | 0.406 | 0.398 | 0.229 | 0.892 | 0.659 |
| Metrics | PMF | TrustMF | DiffNet | DGRec | EATNN | NGCF+ | MHCN | KCGN | SMIN | DSL | %Imp |
| HR@5 | 0.3032 | 0.3133 | 0.3963 | 0.3035 | 0.3259 | 0.4263 | 0.4762 | 0.4361 | 0.4565 | 0.5007 | 35.2 |
| NDCG@5 | 0.2071 | 0.2073 | 0.2650 | 0.1872 | 0.2342 | 0.3020 | 0.3479 | 0.3094 | 0.3298 | 0.3626 | 43.0 |
| HR@10 | 0.4223 | 0.4492 | 0.5544 | 0.4658 | 0.4255 | 0.5629 | 0.5950 | 0.5785 | 0.5852 | 0.6374 | 26.0 |
| NDCG@10 | 0.2464 | 0.2520 | 0.3167 | 0.2401 | 0.2525 | 0.3429 | 0.3805 | 0.3552 | 0.3687 | 0.4065 | 37.2 |
| HR@20 | 0.5565 | 0.6133 | 0.6973 | 0.6193 | 0.5309 | 0.7032 | 0.7418 | 0.7191 | 0.7000 | 0.7683 | 18.6 |
| NDCG@20 | 0.2799 | 0.3020 | 0.3514 | 0.2746 | 0.2838 | 0.3675 | 0.4241 | 0.3844 | 0.3780 | 0.4353 | 31.6 |
4.4 Impact Study of Different Components (RQ2)
In this section, we examine the effects of component-wise ablation and how hyperparameters influence performance.
Model Ablation Study.
To investigate the essential role of our denoised self-supervised learning paradigm in improving performance, we perform an ablation study of key model components. Specifically, we compare our DSL with the following ablated variants: (1) “DSL-d”: disabling cross-view denoised self-supervised learning for mitigating the noisy effects of social-aware collaborative filtering, (2) “DSL-s”: removing social-aware self-supervised augmentation and directly incorporating social user embeddings into user-item interaction prediction, and (3) “DSL-c”: replacing denoised cross-view alignment with contrastive learning to reach agreement for integrating social and interaction views. Results are reported in Table 3. From our results, we observe that our DSL outperforms other variants in most evaluation cases. Based on this, we draw the following key conclusions:
-
•
Comparing DSL with “DSL-d”, the significant performance improvement suggests that social-aware collaborative relation learning is affected by the noise problem when directly incorporating social information.
-
•
The recommendation performance further drops in variant “DSL-s” without the auxiliary learning task of social-aware relation prediction, indicating that incorporating self-supervised signals from user-wise social influence is helpful for enhancing collaborative relational learning.
-
•
The contrastive learning used in variant “DSL-c” attempts to align the social and interaction views, but the irrelevant social connections can mislead the contrastive self-supervision for data augmentation. This observation supports our assumption that social information is inherently noisy for characterizing user preferences.
Parameter Effect Study.
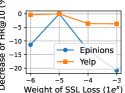
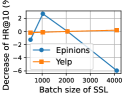
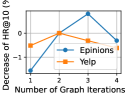
Exploring the influence of key hyperparameters on DSL’s performance, including SSL loss weight, batch size, and the number of graph propagation layers, would be interesting. The results are shown in Figure 2, where the y-axis represents the performance variation ratio compared to the default parameter settings.
-
•
Effect of SSL regularization weight. The SSL loss weight controls the regularization strength of self-supervision signals. It is clear that a proper weight of SSL loss regularization is beneficial for improving model learning on highly-skewed distributed data. However, the SSL regularization does not always improve model representation. As the SSL loss weight increases, the performance worsens. This is because the model gradient learning is biased towards the strongly regularized SSL signals, which has negative effects on the main optimized objective for recommendation.
-
•
Effect of batch size. The best model performance is achieved with a batch size of around 2048. The observed performance differences between Epinions and Yelp stem from their diverse social data densities. Epinions data is more sensitive to batch size due to its sparse social connections. Results on Epinions data indicate that a larger batch size helps alleviate the over-fitting issue during model training. However, worse performance is observed with further increasing batch size, possibly due to local optima.
-
•
Effect of propagation layers #. In GNNs, the number of propagation layers balances the trade-off between informativeness and over-smoothing. When tuning from 1 to 4, other parameters are kept at their default settings. A deeper graph neural network is effective in modeling high-order connectivity through cross-layer message passing to generate informative user and item representations. However, stacking too many propagation layers reduces the model capacity by making many different users identical. The resulting over-smoothed embeddings cannot preserve user uniformity with discriminative representations.
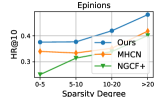
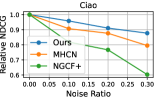
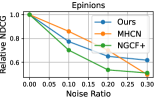
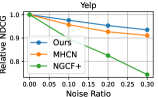
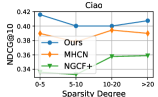
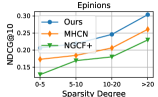
4.5 Model Robustness Evaluation (RQ3)
In this section, we investigate the robustness of our DSL against data sparsity and noise for recommendation.
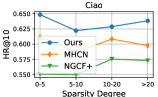
Data Sparsity.
To evaluate the model’s performance on less active users with fewer item interactions, we partitioned the user set into four groups based on their node degrees in the user-item interaction graph , namely (0,5), [5,10), [10,15), and [20, ). We separately measured the recommendation accuracy for each user group, and the evaluation results are reported in Figure 3. We observed that DSL outperformed the best-performing baseline MHCN in most cases, further validating the effectiveness of our incorporated self-supervision signals for data augmentation under interaction label scarcity.
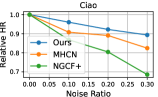
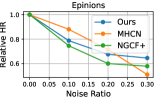
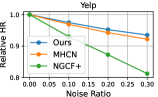
Data Noise.
To investigate the influence of noisy effects on model performance, we randomly generated different percentages of fake edges (i.e., ) to create a corrupted interaction graph as noise perturbation. The relative performance degradation with different noise ratios is shown in Figure 3. Our DSL demonstrates great potential in addressing data noise issues compared to competitors. We attribute this superiority to two reasons: 1) Graph structure learning with social relationships as self-supervision signals, which may alleviate the heavy reliance on interaction labels for representation learning. 2) The cross-domain self-augmented learning distills useful information from the interaction view to debias social connections and learn accurate social-aware collaborative relationships.
These findings address the research question raised in RQ3 by demonstrating that our proposed DSL improves the model’s generalization ability over noisy and sparse data.
4.6 Efficiency Analysis (RQ4)
We conduct additional experiments to evaluate the efficiency of our method for model training when DSL competes with baselines. We measure the computational costs (running time) of different methods on an NVIDIA GeForce RTX 3090 and present the training time for each model in Table 5. The training cost of DSL is significantly lower than most of the compared baselines, demonstrating its potential scalability in handling large-scale datasets in real-life recommendation scenarios. While existing social recommenders (e.g., MHCN and SMIN) leverage SSL for data augmentation, blindly maximizing the mutual information between user embeddings may lead to additional computational costs. In DSL, we enhance the social-aware self-supervised learning paradigm with an adaptive denoising module. This simple yet effective framework not only improves the recommendation quality but also shows an advantage in training efficiency.
| Data | DiffNet | NGCF+ | MHCN | KCGN | SMIN | Our |
| Ciao | 8.1 | 8.2 | 4.92 | 26.9 | 7.8 | 3.2 |
| Epinions | 39.1 | 16.3 | 9.34 | 49.4 | 19.7 | 6.1 |
| Yelp | 692.9 | 124.6 | 56.2 | 132.5 | 75.3 | 58.6 |
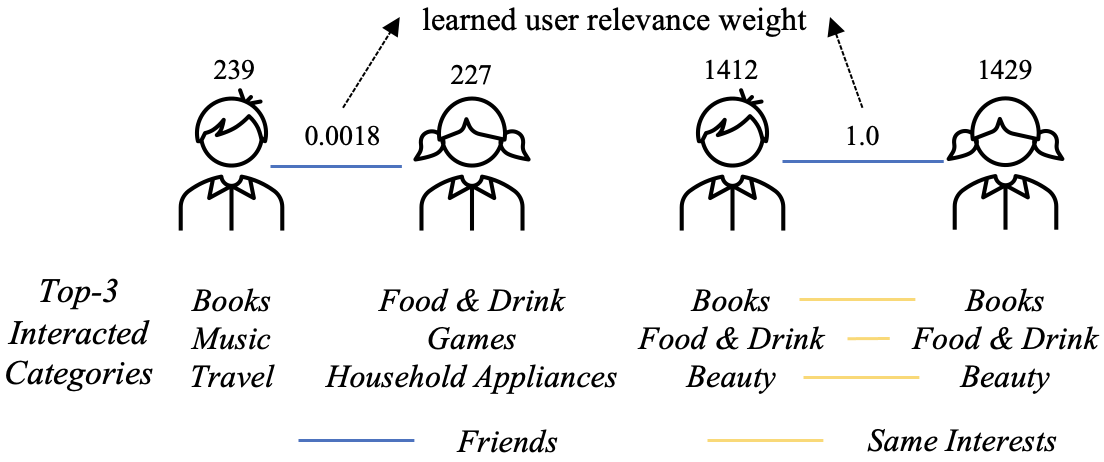
4.7 Case Study
In this section, we conduct a case study in Figure 4 to qualitatively investigate the effects of our cross-view self-augmented learning framework in denoising social connections for user preference learning. Specifically, we sample two user-user pairs from the Ciao dataset and show the top- frequently interacted item categories for each user. From the figure, we observe that the social influence between user 239 and user 227 is identified as weak (i.e., learned lower user relevance weight) with respect to their interaction preference. This is manifested by the fact that they mainly interacted with different item categories, i.e., user 239: Books, Music, and Travel; user 227: Food & Drink, Games, and Household Appliances. On the other hand, the social influence between user 1412 and user 1429 is learned to be strong (i.e., learned higher user relevance weight). Most of their interacted items come from the same categories, i.e., Books, Food & Drink, and Beauty, indicating their similar preferences. This observation aligns with our expectation that DSL can denoise social connections and encode social-aware user interests through meaningful SSL-enhanced representations for recommendation.
5 Conclusion
In this work, we propose a universal denoised self-augmented learning framework that not only incorporates social influence to help understand user preferences but also mitigates noisy effects by identifying social relation bias and denoising cross-view self-supervision. To bridge the gap between social and interaction semantic views, the framework introduces a learnable cross-view alignment to achieve adaptive self-supervised augmentation. Experimental results show that our new DSL leads to significant improvements in recommendation accuracy and robustness compared to existing baselines. Additionally, the component-wise effects are evaluated with ablation study. In future work, we aim to investigate the incorporation of interpretable learning over diverse relations to improve the explainability of denoised self-supervised learners for recommendation. Such incorporation can provide insights into the decision-making process of the social-aware recommender system, enabling users to understand how the system arrives at its recommendation results.
References
- Cai et al. [2023] Xuheng Cai, Chao Huang, Lianghao Xia, and Xubin Ren. Lightgcl: Simple yet effective graph contrastive learning for recommendation. In International Conference on Learning Representations (ICLR), 2023.
- Chen et al. [2019a] Chong Chen, Min Zhang, Yiqun Liu, and Shaoping Ma. Social attentional memory network: Modeling aspect-and friend-level differences in recommendation. In WSDM, pages 177–185, 2019.
- Chen et al. [2019b] Chong Chen, Min Zhang, Chenyang Wang, Weizhi Ma, Minming Li, Yiqun Liu, et al. An efficient adaptive transfer neural network for social-aware recommendation. In SIGIR, pages 225–234, 2019.
- Chen et al. [2020] Lei Chen, Le Wu, Richang Hong, Kun Zhang, and Meng Wang. Revisiting graph based collaborative filtering: A linear residual graph convolutional network approach. In AAAI, volume 34, pages 27–34, 2020.
- Chen et al. [2023] Mengru Chen, Chao Huang, Lianghao Xia, Wei Wei, Yong Xu, and Ronghua Luo. Heterogeneous graph contrastive learning for recommendation. In WSDM, pages 544–552, 2023.
- Epasto and Perozzi [2019] Alessandro Epasto and Bryan Perozzi. Is a single embedding enough? learning node representations that capture multiple social contexts. In WWW, pages 394–404, 2019.
- Fan et al. [2019] Wenqi Fan, Yao Ma, Qing Li, Yuan He, Eric Zhao, et al. Graph neural networks for social recommendation. In WWW, pages 417–426, 2019.
- He et al. [2020a] Kaiming He, Haoqi Fan, Yuxin Wu, et al. Momentum contrast for unsupervised visual representation learning. In CVPR, pages 9729–9738, 2020.
- He et al. [2020b] Xiangnan He, Kuan Deng, et al. Lightgcn: Simplifying and powering graph convolution network for recommendation. In SIGIR, pages 639–648, 2020.
- Huang et al. [2021] Chao Huang, Huance Xu, Yong Xu, Peng Dai, Lianghao Xia, Mengyin Lu, et al. Knowledge-aware coupled graph neural network for social recommendation. In AAAI, volume 35, pages 4115–4122, 2021.
- Liu and Liu [2021] Yixin Liu and Pengfei Liu. Simcls: A simple framework for contrastive learning of abstractive summarization. In ACL, 2021.
- Liu et al. [2019] Ninghao Liu, Qiaoyu Tan, Yuening Li, Hongxia Yang, Jingren Zhou, and Xia Hu. Is a single vector enough? exploring node polysemy for network embedding. In KDD, pages 932–940, 2019.
- Liu et al. [2022] Zhiwei Liu, Liangwei Yang, Ziwei Fan, Hao Peng, and Philip S Yu. Federated social recommendation with graph neural network. TIST, 13(4):1–24, 2022.
- Long et al. [2021] Xiaoling Long, Chao Huang, Yong Xu, Huance Xu, Peng Dai, Lianghao Xia, and Liefeng Bo. Social recommendation with self-supervised metagraph informax network. In CIKM, pages 1160–1169, 2021.
- Mnih and Salakhutdinov [2007] Andriy Mnih and Russ R Salakhutdinov. Probabilistic matrix factorization. NeurIPS, 20, 2007.
- Rendle et al. [2009] Steffen Rendle, Christoph Freudenthaler, et al. Bpr: Bayesian personalized ranking from implicit feedback. In UAI, pages 452–461, 2009.
- Song et al. [2019] Weiping Song, Zhiping Xiao, et al. Session-based social recommendation via dynamic graph attention networks. In WSDM, pages 555–563, 2019.
- Wang et al. [2019] Xiang Wang, Xiangnan He, Meng Wang, Fuli Feng, and Tat-Seng Chua. Neural graph collaborative filtering. In SIGIR, pages 165–174, 2019.
- Wei et al. [2022a] Chunyu Wei, Jian Liang, Di Liu, and Fei Wang. Contrastive graph structure learning via information bottleneck for recommendation. NeurIPS, 35:20407–20420, 2022.
- Wei et al. [2022b] Wei Wei, Chao Huang, Lianghao Xia, Yong Xu, Jiashu Zhao, and Dawei Yin. Contrastive meta learning with behavior multiplicity for recommendation. In WSDM, pages 1120–1128, 2022.
- Wu et al. [2019] Le Wu, Peijie Sun, Yanjie Fu, Richang Hong, Xiting Wang, and Meng Wang. A neural influence diffusion model for social recommendation. In SIGIR, pages 235–244, 2019.
- Wu et al. [2021] Jiancan Wu, Xiang Wang, Fuli Feng, Xiangnan He, Liang Chen, Jianxun Lian, and Xing Xie. Self-supervised graph learning for recommendation. In SIGIR, pages 726–735, 2021.
- Yang et al. [2016] Bo Yang, Yu Lei, Jiming Liu, and Wenjie Li. Social collaborative filtering by trust. TPAMI, 39(8):1633–1647, 2016.
- Yu et al. [2021a] Junliang Yu, Hongzhi Yin, Min Gao, et al. Socially-aware self-supervised tri-training for recommendation. In KDD, pages 2084–2092, 2021.
- Yu et al. [2021b] Junliang Yu, Hongzhi Yin, Jundong Li, Qinyong Wang, et al. Self-supervised multi-channel hypergraph convolutional network for social recommendation. In WWW, pages 413–424, 2021.
- Yuan et al. [2022] Xu Yuan, Hongshen Chen, Yonghao Song, Xiaofang Zhao, Zhuoye Ding, Zhen He, and Bo Long. Improving sequential recommendation consistency with self-supervised imitation. In IJCAI, 2022.
- Zhang et al. [2022] Shengyu Zhang, Lingxiao Yang, Dong Yao, Yujie Lu, et al. Re4: Learning to re-contrast, re-attend, re-construct for multi-interest recommendation. In WWW, pages 2216–2226, 2022.
- Zhou et al. [2020] Kun Zhou, Hui Wang, Wayne Xin Zhao, Yutao Zhu, Sirui Wang, Fuzheng Zhang, Zhongyuan Wang, and Ji-Rong Wen. S3-rec: Self-supervised learning for sequential recommendation with mutual information maximization. In CIKM, pages 1893–1902, 2020.
- Zhu et al. [2021] Yanqiao Zhu, Yichen Xu, Feng Yu, Qiang Liu, Shu Wu, et al. Graph contrastive learning with adaptive augmentation. In WWW, pages 2069–2080, 2021.