Density Functional Theory Study of Solute Cluster Growth Processes in Mg-Y-Zn LPSO Alloys
Abstract
Solute clusters in long period stacking order (LPSO) alloys play a key role in their idiosyncratic plastic behavior, for example kink formation and kink strengthening. Identifying atomistic details of cluster structures is a prerequisite for atomistic modeling of LPSO alloys and is crucial for improving their strength and ductility; however, there is much uncertainty regarding interstitial atoms in the cluster. Although density functional theory calculations have shown that the inclusion of Mg interstitial atoms is energetically most favorable in majority of LPSO alloys, solute elements have also been experimentally observed at interstitial sites. To predict the distributions of interstitial atoms in the cluster and to determine the kind of elements present, it is necessary to identify mechanisms by which interstitial atoms are created. In the present work, we use density functional theory calculations to investigate growth processes of solute clusters, specifically the Mg-Y-Zn LPSO alloy, in order to determine the precise atomistic structure of its solute clusters. We show that a pair of an interstitial atom and a vacancy are spontaneously created when a certain number of solute atoms are absorbed into the cluster, and that all full-grown clusters should include interstitial atoms. We also demonstrate that interstitial atoms are mostly Mg, while the rest are Y; interstitial Zn atoms are negligible. This knowledge greatly simplifies the atomistic modeling of solute clusters in Mg-Y-Zn alloys. Owing to the vacancies emitted from the cluster, vacancy density should be super-saturated in regions where solute clusters are growing, and increased vacancy density accelerates cluster growth.
Keywords: First-principles calculation; LPSO; Cluster Growth; Mg alloy;
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/388d7ea2-f9a4-445b-a8a5-f49b6d7de805/x1.png)
Graphical Abstract
1 Introduction
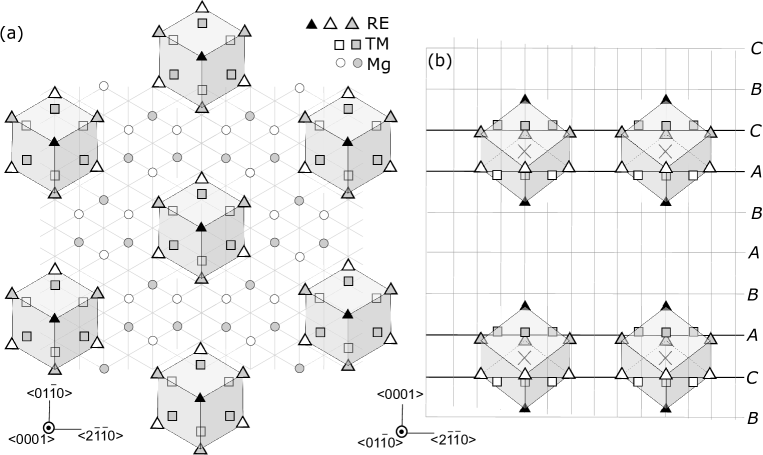
Solute clusters in Mg-based long period stacking order (LPSO) alloys [3, 4] play a key role in their idiosyncratic plastic behavior. Solute atoms form -type clusters [5] as shown in Fig. 1 and are strongly bound and displaced from their original lattice positions; this makes it difficult for dislocations to cut through and allows only slips in the limited basal planes. Although the lack of independent slip planes leads to poor ductility in most materials, LPSO alloys exhibit so-called ”kink deformation” [6, 7, 8], which accommodates plastic deformation in various directions via the structural organization of basal dislocations. It has been reported that these kink structures strengthen the material [9, 10, 11, 12, 13]. It is nonetheless expected that there is much room for improvement in terms of ductility and/or strength of LPSO alloys via optimizing their compositions and the heat-treatment processes through which they are formed. Atomistic modelling of kink structures coupled with macroscopic models of plasticity should give guiding principles for their improvement, and various models have been proposed to account for kink strengthening [14, 15, 16, 17].
Scanning transmission electron microscopy (STEM) observations and density functional theory (DFT) calculations have been used to reveal the atomistic structures of LPSO alloys, including various stacking structures (10H, 12R, 14H, 18R, and 24R), together with their thermodynamic stabilities [18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29] and the inter-cluster ordering along the stacking direction [22, 28, 29, 30]. Nonetheless, there are uncertainties regarding the interstitial atom (IA) in the cluster. Although DFT calculations have shown that the inclusion of Mg-IA is energetically most stable in Mg-Y-Zn and Mg-Y-Ni LPSO alloys [20, 23, 31], solute elements are also observed at interstitial sites in Mg-Y-Zn alloy by STEM [22]. In contrast, for Mg-Y-Al LPSO alloy, DFT calculation indicates that Y-IA is energetically most stable, and STEM observation have shown that about of interstitial sites are occupied by Y atoms [30]. To predict how much of the cluster has IAs and which elements are present, it is necessary to identify the mechanism by which IA is created, because it is implausible to assume that a population of IAs is in thermal equilibrium with its surroundings and can be estimated from static formation energy alone. Rather, IA creation should involve non-equilibrium processes.
Herein, we use DFT calculations to investigate the growth processes of solute clusters, specifically that of the Mg-Y-Zn LPSO alloy, in order to identify the IA formation process. The elementary process of cluster growth involves position exchange of solute atoms mediated by vacancy migration. We calculated the energies of the initial and final states of various elementary steps and estimated the rate of occurrence of each process from these energies. We also show that a pair of an IA and a vacancy are spontaneously created when a certain number of solute atoms are absorbed into the cluster, and that the full-grown cluster should include IAs. Finally, we will show that IAs are mostly Mg atoms, the rest being mostly Y atoms, while Zn IAs are negligible.
This paper is organized as follows. In Section 2, details of DFT calculations are described. In Section 3, results of DFT calculations are presented. Section 4 discusses the consequences deduced from the obtained results. In Section 5, a summary of the results and conclusions is presented.
2 Details of the calculations
2.1 Atomistic model
We investigated the formation energies of single solute clusters embedded in a cell as shown in Fig.2. Periodic boundary conditions were imposed in all directions, using a cell , which contained 10 basal layers and 480 atoms. For simplicity, we used the atomistic configuration of an almost isolated solute cluster, which corresponds to one quarter of the intra-plane cluster density of a fully ordered LPSO structure, in order to avoid complexity arising from inter-cluster interactions.
In the present work, we focus on the formation processes of solute clusters at the stacking fault (SF) region. Each cluster is separated from its periodic images in the direction by 6 basal Mg layers without solute atoms. We confirmed that stacking order of these Mg layers did not significantly affect cluster formation energy, by comparing energies calculated with two different stacking order in the margin area, namely hexagonal 10H cell [ABABACBCBC][ABABACBCBC] and rhombohedral cell [ABABACBCBC][BCBCBACACA]. They differ by meV, which is only of total formation energy. Although other choices for the cell exist, such as 12R and 14H structures, the 10H structure is most convenient to preserve hexagonal symmetry in calculations.
Cell size was determined by minimizing the total energy of the 10H stacking structure without any solute atoms. The calculated cell size was characterized by lattice spacings and , which are slightly larger than those of hcp-Mg. The cell size was fixed to these values for all calculations, allowing the total energy to be compared with a reference configuration. Each case exerts different cell pressures, depending on the local expansion of the solute cluster configuration. The maximum cell pressure is approximately MPa. We estimated the correction to the total energy coming from the interaction between periodic images from cell pressure [32], finding it to be approximately meV. We elected to ignore this effect.
Discussions on the relationship between SF formation and cluster growth have been reported, since each phenomenon promotes the other and it is not clear which takes place first [33, 34]. In the case of Mg-Y-Zn, direct observation of solute segregation near dislocation cores of Shockley partials and the subsequent growth of SF owing to Suzuki effect has been made [35]. Therefore, we assumed that the Y/Zn solute cluster grew on an existing SF and calculated its cluster formation energy in the SF region of the 10H structure.
2.2 DFT calculations
Electronic structure calculations and structural relaxation by force minimization in DFT calculations were performed using the Vienna Ab-initio Simulation Package (VASP) [36, 37] with the projector augmented wave method and ultrasoft pseudopotentials. The exchange correlation energy was calculated using the generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof function [38]. The Methfessel-Paxton smearing method with 0.2-eV width was used. The cutoff energy for the plane-wave basis set was 360 eV, and the convergence of cluster binding energy with respect to increasing cutoff was confirmed. Structural relaxation terminated when the maximum force acting on the movable degrees of freedom became less than meV/.
For the hexagonal supercell, k-points were placed on a Gamma-centered mesh in the XY-plane to preserve hexagonal symmetry; the Monkhorst-Pack k-point mesh was used in the Z-direction. The number of k-points was in all cases. We confirmed that the convergence of cluster-formation energy with respect to the increasing k-point number was rapid, with errors of approximately meV.
3 Results
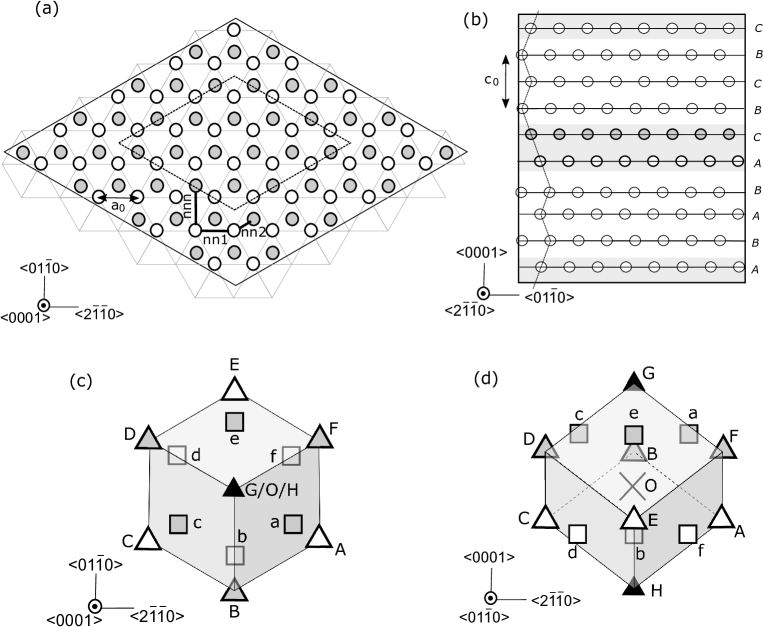
Throughout the paper, we treat a vacancy as a type of solute element denoted by “V”, and thus use expressions such as “site A is occupied by V”. The formation energy of a cluster C containing -Y atoms, -Zn atoms, and -vacancies with respect to a configuration in which each solute atom is isolated in the bulk region is calculated as follows:
| (1) |
where is the total energy of cluster configuration C embedded in a calculation cell of the 10H structure, is the total energy of the same cell without any solute atoms, and is the total energy of the configuration in which one Mg atom in the bulk region is substituted by solute X. When a cluster contains an IA, its formation process involves pair creation of an IA and a vacancy, as will be shown later. Therefore, its reference state contains no IA and one less vacancy. Accordingly, its formation energy is given by
| (2) |
This equation holds regardless of the element species of IA, as well as when the cluster contains no vacancy.
The segregation energy of element X in the SF region, denoted by , is defined as the energy change in which a single solute atom X moves from bulk to SF. We found that eV, eV, and eV. Note that the formation energy given by Eqs. (1) and (2) include the effect of SF segregation. To concentrate on the binding energy between solute atoms, we define cluster binding energy as follows:
| (3) |
where denotes the number of solute atoms X in the SF region.
Table 1 shows the two-body solute-solute interaction energy evaluated using . One can see that both the nearest neighbor Y-Zn and the next nearest neighbor Y-Y interactions are attractive, whereas all other interactions between solute atoms (excluding V) are very small. This result is consistent with previous work calculated using either the hcp or fcc lattice [39]. Table 2 shows the binding energies of various clusters containing up to 6 solute atoms together with a measure of the many-body interaction , where denotes cluster expansion energy calculated using only two-body interactions up to the next nearest neighbor as follows:
| (4) |
where the summation runs through all solute pairs (excluding IA for simplicity), is the relative position of atoms and , and is the two-body solute-solute interaction energy between elements and as shown in Table 1. If is neither the nearest neighbor nor next-nearest neighbor, it is set to zero.
Table 2 also shows the number of tetrahedral sub-clusters made of one Y atom and three Zn/V atoms. One can see that such tetrahedra exhibit significant many-body interactions through which they gain binding energy. A fully formed Y8Zn6 cluster has eight such tetrahedra and it is expected that cluster growth is promoted by the formation of such tetrahedra.
The results shown in Table 2 indicate that vacancies are bound to the cluster as strongly as solute atoms, but the relations between V absorption and solute absorption to the cluster requires careful consideration. Each migration of solute atoms is mediated by V diffusion. When a cluster absorbs a solute atom at a specific site, that site is first occupied by a vacancy, after which that vacancy switches position with a neighbor atom. If the neighbor atom is a solute atom, it is absorbed to the cluster.
The rates of V absorption to a specific site and V emission from that site, denoted by and , respectively, are given as follows:
| (5) | |||||
| (6) |
where is a V jump frequency in bulk, is equilibrium V density in the bulk, is the binding energy of V to the cluster (negative if attractive), is Boltzmann’s constant, and is temperature. Under conditions of thermal equilibrium, , where eV is vacancy-formation energy in bulk as evaluated by DFT calculations. If the absolute value of V binding energy is smaller than , the site is occupied by V with probability in thermal equilibrium conditions. In that case, the absorbed V quickly leaves the cluster, and we can ignore clusters containing vacancies when investigating growth processes.
We consider the rate of V emission followed by solute absorption, together with that of inverse process, denoted by and , respectively. Their ratio is given as follows:
| (7) |
where denotes solute concentration in the bulk and denotes solute binding energy (negative if attractive). The rate of solute absorption is then given by . Solute absorption is possible if , which gives
| (8) |
For example, when and K, Eq. (8) gives eV.
When the absolute value of V-binding energy is greater than V-formation energy, the site is mostly occupied by V. Assuming that solute binding energy is weaker than V-binding energy, the rate of solute absorption and that of the inverse process are given as follows:
| (9) | |||||
| (10) |
Solute absorption is possible if , which gives
| (11) |
For the typical case of and K, this equation gives eV. If this condition is satisfied, the site is initially occupied by V and mostly remains so, until the solute atom enters the neighbor site by diffusion and V swaps its position with the solute atom.
As a cluster grows, Zn atoms in inner sites (a through f) tend to be displaced outwards, whereas Y atoms in outer sites (A through H) tend to be displaced inwards. The octahedral interstitial space at the center of the cluster becomes larger as the cluster grows and, after some threshold, the interstitial atom can be accommodated. Figure 3 shows the migration energy profiles of atoms moving from an inner site to the interstitial site as evaluated by the nudged elastic band method [40] with seven images. When three inner sites are occupied by Zn atoms, the Mg atom in the inner site can move to the interstitial site with a much lower energy barrier than that of vacancy migration in bulk, thereby creating a pair comprising an IA and a vacancy with some energy gain. The Zn atom at the inner site can also move into the interstitial site, but will be subject to a much larger energy barrier and less energy gain.
Table 3 shows the binding energies of various cluster configurations and the energy gain of IA-V pair creation , which gives the difference in between the cluster configurations before and after IA-V pair creation. In cases where one configuration is unstable and relaxes to the other, we adopted a configuration in which the position of IA, or the atom at an inner site that becomes IA, is fixed in structural relaxation, in order to evaluate the energy of an unstable structure by preventing the spontaneous creation or annihilation of the IA-V pair during relaxation. In addition, the position of the inner atom which is most distant from the IA is also fixed to prevent the parallel transport of atoms.
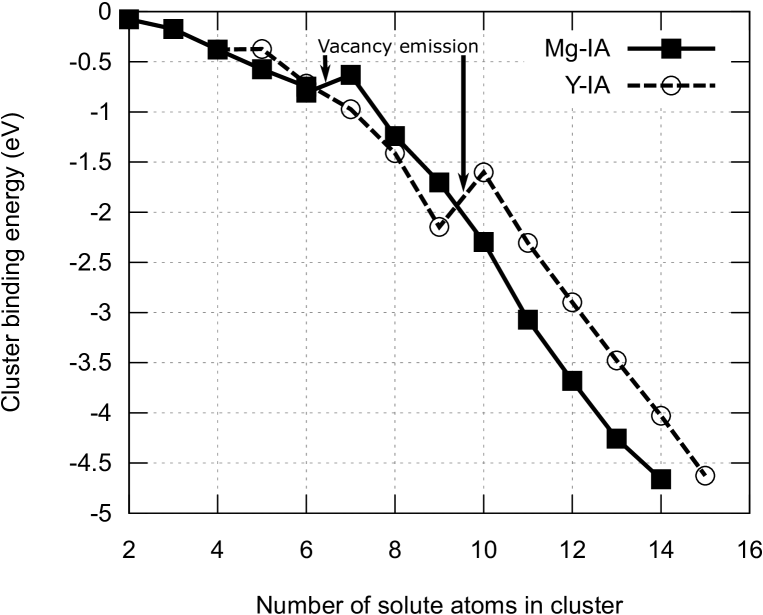
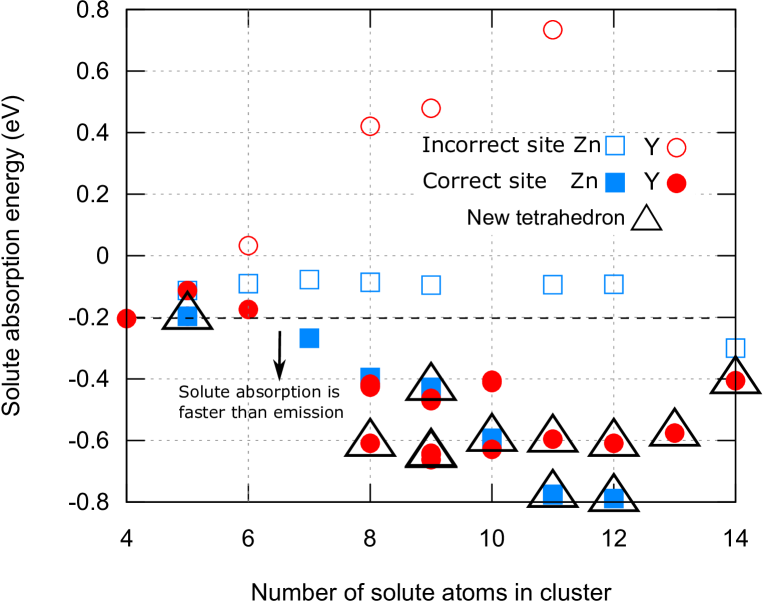
As the cluster grows, the energy barrier becomes lower and the energy gain becomes larger. When four or more inner sites are occupied by Zn atoms, the energy barrier becomes zero and configurations without IA become unstable. From these results, we conclude that every fully-grown cluster should contain IA. The IA atom is most likely to be Mg; the Zn IA is very unlikely because it has a much greater energy barrier for its creation compared to Mg.
Whereas Mg and Zn atoms have two stable positions in the inner site and interstitial site, we found that the Y atom occupying the inner site has only one stable position, which moves toward the interstitial site as other inner sites are occupied by Zn atoms as shown in Fig. 4. Therefore, it is possible that when one inner site is occupied by Y during the growth process, the Y atom becomes an IA. In Table 3, for the Y interstitial case, the distance of the Y atom from the center, denoted by , normalized by the distance of an inner site from the center, denoted by , is shown. for Y-IA case cannot be defined because there is only one stable position for Y atom. Precise estimation of the ratio between Mg-IA and Y-IA requires detailed Monte Carlo simulations and is thus out of scope of the present paper.
Following the formation of an IA-V pair, V leaves the cluster if its binding energy is not comparable to the V formation energy , as discussed above. If the binding energy of the newly created V is comparable to , it remains until substituted by a solute atom, provided that , as discussed previously.
Figure 5 shows the progression of cluster-binding energy during the cluster growth process forming the cluster Y8Zn6 plus IA. For a given configuration, the energy gain of both Y and Zn absorption is investigated at sites where large energy gains are expected via the formation of new attractive pairs of solute atoms and/or a new solute tetrahedron composed of one Y and three Zn atoms. Thereafter, we chose a site and solute atom with maximum absorption energy, included that atom in the cluster, and repeated the process. We confirmed that the solute binding energy satisfies either of the conditions or in all cases.
Figure 6 shows absorption energies at various sites, including “incorrect” absorptions such as Y absorption at inner sites and Zn absorption at sites other than inner or outer sites. Note that Zn absorption at outer sites does not create new Y-Zn neighbor pairs and no energy gain is expected, thus they were excluded from the calculation. We evaluated only the case of Mg-IA. One can see that, following the formation of IA, Y absorption at inner sites becomes highly unfavorable, promoting the absorption of Zn atoms at inner sites. Once the IA is created, “correct” absorptions tend to increase the number of Y1Zn3 tetrahedra and are highly favorable.
3.1 Effect of entropy on absorption
Thus far, we have evaluated the absorption energies of solute atoms to a cluster. Since cluster growth takes place at relatively high temperatures, an entropy effect may modify absorption behavior. In this subsection, we estimate the effect of entropy from vibration and configuration.
Firstly, vibrational entropy is evaluated from the vibrational frequencies of a single atom, either in bulk or in a fully formed cluster with Mg interstitial atom. Solute atoms included in a cluster are bound together by attractive interactions and their amplitudes of vibration are expected to be smaller than those in bulk, resulting in reduced entropy and increased free energy. Vibration frequencies of Mg, Y, and Zn atoms were evaluated using DFT calculations and corresponding vibration free energies as shown in Table 5. was calculated using a quasi-harmonic approximation [41] as follows:
| (12) |
where (Js) denotes the reduced Planck constant. One can see that the vibration frequencies of the Zn atom change significantly when it is absorbed into a cluster, whereas those of the Mg and Y atoms remained virtually unchanged. However, its effect on free energy was at most eV for the Zn atom, even at K. Thus, we conclude that the effect of vibrational entropy on the absorption process is not significant.
Secondly, the configurational entropy of solute atoms is evaluated by assuming that there a periodic array of solute clusters and a uniform distribution of solute atom occur in bulk with concentration . Each cluster is surrounded by bulk Mg atoms, in which ranges from to depending upon the periodicity of clusters. When each cluster absorbs one solute atom, decreases by , and the configurational entropy per atom, , decreases at , and more rapidly for smaller values of . In the extreme case where becomes zero due to absorption and entropy becomes zero, and the change in entropy per cluster is given by . This term is positive and monotonically increases with increasing . For K and , the term is eV. Thus, absorption energy must be greater than eV at . This condition is similar to Eq. (8) derived from more simple considerations of absorption and desorption rates.
4 Discussion
We have shown that a pair comprising an interstitial atom and a vacancy is spontaneously created during the cluster growth process. This entails that vacancy density becomes super-saturated in region where solute clusters are growing. In such a situation, it is possible that vacancies accumulate temporarily at the solute cluster. A precise estimation of the effect of vacancy super-saturation on the cluster growth processes requires mesoscopic scale simulations of vacancy density evolution, and is thus outside of the scope of the present work.
A more straightforward consequence is the acceleration of cluster growth processes, since the elementary process of growth is vacancy diffusion and the growth rate is directly proportional to vacancy density. Normally, the growth rate of the LPSO structure is expected to be proportional to where is migration energy of vacancy. In the super-saturated region, it can be accelerated to .
Another consequence of vacancy super-saturation is the promotion of dislocation climb. When a Shockley partial dislocation absorbs vacancies, it gradually moves in the direction. Accelerated climb motion may assist in the formation of a periodic SF arrangement.
During the growth process of the LPSO structure, experimental observations indicate that the period of stacking order becomes shorter, and solute clusters follow the migration of stacking faults [18]. If cluster migration occurs via the sequential migration of solute atoms, each migration removes a solute atom from the cluster at a cost of approximately eV as shown in Fig. 6, indicating that such migration is quickly reverted. It is more plausible to assume that a fully-grown cluster absorbs further solute atoms to form a fused cluster [26], which then emits extra atoms and becomes an cluster again, but at different position.
5 Conclusion
Using DFT calculations, we have investigated the mechanisms of solute cluster growth in Mg-Y-Zn LPSO alloys, and have found that a tetrahedral cluster made of one Y atom and three Zn atoms is highly stable. A fully-grown cluster contains eight such tetrahedra, and the formation of such tetrahedra is a strong driving force for cluster growth. Similar calculations of other combinations of rare-earth and transition metal elements should reveal the origins of different LPSO structures with various compositions. We also found that a pair comprising an interstitial atom and a vacancy is spontaneously created during this growth process, denoting that every fully-grown cluster contains an interstitial atom. The interstitial atom is most likely Mg, however, some portion can also be Y. Interstitial Zn atoms should be negligible. A vacancy created in the process is emitted from the cluster, and vacancy density should thus become super-saturated during growth of the solute cluster. This may promote dislocation climb and influence the evolution of the LPSO structure. Mesoscopic modelling of cluster growth and vacancy emission, combined with modelling of dislocation glide/climb and stacking fault growth, is expected as the subject of future works.
6 Acknowledgement
The authors are grateful to Hajime Kimizuka for his useful comments. This work was supported by JSPS KAKENHI for Scientific Research on Innovative Areas ”Materials Science of a Mille-feuille Structure” (Grant Numbers 18H05480, 18H05479). Computations were performed on the ICEX at the Japan Atomic Energy Agency. The authors would like to thank Enago (www.enago.jp) for the English language review.
References
- [1]
- [2]
- [3] Y.Kawamura, K.Hayashi, A.Inoue, T.Masumoto, Rapidly solidified powder metallurgy Mg97Zn1Y2 Alloys with excellent tensile yield strength above 600 MPa, Mater Trans 42 (2001) 1172-1176.
- [4] E.Abe, Y.Kawamura, K.Hayashi, A.Inoue, Long-period ordered structure in a high-strength nanocrystalline Mg-1 at% Zn-2 at% Y alloy studied by atomic-resolution Z-contrast STEM, Acta Mater 50 (2002) 3845-3857.
- [5] D.Egusa, E.Abe, The structure of long period stacking/order Mg-Zn-RE phases with extended non-stoichiometry ranges, Acta Mater 60 (2012) 166-178.
- [6] K.Hagihara, N.Yokotani, Y.Umakoshi, Plastic deformation behavior of Mg12YZn with 18R long-period stacking ordered structure, Intermetallics 18 (2010) 267-276.
- [7] M.Yamasaki, K.Hagihara, S.I.Inoue, J.P.Hadorn, Y.Kawamura, Crystallographic classification of kink bands in an extruded Mg-Zn-Y alloy using intragranular misorientation axis analysis, Acta Mater 61 (2013) 2065-2076.
- [8] T.Matsumoto, M.Yamasaki, K.Hagihara, Y.Kawamura, Configuration of dislocations in low-angle kink boundaries formed in a single crystalline long-period stacking ordered Mg-Zn-Y alloy, Acta Mater 151 (2018) 112-124.
- [9] K.Hagihara, A.Kinoshita, Y.Sugino, M.Yamasaki, Y.Kawamura, H.Y.Yasuda, Y.Umakoshi, Effect of long-period stacking ordered phase on mechanical properties of Mg97Zn1Y2 extruded alloy, Acta Mater 58 (2010) 6282-6293.
- [10] K.Hagihara, A.Kinoshita, Y.Fukusumi, M.Yamasaki, Y.Kawamura, High-temperature compressive deformation behavior of Mg97Zn1Y2 extruded alloy containing a long-period stacking ordered (LPSO) phase, Mater Sci Eng A 560 (2013) 71-79.
- [11] C.Xu, T.Nakata, X.Qiao, M.Zheng, K.Wu, S.Kamado, Effect of LPSO and SFs on microstructure evolution and mechanical properties of Mg-Gd-Y-Zn-Zr alloy, Sci Rep 7 (2017) 40846.
- [12] K.Hagihara, Z.Li, M.Yamasaki, Y.Kawamura, T.Nakano, Strengthening mechanisms acting in extruded Mg-based long-period stacking ordered (LPSO)-phase alloys, Acta Mater 163 (2019) 226-239.
- [13] H.Somekawa, D.Ando, M.Yamasaki, Y.Kawamura, Microstructure and mechanical properties of low-temperature wrought-processed Mg-Y-Zn alloy containing LPSO phase, Materialia (2020) 100786.
- [14] T.Mayama, M.Noda, R.Chiba, M.Kuroda, Crystal plasticity analysis of texture development in magnesium alloy during extrusion, Int J Plasticity 27 (2011) 1916-1935.
- [15] T.Mayama, T.Ohashi, Y.Tadano, K.Hagihara, Crystal plasticity analysis of development of intragranular misorientations due to kinking in HCP single crystals subjected to uniaxial compressive loading, Mater Trans 56 (2015) 963-972.
- [16] S.Kobayashi, R.Tarumi, Dislocation-Based Modeling and Numerical Analysis of Kink Deformations on the Basis of Linear Elasticity, Marer Trans 61 (2020) 862-869.
- [17] T.Inamura, Geometry of kink microstructure analysed by rank-1 connection, Acta Mater 173 (2019) 270-280.
- [18] E.Oñorbe, G.Garcés, P.Pérez, P.Adeva, Effect of the LPSO volume fraction on the microstructure and mechanical properties of Mg-Y2X-ZnX alloys, J Mater Sci 47 (2012) 1085-1093.
- [19] K.Kishida, H.Yokobayashi, H.Inui, M.Yamasaki, Y.Kawamura, The crystal structure of the LPSO phase of the 14H-type in the Mg-Al-Gd alloy system, Intermetallics 31 (2012) 55-64.
- [20] J.E.Saal, C.Wolverton, Thermodynamic stability of Mg-based ternary long-period stacking ordered structures, Acta Mater 68 (2014) 325-338.
- [21] M.Yamasaki, M.Matsushita, K.Hagihara, H.Izuno, E.Abe, Y.Kawamura, Highly ordered 10H-type long-period stacking order phase in a Mg-Zn-Y ternary alloy, Scr Mater 78 (2014) 13-16.
- [22] K.Kishida, K.Nagai, A.Matsumoto, A.Yasuhara, H.Inui, Crystal structures of highly-ordered long-period stacking-ordered phases with 18R, 14H and 10H-type stacking sequences in the Mg-Zn-Y system, Acta Mater 99 (2015) 228-239.
- [23] Z.R.Liu, D.Y.Li, Stability and formation of long period stacking order structure in Mg-based ternary alloys, Comput Mater Sci 103 (2015) 90-96.
- [24] Z.Wang, Q.Luo, S.Chen, K.C.Chou, Q.Li, Experimental investigation and thermodynamic calculation of the Mg-Ni-Y system (Y 50 at.%) at 400 and 500 C, J Alloys Compd 649 (2015) 1306-1314.
- [25] M.Tane, H.Kimizuka, K.Hagihara, S.Suzuki, T.Mayama, T.Sekino, Y.Nagai, Effects of stacking sequence and short-range ordering of solute atoms on elastic properties of Mg-Zn-Y alloys with long-period stacking ordered structures, Acta Mater 96 (2015) 170-188.
- [26] J.K.Kim, W.S.Ko, S.Sandlbes, M.Heidelmann, B.Grabowski, D.Raabe, The role of metastable LPSO building block clusters in phase transformations of an Mg-Y-Zn alloy, Acta Mater 112 (2016) 171-183.
- [27] K.Hagihara, T.Okamoto, H.Izuno, M.Yamasaki, M.Matsushita, T.Nakano, Y.Kawamura, Plastic deformation behavior of 10H-type synchronized LPSO phase in a Mg-Zn-Y system, Acta Mater 109 (2016) 90-102.
- [28] C.Liu , Y.Zhu , Q.Luo, B.Liu, Q.Gu, Q.Li, A 12R long-period stacking-ordered structure in a Mg-Ni-Y alloy, J Mater Sci Technol 34 (2018) 2235-2239.
- [29] Q.Luo, Y.Guo, B.Liu, Y.Feng, J.Zhang, Q.Li, K.Chou, Thermodynamics and kinetics of phase transformation in rare earth?magnesium alloys: A critical review, J Mater Sci Technol 44 (2020) 171-190.
- [30] D.Egusa, H.Somekawa, E.Abe, The LPSO Structure with an Extra Order beyond Stacking Periodicity, Mater Trans 61 (2020) 833-838.
- [31] Y.Guo, Q.Luo, B.Liu, Q.Li, Elastic properties of long-period stacking ordered phases in Mg?Zn?Y and Mg?Ni?Y alloys: A first-principles study, Scr Mater 178 (2020) 422-427.
- [32] C.Varvenne, F.Bruneval, M.C.Marinica, E.Clouet, Point defect modeling in materials: Coupling ab initio and elasticity approaches, Phys Rev B 88 (2013) 134102.
- [33] H.Okuda, M.Yamasaki, Y.Kawamura, M.Tabuchi, H.Kimizuka, Nanoclusters first: a hierarchical phase transformation in a novel Mg alloy, Sci Rep 5 (2015) 14186.
- [34] P.Mao, Y.Xin, K.Han, Z.Liu, Z.Yang, Formation of long-period stacking-ordered (LPSO) structures and microhardness of as-cast Mg-4.5 Zn-6Y alloy, Mater Sci Eng A 777 (2020) 139019.
- [35] W.W.Hu, Z.Q.Yang, H.Q.Ye, Cottrell atmospheres along dislocations in long-period stacking ordered phases in a Mg-Zn-Y alloy, Scr Mater 117 (2016) 77-80.
- [36] G.Kresse, J.Hafner, Ab initio molecular dynamics for liquid metals, Phys Rev B 47 (1993) 558.
- [37] G.Kresse, J.Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys Rev B 54 (1996) 11169.
- [38] J.P.Perdew, K.Burke, M.Ernzerhof, Generalized gradient approximation made simple, Phys Rev Lett 77 (1996) 3865-3868.
- [39] H.Kimizuka, M.Fronzi, S.Ogata, Effect of alloying elements on in-plane ordering and disordering of solute clusters in Mg-based long-period stacking ordered structures: A first-principles analysis, Scr Mater 69 (2013) 594-597.
- [40] G.Mills, H.Jonsson, Quantum and thermal effects in H2 dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems, Phys Rev Lett 72 (1994) 1124.
- [41] M.T.Dove, Introduction to lattice dynamics, Cambridge university press, Cambridge, 1993.
| Solute pair | (nn1) | (nn2) | (nnn) |
|---|---|---|---|
| Y-Y | |||
| Zn-Zn | |||
| V-V | |||
| Y-Zn | |||
| Y-V | |||
| Zn-V |
| Label | Y | Zn | V | |||
| C3-1 | G | ac | ||||
| C3-2 | b | ac | ||||
| C3-3 | B | ab | ||||
| C3-4 | B | ac | ||||
| C3-5 | BC | b | ||||
| C3-6 | BG | c | ||||
| C4-1 | AB | ab | ||||
| C4-2 | ACH | b | ||||
| C4-3 | BG | ac | ||||
| C4-4 | G | ace | 1 | |||
| C4-5 | e | Edf | 1 | |||
| C4-6 | B | abc | 1 | |||
| C3-7 | B | ab | c | 1 | ||
| C5-1 | ABe | ab | ||||
| C5-2 | ABC | ab | ||||
| C5-3 | AB | abc | 1 | |||
| C5-4 | ACH | bd | ||||
| C5-5 | BG | abc | 1 | |||
| C5-6 | CH | bdf | 1 | |||
| C6-1 | ABC | abc | 1 | |||
| C6-2 | ABCH | ab | ||||
| C6-3 | ABC | abe | ||||
| C5-7 | ABC | ab | d | |||
| C5-8 | ABC | ab | c | 1 | ||
| C6-4 | ABCe | ab | ||||
| C6-5 | ABe | abc | 1 | |||
| C6-6 | BGd | ace | 1 | |||
| C6-7 | BGb | ace | 1 | |||
| C6-8 | BCG | abc | 1 | |||
| C6-9 | BG | abce | 2 |
| Label | IA | Y | Zn | V | |||
|---|---|---|---|---|---|---|---|
| C4-1 | AB | ab | |||||
| C4-1i | Mg | AB | ab | d | C4-1 | ||
| C5-3 | AB | abc | |||||
| C5-3i | Mg | AB | abc | e | |||
| C6-1 | ABC | abc | |||||
| C6-1i | Mg | ABC | abc | e | |||
| C6-9 | BH | abce | |||||
| C6-9i | Mg | BH | abce | d | C6-9 | ||
| C6-10 | AB | abcf | |||||
| C6-10i | Mg | AB | abcf | e | |||
| C7-1 | ABC | abcd | |||||
| C7-1i | Mg | ABC | abcd | e | |||
| C8-1 | ABCD | abcd | C8-1i | ||||
| C8-1i | Mg | ABCD | abcd | e | |||
| C6-3 | ABC | abe | |||||
| C6-3i1 | Zn | ABC | ab | e | |||
| C6-3i2 | Mg | ABC | abe | f | C6-3 | ||
| C6-3i3 | Mg | ABC | abe | c | C6-3 | ||
| C7-2 | ABC | abce | |||||
| C7-2i1 | Zn | ABC | abc | e | |||
| C7-2i2 | Mg | ABC | abce | d | |||
| Label | IA | Y | Zn | V | |||
| C6-4 | ABCe | ab | |||||
| C6-5 | ABe | abc | |||||
| C7-3 | ABCe | abc | |||||
| C7-3i | Mg | ABCe | abc | d | |||
| C8-2i | Y | ABC | abcd | e | |||
| C9-1i | Y | ABC | abcdf | e |
| Label | IA | Y | Zn | V | ||
|---|---|---|---|---|---|---|
| C6-1i | Mg | ABC | abc | e | ||
| C6-1i2 | Mg | ABC | abc | d | ||
| C6-1i3 | Mg | ABC | abc | |||
| C7-4i | Mg | ABC | abce | |||
| C8-3i | Mg | ABCG | abce | 2 | ||
| C8-4i | Mg | ABC | abcde | 1 | ||
| C8-5i | Mg | ABCH | abce | 1 | ||
| C8-6i | Mg | ABCD | abce | 1 | ||
| C9-2i | Mg | ABCG | abcde | 3 | ||
| C9-3i | Mg | ABCGH | abce | 2 | ||
| C9-4i | Mg | ABCDG | abce | 2 | ||
| C10-1i | Mg | ABCGH | abcde | 3 | ||
| C10-2i | Mg | ABCDGH | abce | 2 | ||
| C11-1i | Mg | ABCGH | abcdef | 5 | ||
| C11-2i | Mg | ABCDGH | abcde | 4 | ||
| C12-1i | Mg | ABCDGH | abcdef | 6 | ||
| C13-1i | Mg | ABCDFGH | abcdef | 7 | ||
| C14-1i | Mg | ABCDEFGH | abcdef | 8 | ||
| C9-1i | Y | ABC | abcdf | e | 3 | |
| C9-1i1 | Y | ABC | abcdf | 3 | ||
| C10-3i | Y | ABC | abcdef | 3 | ||
| C11-3i | Y | ABCD | abcdef | 4 | ||
| C11-4i | Y | ABCG | abcdef | 4 | ||
| C11-5i | Y | ABCH | abcdef | 4 | ||
| C12-2i | Y | ABCDH | abcdef | 5 | ||
| C12-3i | Y | ABCGH | abcdef | 5 | ||
| C13-2i | Y | ABCDGH | abcdef | 6 | ||
| C14-2i | Y | ABCDEGH | abcdef | 7 | ||
| C15-1i | Y | ABCDEFGH | abcdef | 8 |
| Atom | K | K | K | |||
|---|---|---|---|---|---|---|
| Mg bulk | 5.79 | 5.71 | 5.70 | 6 | -149 | -406 |
| Mg cluster | 5.37 | 5.36 | 5.32 | 5 | -155 | -417 |
| Y bulk | 4.01 | 3.92 | 3.90 | 4 | -178 | -464 |
| Y cluster | 3.95 | 3.94 | 3.21 | 4 | -184 | -475 |
| Zn bulk | 2.33 | 2.31 | 2.30 | 2 | -220 | -547 |
| Zn cluster | 4.18 | 4.12 | 3.58 | 4 | -178 | -464 |