Density Spectrum in the Solar Wind Plasma

It is a curious observation that electron density fluctuations in the interstellar medium (ISM) exhibit an omnidirectional Kolmogorov-like (Kolmogorov, 1941) power spectrum $k^{-5/3}$ (or -11/3 spectral index in three dimensions) over a 4 to 5 decade range (Armstrong et al, 1981; Higdon, 1984; Armstrong et al, 1990). The solar wind plasma also possesses density fluctuations that exhibit a Kolmogorov-like $k^{-5/3}$ spectrum (Goldstein et al 1995; Matthaeus & Brown 1988; Zank & Matthaeus 1990; Montgomery et al 1987; Lithwick & Goldreich 2001; Padoan & Nordlund 1999; Shaikh & Zank 2007). Turbulent processes are believed to be responsible for the observed density spectrum in the ISM Armstrong et al (1981); Higdon (1984, 1986); Armstrong et al (1990); Elmegreen (2004); Scalo & Elmegreen (2004); Elmegreen & Scalo (2004) and solar wind Goldstein et al (1995); Matthaeus & Brown (1988); Zank & Matthaeus (1990); Montgomery et al. (1987); Podesta et al (2007, 2006, 2008). The Kolmogorov-like 5/3 spectrum is observed in many fluid, space and astrophysical plasmas as well. For instance, turbulent spectra in the ISM and galaxies are found to exhibit a Kolmogorov-like scaling in wavenumber space Roy et al (2008); Haverkorn (2008); Ryu et al (2008); Rickett (2007); Willett (2005); Elmegreen (1999); Dickey et al (2001); Minter & Spangler (1996). Several MHD and hydrodynamic fluid turbulence simulations show a Kolmogorov-like 5/3 spectrum. Some example of which are Biskamp (2003); Shaikh & Zank (2007); Lithwick & Goldreich (2001); Ghosh et al (1993); Kim & Ryu (2005); Kritsuk (2007). An exhaustive list of references describing a Kolmogorov-like 5/3 spectrum in hydrodynamic fluid and magnetoplasma turbulence is however not possible to cite here. Some good reviews such as McComb (1990); Lesieur (1990); Biskamp (2003); Scalo & Elmegreen (2004); Elmegreen & Scalo (2004) discuss various possible scenarios of turbulence in general. While all of these works show the possiblity of a self-consistent energy exchange between widely disparate length-scales in the presence of waves, nonlinear structures, anisotropy, driving forces etc., the physical processes leading to a Kolmogorov-like turbulent density fluctuation spectrum is not yet fully understood. A great deal of attention has thus focused on understanding the evolution of MHD turbulence spectra in the context of the solar wind and ISM Higdon (1984, 1986); Matthaeus & Brown (1988); Zank & Matthaeus (1990, 1993); Bayly et al (1992); Montgomery et al. (1987); Lithwick & Goldreich (2001); Padoan & Nordlund (1999); Shaikh & Zank (2006, 2007).

Higdon (1984, 1986) interpreted the observed density fluctuations (Armstrong et al, 1981) to be two-dimensional isobaric entropy variations in which temperature and density gradients are directed oppositely and both are orthogonal to the local approximately uniform magnetic field. Based on a pseudosound approximation (Lighthill, 1952), Montgomery et al (1987) related density fluctuations and incompressible magnetohydrodynamics (MHD) velocity and magnetic field fluctuations. This approach, called a pseudosound approximation, assumes that density fluctuations are proportional to the pressure fluctuations through the square of sound speed. The density perturbations in their model are therefore âslavedâ to the incompressible magnetic field and the velocity fluctuations. This hypothesis was further contrasted by Bayly et al. (1992) on the basis of their 2D compressible hydrodynamic simulations by demonstrating that a spectrum for density fluctuations can arise purely as a result of abondoning a barotropic equation of state without even requiring a magnetic field. Bayly’s (1992) work ignores magnetic field effects from the outset and hence does not explain the influence and possible correlation of magnetic field and corresponding magnetized waves on the density fluctuation spectrum. The latter has been investigated in the slow solar wind plasma by Spangler & Spitler (2004) who suggest that there exists a strong correlation between the density and magnetic field fluctuations. The pseudosound fluid description of compressibility, justifying the Montgomery et al. (1987) approach to the density-pressure relationship, was further extended by Matthaeus and Brown (1988) in the context of a compressible magnetofluid (MHD) plasma with a polytropic equation of state in the limit of a low plasma acoustic Mach number (Matthaeus and Brown, 1988). The theory, originally describing the generation of acoustic density fluctuations by incompressible hydrodynamics (Lighthill, 1952), is based on a generalization of Klainerman and Majda’s work (Klainerman and Majda, 1981, 1982; Majda, 1984) and accounts for fluctuations associated with a low turbulent Mach number fluid, unlike purely incompressible MHD. Such a nontrivial finite departure from the incompressibility state is termed a ’nearly incompressible’ fluid description and is put forward to provide a possible explanation of the turbulent density variations that are observed to exhibit a Kolmogorov-like power spectrum in the solar wind plasma (Montgomery et al. 1987; Matthaeus & Brown 1988, Zank & Matthaeus 1990, 1993, Shaikh & Zank 2004a,b). In the context of the ISM, a comparative study of two-dimensional turbulence of self-gravitating supersonic MHD, hydrodynamic and Burgers turbulence by Scalo et al (1998) suggests a power law form of density fluctuations that is close to -1.7. Kim & Ryu (2005) report that the slope of the density power spectra in hydrodynamic turbulence becomes gradually shallower as the rms Mach number increases and it tends towards a Kolmogorov-like slope when the rms (or turbulent) Mach number is unity. The high resoultion simulations of Euler turbulence by Kritsuk et al (2007) suggest that the inertial range velocity scaling in the strongly compressible regime (with a spectral index close to -1.95) deviates substantially from the incompressible Kolmogorov 5/3-law. Kida & Orszag (1990) report that it is only the rotational component of the velocity field in driven hydrodynamic compressible fluid turbulence that exhibits spectra very close to that of the incompressible case even for a large Mach number (close to unity). Lithwick & Goldreich (2001) show that density fluctuations in the ISM plasma are generated by entropy modes while Alfvén waves lead to a Kolmogorov-like spectrum. This, however, is not generic to all Alfvénic Mach numbers ($M_{A}$) (Passot & Vázquez-Semadeni, 2003). While both slow and fast modes introduce density fluctuations at large $M_{A}$, only the slow mode dominates the density-magnetic field anticorrelation at relatively small $M_{A}$ (Passot & Vázquez-Semadeni, 2003). However, the slow mode is known to be strongly Landau damped in a collisionless plasma. The presence of a mean magnetic field introduces additional complexities in the energy cascade processes in MHD turbulence. For instance, the assumption of isotropy breaks down in the presence the mean or large scale magnetic field. Along the direction of this large scale magnetic field Alfvén waves suppress the parallel cascade (Iroshnikov 1963; Kraichnan 1965). The resulting inertial range MHD spectrum is therefore thought to be flattened from $k^{-5/3}$ to $k^{-3/2}$ (Iroshnikov 1963; Kraichnan 1965). Within the paradigm of incompressible MHD turbulence, Goldreich & Sridhar (1995) proposed that parallel ($k_{\parallel}$) and perpendicular ($k_{\perp}$) modes are correlated by $k_{\parallel}\propto k_{\perp}^{2/3}$ and energy in the perpendicular modes follows a Kolmogorov-like spectrum when linear (along $B_{0}$) and nonlinear (across $B_{0}$) frequencies balance. By contrast, Shaikh & Zank (2007) argue that such balance is not obeyed identically by the entire inertial range modes, but only by a few modes that critically balance linear and nonlinear Alfvénic frequency. Boldyrev (2005) proposes a scale dependent anisotropic power law that appears to differ from the in-situ solar wind observations (Podesta et al 2008). While in-situ spacecraft observations of magnetic field fluctuations in solar wind plasma are shown to follow the Kolmogorov-like $k^{-5/3}$ spectrum (Montgomery et al 1987; Zhou et al 1990; Goldstein et al 1995), the velocity field tends to show a close consistency with a $k^{-3/2}$ spectrum (Podesta et al 2006, 2007). The latter is contrasted by Roberts (2007) that the magnetic field and velocity in the solar wind do not evolve in the same way with helocentric distance. Based on Voyager observations, Roberts (2007a,b) argues that velocity spectrum relaxes towards a likely asymptotic state through spectral steepening and acquires a spectral index of -5/3, finally mathching the magnetic field spectrum. Roberts (2007b) further argues that -3/2 is accidental and transient, and that the -5/3 slope is the eventual state of all the fluctuations. In a comprehensive review, Bruno and Carbone (2005) and Veltri (1980) describe that low frequency solar wind velocity fluctuations closely follow a Kolmogorov-like spectrum, and the intermediate region (between high and low frequency) do not allow us to distinguish between a Kolmogorov spectrum (-5/3) and a Kraichnan spectrum (-3/2). Bavassano et al (2005) describe that large scale velocity field fluctuations in the polar solar wind closely follow a Kolmogorov-like 5/3 spectrum.

The discrepancy in the magnetic and velocity field spectra continues to be an unresolved issue. Since our simulations tend to favor a Kolmogorov-like $k^{-5/3}$ velocity spectrum in which density spectrum ($k^{-5/3}$) closely follows the velocity spectrum through a passive convection, we support a $k^{-5/3}$ Kolmogorov-like spectrum for the velocity field fluctuations in solar wind. What is notable in our work is the dissipation of the high frequency component due to the damping (described in Section 2) of compressible plasma motion that suppresses the small scale and high frequency compressive turbulent modes. The MHD plasma therefore evolves towards a nearly incompressible state and the density is convected passively by the velocity field to yield a $k^{-5/3}$ spectrum.

Perhaps, the most striking point about the Kolmogorov-like $k^{-5/3}$ spectrum is its ubiquitous persistence in fluids and plasmas regardless of whether they are (in)compressible, (un)magnetized, (an)isotropic and (un)driven. The observed Kolmogorov-like density spectrum yields two paradoxes; (1) why does a compressible magnetized fluid behaves as though it were incompressible and umagnetized, and (2) Why do the density fluctuations, an apparently quintessential compressive characteristic of magnetized turbulence, yield a Kolmogorov power law spectrum characteristic of incompressible hydrodynamic turbulence? These questions have to be answered if we are to address the origin of the 5/3 spectrum in MHD turbulence in general and the ISM density power law spectrum, in particular. In this paper, we address these issues within the context of fully 3D simulations of compressible, anisotropic, driven Magnetohydrodynamics (MHD) turbulence to understand how and why a supersonic, super Alfvénic, and low plasma $\beta$ ($\beta$ the ratio of plasma pressure and magnetic pressure) compressible MHD fluid should exhibit a Kolmogorov-like wavenumber spectrum in density. We find a strong correlation between the intrinsic MHD waves (i.e. Alfvén, fast & slow magnetoacoustic modes) and nonlinear inertial range turbulent cascades that suggests that nonlinear mode coupling interactions in compressible MHD turbulence tend to dissipate high frequency magnetoacoustic modes. Consquently, the inertial range cascade is governed predominantly by Alfvénic interactions that passively convect the density field to yield a Kolmogorov-like $k^{-5/3}$ spectrum.

In section 2, we describe the governing equations, and critical assumptions of our 3D magnetohydrodynamic simulations. Section 3 describes results from nonlinear fluid simulations of compressible, driven, anisotropic, homogeneous, turbulent magnetohydrodynamic (MHD) plasma. Our simulations demonstrate that density, magnetic and velocity fields in MHD turbulence follow an omnidirectional Kolmogorov-like $k^{-5/3}$ turbulent spectrum. The physical arguments explaining the evolution of a $k^{-5/3}$ spectrum are described in section 4 that deal primarily with turbulent damping of non-solenoidal velocity field fluctuations. In section 5, we outline our results for anisotropic cascades that result from the presence of a mean magnetic field in MHD turbulence. Finally, section 6 summarizes our major results.

Our underlying magnetohydrodynamic (MHD) model assumes that characteristic fluctuations in the magnetofluid plasma are initially isotropic, homogeneous, thermally equilibrated and turbulent. A large scale constant magnetic field is present and drives anisotropic turbulent cascades in an initially isotropic spectral distribution in compressible MHD turbulence. The characteristic turbulent fluctuations in the plasma are assumed in our model to be much bigger than shocks or discontinuities. In other words, we ignore the influence of shock on turbulent fluctuations. Our work incorporating the effect of shocks on turbulent spectra is initiated in Zank et al (2007, 2006). The boundary conditions are periodic, hence mode coupling interactions in the local spatial region are considered.

The fluid model describing nonlinear turbulent processes in the magnetofluid plasma, in the presence of a background magnetic field, can be cast into plasma density ($\rho_{p}$), velocity (${\bf U}_{p}$), magnetic field (${\bf B}$), pressure ($P_{p}$) components according to the conservative form

where,

and

Equations (1) are normalized by typical length $\ell_{0}$ and time $t_{0}=\ell_{0}/V_{A}$ scales in our simulations such that $\bar{\nabla}=\ell_{0}{\nabla},\partial/\partial\bar{t}=t_{0}\partial/\partial t,\bar{\bf U}_{p}={\bf U}_{p}/V_{A},\bar{\bf B}={\bf B}/V_{A}(4\pi\rho_{0})^{1/2},\bar{P}=P/\rho_{0}V_{A}^{2},\bar{e}_{p}=e_{p}/\rho_{0}V_{A}^{2},\bar{\rho}=\rho/\rho_{0}$. The bars are removed from the normalized equations (1). $V_{A}=B_{0}/(4\pi\rho_{0})^{1/2}$ is the Alfvén speed

The rhs in the momentum equation denotes a forcing functions (${\bf f}_{M}({\bf r},t)$) that essentially influences the plasma momentum at the larger length scale in our simulation model. With the help of this function, we drive energy in the large scale eddies to sustain the magnetized turbulent interactions. In the absence of forcing, the turbulence continues to decay freely. While the driving term modifies the momentum of plasma, we conserve density (since we neglect photoionization and recombination). The large-scale random driving of turbulence can correspond to external forces or instabilities for example fast and slow streams, merged interaction region etc in the solar wind, supernova explosions, stellar winds in the ISM, etc. The magnetic field evolution is governed by the usual induction equation, i.e. Eq. (1), and obeys the frozen-in-field theorem unless dissipative mechanism introduces small-scale damping. Note carefully that MHD plasma momentrum equation contains dissipative terms on the rhs. It is the term in the momentum equation (i.e. $\partial(\rho_{p}{\bf U}_{p})/\partial t\cdots$) that is proportional to $\mu\nabla^{2}{\bf U}_{p}+\eta\nabla(\nabla\cdot{\bf U}_{p})$. The latter (along with the other terms in the equation) is divided by the density $\rho_{p}$ field during the evolution to calculate the velocity field.

We have developed a fully three dimensional compressible MHD code to study the nonlinear mode coupling interaction in the context of compressible MHD turbulence. Details of our code are described in (Shaikh & Zank, 2006, 2007). In the simulations, all the fluctuations are initialized isotropically with random phases and amplitudes in Fourier space and an initial spectral shape close to $k^{-2}$ ($k$ is the Fourier mode, which is normalized to the characteristic turbulent length-scale $l_{0}$). We have carried out the simulations for both decaying and driven-dissipative cases with and without external magnetic field $B_{0}$. Since we are interested in a local region of the solar wind magnetofluid plasma, the computational domain employs a normalized three-dimensional periodic box of volume $\pi^{3}$. Other parameters are $\gamma=5/3,\beta=0.1-2.0,M_{A}=1.0-2.0,M_{s}=1.0-2.0,\eta=\mu=10^{-14}-10^{-15},k_{f}<15.0$, where $\gamma,M_{A},M_{s},\eta,\mu$ and $k_{f}$ are respectively the ratio of specific heats, Alfvén Mach number, sonic Mach number, viscosity, magnetic diffusion and energy injection modes. Our MHD model does not include (photo)ionization and radiation terms. Hence source or sink terms corresponding to the density fluctuations are not included in our MHD model. Additionally, the localized dissipation is effective in our simulations at the small-scales where it damps the plasma motions. The small scale dissipation in the local interstellar medium or solar wind may result from e.g. radiative cooling or ion-neutral collisions (Spangler, 1991). Accordingly, the small-scale dissipation in our model corresponds to collisional or viscous effects and is associated with the small-scale damping that is responsible only for the cascade of large-scale energy into the smaller scales thereby producing a well-defined inertial range turbulent spectrum. By contrast, the large-scales and the inertial range turbulent fluctuations remain unaffected by direct dissipation of the smaller scales.

The initial kinetic and magnetic energies are equi-partitioned between the velocity and the magnetic fields. The latter helps treat the transverse or shear Alfvén and fast/slow magnetosonic waves on an equal footing, at least during the early phase of the simulations. Magnetoplasma turbulence evolves under the action of nonlinear interactions in that larger eddies transfer their energy to smaller ones through a forward cascade. According to (Kolmogorov, 1941; Iroshnikov, 1963; Kraichnan, 1965), the cascade of spectral energy is mediated by a local interaction amongst the neighboring Fourier modes that continues until the energy in the smallest turbulent eddies is dissipated due to the finite Reynolds number. This leads to the damping of small scale motions as well. This results in a net decay of the turbulent sonic Mach number $M_{s}$ associated with the large scale fluctuations. If turbulence is not driven at large scales, the turbulent sonic Mach number continues to decay from a supersonic ($\tilde{M}_{s}>1$) to a subsonic ($\tilde{M}_{s}<1$) regime (Shaikh & Zank, 2006). This indicates that nonlinear cascades predominantly cause supersonic MHD plasma fluctuations to become subsonic. In our decaying turbulence simulation, the large-scale energy simply migrates towards the smaller scales by virtue of nonlinear cascades in the inertial range and is dissipated at the smallest turbulent length-scales. On the other hand, spectral transfer in driven turbulence follows a similar cascade process as in the decaying turbulence case. However, the inertial range spectrum in the latter is maintained by a large scale forcing at $k<5$. The spectral transfer of turbulent energy in the neighboring Fourier modes in globally isotropic and homogeneous hydrodynamic and magnetohydrodynamic turbulence is the widely accepted paradigm (Kolmogorov, 1941) that leads to Kolmogorov-like energy spectra, while (Iroshnikov, 1963; Kraichnan, 1965) describe turbulent spectra in the presence of a mean or local $B_{0}$. The most striking effect, however, to emerge from the decay of the turbulent sonic Mach number is that the density fluctuations begin to scale quadratically with the subsonic turbulent Mach number as soon as the compressive plasma enters the subsonic regime, i.e. $\delta\rho\sim{\cal O}(\tilde{M}_{s}^{2})$ when $\tilde{M}_{s}<1$. This was demonstrated in our 3D simulations of a compressible MHD plasma (Shaikh & Zank, 2006). It signifies an essentially weak compressibility in the magnetoplasma, and is consistent with a nearly incompressible state (Matthaeus & Brown, 1988; Zank & Matthaeus, 1990, 1993; Shaikh & Zank, 2006).

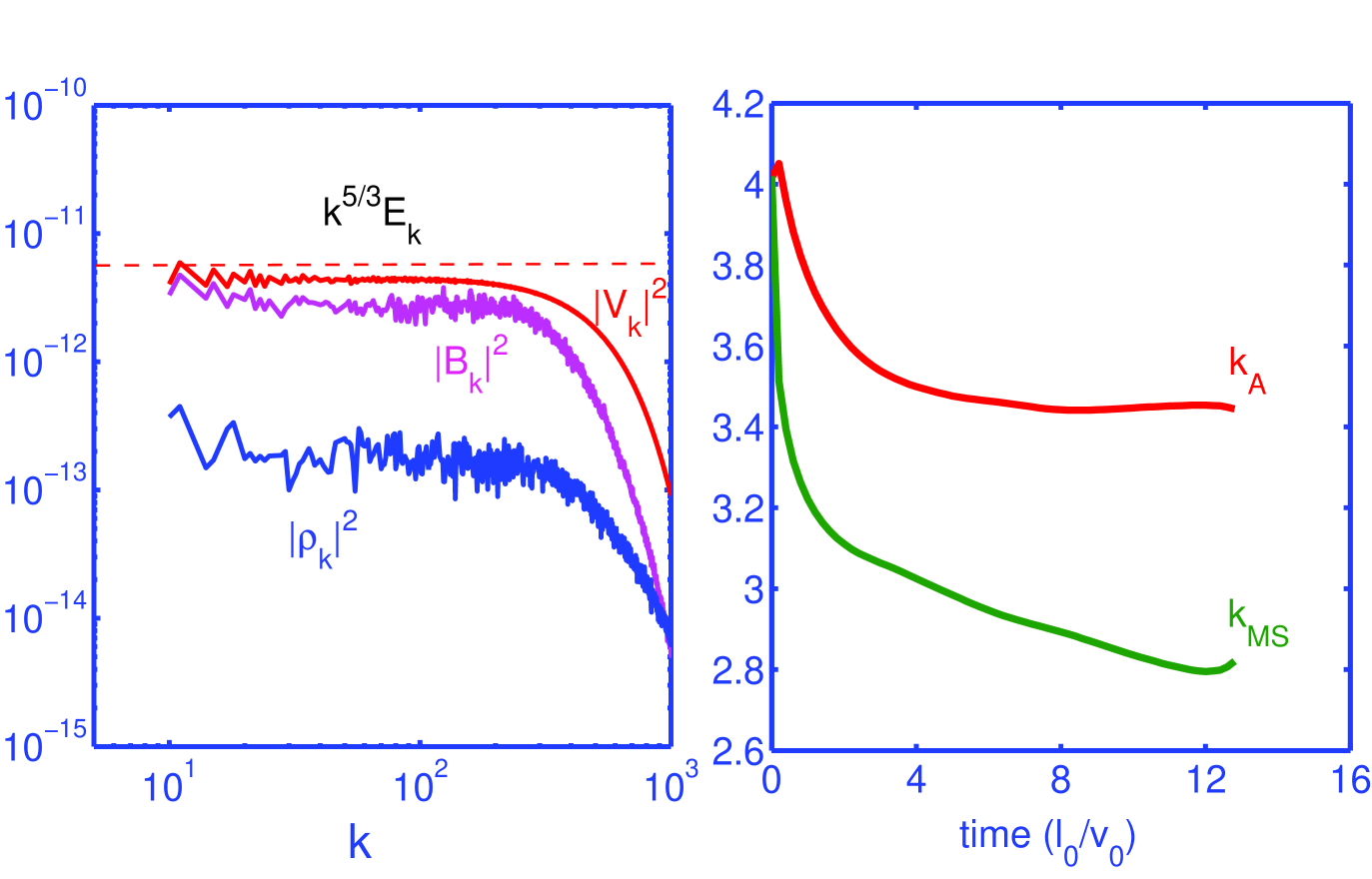
In the context of the magnetoplasma being nearly incompressible, the density fluctations exhibit a weak compressibility in the gas and are convected predominantly passively in the background incompressible fluid flow field. This hypothesis can be verified straightforwardly by investigating the density spectrum which should be slaved to the incompressible velocity spectrum. This is shown in Fig. (1) which illustrates that the density fluctuations follow the velocity fluctuations in the inertial regime over the long time (several Alfvén transit time) evolution of MHD turbulence. The evolution of compressible magnetoplasma from a(n) (initial) supersonic to a subsonic or nearly incompressible regime is gradual and it results in the density field following the velocity fluctuations. In the subsonic regime, compressibility weakens substantially so that density fluctuations are advected only passively. A passively convected fluid exhibits a similar inertial range spectra as that of its background flow field (McComb, 1990). Likewise, subsonic density fluctuations in our simulations exhibit a Kolmogorov-like $k^{-5/3}$ spectrum similar to the background velocity fluctuations in the inertial range. This, we believe, provides a plausible explanation for the Kolmogorov-like density spectrum observed in MHD turbulence i.e. they are convected passively in a field of nearly incompressible velocity fluctuations and acquire identical spectral features [as shown in Fig. (1)]. The passive scalar evolution of the density fluctuations is associated essentially with incompressiblity and can be understood directly from the continuity equation as follows. Expressing the fluid continuity equation as $(\partial_{t}+{\bf U}\cdot\nabla)\ln\rho=-\nabla\cdot{\bf U}$, where the rhs represents compressiblity of the velocity fluctuations, shows that the density field is advected passively when the velocity field of the fluid is nearly incompressible with $\nabla\cdot{\bf U}\simeq 0$. The theoretical basis illustrating the nonlinear damping of the non-solenoidal component of velocity field, i.e. $\nabla\cdot{\bf U}\rightarrow 0$, is described quantitatively in the following section.

Understanding, how an initially non-solenoidal velocity field evolves towards a solenoidal field is important as it explains the evolution of a compressible MHD magnetoplasma from a supersonic to a subsonic or nearly incompressible state that yields a passively advected Kolmogorov-like $k^{-5/3}$ density spectrum. Any given velocity field can be decomposed into solenoidal and non-solenoidal components or, equivalently, longitudinal and transverse components, which we shall here refer to as fast/slow magnetosonic and Alfven components, respectively. The simulations show that the amplitudes of fast/slow magnetosonic components described by the quantity $k_{MS}$ decay more rapidly than the amplitudes of the Alfvenic components. Consequently, they will be inefficient in cascading the corresponding inertial range spectral energy. Hence nonlinear interactions, in the inertial range, are governed predominantly by non-dissipative Alfvénic modes ($k_{A}$) that survive collisional damping in compressible MHD turbulence. This is quantitatively demonstrated in Fig. (1)[right panel].

The damping of a non-solenoidal velocity component, in part, explains the observed Kolmogorov-like $k^{-5/3}$ in our simulations. To this end, it is essential to distinguish the Alfvénic and non-Alfvénic, i.e. corresponding to the compressional or due to slow and fast magnetosonic modes, contributions to the turbulent velocity fluctuations. To identify the distinctive role of Alfvénic and fast/slow (or compressional) MHD modes, we introduce diagnostics that distinguish the energies corresponding to Alfvénic and slow/fast magnetosonic modes. Since the Alfvénic fluctuations are transverse, the propagation wave vector is orthogonal to the velocity field fluctuations i.e. ${\bf k}\perp{\bf U}$, and the average spectral energy contained in these (shear Alfvénic modes) fluctuations can be computed as

The above relationship leads to a finite spectral contribution from the $|{\bf k}\times{\bf U}_{\bf k}|$ characteristic turbulent Alfvénic modes. On the other hand, fast/slow magnetosonic modes propagate longitudinally along the velocity field fluctuations, i.e. ${\bf k}\parallel{\bf U}$ and thus carry a finite component of energy corresponding only to the $i{\bf k}\cdot{\bf U}_{\bf k}$ part of the velocity field, which can be determined from the following relationship

The expression of $k_{MS}$ essentially describes the modal energy contained in the non-solenoidal component of the MHD turbulent modes.

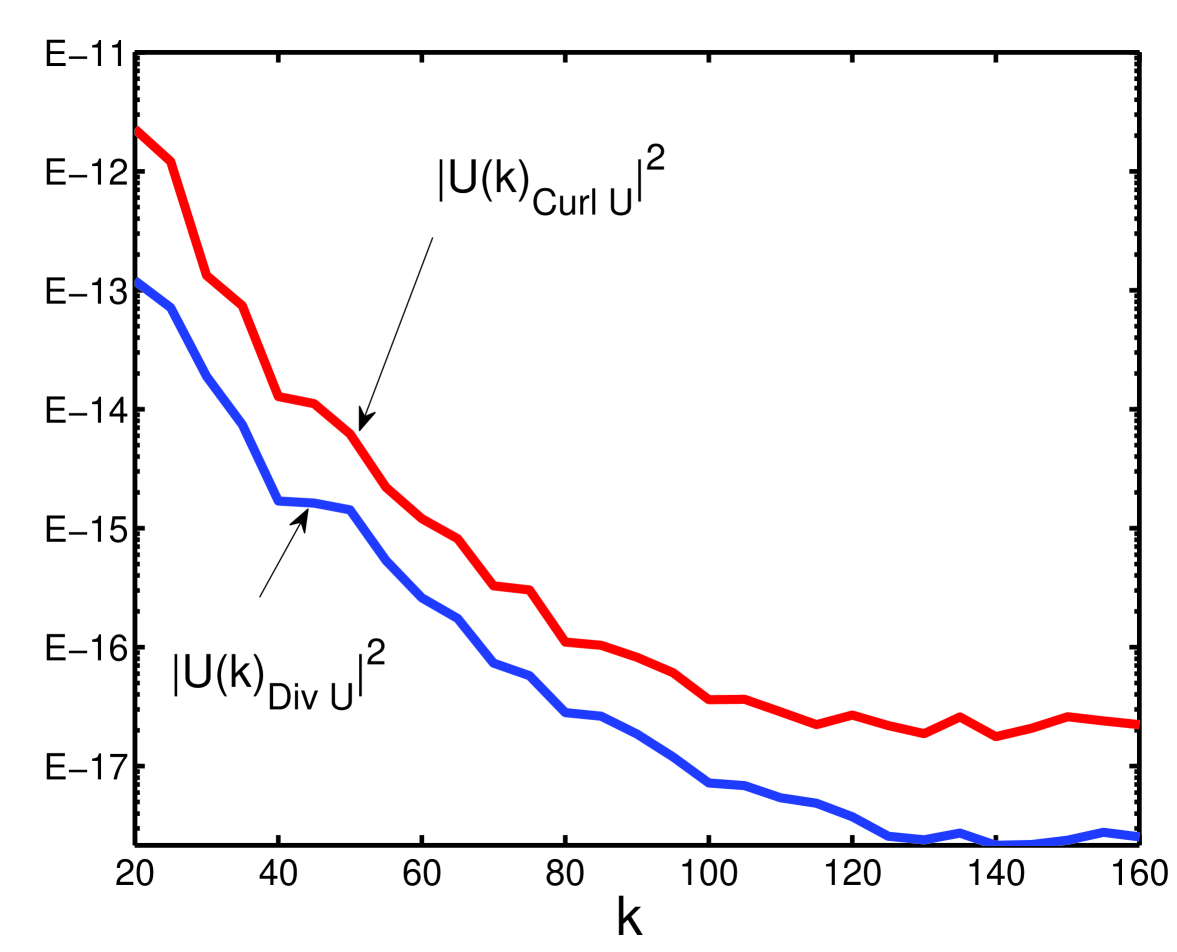
The quantative evolution of the characteristic modes corresponding to the Alfvénic $k_{A}$ and slow/fast compressional magnetosonic $k_{MS}$ modes is depicted in Fig. 1 (right panel). Although the modal energies in $k_{A}$ and $k_{MS}$ modes are identical initially, a disparity in the cascade rate develops, and the energy in longitudinal (or compressional) fluctuations associated with the non-solenoidal velocity field decays far more rapidly than the energy in the Alfvénic modes. The Alfvénic modes, after a modest initial decay, sustain the energy cascade processes by actively transferring spectral power amongst various Fourier modes. By contrast, the fast/slow magnetosonic modes ($k_{MS}$) progressively weaken and suppress their corresponding spectral contribution in the turbulent energy cascades. The difference in the cascades corresponding to $k_{A}$ and $k_{MS}$ modes persists even at long times. The $k_{MS}$ mode represents collectively a dynamical evolution of small-scale fast plus slow magnetosonic cascades. The physical implication, however, that emerges from Fig. 1 is that the fast/slow magnetosonic modes ($k_{MS}$) do not contribute efficiently to the spectral transfer process, and that the cascades are governed predominantly by non-dissipative Alfvénic modes that survive the collisional damping in compressible MHD turbulence. Correspondingly, the turbulent energy associated with the Alfvénic modes makes a dominant contribution to the velocity fluctuation spectrum when compared to the magnetosonic modes. We have made measurements of the turbulent energy in the Alfvénic and fast/slow magnetosonic modes to quantify their respective contributions to the velocity field fluctuation spectrum. This is shown in Fig. (2). In Fig (2), $|U(k)_{\rm CurlU}|^{2}=\sum_{k}|{\bf k}\times{\bf U}_{\bf k}|^{2}/\sum_{k}{k^{2}}$ and $|U(k)_{\rm DivU}|^{2}=\sum_{k}|{\bf k}\cdot{\bf U}_{\bf k}|^{2}/\sum_{k}{k^{2}}$. Clearly, the energy contribution by Alfvénic modes (parallel to $B_{0}$ and orthogonal to the velocity field) is more than 10 times that of the fast/slow magnetosonic modes (parallel to the velocity field). This clarifies that it is the predominance of Alfvénic modes (Fig (1) & (2)) in inertial range cascades that primarily lead to a Kolmogorov-like spectrum. Damping of Alfvén waves is possible by ion-neutral collisions as pointed out by (Kulsrud & Pearce, 1969; Balsara, 1996) in the context of molecular clouds [for more references, see (Shaikh & Zank, 2008)]. In our present simulations, we do not include ion-neutral damping as we focus mainly on the solar wind plasma. This nonetheless suggests that because of the decay of the fast/slow magnetosonic modes in compressible MHD plasmas, supersonic turbulent motions become dominated by subsonic motions and the nonlinear interactions are sustained primarily by Alfvénic modes thereafter; the latter being incompressible. One of the implications of the turbulent damping of non-solenoidal velocity field ($i{\bf k}\cdot{\bf U}_{\bf k}$) in an MHD fluid is that compressible modes make negligible or no contribution to the inertial range energy cascade. The cascade is thus determined primarily by the incompressible Alfvén modes that passively convect the density fluctuations. This point is further consistent with the MHD fluid continuity equation which in $k$ space reads as follows.

The nonlinear mode coupling interations associated with the Dirac delta function $\delta$ are finite only for those interactions that obey the Fourier diad ${\bf k}+{\bf k^{\prime}}=0$ in spectral space. It follows from our simulations that the turbulent damping of the non-solenoidal velocity field on the rhs of the continuity equation makes an insignificant contribution to the inertial range energy cascade. The nonlinear mode coupling interactions in MHD turbulence are therefore dominated by convective transport that leads to a passive convection of density fluctuations. The density fluctuations subsequently follow the inertial range spectrum and are identical to the background nearly incompressible velocity field and thus have a Kolmogorov-like $k^{-5/3}$ spectrum Kolmogorov (1941); McComb (1990); Lesieur (1990) in MHD turbulence. Our simulation results described in Fig. (1) are fully consistent with this scenario.

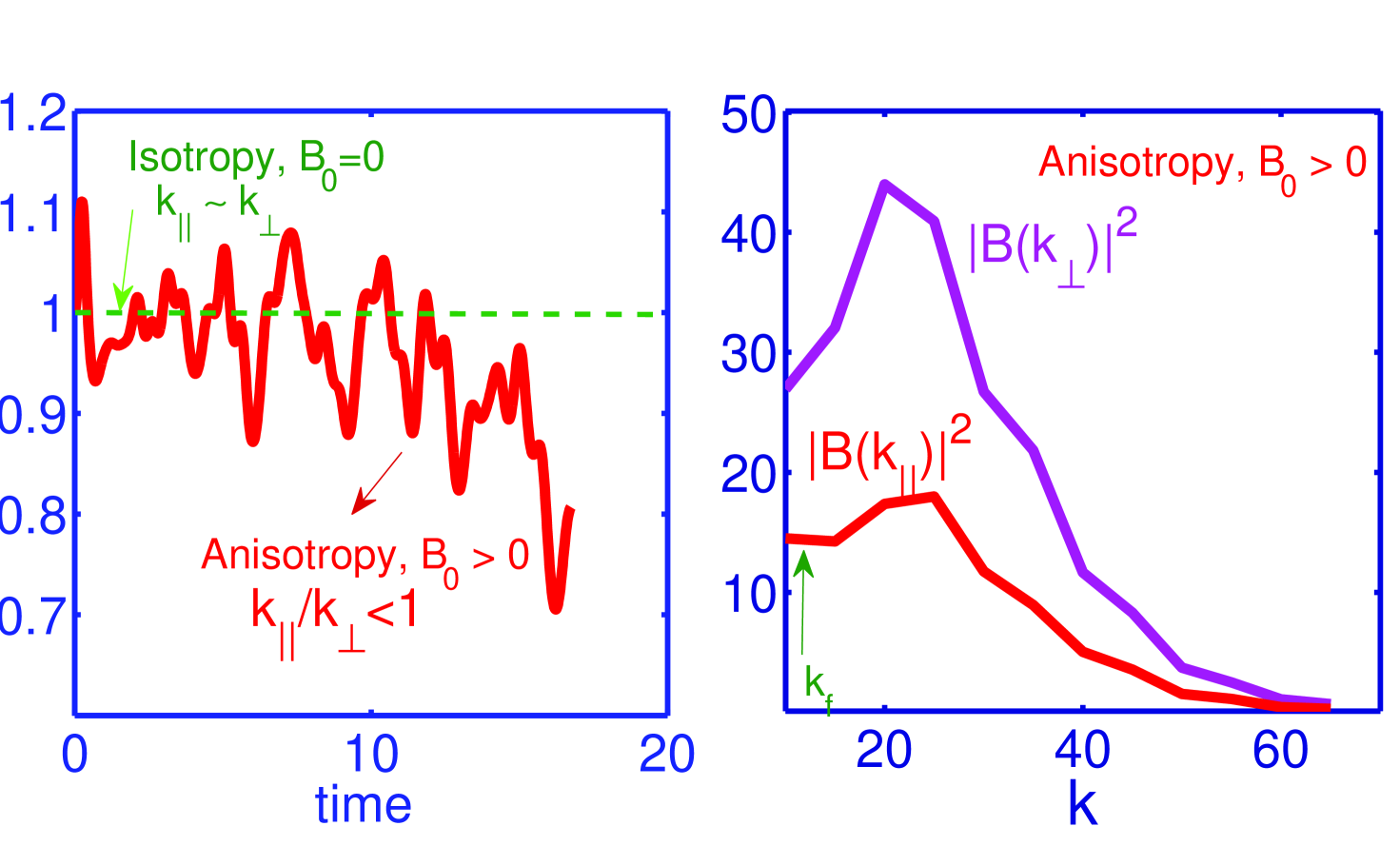
We find that the presence of a large scale magnetic field $B_{0}$ (along the $\hat{z}$-direction) introduces anisotropy in the distribution of energy in wavevector space such that the rms wavenumbers along ($k_{\parallel}$) and across ($k_{\perp}$) the mean magnetic field $B_{0}$ show a discrepancy i.e. $k_{\parallel}\neq k_{\perp}$ [see Fig. (3)]. We employ the following diagnostics to monitor the evolution of the rms wavenumbers $k_{\perp}$ and $k_{\parallel}$ in time. The rms $k_{\perp}$ mode is determined by averaging over the entire turbulent spectrum weighted by $k_{\perp}$, thus

Here $\langle\cdots\rangle$ represents an average over the entire Fourier spectrum, $k_{\perp}=\sqrt{k_{x}^{2}+k_{y}^{2}}$. Similarly, the evolution of the $k_{\parallel}=k_{z}$ (along the $B_{0}$ direction) mode is determined by the following relation,

The wavenumbers $k_{x},k_{y}$ and $k_{z}$ are respectively along the $x,y$ and $z$ directions. It is clear from these expressions that the $k_{\perp}$ and $k_{\parallel}$ modes exhibit isotropy when $k_{\perp}\simeq k_{\parallel}$. Any deviation from this equality corresponds to spectral anisotropy. We follow the evolution of $k_{\perp}$ and $k_{\parallel}$ in our simulations. We find a disparity in the magnetic field fluctuation spectrum along

and across

the mean magnetic field (see Fig. 3, right panel). Note that the discrete summations $\sum_{k_{\parallel}}$ and $\sum_{k_{\perp}}$ are carried over $k_{\parallel}$ and $k_{\perp}$ modes respectively. The presence of the mean magnetic field inhibits turbulent cascades in the parallel (to $B_{0}$) direction and hence the characteristic modes ($k_{\parallel}$) along the mean magnetic field are suppressed, while the modes in the orthogonal direction remain unaffected. The evolution in Fig. (3) therefore shows that the initial isotropic ratio $k_{\parallel}/k_{\perp}\approx 1$ progressively evolves towards anisotropy $k_{\parallel}/k_{\perp}<1$.

The suppression of the $k_{\parallel}$ mode is caused by the excitation of Alfvén waves, which act to weaken spectral transfer along the direction of propagation. This can be understood as follows; We assume that the spectral transfer, mediated by propagating Alfvén waves, can be described by a three wave interaction mechanism, for which the frequency and wavenumber resonance criteria are, respectively, expressed by Shebalin et al. (1983); Matthaeus et al (1998)

and

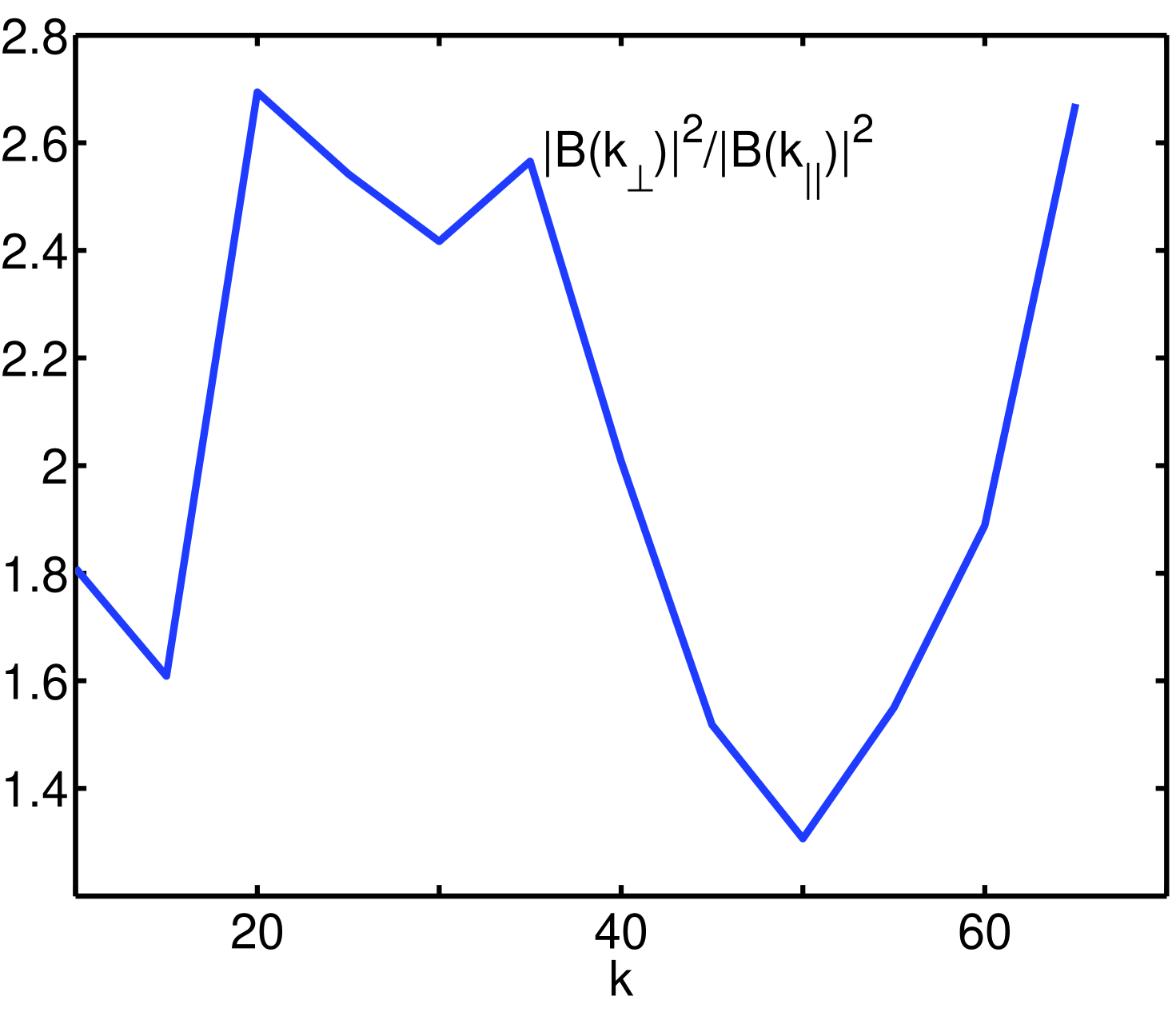
The frequency-wavenumber resonance conditions indicate that two Alfvén waves $(\omega_{1},{\bf k}_{1})$ and $(\omega_{2},{\bf k}_{2})$ mutually interact and give rise to the third wave $(\omega_{3},{\bf k}_{3})$. Such conditions could, in principle, hold for a set of infinite waves as the indices ‘$1$’ and ‘$2$’ are merely dummy indices. With the help of the Alfvén wave dispersion relation ($\omega={\bf k}\cdot{\bf B}_{0}$) and the component of wavenumber matching relation along $B_{0}$, i.e. $k_{3_{\parallel}}=k_{1_{\parallel}}+k_{2_{\parallel}}$, we infer that either the $k_{1_{\parallel}}=0$ or $k_{2_{\parallel}}=0$. It follows from the frequency-wavenumber resonance conditions that either the $k_{1_{\parallel}}=0$ or $k_{2_{\parallel}}=0$. Owing to the absence of one of the parallel (to $B_{0}$) components of the modes, nonlinear mode coupling interaction becomes inefficient in transferring the inertial range spectral energy in the parallel direction. Hence there is very little cascading along the magnetic field direction. Thus, the parallel wavenumbers ($k_{\parallel}$) appear to be suppressed and the spectral cascade mainly occurs in the perpendicular wavenumbers ($k_{\perp}$). Consequently, the magnetic field spectrum along the mean $B_{0}$ is depleted. This, we suggest, explains the wavenumber disparity $k_{\parallel}\neq k_{\perp}$ observed in our simulations [see Fig 3]. While the turbulent cascades are effected locally by the presence of the mean magnetic field, the 3D volume averaged inertial range spectra in our simulations continue to exhibit a power law close to that of Fig. (1).

The question of anisotropic inertial range cascades has long been debated in the context of MHD turbulence. It dates back to the seminal work of Iroshnikov Iroshnikov (1963) and Kraichnan (1965), who first pointed out that the presence of a large-scale or self-consistently generated magnetic field influences the spectral power cascade mechanism in a complicated manner (Iroshnikov, 1963; Kraichnan, 1965). Kraichnan (1965) addressed the interaction of magnetized turbulent eddies with Alfvén waves, excited as a result of a mean magnetic field. Owing to the presence of waves in a MHD fluid, turbulent correlations between velocity and magnetic field and the corresponding energy transfer time are determined primarily by $\tau\sim(b_{0}k)^{-1}$, where $b_{0}$ is a typical amplitude of a local magnetic field and is dimensionally identical to that of the velocity field by virtue of Els$\ddot{\rm a}$sser’s symmetry (Kraichnan 1965). According to Kraichnan (1965), it is this time scale that leads to the modification in the energy transfer (or cascade) because of the wave-turbulent eddy interaction process and without this modification the energy cascade rates would be determined by typical hydrodynamic eddy interaction time. The assumption of isotropy in the Kolmogorov energy spectrum Kolmogorov (1941) was later modified to include the mean or large scale magnetic field (Kraichnan, 1965; Shebalin et al., 1983; Higdon, 1984, 1986; Goldreich & Sridhar, 1995; Matthaeus et al, 1998), in part, because the presence of waves in MHD turbulence can significantly influence the energy cascade dynamics in the wavenumber space. An attractive analysis was presented by Shebalin et al (Shebalin et al., 1983), who demonstrated that the presence of a mean (or dc) magnetic field introduces a spectral anisotropy in the MHD turbulent spectrum. The observed anisotropic cascade in their work was understood to be due to the presence of Alfvén waves, which are excited and propagate along the mean magnetic field. The non-dispersive propagating Alfvén waves in the presence of a mean magnetic field give rise to distinct energy cascade rates along and across the large-scale magnetic field, thereby leading to an asymmetry in the spectral transfer rates. This can be understood as follows; The inertial range energy cascade rates depend on wavenumber (or modes). Since the presence of the background magnetic field depletes the parallel mode (i.e. $k_{\parallel}$ or $k_{z}$) and leaves the perpendicular mode $k_{\perp}$ unaffected, the spectral energy transfer corresponding to the $k_{\parallel}$ mode is suppressed in the direction of the mean or background magnetic field. By contrast, the perpendicular transfer of spectral energy remains unaffected. This is quantified by Fig (3), right panel in which the spectrum of $|B(k_{\parallel})|^{2}$ is suppressed as compared to that of $|B(k_{\perp})|^{2}$. It is because of this disparity, the energy cascades along and across the background magnetic field are distinct. Such asymmetric cascades, in agreement with arguments based on the frequency-wavenumber resonance conditions described as above, produce spectral anisotropy in MHD turbulence (Shebalin et al., 1983; Matthaeus et al, 1998). In the context of the solar wind plasma, fast ($>500$km/s) and slow ($<400$km/s) streams are dominated respectively by $k_{\parallel}$ and $k_{\perp}$ anisotropic modes Dasso et al (2005). A more quantitative treatment of anisotropic cascade was put forward by Goldriech and Sridhar (Goldreich & Sridhar, 1995) for MHD turbulence, suggesting that the Kolmogorov energy spectrum corresponds to wavenumbers perpendicular to the local magnetic field so that $E(k_{\perp})\sim k_{\perp}^{-5/3}$ (where $k_{\perp}$ is wavenumber perpendicular to the local magnetic field), whereas the parallel wave number scales as $k_{\parallel}\propto k_{\perp}^{2/3}$. Boldyrev (2005) proposes that a Goldreich-Sridhar like spectrum Goldreich & Sridhar (1995) results from a weak large-scale magnetic field, while the limit of strong anisotropy, that is, strong large-scale magnetic field, corresponds to the Iroshnikov-Kraichnan Iroshnikov (1963); Kraichnan (1965) scaling of the spectrum. This suggests that there exists an asymmetry in the energy cascade mechanism, which is believed to be due primarily to the presence of large-scale local magnetic fields in the turbulent MHD flow. Our simulation results describing the anisotropic MHD turbulent cascades, depicted in Fig. (3), are further consistent with (Shebalin et al., 1983).

Our work proposes a self-consistent physical paradigm for the development of the density fluctuations spectrum in solar wind plasma in the context of compressible, driven-dissipative, anisotropic 3D MHD turbulence. Understanding turbulent cascades in the MHD plasma is critical to many astrophysical phenomena. These range from understanding the role of waves and nonlinear cascades in the evolution of the solar wind, structure formation at the largest scales, cosmic ray scattering and energization by solar wind turbulence at the smallest scales and the heating of the solar wind (Scalo & Elmegreen 2004, Elmegreen & Scalo 2004, Goldreich & Sridhar 1995, Zank 1999, Goldstein et al 1995, Scalo et al 1998, Goldreich 2001) to problems such as energy transfer across many scales in the ISM Roy et al (2008); Haverkorn (2008); Ryu et al (2008); Rickett (2007); Willett (2005); Elmegreen (1999); Dickey et al (2001); Minter & Spangler (1996).

We find from our 3D (decaying turbulence) simulations that a $k^{-5/3}$ density fluctuation spectrum emerges in fully developed compressible MHD turbulence from nonlinear mode coupling interactions that lead to the migration of spectral energy in the transverse (i.e. ${\bf k}\perp{\bf U}$) Alfvénic fluctuations, while the longitudinal “compressional modes” corresponding to ${\bf k}\parallel{\bf U}$ fluctuations make an insignificant contribution to the spectral transfer of inertial range turbulent energy. The explanation, in part, resides with the evolutionary characteristics of the MHD plasma that governs the evolution of the non-solenoidal velocity field in the momentum field. It is the non-solenoidal component of plasma motions that describes the high frequency contribution corresponding to the acoustic time-scales in the modified pseudosound relationship (Montgomery et al 1987; Matthaeus et al 1988; Zank & Matthaeus 1990; Zank & Matthaeus 1993). What is notable in our present work is we find a self-consistent evolution of a Kolmogorov-like density fluctuation spectrum in MHD turbulence that results primarily from turbulent damping of non-solenoidal modes that constitute fast and slow propagating magnetoacoustic compressional perturbations. These are essentially a higher frequency (compared with the Alfvénic waves) component that evolve on acoustic time-scales and can lead to a “pseudosound relationship” as identified in the nearly incompressible theory (Matthaeus et al 1988; Zank & Matthaeus 1990; Zank & Matthaeus 1993; Bayly et al; Shaikh & Zank 2004a,b,c, 2006, 2007). The most significant point to emerge from our simulation is the diminishing of the high frequency component that is related to the damping of compressible plasma motion. This further leads to the dissipation of the small scale and high frequency compressive turbulent modes. Consequently, the MHD plasma relaxes towards a nearly incompressible state where the density is convected passively by the velocity field and eventually develops a $k^{-5/3}$ spectrum. This physical picture suggests that a nearly incompressible state develops naturally from a compressive MHD magnetoplasma in the solar wind.

The higher resolution in-situ solar wind velocity field observations at 1AU show a typical spectral index in the range from 1.4 to 1.5 (Podesta et al 2007; Tessein et al. 2009). The latter clearly differs from our simulations in which the spectrum of density field is close to 1.67. To this end, we should point out that the solar wind observations at 1 AU contradict the fundamental theme of our model which states that the density fluctuations are convected passively by the velocity field and thereby acquire similar spectral power-law. Owing thus to the differences between the observations and our simulations, our model describing the passive convection of the density field through the nearly incompressible velocity field may not hold near 1 AU. Consequently, the solar wind density fluctuations ($\sim k^{-5/3}$) at 1 AU cannot be correlated with the velocity field ($\sim k^{-3/2}$) through the passive-advection phenomenology. We believe that the deviation of the density and velocity fields, leading thereby to the obvious differences near 1 AU, may arise from a number of physical processes, as noted below. Firstly, the physical processes driving the velocity spectrum near 1 AU are different from those beyond 1 AU. Therefore, the evolutionary characteristics associated with the velocity spectrum near 1 AU (describing a 3/2-like spectrum) can certainly not be representive of the distant outer heliospheric turbulence spectrum. Secondly, close to 1 AU, stream interactions, shear instabilities, compressional modes, and many other physical processes can plausibly alter the velocity field spectrum. It is unclear from the work of Podesta et al (2007) and Tessien et al (2009) whether any of these processes have a significant influence on the observed spectral indices. To further clarify this point, we have carried out more simulations to distinguish the evolution of kinetic energy, and incompressible, compressible, and total velocity spectra (not shown in this paper). We find that the compressive velocity field exhibits a flatter spectrum, while the incompressible velocity field follows a 5/3 spectrum. This could very well mean that the velocity field, if is, driven or dominated by compressive modes, has a spectrum may be a flatter than 5/3. Thirdly, the Alfvénic interactions, often invoked to explain the descrepnacy between the Kolmogorov-like (5/3) and Kraichnan-like (3/2) spectra, are ascribed to Alfvén waves in MHD turbulence (Iroshnikov 1963; Kraichnan 1965; Shebalin et al 1983; Biskamp 2003). The latter inhibits energy cascades along the direction of propagation. The spectral transfer of inertial range turbulent energy is therefore suppressed along the mean $B_{0}$, whereas the perpendicular cascade is governed predominantly by the hydrodynamic-like interactions. Consequently, the energy spectrum is dominated by hydrodynamic-like processes which lead to a Kolmogorov-like (5/3) inertial range turbulent spectrum. Hence a Kolmogorov-like (5/3) spectrum emerges in MHD turbulence when the nonlinear interactions are dominated by hydrodynamic-like eddies. By contrast, magnetic field eddies governing the Alfvénic interactions lead to a Kraichnan-like (3/2) spectrum in MHD turbulence. Thus, the disparate time scales associated with Alfvénic and compressive modes may flatten out the velocity field but not the density field. Our model, thus relating the density to the velocity field spectrum, may not hold near 1 AU in the circumstances where the velocity fluctuations are driven by the processes as described above.

The Kolmogorov-like $k^{-5/3}$ spectrum in density, velocity and magnetic fields resulting from our simulation (see Fig 1) are fully consistent with those of Tilley & Pudritz (2007), Mac Low et al (1998, 1989), Biskamp (2003), Padoan & Nordlund (1999), Stone et al (1998), Goldstein et al (1995), Goldreich & Sridhar (1995) and with others that are described elsewhere in our paper.

The support of NASA(NNG-05GH38) and NSF (ATM-0317509) grants is acknowledged.