¹¹institutetext: University of Minho (CCTC-DI)
Campus de Gualtar, 4710-057 Braga, Portugal
¹¹email: {pcoj, cbm, psa}@di.uminho.pt

Dependability in Aggregation by Averaging

Paulo Jesus Carlos Baquero Paulo Sérgio Almeida

Abstract

Aggregation is an important building block of modern distributed applications, allowing the determination of meaningful properties (e.g. network size, total storage capacity, average load, majorities, etc.) that are used to direct the execution of the system. In the recent years, several approaches have been proposed to compute aggregation functions on distributed settings, exhibiting different characteristics, in terms of accuracy, time and communication complexity. However, the majority of the existing aggregation algorithms exhibit relevant dependability issues, when prospecting their use in real application environments. In this paper, we reveal some dependability issues of aggregation algorithms based on iterative averaging techniques, giving some directions to solve them. This class of algorithms is considered robust (when compared to common tree-based approaches), being independent from the used routing topology and providing an aggregation result at all nodes. However, their robustness is strongly challenged and their correctness often compromised, when changing the assumptions of their working environment to more realistic ones. The correctness of this class of algorithms relies on the maintenance of a fundamental invariant, commonly designated as mass conservation. We will argue that this main invariant is often broken in practical settings, and that additional mechanisms and modifications are required to maintain it, incurring in some degradation of the algorithms performance. In particular, we discuss the behavior of three representative algorithms (Push-Sum Protocol [1], Push-Pull Gossip protocol [2] and Distributed Random Grouping [3]) under asynchronous and faulty (with message loss and node crashes) environments. More specifically, we propose and evaluate two new versions of the Push-Pull Gossip protocol, which solve its message interleaving problem (evidenced even in a synchronous operation mode).

1 Introduction

With the advent of multi-hop ad-hoc networks, sensor networks and large scale overlay networks, there is a demand for tools that can abstract meaningful system properties from given assemblies of nodes. In such settings, aggregation plays an essential role in the design of distributed applications [4], allowing the determination of network-wide properties like network size, total storage capacity, average load, and majorities. Although apparently simple, in practice aggregation has reveled itself to be a non trivial problem, especially when seeking solutions in distributed settings, where no single element holds a global view of the whole system.

In the recent years, several algorithms have addressed the problem from diverse approaches, exhibiting different characteristics in terms of accuracy, time and communication tradeoffs. A useful class of aggregation algorithms is based on averaging techniques. Such algorithms start from a set of input values spread across the network nodes, and iteratively average their values with active neighbors. Eventually all nodes will converge to the same value and can estimate some useful metric. Averaging techniques allow the derivation of different aggregation functions besides average (like count, sum, maximum and minimum), according to the initial combinations of input values. E.g., if one node starts with input $1$ and all other nodes with input $0$ , eventually all nodes will end up with the same average $1/n$ and the network size $n$ can be directly estimated by all of them [5].

The main objective of this work is to expose relevant dependability issues of existing aggregation by averaging algorithms, when challenged by practical implementations in realistic scenarios. For this purpose, we discuss and evaluate the behavior of three representative averaging algorithms, when confronted with practical concerns like communication asynchrony, message loss and node failure. We choose to analyze the following algorithms: Push-Sum Protocol [1] (PSP), Push-Pull Gossip protocol [2] (PPG), and Distributed Random Grouping [3] (DRG). To the best of our knowledge this is the first evaluation of averaging algorithms focusing on dependability and taking into account practical implementation concerns.

The remaining of this paper is organized as follows. We briefly refer to the related work on aggregation algorithms in Section 2. A detailed analysis of some representative averaging aggregation algorithms, concerning their practical implementation on real distributed systems, is discussed in Section 3. In Section 4, we propose two solutions to fix the interleaving issues exhibited by PPG, and compare them with the original algorithm in a common simulation environment. Finally, we make some concluding remarks in Section 5.

2 Related Work

Several aggregation algorithms have been proposed in the last years, tackling the problem for different settings, and yielding different characteristics in terms of accuracy, time and communication complexity.

Classical approaches, like TAG [6], perform a tree-based aggregation where partial aggregates are successively computed from child nodes to their parents until the root of the aggregation tree is reached (requiring the existence of a specific routing topology). This kind of aggregation technique is often applied in practice to Wireless Sensor Network (WSN) [7]. Other tree-based aggregation approaches can be found in [8], and [9]. We should point out that, although being energy-efficient, the reliability of these approaches may be strongly affected by the inherent presence of single-points of failure in the aggregation structure.

Another common class of distributed aggregation algorithms is based on averaging techniques [1, 2, 5, 3, 10]; Here, the values of a variable across all nodes are averaged iteratively. This kind of approaches is independent from the routing topology, often using a gossip-based communication scheme between peers. In this study, we will specifically discuss three of these approaches: PSP [1], PPG [2], and DRG [3].

Alternative aggregation algorithms based on the application of probabilistic methods, can also be found in the literature. This is the case of Extrema Propagation [11] and COMP [12], which reduce the computation of an aggregation function to the determination of the minimum/maximum of a collection of random numbers. These two techniques tend to emphasize speed, being less accurate than averaging approaches.

Specialized probabilistic algorithms can also be used to compute specific aggregation functions, such as count (e.g. to determine the network size). This type of algorithms essentially relies on the results from a sampling process to produce an estimation of the aggregate, using properties of random walks, capture-recapture methods and other statistic tools [13, 14, 15, 16].

3 Analysis

We analyze the practical implementation of aggregation algorithms based on averaging techniques, envisioning their deployment on real distributed network systems (e.g WSN and P2P overlay networks). In particular, we discuss three representative algorithms from this class: PSP [1], PPG [2], and DRG [3]. The performed analysis focuses on the reliability of these algorithms, in order to provide an accurate aggregation estimate, on realistic application scenarios, which are commonly governed by communication asynchrony, and failures. More specifically, this analysis is confined to four main practical settings/concerns:

1.

Synchronous model – refers to the common synchronous operation mode, where the algorithms execution proceeds in lock-step rounds and without faults. In practice, where networks are typically asynchronous, it is possible to implement synchrony over an asynchronous fault-free network (see Chapter 16 of [17]), using a synchronizer. Notice that even under this strong synchrony assumption, algorithms that span more than one round, may see their messages interleaved across rounds;
2.

Asynchronous model – in these settings, message transit takes a finite but unknown time. We consider that nodes communicate using FIFO channels, and no faults will occur. This means that no message in transit can be surpassed by any other message from the same source. Commonly, in practice, the transport communication layer (e.g. TCP) can provide a reliable and ordered message delivery, retransmitting undelivered data packets and using a sequence number to identify their order. Like in previous settings, interleavings may also frequently occur;
3.

Message loss – corresponds to the loss of communication data, due to a temporary link or node failure. In this settings, we consider asynchronous non-FIFO communication, where no guarantee on message delivery is made (like in UDP);
4.

Node Crash – refers to the permanent failure of a node at an arbitrary time – crash-stop model. If a node crashes, it will no longer receive nor send messages, and will be considered as permanently unavailable from that time on.

Aggregation algorithms based on averaging are independent from the network routing topology, and able to produce an estimate of the resulting aggregate at every network node. The main principle of this kind of algorithms is based on an iterative averaging process between small sets of nodes. Eventually, all nodes will converge to the correct value by performing the averaging process among all the network.

The correctness of averaging aggregation algorithms depends on the maintenance of a fundamental invariant, commonly designated as the “mass conservation”. This property states that the sum of the aggregated values of all network nodes must remain constant along the algorithm’s execution, in order for it to converge to the correct result [1].

This kind of aggregation technique intends to be more robust than classical tree-based approaches, by removing the dependency from a specific routing topology, and providing an estimation of the aggregate at every node. For instance, these algorithms are often based on a gossip (or epidemic) communication scheme, which is commonly thought to be robust. Although, similarly to gossip communication protocols [18], the robustness of aggregation algorithms can be challenged, according to the assumptions made on the environment in which they operate.

Next, we discuss and expose dependability issues of some aggregation algorithms operating on a fixed network, but under more realistic assumptions, such as: asynchronous message exchanges, link and node failures.

3.1 Push-Sum Protocol

The PSP [1] is a simple gossip-based aggregation algorithm, essentially consisting on the distribution of shares across the network. Each node maintains and iteratively propagates information of a sum and a weight, which are sent to randomly selected nodes. In more detail: at each time step $t$ (synchronous round), each node $i$ sends to a target node (chosen uniformly at random) and to itself, a pair $(\frac{1}{2}s_{t,i},\frac{1}{2}w_{t,i})$ containing half of its current sum $s_{t,i}$ and weight $w_{t,i}$ ; the values $s_{t,i}$ and $w_{t,i}$ are updated by the sum of all contributions received in the previous time step ( $t-1$ ); an estimate of the aggregation result can be provided at all nodes by the ratio $s_{t,i}/w_{t,i}$ .

Distinct aggregation functions can be computed with these scheme, by varying only on the starting values of the sum and weight variables at all nodes. For instance, considering an initial input value $x_{i}$ at each node $i$ , the following functions can be computed, resorting to distinct initializations: average ( $s_{0,i}=x_{i}$ and $w_{0,i}=1$ for all nodes); sum ( $s_{0,i}=x_{i}$ for all nodes, only one node sets $w_{0,i}=1$ and the remaining $w_{0,i}=0$ ); count ( $s_{0,i}=1$ for all nodes, only one with $w_{0,i}=1$ and the others $w_{0,i}=0$ ).

The continuous execution of this protocol throughout all the network allows the eventual convergence of all nodes estimates to the correct aggregation value, as long as none of the exchanged values are lost. As stated by the authors, the correctness of the algorithm relies on the mass conservation property. In particular, when no messages are in transit, for any time step $t$ , the value $\sum_{\forall i}\frac{s_{t,i}}{w_{t,i}}$ is constant.

Aware from the crucial importance of this invariant, Kempe et al. considered a variation of the algorithm to cope with message loss and the initial failure of some nodes¹¹1Initial failure, refers to nodes that have failed from the beginning of the computation.. They assume that all nodes possess the ability to detect when their messages did not reach their destination, and modified the algorithm to send the undelivered data to the node itself, in order to recover the lost “mass”. Furthermore, they assume that a node can only orderly leave the network, after sending all sums and weights to its peers, not supporting node crashes. In light of these stated assumptions, we extend the discussion of PSP under more realistic settings.

3.1.1 Synchronous model

The proposed algorithm guarantees the maintenance of the mass conservation invariant on a synchronous execution model without faults, assuring its correctness – convergence to the true aggregation result.

3.1.2 Asynchronous model

No issue was identified under asynchronous settings. Message delays may reduce the convergence speed of the algorithm, but will not compromise its correctness (as long as no message is lost). If at some arbitrary point $t$ we stop the execution of the algorithm and wait for all message to be received and processed, we can verify that the ratio $s_{t,i}/w_{t,i}$ will meet the mass conservation property (the value $\sum_{\forall i}\frac{s_{t,i}}{w_{t,i}}$ will be equal to the initial value $\sum_{\forall i}\frac{s_{0,i}}{w_{0,i}}$ ).

3.1.3 Message Loss

As referred by the authors, in order to support message loss, independently from its cause (temporary link/node failure, or initial permanent failures that makes some nodes unreachable), they assume that each node is able to detect messages that have not reached their destination. In this case, the lost mass will be re-sent to the source node itself. This is a very unrealistic assumption. Using an acknowledgement-based scheme to infer message loss, as suggested, would amounts to solving the coordinated attack problem, which in an asynchronous model under possible message loss has been shown to be impossible [19]. Furthermore, even if it were possible, it would introduce additional waiting delays in the protocol, in order to receive a delivery notification for each sent message.

3.1.4 Node Crash

This algorithm does not support node crash. In order to maintain the correctness of the aggregation process, nodes will have to leave the network neatly, after sending all their mass to another node. Such optimistic assumption cannot be often used in practice, since node failures are not likely to be predicted. Nevertheless, one could consider a mechanism in which all the nodes state will be consistently replicated (at each neighbor), enabling alive nodes to subsequently recover the “mass” from a crashed node.

In order to be robust against node failures, G-GAP [10] extended the PSP, implementing a scheme based on the computation of recovery shares and the explicit acknowledgement of mass exchanges between peers. However, this approach provides only a partial support against this type of faults, supporting discontiguous node crashes (assuming that two adjacent nodes do not fail within a short time period of each other).

3.2 Push-Pull Gossip

The PPG protocol described in [5] and [2] is based on an anti-entropy aggregation process, being quite similar to PSP. The main difference of this algorithm relies on its push-pull process, which enforces a symmetric pairwise mass exchange between peers. The induction of this action/reaction pattern, coerces the average settlement between pairs, intending to immediately resolve the differences between nodes. The iterative execution of this push-pull process across all the network will provide the convergence of the algorithm to the correct value (faster, when compared to PSP).

Periodically, each node sends its current aggregation value to another node chosen uniformly at random – push, and waits for the response with the value from the target node – pull – to further apply the aggregation function, obtaining a new estimate of the aggregate. Each time a node receives a push message, it sends back its current value, and only then computes the new aggregate, averaging the received and sent value. At the end of a push-pull operation, both involved nodes will yield the same result.

In [5] the authors do not address mass conservation issues (like the impact of link/node failures), focusing on the efficient implementation of a pair selection method, and considering the extension of the algorithm with a restarting mechanism (executing the protocol during a predefined number of cycles, depending on the desired accuracy) in order to be adaptive and handle network changes (nodes joining/leaving). The subsequent study in [2] proposed a solution for the gossip-based aggregation directed to its practical applicability, considering some modifications to cover some practical issues, like: using timeouts to detect possible faults, ignoring the data exchanges in those situations; executing several instances of the algorithm in parallel to reduce the effect of message loss; making use of a restart mechanism to cope with node crashes.

We should point out that along the discussion carried out by the authors, they intrinsically assume that the core of the push-pull process is atomic, also referred as “the variance reduction step” ( $w_{i}=w_{j}=(w_{i}+w_{j})/2$ ). In practice, additional modifications must be considered to guarantee the atomicity of push-pull. Like common aggregation algorithms by averaging, the correctness of PPG depends from the maintenance of the mass conservation property. Due to its core resemblance with PSP, one could expect to find similar practical issues when prospecting its use in real application scenarios. However, the push-pull process will introduce additional atomicity constraints, that will restrain the use of this algorithm even under a synchronous operation mode.

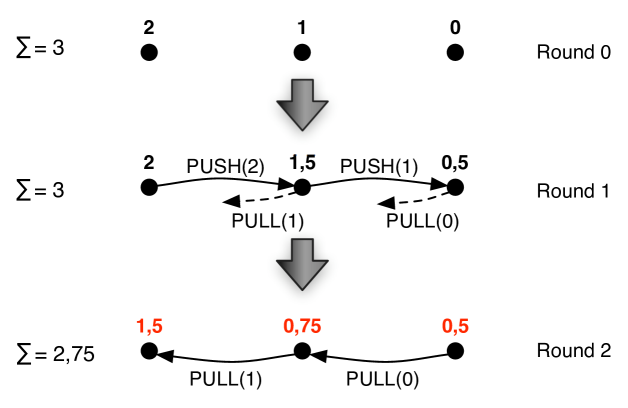
Refer to caption — Figure 1: Violation of the mass conservation invariant in the Push-Pull Gossip protocol, due to message interleaving (approximation values at the end of each round).

3.2.1 Synchronous model

Even in synchronous settings (lock-step execution), the message delivery order may affect the convergence to the true result of PPG. It is fundamental to guarantee the atomicity of the push-pull process in those settings, in order to conserve the mass of the system. If a node starts a push-pull and receives a push message from a third-party node in the middle of the process (after sending the push and before receiving the pull message), then it will first update its approximation value according to the third-party data, before receiving the pull message, and use the result to update its value again with the pull data. This occurrence will introduce an asymmetry in the results produced from the push-pull (different values may be computed by each element), which will incur in a violation of the mass conservation, depending on the involved values (greater as greater is the discrepancy between them). Thus, the correctness of the algorithm is affected by message interleaving, as depicted in Figure 1. We will detail this issue in Section 4, proposing some modifications to the algorithm to guarantee the push-pull atomicity.

3.2.2 Asynchronous model

The interleaving problem of PPG will also be found in asynchronous settings. Moreover, message delays will increase the possibility to interfere in an ongoing push-pull operation, and consequently break the mass invariant as previously described.

3.2.3 Message Loss

In practice, considering the independent failure of a push and pull message, the loss of each one of those messages will yield different effects on the PPG protocol: if the push message is lost, then no node will update its state (the source will timeout and the target will not receive the message) and the mass of the system will be conserved, only slowing down the algorithm convergence; On the other hand, if the pull message is lost (meaning that the push message was successfully received), then only the target node of the exchange process will update its value and the source will timeout waiting for a response, creating an undesirable asymmetry in the process and a consequent violation of the mass conservation invariant.

The authors do not make any assumption regarding the detection of message loss, neither concerning the restoration of the system mass. Instead of that, they consider the concurrent execution of multiple instances of the algorithm, discarding the lower and higher estimates and reporting the average of the remaining executions as the result. This solution does not solve the mass conservation issue due to message loss, and only reduces its impact in the quality of the produced estimate. Further considerations must be made to ensure the algorithm’s correctness in this settings.

3.2.4 Node Crash

The removal of nodes from the system originates a violation of the mass conservation property. In this case, the authors did not show any concern about recovering the mass changes provoked by unpredictable node crashes (not distinguishing crashes from nodes voluntarily leaving the network), but recognize the derivation of a subsequent estimation error. In particular, they specifically characterize the error of the average estimation as a function of the constant proportion of nodes failing (at each cycle), considering that nodes crash before each cycle, and intrinsically assuming (once more) that each variance reduction step is atomic (which is unreasonable in practice).

Indubitably, the introduced estimation error is provoked by the loss of the values held by crashed nodes, and leads to the convergence of the algorithm to an incorrect aggregation result. The authors consider the periodic restart of the PPG algorithm to cope with this issue, reinitializing the execution of the algorithm with clean input values (restoring the correct mass of the system). To detect the possible failure of nodes, they consider the use of a timeout, skipping the exchange step when the timeout expires. Hopefully, the restart mechanism will minimize the effect of the introduced convergence error, being transient to each epoch. Nevertheless, this issue invalidates the continuous use of the algorithm (without restarting), and may incur in unpredictable approximation results, since the correctness of the algorithm will be broken.

3.3 Distributed Random Grouping

A distinct approach based on a Distributed Random Grouping (DRG) is proposed in [3]. Unlike previous gossip-based aggregation algorithms, DRG was designed to take advantage of the broadcast nature of wireless transmissions (where all nodes within radio range will be prone to hear a transmission), directing its use for WSN. In a nutshell, the algorithm essentially consists on the continuous creation of random groups across the network, to successively perform in-group aggregations. Over time, ensuring that the created groups overlap, the estimated values at all nodes will eventually converge to the correct network-wide aggregation result.

DRG defines three different working modes that coordinate its execution: leader, member, and idle. The algorithm operates as follows: according to a predefined probability, each node in idle mode can independently decide to become leader, and broadcast a Group Call Message (GCM), subsequently waiting for joining members; all (remaining) idle nodes respond only to the first received GCM with a Joining Acknowledgment (JACK) tagged with their aggregate estimation, changing their mode to become members of that group; after gathering the estimate values of group members from all received JACKs, the leader computes the new group aggregate and broadcasts the result in a Group Assignment Message (GAM), returning to idle mode and setting its own estimate with the newly calculated value; each member of a group waits for the GAM from its leader to update its local estimate with the result within, not responding to any other request until then, and returning to idle mode afterwards.

The performance of this algorithm is highly influenced by its capacity to create overlapping aggregation groups (size and quantity of groups), which is defined by the probability of a node to become leader. In terms of practical concerns, the authors make some considerations about termination detection for the algorithm, and consider the occurrence of message collisions and link failures, but only analyze their effect at the initial stage of the group creation (at the GCM level). In particular, they assume that link failures only happen between grouping time slots, which is an unrealistic assumption. A thorough analysis of these issues should be performed across the algorithm, considering also their impact at the JACK and GAM level.

3.3.1 Synchronous model

DRG will work in synchronous settings, as long as each node is still only able to join at most one group at each time, which guarantees the maintenance of the mass conservation property.

3.3.2 Asynchronous model

In asynchronous settings, beside the exclusive group entrance, the algorithm must ensure that each node properly completes its participation in the group, receiving an aggregation result that has taken into account its estimated value. Recall that in this model messages are reliably transmitted in FIFO order but can suffer arbitrary finite delays.

Since leaders initiating a GCM call cannot anticipate how many nodes will acknowledge them, there is still a need to consider some timeout for the reception of the JACK responses. This opens the possibility that some nodes that have sent a JACK message will not have this message, and mass, processed in this iteration of the protocol. It is thus necessary that GAM messages are augmented with node and iteration ids, so that only nodes whose JACK reached the leader will consider the subsequent GAM. Iteration ids will also be important so that leaders discard JACK messages from previous GCMs that they initiated.

One can conclude that although there seems to exist no important obstacles for an implementations under this model, several modifications should be considered and the correctness of the resulting approach carefully examined.

3.3.3 Message Loss

In terms of message loss, the authors consider the occurrence of collisions and link failures, but they only consider its effect on GMCs, with impacts on the creation of groups, reducing its expected size. For instance, they assume that link failures only happen between iterations of the protocol, which is unrealistic since links can unpredictably fail at any point of the algorithm execution, provoking the loss of any type of message.

In this setting, timeouts are needed in the receptions steps for expected JACK and GAM messages. The loss of a GCM will have no impact on the correctness of the algorithm, only preventing nodes from joining the group. However, loosing a JACK from a node but delivering the subsequent GAM to that same node will most probably violate mass conservation. The same happens if GAMs are lost.

Extensions that assign iteration ids and node ids to the protocol messages can possibly address some of these issues, but the need to have a successful GAM reception on nodes that contributed their mass in a successfully delivered JACK message points again to the coordinated attack problem.

3.3.4 Node Crash

Similarly to previous approaches, this algorithm does not support node crashes (not addressed by the authors). The impact of the removal of a node from the network will be proportional to the contribution of its value to the computation of the global aggregate. As already mentioned before, the unpredicted failure of a node will alter the total mass of the system, breaking the mass conservation invariant, and leading the system to converge to a wrong result.

4 Case Study: Push-Pull Gossiping

In the previous section, we argue that most aggregation algorithms by averaging have practical implementation issues in realistic environments. In order to solve the exposed issues and ensure the algorithms dependability, important modifications must be introduced to their implementation. However, these additional modifications will incur in some degradation of their performance. We now choose to address in more detail PPG, since it is the only one that does not converge to the true aggregation result in a synchronous operation mode, as depicted by simulation results of Figure 2.

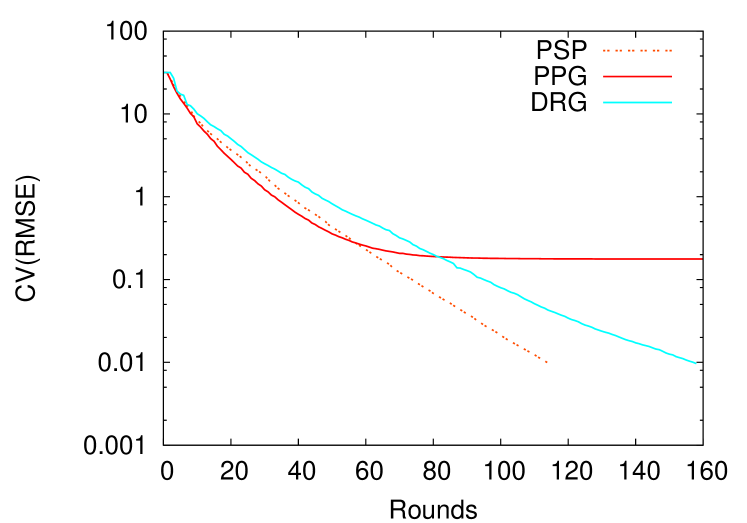
We use a custom high level simulator to evaluate the execution of the analyzed algorithms in a synchronous operation mode²²2synchronous model as in Chapter 2 of [17], providing a fair comparison of them. However, the simulation level was detailed enough to observe some effects on messages passing (in particular, interleaving), since we assume that all the messages received in a common round will be processed by the target node in some arbitrary order. The depicted results correspond to the average values (number of rounds or messages) required to reach a specific accuracy (coefficient of variation of the root mean square error), obtained from 50 trials of the execution of the algorithms under identical settings. In each trial different networks with a random topology (generated according to the Erdős–Rényi model [20]) and the same characteristics (network of size 1000 and average connection degree of 5) are used. We implement the Count version of each simulated algorithm (to determine the network size) and tune all its parameters (e.g. the probability to become leader in DRG) to obtain its best performance in each simulation scenario.

As previously referred (in Section 3.2) and confirmed by simulations (see Figure 2), the correctness of PPG (mass conservation) is affected by the occurrence of messages interleaving in push-pull operations, occurring even in synchronous rounds settings. In practice, in order to guaranty the convergence of PPG to the correct result, an additional property must be considered: the push-pull process must be atomic, and the approximation value cannot be update by any concurrent process before the end of an already initiated push-pull procedure. We propose two concrete alternative versions of the algorithm that tackle this problem, and guarantee the consistency of the push-pull process: Push-Pull Back Cancellation (PPBC), and Push-Pull Ordered Wait (PPOW).

4.1 Push-Pull Back Cancellation

This version of the algorithm is based on a message cancellation mechanism, to guaranty that no other process will interfere in an ongoing push-pull operation. In this scheme, after sending a push message to the chosen target, all the received messages will be ignored (without any local state update) by the source node, until the awaited pull message is received. The cancelation mechanism is implemented by sending a pull message with the same value received in the push one, skipping the correspondent state update. By reflecting back the received approximation value, the update performed by the initiator will not change its approximation value. The main drawback of this mechanism is the execution of dummy push-pulls (that will not contribute to the system convergence), all in order to ensure a consistent state update of ongoing push-pull operations.

4.2 Push-Pull Ordered Wait

This version of the algorithm adds a message buffering process to the original version of the algorithm. All push messages received while a push-pull operation has already been initiated by a node are locally buffered, and will only be processed after the conclusion of the ongoing push-pull. Notice that, simply considering this buffering mechanism could incur in deadlocks across the network, due to possible creation of waiting cycles between nodes. E.g. If node $n_{1}$ is waiting for node $n_{2}$ , which is waiting for node $n_{3}$ , and by is turn $n_{3}$ is waiting for $n_{1}$ , ending all locked waiting for each other.

Additional requirements must be considered to avoid this cyclic waiting situation. For instance, we define a total order between nodes (by setting a UID to each node), and stipulate that each node can only initiate a push-pull operation with nodes from a specific order (inferior or superior). For example, considering the order between nodes $n_{1}<n_{2}<n_{3}$ (defined by their UID, from lower to higher ID values), and imposing that push messages can only be sent to nodes with a higher ID: node $n_{3}$ could never be waiting for $n_{1}$ (breaking the previous cycle), since it has a lower ID and consequently no push messages can be sent to it by $n_{3}$ . Although, this scheme restrains the execution of push-pull in some directions, unlike the previous version it does not wast concurrent push-pulls, and makes the most of their contributions to the convergence of the algorithm.

4.3 Simulation Results

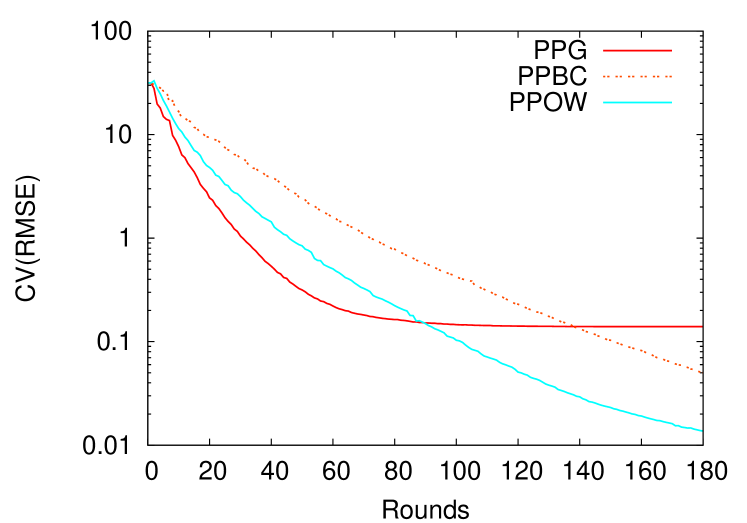
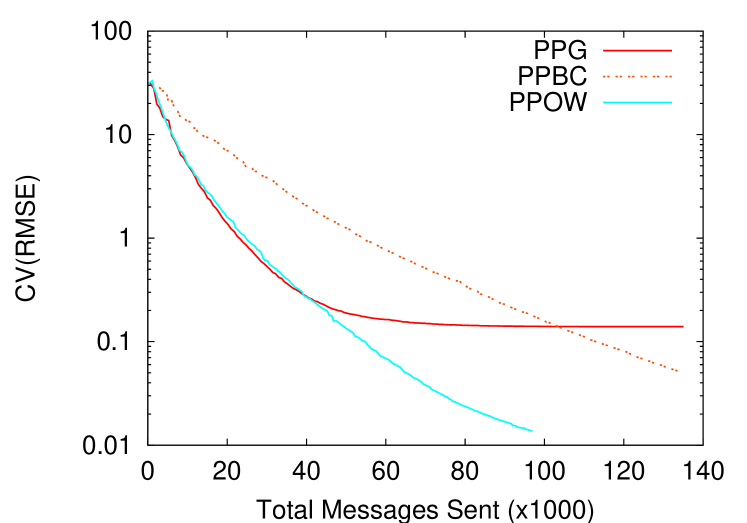
As depicted by Figure 3, the modifications introduced to the original algorithm solve the convergence problem of the algorithm, but at the cost of a performance degradation in terms of convergence speed (see Figure 3(a)). As expected PPOW performs better than PPBC, since its buffering mechanism allows the integration of all the received contributions to the aggregation process. By making all contributions (messages) count, PPOW exhibits similar results than the original algorithms in terms of overhead (number of message needed to reach a common accuracy), as showed in Figure 3(b).

5 Conclusion

In this study, we expose important implementation and dependability issues in averaging based aggregation algorithms. Issues that are often overlooked in the abstract modeling of the algorithms and that must be addressed in any concrete real scenario.

In particular, we discuss three established algorithms from this class under practical settings, namely the Push-Sum Protocol [1], Push-Pull Gossip protocol [2] and Distributed Random Grouping [3]. All algorithms evidence some dependability issues, that compromise their correctness, when exposed to asynchronous and faulty (e.g. with message loss or node crash) environments.

Supplementary mechanisms and modifications must be added to the discussed aggregation algorithms, in order to provide fault tolerance and enable their practical use. These additional provisions will result in a degradation of the algorithms performance. In particular, we extend the Push-Pull Gossip protocol, which exhibit issues even on synchronous settings, and propose two concrete version of the protocol to solve its interleaving problems: Push-Pull Back Cancellation, and Push-Pull Ordered Wait. As showed by the results obtained from simulations, the proposed algorithms solve the convergence problem of the original algorithm, but exhibit a worse global performance (especially in terms of convergence speed).

The depicted vulnerability of current averaging algorithms, and their importance when seeking high precision aggregates, also served as a motivation for our ongoing research on Flow Updating [21], a fast fault tolerant averaging algorithm that is, by design, resilient to message loss.

References

[1] D Kempe, A Dobra, and J Gehrke. Gossip-based computation of aggregate information. Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, pages 482–491, 2003.
[2] M Jelasity, A Montresor, and O Babaoglu. Gossip-based aggregation in large dynamic networks. ACM Transactions on Computer Systems (TOCS), 23(3):219 – 252, Aug 2005.
[3] Jen-Yeu Chen, G Pandurangan, and Dongyan Xu;. Robust computation of aggregates in wireless sensor networks: Distributed randomized algorithms and analysis. IEEE Transactions on Parallel and Distributed Systems, 17(9):987 – 1000, 2006.
[4] Robbert Van Renesse. The importance of aggregation. Future Directions in Distributed Computing, Lecture Notes in Computer Science, 2584:87–92, 2003.
[5] M Jelasity and A Montresor. Epidemic-style proactive aggregation in large overlay networks. 24th International Conference on Distributed Computing Systems, pages 102 – 109, Jan 2004.
[6] Samuel Madden, Michael Franklin, Joseph Hellerstein, and Wei Hong. TAG: a Tiny AGgregation service for ad-hoc sensor networks. ACM SIGOPS Operating Systems Review, 36(SI):131–146, Dec 2002.
[7] S Madden, R Szewczyk, M Franklin, and D Culler. Supporting aggregate queries over ad-hoc wireless sensor networks. Proceedings of the 4th IEEE Workshop on Mobile Computing Systems and Applications, pages 49–58, 2002.
[8] J Li, K Sollins, and D Lim. Implementing aggregation and broadcast over distributed hash tables. ACM SIGCOMM Computer Communication Review, 35(1):81–92, 2005.
[9] Yitzhak Birk, Idit Keidar, Liran Liss, Assaf Schuster, and Ran Wolff. Veracity radius: capturing the locality of distributed computations. PODC ’06: Proceedings of the 25th annual ACM symposium on Principles of distributed computing, 2006.
[10] Fetahi Wuhib, Mads Dam, Rolf Stadler, and Alexander Clemm. Robust monitoring of network-wide aggregates through gossiping. 10th IFIP/IEEE International Symposium on Integrated Network Management, pages 226 – 235, 2007.
[11] Carlos Baquero, Paulo Sérgio Almeida, and Raquel Menezes. Fast estimation of aggregates in unstructured networks. International Conference on Autonomic and Autonomous Systems (ICAS), Valencia, Spain, Apr 2009.
[12] D Mosk-Aoyama and D Shah. Computing separable functions via gossip. PODC ’06: Proceedings of the 25th annual ACM symposium on Principles of Distributed Computing, pages 113–122, 2006.
[13] Laurent Massoulié, Erwan Merrer, Anne-Marie Kermarrec, and Ayalvadi Ganesh. Peer counting and sampling in overlay networks: random walk methods. PODC 06: Proceedings of the 25th annual ACM symposium on Principles of Distributed Computing, 2006.
[14] A Ganesh, A Kermarrec, E Le Merrer, and L Massoulié. Peer counting and sampling in overlay networks based on random walks. Distributed Computing, 20(4):267–278, Nov 2007.
[15] Sandeep Mane, Sandeep Mopuru, Kriti Mehra, and Jaideep Srivastava. Network size estimation in a peer-to-peer network. Technical report, Department of Computer Science - University of Minnesota, page 12, Sep 2005.
[16] D Kostoulas, D Psaltoulis, Indranil Gupta, K Birman, and Al Demers. Decentralized schemes for size estimation in large and dynamic groups. 4th IEEE International Symposium on Network Computing and Applications, pages 41–48, 2005.
[17] Nancy A Lynch. Distributed Algorithms. Morgan Kaufmann Publishers Inc., 1996.
[18] Lorenzo Alvisi, Jeroen Doumen, Rachid Guerraoui, Boris Koldehofe, Harry Li, Robbert Renesse, and Gilles Tredan. How robust are gossip-based communication protocols? ACM SIGOPS Operating Systems Review, 41(5), Oct 2007.
[19] Jim Gray. Notes on data base operating systems. In Operating Systems, An Advanced Course. Lecture Notes in Computer Science, Vol. 60, pages 393–481, London, UK, 1978. Springer-Verlag.
[20] Paul Erdős and Alfréd Rényi. On the evolution of random graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences, 5:17–61, 1960.
[21] Paulo Jesus, Carlos Baquero, and Paulo Sérgio Almeida. Fault-tolerant aggregation by flow updating. In 9th IFIP International Conference on Distributed Applications and Interoperable Systems (DAIS), volume 5523 of Lecture Notes in Computer Science, pages 73–86, Lisbon, Portugal, June 2009. Springer.