Designing Heaven’s Will:
The job assignment in the Chinese imperial civil service
Abstract.
We provide an original analysis of historical documents to describe the assignment procedures used to allocate entry-level civil service jobs in China from the tenth to the early twentieth century. The procedures tried to take different objectives into account through trial and error. By constructing a formal model that combines these procedures into a common framework, we compare their effectiveness in minimizing unfilled jobs and prioritizing high-level posts. We show that the problem was inherently complex such that changes made to improve the outcome could have the opposite effect. Based on a small modification of the last procedure used, we provide a new mechanism for producing maximum matchings under constraints in a transparent and public way.
Keywords: Civil service assignment; Matching; Market design; History of civil service
JEL: D73; J45; C78; D47; N15
1. Introduction
Bureaucrats are a core component of state capacity, as they are responsible for raising taxes, implementing policies, and delivering public services (Besley and Persson, 2009; Rauch and Evans, 2000). Studying the institutional rules that govern the appointments of these bureaucrats is therefore crucial to gain insights for understanding the functioning of the administration, as well as the impacts on the society’s political and economic life. The civil service assignment in Imperial China provides a rich opportunity for this purpose. In particular, the assignment rules have evolved over time, in response to various challenges arising from the complexity in personnel as a result of its objectives and constraints.
In this paper, we draw on historical documents and studies to present the first formal description for one of the earliest and longest-used assignment schemes that systematically assigned candidates to government jobs from the mid-tenth century to the early twentieth century in China. After describing in details various changes made to the assignment procedure since its first introduction, we provide a unified theoretical framework for analyzing these procedures, which helps to understand the trade-offs behind each change.
An important step in the evolution of the Chinese civil service was the introduction of a meritocratic selection system in the late sixth century that made it possible to select competent candidates from the general population to work for the state on various tasks at national, provincial, and prefectural levels. While the exam-based selection determined who would be qualified for the government jobs, the decisions regarding which jobs were taken by which candidates were not institutionalized until the mid-tenth century. Following the establishment of a professional career system around this period, recruitment via examinations expanded significantly, thus encouraging the use of more systematic rules to allocate newly recruited candidates to government jobs. There were a few challenges in finding the right candidates for jobs, that are not uncommon to today’s world. First, given that there were candidates who obtained different levels of degrees, and jobs with different levels of importance, how to assign them systematically while ensuring the functioning of the bureaucracy? Second, appointing candidates to jobs in their home regions requires a careful balance between the benefit from the local knowledge and the threat of local capture. Last but not least, how to prevent the appointments from falling prey to corruption and influence-peddling?
Our historical investigation identifies three criteria that were taken into consideration by the assignment procedures of the Chinese civil service in addressing the challenges mentioned above. First, the eligibility criterion, which defines for qualified candidates, depending on their competence measured by degrees, the types of government jobs they could be assigned to. Second, rule of avoidance, which prohibits candidates from being assigned to jobs located in their home regions. Finally, randomness, which was desirable when producing the matches, as it limits the impact of personal influences and balances the demands of different political groups. These three criteria were desirable properties—also resilient over time—when making the appointments, yet there were complicated questions regarding how to best implement them, as illustrated in the following quote from the court discussions between Emperor Chongzhen and his ministers in 1628. Curiously then, this important decision was thought to be best left to Heaven’s Will—the drawing of lots.
“Finding the right men for the grand secretariat benefits greatly the empire. I do not dare to make the decision myself, therefore, I ask for Heaven’s will.” — Sun (1777)111Grand secretaries were cabinet members of the central administration. Lots-drawing was used mainly for assigning entry-level jobs which we will describe in more details later. It was however occasionally used for middle or high rank jobs.
The first formal assignment procedure emerged around the mid-tenth century during the Song dynasty (960–1279).222To assist readers when following the chronological order of the Chinese dynasties involved in our paper, we add a superscript of a number next to the dynasty to indicate the order: Song precedes Ming , which again precedes Qing . The Song procedure allowed candidates to express their preferred jobs and they were assigned one by one in public following an order determined by their degrees and exam results. This feature of sequential assignment was kept in all subsequent procedures—as it provided transparency, while several major changes were developed.
The first change occurred around the late fourteenth century, in the wake of the transition to the new Ming Dynasty. In the previous Song procedure, the preferences of candidates could result in a situation where a higher-degree candidate—eligible to both lower-level and higher-level jobs—was assigned to a lower-level job, while a higher-level job was left unassigned with a lower-degree candidate—eligible only to the lower-level job. In an effort to assign more candidates to jobs matching their competence, preferences were no longer taken into account. Instead, a job was decided for each of them after assessing the fit between the candidate and the job. We refer to this procedure as the First Ming procedure. The second change took place in the late sixteenth century, with the intention of reducing personal interference and balancing factional politics. The assignments were, for the first time, determined by drawing matches randomly from tubes. We refer to this procedure as the Second Ming procedure. While installing impartiality in the assignment process, the Second Ming procedure was criticized for, among other aspects, its failure in finding candidates with the right competence to jobs, a situation similar to what occurred under the Song procedure.
Nevertheless, lots-drawing survived dynastic changes and became the norm in the following centuries. Indeed, the focus of debates at that time shifted from whether lots-drawing should be used to how its performance could be improved. Amid this climate, and soon after another dynastic transition, a partitioned lots-drawing system was introduced around the mid-seventeenth century—the third change, and once again with the objective of assigning more candidates to jobs matching their competence. In this procedure, which we refer to as the First Qing procedure, the assignment was partitioned into multiple smaller assignments, where each of them contained one type of job and a list of candidates who were eligible to them. This could prevent some of the mismatches of skills present in the previous procedure. The final change—which occurred in the early nineteenth century—responded to a different concern that was known but not handled until then. The procedures used up until then could produce assignments that leave candidates and jobs unmatched, while alternative assignments could match more candidates to jobs. The change involved first matching candidates who had regions to avoid among the jobs present in the procedure. We refer to the last procedure as the Second Qing procedure.
To understand the trade-offs behind these changes, we introduce a formal model that captures the key elements of different assignment procedures used in history. Two measures are our focus when evaluating these procedures, minimizing the number of unfilled jobs, and prioritizing high-levels—favoring the match of high-level candidates, as measured by their degrees, to high-level jobs. These two objectives were mentioned in the historical context either explicitly or implicitly. They ensure that, first, jobs were assigned—unassigned candidates needed to wait for the next appointment months later, and second, jobs were assigned to candidates with the right competence.
When implementing matches sequentially, there is, generally speaking, a tension between these objectives and the two compatibility constraints—eligibility and rule of avoidance (see Example 1). To evaluate different procedures, we need to be careful with the interaction of the two compatibility constraints. We therefore separate our analysis by considering two variations of the compatibilities between candidates and jobs. We show that if one considers only eligibility constraint—aiming at matching candidates to jobs that fit their qualifications— the changes in the procedures show a series of adjustments in the right direction. Indeed, while the Song procedure might fail to minimize unfilled jobs and prioritize high-levels—due to candidates’ preferences—and in the Second Ming procedure—due to randomness—these issues are mitigated in both the First Ming and the two Qing procedures.
Perhaps surprisingly, however, when taking the rule of avoidance into account in addition to eligibility, both the change from the Song procedure to the First Ming procedure and the change from the Second Ming procedure to the First Qing procedure could lead to more unfilled jobs and failure to prioritize high-levels. This can happen because these two types of constraints can interact in a unintuitive way, such that decisions that were made with the prioritization of high-levels in mind but without evaluating its interaction with the rule of avoidance could lead to worse outcomes in both measures.
The final change, from First to Second Qing , was the only change motivated by the concern of unfilled jobs that the rule of avoidance introduced. It consisted of first matching candidates who had incompatible jobs within the assignment, and only after that matching the remaining ones. We show that this change unambiguously reduces the number of unfilled jobs, without affecting the prioritization of high-levels. While the extent to which the problems related to unfilled jobs and prioritization of high-levels depend crucially on the specific combinations of candidates, jobs, and their regions and degree types, we provide anecdotal indications that minimizing unfilled jobs was a concern, and that in particular the change from First to Second Qing might have reduced the likelihood that a candidate was left unmatched.
Finally, we make a small modification of Second Qing procedure, resulting in a simple procedure that produces matchings randomly, and under certain assumptions, matches the maximum number of candidates to jobs for any realization of chance. Random assignments, often subject to some types of constraints, are often used in real-life. Examples include allocating refugees to hosting families who have facility constraints (Andersson and Ehlers, 2017), assigning judges who have different specializations to cases (Thorley, 2020), and public house allocation with size differences (Arnosti and Shi, 2020). Randomness in the form of drawing lots has also been proposed by political scientists to distribute positions within the European Commission among member states (Buchstein and Hein, 2009; Berger et al., 2020). Our new procedure can be applied when matchings need to be produced randomly in a simple and transparent way.
1.1. Related Literature
It has long been recognized that effective state bureaucracies require meritocratic recruitment, competitive compensation, and systematic rules for appointments and promotions that shield away from personal influences (Weber, 1964, 1978). Despite the importance of assignment rules in the bureaucratic system, economic analyses of the civil service have primarily focused on the selection and incentives of civil servants (Dal Bó et al., 2013; Bai and Jia, 2016), while relatively little has been done to understand the rules that determine how selected personnel were appointed to specific jobs. Indeed, economists tend to presume sufficient institutions exist to deploy civil servants in posts and thus enabling them to execute administration tasks. In contrast, historians tend to focus more on why institutions exist and how institutions evolve. In the context of the Chinese civil service, Will (2002) is the first historical study that reviews the origin and evolution of the lots-drawing procedure in imperial China since the late sixteenth century. Watt (1972) offers a panoramic view of the career path for county magistrates—from first-time appointment, promotion, and re-appointment to demotion—during the period between the late eighteenth and the early nineteenth century. Similarly, Gong (1997), Pan (2005) and Zhang (2010) review the civil service systems for Song , Ming and Qing respectively. These historical studies mainly analyze the societal and political background of the appointment systems, but have not evaluated the properties of the appointment procedures. A few recent economics papers evaluate empirically how the appointment methods, and in particular patronage—by means of discretionary appointments through connections, contrary to our focus of rule-based assignment—affect public service, and find that patronage generally leads to worse economic performance or the selection of less competent officials (Xu, 2018; Colonnelli et al., 2020). Thakur (2020) studies a formal assignment procedure currently used in the Indian Administrative Service, focusing its distributional issues and the effect on bureaucratic and economic performance.
By formalizing the civil service assignment as a matching problem, our paper connects to the literature in matching and market design, which has a long tradition of applying formal economic theory to study properties of allocation mechanisms used in real-life applications. Examples include the entry labor market for medical residents (Roth, 1984), the military career in the U.S. (Sönmez, 2013; Sönmez and Switzer, 2013), lawyers to courts in Germany (Dimakopoulos and Heller, 2019), school choice (Abdulkadiroğlu and Sönmez, 2003), and kidney exchange (Roth et al., 2004). Some of the issues that we identify regarding the way in which the matchings are produced sequentially are indirectly related to, for example, the topic of reserve design. Dur et al. (2018) show how the processing order of reserves in school choice design matters and how some processing orders can cause unintended consequences. Other papers include Sönmez et al. (2021) on affirmative action policies in Indian civil service, Pathak et al. (2020a) on H-1B visa allocation rules, and Pathak et al. (2020b) on medical resources allocations. In addition, the search for procedures that guarantee minimize unfilled jobs relates to maximum matchings in random environments. Bogomolnaia and Moulin (2004) look at maximum matchings when randomizing over dichotomous preference. Boczoń and Wilson (2018) study the UEFA Champions League group drawing method, a problem in which matchings are also determined by drawing lots and where there is a concern about maximality.
More broadly speaking, our paper also relates to a burgeoning literature that applies economic theory to analyze important economic and societal institutions in history. Greif (1993) is perhaps the first paper in the field, applying contract theory to analyze contractual relations in eleventh-century Mediterranean trade. Other studies include Greif et al. (1994) on the contract enforcement problem faced by merchants in late medieval Europe, Börner and Hatfield (2017) on the debt-clearing financial mechanisms in preindustrial Europe, and Mackenzie (2019) on the succession rules of Popes. Our paper follows this approach in that we use the toolbox from matching theory to analyze the civil service assignment procedures—another important historical institution—in order to shed light on its properties.
The remainder of the paper is as follows. The next section provides background information on the selection and appointment of civil servants in the historical context. Section 3 describes in detail the assignment procedures used throughout history. Section 4 presents our theoretical framework and formalizes the previously described assignment procedures. Section 5 develops and evaluates comparative static results of the assignments procedures. In Section 6, we conclude and indicate potential theoretical and empirical future work.333We also provide some additional background information related to the selection and appointment of civil servants and a documentation of original sources and data used in our historical research in an online supplementary material.
2. Selection and appointment of civil servants:
A historical background
Evidence of state bureaucracy in China can be traced back to as early as the third century BC (Creel, 1964). A large body of bureaucrats was needed to implement various tasks, ranging from tax collection and juridical investigation to miscellaneous administrative chores. The way in which these bureaucrats were selected has evolved over time, starting from a hereditary system to a recommendation-based system in 134, and finally to an examination-based system in 589, known as the Civil Service Exams. It lasted until 1905,444The exam system was interrupted during the Yuan dynasty (1279–1368), a Mongol-led dynasty. It was re-established in 1315, not long before the fall of the Yuan dynasty. and was abolished following a series of modernization reforms shortly before the fall of Imperial China. The Civil Service Exams allowed any man to register for the exams, without recommendation or patronage by incumbent officials, and registered candidates were selected through a series of standardized exams that primarily focused on Confucian classics. It was hoped that these exams would install impartial evaluation and select candidates by merit rather than birth or class. Selection by exams was initially used on a small scale for the civil service,555Besides examination, one could qualify for the civil service through other channels. This includes clerks who were hired by local governments on term-limited contracts, people who were qualified in recognition of distinguished services by their fathers, and those who were qualified by paying a tribute to the government. These candidates needed to pass separate exams before being considered for appointments. but started to gain importance in the Song dynasty (960–1279). The Song administration gradually established a career civil service system, where candidates were first selected by merit, and once qualified they could follow a career ladder for promotion and remain on the payroll of the central government until retirement, even if no specific tasks or posts were available (Gong, 1997). In addition, rules were introduced to safeguard impartiality in exams, which remained in the following dynasties. For instance, names of candidates were obfuscated, and their exam answers were transcribed before evaluation, all to make sure that the candidates were not able to be identified directly or indirectly through handwriting (Elman, 2000).666Prior to the changes, candidates were asked to write down their names on their papers. Since this information could be seen by the examiners during the evaluation phase, officials or local gentries could still interfere in the selection process. Selection by exams became the dominant method in the Ming dynasty (1368–1644) and the succeeding Qing dynasty (1644–1912), and was regarded as the “regular” path to qualify for civil service, in contrast to other paths of qualifications. In the remainder of the paper, we focus on the appointments of candidates who obtained their qualifications through examination, unless otherwise mentioned.
The Civil Service Exams included multiple levels of qualification exams. After passing the entry-level exam, held locally and twice every three years, candidates were given the degree of licentiate (“xiu cai”). Licentiates could then proceed to the next levels of triennial exams which offered opportunity for centrally appointed government jobs. The second level was a provincial-level examination in the provincial capital, and candidates who passed these were awarded the degree of recommended men (“ju ren”). Recommended men could proceed to the third-level exam held in the capital. Successful candidates were awarded the provisory title of tribute scholars (“gong shi”). They were re-examined and ranked in the imperial palace, under the supervision of ministers and often the emperor himself. These candidates were eventually awarded the degree of advanced scholars (“jin shi”). During a typical year of examinations in Ming and Qing dynasties, more than 1,000 candidates received the degree of recommended men, while about 100 went on to obtain the degree of advanced scholar.
Recommended men, tribute and advanced scholars were then appointed by the Ministry of Personnel to various important government jobs located in or outside the capital. These jobs were entry-level civil service jobs, while higher-level jobs were reserved for the promotion of more experienced officers. Once assigned, the new officials would serve three years in their positions, and after that, depending on their evaluations, they could be promoted, transferred, or demoted. Typical entry-level jobs in the capital included editors at Hanlin Academy—an elite scholastic institute whose main task was to interpret the Confucian classics—secretaries in various ministries, officers at various departments and courts, etc. Typical jobs outside the capital included magistrates and judges in prefectures, sub-prefectures, and counties.777From the Song to the Qing dynasty, the central administrative divisions were such that outside the capital city, province was the primary division. Under the level of province were prefectures, followed by sub-prefectures. The smallest administrative unit was county. Each level of the administrative units was typically headed by a magistrate, who was assisted by a judge in charge of investigating civil and criminal cases. Among all jobs, the most common ones were county magistrates, who were responsible for the overall management of a county, including mostly but not exclusively tax collection, law enforcement, school inspection, and disaster relief. There were roughly 1,300 to 1,500 counties during our periods of interest, and most of the open posts were reserved for the newly selected candidates, with some remaining for transfer or re-appointment posts. For instance, about two-thirds of the posts were for newly selected candidates during the early Qing period (Will, 2002).
The overall goal of the appointment was to “find the right person for the right job.” There are of course different interpretations on what should be considered an appropriate match. We observe three criteria that emerged over time, and were respected by the appointment system, though to different extents. While the first two criteria were present in all procedures, the third one appeared as of the late sixteenth century.
Eligibility.
Qualified candidates, depending on their degree, were eligible for different sets of civil service jobs. In general, candidates with higher degrees were appointed to jobs with higher ranks. That is, advanced scholars were more likely to be assigned to more important jobs than tribute scholars or recommended men. Early debates often centered around whether academic achievement should be the sole consideration for measuring one’s competence. However, over time, academic achievement was gradually accepted as the main desideratum, as it provided clear incentives to follow the career system and gave legitimacy to the government rule. Since the precise eligibility requirement varied with time, we will elaborate on the details in Section 3 when discussing the assignment procedures.
Rule of Avoidance.
This additional criterion could prevent one candidate from being assigned to a particular job even if he was eligible. The rule of avoidance, in fact much older than the civil service appointment, dates back to the second century. Despite the various forms it took over time, avoidance of localities is the most fundamental one for the entry-level jobs (Wei, 1992). It stated that a candidate was prohibited from being appointed to his native province.888The other types of avoidance can overlap with avoidance of localities or involve smaller sets of people. For instance, the avoidance of family, which prevented a candidate from being assigned to a job where he and an incumbent official were direct or indirect family members. Since most people’s families came from the same region, avoidance of localities was often sufficient. The other type was avoidance of teacher and student, which prevented a candidate from serving in a job where he was the student or the teacher of an incumbent officer. Bureaucrats originating from a particular region naturally had an information advantage about their home regions, and therefore assigning them there could be beneficial to the local management. However, as they were also more connected to local elites, this also posed a threat of local capture, especially in the days when regions were more isolated due to communication and transportation constraints. Rule of avoidance was thus intended to prevent the formation of local powers, which was regarded as a major impediment and challenge to unification throughout the Chinese history.
Randomness.
Starting from the late Ming dynasty, candidates were appointed randomly to compatible jobs by drawing them from tubes. Though it might seem odd to randomly assign civil servants to posts, it is a way by which the emperor could essentially eliminate the possibility that local clans would extend their power by influencing these assignments, without taking on the decisions himself. On the other hand, the lack of criteria when deciding individual assignments reduces the ability of matching highly qualified candidates to higher-level jobs. It seems, however, that randomness was gradually accepted as a desirable property from the late sixteenth century onward.999Random assignments have a surprising history in the political sphere. As early as the democratic period of ancient Athens, random assignments were used to select citizens to serve in the Boule (a council appointed to run the daily affairs of the city) and various state offices, through a randomization device known as Kleroterion (Headlam, 1891). In recent years, political scientists have also advocated for a lot-drawing procedure for assigning EU commissioners (Buchstein and Hein, 2009).
3. Assignment procedures through history
We focus in this section on the methods that were used from the tenth to the early twentieth century to determine, for each of the candidates selected by exams, which jobs they were assigned to. In order to obtain an overview on how the assignment procedures worked, we combine both official documents as well as secondary sources. Official documents for dynasties before the tenth century do not inform us about the details of the appointment procedure, perhaps due to its small scale, and assignments were more ad-hoc. The earliest official regulations describing the assignment procedures in detail are from the Song dynasty.101010Note that official documents were often compiled in the succeeding dynasty by the order of the new emperors. Writing “official dynastic history” of its predecessor is a convention established by the state historian Sima Qian from Han dynasty (202BC–-220), which, even though it might be biased, provides invaluable sources to study institutions in earlier times. Parts of the original official documents from the Ming dynasty and the majority of original official documents from the Qing dynasty are preserved today. The treatises on selection and appointment from the History of Song (SS, 1343)—the official dynastic history—describe the types of civil service jobs that candidates were assigned to, which draws a blueprint for the dynasties to follow, though details are often vague. Rules of Ministry of Personnel from Yongle Encyclopedia (Yao, 1408) offer supplementary materials for understanding how the assignment procedure was actually carried out during this period. For the following Ming dynasty, in addition to treatises on selection and appointment from the History of Ming (MS, 1739), Collected Statutes of Ming (MHD, 1587)—the official code of administration from the Ming dynasty documenting regulations for six ministries, including the Ministry of Personnel, and Regulations of Ministry of Personnel (LBZZ, 1614)—both provide additional descriptions of the types of jobs candidates were eligible for and the assignment procedure. Lastly, with the maturing of the assignment system, the Qing dynasty produced the most detailed official sources on the assignment procedure, including how it was carried out and how eligibility and rule of avoidance were respected in the procedure, as well as related policy changes (see Collected Statutes of Qing (DQHD, 1886) and Regulations of Ministry of Personnel (QDLBQXZL, 1886)). Our secondary sources include court debates, correspondences between emperors and ministers, and handbooks preparing students for the career system (Huang, 1694). These sources allow us to validate implementation details mentioned in the official documents.
3.1. The Song procedure (960-1279)
With the expansion of the selection of candidates by exams, a more formal assignment procedure started to emerge. From the official documents, we know that selected candidates were eligible for entry-level jobs, including clerks in various ministries in the capital and county magistrates in the provinces, though we do not observe clear rules that define eligible jobs by the categories of degrees candidates obtained.
Selected candidates were appointed four times a year. The assignment procedure was priority-based, and in most cases priorities were determined first by the candidates’ degrees—starting with the advanced scholars then other degree categories—and then by their exam results within each degree category.111111A hybrid system that combines both merit and patronage was used by the Song dynasty. In addition to exam results, candidates were given higher priority if they were endorsed by incumbent officials. This practice was not continued in the following procedures. All vacancies were announced before the assignment, so that candidates could consider their preferred jobs. During the initial appointment round, officials from the Ministry of Personnel chanted out a candidate’s name following the priority order, who then needed to indicate a job of interest that was still available. The officials in charge would then announce “approve” or “not approve.” An extra round of appointment was organized afterwards for the unassigned candidates and unassigned jobs, using a similar mechanism. If there were still unassigned candidates or jobs, they would be assigned in the next appointment phase three months later.
3.2. The First Ming procedure (1368-1594)
A priority mechanism continued to be used in the Ming dynasty. However, candidates were no longer asked to express their preferred jobs. Instead, the Ministry of Personnel would assess the candidate, and then decide a suitable job for him. The frequency of the assignment was increased to monthly, with first-time appointments being organized in even months, and promotions or transfers organized in odd months. This organization of monthly appointments continued in the following centuries.
As the civil service system grew in size and importance, the rules on eligibility were clarified. Table 3.1 presents the details. In addition to the general distinction between advanced scholars and tribute scholars together with recommended men, advanced scholars were further differentiated into three grades. The top grade, consisting of three people, were immediately assigned to editor jobs in the Hanlin academy. The rest of the candidates were only appointed upon completion of internships in different ministries and departments in the capital that usually lasted for half a year. Among them, those in the second grade were considered for secretaries in various ministries in the capital, or sub-prefecture magistrates outside the capital. The third-grade advanced scholars were eligible for, among metropolitan jobs, secretaries to the emperor, and officers at various departments and courts. Furthermore, they were eligible for, among jobs outside the metropolitan area, prefecture judges and county magistrates. Finally, tribute scholars and recommended men were eligible only for non-metropolitan jobs, which included prefecture judges, county magistrates, and various study officers.121212For candidates qualified through non-examination paths, similar guidelines also existed. It is clear from the table that some jobs such as ministry secretaries only considered advanced scholars, but not candidates with lower degrees, and some jobs such as study officers only considered tribute scholars and recommended men. Other jobs, such as county magistrates and prefecture judges, could be assigned to candidates with all three degrees.
| Jobs | |||
|---|---|---|---|
| Metropolitan | Non-metropolitan | ||
| Advanced scholars | First grade | Senior and junior editors at Hanlin Academy | |
| Second grade | Ministry secretaries | Sub-prefecture magistrates | |
| Third grade | Secretaries to the emperor, officers at Department of Foreign Affairs, officers at Court of Judicature Review, officers at Court of Ceremonials | Prefecture judges, and county magistrates | |
| Tribute scholars and recommended men | Prefecture judges, county magistrates, and study officers | ||
Like the Song procedure, the First Ming procedure followed an order over the candidates when determining their jobs. Advanced scholars had the highest priority, followed by tribute scholars and recommended men, and they were ranked by exam results within each degree category. Following this strict priority order, the Ministry of Personnel looked to place each candidate at a job that he was entitled to, while respecting the rule of avoidance. In general, the ministry tried to look for a job matching the candidate’s skill as measured by exam result. Therefore, higher-ranked jobs were more likely to be assigned to those with higher exam results.
The First Ming procedure could, in principle, handle both eligibility and rule of avoidance well; however, it provided enough leeway for officials or political clans to interfere with the final assignment. It was evident that, by the late sixteenth century, such interference was ubiquitous, to the point that appointment decisions were no longer focusing on one’s competence, but rather which clan he belonged to. This unavoidably undermined the effectiveness of selecting individuals by merit, and as a consequence, reduced competence of governance and fragmented central control (Will, 2002).
3.3. The Second Ming procedure (1594-1644)
The lots-drawing procedure was introduced in 1594. Instead of being evaluated case by case, appointments began to be determined by drawing lots. This was the first procedure that systematically assigned selected candidates to entry-level civil service jobs via lotteries. Information on which candidates were eligible for which jobs was publicly announced before the assignment. Job titles were written on bamboo sticks and were then put into tubes. The procedure then proceeded as follows.
-
•
Advanced scholars drew first, in descending order of their examination results. Each candidate drew a job from a tube filled with jobs that they were eligible for.
-
•
Only after all advanced scholars had a chance to draw, the tribute scholars could proceed to draw. They drew jobs from a tube that filled with jobs that they were eligible for, also following the order determined by their exam results.
-
•
Finally, after all tribute scholars had a chance to draw, the recommended men drew. They drew jobs from a tube filled with jobs that they were eligible for, again following the order determined by their exam results.131313Details about the order in which the candidates draw their jobs were vague in the official documents around this time. But from secondary sources, we could infer this drawing order. For example, a report in 1602 written by Li Dai, minister of the Ministry of Personnel at the time, mentions that lots left by the advanced scholars are kept for tribute students and recommended men, while lots left by them are kept for other types candidates (Wu (1609), vol.59).
The Ming lots-drawing procedure respects the eligibility criteria due to the fact that the tubes from which a candidate would draw their job only contained jobs for which they were eligible. So, for example, when matching advanced scholars, the tube with jobs would only contain those that satisfied their eligibility. The official documents around this time mention that the rule of avoidance had to be respected. The documentation is not precise about how that restriction was implemented. From the context, however, and from the descriptions documenting how this restriction was implemented later in the Qing dynasty, it is most plausible that if one drew an incompatible job due to rule of avoidance, he would be allowed to continue drawing until a compatible job was found.
Compared to the First Ming procedure, this lots-drawing procedure limited personal decisions and interference. Moreover, the randomness introduced by lotteries balanced demands from different political clans to place their own people in their home regions. Besides, the drawing of lots has been part of culture in China. Indeed, drawing lots was already used in the assignment of some military posts, as well as the assignment of interns to offices in the capital in earlier times (Will, 2002).
Nevertheless, the new procedure received fierce criticisms from the outset. It was attacked for lack of control in finding the right match (Gu, 1670). One primary issue is that, depending on the realization of chance, higher-priority candidates could draw medium-ranked jobs (i.e. jobs that are also compatible with lower-ranked candidates) while there were still higher-ranked jobs to be filled. Furthermore, it did not take long before the new procedure fell victim to corruption. It was reported that officials selected the best jobs and placed them in a way that, when it was the turn for candidates who bribed them to draw, they could draw the most desirable jobs (Shen, 1619).
3.4. The First Qing procedure (1644-1824)
Despite the change of dynasty, the lots-drawing procedure survived, as using random assignment to diffuse regional powers was seen as a desirable method to reinforce the unification of the country by the newly founded administration, led by the Manchu ethnic minority.
Besides slight modification on eligibility rules (see Table 3.2), there were a few further developments in the procedure. To begin, additional security measures were introduced to ensure impartiality. First, it was stressed that in addition to executing the lots-drawing procedure publicly, officials from the Censorate, a supervisory agency, were present to oversee the appointments. Second, names of candidates and jobs were sealed before putting them into the tubes. Additionally, to cope with corruption and rigging in the drawing process, candidates no longer followed the order determined by their results when drawing jobs. Instead, they followed a random order also determined by lotteries.
| Jobs | |||
|---|---|---|---|
| Metropolitan | Non-metropolitan | ||
| Advanced scholars | First grade | Senior and junior editors at Hanlin Academya | |
| Second and third grade | Ministry secretaries | County magistrates, and prefecture study officers | |
| Tribute scholars and recommended men | County magistrate, department and county study officers | ||
Notes: aA small number of top performers among the second and third grade advanced scholars were selected to study first at the Hanlin Academy. Upon passing the academy exam, one could be appointed to be an editor at the Hanlin Academy as well. As an additional exam was required and there were very few of these jobs, we do not include editors as eligible jobs for candidates who achieved second or third grade advanced scholars.
A more fundamental change was the use of a system of partitioned assignments, which reduced the chance of being matched to a lower-ranked job when a high-ranked job was still available, a main concern in the Second Ming procedure. The appointment for newly selected candidates was organized in every even month, as in the Ming dynasty. The Ministry of Personnel first registered all vacancies reported by different administrative units.141414We focus on the Han jobs. Civil service jobs were reserved for different ethnic groups in Qing dynasty: the Manchu jobs (Manchus were the ruling ethnic minority), the Mongol jobs (Mongols were the crucial ally of Manchus), and the Han jobs. The majority of the jobs, especially the entry-level jobs, were Han jobs. Assignment procedures to the Manchu and Mongol jobs were similar to the Han jobs procedure. Vacancies were categorized by their types—for instance, secretaries in various ministries counted as one type, and county magistrates in various locations counted as another. After preparing the list of vacant jobs, the ministry then drew up, for each type of job, a list of candidates—matching the number of jobs— who were eligible. Whenever there were multiple categories of eligible candidates, quotas for each category were specified.151515We provide an illustration for county magistrates taken from Regulations of Ministry of Personnel (QDLBQXZL, 1886). Candidates qualified through other non-examination channels were also considered for the appointment of county magistrates in the Qing dynasty. The quotas for both candidates selected through exams and other channels were as follows: 5 advanced scholars, 5 recommend men, 4 candidates who paid financial tribute (if none, then substitute with recommended men), 3 candidates who were promoted from clerks. These 17 people formed one “class.” Next, we describe, for a given type of job and a given list of candidates, how the First Qing procedure was applied.
-
•
A supervisor in charge of the appointment first drew a stick from the tube of candidates, then drew a stick from the tube of jobs.
-
•
If the pair of candidate and job did not violate the rule of avoidance, then the supervisor would declare the match.
-
•
If the pair did violate the rule of avoidance, then the job stick was put aside, and the official would keep drawing a new job until the candidate did not need to avoid it. After the match, the ineligible job(s) would be put back into the tube.
-
•
The appointment resumed until all candidates were drawn and matched to a job, or all remaining jobs and candidates are mutually incompatible.
Finally, unassigned candidates would be returned to their queues, waiting for the next appointment. Unassigned jobs would also be added to the vacancy lists in the next appointment.
This system of partitioned assignments increased the chance that a higher-priority candidate would end up with a higher-ranked job. Indeed, given that now each partitioned assignment consisted of only one type of job and eligible candidates, and given the way in which the jobs were processed as well as the way in which the contents inside each tube were determined, candidates with higher degrees had a higher chance to draw a job with a higher rank. The lottery only randomized which exact job one eventually got within the same type (and same rank) of job. The Qing administration seemed willing to sacrifice some randomness in the matches to improve the matching quality.
Yet, the partitioned assignments led to another problem. Unlike the Second Ming procedure, where a candidate who first drew an incompatible job had more jobs available next, now the candidate could only draw from a smaller pool of jobs. This reduced the chance of finding a compatible job. Similarly, it also increased the chance that a job was left unassigned. A situation with increasing numbers of unassigned candidates and unserved jobs was not ideal for the functioning of bureaucracy. Of course, this problem was exacerbated by the rule that unassigned candidates could not be considered for other type of jobs in the current assignment. This rule, on the other hand, can be seen as a means to guarantee that candidates would not be assigned to lower-ranked jobs when they could be considered for higher-ranked jobs in the next appointment.
3.5. The Second Qing procedure (1824-1905)
To address problems related to unfilled jobs introduced by the partitioned assignments, the procedure was changed in 1824 such that instead of all candidates being matched at the same time, for a given type of job, those with incompatible jobs among those in their corresponding tube were required to draw first. Only after the prioritized candidates finished drawing could the rest of the candidates proceed to draw jobs. The other aspects of the procedure remained the same as the previous procedure. The following quote taken from the Collected Statutes of Qing (DQHD, 1886) recorded this change:
“1824, it was approved after discussions, for the people who draw lots in the monthly appointment, those who have home provinces to avoid draw first. If they still draw a job that needs to be avoided, remove this job and ask [the candidates] to draw another job. Until a [compatible] lot is drawn, let those who do not need to avoid home provinces draw.”
By prioritizing the candidates who had regions to avoid, their chance of finding a compatible job was increased, and more jobs were matched, as the only factor driving incompatibility in a partitioned assignment is the rule of avoidance.
While we do not have data that would allow us to estimate whether this change had measurable impact on the cardinality of the matchings, there are indications that there was a reduction in the time it took candidates to be matched to a job after the change was introduced. Based on the calculations by Wang (2016) using the archived curricula vitae of civil servants in the Qing dynasty, the average waiting time for advanced scholars to become county magistrates was reduced from 8 years between 1796 and 1820 to 5.5 years between 1821 to 1850. This provides some suggestive evidence of the possible impact of the procedure change.
To sum up before analysing these procedures, the historical account presented in this section elucidates that the assignment procedures gradually moved away from personal influences and resorted to more systematic rules in deciding who should get which job. Despite the fact that candidates’ preferences were considered in the initial Song procedure, they were no longer taken into account by the later procedures, mainly because individual preferences could come into conflict with the prioritization of high-levels. From the late sixteenth century onward, drawing lots was accepted and routinized in the civil service appointments, and developments were therefore made to balance the prioritization of high-levels and the number of total matches, while respecting eligibility, rule of avoidance, and to some extent, randomness.
It is worth mentioning that there are a few common features present in the design of all procedures. First, it was emphasized in all procedures that the assignments should be done publicly, as a means of transparency and, consequently, legitimacy for the assignment outcomes. Second, and perhaps more importantly, all procedures were carried out sequentially, and appointments were declared once a match was found. This provided a simple and intuitive way to produce desirable matchings. When using lots-drawing, for instance, even if there are other ways in theory to find randomized compatible matchings, appointments in the historical practice were made sequentially one at a time using specific priority orders.
4. Assignment procedures: A theoretical framework
Analysing the functioning of the assignment procedures used in several historical episodes is challenging. Our analyses focus on the main procedures described above. The historical records indicate that sometimes adjustments were made after the use of the standard method.161616For instance, in a letter between Wang Shu—minister of the Ministry of Personnel from 1487 to 1505—and the court, such a case was mentioned (Chen et al., 1638). Shi Cunli, aged 22, was awarded with the advanced scholar title. Under the First Ming procedure, he could have been assigned to a county magistrate. However, the ministry worried that he could not manage the heavily populated county due to his lack of experience, and therefore recommended sending him back for internship in the foreign affairs department, where he was eventually appointed with a secretary job. Similarly, it was documented that in the Qing dynasty, candidates who were initially appointed through the standard procedure had to present themselves in the court and in front of the emperor for audition (QDLBQXZL, 1886). Based on the audition and the difficulty level of the job one was assigned to, the initial assignment could be changed. We abstract away from these adjustments as they are difficult to model due to their ad-hoc nature. We construct a simple model that allows us to compare the main assignment procedures across time. While our application is motivated by the civil service assignment, our theoretical framework follows the terminology used in matching literature.171717Throughout the text, we use the terms worker and candidate interchangeably.
4.1. Model
A set of workers is to be matched to a set of jobs . A matching is a function such that each worker (job) is assigned either to one job (worker) or is left unassigned, and a worker is matched to a job if and only if the job is also matched to him, that is, for any and , . To account for the restrictions on what matches are acceptable, let be a compatibility correspondence that defines which jobs are compatible with each worker. In our application, compatibility could be determined by eligibility or the rule of avoidance. In addition, we say that a matching is feasible if workers only receive jobs that they are compatible with, that is, for any and , . The set of all feasible matchings is denoted by . We refer to a triple as a market.
For any matching and any subset of jobs , let be the set of workers matched to some job in under matching . That is, . Denote by the cardinality or the size of , that is, .
Definition 1.
A matching minimizes unfilled jobs if for any , .
This definition says that a matching minimizes unfilled jobs if there is no other feasible matching that matches more workers to jobs. Notice that since a worker can only be matched to a job, minimizing unfilled jobs is equivalent to minimizing unmatched candidates. For our application, it is important to assign as many qualified candidates as possible to jobs, since both unassigned candidates and unfilled jobs could leave important resources idle until the next appointment, typically executed two months later.
An assignment plan is a pair , where is a strict total order over the set of workers, and each element of is a strict total order over the set of jobs. Assignment plans are a key concept that unifies all of the five procedures that we evaluate into a common framework. Depending on the specific application, they can represent a design decision or a realization of chance when drawing lots. The first element of the assignment plan, the order , tells for each pair of workers ,, who will be considered for a matching first. In the Song , First, and Second Ming procedures, for instance, an assignment plan in which represents the situation in which worker obtained a higher exam grade than , and therefore if both obtained the same title (for example, advanced scholar), both procedures will match to a job (if any) before .181818Note, however, that does not say that will be matched immediately after , but that will not be considered for a match before . In the Qing procedures, indicates the order in which workers in the same tube are drawn. So if, for example, a tube contains workers , then represents the realization of chance in which these workers are drawn from that tube in that order. All possible orderings in which workers can be drawn from that tube are represented by all the permutations of . Importantly, a uniform distribution over all of these permutations represents the distribution in which these orders take place in the real-life procedure.
The second element of the assignment plan, the orders over jobs , represents the order in which jobs are considered, for each worker. Given a worker and two jobs , says that, when considering a match for worker , if both jobs are being considered and the worker is matched to , it must be that is not available anymore or is incompatible with . In the Song procedure, represents worker ’s preference over the jobs: if both and are still available when his turn comes, and is compatible with him, he will choose instead of . In the First Ming procedure, it represents whatever criterion was used to choose among eligible jobs. Finally, in the Second Ming and the Qing procedures, orders over jobs also represent a realization of chance of the order of drawing of jobs from the corresponding tube. So if worker is such that , and these three jobs are in the tube from which he will draw, he will first draw . If is an eligible job that does not violate the rule of avoidance, he will be matched to that job. If, say, is incompatible with , then he will next draw , and so on. As in the order over workers, drawing uniformly from the possible permutations over a set of jobs results in the same distribution of outcomes that result from the real-life procedure when is facing a tube with these contents. Note that, as opposed to the order over workers, which is unique, here each worker might be associated with a different order over jobs. This represents the fact that the drawings of jobs from a tube are independent draws—conditional, of course, on the contents of the tube.
The other key concept when modeling the procedures is an assignment arrangement. An assignment arrangement is a list that partitions a market into independent sub-markets. Each element of the list is a sequence of tubes, consisting of a list of subsets of workers and a list of subsets of jobs . These sets of workers and jobs, which we denote by tubes, are such that:
and for every or , and . In other words, the sets listed in the sequences of tubes partition the sets of workers and jobs.
An assignment arrangement represents two aspects of the assignment procedure. First, it allows for the problem to be partitioned into independent sub-markets. This is what is done in the Qing procedures: candidates and jobs are split into separate and independent matching sub-problems for each type of job. Second, it represents the order in which different subsets of candidates and jobs are considered. A sequence of tubes , for example, indicates that first the workers in will be considered and matched to jobs. Only after all the workers in are matched to a job (or are left without any remaining compatible job), the workers in will be considered. When it comes to jobs, take any worker (regardless of whether it is a worker in or ), jobs in will only be considered if there are no jobs compatible with that worker among those remaining in . This representation not only allows the modeling of all the procedures, but also the extension to a new procedure that improves upon the Second Qing procedure in Section 5.2.
Given a market, an assignment plan together with an assignment arrangement can be combined to represent an execution of the matching procedures that we model. Consider a market and an assignment plan . We next describe how the assignment arrangement produces a matching of workers to jobs. To do so, it is helpful to use the following notation. Given a set and an order , we denote as the top element of in the order , that is, .
For each element in the assignment arrangement, the steps below are followed to produce a matching :
-
(1)
Let .
-
(2)
For each , let and repeat the following procedure until :
-
•
Let and remove from . There are two cases:
-
–
: let .
-
–
: let be the lowest value of such that , and . Let , and remove from .
-
–
-
•
In other words, given in the assignment arrangement, we follow the order of tubes of workers in , matching the workers in first, and only after considering all of them do we move to the next subset of workers , and so on. Within each tube, the order in which workers are chosen is determined by . Each worker is matched to a job in the first tube of jobs that still contains a compatible job. If that tube contains more than one compatible job, then he is matched to the job with highest priority in that tube with respect to . If, however, there is no compatible job left, then he is left unmatched. We repeat these steps for each in the assignment arrangement, which produces a matching of workers to jobs. We refer to the combination of an assignment arrangement with a method of producing an assignment plan as a procedure.
The key advantage of this model, for our purposes, is that it allows us to perform reliable comparative statics between procedures. By fixing an assignment plan and evaluating the matchings produced by two different assignment arrangements, we are able to compare, for example, two random procedures without picking different realizations of chance. Moreover, we are even able to compare deterministic procedures, such as the Song , to a random one, such as the Second Ming . If we are able to analyze the outcomes produced by these two procedures for any fixed assignment plan, then the fact that one is deterministic and the other is random is inconsequential for the analysis.
To facilitate our analysis of the procedures used in history, we consider in what follows a simplified setting where there are two categories of workers, (representing advanced scholars), and (representing tribute scholars and recommended men).191919While there was an extra division within the category of advanced scholars during the Song and Ming dynasties, our simplified version is equivalent, for our analysis, to the one used during the Qing dynasty. On the other side, jobs are partitioned according to eligibility: jobs in and are eligible for workers in and respectively, and jobs in are eligible to all workers. The partition reflects the fact that, in our application, some jobs were assigned only to advanced scholars, and some only to tribute scholars and recommended men, while some others could be matched to candidates from both categories. This simplification allows us to capture the main features of the civil service assignment without unnecessary complications that are not crucial to our results.
To capture the objective of assigning candidates with different degrees to jobs with matching levels, we formulate the following definition when evaluating a matching with respect to our simplified setting.
Definition 2.
A matching prioritizes more high-levels than if , , , and . A matching prioritizes high-levels if there does not exist another matching that prioritizes more high-levels than .
In other words, a matching prioritizes more high-levels than another matching if (i) does not match fewer workers than , (ii) does not match fewer workers from than , (iii) does not match less workers from to jobs in than , and (iv) it does not match less workers from to jobs in , except when compensated by an increase in workers from matched to these jobs. This definition captures, with relatively simple conditions, the objective of prioritizing the matching of higher-level jobs over lower-level ones, and of higher-level candidates over lower-level ones. Given that eligibility constraints are always satisfied, it guarantees the trade-offs that remain between which candidates and jobs to match are resolved toward matching more advanced jobs to more advanced candidates.
Finally, for our historical analysis, it will be helpful to consider two different compatibility correspondences. The first one, denoted by , considers only the constraint on eligibility. That is, for any and , if and only if and or and . The second one, denoted by , considers both the constraints of eligibility and rule of avoidance. That is, for any and , if and only if and is not in worker ’s native region.
4.2. Models of the procedures
We will use our baseline model of markets, assignment plans, and assignment arrangements to describe the five procedures presented in Section 3 as instances of the model. It should go without saying that, given the nature of the sources that we used, some simplifications and additional assumptions are unavoidable. We are, however, explicit whenever they are consequential, and made a conscious effort to make them parsimonious. If there is a gap in the description of some procedure but is present in a previous or later procedure, then we assumed continuity of that element. Finally, whenever possible we opted for assumptions that make the procedures more similar to each other, as opposed to different, to reduce the reliance of the differences that we obtained on those assumptions. That being said, the vast majority of the elements in the descriptions below can be traced back to the descriptions in the historical documents we used.
4.2.1. The Song Procedure
First, the workers in would be matched first, following a single ordering based mainly on their exam result. Then the workers in , also following a single ordering based mainly on their exam result. During their turn, workers are able to choose, in principle, any available unmatched job. This choice could then be approved or rejected. To the extent of our knowledge, there were no systematic rules for approving or rejecting a choice. We therefore make the assumption that, as long as the worker is compatible with the job in terms of both eligibility and rule of avoidance, the choice would be approved.
The Song assignment arrangement therefore contains only one sequence of tubes, . The assignment plan used in the Song procedure is such that if workers and belong to the same category and obtained a better exam result than , then . As for each worker , represented that worker’s strict preference ordering over the jobs in .
4.2.2. The First Ming Procedure
Workers are matched following the same ordering as the Song procedure: first those in , and then those in , and within each category their order is based on their exam results. Workers, however, do not have a say on the job that they will be matched to. Instead, the ministry matches a job that better fits one’s skill, in an attempt to make the matching prioritize high-levels. More specifically, this implies that the ministry first tries to match as many workers in to jobs in , and when that is not possible, to jobs in . After trying to match all the workers in , they would try to match those in , first to the remaining jobs in (if any) and then to those in .
The First Ming assignment arrangement thus contains still one sequence of tubes but with different partitions: . The assignment plan used in the First Ming procedure is such that if workers and belong to the same category and obtained a better exam result than , then . None of our results depend on the orders over jobs , so there is no need to have an explicit model of that part of the assignment plan. Therefore, any list of ordering over jobs can be an assignment plan under the First Ming procedure.
4.2.3. The Second Ming Procedure
As in the previous procedures, workers in were matched first in the Second Ming procedure, and then those in , and their order within each category is based on their results from the examination. The difference comes to the choice of jobs to be matched to each worker: workers draw their jobs from a tube containing all of the jobs that are compatible with the worker.
The Second Ming assignment arrangement is the same as that of the Song procedure. The assignment plan used in the Second Ming procedure is such that is the same as the First Ming procedure, but where each ordering in is independently drawn from a uniform distribution over the set of all orderings over .
4.2.4. The First Qing Procedure
The First Qing procedure differs in multiple ways from the previous ones. First, the set of workers and jobs are partitioned between multiple sequences of tubes, each of them matching workers to only one type of job. For example, one sequence of tubes has only ministry secretaries as jobs and workers compatible with that job, namely, advanced scholars; another sequence of tubes has only county magistrates as jobs and workers compatible with that job, namely, both advanced scholars and tribute scholars together with recommended men, etc.
Without loss of generality, we abstract away from the specific type of jobs, and consider still the three categories of jobs, , , and .202020From Table 3.2, we know that there were two types of jobs, one type of job, and one type of job. Since the Qing practice did not allow unmatched candidates to be considered for the next type of jobs, that is, assignment of each type of job was independent, this simplification does not change the qualitative aspects of our results. Further, to account for the fact that workers in are compatible with both jobs in and , we denote by and two sets of such that . Similarly, denote by and two sets of such that .
Then, the First Qing assignment arrangement contains the following three sequences of tubes:
where the sets in the assignment arrangement are such that , and . These assumptions are in line with the design of the Qing procedure, in which the number of workers in each sequence of tubes matches the number of jobs.212121Differently from the Ming procedures, here the number of workers put into urns was based on the number of jobs to be matched. These assumptions, moreover, prevent situations in which the qualitative results depend on “misguided” choices while setting up these sequences of urns. For example, if , , and , even in the absence of incompatibilities due to the rule of avoidance the outcome will not prioritize high-levels simply because jobs in will be left unmatched, while workers in could be matched to them instead of the jobs in .
The second difference involves the method of constructing the assignment plan, and in particular when it comes to the way of ordering the workers. The assignment plan used in the First Qing procedure is such that is independently drawn from a uniform distribution over the set of all rankings over , and each ranking in is independently drawn from a uniform distribution over the set of all rankings over .
4.2.5. The Second Qing Procedure
The Second Qing procedure differs from the First Qing procedure in only one aspect: instead of having only one tube of workers in each sequence of tubes, there are two tubes of workers. More specifically, the assignment arrangement in the Second Qing procedure has the following three sequences of tubes:
In the sequences of tubes above, there are two tubes of workers in each sequence of tubes. The first one contains the workers who are incompatible with some job in the tube of jobs and therefore prioritized in the assignment, and the second one contains workers who are compatible with all jobs in the tube of jobs and thus are not prioritized in the assignment. Formally, take the sequence of tubes in the First Qing procedure, which partition the set of workers as and the set of jobs as . The tubes in the Second Qing procedure are such that, for , , , , and , where the superscripts and stand for priority and non-priority, respectively. Notice here that each sequence of tubes contains workers and jobs that are mutually compatible in terms of eligibility by construction, thus the sole criterion for splitting the tubes of workers is the rule of avoidance.
As in the First Qing procedure, the assignment plan used in the Second Qing procedure is such that is independently drawn from a uniform distribution over the set of all rankings over , and each ranking in is independently drawn from a uniform distribution over the set of all rankings over .
5. Analysis of the assignment procedures and the changes
In this section, we present comparative static results, showing how the matchings produced by the five procedures perform in terms of minimization of unfilled jobs and prioritization of high-levels, and how the changes that were made over time affect these properties.
We replicate each analysis for the cases in which and are each used as compatibility correspondences. By doing this, we are able to compare how the changes in the procedure being used impact the assignments if we only consider eligibility concerns () or those concerns combined with the rule of avoidance (). When combined, these results will show how the interaction between these two sets of constraints yields a very different conclusion about the potential impacts of these changes.
5.1. Properties of the assignment procedures and comparative statics
All the procedures we evaluate were implemented by matching workers to jobs sequentially. Despite its transparency and simplicity, this type of mechanism may suffer from some shortcomings due to the “greedy” way in which they process the matchings.
More specifically, both the minimization of unfilled jobs and the prioritization of high-levels are properties that, in general, are incompatible with matching each worker with an arbitrary compatible job, one at a time. To see this, consider the example below.222222While the example considers eligibility constraints, one can easily construct an analogous one using only the rule of avoidance.
Example 1.
Consider a market of two workers and two jobs . The subscript index indicates the category of worker and job; thus, worker is eligible for both jobs and , while worker is only eligible for . If in a procedure, is matched first to , then is left unassigned as he is incompatible with the remaining job . However, we know there is another matching where both workers can be matched to both jobs: , and .
The issue in the example resides in the fact that if worker is matched before , ignoring the relationship between the sets of compatible jobs of both workers, might not minimize unfilled jobs. At first sight, this problem could be solved (or at least mitigated) if some of the matchings could be revised. If at worker ’s turn only job is available, both workers could “exchange” their draws in a mutually compatible way. In fact, this possibility was discussed in the early years of the Second Ming procedure. In 1602, in a correspondence to the court by Li Dai—the minister of the Ministry of Personnel at the time, it was suggested that a candidate who either draws an incompatible job or ends up with no compatible jobs left would be able to exchange his assignment with some candidate matched with a compatible job in a mutually acceptable way (Wu, 1609). However, there is no indication that such exchanges were carried out. One natural interpretation for the reason why these exchanges were not implemented is that making exchanges after a matching was determined reduces at least the perception of transparency. Additionally, revising matchings that were determined randomly goes in the opposite direction of the purpose of the introduction of randomness, bringing back arguably arbitrary changes to the outcome.
Notice that the discussion on the exchange method also provides one more indication that minimizing the number of unfilled jobs were an actual concern at the time. One additional indication that unfilled jobs were an issue affecting the assignments was that from the mid-Qing, one or two extra candidates were added when constructing the list, as a means to reduce the number of unfilled jobs (QDLBQXZL, 1886).
The challenges faced by the designers of these procedures were, in fact, extremely complex even for today’s standards. The first feasible algorithm for finding a maximum matching—the “Hungarian method”— was published in the 1950s (Kuhn, 1955). The literature on “online matching,” which covers methods for determining matchings “greedily” one by one in an attempt to produce approximately maximum matchings, is still evolving (Feng, 2014). Even if one considers only the rule of avoidance, the determination of which workers should be matched to which jobs is a relatively complex combinatorial problem that depends on the numbers of jobs and workers from each region. Given these facts, therefore, it should not come as a surprise that the procedures in general are not optimal. We will show, however, that the designers were relatively close to that in the end.
Our first result shows that, when considering only eligibility constraints, the changes in the procedures were consistent with the objective of minimizing unfilled jobs.
Proposition 1.
When considering only compatibility in terms of eligibility , the First Ming , First Qing , and Second Qing procedures produce matchings that minimize unfilled jobs, while there are markets and assignment plans for which the Song and the Second Ming procedures produce matchings that do not minimize unfilled jobs.
Proof.
First, recall that the First Ming procedure tries to match workers to jobs that fit their degrees, following the order to match as many workers in first to jobs in and then to , and afterwards, match as many workers in to jobs in the remaining jobs and then to . Therefore, (i) jobs in will only be left unmatched if , (ii) jobs in will only be left unmatched if every worker is matched, and (iii) jobs in will only be left unmatched if all workers in are matched. One can clearly see that when some job is left unmatched, the three observations above imply that there is no alternative matching that could match that job without leaving another unmatched.
Second, notice that every sequence of tubes under the First and Second Qing procedures contains workers and jobs that are mutually compatible with respect to . Since the number of workers and jobs are equal in each one of these sequences of tubes, every worker is matched to a job, and therefore the matching produced by these two procedures does not minimize unfilled jobs.
Next, to see that the matchings produced by the Song and Second Ming procedures might not minimize unfilled jobs, consider a market where there is an equal number of workers, workers, jobs, and jobs, and with . Consider moreover an assignment plan, where workers are assigned before workers, and for every worker, jobs are considered before jobs. That is, for every and , ; and for every , and , .
The matchings produced by both the Song and the Second Ming procedures match the workers in to the jobs in , leaving all the workers in and jobs in unmatched. Notice, however, that there is an alternative matching that matches every worker and every job: match all workers in to the jobs in , and all workers in to the jobs in . ∎
The proposition below shows that when both eligibility and rule of avoidance are considered, the story changes.
Proposition 2.
When considering compatibility in terms of both eligibility and rule of avoidance , there are markets and assignment plans for which all the procedures produce matchings that do not minimize unfilled jobs.
Proof.
Let there be three regions: , , and . Moreover, let () be the set of workers (jobs) from region , and define the same for and respectively. Consider a market where there is an equal number of workers and jobs, with and , and there are no workers nor or jobs. In addition, within workers, there are from region and from region . On the job side, within jobs, we have from region , from region , and 1 from region . Moreover, consider an assignment plan where for every and , ; and for every , , , and , and . Put differently, the assignment plan is such that all workers from region are assigned before all workers from region , and for every worker, jobs from region are considered before jobs from region , which are considered before jobs from region .
Then, the matchings produced by all the procedures that we are evaluating match the workers in to the jobs in , and one worker in to the job in , leaving all the remaining workers in , and the jobs in unmatched. Notice, however, that there is an alternative matching that matches every worker and every job: match workers in to jobs in , one worker in to the job in , workers in to jobs in , and one worker in to a job in . Therefore, the matchings produced by all the procedures do not minimize unfilled jobs when taking both eligibility and rule of avoidance into count. ∎
Next, we consider the extent to which the matchings produced by all the procedures prioritize high-levels. As before, we first discuss the case where we only take eligibility into account.
Proposition 3.
When considering only compatibility in terms of eligibility , the First Ming , First Qing , and Second Qing procedures produce matchings that prioritize high-levels, while there are markets and assignment plans for which the Song and the Second Ming procedures produce matchings that do not prioritize high-levels.
Proof.
First, recall in the First and Second Qing procedures, workers and jobs are partitioned into three sequences of tubes in which they are all compatible with respect to . Since the number of workers and jobs is equal in each one of these sequences of tubes, every worker is matched to a job. Moreover, every job in is matched to a worker in . These two facts together imply that this matching prioritizes high-levels.
Next, consider the First Ming procedure. Regardless of the assignment plan, the following observations can be made about the matching produced:
-
(1)
An unmatched job in is possible only if there are less workers than jobs, .
-
(2)
If , then every job in is matched to a worker in , and every worker in is matched either to a job in or .
-
(3)
If , then every job in and is matched to a worker in .
-
(4)
If a job in is left unmatched, then every worker is already matched to a job. If a worker in is left unmatched, then every job in is already matched to a worker.
These observations combined imply that the matching produced by the First Ming procedure prioritizes high-levels.
Finally, to see that the Song and the Second Ming procedures may not prioritize high-levels, consider the case in which and . Moreover, let the assignment plan be such that for every and , ; and for every , , , . That is, all workers in are matched before all workers in , and for every worker, all jobs in are considered before all jobs in . Then, the matching produced by the Song and the Second Ming procedures matches the workers in to the jobs in , leaving all the remaining workers in , and the jobs in unmatched. Notice, however, that an alternative matching that matches every worker in to the jobs in and every worker in to the jobs in prioritizes more high-levels than the one produced either by the Song or the Second Ming procedure. ∎
As for the minimization of unfilled jobs, rule of avoidance also affects the prioritization of high-levels. The following shows that when we consider both eligibility and rule of avoidance as compatibility constraints, all procedures can result in matchings that do not prioritize high-levels. This result follows immediately from markets constructed from the proof of Proposition 2, and therefore the proof is omitted.
Proposition 4.
When considering compatibility in terms of both eligibility and rule of avoidance , there are markets and assignment plans for which all the procedures produce matchings that do not prioritize high-levels.
Notice that if we consider only the results involving compatibility in terms of eligibility, we would conclude that both the changes from the Song procedure to the First Ming procedure and from the Second Ming procedure to the First Qing procedure would unambiguously improve the matchings that were produced, both in terms of the minimization of unfilled jobs and prioritization of high-levels. However, when we compare with respect to compatibility in terms of eligibility and rule of avoidance, the same conclusion can no longer be made. In fact, we show in the theorem below that the changes might have resulted in the opposite effect, even while considering the same market and assignment plan.
Theorem 1.
When considering compatibility in terms of both eligibility and rule of avoidance , there are markets and assignment plans for which the matching produced by both the Song and the Second Ming procedures prioritizes high-levels and leave no worker unmatched, but under the First Ming , the First and Second Qing procedures do not prioritize high-levels and leave half of the workers unmatched.
Proof.
Let there be three regions: , , and . Let, moreover, be the set of workers (jobs) from region , and the same for and . Consider then a market where , and , with . Among the workers, of them come from region , and the other of them come from region . Among the jobs, of the jobs are from region , and of the jobs are from region .
Consider the following assignment plan , where for every and ; for every , , , . That is, all workers in are assigned before all workers in ; and for every worker, all jobs in are assigned before all jobs in .
The matching produced by both the Song and Second Ming procedures matches the workers in to the jobs in , and the workers in to the jobs in . Notice that prioritizes high-levels and minimizes unfilled jobs.
The matching produced by the First and Second Qing depends on the specific way in which the workers in are partitioned.232323In practice, this followed the candidates’ exam grades, so that those with higher grades were put into the sequence of tubes with the jobs, and those with lower grades to the remaining jobs. The arrangement we use relies, therefore, on the workers from region having lower grades. We will consider the case in which the sequence of tubes for the jobs is and for the jobs .
The matching produced by the First Ming and the First and the Second Qing procedures—with the sequence of tubes above—matches the workers in to the jobs in , but leaves the workers in and the jobs in unmatched. Notice that the matching leaves no worker or job unmatched, and prioritizes more high-levels than . ∎
Even though the First Ming and First Qing procedures were motivated by the need to improve the prioritization of high-levels, our result suggests that there are situations where both procedures lead to worse outcomes, due to its interaction with the rule of avoidance. Moreover, the magnitude of the problem can be substantial, as large as half of the workers.
A striking consequence of the results we produced so far is that the changes of mechanisms might have opposite effects on the minimization of unfilled jobs and prioritization of high-levels, depending on which constraints are being considered, for the same market and assignment plan. That is, this difference is not driven by different orders or realizations of chance, but by whether the rule of avoidance is being considered or not.
Finally, we show that, the change from the First to the Second Qing procedure nonetheless resulted in an improvement in the cardinality of the matchings produced. The proposition below describes this result.
Theorem 2.
Consider any market and assignment plan, and let and be the matchings produced by the First and Second Qing procedures, respectively. Then, . Moreover, there are markets and assignment plans for which .
Proof.
Let be any of the sequences of tubes in the First Qing , and then let be the corresponding sequences of tubes in the Second Qing .242424For the purposes of this proof, the categories of the workers and jobs involved in these sequences of tubes is inconsequential, since from the perspective of these categories every worker is compatible with every job.
First, notice that since workers in the set are compatible with every job in , the only way that some worker in is left unmatched in both procedures is if all jobs are matched. Therefore, one way to show that is to show that every worker in who is matched to a job under the First Qing is also matched to a job under the Second Qing .
Let be any assignment plan, and be the ranking restricted to the set of prioritized workers . In addition, let , and be the -th highest-ranking worker in the ranking . We now show by induction that, for every worker , the set of jobs that are still available in the step where is matched to a job under the First Qing procedure, denoted by , is a subset of the jobs that are available when matching under the Second Qing , denoted by .
Base: Let . Under the Second Qing Procedure, the set of jobs still available when matching , the highest-ranking worker among the prioritized workers, is . Therefore, .
Step: Assume that for every and , , and consider a worker . Suppose, for a contradiction, that there is a job that is available when matching him under the First Qing procedure but not when matching him under the Second Qing procedure, that is, formally, but . By induction assumption and the fact that , and therefore . By construction of the Second Qing procedure, the only way that this can happen is if the job is matched to worker in the Second Qing procedure. That is, . Moreover, we know as a result of the immediate assignment by the procedure that . By the contradiction assumption , we therefore have . On the other hand, the contradiction assumption implies that . But this is a contradiction with , since by induction assumption .
Finally, to observe that there are some situations where , we consider the following market. There are three regions: , , and . Moreover, let () be the set of workers (jobs) from region , and the same for and . Let and .
Consider the following assignment plan , where for every and , for every , , , .
The matching produced by the First Qing procedure matches the workers in to the jobs in , but leaves the remaining workers in and jobs in unmatched.
The matching produced by the Second Qing procedure matches the workers in to the jobs in , and the workers in to the jobs in . ∎
Figure 1 summarizes the above results. Note that we know from Proposition 2, despite the improvement yielded by the Second Qing procedure, in general the Second Qing procedure may still not match as many candidates as possible. In the section below, however, we show that in certain markets the addition of a single tube of jobs could result in a procedure that produces matchings that minimizes unfilled jobs and prioritize high-levels in every realization of chance.
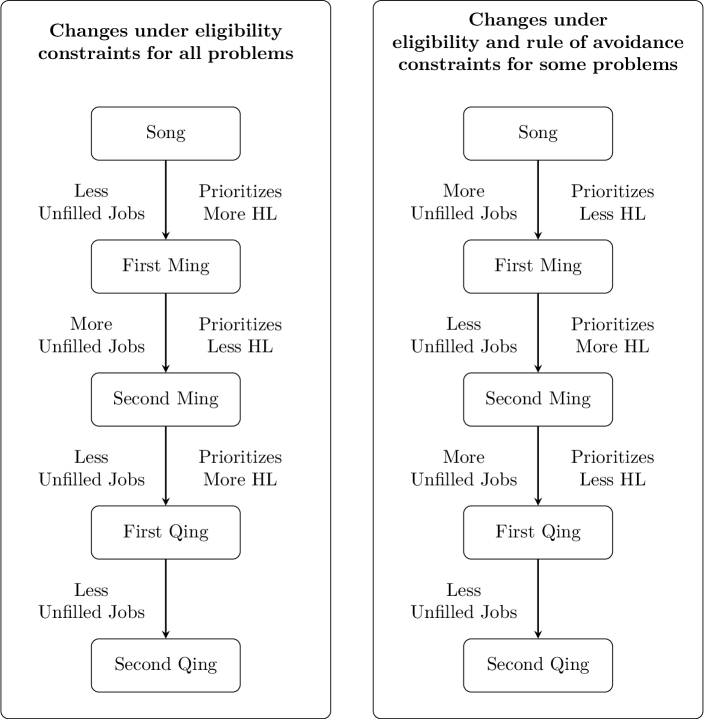
5.2. A simple lots-drawing procedure that minimizes unfilled jobs
We will now show that, under a relatively simple assumption on the numbers of workers and jobs per region, there is a modification of the Second Qing procedure that always yields matchings that minimize unfilled jobs in each sub-market.
The problems regarding the minimization of unfilled jobs in the Second Qing procedure is driven solely by one of the compatibility constraints—namely, rule of avoidance. Therefore, for ease of illustration, we will consider just one category of workers and jobs that are mutually compatible in terms of degrees. Let be the set of regions to which workers and jobs might belong to, and and denote the set of workers and jobs from region , respectively. In addition, let be the set of all workers except . Similarly, denote the set of all jobs except by .
Definition 3.
A market is regionally-sufficient if for every for which and , .
This condition requires, therefore, that for each region that has both workers and jobs in the market, there are no more jobs than workers.252525Notice that this is a condition involving mutually incompatible sets, and therefore are independent of the conditions for the existence of a matching that covers all workers or all jobs (Hall, 1935).
Without loss of generality, let be the set with the largest number of workers (that is, for all , .), and consider the following sequence of tubes:
where contains the jobs from the region with the largest number of workers, and contains the jobs from the other regions. In this ordering, workers from the region that has the largest number of workers are given priority to draw a job over the rest of the workers, and the jobs from this region are put into the second tube of jobs.262626If we do include workers from regions that do not have jobs, then we include them in the second tube on the workers’ side, together with . If we include jobs from regions that do not have workers, then we also include them in the first tube of jobs, together with .
Theorem 3.
If the market is regionally-sufficient, the matchings produced by the sequence of tubes minimize unfilled jobs for any assignment plan. Moreover, if , then every job is matched to a worker.
Proof.
Without loss of generality, we assume that the sets of workers are ordered such that .
In a first step, we show that all jobs in the first tube, , will be matched. Suppose that some job in is left unmatched. Let this unmatched job be located in region , a region that does not have the largest number of workers. That is, formally, , with . It must then be that all workers who can be matched to , including all workers in and all workers in except (who are incompatible with jobs in ), are already matched to jobs in . This implies that, for any , the following condition must hold:
where . The condition says that there are more jobs in than there are total workers excluding those from region , where the unmatched job is located. Since by construction the workers are ordered such that , then we must have:
which is a contradiction with the market being regionally-sufficient. Indeed, over-demand implies for all , and therefore .
In a second step, we consider the jobs in the second tube, . Notice that if no job in is left unmatched, then all jobs are matched to workers, therefore minimizing unfilled jobs. Suppose then that some job in is left unmatched. A first observation is that it must be the case that all workers in (who are compatible with ) are matched. Otherwise, there would be no job left unmatched in .
There are then two cases to consider. First, there is no worker in left unmatched. If that’s the case, then all workers are matched and therefore the matching minimizes unfilled jobs.
Second, there is some worker in left unmatched. Since he is in the first tube of workers, it must be that workers in exhausted all jobs in . In that case, however, by the time the workers in are drawn, all jobs available (those in ) are compatible with them.
Here, if , we have a contradiction with some job in being left unmatched. In this case, all jobs are matched.
If , then it is still possible that some job in is left unmatched. To see that the matching is still minimizing unfilled jobs in this case, we will represent the market as a bipartite graph, where are vertices on one side and each vertex represents a worker, are the vertices on the other side and each vertex represents a job, and an edge connects and if and only if they are compatible, i.e., they are from different regions. A matching is then a set of the edges such that each worker or job can only appear in at most one of the edges in that set. An augmenting path is a path with an odd number of edges in which both ends are unmatched vertices and the edges alternate between edges inside and outside the matching. The following lemma is useful to show our result.
Lemma 1 (Berge’s Lemma).
A matching minimizes unfilled jobs if and only if it contains no augmenting path.
Suppose the resulting matching does not minimize unfilled jobs. Then, by Berge’s Lemma, this implies there is an augmenting path connecting an unmatched worker in and an unmatched job in . An alternating path that starts at a worker in , however, never includes an element of . To observe this, consider an unmatched worker in . That worker is connected to the jobs in . Since the next edge in the augmenting path must be in the matching, it connects next to a worker in (since all jobs in are matched to workers in ). Therefore, if we keep adding edges to the augmenting path we will always alternate between vertices in and . Therefore, there is no augmenting path connecting an unmatched worker in and an unmatched job in —a contradiction with the matching not minimizing unfilled jobs. ∎
The theorem above suggests that, if considering the civil service application, a procedure that minimizes unfilled jobs could involve ordering two tubes for each side of the market, in what could be considered a small departure from the Second Qing procedure. Interestingly, this extension involving the use of two ordered tubes of jobs is not only a natural extension of the original procedures, but similar to an extension that was briefly experimented while implementing the Second Ming procedure. In it, instead of having a single tube of jobs, there were four tubes, each representing four divisions of the empire—northwest, northeast, southwest, and southeast (Will, 2002). Candidates would draw first from the tube containing jobs from the division where their home province was before proceeding to the other ones. The intention was to offer a compromise between the use of the rule of avoidance (which was still in place) and an attempt to place candidates in locations that were not too far from their hometown. The four-tube system, however, stopped briefly after its introduction. One reason seemed to be that corruption became rife after the drawing procedure became more complicated (Shen, 1619). The need for considering proximity was no longer mentioned in the Qing discussions.
It is important to note that the markets used to prove Proposition 2 are regionally-sufficient. Therefore, this assumption does not mitigate the problems of the procedures that we identified regarding the minimization of unfilled jobs. It is also worthy of noting that the procedure above is not only an interesting extension of the Second Qing procedure, but also a simple and transparent proposal for producing, in the present, maximum matchings under these type of constraints.
6. Discussion
This paper presented the evolution of the civil service assignment procedures that were used for more than a thousand years to match qualified candidates to government jobs. We presented detailed descriptions of these procedures and the discussions that lead to their changes. We also provided a unified theoretical framework for describing and evaluating the procedures and their characteristics, helping us to understand the trade-offs behind each change. Due to the challenges in balancing different objectives, some of the changes, despite their motivations, could have led to unintended consequences.
The careful assessment of the details of procedures such as the ones we mapped in this paper is valuable for multiple reasons. One is that it allows us to, through the mathematical properties that they have, look behind the curtain and find traces of issues and concerns that the designers were handling. Another reason is that it provides a toolkit for further analysis about the subject in ways that prevent procedural misspecification. For instance, the fact that civil servants were randomly matched to important roles in the empire for hundreds of years in China presents an exciting opportunity for empirical work.272727This is especially true in China, which has preserved an extensive amount of relevant historical records. But the reliability of estimations that could be made are likely sensitive to the extent to which the distributions over the matchings reflect the specific constraints and procedural details.
Finally, we believe that historical studies related to the design of matching procedures or other types of markets can provide important insights not only into what seems to work in the short or long term, but also which parts of a design persist even when the institutions around it also change and evolve. These resilient properties are likely to be desirable when designing new procedures.
References
- Abdulkadiroğlu and Sönmez (2003) Abdulkadiroğlu, A. and Sönmez, T. (2003). School choice: A mechanism design approach. American economic review, 93 (3), 729–747.
- Andersson and Ehlers (2017) Andersson, T. and Ehlers, L. (2017). Assigning refugees to landlords in sweden: Efficient stable maximum matchings. The Scandinavian Journal of Economics.
- Arnosti and Shi (2020) Arnosti, N. and Shi, P. (2020). Design of lotteries and wait-lists for affordable housing allocation. Management Science, 66 (6), 2291–2307.
- Bai and Jia (2016) Bai, Y. and Jia, R. (2016). Elite recruitment and political stability: The impact of the abolition of china’s civil service exam. Econometrica, 84 (2), 677–733.
- Berger et al. (2020) Berger, J., Osterloh, M., Rost, K. and Ehrmann, T. (2020). How to prevent leadership hubris? comparing competitive selections, lotteries, and their combination. The Leadership Quarterly, 31 (5), 101388.
- Besley and Persson (2009) Besley, T. and Persson, T. (2009). The origins of state capacity: Property rights, taxation, and politics. American Economic Review, 99 (4), 1218–44.
- Boczoń and Wilson (2018) Boczoń, M. and Wilson, A. (2018). Goals, constraints, and public assignment: A field study of the UEFA Champions League.
- Bogomolnaia and Moulin (2004) Bogomolnaia, A. and Moulin, H. (2004). Random matching under dichotomous preferences. Econometrica, 72 (1), 257–279.
- Börner and Hatfield (2017) Börner, L. and Hatfield, J. W. (2017). The design of debt-clearing markets: Clearinghouse mechanisms in preindustrial europe. Journal of Political Economy, 125 (6), 1991–2037.
- Buchstein and Hein (2009) Buchstein, H. and Hein, M. (2009). Randomizing europe: the lottery as a decision-making procedure for policy creation in the eu. Critical Policy Studies, 3 (1), 29–57.
- Chen et al. (1638) Chen, Z., Xu, F. and Song, Z. (1638). Ming jing shi wen bian (A collection of Ming dynasty’s statecraft essays), vol. 39.
- Colonnelli et al. (2020) Colonnelli, E., Prem, M. and Teso, E. (2020). Patronage and selection in public sector organizations. American Economic Review, 110 (10), 3071–99.
- Creel (1964) Creel, H. G. (1964). The beginnings of bureaucracy in China: The origin of the Hsien. The Journal of Asian Studies, 23 (2), 155–184.
- Dal Bó et al. (2013) Dal Bó, E., Finan, F. and Rossi, M. A. (2013). Strengthening state capabilities: The role of financial incentives in the call to public service. The Quarterly Journal of Economics, 128 (3), 1169–1218.
- Dimakopoulos and Heller (2019) Dimakopoulos, P. D. and Heller, C.-P. (2019). Matching with waiting times: The german entry-level labor market for lawyers. Games and Economic Behavior, 115, 289–313.
- DQHD (1886) DQHD (1886). Da qing huidian (The Collected Statutes of Qing), vol. 44.
- Dur et al. (2018) Dur, U., Kominers, S. D., Pathak, P. A. and Sönmez, T. (2018). Reserve design: Unintended consequences and the demise of boston’s walk zones. Journal of Political Economy, 126 (6), 2457–2479.
- Elman (2000) Elman, B. A. (2000). A cultural history of civil examinations in late imperial China. University of California Press.
- Feng (2014) Feng, X. (2014). Online bipartite matching: a survey and a new problem. mimeo.
- Gong (1997) Gong, Y. (1997). Songdai guanzhi cidian (A dictionary of the Song civil service system). Zhonghua book company.
- Greif (1993) Greif, A. (1993). Contract enforceability and economic institutions in early trade: The maghribi traders’ coalition. American economic review, pp. 525–548.
- Greif et al. (1994) —, Milgrom, P. and Weingast, B. R. (1994). Coordination, commitment, and enforcement: The case of the merchant guild. Journal of Political Economy, 102 (4), 745–776.
- Gu (1670) Gu, Y. (1670). Ri zhi lu (Records of daily knowledge).
- Hall (1935) Hall, P. (1935). On representatives of subsets. Journal of the London Mathematical Society, 1 (1), 26–30.
- Headlam (1891) Headlam, J. W. (1891). Election by lot at Athens. 4, The University Press.
- Huang (1694) Huang, L. (1694). Fuhui quanshu (A Complete Book Concerning Happiness and Benevolence). reprint of Japanese 1850 edition, Kyuko shoin, Tokyo.
- Kuhn (1955) Kuhn, H. W. (1955). The hungarian method for the assignment problem. Naval Research Logistics Quarterly, 2 (1-2), 83–97.
- LBZZ (1614) LBZZ (1614). Libu zhizhang (Regulations of Ministry of Personnel).
- Mackenzie (2019) Mackenzie, A. (2019). An axiomatic analysis of the papal conclave. Economic Theory, pp. 1–31.
- MHD (1587) MHD (1587). Ming huidian (Collected Statutes of Ming), vol. 2-13.
- MS (1739) MS (1739). Ming shi (History of Ming), vol. 71.
- Pan (2005) Pan, X. (2005). Mingdai wenguan quanxuan zhidu yanjiu (A study on the appointments of civil service system in Ming dynasty). Peking University Press.
- Pathak et al. (2020a) Pathak, P. A., Rees-Jones, A. and Sönmez, T. (2020a). Immigration Lottery Design: Engineered and Coincidental Consequences of H-1B Reforms. Tech. Rep. 26767, National Bureau of Economic Research.
- Pathak et al. (2020b) —, Sönmez, T., Ünver, M. U. and Yenmez, M. B. (2020b). Fair allocation of vaccines, ventilators and antiviral treatments: leaving no ethical value behind in health care rationing. arXiv preprint arXiv:2008.00374.
- QDLBQXZL (1886) QDLBQXZL (1886). Qin ding li bu quan xuan ze li (Rules and Regulations for the Appointments by the Ministry of Civil Appointments), vol. 43.
- Rauch and Evans (2000) Rauch, J. E. and Evans, P. B. (2000). Bureaucratic structure and bureaucratic performance in less developed countries. Journal of Public Economics, 75 (1), 49–71.
- Roth (1984) Roth, A. E. (1984). The evolution of the labor market for medical interns and residents: a case study in game theory. Journal of Political Economy, 92 (6), 991–1016.
- Roth et al. (2004) —, Sönmez, T. and Ünver, M. U. (2004). Kidney exchange. The Quarterly Journal of Economics, 119 (2), 457–488.
- Shen (1619) Shen, D. (1619). Wanli yehuo bian (Unofficial matters from the Wanli reign).
- Sönmez (2013) Sönmez, T. (2013). Bidding for army career specialties: Improving the rotc branching mechanism. Journal of Political Economy, 121 (1), 186–219.
- Sönmez and Switzer (2013) Sönmez, T. and Switzer, T. B. (2013). Matching with (branch-of-choice) contracts at the united states military academy. Econometrica, 81 (2), 451–488.
- Sönmez et al. (2021) —, Yenmez, M. B. et al. (2021). Affirmative action in India via vertical, horizontal, and overlapping reservations. Working paper.
- SS (1343) SS (1343). Song shi (History of Song), vol. 158.
- Sun (1777) Sun, C. (1777). Chunming meng yulu (A Collective Memories of Ming). Si ku quan shu (Complete Library in Four Treasures), Vol. 24.
- Thakur (2020) Thakur, A. (2020). Matching in the civil service: A market design approach to public administration and development. Working paper.
- Thorley (2020) Thorley, D. (2020). Randomness pre-considered: Recognizing and accounting for “de-randomizing” events when utilizing random judicial assignment. Journal of Empirical Legal Studies, 17 (2), 342–382.
- Wang (2016) Wang, Z. (2016). Qingdai zhiguan renshi yanjiu (A study on the government personnel in Qing dynasty). Shanghai Bookstore Publishing House.
- Watt (1972) Watt, J. R. (1972). The district magistrate in late imperial China. Columbia University Press.
- Weber (1964) Weber, M. (1964). The Theory of Social and Economic Organization: Transl. by AM Henderson and Talcott Parsons. Free Press.
- Weber (1978) — (1978). Economy and society: An outline of interpretive sociology, vol. 2. Univ of California Press.
- Wei (1992) Wei, X. (1992). Qingdai renguan zhi jiguan huibi zhidu (avoidance of home region in qing appointments). Institute of Modern History working papers, Academia Sinica, 3.
- Will (2002) Will, P.-É. (2002). Creation, conflict, and routinization: The appointment of officials by drawing lots, 1594–1700. Ming Qing Yanjiu, pp. 73–121.
- Wu (1609) Wu, L. (1609). Wanli shuchao (A collection of the Wanli coourt debates), vol. 21.
- Xu (2018) Xu, G. (2018). The costs of patronage: Evidence from the British Empire. American Economic Review, 108 (11), 3170–98.
- Yao (1408) Yao, G. (1408). Yongle da dian (Yongle Ecyclopedia), vol. 14626.
- Zhang (2010) Zhang, Z. (2010). Qingdai wenguan xuanren zhidu yanjiu (A study on the appointments of civil service system in Qing dynast). Ph.D. thesis, Nankai University.