Designing High-Power, Octave Spanning Entangled Photon Sources for Quantum Spectroscopy
Abstract
Entangled photon spectroscopy is a nascent field that has important implications for measurement and imaging across chemical, biology, and materials fields. Entangled photon spectroscopy potentially offers improved spatial and temporal-frequency resolutions, increased cross sections for multiphoton and nonlinear measurements, and new abilities in inducing or measuring quantum correlations. A critical step in enabling entangled photon spectroscopies is the creation of high-flux entangled sources that can use conventional detectors, as well as provide redundancy for the losses in realistic samples. Here, we report a periodically poled, chirped, lithium tantalate platform that generates entangled photon pairs with a efficiency. For a near watt level diode laser, this results in a near W-level flux. The single photon per mode limit that is necessary to maintain non-classical photon behavior is still satisfied by distributing this power over up to an octave-spanning bandwidth. The spectral-temporal photon correlations are observed via a Michelson-type interferometer that measures the broadband Hong-Ou-Mandel two-photon interference. A coherence time of 245 fs for a 10 nm bandwidth in the collinear case and a 62 fs for a 125 nm bandwidth in the non-collinear case is measured using a CW pump laser, and, essentially, collecting the full photon cone. We outline in detail the numerical methods used for designing and tailoring the entangled photons source, such as changing center wavelength or bandwidth, with the ultimate aim of increasing the availability of high-flux UV-Vis entangled photon sources in the optical spectroscopy community.
I Introduction
An entangled photon pair is generated by splitting a single photon into two photons via spontaneous parametric down conversion (SPDC) Burnham and Weinberg (1970). The quantum correlations between the two photons have several effects. First, when coherently recombined in time and space, the two entangled photons behave as the initial pump photon. In other words, the two entangled photons can be thought of as acting like a single photon in light-matter interactions Szoke et al. (2020). As a result, two entangled photons leave the same side of a beamsplitter Hong, Ou, and Mandel (1987) and diffract from a grating at the wavelength of the pump photon Mitev et al. (2020); Shimizu, Edamatsu, and Itoh (2003); Abouraddy et al. (2001). Entangled photon pairs also linearize multiphoton and nonlinear spectroscopy, as has been well-studied in two photon absorption and fluorescence Javanainen and Gould (1990); Dayan et al. (2005); Villabona-Monsalve, Burdick, and Goodson (2020); Raymer et al. (2013); Tabakaev et al. (2021); Li et al. (2020); Kang et al. (2020). Entangled photons also have non-Fourier reciprocal spectral-temporal resolutions and are able to yield spatial resolutions which scale inversely with the number of correlated entangled photons N Boto et al. (2000); Steuernagel (2004); Oka (2011, 2018); Schlawin, Dorfman, and Mukamel (2018).
These properties, plus the more well known sub-shot noise and classical light rejection behaviors, make entangled photons tempting for use in ultrafast laser spectroscopy Dorfman, Schlawin, and Mukamel (2016); MacLean, Schwarz, and Resch (2019). The fragility of the entangled states, and the difficulty and expense associated with single photon counting, necessitates a need for high flux (nW-W) entangled photon sources that would easily interface with existing ultrafast optics setups Nasr et al. (2005). However, commonly used nonlinear crystals (BBO, KDP), usually have entangled photon creation efficiencies in the to range Kwiat et al. (1995); Friberg, Hong, and Mandel (1985); Kwiat et al. (1999). Reliance on ’birefringent phase matching’ limits the highest usable nonlinear coefficients of the crystal as well as the bandwidth of entangled photons that can be created Karan et al. (2020); Nikogosyan (1991); Midwinter and Warner (1965). The possible phase-matching conditions result in bandwidths in the tens of nanometers range, which corresponds to 100s of femtoseconds to picoseconds in correlation times in experiments. Given the current assumption that the entangled photon correlation time must be less than a molecule or material’s dephasing time to allow a nonlinear or multiphoton enhancement, the narrow bandwidth of birefringent phase matching presents critical limits on entangled spectroscopy’s feasibility Dorfman, Schlawin, and Mukamel (2016); Roslyak and Mukamel (2009).
In contrast, the ferroelectric properties of materials such as KTP and lithium niobate allow the crystals to be periodically poled and utilize a ’quasi phase-matching’ (QPM) technique Wang et al. (1999); Yu et al. (2002); Lin et al. (2019). Quasi-phase-matching allows the use of Type-0 collinear phase matching Chen et al. (2009), SPDC efficiencies of to Bock et al. (2016); Shi and Tomita (2004), a broadly tunable center wavelength (set by the grating period instead of crystal angle) Armstrong et al. (1962), and easy implementation of waveguides that can saturate single photon detectors with mW of CW diode laser input power Tanzilli et al. (2001). Broad bandwidth phase matching is achieved by introducing a chirp into the poling period of the structure. The nonlinear poling allows for more wavelengths to be phase matched, while also retaining the benefits associated with longer crystals, namely a larger downconverted photon flux. The increased bandwidth directly affects the effective temporal resolution of experiments Nasr et al. (2008); Pe’er et al. (2005); Ou and Lu (1999).The broad bandwidth also allows increased power densities, as the the single photon per wavelength mode occupation limit necessary for non-classical effects is not exceeded (calculated as the flux in photons/s divided by the bandwidth in Hz) Hadfield (2009). While KTP and lithium niobate have been the primary workhorse for entangled photon generation in quantum information system settings, they have limitations with regards to their damage thresholds and UV cut-offs. In contrast, lithium tantalate is more ideal for physical chemistry and materials research because it has higher power handling capabilities (240 MW/cm2) Zverev et al. (1972) and a lower UV absorption edge (280 nm) Antonov et al. (1975); Meyn and Fejer (1997).
To accelerate the adoption of entangled photon techniques, we outline how to create an entangled photon source that can achieve near W powers of entangled photons down to UV wavelengths with temporal resolutions of tens of femtoseconds. These entangled photon fluxes are high enough to be visible by eye when starting from a 1W CW pump laser, greatly facilitating the alignment of entangled experiments. Here, the generated photon pairs are centered around a degenerate wavelength of 812 nm, resulting from a 406 nm pump source, but this wavelength can be tuned as outlined by the formulas in the paper. The 8% MgO doped congruent lithium tantalate (CLT) gratings use a Type-0, collinear quasi-phase matching configuration. A Michelson type interferometric scheme Lopez-Mago and Novotny (2012) measures the fourth-order interference of the entangled photons and gives coherence times of 245 fs for a bandwidth of 10 nm and 62 fs for a bandwidth of 125 nm. Of course, simply producing a broad bandwidth of entangled photons is not the same as carrying out experiments using them. We discuss our attempts to utilize the full SPDC cone and bandwidth in subsequent experiments, emphasizing where optics development is still needed to achieve maximum temporal resolution and flux. Using the full cone is in contrast to most experiments where irises are used to select two points from the SPDC cone, thereby severely reducing the total photon flux at the gain of state purity. The paper aims to give quick access to the sources needed for the emerging field of nonlinear entangled photon optics as well as outlining the next steps needed in the field.
II Theory
II.1 Designing Broadband SPDC in chirped nonlinear materials
Prior to quantifying the experimental behavior of the SPDC sources, we lay out the theoretical and numerical details used in their design.
In SPDC, the creation of two entangled photons arises from the quantum mechanical process of a single pump photon mixing with the underlying vacuum state. The two down-converted daughter photons display strong correlations in time, energy, and momentum due to the parametric mixing process Burnham and Weinberg (1970); Klyshko, Penin, and Polkovnikov (1970). The time and energy correlations originate from the individual photons being generated simultaneously from the pump photon:
| (1) |
| (2) |
where , , and are the frequencies of the pump, signal, and idler photon respectively. The momentum correlation is dictated by the phase matching condition, which is a consequence of the wave-like nature of the interacting fields. Each field has a corresponding wave vector defined via its respective phase velocity in the medium:
| (3) |
with being the frequency and temperature dependent refractive index of the material. The following vector sum, the longitudinal component of which is depicted in Fig.1, should be satisfied in order to ensure that a proper phase relationship between the interacting waves is maintained throughout the nonlinear crystal.
| (4) | |||
It is only when this relationship holds true that constructive interference between the propagating waves can occur and energy is transferred dominantly in one direction, rather than oscillating back and forth between the two optical modes Boyd and Prato (2008).
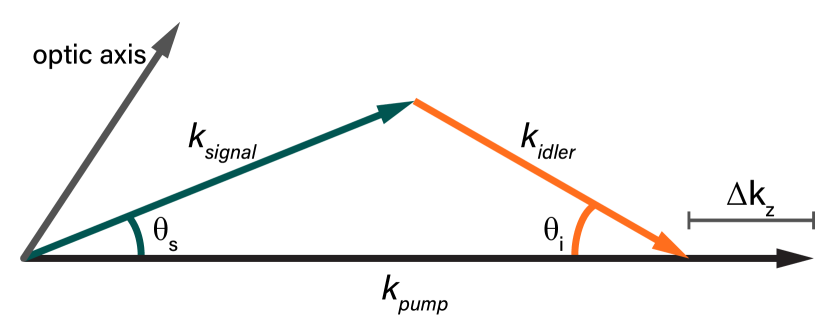
A natural extension of this phase-matching principle, termed quasi-phase-matching, is apparent if one considers the duality between position and momentum space. A periodic lattice in position space directly corresponds to a well-defined wave vector k in momentum space via a Fourier transform. Therefore, if the nonlinear dielectric tensor domains of ferroelectric nonlinear crystal are modulated with a specific periodicity , a quasi-momentum term arises, which can be used to satisfy a non-phase-matched nonlinear interaction.
| (5) |
The quasi-phase-matching term also has an additional advantage, in that it can be chosen to be higher-order. Here, the order of the configuration is defined by m.
| (6) |
This serves a particular experimental benefit as it allows for nonlinear interactions to be phase-matched (albeit with lower efficiency), even if the required order periodicity is too small to be fabricated Fejer et al. (1992).
We now describe the design of a grating in congruent lithium tantalate with the design goal of a 406 nm pump wavelength that creates a >400 nm bandwidth around the degenerate 812 nm SPDC point. The source must also be capable of creating near W powers given a 1 W input power. The first step is to obtain the Sellmeier equations that describe the frequency and temperature dependent refractive indices of the material Moutzouris et al. (2011). The numeric values and a representative plot are found in the supplementary information. Using the Sellmeier equations, the phase mismatch (Eq.5) is then evaluated for a wide range of pump-signal/idler wavelength configurations while keeping one entangled photon frequency a constant. External conditions such as the desired temperature range and minimum achievable poling periodicity are also enforced such that the parameter space remains within experimentally realistic boundaries. The root of Eq.5 can then be found by a root-finding algorithm. For the congruent lithium tantalate and a 406-812 SPDC process, and imposing a realistic < 200°C temperature condition, solving for the root of Eq.5 yields a poling period of 9.5 m at 133°C (see figure in SI for the graphical solution).
Quasi-phase-matching is a strongly temperature dependent technique. By solving Eq.5 for a range of temperatures near the calculated degeneracy point (133°C), the splitting and tuning of the SPDC spectrum can be calculated. Tuning the SPDC spectrum via the crystal temperature is useful for controlling what intermediate states are involved in, the magnitude of, and the temporal resolution of an entangled two photon process. The temperature dependent behavior is shown in Fig.2. Here, the transition between the degenerate and non-degenerate domains is clearly observable, with lower temperatures corresponding to a weaker degenerate emission profile. The lower plot of Fig.2 also clearly shows a very strong narrowing of the signal and idler bandwidths as one temperature tunes further away from degeneracy.
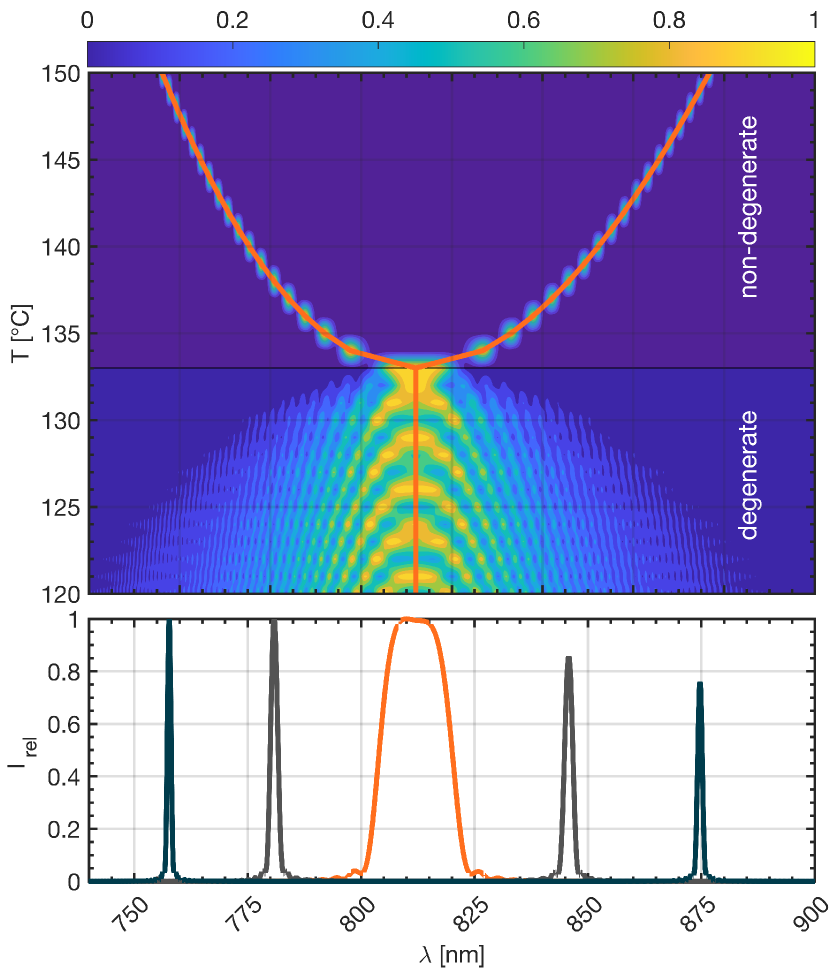
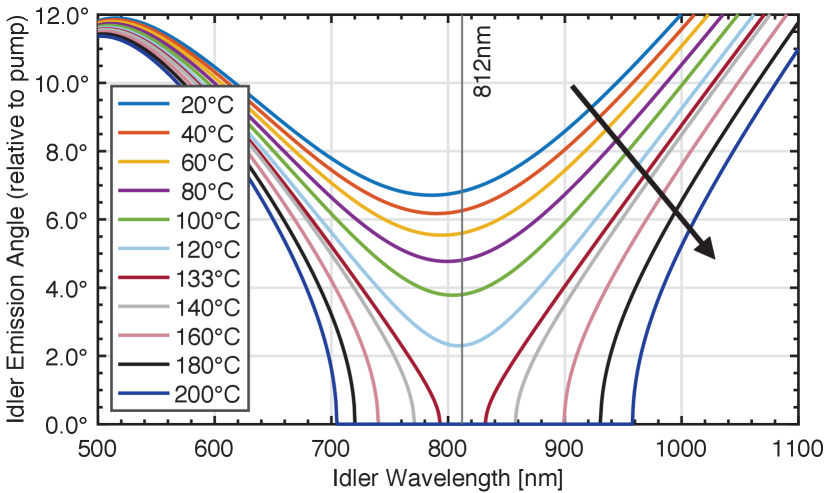
Additionally, both signal and idler have an inherent angular emission property determined by the momentum conservation condition in Eq.5. The strong frequency dependence of the outgoing angles can be numerically calculated from the momentum conservation equation if one decomposes the wave vectors into their longitudinal and transverse components, and solves the trigonometric equations for transverse phase-matching. Subsequently computing the emission angle for each frequency of interest, in conjunction with the frequency dependent refractive index of the nonlinear crystal, the SPDC cone’s spectral characteristic for various crystal temperatures can be plotted (Fig.3). As predicted, at the degenerate emission temperature of 133°C, the plot shows that the emission angle of the 812 nm signal and idler photons is 0°. More importantly however, comparing the results to those in Fig.2, the shaded non-degenerate region also corresponds to a collinear emission profile. Vice versa, temperatures below 133°C display a (albeit weak) degenerate, non-collinear character.
In a chirped crystal, the bandwidth of the down-converted entangled photons is increased by changing the poling period throughout the crystal. The increasing width elements correspond to different phase-matched wavelength configurations of Eq.5 (Fig.4). The photons still add up to the narrow linewidth of the pump laser but the temporal resolution is given by the temporal alignment and down-converted bandwidth of the entangled photons. This is why entangled photon experiments are said to have independent spectral and temporal resolutions. The importance of the pump laser’s linewidth in determining the entangled photon state’s purity, and thus the access to non-classical spectroscopic properties, is discussed in the SI.
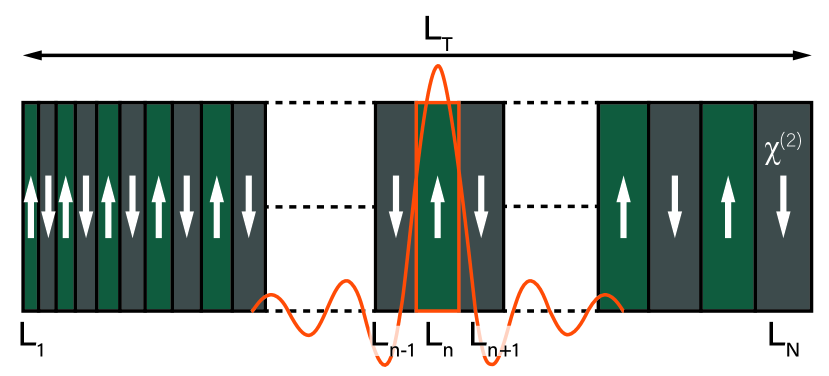
Following a similar treatment to Di Giuseppe et al. (2002), the crystal can be decomposed into its individual domains, in each of which the downconversion amplitude follows the usual sinc function-like phase-matching dependence Burlakov et al. (1997). This is attributed to the Fourier transform of a rectangular function in real-space representing the probability of a downconversion event occurring inside the crystal element.
| (7) |
With being the length of the crystal element. Similarly, a cumulative-phase term can be defined, which is related to a forward propagating wave with phase-mismatch traversing a crystal length after it has been generated in the SPDC process at crystal element n.
| (8) |
Carrying out a sum over all individual crystal elements then allows for the resulting SPDC spectrum to be calculated (Eq.9) and thereby observe the effects of different chirping parameters. For lithium tantalate, this is shown in Fig.5. In the case of CLT, a 10% chirp around the degenerate poling periodicity calculated above yields a full octave spanning SPDC bandwidth. Trivially, in the limit of no chirp, where all crystal elements are equal in size, the solution for a periodically poled crystal of length L is recovered.
| (9) | |||
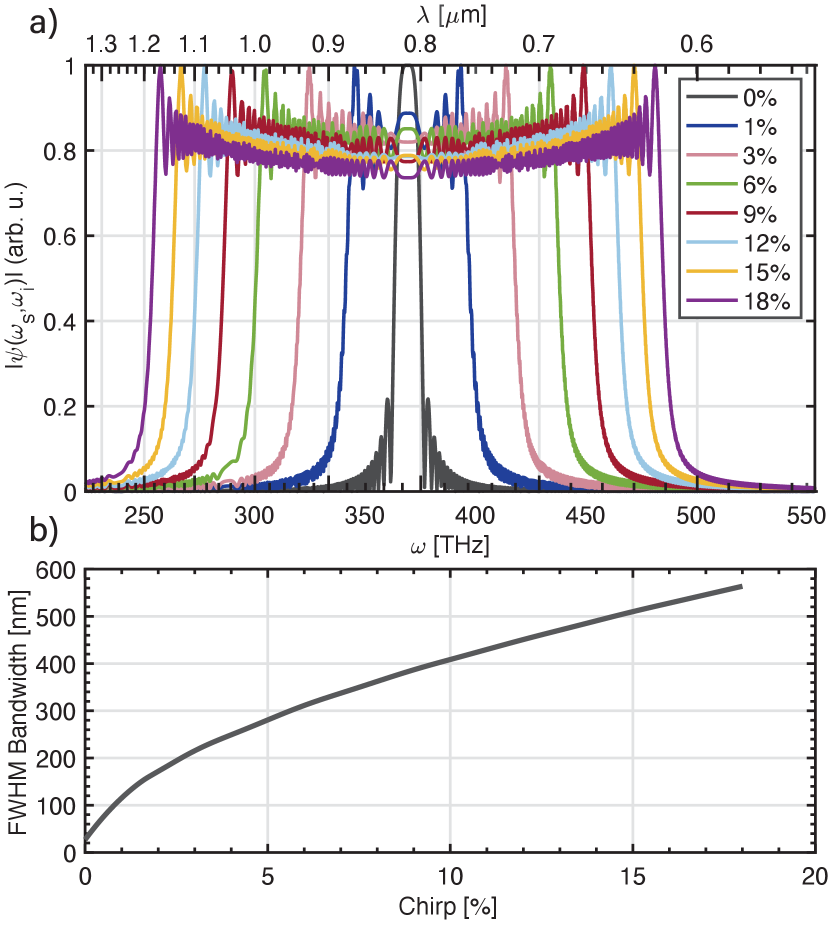
By plotting the solution of Eq.9 as a function of the position inside the crystal along the propagation direction, we can gain some intuition for how the constructive interference results in a broadened spectrum. In the case of CLT, a 10% chirp around the degenerate poling periodicity calculated above yields a full octave spanning SPDC bandwidth as shown in Fig.6. Here we used a total grating length of 18 mm equal to the chip used in subsequent experiments.
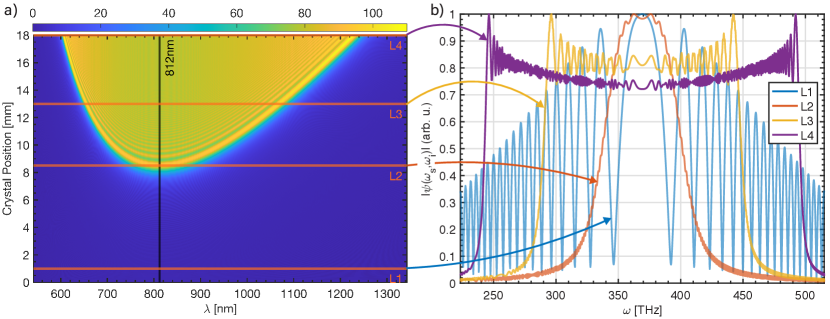
The 2D plot in Fig.6 provides some additional insight into how modulation of the poling period affects the build-up of the emitted spectrum. In particular, it’s important to note that while the first 8mm length of the crystal appears to show no downconversion taking place, this is indeed not the case. While all crystal elements in this region satisfy a particular phase-matching condition, it is only after a certain propagation length that the phases of each spectral mode coherently sum to a strong enough amplitude that would be perceivable on the plot. Furthermore, the broadening of the downconverted bandwidth does have a particular drawback, in that the frequencies close to degeneracy become weaker in intensity. This is best observed in the line cuts for positions L3 and L4, where instead of a constant intensity across all frequencies, the emission spectrum peaks at the lower and higher cut-offs but begins to droop more severely as the bandwidth increases. Thus, increasing the chirping of the poling period indefinitely does not necessarily yield a flat power spectral density. It should be pointed out that this issue can be addressed via chirp profiles which follow not a linear but some higher order functional form Brańczyk et al. (2011).
In contrast to narrowband SPDC where the emission angles for the photon pairs are well confined within the two narrow arcs satisfying momentum conservation, such extremely broadband downconversion poses inherent difficulties in the spatial degree of freedom due angular (chromatic) dispersion of the resulting beam. As Fig.3 shows, the emission angles increase quickly away from degeneracy. This presents several experimental issues, as the beam no longer represents an ideal point source, which will be discussed in the experimental section below. Taking into account the physical dimensions of the grating cross section (detailed in the experimental section below), it is easy to see that the output aperture of the grating can at most only accommodate of emission in the horizontal axis, and along the vertical axis relative to the center point of the crystal where we focus. Beyond this, large parts of the SPDC emission cone will begin to interact with the domain boundaries which form the grating channel. While in principle the refractive index is the same for both un-poled and poled crystal regions, the periodic poling process causes some stress at the domain walls. Therefore, the edge of the each pattern in the lateral direction acts as a kind of scattering center, possibly resulting in unwanted interference patterns. Therefore special attention should be paid to accommodate the spatial distribution of the cone as it diverges inside the channel.
A final point to consider is the total length of the grating.is to be chosen by considering two interlinked criteria. Firstly, the expected power spectral density of the entangled photons at the output scales as . Emission intensity can therefore be significantly increased by utilizing longer structures. Conversely, the expected power spectral density also depends on a multiplicative factor. Hence, longer gratings result in narrower emission bandwidths. This ‘dual’-argument also applies to poling patterns which have a chirp, as while increasing the amount of variation in the poling periodicity serves to broaden the emission bandwidth, each spectral component will be less populated with photons and thus less brilliant.
III Experiment
III.1 SPDC Characterization
The periodically poled congruent lithium tantalate gratings were manufactured by HC Photonics. The unchirped chip consists of 8 gratings with different poling periods (8.5, 9, 9.5, 10, 10.5, 11, 11.5, 12 m). It is 20 mm long and each channel has a 0.9 mm by 0.5 mm cross section. The chirped chip consists of 6 gratings with varying chirp parameters and entrance poling periods (Table 1). Each grating is 18 mm long and has a 1 mm by 0.3 mm cross section. The gratings are AR-coated on both input and output faces at 406nm(R<0.5%)/812nm(R<0.5%).
| Grating | [m] | [m] | [m] | Chirp |
|---|---|---|---|---|
| 1 | 9.000 | 9.45 | 9.900 | 10% |
| 2 | 9.048 | 9.50 | 9.952 | 10% |
| 3 | 9.095 | 9.55 | 10.005 | 10% |
| 4 | 9.143 | 9.60 | 10.057 | 10% |
| 5 | 9.190 | 9.65 | 10.110 | 10% |
| 6 | 9.238 | 9.70 | 10.162 | 10% |
The experimental setup, as illustrated in Fig.8, consisted of a computer-tunable, CW Ti:Sapphire laser (M2 SolsTiS) and an external SHG cavity to act as the pump source. The maximal output power of the SHG at 406 nm was 1.15 W with a 0.89 nm linewidth. The pump beam is focused through the ppCLT grating using an aspheric lens with a 40 cm focal length. This focal length is chosen such that the size of the focused beam was smaller than the grating’s cross sectional dimension and further optimized for peak SPDC brightness. The position of the crystal can be finely adjusted in the XYZ directions using a piezoelectric stage, which is critical for maximizing the entangled photon flux. The angular deviation of the grating’s long axis relative to the input beam was not as crucial as the X-Y centering of the chip around the focused beam and the z-control over exact focal point positioning. The temperature of the crystal is controlled by a ceramic heater and PID loop (Covesion) to an accuracy of 10 mK.
To measure the SPDC spectrum as well as the power of the downconverted flux, the output of the grating is passed through a total of three OD-4 500 nm longpass filters (Edmund Optics) to eliminate the residual 406 nm pump. The SPDC cone is collimated with an off-axis parabolic mirror and then focused into a USB spectrometer (Thorlabs). For more detailed characterization, the SPDC cone is collimated with a telephoto lens and then focused into a spectrometer (Princeton Instruments IsoPlane) with a 15cm focal length lens. In this configuration, spectral and power measurements are performed with an electron multiplying intensified CCD camera (emICCD, Princeton Instruments MAX4). For the broadband spectral measurements, spectra are collected and stitched together as a 800 nm blazed grating with 150 grooves/mm is scanned across several center wavelengths. These spectra are then background corrected, quantum efficiency corrected according to the detection efficiency of the emICCD camera, and normalized.
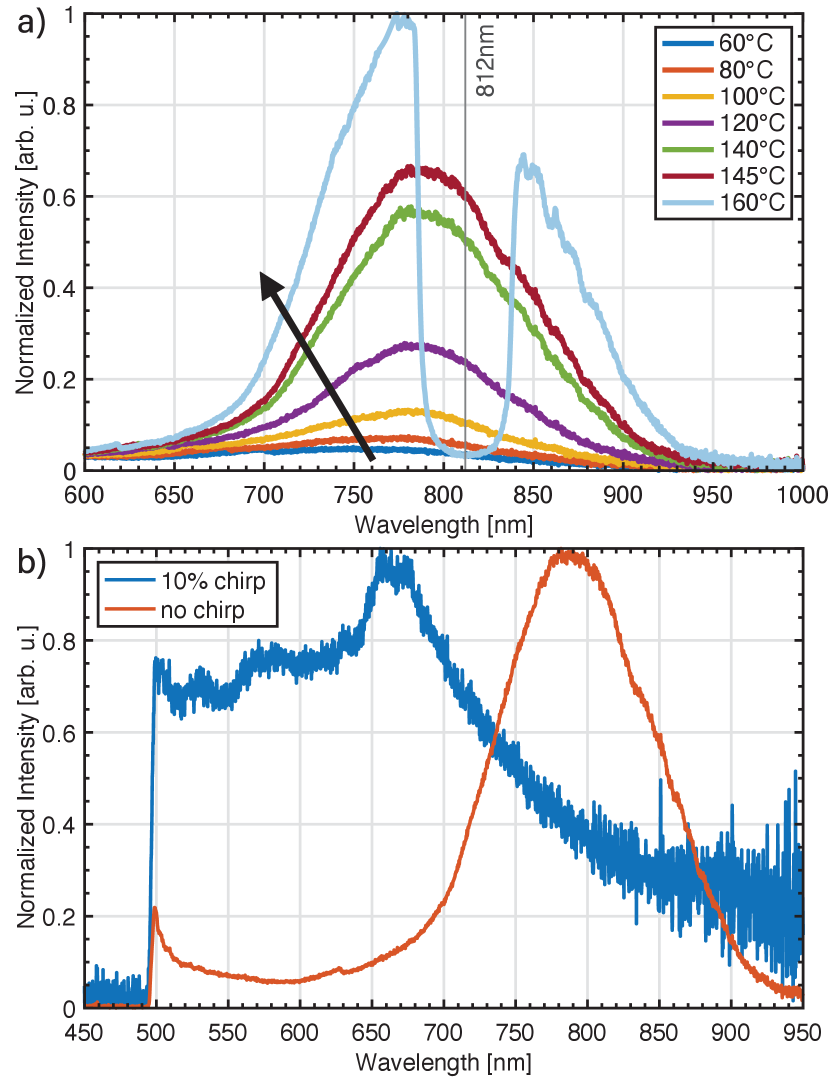
Fig.7 (a) depicts the SPDC spectra for the 9.50 µm unchirped grating as the temperature of the crystal is varied from 60°C to 160°C. Above 150°C, the shift from degenerate to non-degenerate emission conditions is apparent from the decrease in intensity around the degenerate wavelength region of 812 nm (gray dashed line). In comparison, as shown in Fig.7 (b), at 145 °C, the chirped chip (blue curve) exhibits much broader and flatter emission than the unchirped counterpart (red curve).
III.2 Two-Photon Interference
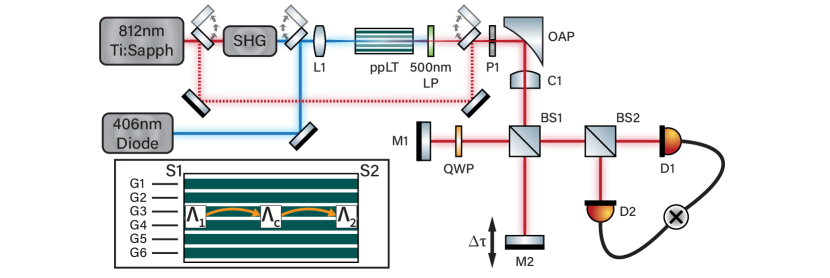
The fourth-order interference between entangled photon pairs was quantified with a two-photon Michelson interferometer, depicted in Fig.8. The Michelson interferometer is chosen because the configuration allows a broader bandwidth of the SPDC cone to be easily utilized, in contrast to a Mach-Zehnder configuration. Following the end of the ppLT chip, the entangled photons are collimated with an off-axis parabolic mirror and a cylindrical lens. These photons are directed through a broadband nonpolarizing 50:50 beamsplitter (BS1, Layertec) which separates the incident photons into two paths. In the reflected path, the photons pass through an achromatic quarter-waveplate (Thorlabs) twice to rotate their polarizations. The optical path length difference between the two arms is adjusted by scanning a mirror mounted to a linear stage in the transmitted arm. Coincidence counts vs. optical path length difference are then collected at one of the output arms of BS1. The coincidence counting setup consists of a second broadband 50:50 beamsplitter (BS2, Layertec), and two free-space-to-fiber coupling setups connecting to single-photon avalanche diodes (SPADs, Laser Component COUNT) and time-tagging electronics (PicoHarp 300). Because of the high SPDC flux, the pump beam must first be dimmed by six orders of magnitude to avoid SPAD saturation (counting rate photons/s). Full counting rate experiments can be completed using the CCD alone Reichert, Defienne, and Fleischer (2018); Zhang et al. (2020) but were not implemented at the time of writing this paper.
The free-space-to-fiber coupling setups each consist of 2 mirrors to align the beamsplitter outputs through a 4.51 mm focal length asphere, which then focuses the beam into a multimode fiber (105 core diameter, 0.22 NA) connected to the SPADs. For these measurements, the coincidence time-bin resolution is set to 8 ps and coincidences are summed within a 10 ns window. Fourth-order interferograms were measured for different bandwidths of entangled photon pairs. For the first experiment, bandpass filters centered at 810 nm with a 10 nm FWHM are mounted to the front of each of the fiber coupling units. Note that this filter is not at the 812nm degenerate wavelength and reduces the degree of entanglement. For the second experiment, the 810 nm bandpass filters are removed to couple the broadband, collinear SPDC into the SPADs. Finally, the oven is allowed to cool to the non-collinear but degenerate temperature of 150°C, and broadband two-photon interference was measured again. Note that due to the large bandwidth of the SPDC, the fiber coupling efficiency of the non-degenerate photons is also poor at less than 10 of total power. As discussed at the end of this section, optics development is still needed similar to using classical broadband ultrafast lasers.
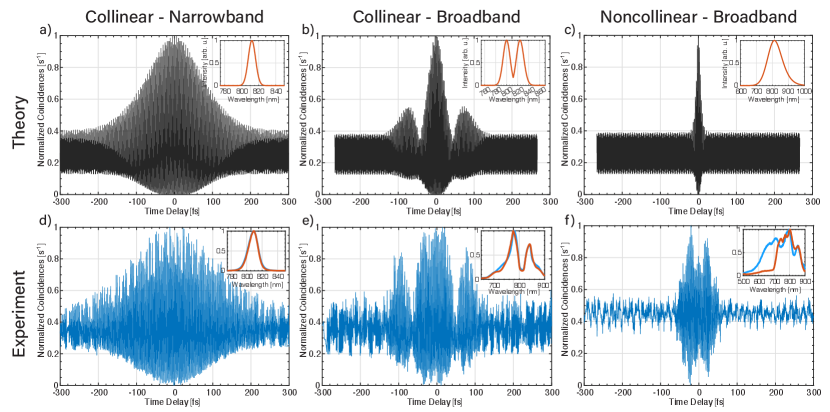
Fig.9 shows the simulated fourth-order interferences using the produced bandwidth of the SPDC source and then the measured fourth-order interferences for two collinear bandwidths and a third non-collinear, full spectrum measurement. When the quarter-wave plate is set to 0°, the photons arriving at BS1 have the same polarization, and interfere coherently as correlated pairs. The interference pattern is robust against pump power fluctuations. When the quarter-wave plate is rotated to 45°, the reflected arm becomes perpendicularly polarized to the transmitted arm, the interference pattern disappears, and the coincidence counts follow the average pump power reading collected before and after the coincidence detection (SI Fig.8-9). The resulting coherence length of the total flux can be determined from the width of the interference peak. Table 2 summarizes the theoretical and measured coherence lengths.
| Collinear narrowband | Collinear broadband | Non-collinear broadband | |
|---|---|---|---|
| Theoretical coherence time [fs] | 200 | 45 | 18 |
| Measured coherence time [fs] | 245 | 57.4 | 62 |
For the measurement with 810-(10) nm bandpass filters mounted to the front of the fiber coupling units, shown in Fig.9(d), the coherence length is approximately 73 µm (or 245 fs). The simulated interference pattern as well as the coherence length of 60µm (200 fs), shown in Fig.9(a), agree fairly with the measurement given that the 10nm bandpass filter is offset from the degenerate wavelength of 812 nm. Note that the measured bandwidth after the fiber is roughly double what it actually is because the spectrometer slit had to be run wide to get sufficient flux for spectral analysis after the fiber coupling. The theoretical plot uses the correct bandwidth. Fig.9(e) shows the interference from collinear broadband SPDC flux without bandpass filters. The bandwidth is reduced and the SPDC spectrum is split (nondegenerate) because the phase matching temperature is maintained at the elevated collinear emission (Fig.2). From the width of the center peak, the coherence length is approximately 17.2 µm (or 57.4 fs). For reference, the simulated coherence length is approximately 13 µm (45 fs). Similarly, Fig.9(f) shows the lower temperature non-collinear broadband interference. Here, the full 200 nm bandwidth of the SPDC source is attempted to be used (expected temporal width 8fs). However the spectrum reaching the detector is limited to 125 nm because of collimation issues, upstream optics, and fiber coupling. The coherence length calculated from the measured width of the peak is 18.9 µm (or 62 fs). This indicates that the degree of entanglement has degraded due to poor fiber coupling at non-collinear temperatures and other upstream optics. For example, the spectrum after the multiple beamsplitters is not balanced (Fig.9(f), inset) as compared to the other cases. The increased temporal width is also indicative of the need for dispersion management upstream, just as is similar to a broadband ultrafast laser pulse of an expected 20 fs pulse. The same would be true for the chirped (>200 nm) SPDC source so an interferometer is not shown here.
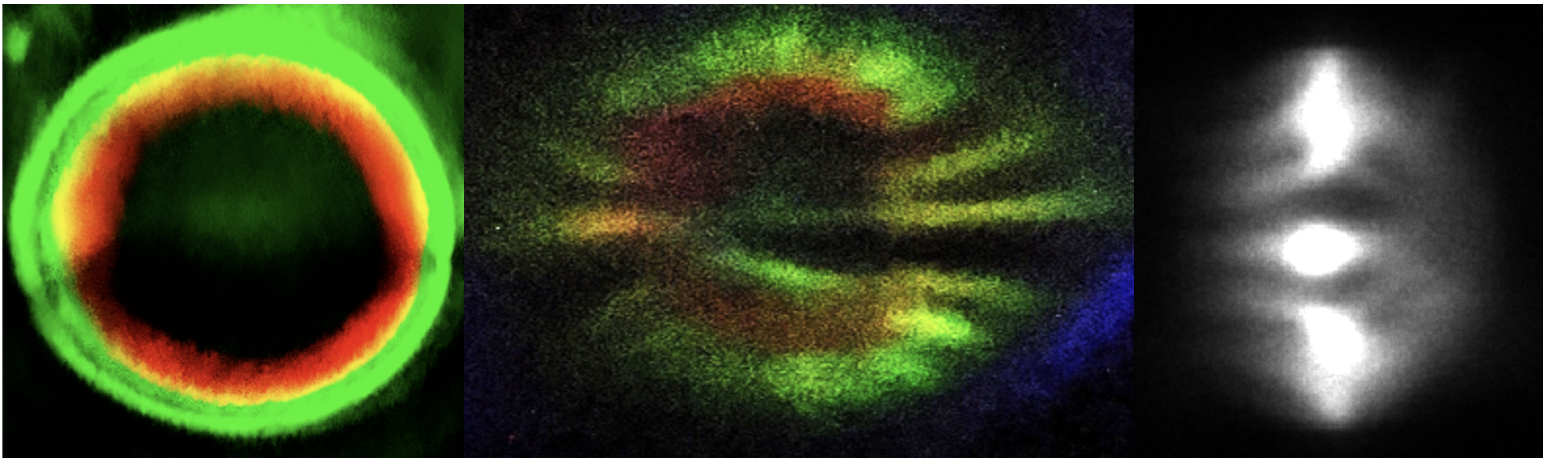
The lack of fiber coupling efficiency in the broadband, non-collinear case is not simply one of input optics. Immediately following the chip, the spatial profile of the entangled photons is cone-like with a wavelength-dependent distribution (Fig.10 left). The measured angular deviation with wavelength matches the simulated entangled photon emission. Within a non-degenerate pair, the idler photon has a larger emission angle than the signal photon. The wavelength-dependent angular emission cone present a challenge in the implementation of free-space broadband entangled photon setups because the emission does not act like single point source. We attempted to collimate the emission cone using a variety of free-space optical configurations and found that a telephoto lens or an off-axis parabolic mirror (sometimes with an additional cylindrical lens for beam shaping) provides the best long range spatial profiles. After a propagation length of 45 cm into the far field, the entangled photon cone collapses (Fig.10 middle). This spatial profile collapse is most likely due to the interference of photon pairs created along the length of the crystal and scattering effects near the domain boundaries of the grating. The end result shows characteristics of somewhere between a Laguerre and a Hermite mode which would match the circular emission in a square profile created by the source. The beam profile will likely be improved by using adaptive optics. The far field effects could also be reduced by using a waveguide instead of a grating; however, nanophotonic implementations cannot handle the high input powers used in this paper and fiber coupling of the broadband emission spectrum from the waveguide is not well developed. Another obvious option is, instead of using fiber coupled SPADs for the detection, is to move to emICCD photon counting techniques that would not require focusing of the collapsed beam profile. However, this approach still needs exploration and requires an emICCD even more costly than SPADs. Further investigation into the creation and collimation of broadband entangled photons is critical for the implementation of short temporal length, high flux entangled photon spectroscopy.
IV Conclusion
Quasi-phase-matching in periodically poled crystals offers significant benefits in the experimental implementation of broadband entangled photon sources for use in spectroscopy. Simulated parameters for unchirped, periodically poled lithium tantalate gratings were utilized to design and construct a broadband entangled photon source spanning nearly an octave in frequency. This broadband source was characterized by measuring the output spectra of the grating and the fourth order interference by a two-photon Michelson interferometer. The two-photon Michelson interferometer was used to emphasize where further optics and detector development is still need to utilize the broadband and short temporal width sources. As in, the SPDC spectrum can be reliably created from the designed chip, however, the down-stream optics and detectors still need development to fully utilize this source. Given the theoretical and experimentally demonstrated advantages of entangled photons in studies of chemical, biological, and material systems, we anticipate the widespread applicability of this particular energy-time entangled photon source.
Acknowledgment
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0020151.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- Burnham and Weinberg (1970) D. C. Burnham and D. L. Weinberg, “Observation of simultaneity in parametric production of optical photon pairs,” Phys. Rev. Lett. 25, 84–87 (1970).
- Szoke et al. (2020) S. Szoke, H. Liu, B. P. Hickam, M. He, and S. K. Cushing, “Entangled light–matter interactions and spectroscopy,” J. Mater. Chem. C 8, 10732–10741 (2020).
- Hong, Ou, and Mandel (1987) C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between two photons by interference,” Phys. Rev. Lett. 59, 2044–2046 (1987).
- Mitev et al. (2020) V. Mitev, L. Balet, N. Torcheboeuf, P. Renevey, and D. L. Boiko, “Discrimination of entangled photon pair from classical photons by de broglie wavelength,” Scientific Reports 10, 7087 (2020).
- Shimizu, Edamatsu, and Itoh (2003) R. Shimizu, K. Edamatsu, and T. Itoh, “Quantum diffraction and interference of spatially correlated photon pairs generated by spontaneous parametric down-conversion,” Phys. Rev. A 67, 041805 (2003).
- Abouraddy et al. (2001) A. F. Abouraddy, B. E. A. Saleh, A. V. Sergienko, and M. C. Teich, “Double-slit interference of biphotons generated in spontaneous parametric downconversion from a thick crystal,” Journal of Optics B: Quantum and Semiclassical Optics 3, S50–S54 (2001).
- Javanainen and Gould (1990) J. Javanainen and P. L. Gould, “Linear intensity dependence of a two-photon transition rate,” Phys. Rev. A 41, 5088–5091 (1990).
- Dayan et al. (2005) B. Dayan, A. Pe’er, A. A. Friesem, and Y. Silberberg, “Nonlinear interactions with an ultrahigh flux of broadband entangled photons,” Phys. Rev. Lett. 94, 043602 (2005).
- Villabona-Monsalve, Burdick, and Goodson (2020) J. P. Villabona-Monsalve, R. K. Burdick, and T. Goodson, “Measurements of entangled two-photon absorption in organic molecules with cw-pumped type-i spontaneous parametric down-conversion,” The Journal of Physical Chemistry C 124, 24526–24532 (2020), https://doi.org/10.1021/acs.jpcc.0c08678 .
- Raymer et al. (2013) M. G. Raymer, A. H. Marcus, J. R. Widom, and D. L. P. Vitullo, “Entangled photon-pair two-dimensional fluorescence spectroscopy (epp-2dfs),” The Journal of Physical Chemistry B 117, 15559–15575 (2013), pMID: 24047447, https://doi.org/10.1021/jp405829n .
- Tabakaev et al. (2021) D. Tabakaev, M. Montagnese, G. Haack, L. Bonacina, J.-P. Wolf, H. Zbinden, and R. T. Thew, “Energy-time-entangled two-photon molecular absorption,” Phys. Rev. A 103, 033701 (2021).
- Li et al. (2020) T. Li, F. Li, C. Altuzarra, A. Classen, and G. S. Agarwal, “Squeezed light induced two-photon absorption fluorescence of fluorescein biomarkers,” Applied Physics Letters 116, 254001 (2020).
- Kang et al. (2020) G. Kang, K. Nasiri Avanaki, M. A. Mosquera, R. K. Burdick, J. P. Villabona-Monsalve, T. Goodson, and G. C. Schatz, “Efficient modeling of organic chromophores for entangled two-photon absorption,” Journal of the American Chemical Society 142, 10446–10458 (2020).
- Boto et al. (2000) A. N. Boto, P. Kok, D. S. Abrams, S. L. Braunstein, C. P. Williams, and J. P. Dowling, “Quantum interferometric optical lithography: Exploiting entanglement to beat the diffraction limit,” Phys. Rev. Lett. 85, 2733–2736 (2000).
- Steuernagel (2004) O. Steuernagel, “On the concentration behaviour of entangled photons,” J. Opt. B: Quantum Semiclass 6, S606–S609 (2004).
- Oka (2011) H. Oka, “Selective two-photon excitation of a vibronic state by correlated photons,” The Journal of Chemical Physics 134, 124313 (2011), https://doi.org/10.1063/1.3573565 .
- Oka (2018) H. Oka, “Enhanced vibrational-mode-selective two-step excitation using ultrabroadband frequency-entangled photons,” Phys. Rev. A 97, 063859 (2018).
- Schlawin, Dorfman, and Mukamel (2018) F. Schlawin, K. E. Dorfman, and S. Mukamel, “Entangled two-photon absorption spectroscopy,” Accounts of Chemical Research 51, 2207–2214 (2018), pMID: 30179458, https://doi.org/10.1021/acs.accounts.8b00173 .
- Dorfman, Schlawin, and Mukamel (2016) K. E. Dorfman, F. Schlawin, and S. Mukamel, “Nonlinear optical signals and spectroscopy with quantum light,” Rev. Mod. Phys. 88, 045008 (2016).
- MacLean, Schwarz, and Resch (2019) J.-P. W. MacLean, S. Schwarz, and K. J. Resch, “Reconstructing ultrafast energy-time-entangled two-photon pulses,” Phys. Rev. A 100, 033834 (2019).
- Nasr et al. (2005) M. B. Nasr, G. D. Giuseppe, B. E. Saleh, A. V. Sergienko, and M. C. Teich, “Generation of high-flux ultra-broadband light by bandwidth amplification in spontaneous parametric down conversion,” Optics Communications 246, 521–528 (2005).
- Kwiat et al. (1995) P. G. Kwiat, K. Mattle, H. Weinfurter, A. Zeilinger, A. V. Sergienko, and Y. Shih, “New high-intensity source of polarization-entangled photon pairs,” Phys. Rev. Lett. 75, 4337–4341 (1995).
- Friberg, Hong, and Mandel (1985) S. Friberg, C. K. Hong, and L. Mandel, “Measurement of time delays in the parametric production of photon pairs,” Phys. Rev. Lett. 54, 2011–2013 (1985).
- Kwiat et al. (1999) P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard, “Ultrabright source of polarization-entangled photons,” Phys. Rev. A 60, R773–R776 (1999).
- Karan et al. (2020) S. Karan, S. Aarav, H. Bharadhwaj, L. Taneja, A. De, G. Kulkarni, N. Meher, and A. K. Jha, “Phase matching in beta-barium borate crystals for spontaneous parametric down-conversion,” Journal of Optics 22, 083501 (2020).
- Nikogosyan (1991) D. N. Nikogosyan, “Beta barium borate (bbo),” Applied Physics A 52, 359–368 (1991).
- Midwinter and Warner (1965) J. E. Midwinter and J. Warner, “The effects of phase matching method and of crystal symmetry on the polar dependence of third-order non-linear optical polarization,” British Journal of Applied Physics 16, 1667–1674 (1965).
- Roslyak and Mukamel (2009) O. Roslyak and S. Mukamel, “Multidimensional pump-probe spectroscopy with entangled twin-photon states,” Phys. Rev. A 79, 063409 (2009).
- Wang et al. (1999) S. Wang, V. Pasiskevicius, J. Hellström, F. Laurell, and H. Karlsson, “First-order type ii quasi-phase-matched uv generation in periodically poled ktp,” Opt. Lett. 24, 978–980 (1999).
- Yu et al. (2002) N. E. Yu, J. H. Ro, M. Cha, S. Kurimura, and T. Taira, “Broadband quasi-phase-matched second-harmonic generation in mgo-doped periodically poled linbo3 at the communications band,” Opt. Lett. 27, 1046–1048 (2002).
- Lin et al. (2019) J. Lin, N. Yao, Z. Hao, J. Zhang, W. Mao, M. Wang, W. Chu, R. Wu, Z. Fang, L. Qiao, W. Fang, F. Bo, and Y. Cheng, “Broadband quasi-phase-matched harmonic generation in an on-chip monocrystalline lithium niobate microdisk resonator,” Phys. Rev. Lett. 122, 173903 (2019).
- Chen et al. (2009) J. Chen, A. J. Pearlman, A. Ling, J. Fan, and A. Migdall, “A versatile waveguide source of photon pairs for chip-scale quantum information processing,” Opt. Express 17, 6727–6740 (2009).
- Bock et al. (2016) M. Bock, A. Lenhard, C. Chunnilall, and C. Becher, “Highly efficient heralded single-photon source for telecom wavelengths based on a ppln waveguide,” Opt. Express 24, 23992–24001 (2016).
- Shi and Tomita (2004) B.-S. Shi and A. Tomita, “Highly efficient generation of pulsed photon pairs with bulk periodically poled potassium titanyl phosphate,” J. Opt. Soc. Am. B 21, 2081–2084 (2004).
- Armstrong et al. (1962) J. A. Armstrong, N. Bloembergen, J. Ducuing, and P. S. Pershan, “Interactions between light waves in a nonlinear dielectric,” Phys. Rev. 127, 1918–1939 (1962).
- Tanzilli et al. (2001) S. Tanzilli, H. D. Riedmatten, W. Tittel, H. Zbinden, P. Baldi, M. D. Micheli, D. Ostrowsky, and N. Gisin, “Highly efficient photon-pair source using periodically poled lithium niobate waveguide,” Electronics Letters 37, 26–28 (2001).
- Nasr et al. (2008) M. B. Nasr, S. Carrasco, B. E. A. Saleh, A. V. Sergienko, M. C. Teich, J. P. Torres, L. Torner, D. S. Hum, and M. M. Fejer, “Ultrabroadband biphotons generated via chirped quasi-phase-matched optical parametric down-conversion,” Phys. Rev. Lett. 100, 183601 (2008).
- Pe’er et al. (2005) A. Pe’er, B. Dayan, A. A. Friesem, and Y. Silberberg, “Temporal shaping of entangled photons,” Phys. Rev. Lett. 94, 073601 (2005).
- Ou and Lu (1999) Z. Y. Ou and Y. J. Lu, “Cavity enhanced spontaneous parametric down-conversion for the prolongation of correlation time between conjugate photons,” Phys. Rev. Lett. 83, 2556–2559 (1999).
- Hadfield (2009) R. H. Hadfield, “Single-photon detectors for optical quantum information applications,” Nature Photonics 3, 696–705 (2009).
- Zverev et al. (1972) G. M. Zverev, E. A. Levchuk, V. A. Pashkov, and Y. D. Poryadin, “Laser-radiation-induced damage to the surface of lithium niobate and tantalate single crystals,” Soviet Journal of Quantum Electronics 2, 167–169 (1972).
- Antonov et al. (1975) V. A. Antonov, P. A. Arsenev, I. G. Linda, and V. L. Farstendiker, “Colour centres in single crystals of lithium tantalate,” physica status solidi (a) 28, 673–676 (1975), https://onlinelibrary.wiley.com/doi/pdf/10.1002/pssa.2210280234 .
- Meyn and Fejer (1997) J.-P. Meyn and M. M. Fejer, “Tunable ultraviolet radiation by second-harmonic generation in periodically poled lithium tantalate,” Opt. Lett. 22, 1214–1216 (1997).
- Lopez-Mago and Novotny (2012) D. Lopez-Mago and L. Novotny, “Coherence measurements with the two-photon michelson interferometer,” Phys. Rev. A 86, 023820 (2012).
- Klyshko, Penin, and Polkovnikov (1970) D. N. Klyshko, A. N. Penin, and B. F. Polkovnikov, “Parametric luminescence and light scattering by polaritons,” JETP Lett. 11, 11–14 (1970).
- Boyd and Prato (2008) R. Boyd and D. Prato, Nonlinear Optics, 3rd ed. (Elsevier Science, 2008).
- Fejer et al. (1992) M. M. Fejer, G. A. Magel, D. H. Jundt, and R. L. Byer, “Quasi-phase-matched second harmonic generation: tuning and tolerances,” IEEE Journal of Quantum Electronics 28, 2631–2654 (1992).
- Moutzouris et al. (2011) K. Moutzouris, G. Hloupis, I. Stavrakas, D. Triantis, and M.-H. Chou, “Temperature-dependent visible to near-infrared optical properties of 8 mol% mg-doped lithium tantalate,” Opt. Mater. Express 1, 458–465 (2011).
- Di Giuseppe et al. (2002) G. Di Giuseppe, M. Atatüre, M. D. Shaw, A. V. Sergienko, B. E. A. Saleh, and M. C. Teich, “Entangled-photon generation from parametric down-conversion in media with inhomogeneous nonlinearity,” Phys. Rev. A 66, 013801 (2002).
- Burlakov et al. (1997) A. V. Burlakov, M. V. Chekhova, D. N. Klyshko, S. P. Kulik, A. N. Penin, Y. H. Shih, and D. V. Strekalov, “Interference effects in spontaneous two-photon parametric scattering from two macroscopic regions,” Phys. Rev. A 56, 3214–3225 (1997).
- Brańczyk et al. (2011) A. M. Brańczyk, A. Fedrizzi, T. M. Stace, T. C. Ralph, and A. G. White, “Engineered optical nonlinearity for quantum light sources,” Opt. Express 19, 55–65 (2011).
- Reichert, Defienne, and Fleischer (2018) M. Reichert, H. Defienne, and J. W. Fleischer, “Massively parallel coincidence counting of high-dimensional entangled states,” Scientific Reports 8, 2045–2322 (2018).
- Zhang et al. (2020) Y. Zhang, D. England, A. Nomerotski, P. Svihra, S. Ferrante, P. Hockett, and B. Sussman, “Multidimensional quantum-enhanced target detection via spectrotemporal-correlation measurements,” Phys. Rev. A 101, 053808 (2020).