J.H and Q.L contributed equally to this work.
Designing the Quantum Channels Induced by Diagonal Gates
Abstract
The challenge of quantum computing is to combine error resilience with universal computation. Diagonal gates such as the transversal gate play an important role in implementing a universal set of quantum operations. This paper introduces a framework that describes the process of preparing a code state, applying a diagonal physical gate, measuring a code syndrome, and applying a Pauli correction that may depend on the measured syndrome (the average logical channel induced by an arbitrary diagonal gate). It focuses on CSS codes, and describes the interaction of code states and physical gates in terms of generator coefficients determined by the induced logical operator. The interaction of code states and diagonal gates depends very strongly on the signs of -stabilizers in the CSS code, and the proposed generator coefficient framework explicitly includes this degree of freedom. The paper derives necessary and sufficient conditions for an arbitrary diagonal gate to preserve the code space of a stabilizer code, and provides an explicit expression of the induced logical operator. When the diagonal gate is a quadratic form diagonal gate (introduced by Rengaswamy et al.), the conditions can be expressed in terms of divisibility of weights in the two classical codes that determine the CSS code. These codes find application in magic state distillation and elsewhere. When all the signs are positive, the paper characterizes all possible CSS codes, invariant under transversal -rotation through , that are constructed from classical Reed-Muller codes by deriving the necessary and sufficient constraints on . The generator coefficient framework extends to arbitrary stabilizer codes but there is nothing to be gained by considering the more general class of non-degenerate stabilizer codes.
1 Introduction and Review111Section 2 introduces notation and provides technical background for the results described in this section.
We approach quantum computing through fault tolerant implementation of a universal set of gates. There are many finite sets of gates that are universal, and a standard choice is to augment the set of Clifford gates by a non-Clifford unitary [7] such as the gate ( rotation). Gottesman and Chuang [20] introduced the Clifford hierarchy of unitary operators. The first level is the Pauli group. The second level is the Clifford group, which consists of unitary operators that normalize the Pauli group. The -th level consists of unitary operators that map Pauli operators to the -th level under conjugation. The teleportation model of quantum computation introduced in [20] is closely related to the structure of the Clifford hierarchy (for details, see [42, 4, 5, 1, 15, 36, 33]). The diagonal gates in the Clifford hierarchy form a group [42, 15], and the diagonal entries are -th roots of unity raised to some polynomial function of the qubit state. Cui et al. [15] determined the level of a diagonal gate in the Clifford hierarchy in terms of and the degree of the polynomial function. Quadratic form diagonal (QFD) gates are a family of diagonal gates associated with quadratic forms. The class of QFD gates includes transversal -rotations through , and encompasses all -local gates in the hierarchy [36].
Quantum error-correcting codes (QECCs) protect information as it is transformed by logical gates. In general, a logical non-Clifford gate is more difficult to implement than a logical Clifford gate [19]. Any non-Clifford operation on the logical qubits of an QECC must be induced by a non-Clifford operation on the physical qubits [15]. We derive a global necessary and sufficient condition for any diagonal physical gate to preserve the code space of a stabilizer code [18, 11]. A transversal gate [18] is a tensor product of unitaries on individual code blocks. In the case of transversal -rotation through , we show that this global condition is equivalent to the local trigonometric conditions derived by Rengaswamy et al. [35]. Our approach has the advantage of providing insight into the induced logical operator.
It is essential that a set of gates be both universal and fault-tolerant. Fault-tolerance of transversal gates follows from the observation that uncorrelated errors remain uncorrelated in code blocks. The Eastin-Knill Theorem [17] reveals that we cannot implement a universal set of logical operations on a QECC using transversal operations alone. Magic state distillation (MSD) combines transversal gates with an ancillary magic state to circumvent this restriction [10, 34, 9, 2, 13, 26, 14, 22, 25, 39]. If the initial fidelity of magic state exceeds a certain threshold, then it can be purified by successive application of the quantum teleportation protocol on stabilizer codes that are able to realize a logical non-Clifford gate. (Generalized) triorthogonal codes [9, 22] are Calderbank-Shor-Steane (CSS) codes [12, 37] designed to implement a non-Clifford logical gate (up to some diagonal Clifford logical gates). Hamming weights in the classical codes that determine the CSS codes are required to satisfy certain divisibility properties [13, 26, 21, 39, 31]. Many examples employ Reed-Muller (RM) codes. In Section 5 we characterize CSS codes constructed from classical RM codes that are fixed by transversal -rotation through .
MSD provides a path to universal fault tolerant computation, where success depends on engineering the interaction of code states and physical gates. Here we consider the interaction of a diagonal physical gate with the code states of a stabilizer code, as shown in Figure 1. We prepare an initial code state, apply a physical gate, then measure a code syndrome , and finally apply a correction based on . For each syndrome, we expand the induced logical operator in the Pauli basis to obtain the generator coefficients that capture state evolution. Intuitively, the diagonal physical gate preserves the code space if and only if the induced logical operator corresponding to the trivial syndrome is unitary.
The effectiveness of magic state distillation (MSD) depends on the probability of observing a given syndrome, and it is possible to combine syndrome measurement with a decoder (see Krishna and Tillich [25] for example). Generator coefficients provide a framework for investigating the effectiveness and the threshold of distillation. We describe the design space that is available through a running example.
Example 1 (The Steane code).
Reichardt [34] demonstrated that it is possible to distill the magic state by post-selecting on the trivial syndrome, even though the Steane code is not perfectly preserved by the transversal T gate. He also demonstrated the distillation threshold is optimal for . In Section 4, we use generator coefficients to describe the average-logical channel induced by the transversal gate on the Steane code. When we observe the trivial syndrome, the induced logical operator is . Otherwise it is a logical Pauli followed by a logical . The induced logical operator becomes for all syndromes after applying a logical Pauli correction to all non-trivial syndromes. However, the distillation protocol no longer converges, despite the higher probability of success333See Appendix A. Generator coefficients encode the probabilities of observing different syndromes, which can be used to analyze variants of the Steane protocol (such as applying a decoder to subsets of syndromes), as well as MSD protocols that use different codes (such as the code).
The introduction of magic state distillation by Bravyi and Kitaev [10] led to the construction of CSS codes where the code space is preserved by a transversal -rotation of the underlying physical space [10, 34, 9, 13, 26, 14, 22, 39]. The approach taken in each paper is to examine the action of a transversal -rotation on the basis states of a CSS code. This approach results in sufficient conditions for a transversal -rotation to realize a logical operation on the code space. In contrast we derive necessary and sufficient conditions by analyzing the action of a transversal diagonal gate on the stabilizer group that determines the code. In effect, we study the code space by studying symmetries of the codespace.
The interaction of transversal physical operators and code states depends very strongly on the signs of stabilizers [23, 16]. Consider for example, the design of CSS codes that are oblivious to coherent noise. We can model the effective error as a uniform -rotation on each qubit through some (small) angle . We require the noise to preserve the code space and to act trivially (as the logical identity operator). It is possible to demonstrate the existence of weight- -stabilizers, and to show that their signs must be balanced [23]. Our generator coefficient framework includes the freedom to choose signs and this degree of freedom is relatively unexplored. We describe the design space that is available through a running example.
Example 2 (The code).
Generator coefficients encode correlation between the initial code state and syndrome measurement, which may result in loss of logical information. The code shows that correlation can depend very strongly on the signs of -stabilizers. The stabilizer group is . In Section 4 we show that if has a positive sign, then there is an embedded decoherence free subspace spanned by the three encoded basis states , , and . We also show that syndrome measurement collapses logical information. If has a negative sign, then we show that logical information does not collapse, but the embedded decoherence free subspace disappears. Generator coefficients encode the different ways that code states can evolve.
We now summarize our main technical contributions.
-
1)
We derive an explicit expression for the logical channel induced by a diagonal physical gate (Section 4, (94) describes the induced logical operator for each syndrome and (112) describes the probability of observing ). We quantify the correlation between initial code state and measured syndrome by separating the probability of observing a given syndrome into two components, one depending on the generator coefficients, the other on the choice of initial state (Section 4.2). We analyze the code (Example 2) to show that each component depends strongly on the choice of signs in the stabilizer code, and that we can choose signs to create a embedded decoherence free subspace.
-
2)
We derive necessary and sufficient conditions for an arbitrary diagonal physical gate to preserve the codespace of a CSS code with arbitrary signs (Section 5, Theorem 7), and describe the logical operator that results (Section 5, Remark 8). These conditions generalize earlier conditions found by Rengaswamy et al [35] for transversal -rotation through .
-
3)
We further simplify the necessary and sufficient conditions for a QFD gate to preserve the code space of a CSS code (Section 5, Theorem 9). These conditions govern divisibility of Hamming weights in the classical codes that determine the CSS codes. In the case of transversal -rotation through applied to CSS codes with positive signs, we show the necessity of divisibility conditions derived in [26, 39].
-
4)
We characterize all CSS codes with positive signs, invariant under transversal -rotation through , that are constructed from classical Reed-Muller (RM) codes (and their derivatives obtained by puncturing or removing the first coordinate). We derive necessary and sufficient conditions that relate to the parameters of the component RM codes (Section 5, Theorem 14 and Remark 15).
-
5)
We extend the generator coefficient framework to stabilizer codes (Appendix B). This extension shows that given an non-degenerate stabilizer code preserved by a diagonal gate , we can construct an CSS code preserved by with the same induced logical operator. Note that (the minimum weight of any nontrivial -logical Pauli operator) is the relevant distance for MSD. Recall that an stabilizer code is non-degenerate if the weight of every stabilizer element is at least .
The rest of the paper is organized as follows. Section 2 introduces notation and provides the necessary background. Our review of stabilizer codes takes account of the freedom to choose signs in the stabilizer group, and provides the general encoding map and logical Pauli operators for CSS codes with arbitrary signs. Section 3 introduces the generator coefficients that describe how a diagonal gate acts on a CSS code. Section 4 describes how generator coefficient govern the average logical channel. Section 5 establishes necessary and sufficient conditions for a CSS code to support a diagonal physical gate, and derives the induced logical operator. We then derive the divisibility conditions and introduce RM constructions. Section 6 concludes the paper and discusses future directions. In Appendix B, we extends the generator coefficient framework to general stabilizer codes and show that CSS codes perform at the least as well as non-degenerate stabilizer codes for diagonal gates.
2 Preliminaries and Notation
2.1 Classical Reed-Muller Codes
Let denote the binary field. Let , and let , , , be binary variables (monomials of degree ). Monomials of degree can be written as where are distinct. A boolean function with degree is a binary linear combination of monomials with degrees at most . There is a one-to-one correspondence between boolean functions and evaluation vectors . The degree boolean function corresponds to the constant evaluation vector .
For , the Reed-Muller code RM is the set of all evaluation vectors associated with boolean functions of degree at most , The length of the RM code is , the dimension is given by , and the minimal distance is . The dual of RM is RM, and we can construct the RM codes by a recursively observing RM [28]. Note that all weights in RM() are multiples of [3, 29, 28], and the highest power of that divides all weights of codewords in RM() is exactly [6].
2.2 The MacWilliams Identities
Let be the imaginary unit. We denote the Hamming weight of a binary vector by . The weight enumerator of a binary linear code is the polynomial
| (1) |
The MacWilliams Identities [27] relate the weight enumerator of a code to that of the dual code , and are given by
| (2) |
Given an angle , we make the substitution and , and define
| (3) | ||||
| (4) |
2.3 The Pauli Group
Any Hermitian matrix can be uniquely expressed as a real linear combination of the four single qubit Pauli matrices/operators
| (5) |
and . The operators satisfy
Let denote the Kronecker product (tensor product) of two matrices and . Let and . Given binary vectors and with or , we define the operators
| (6) | ||||
| (7) |
We often abuse notation and write , though entries of vectors are sometimes interpreted in . Note that can have order or , but . The -qubit Pauli group is defined as
| (8) |
where . The -qubit Pauli matrices form an orthonormal basis for the vector space of complex matrices () under the normalized Hilbert-Schmidt inner product [18].
We use the Dirac notation, to represent the basis states of a single qubit in . For any , we define , the standard basis vector in with in the position indexed by and elsewhere. We write the Hermitian transpose of as . We may write an arbitrary -qubit quantum state as , where and . The Pauli matrices act on a single qubit as
The symplectic inner product is . Since , we have
| (9) |
2.4 The Clifford Hierarchy
The Clifford hierarchy of unitary operators was introduced in [20]. The first level of the hierarchy is defined to be the Pauli group . For , the levels are defined recursively as
| (10) |
where is the group of unitary matrices. The second level is the Clifford Group, , which can be generated (up to overall phases) using the “elementary" unitaries Hadamard, Phase, and either of Controlled-NOT (C) or Controlled- (C) defined respectively as
| (11) |
| (12) | ||||
| (13) |
Note that Clifford unitaries in combination with any unitary from a higher level can be used to approximate any unitary operator arbitrarily well [7]. Hence, they form a universal set for quantum computation. A widely used choice for the non-Clifford unitary is the gate in the third level defined by
| (14) |
2.5 Stabilizer Codes
We define a stabilizer group to be a commutative subgroup of the Pauli group , where every group element is Hermitian and no group element is . We say has dimension if it can be generated by independent elements as , where and . Since is commutative, we must have .
Given a stabilizer group , the corresponding stabilizer code is the fixed subspace . We refer to the subspace as an stabilizer code because it encodes logical qubits into physical qubits. The minimum distance is defined to be the minimum weight of any operator in . Here, the weight of a Pauli operator is the number of qubits on which it acts non-trivially (i.e., as or ), and denotes the normalizer of in defined by
| (15) |
Note that the second equality defines the centralizer of in , and it follows from the first since Pauli matrices commute or anti-commute.
For any Hermitian Pauli matrix and , the operator projects onto the -eigenspace of . Thus, the projector onto the codespace of the stabilizer code defined by is
| (16) |
where is a character of the group , and is determined by the signs of the generators that produce : for a unique .
Let , be the protected logical state. We define the generating set for the logical Pauli operators by the actions
| (17) |
where
| (20) |
and Let be the -qubit operators which are physical representatives of for . Then commute with the stabilizer group and satisfy
| (23) |
Remark 1.
A stabilizer code determines a resolution of the identity with the different subspaces fixed by different signings of the stabilizer generators. When we correct stochastic and independent Pauli errors, different signings of stabilizer generators lead to quantum codes with identical performance. However, when we consider correlated errors such as the coherent errors (rotations of axis for any angle ), the signs of stabilizers play an important role [23, 16].
Example 3 (-qubit bit flip code with negative signs).
Consider the stabilizer code defined by the group , which differs from the stabilizer group of the -qubit bit flip code, , just by the sign of . The encoding circuit of consist of C and C gates, which maps to and to . Since , the encoding circuit of has an extra gate on the first qubit, which has and . Moreover, the physical representation of logical Pauli and for is and respectively, i.e., .
2.6 CSS Codes
A CSS (Calderbank-Shor-Steane) code is a particular type of stabilizer code with generators that can be separated into strictly -type and strictly -type operators. Consider two classical binary codes such that , and let , denote the dual codes. Note that . Suppose that is an code and is an code. Then, the corresponding CSS code has the stabilizer group
where . The CSS code projector can be written as the product:
| (24) |
where
| (25) |
and
| (26) |
Each projector defines a resolution of the identity, and we focus on since we consider diagonal gates. Note that any -qubit Pauli operator can be expressed as for a -stabilizer representation , a -logical representation , and a -syndrome representation . For , we define
| (27) | ||||
| (28) |
Then, we have
| (31) | |||
| (32) |
If and can correct up to errors, then defines an CSS code with , which we will represent as CSS(). If and are the generator matrices for and respectively, then the matrix
| (33) |
generates .
2.7 General Encoding Map for CSS codes
Given an CSS() code with all positive signs, let be the generator matrix for all coset representatives for in (note that the choice of coset representatives is not unique). The canonical encoding map is given by . Note that the signs of stabilizers change the fixed subspace by changing the eigenspaces that enter into the intersection. Thus, the encoding map needs to include information about nontrivial signs.
We capture sign information through character vectors (note that the choice of coset representatives is not unique) defined for -stabilizers and -stabilizers respectively by
| (34) |
and
| (35) |
Then, for , we have and . In Example 3, we may choose the character vectors (character vector of -stabilizers) and (character vector of -stabilizers).
The generalized encoding map is defined by
| (36) |
To verify that the image of the general encoding map is in , we show that for (that is , , , and ),
| (37) |
2.8 General Logical Pauli Operators for CSS codes
Given the choice of , there exists a unique set of vectors , where is the standard basis of . If is the -the row of generator matrix , then
| (38) |
Assume we have
| (47) |
Thus, we have for
| (48) |
and
| (49) |
where the second to last step follows from (38). Thus we can choose
| (50) |
where are the -th rows of the above coset generator matrices , respectively.
Remark 2.
Applying appropriate Pauli operators takes care of different signs in the stabilizer group and changes the sign of logical Pauli operators. Although the sign for a single logical Pauli operator is not observable, a general logical operator is a linear combination of logical Pauli operators, which may bring the global sign into some local phase.
Example 2 (The basis state and logical Pauli operators of the code).
Consider the CSS() code with . We may choose the generator matrices of and as
| (51) |
The encoded basis states and logical Pauli operators for two choices of the signs are given below. If (), we have
When (, ), we have
2.9 Quantum Channels
The quantum states defined in Section 2.3 are called pure states. When a system contains multiple pure states with probabilities , the ensemble , is described by a density operator given by
| (52) |
Every density operator is Hermitian, positive semi-definite, with unit trace. Conversely, any operator with these three properties can be written in the form (52). Every ensemble determines a unique density operator but a density operator can describe different ensembles.
Suppose we measure the density operator with a finite set of projectors forming a resolution of the identity. If the initial state in the ensemble is , then we observe the outcome with probability and obtain the reduced state . From the perspective of density operators, we observe the outcome with probability and the density operator evolves to be . Thus, after measurement, we have a ensemble of ensembles described by a new density operator given by [40]
| (53) |
A quantum channel is linear, completely-positive, and trace-preserving, and can be characterized by a Kraus representation [32, 40]. A map is linear, completely-positive, and trace-preserving if and only if there exists a finite set of operators (from to ) such that for any
| (54) |
The operators are called Kraus operators and satisfy
| (55) |
and
| (56) |
Note that the Kraus representation of a quantum channel is not unique.
3 Generator Coefficients
Starting from the general encoding map and logical Pauli operators of CSS codes introduced in Section 2.7, we study gates interacting with these codes. We consider quantum gates for which the Pauli expansion consists only of tensor products of Pauli ’s (or Pauli ’s). We partition into cosets of the -stabilizers (or -stabilizers), and define generator coefficients that take advantage of the structure of stabilizer group. The framework of generator coefficients provides insight into the average logical channel, the necessary and sufficient conditions for a CSS code to be invariant under a particular gate, and the induced logical operator. We extend the framework of generator coefficients to general stabilizer codes in Appendix B.
Consider a unitary matrix (quantum gate) , where . Since
| (57) |
we have
| (58) |
We define the generator coefficients for acting on a given CSS code as follows.
Definition 3 (Generator Coefficients for ).
Let CSS() be an stabilizer code defined by the stabilizer group and the character vector for -stabilizers. Let be any -syndrome and be any -logical. Then, for any pair , , we define the generator coefficient corresponding to the diagonal unitary gate by
| (59) |
where .
Note that given a CSS code with not all positive signs, the character vector is unique up to an element of . A different choice of the coset representatives of in only changes the signs of , and leads to a global phase in the logical quantum channel induced by , which is given in Section 4.
By partitioning into cosets of , we gain insight into the interaction of syndromes and logicals. The code projector is , and we have
| (60) |
In the above summations, and , and is given by (59). We now study the generator coefficients associated with two different types of quantum gate .
3.1 Transversal -Rotations
There are two reasons to study how acts on the states within a quantum error-correcting code. The first is that when is not a multiple of , may realize a non-Clifford logical gate, and the second is that coherent noise can be modeled as . The Pauli expansion of is
| (61) |
As , we substitute it in (59), and obtain the generator coefficients of ,
| (62) |
We now compute the generator coefficients for the Steane code.
Example 1 (Generator Coefficients for applied to the Steane code).
The Steane code is a perfect CSS() code with all positive signs and generator matrix
| (65) |
where is the parity-check matrix of the Hamming code:
| (69) |
Then, we have , where are the vectors of all ones and all zeros respectively. If we compute the generator coefficients directly from (3.1), then we need the weight enumerators of all cosets of . We may simplify these calculations using the MacWilliams Identities. Consider for example the case and , where we may write
| (70) |
where is defined in (4). We apply the MacWilliams Identities to to obtain
| (71) |
We simplify the term in the same way,
| (72) |
It follows from (1), (71), and (72) that
| (73) | ||||
| (74) |
where (74) is obtained from (73) by substituting in the weight enumerator of
We compute all the generator coefficients for the Steane code in Table 1. We return to this data in Section 4.1 to provide more insight into the logical channel determined by , and in Section 4.2 to calculate the probabilities of observing different syndromes.
Before introducing the Kraus decomposition of acting on a CSS code, we provide an alternative definition of generator coefficients which simplifies calculations. We first write as a linear combination of weight enumerators, then apply the MacWilliams Identities.
Lemma 4 (Simplified Definition of Generator Coefficients).
Consider a CSS() code, where is the character vector for the -stabilizers . Then, the generator coefficients defined in (3.1) can be written as
| (75) |
Remark 5.
Proof.
See Appendix C.1. ∎
3.2 Quadratic Form Diagonal Gates
Rengaswamy et al. [36] considered diagonal unitaries of the form
| (76) |
where is an integer, , and is an symmetric matrix with entries in , the ring of integer modulo . Note that the exponent . When and is binary, we obtain the diagonal Clifford unitaries. QFD gates defined by (76) include all -local and -local diagonal unitaries in the Clifford hierarchy, and they contain for , where is an integer.
Recall that Pauli matrices form an orthonormal basis for unitaries of size with respect to the normalized Hilbert-Schmidt inner product . Hence,
| (77) |
and the Pauli expansion of a QFD gate becomes
| (78) |
where
| (79) |
Example 4.
If , then we have , , and
Example 5.
Consider , and . If , then and If , then and
| (80) |
We substitute (79) in (59), and obtain the generator coefficients for QFD gates
| (81) |
Let be the character vector . Changing the order of summation, we have
| (82) |
where
| (83) |
Substituting (83) in (82), we obtain
| (84) |
When , we obtain the transversal -rotation up to a global phase. We now use (84) to calculate generator coefficients of the code.
Example 2 (Generator Coefficients of C and C for the code).
The code is a CSS code with . The -logical and the -syndrome . Assume all the stabilizers have positive signs (the character vector ). Set
| (85) |
Setting , we list the generator coefficients for C in Table 2. Note that C and C shared the same symmetric matrix but the level is different. Table 3 lists the generator coefficients for C.
4 Average Logical Channel
We investigate the effect of acting on a CSS codespace by considering the following steps:
-
1.
Choose any initial density operator in the CSS codespace . Then, we have .
-
2.
Apply physically. Then the system evolves to
(86) -
3.
Measure with -stabilizers to obtain the syndrome . It follows from (53) that the system evolves to
(87) -
4.
Based on the syndrome , we apply a Pauli correction to map the state back to . This correction may introduce some logical operator . The final state is in the CSS codespace.
Generator coefficients help describe the average logical channel resulting from acting on a CSS codespace (steps 1-4). We extend our approach to arbitrary stabilizer codes in Appendix B.
4.1 The Kraus Representation
Kraus operators describe the logical channels obtained by averaging the action of over density operators in . Generator coefficient appear as the coefficients in the Pauli expansion of Kraus operators. We use generator coefficients to simplify the term in (86). It follows from (60) and the derivation in Appendix C.2 that
| (88) |
where as described in (27), and
| (89) |
Since the projectors are pairwise orthogonal, it follows from that for any fixed , we have
| (90) |
Since describes an ensemble of states in the codespace , it follows from that for fixed , we have
| (91) |
where . Thus, we may write as
| (92) |
where . Although the sign does not matter here, we carry it along for consistency with the logical Pauli operators derived in (50). Based on the syndrome , the decoder applies a correction and maps the quantum state back to the codespace . This correction might induce some undetectable -logical with . Hence, the final state after step 4 becomes
| (93) |
where
| (94) |
is the effective physical operator corresponding to syndrome . It follows from (50) that for , is a logical Pauli , and (93), (94) can be considered just in the logical space.
Note that the evolution described in (93) works for any initial code state in step 1. The interaction between the diagonal gate and the structure of CSS code in step 2 is captured in the generator coefficients . The syndrome of the measurement in step 3 is reflected by the sum in (93), and the decoder chosen in step 4 is expressed by some logical Pauli determined by for each syndrome.
To show is the set of Kraus operators, we need to verify that
| (95) |
We may simplify the summation as
| (96) |
where the new variable . In Theorem 6, we verify (95) by showing that the coefficient of is 1 and that the coefficients of are all zero. Theorem 6 describes the general property of generator coefficients, which mainly because quantum gates are unitaries.
Theorem 6.
Suppose that a -unitary gate induces generator coefficients on a CSS() code. If , then
| (99) |
Proof.
See Appendix C.4. ∎
We conclude that the Kraus operators describing the action of on a CSS code are given by (94).
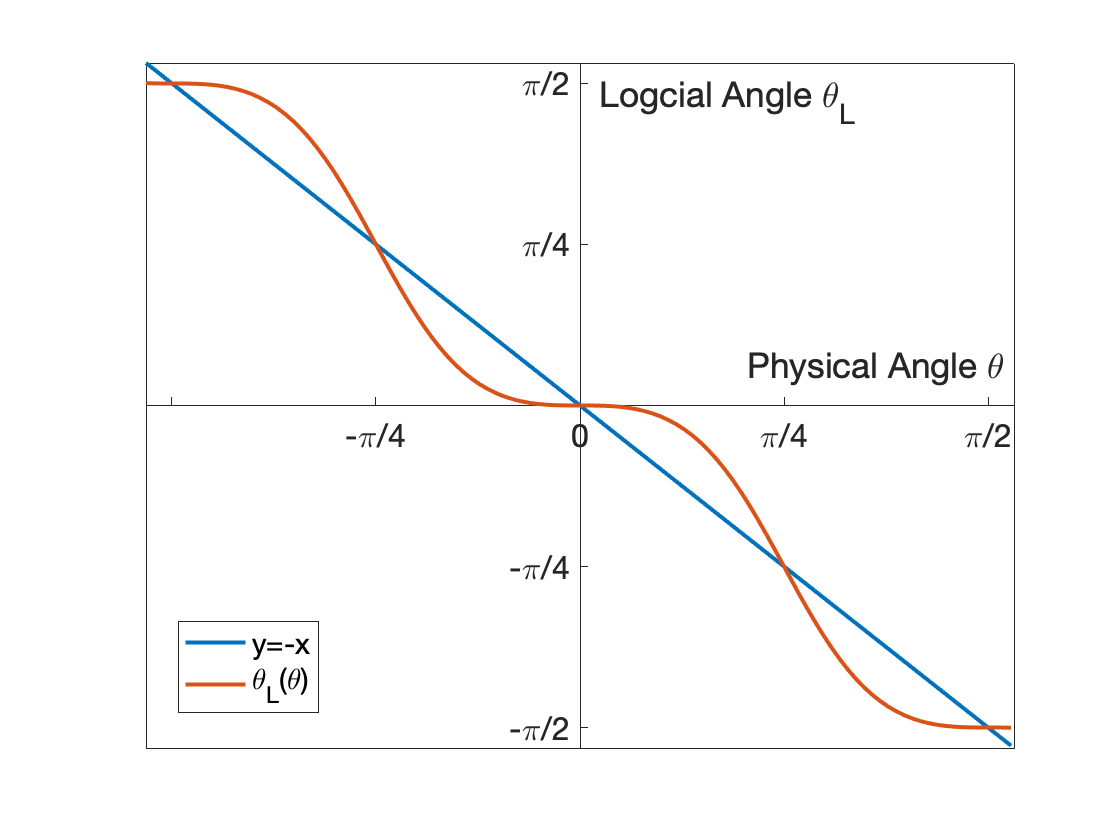
When , the generator coefficients take the form (3.1). Consider now a one-logical-qubit system, where one of the pair is real and the other is pure imaginary. Then the logical qubit is rotated with angle and we can express in terms of the physical rotation angle [16] as
| (100) |
See Appendix C.3 for details. We again take the Steane code as an example, substitute the values from Table 1 and obtain the logical rotation angle
| (101) |
Figure 2 plots displaying third-order convergence about . Note that . In Appendix A, we explain how supports magic state distillation with the aid of a logical Phase gate. When , , and the Steane code might be applied to convert 7 noisy copies of the state into 1 copy of the state with higher fidelity.
We now compute all Kraus operators induced by acting on the Steane code.
Example 1 (continued).
We take the data in Table 1 and substitute to obtain
| (102) |
We assume for all , and use these generator coefficients to compute the Kraus operators
| (103) | ||||
| (104) |
which describe the average logical channel corresponds to the transversal gate. Reichardt [34] discussed the Steane code in magic state distillation. The computed average logical channel makes it clear that we can choose proper corrections based on syndromes ( for ) to obtain the logical operator from all the syndromes.
Note that the Steane code is not a triorthogonal code [9], but it can be used in state distillation [34]. The generator coefficients framework may help to characterize codes that are not preserved by transversal but realize a logical gate when the trivial syndrome is observed. Recently, Vasmer and Kubica [38] introduced a new code by morphing the quantum Reed-Muller code [24, 10] and the color code [14]. It provides the first protocol in state distillation that supports a fault-tolerant logical gate from a diagonal physical gate that is not transversal . The generator coefficient framework applies to arbitrary diagonal gates, and may facilitate finding more examples of distillation.
4.2 Probability of Observing Different -Syndromes
The Kraus operators derived in Section 4.1 describe logical evolution conditioned on different outcomes from stabilizer measurement, and it is natural to calculate the probability of observing different syndromes . Generator coefficients provide a means of calculating these probabilities that illuminates dependence on the initial state, and we will provide examples where the initial state and the outcome of syndrome measurement are entangled.
Consider a CSS() code with codespace . For any fixed , we first apply , and then measure with projectors , where . Then the probability of obtaining a syndrome is
| (105) |
It follows from equation (60) that
| (106) |
and similarly
| (107) |
For any fixed , since , we have
| (108) |
It follows from the simplification in Appendix C.5 of the later half in (108) that
| (109) |
where . Note that since and , the inner summation is nonzero only when so that
| (110) |
Similarly, we have
| (111) |
Thus, the probability of observing the syndrome can be written as
| (112) |
Note that only the second term depends on the initial state. If some in the initial state , then the second term (the cross terms) in (112) vanishes since every with is some nontrivial Pauli logical. Note that it follows from Theorem 6 that . Since for any initial state , it follows that the sum of the second term over all the -syndromes is 0, that is,
| (113) |
Note that Pauli logicals only change signs in the basis. If the second term is the same for all computational basis states in the codespace, then the probability of observing different syndromes is the same for different initial states . If not, the probabilities depend on the initial state, and encode the mutual information between initial state and syndrome measurement. In these circumstances, we cannot find a recovery operator for that is good for the entire codespace. An important special case is when a decoherence-free subspace is embedded in the codespace (useful for passive control of coherent errors ).
We now introduce two examples to illustrate how (112) provides insight into invariance of the codespace, the probability of success in magic state distillation, and existence of an embedded decoherence-free subspace. Continuing Example 1 below, we compute the probabilities of observing different syndromes for the Steane code and discuss implications. Continuing Example 2 below, we demonstrate that by changing signs of -stabilizers in the code, we can switch from the case where the second term is the same for every initial state to the case of an embedded decoherence-free subspace.
Example 1 (continued).
The Steane code has only one logical qubit, and we let , denote the the two computational basis states. Given a syndrome , we observe that one of the generator coefficients , , is real and the other is purely imaginary, so that the crossterms vanish in (112). Hence, the probabilities of observing different syndromes are constant for different initial states and are given by
| (114) |
It is not hard to verify that for all and for all . Figure 3 plots the probability of observing the trivial syndrome as a function of the rotation angle.
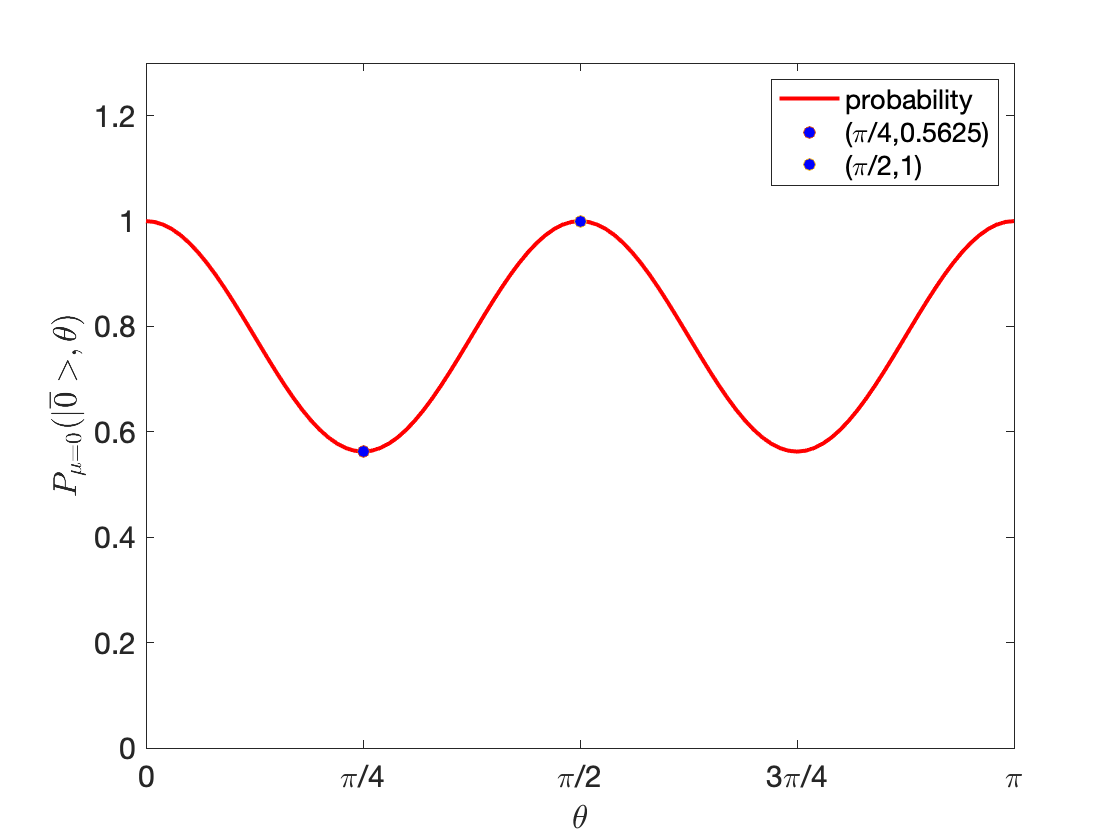
We observe from Figure 3 that when is a multiple of , for all the states in the Steane codespace , which implies that preserves . The angle minimizes the probability of obtaining the zero syndrome and this minimum value relates to the probability of success in magic state distillation. Substituting , we obtain for all .
Example 2 (continued).
Recall the CSS() code with two different choices of signs defined by the character vectors (all positive signs), and (negative in the stabilizer group).
Table 4 lists the generator coefficients for all positive signs (). We now use the data to calculate the probabilities of observing different syndromes as described in (112). For the encoded state, we have
| (115) |
| 0 | 0 | 0 | ||
The remaining three states have the same probabilities of observing -syndromes:
| (116) | |||
| (117) |
If the initial state is among , then it evolves within the codespace for all angles , which implies that forms a embedded decoherence-free subspace (DFS) inside the codespace [23].
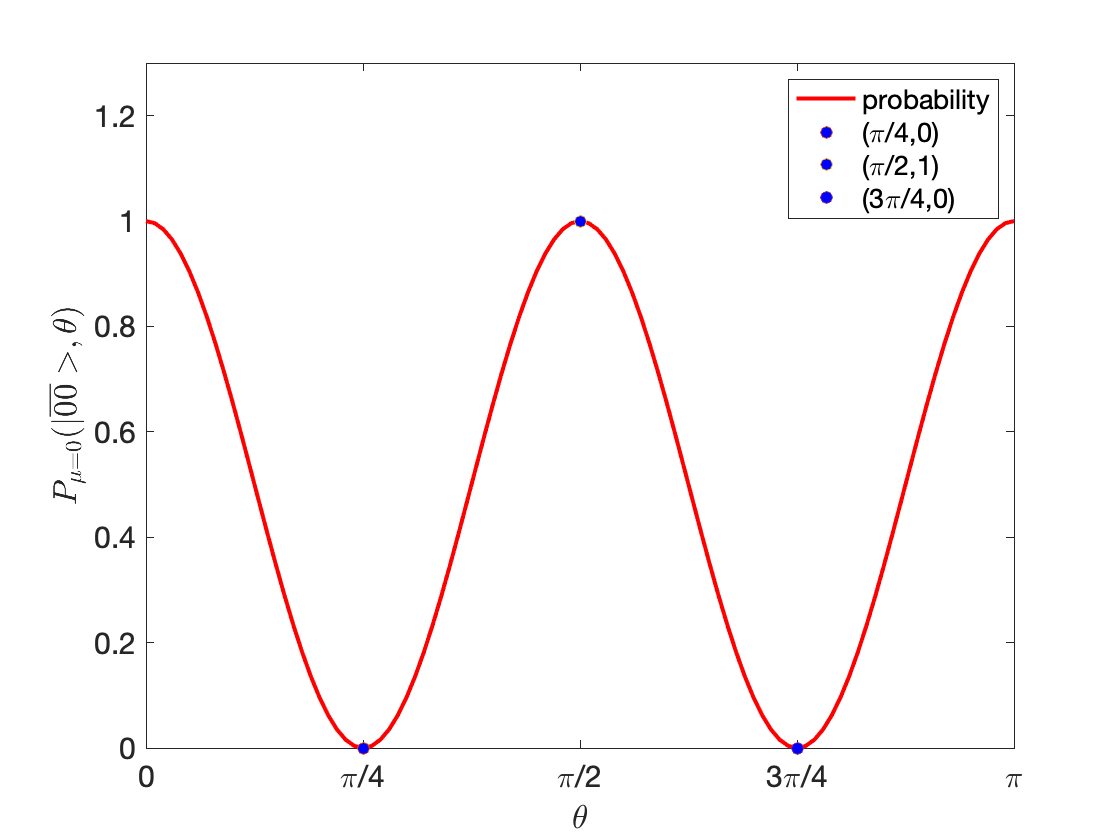
Figure 4 plots (2) for different physical angles . When for some integer , syndrome measurement acts as projection from to the embedded DFS, and we are able to learn whether the initial state was ; When for some integer , the measurement outcome is always the zero syndrome, which implies that perserve the codespace and some logical operator is induced. The Kraus operators derived in (94) imply that the induced logical operator is
| (118) |
Next, we compute the generator coefficients for the same code but with nontrivial signs (character vector ).
In prior work [23], we have derived criteria that ensure a stabilizer code is a DFS, and (112) opens the door to developing criteria for embedded DFS, in which the second term acts as an amendment to the first term and implies the probability is either or for a subset of initial -basis state in the codespace.
5 CSS codes Preserved by
When a CSS code is preserved by a unitary , the probability of observing the zero syndrome is 1, and the Kraus operators capture evolution of logical states. Theorem 7 provides necessary and sufficient conditions for a unitary to preserve a CSS code.
We prove Theorem 7 by writing as a product , where commutes with the -projector , and we then translate commutativity to conditions on generator coefficients. We generalize these conditions to arbitrary stabilizer codes in Appendix B.
Theorem 7.
Let CSS() be an CSS code defined by the stabilizer group with code projector . Then the unitary preserves (i.e. ) if and only if
| (119) |
Proof.
See Appendix C.6. ∎
Remark 8 (Logical Operator induced by ).
We assume that for a CSS code defined by . By Theorem 7, (119) holds, so that by Theorem 6 we only have one Kraus operator left in (94) that is given by
| (120) |
Note that and we have a bijective map defined by , where is the generator matrix selected. Let be the logical operator induced by , and let be the th entry of the vector . Then, using (50), we translate the Kraus operator into the logical space as
| (121) |
Thus, if a CSS code is preserved by , then the generator coefficients corresponding to the zero syndrome are simply the coefficients in the Pauli expansion of the induced logical operator. We also observe that given in (121) is unitary if and only if (119) holds.
In the following subsections, we simplify (119) in special cases when is a QFD gate, and when for some integer . We then provide necessary and sufficient conditions for quantum Reed-Muller codes to be preserved by , and connect to the conditions in [35, Theorem 17].
5.1 QFD Gates
Theorem 9 below specializes Theorem 7 to the broad class of diagonal level- QFD gates determined by symmetric matrices . Note that Theorem 9 applies to CSS codes with arbitrary signs and form a subset of QFD gates. Theorem 9 includes the divisibility conditions derived in [43, 26, 39] as a special case.
Theorem 9.
Consider a CSS()code, where is the character vector of the -stabilizers. Then, a QFD gate preserves the codespace if and only if
| (122) |
for all such that .
Proof.
Remark 10.
When , then and the divisibility condition simplifies to the condition previously obtained for . If a CSS code is preserved by for all , then it follows (122) that for any fixed , all elements in the coset have the same Hamming weight. It then follows from the generalized encoding map given in (36) that any CSS code invariant under for all is a constant-excitation code [41].
We now explore the influence of signs by analyzing and separating the effect of the character vector .
Lemma 11.
Consider a CSS() code, where is the character vector of the -stabilizers. Then, (122) holds for all such that if and only if
| (126) |
| (127) |
for all and
Proof.
See Appendix C.7. ∎
Note that only (126) depends on the character vector , and its contribution is moving the divisible requirement for a set to that for a coset.
Note that by varying the level , the same symmetric matrix can determine different gates (for example, the gates C and C in Example 5). The divisibility conditions corresponding to successive levels differ by a factor of . This suggests using concatenation to lift a code preserved by a level QFD gate determined by to a code preserved by a level QFD gate determine by . We defer investigation to future work.
5.2 Transversal -Rotation
5.2.1 and RM Constructions
If the physical rotation angle is a fraction of , then the constraint on generator coefficients in (119) is equivalent to conditions on the Hamming weights that appear in the classical codes and that determine the quantum CSS code.
Theorem 12.
Let . Then preserves the CSS() codespace if and only if
| (128) |
for all and all , where is the character vector that determines signs of -stabilizers and is the coordinate-wise product of and .
Proof.
See Appendix C.8. ∎
Remark 13 (Transversal -rotation).
Assume positive signs (character vector ) and set for some integer . Since and , it follows from Theorem 12 that preserves a CSS codespace if and only if
| (129) |
| (130) |
This result coincides with the sufficient conditions in [39, Proposition 4], which is a special case of the quasitransversality introduced earlier by Campbell and Howard [14]. For example, if a CSS code with all positive stabilizers is invariant under , then the weight of every -stabilizers needs to be divisible by 8. We note that the color code is the smallest error-detecting CSS code with all positive signs that is preserved by . We defer the study of non-trivial character vectors to future work.
The divisibility conditions (129), (130) suggest constructing CSS codes from classical Reed-Muller codes.
Theorem 14 (Reed-Muller Constructions).
Consider Reed-Muller codes with . The CSS() code with all positive stabilizers is preserved by if and only if
| (131) |
Proof.
Note that all -stabilizers have positive signs corresponding to the case in Theorem 12. Then, preserves a CSS codespace if and only if (129) and (130) hold.
Let and . If , then and . It follows from McEliece [29] (see also Ax [3]) that
| (132) |
and this bound is tight. The two conditions become .
If , then it follows from McEliece [30, 6] that is the highest power of that divides for all . We first show (131) is necessary. It follows from (129) that
| (133) |
We need to understand divisibility of weights where and . The codeword is the evaluation vector of a sum of monomials, and we start by considering the case of a single monomial. Consider a codeword corresponding to the evaluation of a monomial of degree . For all , we observe that is a codeword in RM supported on . Then, is the highest power of that divides for all . Note that since takes values from to , we have
| (136) |
We now consider such that , where , are evaluation vectors correspond to monomials in . Then, for , we have
| (137) |
Since , it follows from (130) that divides , and so . By (5.2.1), we have
| (138) |
Since is the evaluation vector of a monomial with degree , is a codeword in RM supported on . Then, is the highest power of that divides for all . The extremum is achieved when the monimials corresponding to and have degree and do not share a variable. Hence,
| (139) |
It remains to consider the case , where each is the evaluation vector of a monomial. We use inclusion-exclusion to rewrite (130) as
| (140) |
We now use induction. Assume for , we have
| (143) |
Note that for , corresponds to a monomial with degree , hence is a codeword in RM() supported on . Then, we have
| (144) |
in which the bound on the exponent is tight since we can choose to be evulations vectors corresponding to disjoint monomials of degree . Hence, divides all terms in (140) for . Hence, for the last term, we must have
| (145) |
which implies that
| (148) |
and the induction is complete. Note that since , we have
| (149) |
and the necessary condition reduces to
| (150) |
To prove the sufficiency of the case , we simply reverse the steps. ∎
Remark 15 (Puncturing RM codes by removing the first coordinate).
Consider the classical RM code, and two elementary operations on its generator matrix: 1. removing the first column which is ; 2. removing the first row of all 1s. After either of the two operations, we observe that is still the highest power of that divides all of its weights. Hence, the RM constructions described in Theorem 14 can be extended to punctured RM codes. If operation 1 is applied on , and operations 1 and 2 are applied on , then we can relax the relation between and as . It follows from the same arguments that the resulting CSS code is preserved by with the same constraint on as described in (131). This family contains the triorthogonal codes described in [9].
Remark 16 (QRM Codes).
We now illustrate Theorem 7 and Theorem 12 through two CSS codes preserved by , one with a single logical qubit, the other with multiple logical quibts.
Example 6 (The punctured quantum Reed-Muller code [24, 10]).
Consider the CSS() code defined by and , with the first coordinate removed in both and . It is well-known [10, 35] that preserves the CSS codespace when the signs of -stabilizers are trivial. Since , for and for ), the code satisfies the divisibility conditions in Theorem 12. We compute the induced logical operator by computing the generator coefficients for the zero syndrome. Note that . The weight enumerators of and are given by
We have
| (152) |
The constraint on generator coefficients in (119) is satisfied:
It follows from (121) that the logical operator induced by is
Example 7 (The code).
The color code [14] is defined on qubits which we identify with vertices of the cube. All vertices participate in the X-stabilizer and generators of the Z-stabilizers can be identified with 4 independent faces of the cube. The signs of all the stabilizers are positive. The color code can also be thought as a Reed-Muller CSS() code with generator matrix
| (158) |
The code can be used in magic state distillation for the controlled-controlled- (CCZ) gate in the third-level of Clifford hierarchy. To verify that the code is preserved by and the induced logical operator is CC (up to some logical Pauli ), we first compute the generator coefficients corresponding to the trivial syndrome. The weight enumerators of and for are given by
so that
| (159) |
for all the seven non-zero . Then,
so (119) holds, and the induced logical operator is
| (160) |
5.2.2 Generator Coefficients and Trigonometric Identities
When for some integer , Rengaswamy et al. [35] derived necessary and sufficient conditions for a stabilizer code to be invariant under . This derivation depends on prior work characterizing conjugates of arbitrary Pauli matrices by [36]. The necessary and sufficient conditions provided in [35, Theorem 17] are expressed as two types of trigonometric identity. We now show that our constraint on generator coefficients is equivalent to the first trigonometric identity, and that the second trigonometric identity follows from the first. Our main tool is the MacWilliams Identities [27], and our analysis extends from CSS codes to general stabilizer codes.
We demonstrate equivalence through a sequence of three lemmas.
Lemma 17.
Given a CSS() code, let and . For all nontrivial , define . Let . Then, (119) holds if and only if for all non-zero
| (161) |
Proof.
See Appendix C.9. ∎
The support of a binary vector is the set of coordinates for which the corresponding entry is non-zero. Given two binary vectors , , we write to mean that the support of is contained in the support of . Let be the support of . We define to be the truncated binary vector that drops all the coordinates outside . Given a space , we denote . The next lemma finds equivalent representations of the cosets for non-zero .
Lemma 18.
Given a CSS() code, define and as above. For any non-zero , define and . Define (resp. ) by adding all the zero coordinates outside back into (resp. ). Note that . Define such that . Then for all nontirvial ,
| (162) |
Proof.
See Appendix C.10. ∎
Lemma 19.
Given a CSS() code, let , and define , , , , as above. Recall that . For any and any nontrivial ,
| (163) |
if and only if
| (164) |
Proof.
See Appendix C.11. ∎
Theorem 20.
The unitary realizes a logical operation on the codespace of an CSS() code if and only if for all non-zero ,
| (165) |
Proof.
Remark 21.
Rengaswamy [35, Theorem 17] derived a pair of necessary and sufficient conditions for a CSS code to be invariant under . Theorem 20 shows that the first of these conditions implies the second and also generalizes the first condition to arbitrary angle . Note that the trigonometric conditions are local whereas the square sum constraint on generator coefficients is global.
6 Conclusion
We have introduced a framework that describes the process of preparing a code state, applying a diagonal physical gate, measuring a code syndrome, and applying a Pauli correction. We have described the interaction of code states and physical gates in terms of generator coefficients determined by the induced logical operator, and have shown that this interaction depends strongly on the signs of -stabilizers in a CSS code. We have derived necessary and sufficient conditions for a diagonal gate to preserve the code space of a CSS code, and have provided an explicit expression of its induced logical operator. When the diagonal gate is a transversal -rotation through an angle , we derived a simple global condition that can be expressed in terms of divisibility of weights in the two classical codes that determine the CSS code. When all signs in the CSS code are positive, we have proved the necessary and sufficient conditions for Reed-Muller component codes to construct families of CSS codes invariant under transversal Z-rotation through . It remains open to investigate the constraints for a CSS code determined by two classical decreasing monomial codes to be invariant under transversal -rotation.
The generator coefficient framework provides a tool to analyze the evolution under any given diagonal gate of stabilizer codes with arbitrary signs, and we are working to characterize more valid CSS codes can be used in magic state distillation.
Acknowledgement
We would like to thank Ken Brown, Dripto Debroy, and Felice Manganiello for helpful discussions. Ken Brown suggested we look at the method of simulating coherent noise for surface codes described in [8], and this led to our generator coefficient framework, and its use in analyzing the average logical channel. Dripto Debroy encouraged us to interpret the decoherence-free subspace appearing in Example 2 in terms of entanglement of initial states and syndrome measurements. Felice Manganiello shared his construction of CSS codes with RM components that are preserved by a transversal gate, and this led to our construction of CSS codes with RM components that are preserved by transversal -rotations.
The work of the authors was supported in part by NSF under grants CCF-1908730 and CCF-2106213.
References
- [1] Jonas T. Anderson and Tomas Jochym-O’Connor. Classification of transversal gates in qubit stabilizer codes. Quantum Info. Comput., 16(9–10):771–802, Jul 2016. doi:10.26421/qic16.9-10-3.
- [2] Hussain Anwar, Earl T. Campbell, and Dan E Browne. Qutrit magic state distillation. New J. Phys., 14(6):063006, 2012. doi:10.1088/1367-2630/14/6/063006.
- [3] James Ax. Zeroes of polynomials over finite fields. Am. J. Math., 86(2):255–261, 1964. doi:10.2307/2373163.
- [4] Salman Beigi and Peter W Shor. , semi-Clifford and generalized semi-Clifford operations. Quantum Inf. Comput., 10(1&2), 2010. doi:10.26421/QIC10.1-2-4.
- [5] Ingemar Bengtsson, Kate Blanchfield, Earl T. Campbell, and Mark Howard. Order 3 symmetry in the Clifford hierarchy. J. Phys. A Math. Theor., 47(45):455302, 2014. doi:10.1088/1751-8113/47/45/455302.
- [6] Yuri L. Borissov. On Mceliece’s result about divisibility of the weights in the binary Reed-Muller codes. In Seventh International Workshop, Optimal Codes and related topics, pages 47–52, 2013. URL: http://www.moi.math.bas.bg/oc2013/a7.pdf.
- [7] P. Oscar Boykin, Tal Mor, Matthew Pulver, Vwani Roychowdhury, and Farrokh Vatan. On universal and fault-tolerant quantum computing: a novel basis and a new constructive proof of universality for shor’s basis. In 40th Annu. Symp. Found. Comput. Sci. (Cat. No.99CB37039), pages 486–494. IEEE, 1999. doi:10.1109/sffcs.1999.814621.
- [8] Sergey Bravyi, Matthias Englbrecht, Robert König, and Nolan Peard. Correcting coherent errors with surface codes. Npj Quantum Inf., 4(1):1–6, 2018. doi:10.1038/s41534-018-0106-y.
- [9] Sergey Bravyi and Jeongwan Haah. Magic-state distillation with low overhead. Phys. Rev. A, 86(5):052329, 2012. doi:10.1103/physreva.86.052329.
- [10] Sergey Bravyi and Alexei Kitaev. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A, 71(2):022316, 2005. doi:10.1103/physreva.71.022316.
- [11] Robert A. Calderbank, Eric M. Rains, Peter W. Shor, and Neil J.A. Sloane. Quantum error correction via codes over (4). IEEE Trans. Inf. Theory, 44(4):1369–1387, 1998. doi:10.1109/isit.1997.613213.
- [12] Robert A. Calderbank and Peter W. Shor. Good quantum error-correcting codes exist. Phys. Rev. A, 54:1098–1105, Aug 1996. doi:10.1103/physreva.54.1098.
- [13] Earl T. Campbell, Hussain Anwar, and Dan E Browne. Magic-state distillation in all prime dimensions using quantum Reed-Muller codes. Phys. Rev. X, 2(4):041021, 2012. doi:10.1103/physrevx.2.041021.
- [14] Earl T. Campbell and Mark Howard. Unified framework for magic state distillation and multiqubit gate synthesis with reduced resource cost. Phys. Rev. A, 95(2):022316, 2017. doi:10.1103/physreva.95.022316.
- [15] Shawn X. Cui, Daniel Gottesman, and Anirudh Krishna. Diagonal gates in the Clifford hierarchy. Phys. Rev. A, 95(1):012329, 2017. doi:10.1103/physreva.95.012329.
- [16] Dripto M. Debroy, Laird Egan, Crystal Noel, Andrew Risinger, Daiwei Zhu, Debopriyo Biswas, Marko Cetina, Chris Monroe, and Kenneth R. Brown. Optimizing stabilizer parities for improved logical qubit memories. Phys. Rev. Lett., 127(24), Dec 2021. doi:10.1103/physrevlett.127.240501.
- [17] Bryan Eastin and Emanuel Knill. Restrictions on transversal encoded quantum gate sets. Phys. Rev. Lett., 102(11):110502, 2009. doi:10.1103/physrevlett.102.110502.
- [18] Daniel Gottesman. Stabilizer codes and quantum error correction. California Institute of Technology, 1997. doi:10.48550/arXiv.quant-ph/9705052.
- [19] Daniel Gottesman. The heisenberg representation of quantum computers. arXiv preprint quant-ph/9807006, 1998. doi:10.48550/arXiv.quant-ph/9807006.
- [20] Daniel Gottesman and Isaac L. Chuang. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature, 402(6760):390–393, 1999. doi:10.1038/46503.
- [21] Jeongwan Haah. Towers of generalized divisible quantum codes. Phys. Rev. A, 97(4):042327, 2018. doi:10.1103/physreva.97.042327.
- [22] Jeongwan Haah and Matthew B. Hastings. Codes and protocols for distilling , controlled-, and toffoli gates. Quantum, 2:71, 2018. doi:10.22331/q-2018-06-07-71.
- [23] Jingzhen Hu, Qingzhong Liang, Narayanan Rengaswamy, and Robert Calderbank. Mitigating coherent noise by balancing weight- -stabilizers. IEEE Trans. Inf. Theory, 68(3):1795–1808, 2022. doi:10.1109/tit.2021.3130155.
- [24] Emanuel Knill, Raymond Laflamme, and Wojciech Zurek. Accuracy threshold for quantum computation. arXiv quant-ph/9610011, 1996. doi:10.48550/arXiv.quant-ph/9610011.
- [25] Anirudh Krishna and Jean-Pierre Tillich. Towards low overhead magic state distillation. Phys. Rev. Lett., 123(7):070507, 2019. doi:10.1103/physrevlett.123.070507.
- [26] Andrew J. Landahl and Chris Cesare. Complex instruction set computing architecture for performing accurate quantum rotations with less magic. arXiv preprint arXiv:1302.3240, 2013. doi:10.48550/arXiv.1302.3240.
- [27] Florence J. MacWilliams. A theorem on the distribution of weights in a systematic code. Bell Labs Tech. J., 42(1):79–94, January 1963. doi:10.1002/j.1538-7305.1963.tb04003.x.
- [28] Florence J. MacWilliams and Neil J. A. Sloane. The theory of error correcting codes, volume 16. Elsevier, 1977.
- [29] Robert J. McEliece. On periodic sequences from GF(). J. Comb. Theory Ser. A., 10(1):80–91, 1971. doi:10.1016/0097-3165(71)90066-5.
- [30] Robert J. McEliece. Weight congruences for p-ary cyclic codes. Discrete Math, 3(1):177–192, 1972. doi:10.1016/0012-365X(72)90032-5.
- [31] Sepehr Nezami and Jeongwan Haah. Classification of small triorthogonal codes. Phys. Rev. A, 106:012437, Jul 2022. doi:10.1103/PhysRevA.106.012437.
- [32] Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2011.
- [33] Tefjol Pllaha, Narayanan Rengaswamy, Olav Tirkkonen, and Robert A. Calderbank. Un-weyl-ing the Clifford hierarchy. Quantum, 4:370, 2020. doi:10.22331/q-2020-12-11-370.
- [34] Ben W. Reichardt. Quantum universality from magic states distillation applied to css codes. Quantum Inf. Process., 4(3):251–264, 2005. doi:10.1007/s11128-005-7654-8.
- [35] Narayanan Rengaswamy, Robert A. Calderbank, Michael Newman, and Henry D. Pfister. On optimality of CSS codes for transversal . IEEE J. Sel. Areas in Inf. Theory, 1(2):499–514, 2020. doi:10.1109/jsait.2020.3012914.
- [36] Narayanan Rengaswamy, Robert A. Calderbank, and Henry D. Pfister. Unifying the Clifford hierarchy via symmetric matrices over rings. Phys. Rev. A, 100(2):022304, 2019. doi:10.1103/physreva.100.022304.
- [37] A. M. Steane. Simple quantum error-correcting codes. Phys. Rev. A, 54(6):4741–4751, 1996. doi:10.1103/PhysRevA.54.4741.
- [38] Michael Vasmer and Aleksander Kubica. Morphing quantum codes. PRX Quantum, 3(3), Aug 2022. doi:10.1103/prxquantum.3.030319.
- [39] Christophe Vuillot and Nikolas P. Breuckmann. Quantum pin codes. IEEE Trans. Inf. Theory, 68(9):5955–5974, Sep 2022. doi:10.1109/tit.2022.3170846.
- [40] Mark M Wilde. Quantum information theory. Cambridge University Press, 2013.
- [41] Paolo Zanardi and Mario Rasetti. Noiseless quantum codes. Phys. Rev. Lett., 79(17):3306, 1997. doi:10.1103/PhysRevLett.79.3306.
- [42] Bei Zeng, Xie Chen, and Isaac L. Chuang. Semi-Clifford operations, structure of hierarchy, and gate complexity for fault-tolerant quantum computation. Phys. Rev. A, 77(4):042313, 2008. doi:10.1103/physreva.77.042313.
- [43] Bei Zeng, Andrew Cross, and Isaac L. Chuang. Transversality versus universality for additive quantum codes. IEEE Trans. Inf. Theory, 57(9):6272–6284, 2011. doi:10.1109/tit.2011.2161917.
Appendix A Magic State Distillation Using the Steane Code
We use the Steane code as an example to show the trade-off between fidelity and the probability of success in magic state distillation. Classical magic state distillation post-selects on the trivial syndrome without considering the error correction. If we follow this procedure, then the Steane code can be used to distill the state with linear convergence as described in Case 1. In Case 2, we try to increase the probability of success by introducing error-correction instead of post-selecting on the trivial syndrome. In Case 3, we consider only correcting one of non-trivial syndromes.
Case 1: Reichardt [34] calculated error rate by tracking evolution of code states. The generator coefficient framework makes it possible to calculate the output error rate by tracking operators.
-
(i)
Encode to get the of the Steane codestate.
-
(ii)
Given seven copies of and ancillary qubits, we can realize the phsyical transversal with the help of Clifford gates and Pauli measurements. If the states are exact, the probability of observing the trivial syndrome is and the probability of observing each non-trivial syndrome is (Take in (114)). When the trivial syndrome is observed, it follows from Example 1 that the induced logical operator is . We then apply a physical representation of the logical hase gate to obtain . In practice, each of the input magic states is noisy. We assume dephasing noise: with the same probability of a Pauli error for each of the seven physical qubits. The probability of observing the trivial syndrome involves two terms. The first term captures the event that upon observing the trivial syndrome , the dephasing error is undetectable. The second term captures the event that upon observing the non-trivial syndrome , the dephasing error cancels the observed syndrome. The probability of success is given by
(166) (167) (168) (169) Note that the cosets corresponding to non-trivial syndromes have identical weight enumerators.
-
(iii)
If we observe the non-trivial syndrome , we declare failure and restart. Upon observing the trivial syndrome, we decode and the output mixed state is
(170) where
(171) (172) (173) The first term captures the event that upon observing the the trivial syndrome , the dephasing error acts as a -stabilizer (). The second captures the event that upon observing the the non-trivial syndrome , the dephasing error lies in (). In this case, the dephasing error appears as the error correction that maps back to the code space and results in a logical gate. We now write the output error rate as a function of the initial error rate , and calculate its Taylor expansion at
(174) This implies that the threshold for the initial error rate is (the same as [34]), while that of the code is [10].
Case 2: Note that probability of success in Case 1 is upper bounded by . It is natural to ask whether we may introduce error correction to increase the probability of success. It follows from (102) that we can choose proper corrections based on syndromes ( for ) to obtain the logical operator with probability if the physical transversal is exact. The output error-rate now becomes
| (175) |
The output error rate does not fall below the line in the positive orthant, and we say that the protocol does not converge.
Case 3: We balance Case 1 and Case 2 by implementing error correction for only one of the seven non-trivial syndromes, say . Although the probability of success increases slightly to
| (176) |
the prefactor of the linear term of the output error rate is greater than 1. We conclude that the protocol does not converge.
The same analysis can be performed for a code that is perfectly preserved by the transversal gate, such as the code. The analysis provides insight into the trade-off between the probability of success and the fidelity of the output magic states.
Appendix B Generator Coefficient Framework for Stabilizer codes
We described the generator coefficient framework for CSS code and we now extend it to arbitrary stabilizer codes. We consider a general stabilizer code generated by the matrix
| (180) |
where such that is the -component of and is the -component of . We assume that the row space of contains no non-zero vector with or . Assume the dimensions of , , and are respectively. Then, we have
| (181) |
where
| (182) |
| (183) |
Let . Then, as described below.
Then (60) becomes
| (184) |
and the generator coefficients of for the stabilizer code are given by
| (185) |
where and . These generalized generator coefficients inherit the properties described in Theorem 6, that is,
| (188) |
for . Grouping together the projectors and , we consider the new family of projectors
| (189) |
For , we write
| (190) |
and note that is a resolution of identity.
Replacing the resolution of identity by , we conclude that the generator coefficients describe the same average logical channel as in (93) and (94) since the logical Pauli for stabilizer codes can be chosen as up to a sign. Based on the description of the average logical channel, we study the conditions for the invariance of a stabilizer code as below.
Theorem 22.
Consider a general stabilizer code defined by (180). Consider , and we have . Then, a -unitary gate preserves (i.e. ) if and only if
| (191) |
Proof.
Theorem 23.
Proof.
From the construction of , the number of physical qubits does not change (). Also, follows from the fact that . It remains to show that the new -distance .
Assume there exists such that and , where is the Pauli weight (number of nontrivial Pauli matrices) defined by
| (194) |
Then, and , which implies that . Also by definition, we have and thus . However, by assumption the distance of is and thus has minimum weight , which is a contradiction. Therefore, . ∎
Remark 24.
Note that the values of generator coefficients are the same for the stabilizer code and the CSS code. The induced logical operator by remains the same. It follows from Theorem 23 that given an non-degenerate stabilizer code supporting a physical quantum (unitary) gate, there exists an equivalent CSS code (since the Pauli expansion of the physical gate has support only on Pauli , we only compare the distance of stabilizer code with the -distance of the equivalent CSS code) supporting the same operation. Note that a similar argument applies to .
Appendix C Proofs for All Results
C.1 Proof of Lemma 4
Setting , we have . Setting
| (195) |
and
| (196) |
we may rewrite (3.1) as
| (197) |
Since and , we have
| (198) |
We may apply the MacWilliams Identities to obtain
| (199) |
and similarly
| (200) |
We combine (199) and (200) to obtain
| (201) |
Similarly,
| (202) |
Since , it follows from (198), (201), (202) that
| (203) |
which completes the proof.∎
C.2 Derivation of (88)
| (204) |
where . ∎
C.3 Derivation of
Since there is only one logical qubit, is either zero or non-zero. It then follows from (76) and (77) that the effective physical operator corresponding to the syndrome is
| (205) |
Thus, if we observe the trivial syndrome, then the induced logical portion is
| (206) |
Since we also assume that one of the pair is real and the other is pure imaginary, we can consider as a -rotation with angle up to some logical Pauli :
| (209) |
with
C.4 Proof of Theorem 6
C.5 Derivation of (109)
| (212) |
where (212) follows from the fact . ∎
C.6 Proof of Theorem 7
Recall from (60) that simplifies to
| (213) |
C.7 Proof of Lemma 11
C.8 Proof of Theorem 12
C.9 Proof of Lemma 17
C.10 Proof of Lemma 18
We first show that . Let . Then, . Let . We observe
| (227) |
where the last step follows from . Since and , . We consider two cases. If , then and . Otherwise, . Then and . For both cases, . Thus, , which implies that . Then, we have .
It remains to show that . We observe that . Thus, which completes the proof. ∎