Detail-Preserving Transformer for Light Field Image Super-Resolution
Abstract
Recently, numerous algorithms have been developed to tackle the problem of light field super-resolution (LFSR), i.e., super-resolving low-resolution light fields to gain high-resolution views. Despite delivering encouraging results, these approaches are all convolution-based, and are naturally weak in global relation modeling of sub-aperture images necessarily to characterize the inherent structure of light fields. In this paper, we put forth a novel formulation built upon Transformers, by treating LFSR as a sequence-to-sequence reconstruction task. In particular, our model regards sub-aperture images of each vertical or horizontal angular view as a sequence, and establishes long-range geometric dependencies within each sequence via a spatial-angular locally-enhanced self-attention layer, which maintains the locality of each sub-aperture image as well. Additionally, to better recover image details, we propose a detail-preserving Transformer (termed as DPT), by leveraging gradient maps of light field to guide the sequence learning. DPT consists of two branches, with each associated with a Transformer for learning from an original or gradient image sequence. The two branches are finally fused to obtain comprehensive feature representations for reconstruction. Evaluations are conducted on a number of light field datasets, including real-world scenes and synthetic data. The proposed method achieves superior performance comparing with other state-of-the-art schemes. Our code is publicly available at: https://github.com/BITszwang/DPT.
Introduction
Light field (LF) imaging systems offer powerful capabilities to capture the 3D information of a scene, and thus enable a variety of applications going from photo-realistic image-based rendering to vision applications such as depth sensing, refocusing, or saliency detection. However, current light field cameras naturally face a trade-off between the angular and spatial resolution, that is, a camera capturing views with a high angular sampling typically at the expense of a limited spatial resolution, and vice versa. This limits the practical applications of LF, and also motivates many efforts to study super-resolution along the angular dimension (i.e., to synthesize new views) or the spatial dimension (i.e., to increase the spatial resolution). Our work focuses on the latter one.
In comparison with the traditional 2D photograph that only records the spatial intensity of light rays, a light field additionally collects the radiance of light rays along with different directions, offering a multi-view description of the scene. A naive solution of light field super-resolution (LFSR) is to super-resolve each view independently using single image super-resolution (SISR) techniques. However, despite the recent progress of SISR, the solution is sub-optimal mainly because it neglects the intrinsic relations (i.e., angular redundancy) of different light field views, possibly resulting in angularly inconsistent reconstructions. To address this, many studies exploit complementary information captured by different sub-aperture images for high-quality reconstruction. The seminal learning-based method, i.e., (Yoon et al. 2015), directly stacks 4-tuples of sub-aperture images together as an input of a SISR model. Subsequent efforts develop more advanced techniques, e.g., to explore the geometric property of a light field in multiple network branches (Zhang, Lin, and Sheng 2019), to align the features of the center view and its surrounding views with deformable convolutions (Wang et al. 2021d), to encourage interactions between spatial and angular features for more informative feature extraction (Wang et al. 2020), to combinatorially learn correlations between an arbitrary pair of views for super-resolution (Jin et al. 2020), or to gain an efficient low-rank light field representation for restoration (Farrugia and Guillemot 2019).
Despite the encouraging results of these approaches, they are all based on convolutional network architectures, thus inherently lack strong capabilities to model global relations among different views of light field images. In light of the ill-posed nature of the super-resolution problem, we believe that an ideal solution should take into account as much informative knowledge in the LR input as possible.
Motivated by the above analysis, we propose, to the best of our knowledge, the first Transformer-based model to address LFSR from a holistic perspective. In stark contrast to existing approaches, our model treats each light field as a collection of sub-aperture image (SAI) sequences (captured along horizontal or vertical directions), and exploits self-attention to reveal the intrinsic geometric structure of each sequence. Despite the advantages of Transformers in long-range sequence modeling, it is non-trivial to apply vanilla Transformers (e.g., ViT (Dosovitskiy et al. 2020)) for super-resolution tasks, mainly because 1) they represent each input image with small-size (e.g., or ) patches (i.e., tokens), which may damage fundamental structures (e.g., edges, corners or lines) in images, and 2) the vanilla fully connected self-attention design focus on establishing long-range dependencies among tokens, however, ignoring the locality in the spatial dimension. To address these problems, we introduce spatial-angular locally-enhanced self-attention (SA-LSA), which strengths locality using convolutions first, then promotes non-local spatial-angular dependencies of each SAI sequence.
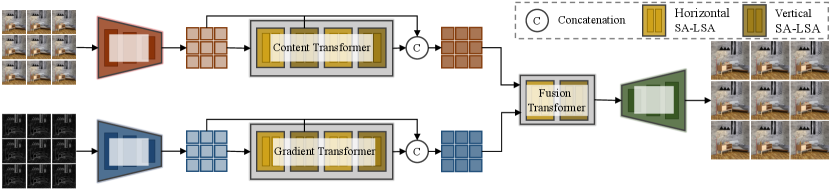
Based on SA-LSA, we design a novel Transformer-based LFSR model, i.e., DPT, which simultaneously captures local structures within each SAI and global structures of all SAIs in the light field. Concretely, DPT consists of a content Transformer and a gradient Transformer to learn spatial-angular dependencies within each light field and the corresponding gradient images, respectively. It is also equipped with a cross-attention fusion Transformer to aggregate feature representations of the two branches, from which a high-resolution light field is reconstructed.
In a nutshell, our contributions are three-fold: 1) We reformulate the problem of LFSR from a sequence-to-sequence learning perspective, which is differentiated to prior works in a sense that it fully explores non-local contextual information among all sub-aperture images, better characterizing geometric structures of light fields; 2) We design a spatial-angular locally-enhanced self-attention layer, which, in comparison with its vanilla fully-connected counterparts, offers our Transformer a strong ability to maintain crucial local context within light fields; 3) We finally introduce DPT as a novel Transformer-based architecture, which not only mines non-local contexts from multiple views, but also preserving image details for each single view. Our DPT demonstrates the promising performance on multiple benchmarks, while maintaining similar network parameters and computational cost as existing convolution-based networks.
Related Work
Light Field Super-Resolution. Early deep learning-based methods usually respectively learn the spatial and angular information with two independent subnetworks: one subnetwork captures the spatial information and another one learns the angular information. For example, (Yoon et al. 2017) adopted the SRCNN (Dong et al. 2014) to separately process each SAI for spatial super-resolution and interpolated novel views for angular super-resolution with the angular super-resolution network. (Yuan, Cao, and Su 2018) utilized a single image super-resolution network to enlarge the spatial resolution of each SAI, and applied the proposed EPI enhancement network to restore the geometric consistency of different SAIs. Recently, many researchers seek to simultaneously capture the spatial and angular information with a unified framework. (Wang et al. 2018) built a horizontal and a vertical recurrent network to respectively super-resolve 3D LF data. (Zhang, Lin, and Sheng 2019) stacked the SAIs from different angular directions as inputs and sent them to a multi-branch network to capture the spatial and angular information. (Wang et al. 2021d) used the deformable convolution (Dai et al. 2017) to align and aggregate the center-view and surrounding-view features to conduct LFSR. (Wang et al. 2020) developed a spatial-angular interaction network to learn the spatial-angular information from the macro-pixel image constructed with different SAIs. However, a major drawback of these approaches is that they fail to consider the long-range dependency among multiple SAIs in learning rich spatial-angular representations. To address this issue, we propose a Transformer based LFSR model, in which three proposed Transformers are leveraged to establish the non-local relationship of different SAIs for more effective representation learning.
Transformer for Image Super-Resolution. Attention-based models have demonstrated great successes in diverse vision tasks (Wang et al. 2021a; Zhou et al. 2020; Mou et al. 2021; Zhou et al. 2021a; Wang et al. 2021c, b; Zhou et al. 2021b) due to their powerful representative abilities. Some attention-based methods have been recently proposed to address the super-resolution tasks. These works can be roughly grouped into two categories: Transformer for single image super-resolution and Transformer for multiple image super-resolution. The former one mainly uses the Transformer to mine the intra-frame long-range dependency for high quality image reconstruction, i.e., IPT (Chen et al. 2021), SwinIR (Liang et al. 2021), and ESRT (Lu et al. 2021). The latter one adopts the Transformer to explore the inter-frame context information for accurate image reconstruction. i.e.,TTSR (Yang et al. 2020) for reference-based image super-resolution and VSR (Cao et al. 2021) for video super-resolution. Motivated by these approaches, we devise the first Transformer based architecture for LFSR.
Our Approach
Problem Formulation. We treat the task of LFSR as a high-dimensional reconstruction problem, in which each LF is represented as a 2D angular collection of sub-aperture images (SAIs). Formally, considering an input low-resolution LF as with angular resolution of and spatial resolution of , LFSR aims at reconstructing a super-resolved LF with the upsampling factor. Following (Yeung et al. 2018; Zhang, Lin, and Sheng 2019; Wang et al. 2020, 2021d), we consider the case that SAIs distribute in a square array, i.e., , where indicates the angular resolution along the horizontal or vertical direction.
Network Overview. The overall architecture of DPT is shown in Fig. 1. Given as the network input, we compute a gradient map for each 2D SAI, and organize them together as a gradient field . and are separately fed into two small CNNs for convolutional feature extraction, following by two unimodal Transformers (i.e., a content Transformer and a gradient Transformer) to learn richer feature representations. To better learn relevant visual patterns among different SAIs, we treat (or ) as a collection of horizontal and vertical angular sequences, and each sequence includes consecutive SAIs collected along one direction. Our content (or gradient) Transformer processes these sequences in (or ) one by one to avoid expensive computations as well as redundant interactions among irrelevant SAIs. Next, DPT aggregates the output features of the two Transformers via a cross-attention fusion Transformer, yielding a more comprehensive representation that is able to well preserve image details, which in final leads to better reconstruction.
In the following, we first provide a detailed description of DPT. Then, we elaborate on the proposed spatial-angular locally-enhanced self-attention layer, which is an essential component of our Transformer.
Detail-Preserving Transformer (DPT)
Convolutional Feature Extraction. Given the light field input as well as its gradient field , two CNNs and are leveraged to separately extract
| (1) | ||||
per-SAI embeddings and at spatial resolution and with embedding channel .
Content and Gradient Transformer. The convolutional feature embeddings (i.e., and ) capture local context within each SAI independently but lack global context across different SAIs. We use Transformers (Dosovitskiy et al. 2020) to enrich the embeddings with sequence-level context. We start by learning unimodal contextualized representations and using a content Transformer and a gradient Transformer :
| (2) | ||||
Note that the two transformers share the same network structure. For simplicity, we only describe in the following.
The is comprised of spatial-angular attention blocks. Each block includes two consecutive SA-LSA layers (detailed in the next section), which exploit global relations within each horizontal or vertical sequence of the input LF image, respectively.
In particular, in the -th block, we treat its input as a set of horizontal (or row-wise) sequences, i.e., , where indicates a sequence of convolutional features, corresponding to the -th row in the input. The first horizontal SA-LSA layer aims to explore the dependencies within each sequence independently. Specifically, for each horizontal sequence , we obtain a non-local representation as follows:
| (3) |
After processing all horizontal sequences in , we obtain a horizontal-enhanced content representation for the light field:
| (4) |
where ‘[ ]’ denotes the concatenation operation.
Next, the second vertical SA-LSA layer accepts as input, and explores the long-range relations of vertical (or column-wise) sequences, i.e., , where indicates sequences of convolutional features, corresponding to the -th column in . Similarly, the vertical sequences in are transformed via to produce a vertical-enhanced content representation :
| (5) |
where is the non-local representation of . Our content Transformer uses spatial-angular attention blocks to aggregate informative contextual knowledge among SAIs, eventually yielding a more comprehensive content representation .
Our gradient Transformer performs in a similar way as the content Transformer. It accepts as its input, and utilizes spatial-angular attention blocks to deliver a gradient representation .
Cross-Attention Fusion Transformer. While the content and gradient Transformers process each modality separately, we design a fusion Transformer to aggregate together their representations. To obtain more comprehensive unimodal representations, we obtain the inputs of fusion Transformer by combining all intermediate features in the content or gradient Transformers:
| (6) | |||
Different from and which capture non-local dependencies of tokens within the same sequence, our fusion Transformer aims to explore the relations between tokens of two sequences. In particular, for the -th horizontal (or vertical) sequences in and , i.e., and , the achieves a detail-preserved representation as:
| (7) |
The performs cross-attention between its inputs, with query generated from , key and value from , to gather high-frequency information as a compensation of the content representation. We concatenate the outputs together to obtain the fusion output . Note that our fusion Transformer only includes one spatial-angular attention block, and we see minor performance improvement when adding additional blocks.
SAI Reconstruction. Finally, we leverages a reconstruction module over to obtain a high-resolved LF :
| (8) |
Here, is separately applied to each SAI.
Remark. Our DPT employs Transformers to enrich convolutional features and (Eq. 2) into richer representations and , respectively, which are further aggregated together via a fusion Transformer. In this manner, our network is able to collect informative non-local contexts within each SAI and across different SAIs, allowing for higher-quality reconstruction.
In addition, our Transformers process each sequence (or sequence fusion) independently rather than directly process all sequences together. This enables our model to meet hardware resource constraints, and more importantly, avoid redundant interactions among irrelevant sub-aperture images.
In Transformer architectures (e.g., ViT (Dosovitskiy et al. 2020)), fully-connected self-attention is extensively employed to explore non-local interactions among input tokens. However, the vanilla self-attention layer neglects local spatial context within each input token, which is crucial for image reconstruction. To remedy this limitation, we introduce a spatial-angular locally-enhanced self-attention layer to offer our Transformer a strong capability in modeling locality.
Spatial-Angular Locally-Enhanced Self-Attention
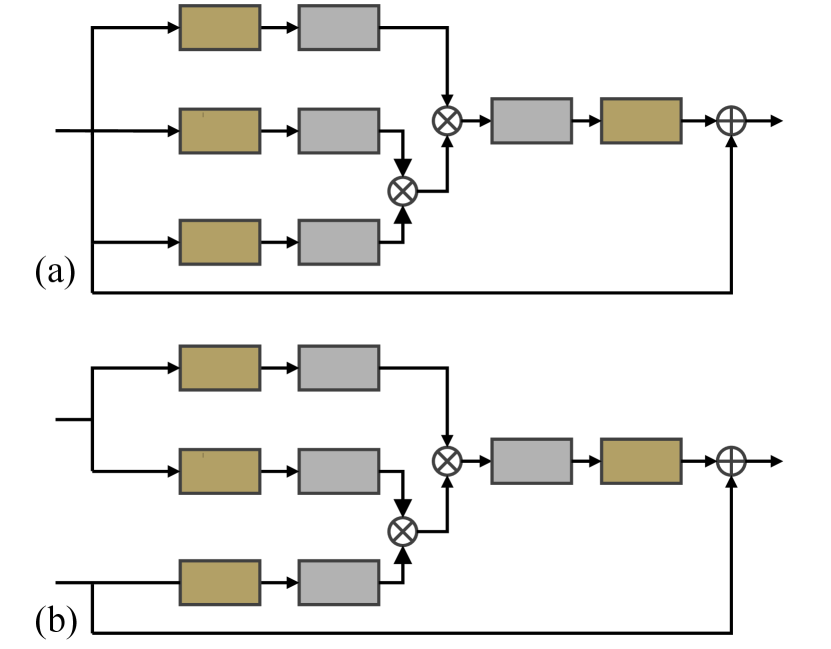
Inspired by VSR (Cao et al. 2021), our SA-LSA layer includes three sequential operations: spatial-angular convolutional tokenization, spatial-angular self-attention, as well as spatial-angular convolutional de-tokenization. Its structure is illustrated in Fig. 2 (a).
Spatial-Angular Convolutional Tokenization. ViT-like architectures (Dosovitskiy et al. 2020) leverage a linear projection layer to achieve input tokens at a very early stage. In contrast, our proposed convolutional tokenization mechanism obtains the tokens in the self-attention layer, yielding a multi-stage hierarchy like CNNs. This allows our Transformer to capture local contexts from low-level features to high-level semantic representations.
In particular, denote as the spatial-angular representation of an angular sequence, where is the length of the sequence, denotes feature dimension, and is the spatial dimension. The convolutional tokenization module generates query , key and value at each self-attention layer as follows:
| (9) |
It produces the inputs of a self-attention layer via two steps. First, the input is fed into three independent convolutional layers (i.e., , and ). We implement each layer with kernel size .
Next, a function is designed to obtain spatial-angular tokens. In particular, it extracts a collection of overlapping patches with size . Thus, we are able to obtain a sequence of tokens, and each token with a feature dimension .
Spatial-Angular Self-Attention. The fully-connected self-attention layer is applied on to explore the non-local spatial-angular relations among the tokens as follows:
| (10) |
where Attention denotes a standard self-attention layer as in (Vaswani et al. 2017; Dosovitskiy et al. 2020).
Spatial-Angular Convolutional De-Tokenization. To enable the application of convolutional tokenization in each self-attention layer, we further de-tokenize the attended feature sequence to fold the patches into a large feature map with the same dimension as :
| (11) |
where denotes the de-tokenization operation, and is a convolutional layer as Eq. 9. A residual layer is also used to avoid the loss of important features. Here, well encodes the local (in the spatial dimension) and global (in both spatial and angular dimensions) context of the input angular sequence, which could be expected to help produce better reconstruction results.
Note that in the fusion Transformer, we improve SA-LSA into a cross-attention SA-LSA layer to support the computation of cross-attention between the two modalities. Fig. 2 shows the detailed structure.
| Method | Scale | EPFL | HCInew | HCIold | INRIA | STFgantry |
|---|---|---|---|---|---|---|
| Bicubic | 29.50 / 0.9350 | 31.69 / 0.9335 | 37.46 / 0.9776 | 31.10 / 0.9563 | 30.82 / 0.9473 | |
| VDSR (Kim, Lee, and Lee 2016) | 32.50 / 0.9599 | 34.37 / 0.9563 | 40.61 / 0.9867 | 34.43 / 0.9742 | 35.54 / 0.9790 | |
| EDSR (Lim et al. 2017) | 33.09 / 0.9631 | 34.83 / 0.9594 | 41.01 / 0.9875 | 34.97 / 0.9765 | 36.29 / 0.9819 | |
| RCAN (Zhang et al. 2018) | 33.16 / 0.9635 | 34.98 / 0.9602 | 41.05 / 0.9875 | 35.01 / 0.9769 | 36.33 / 0.9825 | |
| LFBM5D (Alain and Smolic 2018) | 31.15 / 0.9545 | 33.72 / 0.9548 | 39.62 / 0.9854 | 32.85 / 0.9695 | 33.55 / 0.9718 | |
| GB (Rossi and Frossard 2018) | 31.22 / 0.9591 | 35.25 / 0.9692 | 40.21 / 0.9879 | 32.76 / 0.9724 | 35.44 / 0.9835 | |
| resLF (Zhang, Lin, and Sheng 2019) | 32.75 / 0.9672 | 36.07 / 0.9715 | 42.61 / 0.9922 | 34.57 / 0.9784 | 36.89 / 0.9873 | |
| LFSSR (Yeung et al. 2018) | 33.69 / 0.9748 | 36.86 / 0.9753 | 43.75 / 0.9939 | 35.27 / 0.9834 | 38.07 / 0.9902 | |
| LF-InterNet (Wang et al. 2020) | 34.14 / 0.9761 | 37.28 / 0.9769 | 44.45 / 0.9945 | 35.80 / 0.9846 | 38.72 / 0.9916 | |
| LF-DFnet (Wang et al. 2021d) | 34.44 / 0.9766 | 37.44 / 0.9786 | 44.23 / 0.9943 | 36.36 / 0.9841 | 39.61 / 0.9935 | |
| DPT (Ours) | 34.48 / 0.9759 | 37.35 / 0.9770 | 44.31 / 0.9943 | 36.40 / 0.9843 | 39.52 / 0.9928 | |
| Bicubic | 25.14 / 0.8311 | 27.61 / 0.8507 | 32.42 / 0.9335 | 26.82 / 0.8860 | 25.93 / 0.8431 | |
| VDSR (Kim, Lee, and Lee 2016) | 27.25 / 0.8782 | 29.31 / 0.8828 | 34.81 / 0.9518 | 29.19 / 0.9208 | 28.51 / 0.9012 | |
| EDSR (Lim et al. 2017) | 27.84 / 0.8858 | 29.60 / 0.8874 | 35.18 / 0.9538 | 29.66 / 0.9259 | 28.70 / 0.9075 | |
| RCAN (Zhang et al. 2018) | 27.88 / 0.8863 | 29.63 / 0.8880 | 35.20 / 0.9540 | 29.76 / 0.9273 | 28.90 / 0.9110 | |
| LFBM5D (Alain and Smolic 2018) | 26.61 / 0.8689 | 29.13 / 0.8823 | 34.23 / 0.9510 | 28.49 / 0.9137 | 28.30 / 0.9002 | |
| GB (Rossi and Frossard 2018) | 26.02 / 0.8628 | 28.92 / 0.8842 | 33.74 / 0.9497 | 27.73 / 0.9085 | 28.11 / 0.9014 | |
| resLF (Zhang, Lin, and Sheng 2019) | 27.46 / 0.8899 | 29.92 / 0.9011 | 36.12 / 0.9651 | 29.64 / 0.9339 | 28.99 / 0.9214 | |
| LFSSR (Yeung et al. 2018) | 28.27 / 0.9080 | 30.72 / 0.9124 | 36.70 / 0.9690 | 30.31 / 0.9446 | 30.15 / 0.9385 | |
| LF-InterNet (Wang et al. 2020) | 28.67 / 0.9143 | 30.98 / 0.9165 | 37.11 / 0.9715 | 30.64 / 0.9486 | 30.53 / 0.9426 | |
| LF-DFnet (Wang et al. 2021d) | 28.77 / 0.9165 | 31.23 / 0.9196 | 37.32 / 0.9718 | 30.83 / 0.9503 | 31.15 / 0.9494 | |
| DPT (Ours) | 28.93 / 0.9167 | 31.19 / 0.9186 | 37.39 / 0.9720 | 30.96 / 0.9502 | 31.14 / 0.9487 |
Detailed Network Architecture
Convolutional Feature Extraction. The convolutional modules and (Eq. 2) share a similar network structure. Following (Wang et al. 2021d), each of them consists of two residual blocks and two residual atrous spatial pyramid pooling blocks organized in an intertwine manner, following by an angular alignment module without using deformable convolution to align the convolutional features of different views.
Transformer Networks. In the content and gradient Transformers, we set the number of attention blocks to by default. For , Eq. 9 is slightly modified to enable the exploration of cross-attention by generating query from the content representation, while key and value from the gradient representation.
Reconstruction Module. The reconstruction module (Eq. 8) is implemented as a cascaded of five information multi-distillation blocks, following with a upsampling layer, which consists of a pixel shuffle operation combined with two convolution layers, to generate the super-resolved SAIs (Wang et al. 2021d).

Experiment
Datasets and Evaluation Metrics
We conduct extensive experiments on five popular LFSR benchmarks, i.e., EPFL (Rerabek and Ebrahimi 2016), HCInew (Honauer et al. 2016), HCIold (Wanner, Meister, and Goldluecke 2013), INRIA (Le Pendu, Jiang, and Guillemot 2018), and STFgantry (Vaish and Adams 2008). All of the light field images from the above benchmarks have a 99 angular resolution (i.e., ). PSNR and SSIM are chosen as the evaluation metrics. For a testing dataset with scenes, we first obtain the metric values of sub-aperture images, and average the summation results of to obtain the final metric score.
Implementation Details
Following (Wang et al. 2021d), we convert the light field images from the RGB space to the YCbCr space. Our model only super-resolves Y channel images, and uses the bicubic interpolation to super-resolve Cb and Cr channels images, respectively. The gradient maps are extracted from Y channel of each SAI along the spatial dimension with the function provided by (Ma et al. 2020). We perform and SR with angular resolution on all benchmarks. In the training stage, the patches are cropped from each sub-aperture image, and we apply the bicubic interpolation to generate and patches. We use random horizontal rotation, vertical rotation and rotation to augment the training data. Spatial and angular resolution are processed simultaneously for preserving the LF structure. The loss is used to optimize our network. We use the Adam optimizer to train our network, with a batch size of 8. The initial learning rate is set to and it will be halved every 15 epochs. We train the network for 75 epochs in total. All experiments are carried out on a single Tesla V100 GPU card.
Comparisons with State-of-the-Art
To evaluate the effectiveness of DPT, we compare it with the several state-of-the-art LFSR methods ( i.e., LFBM5D (Alain and Smolic 2018), GB (Rossi and Frossard 2018), resLF (Zhang, Lin, and Sheng 2019), LFSSR (Yeung et al. 2018), LF-InterNet (Wang et al. 2020), and LF-DFNet (Wang et al. 2021d)) and single image super-resolution methods ( i.e., VDSR (Kim, Lee, and Lee 2016), EDSR (Lim et al. 2017), and RCAN (Zhang et al. 2018)) on five LFSR benchmarks. Following (Wang et al. 2021d), we treat Bicubic upsampling as the baseline.
Quantitative Results. The quantitative performance comparisons are reported in Table 1. As seen, DPT achieves a promising performance in comparison with other methods. Single image super-resolution methods (i.e., VDSR (Kim, Lee, and Lee 2016), EDSR (Lim et al. 2017) and RCAN (Zhang et al. 2018)) super-resolve each view separately. DPT outperforms all of them, which can be attributed to its outstanding capability to capture the complementary information of different views.
Furthermore, compared with other CNN-based methods, e.g., resLF (Zhang, Lin, and Sheng 2019), LFSSR (Yeung et al. 2018), LF-InterNet (Wang et al. 2020), our DPT outperforms all of them for SR. The reason lies in that these methods are still weak in modeling global relations of different views. In contrast, our DPT can establish the global relations among different SAIs with the Transformer for efficient spatial-angular representations.
Specifically, compared with the current leading approach LF-DFNet (Wang et al. 2021d), DPT obtains superior results on EPFL (Rerabek and Ebrahimi 2016), HCIold (Wanner, Meister, and Goldluecke 2013) and INRIA (Le Pendu, Jiang, and Guillemot 2018) for SR. The reason is that, LF-DFNet only models the short-range dependencies between each side-view SAI and the center-view SAI, while our DPT explores long-range relations among all SAIs.
| Method | Scale | # Param (M) / FLOPs (G) | PSNR / SSIM |
|---|---|---|---|
| resLF | 2 | 6.35 / 37.06 | 32.75 / 0.9672 |
| LFSSR | 2 | 0.81 / 25.70 | 33.69 / 0.9748 |
| LF-InterNet | 2 | 4.80 / 47.46 | 34.14 / 0.9761 |
| LF-DFNet | 2 | 3.94 / 57.22 | 34.44 / 0.9766 |
| DPT (Ours) | 2 | 3.73 / 57.44 | 34.48 / 0.9759 |
| resLF | 4 | 6.79 / 39.70 | 27.46 / 0.8899 |
| LFSSR | 4 | 1.61 / 128.44 | 28.27 / 0.9080 |
| LF-InterNet | 4 | 5.23 / 50.10 | 28.67 / 0.9143 |
| LF-DFNet | 4 | 3.99 / 57.31 | 28.77 / 0.9165 |
| DPT (Ours) | 4 | 3.78 / 58.64 | 28.93 / 0.9167 |
| # | Content Transformer | Gradient Transformer | Fusion Mechanism | # Param (M) | PSNR / SSIM | ||
| Sum | Transformer (image) | Transformer (sequence) | |||||
| 1 | 3.99 | 28.77 / 0.9165 | |||||
| 2 | ✓ | 2.62 | 28.77 / 0.9142 | ||||
| 3 | ✓ | ✓ | ✓ | 3.72 | 28.86 / 0.9153 | ||
| 4 | ✓ | ✓ | ✓ | 3.75 | 28.81 / 0.9149 | ||
| 5 | ✓ | 3.83 | 28.72 / 0.9139 | ||||
| 6 | ✓ | ✓ | ✓ | 3.91 | 28.89 / 0.9157 | ||
| 7 | ✓ | ✓ | ✓ | 3.78 | 28.93 / 0.9167 | ||
Qualitative Results. Fig. 3 depicts some representative visual results of different approaches for SR. As seen, LF-InterNet (Wang et al. 2020) and LF-DFNet (Wang et al. 2021d) produce distorted results for the structures of the telescope stand in the Bicycle scene and the flowerbed edge in the Sculpture scene. In contrast, our DPT yields much better results, with all above regions being well preserved.
Computational Analysis. Table 2 provides a detailed analysis of the LFSR models in terms of parameters, FLOPs, and reconstruct accuracy on EPFL. Following (Wang et al. 2021d), we set the size of the input LF image as for the computation of the FLOPs. As can be seen, DPT shows the best trade-off between reconstruction accuracy and model efficiency. For SR, DPT has fewer parameters while better accuracy, in comparison with LF-DFNet (Wang et al. 2021d). This result further confirms the effectiveness of DPT, not only in better performance but also its efficiency.
Ablation Study
To gain more insights into our model, we conduct a set of ablative experiments on the EPFL dataset for SR. The results are reported in Table 3. We show in the st row the performance of baseline model (i.e., LF-DFNet (Wang et al. 2021d)), and the th row the results of our full model.
Content Transformer. We first investigate the effect of the content Transformer by constructing a network which is implemented with the convolution feature extraction module , content Transformer and the image reconstruction module . Its results are given in the 2nd row. We can see that the content Transformer itself can lead to a similar performance as the baseline model, however, our content Transformer has fewer parameters. This confirms that global relations among different views brought by the content Transformer are benefical to LFSR.
Gradient Transformer. Furthermore, we combine the gradient Transformer into the content Transformer, with the results being shown in the rd row. As we can see, by introducing the gradient Transformer, the performance of the content Transformer (the 2nd row) improves by 0.09dB in terms of PSNR and 0.0011 improvement in terms of SSIM, respectively. Moreover, the models with dual transformers (the 4th, the 6th and the 7th rows) outperform the model with only a content Transformer (the 2nd row), which further confirms the effectiveness of gradient Transformer. Finally, we replace the content Transformer and gradient Transformer of DPT with residual blocks while maintaining the network parameters almost unchanged. Its results are given in the 5th row. The dual branches in DPT are equivalent to two convolutional neural networks for feature extraction. As reported in Table 3, DPT has a 0.21 dB PSNR drop, demonstrating the effectiveness of the proposed Transformers.
Impact of Fusion Mechanism. To explore the effect of fusion mechanism for content and gradient feature aggregation, we construct two model variants, which generates the detailed-preserved representation in Eq. 7 by the element-wise summation (the 3rd row) and the Transformer for a single view non-local dependencies exploration (the 4th row), respectively. As can be observed, our cross-attention fusion Transformer (the 7th row) brings a promising performance improvement over the results of 3rd row and the 4th row in PSNR and SSIM, which is attributed to its effectiveness for the complementary non-local information exploration of the content and gradient features.
Efficacy of SA-LSA. We study the effect of the SA-LSA layers by replacing them with the vanilla fully-connected self-attention layers in DPT (the 6th row). As seen, the model with SA-LSA layers (the 7th row) obtains a better performance with fewer parameters, proving the effectiveness of local spatial context for SAI reconstruction.
Number of Attention Blocks . At last, we study the performance of DPT with respect to the number of spatial-angular attention blocks in the content Transformer (or the graidient Transformer). Table 4 reports the comparison results. As seen, DPT achieves the best results at . Thus, we choose as the default number of spatial-angular attention blocks in DPT.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| PSNR (dB) | 28.69 | 28.93 | 28.78 | 28.74 |
| # Param (M) | 2.89 | 3.78 | 5.00 | 6.56 |
Conclusion
This work proposes a Detail Preserving Transformer (DPT), as the first application of Transformer for LFSR. Instead of leveraging a vanilla fully-connected self-attention layer, we develop a spatial-angular locally-enhanced self-attention layer (SA-LSA) to promote non-local spatial-angular dependencies of each sub-aperture image sequence. Based on SA-LSA, we leverage a content Transformer and a gradient Transformer to learn spatial-angular content and gradient representations, respectively. The comprehensive spatial-angular representations are further processed by a cross-attention fusion Transformer to aggregate the output of the two Transformers, from which a high-resolution light field is reconstructed. We compare the proposed network with other state-of-the-art methods over five commonly-used benchmarks, and the experimental results demonstrate that it achieves favorable performance against other competitors.
References
- Alain and Smolic (2018) Alain, M.; and Smolic, A. 2018. Light field super-resolution via LFBM5D sparse coding. In ICIP, 2501–2505.
- Cao et al. (2021) Cao, J.; Li, Y.; Zhang, K.; and Van Gool, L. 2021. Video Super-Resolution Transformer. arXiv preprint arXiv:2106.06847.
- Chen et al. (2021) Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; and Gao, W. 2021. Pre-trained image processing transformer. In CVPR, 12299–12310.
- Dai et al. (2017) Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; and Wei, Y. 2017. Deformable convolutional networks. In ICCV, 764–773.
- Dong et al. (2014) Dong, C.; Loy, C. C.; He, K.; and Tang, X. 2014. Learning a deep convolutional network for image super-resolution. In ECCV, 184–199.
- Dosovitskiy et al. (2020) Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. 2020. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In ICLR.
- Farrugia and Guillemot (2019) Farrugia, R. A.; and Guillemot, C. 2019. Light field super-resolution using a low-rank prior and deep convolutional neural networks. IEEE TPAMI, 42(5): 1162–1175.
- Honauer et al. (2016) Honauer, K.; Johannsen, O.; Kondermann, D.; and Goldluecke, B. 2016. A dataset and evaluation methodology for depth estimation on 4d light fields. In ACCV, 19–34.
- Jin et al. (2020) Jin, J.; Hou, J.; Chen, J.; and Kwong, S. 2020. Light field spatial super-resolution via deep combinatorial geometry embedding and structural consistency regularization. In CVPR, 2260–2269.
- Kim, Lee, and Lee (2016) Kim, J.; Lee, J. K.; and Lee, K. M. 2016. Accurate image super-resolution using very deep convolutional networks. In CVPR, 1646–1654.
- Le Pendu, Jiang, and Guillemot (2018) Le Pendu, M.; Jiang, X.; and Guillemot, C. 2018. Light field inpainting propagation via low rank matrix completion. IEEE TIP, 27(4): 1981–1993.
- Liang et al. (2021) Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; and Timofte, R. 2021. SwinIR: Image restoration using swin transformer. arXiv preprint arXiv:2108.10257.
- Lim et al. (2017) Lim, B.; Son, S.; Kim, H.; Nah, S.; and Mu Lee, K. 2017. Enhanced deep residual networks for single image super-resolution. In CVPRW, 136–144.
- Lu et al. (2021) Lu, Z.; Liu, H.; Li, J.; and Zhang, L. 2021. Efficient Transformer for Single Image Super-Resolution. arXiv preprint arXiv:2108.11084.
- Ma et al. (2020) Ma, C.; Rao, Y.; Cheng, Y.; Chen, C.; Lu, J.; and Zhou, J. 2020. Structure-preserving super resolution with gradient guidance. In CVPR, 7769–7778.
- Mou et al. (2021) Mou, C.; Zhang, J.; Fan, X.; Liu, H.; and Wang, R. 2021. COLA-Net: Collaborative Attention Network for Image Restoration. IEEE TMM.
- Rerabek and Ebrahimi (2016) Rerabek, M.; and Ebrahimi, T. 2016. New light field image dataset. In 8th International Conference on Quality of Multimedia Experience, CONF.
- Rossi and Frossard (2018) Rossi, M.; and Frossard, P. 2018. Geometry-consistent light field super-resolution via graph-based regularization. IEEE TIP, 27(9): 4207–4218.
- Vaish and Adams (2008) Vaish, V.; and Adams, A. 2008. The (new) stanford light field archive. Computer Graphics Laboratory, Stanford University, 6(7).
- Vaswani et al. (2017) Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A. N.; Kaiser, Ł.; and Polosukhin, I. 2017. Attention is all you need. In NeurIPS, 5998–6008.
- Wang et al. (2021a) Wang, S.; Zhou, T.; Lu, Y.; and Di, H. 2021a. Contextual Transformation Network for Lightweight Remote Sensing Image Super-Resolution. IEEE TGRS.
- Wang et al. (2021b) Wang, W.; Zhou, T.; Qi, S.; Shen, J.; and Zhu, S.-C. 2021b. Hierarchical human semantic parsing with comprehensive part-relation modeling. IEEE TPAMI.
- Wang et al. (2021c) Wang, W.; Zhou, T.; Yu, F.; Dai, J.; Konukoglu, E.; and Van Gool, L. 2021c. Exploring Cross-Image Pixel Contrast for Semantic Segmentation. In ICCV, 7303–7313.
- Wang et al. (2018) Wang, Y.; Liu, F.; Zhang, K.; Hou, G.; Sun, Z.; and Tan, T. 2018. LFNet: A novel bidirectional recurrent convolutional neural network for light-field image super-resolution. IEEE TIP, 27(9): 4274–4286.
- Wang et al. (2020) Wang, Y.; Wang, L.; Yang, J.; An, W.; Yu, J.; and Guo, Y. 2020. Spatial-angular interaction for light field image super-resolution. In ECCV, 290–308.
- Wang et al. (2021d) Wang, Y.; Yang, J.; Wang, L.; Ying, X.; Wu, T.; An, W.; and Guo, Y. 2021d. Light field image super-resolution using deformable convolution. IEEE TIP, 30: 1057–1071.
- Wanner, Meister, and Goldluecke (2013) Wanner, S.; Meister, S.; and Goldluecke, B. 2013. Datasets and benchmarks for densely sampled 4D light fields. In Vision, Modelling and Visualization, volume 13, 225–226.
- Yang et al. (2020) Yang, F.; Yang, H.; Fu, J.; Lu, H.; and Guo, B. 2020. Learning texture transformer network for image super-resolution. In CVPR, 5791–5800.
- Yeung et al. (2018) Yeung, H. W. F.; Hou, J.; Chen, X.; Chen, J.; Chen, Z.; and Chung, Y. Y. 2018. Light field spatial super-resolution using deep efficient spatial-angular separable convolution. IEEE TIP, 28(5): 2319–2330.
- Yoon et al. (2017) Yoon, Y.; Jeon, H.-G.; Yoo, D.; Lee, J.-Y.; and Kweon, I. S. 2017. Light-field image super-resolution using convolutional neural network. IEEE SPL, 24(6): 848–852.
- Yoon et al. (2015) Yoon, Y.; Jeon, H.-G.; Yoo, D.; Lee, J.-Y.; and So Kweon, I. 2015. Learning a deep convolutional network for light-field image super-resolution. In ICCVW.
- Yuan, Cao, and Su (2018) Yuan, Y.; Cao, Z.; and Su, L. 2018. Light-field image superresolution using a combined deep CNN based on EPI. IEEE SPL, 25(9): 1359–1363.
- Zhang, Lin, and Sheng (2019) Zhang, S.; Lin, Y.; and Sheng, H. 2019. Residual networks for light field image super-resolution. In CVPR, 11046–11055.
- Zhang et al. (2018) Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; and Fu, Y. 2018. Image super-resolution using very deep residual channel attention networks. In ECCV, 286–301.
- Zhou et al. (2020) Zhou, T.; Li, J.; Wang, S.; Tao, R.; and Shen, J. 2020. Matnet: Motion-attentive transition network for zero-shot video object segmentation. IEEE TIP, 29: 8326–8338.
- Zhou et al. (2021a) Zhou, T.; Li, L.; Li, X.; Feng, C.-M.; Li, J.; and Shao, L. 2021a. Group-Wise Learning for Weakly Supervised Semantic Segmentation. IEEE TIP.
- Zhou et al. (2021b) Zhou, T.; Qi, S.; Wang, W.; Shen, J.; and Zhu, S.-C. 2021b. Cascaded parsing of human-object interaction recognition. IEEE TPAMI.