Determination of Chain Strength induced by Embedding in D-Wave Quantum Annealer
Abstract
The D-wave quantum annealer requires embedding with ferromagnetic (FM) chains connected by several qubits, because it cannot capture exact long-range coupling between qubits, and retains the specific architecture that depends on the hardware type. Therefore, determination of the chain strength required to sustain FM order of qubits in the chains is crucial for the accuracy of quantum annealing. In this study, we devise combinatorial optimization problems with ordered and disordered qubits for various embeddings to predict appropriate values. We analyze the energy interval and between ground and first excited states in the combinatorial optimization problems without and with chains respectively, using the exact approach. We also measure the probability that the exact ground energy per site is observed in many simulated annealing shots. We demonstrate that the determination of is increasingly sensitive with growing disorder of qubits in the combinatorial optimization problems. In addition, the values of appropriate , where the values of are at a maximum, increase with decreasing . Finally, the appropriate value of is shown to be observed at approximately and in the ordered and disordered qubits, respectively.
pacs:
71.10.Fd,71.27.+a,71.30.+hI Introduction
The recent progress in quantum technology has brought about the dawn of quantum machines. Machines based on qubits rather than classical binary digits are being developed and built more frequently than ever Preskill2018 . One such machine is the D-wave quantum annealer (DQA) Johnson2011 . Unlike gate-type quantum machines using circuits, the DQA implements a quantum annealing (QA) process in the parameterized Hamiltonian of a transverse-field Ising model, composed of binary superconducting qubits Johnson2011 ; Kadowaki1998 . The primary advantage of this architecture is that it is much easier to add qubits than that in the case of gate-type quantum computers while maintaining the accuracy of results King2022 . Thus, the emerging DQA, which has seen rapid increments in qubit capacity, is catching up to the computational speed of the classical digit machine in an annealing process. Consequently, it has been extensively employed in combinatorial optimization problems requiring an annealing process as well as in the research of the Ising model, which shows unconventional phases at zero temperature Amin2018 ; Isakov2016 ; Mazzola2017 ; Inoue2021 ; Kairys2020 ; King2021 ; Irie2021 ; Park2022 ; Ronnow2014 ; Albash2018 ; Ronnow2014(1) .
However, the DQA cannot technically describe exact couplings between long distance qubits. It also retains specific architectures such as Pegasus and Kimera graphs dependent on DQA hardware types. These situations demand a physical embedding of the problem into the DQA, such that the architecture of the original problem topologically matches with one on the DQA Lanthaler2021 ; Konz2021 . Additionally, the chain with ferromagnetic (FM) coupling between several qubits necessitates that one variable in the architecture of the original problem be introduced in the embedding. Therefore, energetically competes with the coupling given in the original combinatorial optimization problem. The weak or strong induce the brokenness or the clustering of chains, respectively, which lower the accuracy of results measured by the DQA. This can be improved by appropriate selection of .
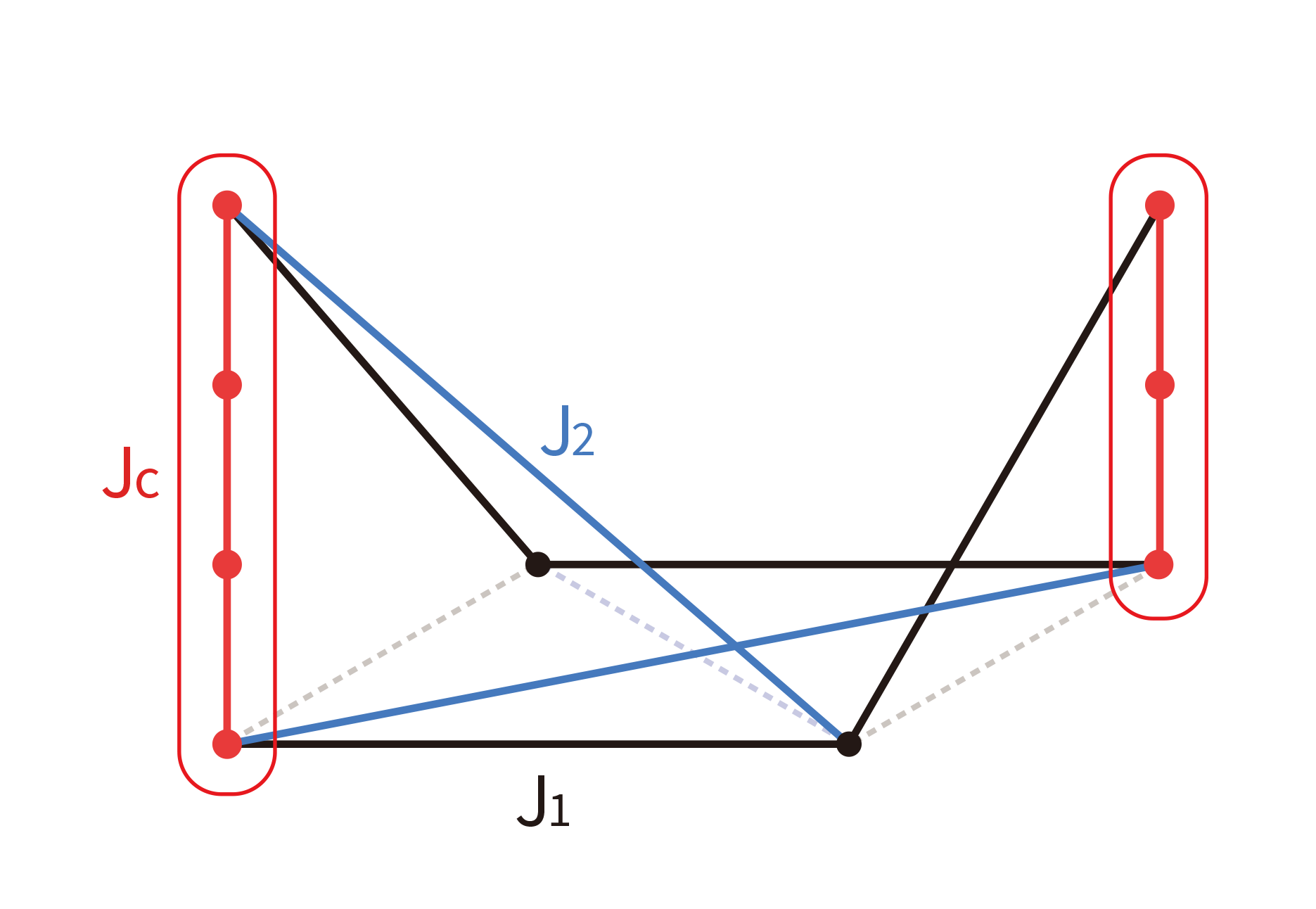
In this study, we devise artificial ordered and disordered systems to estimate the appropriate between qubits in the chains appearing in various embeddings. The qubits for the combinatorial optimization problem are put on two-dimensional (2D) square architecture. The chains are made on the three-dimensional (3D) -direction of the initially 2D architecture. The qubits in the original problem of 2D architecture are connected on edge qubits of the chains in the -direction. The devised systems cover all embeddings of 2D by adjustment of the composition of qubits in the chains. We consider the 2D frustrated and disordered Ising model as the combinatorial optimization problem, where the intervals between ground and first excited energies are systematically tuned by strength of frustration. Fig. 1 shows the schematic unit cell of qubits on two- dimensional (2D) square structure with the nearest-neighbor interaction of and diagonal-neighbor interaction of . The chains are marked as circles. We control various parameters such as the distance, position, and number of the chains to provide information of approximate in many cases. We analyze the energetic model without the constraint of the penalty function, through the exact and simulated annealing (SA) approaches Kirkpatrick1983 ; Santoro2002 .
We calculate the full energy spectrum in 2D ordered qubits with nine qubits in the chains using the exact method. We also analyze the probability happened exact ground energy per site in many SA shots in 2D ordered and disordered qubits with several chain strengths of various embeddings. We find that the energy gap between ground and first excited states in the combinatorial optimization problem with chains of DQA are systematically controlled by in the ordered qubits. We confirm that is less sensitive in the ordered combinatorial optimization problem with large , while it is highly sensitive in the disordered one with . We confirm that the most appropriate , with the maximum values of for stable QA, increases with decreasing . Finally, we find that it occurs at and in the ordered phase and disordered phase, respectively, with .
The paper is organized as follows: Section II gives a detailed description of the combinatorial optimization problem with ordered and disordered qubits for various embeddings. In Section III, we predict for various parameters of the chains via exact and SA tools, and discuss results. Finally, we present the conclusions in Section IV.
II Artificial combinatorial optimization model for Embedding
The Hamiltonian of the DQA is given as
| (1) |
where and are the parts of the combinatorial optimization problem and the chain, respectively. Here, is expressed as
| (2) |
where means the chain coupling of FM order between and qubits and is the number of qubits at the chain of -site. The total number of qubits in all chains is given as . Unlike the realistic DQA with a specific architecture of qubits such as the Pegasus graph, we put the qubits of the combinatorial optimization problem and of the chains in on a 2D square lattice and in in the 3D -direction, respectively. These architectures cover all embeddings of 2D by control of the composition and number of qubits in the chains. To account for various embeddings, and are randomly selected in the and in the size of , respectively.
To estimate appropriate , as a simple example we consider the combinatorial optimization problem with the frustrated and disordered qubits tuned by diagonal couplings. The Hamiltonian of the combination optimization problem is defined as
| (3) |
where nearest- and diagonal-neighbors are denoted by and , respectively. The qubits of Eq. (3) without chains display the antiferromagnetic (or PM) and stripe orders for and at zero temperature, respectively Jin2012 ; Jin2013 . The value of systematically tunes . Note that another gap appears in the full DQA Hamiltonian in Eq. (1), where controls . The total number of qubits used in the DQA computation is . The total ground energy of Eq. (1) is given as .
III Result
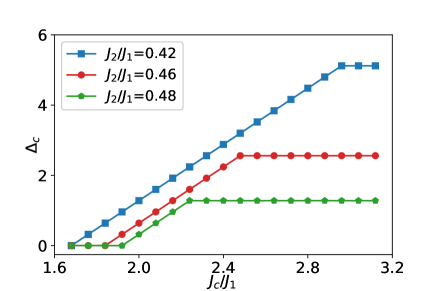
We first search for the critical chain strength occurred the chain brokenness in the 2D optimization problem with increasing the distance and number of the chains through exact approach. Surprisingly, we confirm that is not dependent on those of the chains in the regions of (or ) with antiferromagnetic (or PM) order of qubits. Fig. 2 shows as a function of for , and . Two kinks are evident in Fig. 2. with the first kink at are , and for , and , respectively. increases with increasing . The second kink when are , and , appears , and , respectively. of these are exactly equal to calculated by Eq. (3) without the chains. We propose that the brokenness and clustering of the chains would appear below and above , respectively. The regime between and expected the stable QA computations is shrinking with increasing . This relationship breaks down at the combinatorial optimization problem of fully frustrated qubits with .
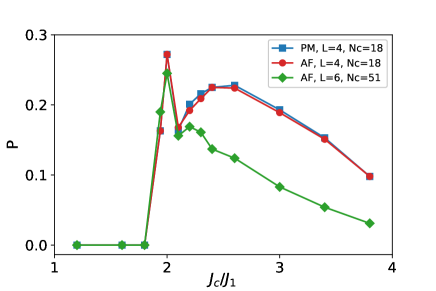
Next, we analyze the probability that is observed. This is done in many SA shots to confirm the validity of the exact results calculated above. Fig. 3 displays as a function of for and with PM and antiferromagnetic orders of qubits. PM and antiferromagnetic orders are observed at and , respectively. The positions and distances of the qubits in the chains are randomly selected in -site on the 2D qubits and on -direction of -site, respectively. used in Fig. 3 is and for and , respectively. As expected, in all cases, is zero at the brokenness state of the chains below the value of predicted by the exact results. Note that we do not insert of small values with the chain brokenness, which observe in the first or second excited states of the SA computations, in Fig. 3. gradually decreases in the clustering state of the chains above . The values of at PM order with are equal to those at antiferromagnetic order within numerical deviations. Overall, decreases with increasing and . The highest values of are observed at in all cases.
In the following section, we investigate why the highest peaks of are observed at in the stable QA region between the brokenness and clustering regions. We plot as a function of for , and in Fig. 4. Here, in terms of energy gaps, is equal to in the antiferromagnetic (or PM) regions. The values of in all cases are decreasing with increasing . They at are always higher than those at and , even though they converge at with a tiny . We surmise that is the optimized point without any bias between energy of the combinatorial optimization problem and the chain in Eq. (2) and Eq. (3), respectively.
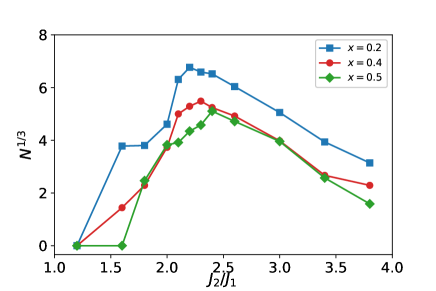
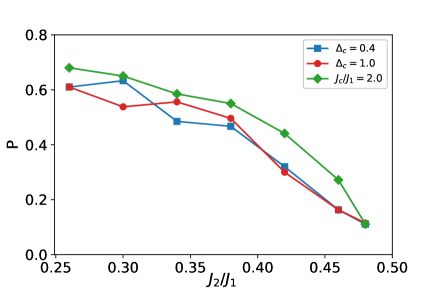
Finally, we would like to search for appropriate in the realistic DQA, because most combinatorial optimization problems would be described using disordered qubits, while the above results use ordered qubits. For disordered systems, we consider the combinatorial optimization problem with competition between antiferromagnetic and stripe orders of the qubits. For those, we introduce an ratio to select and in the diagonal bond of Eq. (3). For instance, and are selected according to the same ratio of in the maximally disordered states of the qubits. We count the number of cases where is observed in 2000 times SA shots. Fig 5 shows as a function of at for , and . The ordered and disordered qubits first appear at and , respectively. The maximally disordered qubits are seen at . The averaged energy of ensembles is , and for , and , respectively. As expected, the number of cases where is observed as a function of is much larger in the ordered qubits with than in the disordered ones with and . appeared the highest number of cases are , and for , and , respectively. This means that the determination of appropriate is increasingly sensitive with growing disorder and that the appropriate value of increases with increasing disorder. We guess that the appropriate is observed at approximately in the disordered qubits.
IV Conclusion
The DQA, with its recent rapid increase in qubit capacity, displays much potential and has been extensively applied in the solution of various combinatorial optimization problems. However, as a limitation, the physical embedding with FM chains of several qubits is required to consider exact long-range coupling between qubits ignored in the DQA. Brokenness and clustering of qubits in the chains lowers the accuracy of results measured by the DQA. To minimize this, appropriate determination of to keep the FM ordered qubits in the chains is crucial.
We designed the ordered and disordered qubits on the 2D square structure as the combinatorial optimization problem. The chains with FM ordered qubits were composed on the 3D -direction of the 2D architecture for examination of various embeddings. We used the exact method to compute the and , at which chain brokenness and clustering happened, respectively. We analyzed the probability that occurred in the combinatorial optimization problems with ordered and disordered qubits to estimate appropriate in various embeddings through the SA approach. We found that is less sensitive in the ordered qubits with large , while it is highly sensitive in the disordered ones with . In addition, we found that the most appropriate , with the maximum values of , increases with decreasing . Finally, we confirm that the appropriate is found at approximately and in the ordered and disordered qubits with , respectively.
We would like to note that before this work, we measured the qubit configurations of Eq. (3) using the DQA with 5000+ qubits composed on the Pegasus graph Park2022 . In our experience the QA on hardware shows stronger chain brokenness than SA on classical machine. Therefore, occasionally occurred within the chain brokenness phase, which is smaller than . Nevertheless, the overall tendency of measured by DQA is qualitatively consistent with that of computed by the SA approach.
V Acknowledgements
We would like to thank Hayun Park and Myeonghun Park for useful discussions. This work was supported by Ministry of Science through NRF-2021R1111A2057259. We acknowledge the hospitality at APCTP where part of this work was done.
References
- (1) J. Preskill, Quantum Computing in the NISQ era and beyond, Quantum 2, 79 (2018).
- (2) M. W. Johnson, M. H. S. Amin, S. Gildert, T. Lanting, F. Hamze, N. Dickson, R. Harris, A. J. Berkley, J. Johansson, P. Bunyk, et al., Quantum annealing with manufactured spins, Nature 473, 194 (2011).
- (3) Tadashi Kadowaki and Hidetoshi Nishimori, Quantum annealing in the transverse Ising model, Phys. Rev. E 58, 5355 (1998).
- (4) A.D. King, S. Suzuki, J. Raymond et al., Coherent quantum annealing in a programmable 2000 qubit Ising chain, Nature Phys. 102, 1745 (2022).
- (5) M.H. Amin, E. Andriyash, J. Rolfe, B. Kulchytskyy, and Roger Melko, Quantum Boltzmann Machine, Phys. Rev. X 8, 021050 (2018).
- (6) Sergei V. Isakov, Guglielmo Mazzola, Vadim N. Smelyanskiy, Zhang Jiang, Sergio Boixo, Hartmut Neven, and Matthias Troyer, Understanding Quantum Tunneling through Quantum Monte Carlo Simulations, Phys. Rev. Lett. 117, 180402 (2016).
- (7) Guglielmo Mazzola, Vadim N. Smelyanskiy, and Matthias Troyer, Quantum Monte Carlo tunneling from quantum chemistry to quantum annealing, Phys. Rev. B 96, 134305, (2017).
- (8) Inoue, D., Okada, A., Matsumori, T. et al., Traffic signal optimization on a square lattice with quantum annealing, Sci Rep 11, 3303 (2021).
- (9) Paul Kairys, Andrew D. King, Isil Ozfidan, Kelly Boothby, Jack Raymond, Arnab Banerjee, and Travis S. Humble, Simulating the Shastry-Sutherland Ising Model Using Quantum Annealing, PRX Quantum 1, 020320 (2020).
- (10) King, A.D., Raymond, J., Lanting, T. et al., Scaling advantage over path-integral Monte Carlo in quantum simulation of geometrically frustrated magnets, Nat. Commun. 12, 1113 (2021).
- (11) Irie, H., Liang, H., Doi, T. et al. Hybrid quantum annealing via molecular dynamics. Sci Rep 11, 8426 (2021).
- (12) H. Park, and H. Lee, Frustrated Ising Model on D-wave Quantum Annealing Machine J. Phys. Soc. Jpn. 91, 074001 (2022).
- (13) Troels F. Ronnow, Zhihui Wang, Joshua Job, Sergio Boixo, Sergei V. Isakov, David Wecker, John M. Martinis, Daniel A. Lidar and Matthias Troyer, Defining and detecting quantum speedup, Science 345, 420 (2014).
- (14) Tameem Albash and Daniel A. Lidar, Demonstration of a Scaling Advantage for a Quantum Annealer over Simulated Annealing, Phys. Rev. X 8, 031016 (2018).
- (15) Boixo, S., Ronnow, T., Isakov, S. et al., Evidence for quantum annealing with more than one hundred qubits, Nature Phys 10, 218 (2014).
- (16) M. Lanthaler and W. Lechner, Minimal constraints in the parity formulation of optimization problems, New J. Phys. 23 083039 (2021).
- (17) M. S. Konz, W. Lechner, H. G. Katzgraber, and M. Troyer, Embedding Overhead Scaling of Optimization Problems in Quantum Annealing, PRX Quantum 2, 040322 (2021).
- (18) S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi, Optimization by simulated annealing, Science 220, 671 (1983).
- (19) Giuseppe E. Santoro, Roman Martonak, Erio Tosatti and Roberto Car, Theory of Quantum Annealing of an Ising Spin Glass, Science 295, No. 5564, 2427 (2002).
- (20) Songbo Jin, Arnab Sen, and Anders W. Sandvik, Ashkin-Teller Criticality and Pseudo-First- Order Behavior in a Frustrated Ising Model on the Square Lattice, Phys. Rev. Lett. 108, 045702 (2012).
- (21) Songbo Jin, Arnab Sen, Wenan Guo, and Anders W. Sandvik, Phase transitions in the frustrated Ising model on the square lattice, Phys. Rev. B 87, 144406 (2013).