Deterministic Leader Election Among Disoriented Anonymous Sensors
Abstract
We address the Leader Election (LE) problem in networks of anonymous sensors sharing no kind of common coordinate system. Leader Election is a fundamental symmetry breaking problem in distributed computing. Its goal is to assign value 1 (leader) to one of the entities and value 0 (non-leader) to all others.
In this paper, assuming disoriented anonymous sensors, we provide a complete characterization on the sensors positions to deterministically elect a leader, provided that all the sensors’ positions are known by every sensor.
More precisely, our contribution is twofold: First, assuming anonymous sensors agreeing on a common handedness (chirality) of their own coordinate system, we provide a complete characterization on the sensors positions to deterministically elect a leader. Second, we also provide such a complete chararacterization for sensors devoided of a common handedness.
Both characterizations rely on a particular object from combinatorics on words, namely the Lyndon Words.
Keywords: Distributed Leader Election, Sense of Direction, Chirality, Sensor Networks, Lyndon Words.
1 Introduction
In distributed settings, many problems that are hard to solve become easier to solve with a leader to coordinate the system. The problem of electing a leader among a set of computing units is then one of the fundamental tasks in distributed systems. The Leader Election (LE) Problem consists in distinguishing among a set of entities exactly one of them. The leader election problem is covered in depth in many books related to distributed systems, e.g., [Lyn96, San07].
The distributed systems considered in this paper are sensor networks. Sensor networks are dense wireless networks that are used to collect (to sense) environmental data such as temperature, sound, vibration, pressure, motion, etc. The data are either simply sent toward some data collectors or used as an input to perform some basic cooperative tasks. Wireless Sensor Networks (WSN) are emerging distributed systems providing diverse services to numerous applications in industries, manufacturing, security, environment and habitat monitoring, healthcare, traffic control, etc. WSN aim for being composed of a large quantity of sensors as small, inexpensive, and low-powered as possible. Thus, the interest has shifted towards the design of distributed protocols for very weak sensors, i.e., sensors requiring very limited capabilities, e.g., uniformity (or, homogeneity — all the sensors follow the same program —, anonymity — the sensors are a priori indistinguishable —, disorientation — the sensors share no kind of coordinate system nor common sense of direction.
However, in weak distributed environments, many tasks have no solution. In particular, the Pattern Formation problem for sensors having the additional capability of mobility is not always solvable. The Pattern Formation problem consists in the design of protocols allowing autonomous mobile sensors to form a specific class of patterns, e.g., [SY99, FPSW99, FPSW01, DK02, Kat05, DP07a, DLIP08]. Such mobile sensors are often referred to as robots or agents. In [FPSW99], the authors discuss whether the pattern formation problem can be solved or not according to the capabilities the robots are supposed to have. They consider the ability to agree on the direction and orientation of one axis of their coordinate system (North) (Sense of Direction) and a common handedness (Chirality). Assuming sense of direction, chirality, and Unlimited Visibility — each robot is able to locate all the robots —, they show that the robots can form any arbitrary pattern. Then, they show that with the lack of chirality, the problem can be solved in general with an odd number of robots only. With the lack of both sense of direction and chirality, the pattern formation problem is unsolvable in general.
In [FPSW01] and [DPV10], the authors show the fundamental relationship between the Pattern Formation problem and the Leader Election problem. In the first paper, it is shown that, for a group of robots, pattern formation problem cannot be solved if the robots cannot elect a leader. In the second one, the authors aim at knowing whether the reverse is true or not. In other words, if the robots can elect a leader, can they solve the pattern formation problem? The authors prove that this property holds for robots in the asynchronous model CORDA, provided the robots share the same chirality.
In [FPSW01], they show that under sense of direction and chirality, Leader Election can be solved by constructing a total order over the coordinates of all the agents. By contrast, with no sense of direction and lack of chirality, Leader Election is unsolvable (in general). Informally, the results in [FPSW99, FPSW01] come from the fact that starting from a totally symmetric configuration where the positions of the robots coincide with the vertice of a regular -gon, no robot can be distinguished. Nevertheless, no characterization of the geometric configurations allowing to elect a leader, among disoriented sensors, is given.
In a first approach, the possibility of electing a leader among disoriented sensors seems to be related to the absence of some kind of symmetry in the configuration. Besides, this way would be in line with the result of Angluin [Ang80] showing that, in uniform interconnected networks, the impossibility of breaking a possible symmetry in the initial configuration makes the leader election unsolvable deterministically. However, this approach does not turn out to be appropriate in our context. Indeed, as depicted in Figure 1, some symmetric configurations do not prevent the sensors from distinguishing a leader. This raises the following question : “Given a set of weak sensors scattered on the plane, what are the (minimal) geometric conditions to be able to deterministically agree on a single sensor?”
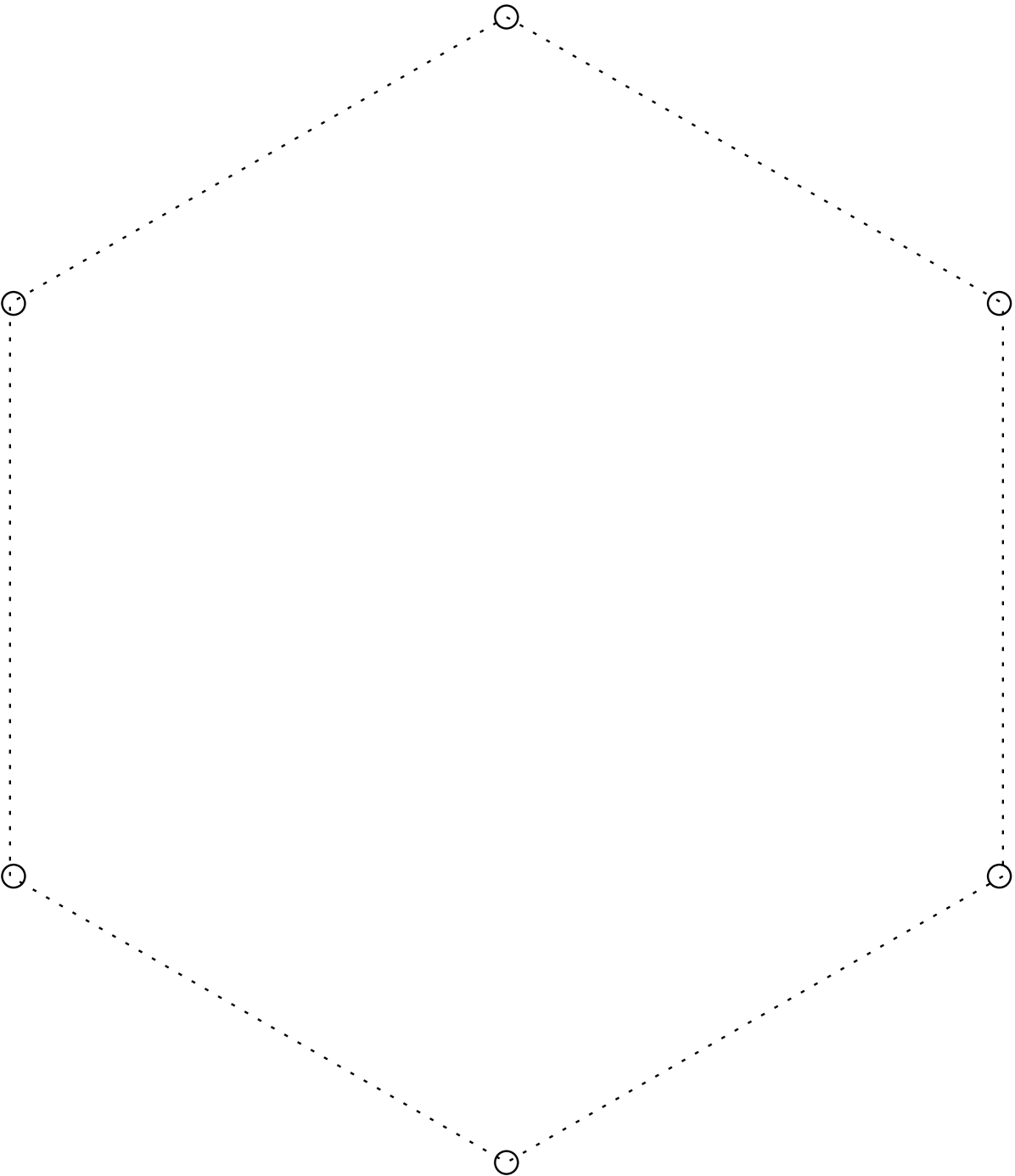
() Symmetric Configuration : a regular -gon
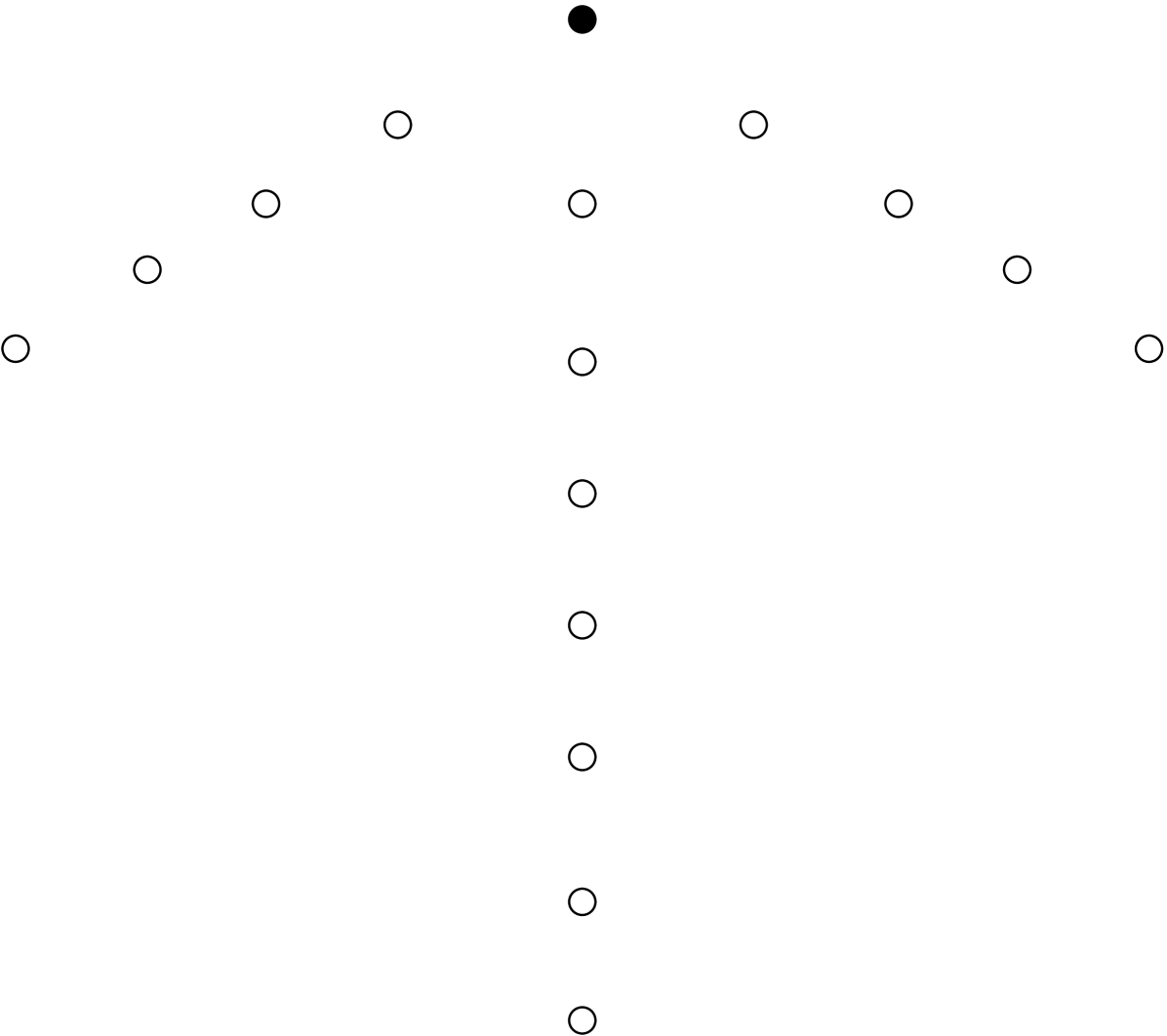
() Symmetric Configuration : an arrow
In this paper, this question is addressed under very weak assumptions: in particular, the sensors share no kind of common coordinate system. More precisely, they are not required to share any unit measure, common orientation or direction and even any common sense of rotation, say chirality.
We provide a complete characterization (necessary and sufficient conditions) on the sensors positions to deterministically elect a leader. Our result holds for any , provided that the sensors know all the positions and are able to make real computations. The sufficient condition is shown by providing a deterministic algorithm electing a leader.
The proof is based on the ability for the sensors to construct a Lyndon word from the sensors’ positions as an input. A Lyndon word is a non-empty word strictly smaller in the lexicographic order than any of its suffixes, except itself and the empty word. Lyndon words have been widely studied in the combinatorics of words area [Lot83]. However, only a few papers consider Lyndon words addressing issues in other areas than word algebra, e.g., [Che04, DR04, SM90, DP07a]. In [DP07a], we already showed the power of Lyndon words to build an efficient and simple deterministic protocol to form a regular -gon with a prime number of robots.
In the next section (Section 2), we formally describe the distributed model and the words considered in this paper. In Section 3, for convenience, we present a preliminary result assuming sensors with chirality. The lack of chirality is addressed in Section 4. Finally, we conclude this paper in Section 5.
2 Preliminaries
In this section, we define the distributed system considered in this paper. Next, we review some formal definitions and basic results on words and Lyndon words.
2.1 Model
Consider a set of sensors arbitrarily scattered on the plane such that no two sensors are located at the same position. A configuration is a set of positions occupied by the sensors. The sensors are uniform and anonymous, i.e, they all execute the same program using no local parameter (such as an identity) allowing to differentiate any of them. However, we assume that each sensor is a computational unit having the ability to determine the positions of the sensors within an infinite decimal precision. We assume no kind of communication medium. Each sensor has its own local - Cartesian coordinate system defined by two coordinate axes ( and ), together with their orientations, identified as the positive and negative sides of the axes.
In this paper, we assume that the sensors have no Sense of Direction and we discuss the influence of Chirality in a sensor network.
Definition 2.1 (Sense of Direction)
A set of sensors has sense of direction if the sensors agree on a common direction of one axis ( or ) and its orientation. The sense of direction is said to be partial if the agreement relates to the direction only —i.e., they are not required to agree on the orientation.
In Figure 2, the sensors have sense of direction in the cases () and (), whereas they have no sense of direction in the cases () and ().
Given an - Cartesian coordinate system, the handedness is the way in which the orientation of the axis (respectively, the axis) is inferred according to the orientation of the axis (resp., the axis).
Definition 2.2 (Chirality)
A set of sensors has chirality (or the sensors have chirality) if the sensors share the same handedness.
In Figure 2, the sensors have chirality in the cases () and (), whereas they have no chirality in the cases () and ().
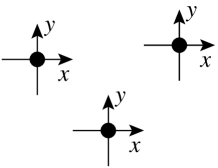
() Sense of Direction and Chirality
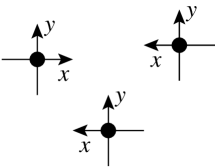
() Sense of Direction and No Chirality
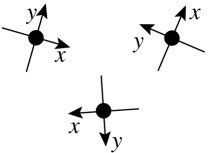
() No Sense of Direction and Chirality
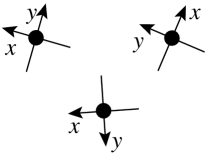
() No Sense of Direction and No Chirality
2.2 Words and Lyndon Words
Let an alphabet be a finite set of letters. A non empty word over is a finite sequence of letters , . The concatenation of two words and , denoted simply by , is equal to the word such that and . Let be the empty word such that for every word , . The length of a word , denoted by , is equal to the number of letters of ().
Suppose the alphabet is totally ordered by the relation . Then a word is said to be lexicographically smaller than or equal to a word , denoted by , iff there exists either a word such that or three words and two letters such that , , and . We write when and .
Let and be two positive integers. The power of a word is the word denoted by such that , and . A word is said to be primitive if and only if . Otherwise ( and ), is said to be strictly periodic.
The rotation of a word , notation , is defined by:
Note that .
Lemma 2.3
[Lot83] Let and be a word and a rotation of , respectively. The word is primitive if and only if is primitive.
A word is said to be minimal if and only if , .
Definition 2.4 (Lyndon Word)
A word is a Lyndon word if and only if is nonempty, primitive and minimal, i.e., and .
For instance, if , then , , , , are Lyndon words, whereas , and are not — is not minimal () and is not primitive ().
2.3 Leader Election.
The leader election problem considered in this paper is stated as follows: Given a configuration of sensors, the sensors are able to deterministically agree on a same sensor called the leader.
3 Leader Election with Chirality
In this section, we consider a sensor network having the property of chirality. The results we propose in this section have been presented in [DP07b].
In Subsection 3.1, we provide general definitions and establish some results with respect to configurations and words. We then show in Subsection 3.2 the relationship between the presence (the lack) of a leader and the existence (the absence) of a Lyndon word.
3.1 Configurations and Words
Given a configuration , denotes the smallest enclosing circle of the positions of the sensors in . The center of is denoted by . The distance from to any point on , the radius of , is denoted by . In any configuration , is unique and can be computed by any sensor in linear time [Meg83, Wel91]. It passes either through two of the positions that are on the same diameter (opposite positions), or through at least three of the positions in . Note that if , then passes both sensors and no sensor can be located inside , in particular at .
Given a smallest enclosing circle , the radii are the line segments from the center of to the boundary of . Let be the finite set of radii such that a radius belongs to iff at least one sensor is located on but . Denote by the number of radii in . In the sequel, we will abuse language by considering radii in only. Given two distinct positions and located on the same radius (), denotes the Euclidean distance between and .
Since and the set of positions are finite, the set of different distances between positions of sensors on the radii in is finite. Every robot codes each of these distances using a fonction such that the output of is a letter of an arbitrary alphabet provided with an order relation, and the code respects the natural order on distances (i.e. for letters , and distances , , if and only if ). A similar code is used for the angles in Definition 3.3.
Definition 3.1 (Radius Word)
Let be the position of , be the respective positions of sensors located on the same radius . Let be the radius word such that
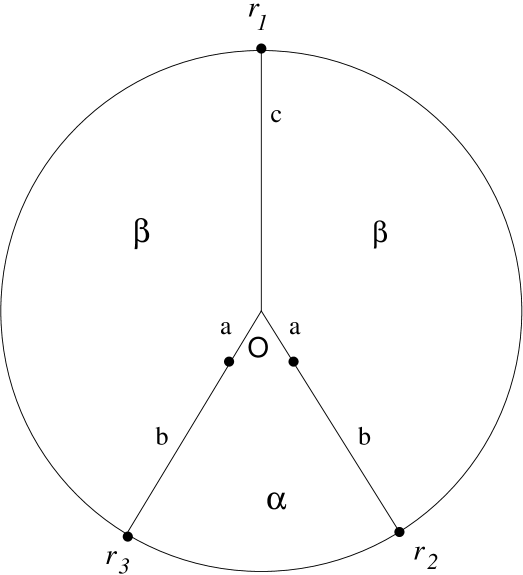
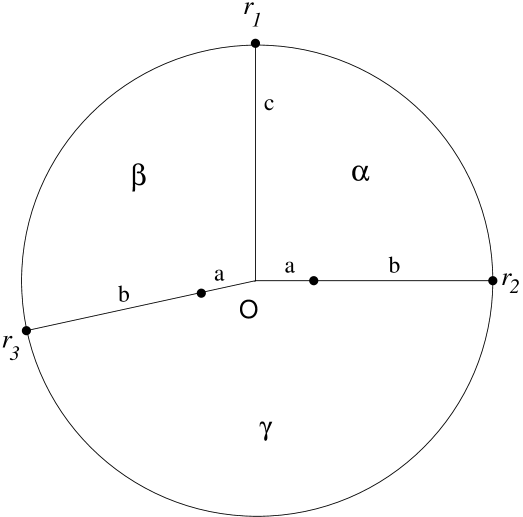
Note that all the distances are computed by each sensor with respect to its own coordinate system, i.e., proportionally to its own measure unit. So, for any radius , all the sensors compute the same word . For instance, in Figure 3, for every sensor, and .
Remark 3.2
If there exists one sensor on (), then for every radius , .
Denote by an arbitrary orientation of , i.e., denotes either the clockwise or the counterclockwise direction111Note that the clockwise (resp. counterclockwise) direction may be the counterclockwise (resp. clockwise) direction for the robots depending on their handedness. However, without loss of generality, we can assume that both directions are those we commonly use.. Given an orientation of , denotes the opposite orientation. Let be a radius in , the successor of in the direction, denoted by , is the next radius in , according to . The successor of , denoted by , is the radius such that , and . Given and its successor , denotes the angle between and following the direction.
Definition 3.3 (Configuration Word)
Let be a radius in . The configuration word of with respect to , an arbitrary orientation of , denoted by , is defined by:
such that, is the radius word of , is a code (similar as for the distances) of the angle between and its successor in following , and for every , being the successor of in following , is the radius word of and is the code of the angle between and its successor in following .
In the sequel, by abuse of language, we will refer to distances and angles without explicitely mentionning the code, to ease the reading.
In Figure 3, assuming that denotes the clockwise direction, then:
,
,
,
,
, and
.
Definition 3.4
A configuration of sensors is said to be periodic if there exists a rotation of center and of angle , such that , (i.e, the configuration is superimposed on ). Let be a configuration with no robot at the position . A construction of configuration words on is said to be period-free when the configuration words corresponding to are not periodic when is not periodic. In other words, if the configuration words corresponding to a configuration are strictly periodic, then is periodic.
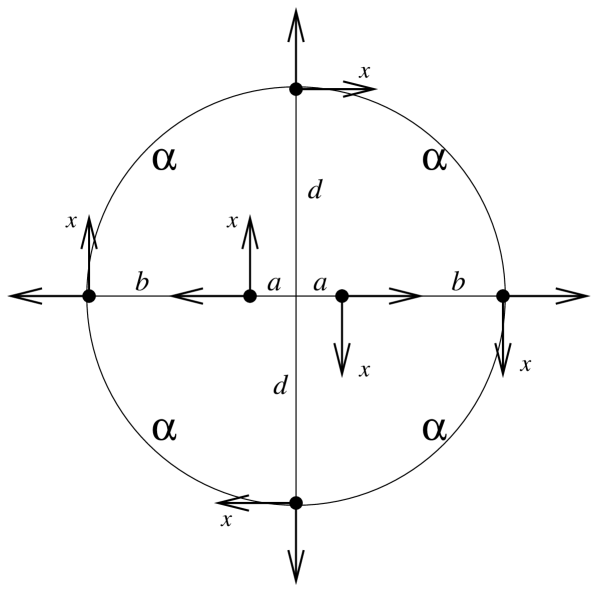
In Figure 4, configuration words are strictly periodic (we can distinct two configuration words, and ) and the figure is periodic since the set of positions of the sensors is preserved by the rotation of center and of angle .
Notice the following important fact, which is fondamental for the statement of the following results:
Remark 3.5
The construction of configuration words stated in Definition 3.3 is period-free.
Proof. Let be a configuration of sensors. If is strictly periodic for some radius , that is for some integer and a word , then there exists rotations , of center and of angle such that .
In this section, we consider sensors with chirality. In particular, they are able to agree on a common orientation of . Let be the set of configuration words computed by the sensors over according to . Since for every sensor, there is no ambiguity on , in the sequel of this section, we omit in the notations when it is clear in the context. For instance in Figure 3,
Remark 3.6
The following propositions are equivalent:
-
1.
There exists one sensor on
-
2.
For every radius ,
-
3.
Remark 3.7
Given an orientation , for every pair in , is a rotation of .
The lexicographic order on the set of radius words over is naturally built over the natural order on the set of codes of distances (we recall that is is compatible with the natural order on real numbers).
Definition 3.8
Let be the set of letters appearing in . Let and be any two letters in . Define the order over as follows:
The lexicographic order on is built over .
Lemma 3.9
Given an orientation , if there exist two distinct radii and in such that both and are Lyndon words (), then .
Proof. Assume by contradiction that, given an orientation , two distinct radii and exist such that both and are Lyndon words and . By Remark 3.6, there exists no sensor located at . By Remark 3.7, (respectively, ) is a rotation of (resp. ). So, by Definition 3.3, and . A contradiction.
Corollary 3.10
Given an orientation , if there exists (at least) one radius such that is a Lyndon word strictly greater than , then is unique.
3.2 Chirality, Leader Election and Lyndon Words
In this section, we show that the problems of the existence of a unique Lyndon word and of the existence of a deterministic Leader Election protocol are equivalent.
Lemma 3.11
If there exists such that is a Lyndon word, then the sensors are able to deterministically agree on a same sensor .
Proof. Directly follows from Corollary 3.10: If there is a sensor located on , then the sensors are able to agree on . Otherwise, there exists a single radius such that is a Lyndon word. In that case, all the sensors are able to agree on the sensor on that is the nearest one from .
Lemma 3.12
If there exists no radius such that is a Lyndon word, then there exists no deterministic algorithm allowing the sensors to agree on a same sensor .
Proof. Assume by contradiction that no radius exists such that is a Lyndon word and that there exists an algorithm allowing the sensors to deterministically agree on a same sensor . From Remark 3.6, there is no sensor located on , otherwise for all , would be a Lyndon word.
Let be a word in such that , . That is, is minimal. Assume first that is primitive. Then, is a Lyndon word that contradicts the assumption. So, is a strictly periodic word (there exist and such that ) and, from Lemma 2.3, we deduce that for all , is also strictly periodic. Since by Remark 3.5 our construction is period-free, this implies that the configuration is periodic. Thus, for every , there exists at least one radius such that and . So if an algorithm elects a leader on in a deterministical way, this algorithm distinguishes another leader on . In that case, cannot allow the sensors to deterministically agree on a same sensor .
Figure 4 presents an example of a configuration where the sensors have the same measure unit and their axis meets the radius on which they are located. In this case, no radius exists such that is a Lyndon word and, with respect to Lemma 3.12, sensors are not able to deterministically agree on a same sensor .
Theorem 3.13
Given a configuration of any number of disoriented sensors with chirality scattered on the plane, the sensors are able to deterministically agree on a same sensor if and only if there exists a radius such that is a Lyndon Word.
The acute reader will have noticed that when electing a leader is straightforward. On the other hand, when , it is impossible to elect a unique leader in a deterministic way: Our theorem confirms this fact as the two words obtained for the two radii are the same in such a configuration (actually each of both words consists in the concatenation of two identical letters).
4 Leader Election without Chirality
In this section, the lack of chirality among the sensors is considered. A first result presented in [DP07b] shows that the Configuration Word construction described in Section 3 is not enough to deal with an even number of sensors without chirality. We now show how to extend the Configuration Word so that we obtain a general characterization.
In Subsection 4.1, general definitions and results are given. They are then used to show in Subsection 4.2 the relationship between Leader Election and Lyndon words.
4.1 Words and Lack of Chirality
Devoid of chirality, the sensors are no longer able to agree on a common orientation of . In other words, with respect to their handedness, some of the sensors may assign to the actual clockwise direction, whereas some other may assign to the counterclockwise direction. As a consequence, given a radius and two sensors and on , the configuration word computed by may differ from the one computed by , depending on whether and share the same handedness or not. For instance, in Figure 3, the configuration word (as defined by Definition 3.3) is equal to either or , depending on the fact denotes the clockwise direction or the counterclockwise, respectively.
Furthermore, given a radius , if there exists a radius such that , then there exists an axial symmetry which corresponds to the bissectrix of . Otherwise (i.e., no radius exists such that ), no such axial symmetry exists. This observation leads us to provide the following definition in order to classify the radii.
Definition 4.1 (Type of symmetry)
A radius is of type (of symmetry) if there exists such that . Otherwise (when , that is there is no symmetry axis or the axis corresponds to the radius itself), is said to be of type . A radius of type is said to be -symmetric.
We use the type of symmetry to define the strong configuration word of any radius in as follows:
Definition 4.2 (Strong Configuration Word)
Let be a radius in . The strong configuration word of with respect to , an arbitrary orientation of , denoted by , is defined by:
such that, is the type of , is the radius word of , is the angle between and its successor in following , and for every , being the successor of in following , is the type of symmetry of , is the radius word of , and is the angle between and its successor in following .
Note that the (weak) configuration words used in Section 3 (Definition 3.3) could have been defined as strong configuration words by using Constant as type of symmetry, i.e., by mapping each letter to . We discuss this issue in more details in the next section.
Notice also that the construction of strong configuration words has obviously the same important property as the construction of weak configuration words:
Remark 4.3
The construction of strong configuration words stated in Definition 4.2 is period-free.
Definition 4.4 (Type of word)
A word is said to be of type if and only if its first letter is equal to for any .
Devoid of chirality, the sensors cannot agree on a common orientation of . So, for each radius , each sensor computes two strong configuration words, one for each direction, and . Let be the set of strong configuration words computed in both directions by the sensors for each radius in . In Figure 3, all the sensors compute the following set:
Remark 4.5
The following propositions are equivalent:
-
1.
There exists one sensor on
-
2.
For every radius ,
-
3.
Similarly to Section 3, we build the lexicographic order on the set of radius words over as follows:
Definition 4.6
Let be the set of letters appearing in . Let and be any two letters in . Define the order over as follows:
The lexicographic order on is built over .
The proof of the following lemma is similar to the one of Lemma 3.9:
Lemma 4.7
Given an orientation , if there exist two distinct radii and in such that both and are Lyndon words (), then .
Corollary 4.8
Given an orientation , if there exists (at least) one radius such that is a Lyndon word strictly greater than , then is unique.
4.2 Leader Election and Lyndon Words
Let be the subset of radii such that is a Lyndon word in the clockwise or in the counterclockwise orientation. Denote by the number of radii in .
Lemma 4.9
If for some orientation of in , there exists such that , then for all , and the leader is the sensor at the center of .
Note that Lemma 4.9 applies necessarily when . Indeed, this means that there exists at least two distinct radii and such that and are Lyndon words for a common orientation and by Lemma 3.9, this implies that , so that . So, in the remainder of this section, we study the case .
Lemma 4.10
If for all , , , and , the sensors are able to deterministically agree on a same sensor .
Proof. The leader is the nearest sensor to , on .
Note that, in this case, is necessarily -symmetric. An example of such a configuration is given by Figure 3: is a Lyndon word. The leader is the sensor on .
Lemma 4.11
If for all , , , and , the sensors are able to deterministically agree on a same sensor if and only if and are of type .
Proof. Without loss of generality we can consider that and are Lyndon words. We have three cases to consider:
-
1.
Radii and cannot be of different types. Assume by contradiction they can. Without loss of generality we can consider that is of type and is of type . So, from Definition 4.1, we deduce there is another radius of type which is also a Lyndon word. So, we would have three radii corresponding to a Lyndon word, which contradicts Corollary 4.8.
-
2.
For the same reason, if and are both -symmetric, then necessarily . In this case, if an algorithm elects a leader on in a deterministical way, this algorithm distinguishes another leader on —refer to Figure 5 for an example of such a configuration. So an algorithm cannot allow the sensors to deterministically agree on a same sensor .
-
3.
If and are both -symmetric, then . Without loss of generality, we can consider that . Then the sensors are able to deterministically agree on the sensor that is the nearest to on .
Example 4.12
Figure 5 shows a configuration where each radius is -symmetric; and so no leader exists. Notice that a case like this one can occur only when the number of sensors is even.
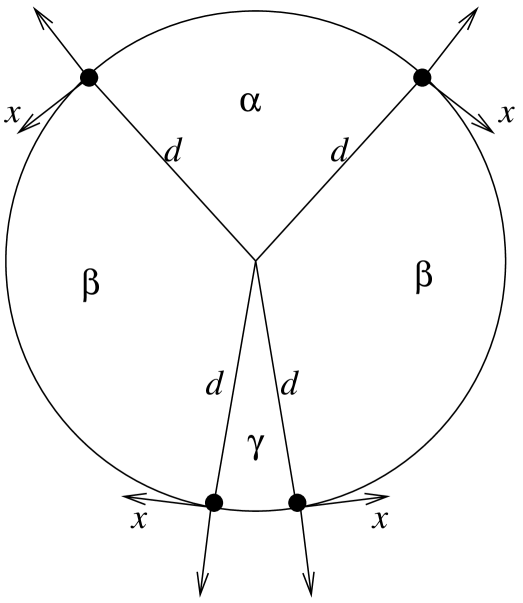
Example 4.13
and are Lyndon word, is the smallest one, so the leader is the sensor that is the nearest to on .
Lemma 4.14
If for all , , , and , then there exists no deterministic algorithm allowing the sensors to agree on a same sensor .
Proof. Assume by contradiction that there exists no radius on the center of or such that or is a Lyndon word and that there exists an algorithm allowing the sensors to deterministically agree on a same sensor . Let be a word in such that , . Suppose w.l.o.g. that . That is, is minimal. Assume first that is primitive. Then it is a Lyndon word that contradicts the assumption. So, is a strictly periodic word and from Lemma 2.3, we deduce that for all , is also strictly periodic. Since by Remark 4.3 our construction is period-free, this implies that the configuration is periodic. Thus, for every , there exists at least one radius such that and .
So if an algorithm elects a leader on in a deterministical way, this algorithm distinguishes another leader on . In that case, cannot allow the sensors to deterministically agree on a same sensor .
The four previous lemmas lead to:
Theorem 4.15
Given a configuration of any number of disoriented sensors without chirality scattered on the plane, the sensors are able to deterministically agree on a same sensor if and only if there exists such that is of type 0 and is a Lyndon word of type .
Remark 4.16
Notice that our construction does not necessarily give the same leader for one given configuration whether there is chirality or not. For instance in Figure 3, with chirality, if the orientation is , the chosen leader is the nearest sensor to on and if the orientation is , it is the nearest sensor to on . Without chirality, the chosen leader is the sensor on .
As noticed in this section, the (weak) configuration words built in Section 3 (Definition 3.3) can be easily defined in terms of strong configuration words (Definition 4.2) by mapping each pair to . Thus, Theorem 3.13 also holds over the strong configuration words built on assuming chirality.
Theorem 4.17
Given a configuration of any number of disoriented sensors scattered on the plane and a period-free construction of strong configuration words , the sensors are able to deterministically agree on a same sensor if and only if there exists a Lyndon word of type among the configuration words.
5 Conclusion
In this paper, we studied the leader election problem in networks of anonymous sensors sharing no kind of common coordinate system. Because of the anonymity, the problem is impossible to solve in a deterministic way, in general. Nevertheless, some specific geometric configurations allows to elect a leader. Using properties of Lyndon words, we give a complete characterization on the sensors positions to deterministically elect a leader for any number of anonymous sensors, assuming chirality or not. This result is based on a specific coding of planar configurations involving Lyndon words which ensures to keep the properties allowing to distinguish a unique leader, if any, while not creating new ones. In the light of our study, the leader provided by our construction turns out to be one of the sensors closest to the center of among either all the sensors or only those that are located on the unique symmetry axis of a configuration. In the case where the sensors share a common handedness, this feature has been used to facilitate the resolution of the arbitrary pattern formation problem as it is shown in [DPV10]. We conjecture that it can also be used in the case where the agents do not share a common handedness. However it should be noted that, according to the distributed tasks to be solved, it might be sometimes more judicious to obtain a leader having other geometrical characteristics. This is particularly the case for the flocking tasks among mobile agents (which consist in moving as a group while following a leader) which a leader initially closest to the boundary of would be more adapted to achieve. Therefore, it is worth emphasizing that we may slightly modify our coding in order to take into account the following distributed task to be achieved: For example by giving higher priority to angles instead of distance or more generally, by changing the order over the set of letters.
As a future work, we will concentrate on finding similar characterizations for other collaborative tasks in mobile sensor networks such as localization problem for which we know that no solution exists in general [DLIP10]. We will also study how the solvability of the election problem impacts the solvability of other fundamental distributed tasks in sensor networks.
References
- [Ang80] D Angluin. Local and global properties in networks of processors. In Proceedings of the 12th Annual ACM Symposium on Theory of Computing (STOC ’80), pages 82–93, 1980.
- [Che04] M Chemillier. Periodic musical sequences and Lyndon words. Soft Computing, 8(9):611–616, 2004.
- [DK02] X Defago and A Konagaya. Circle formation for oblivious anonymous mobile robots with no common sense of orientation. In 2nd ACM International Annual Workshop on Principles of Mobile Computing (POMC 2002), pages 97–104, 2002.
- [DLIP08] Y Dieudonné, O Labbani-Igbida, and F Petit. Circle formation of weak mobile robots. TAAS, 3(4), 2008.
- [DLIP10] Y Dieudonné, O Labbani-Igbida, and F Petit. Deterministic robot-network localization is hard. IEEE Transactions on Robotics, 26(2):331–339, 2010.
- [DP07a] Y Dieudonné and F Petit. Circle formation of weak robots and Lyndon words. Information Processing Letters, 104(4):156–162, 2007.
- [DP07b] Yoann Dieudonné and Franck Petit. Deterministic leader election in anonymous sensor networks without common coordinated system. In OPODIS, pages 132–142, 2007.
- [DPV10] Y Dieudonné, F Petit, and V Villain. Leader election problem versus pattern formation problem. In DISC, pages 267–281, 2010.
- [DR04] O Delgrange and E Rivals. Star: an algorithm to search for tandem approximate repeats. Bioinformatics, 20(16):2812–2820, 2004.
- [FPSW99] P Flocchini, G Prencipe, N Santoro, and P Widmayer. Hard tasks for weak robots: The role of common knowledge in pattern formation by autonomous mobile robots. In 10th Annual International Symposium on Algorithms and Computation (ISAAC 99), pages 93–102, 1999.
- [FPSW01] P Flocchini, G Prencipe, N Santoro, and P Widmayer. Pattern formation by autonomous robots without chirality. In VIII International Colloquium on Structural Information and Communication Complexity (SIROCCO 2001), pages 147–162, 2001.
- [Kat05] B Katreniak. Biangular circle formation by asynchronous mobile robots. In 12th International Colloquium on Structural Information and Communication Complexity (SIROCCO 2005), pages 185–199, 2005.
- [Lot83] M Lothaire. Combinatorics on words. Addison-Wesley, 1983.
- [Lyn96] N Lynch. Distributed algorithms. Morgan Kaufmann, 1996.
- [Meg83] N Megiddo. Linear-time algorithms for linear programming in and related problems. SIAM Journal on Computing, 12(4):759–776, 1983.
- [San07] N Santoro. Design and Analysis of Distributed Algorithms. John Wiley & Sons, Inc., 2007.
- [SM90] R Siromoney and L Mathew. A public key cryptosystem based on Lyndon words. Information Processing Letters, 35(1):33–36, 1990.
- [SY99] I Suzuki and M Yamashita. Distributed anonymous mobile robots - formation of geometric patterns. SIAM Journal of Computing, 28(4):1347–1363, 1999.
- [Wel91] E Welzl. Smallest enclosing disks (balls and ellipsoids). In LNCS 555, editor, New Results and New Trends in Computer Science, pages 359–370, 1991.