Devitalizing noise-driven instability of entangling logic in silicon devices with bias controls

The spin of electrons in isotopically enriched silicon (Si) has been regarded as a promising mechanism for encoding quantum information due to its extremely long coherence time [1, 2, 3, 4] that is highly advantageous for stable manipulations of quantum bits (qubits). In particular, a great amount of effort has been put in by researchers to physically realize universal logic gate devices with electron spins in Si-based quantum dot (QD) structures [3, 4, 5, 6, 7, 8, 9, 10, 11] whose confinement is controlled with external electric and magnetic fields. The preciseness of corresponding logic operations has been continuously improved so single qubit rotations can be now conducted with a fidelity larger than 99% [3, 4, 5, 6, 7, 11], and recently a 98% fidelity is reported for 2-qubit SWAP operations [8]. Elaborated designs of gate devices that generate quantum entanglement [12, 13], the most celebrated quantum resource being widely used in various applications [14, 15, 16], have been also reported but their accuracy so far is generally not as good as the non-entangling cases so the fidelity of 2-qubit Bell-states generated from double quantum dot (DQD) platforms stays in 78%-89% [9, 10, 11]. With a rapid progress in pulsing technologies [6, 17], the speed of DQD-based gating operations reached a sub-microsecond level, and it is shown that a controlled-X (CNOT) operation, the most crucial entangling logic for universal quantum computing, can be conducted in less than 200 nanoseconds (nsec) with a single microwave pulse [10].

In general, the quality of spin qubits in solid-based platforms highly depends on material-inherent noises [18, 19, 20, 21, 22] that are mainly due to the fluctuation in local electric and magnetic fields around qubits. In the Si-based case, noises of magnetic fields (spin noises) can be suppressed with purification of ²⁸Si crystals, and latest works have shown 12-inch ²⁸Si wafers that contain 100ppm or less of spin-carrying ²⁹Si atoms [23, 24]. Suppressing noises of electric fields (charge noises), however, is more difficult than the case of spin noises since its origins have not been fully understood yet. Accordingly, state-of-the-art ideas have been proposed to increase the robustness of spin qubits to existing charge noises in Si devices such as, for example, placing qubits far away from surface oxides [22] that can serve as a source of low-frequency charge noises [19], increasing spin resonance frequencies [7], and biasing DQDs symmetrically to reduce the sensitivity of qubit interactions to charge noises [10, 25]. In spite of the non-trivial contribution driven with these ideas, the up-to-date fidelity of entangling operations in Si devices is not yet in a level where the accuracy in computations can be generally guaranteed, and the motivation for sound studies on technical strategies that can enhance the fidelity of entangling operations under charge noises, therefore, should be huge.

In this work, we elaborately examine the engineering-driven possibilities for devitalizing negative effects that charge noises have against entangling operations implemented with Si QD devices, where the focal point of engineering is the real-time pattern of control signals that has been rarely discussed in detail by the strategies proposed in previous studies [7, 22, 25]. For this purpose, we computationally explore Si DQD structures with our in-house simulation code package that can describe device operations in a full-scale from initializations and time-dependent behaviors of electron spin qubits. As a baseline for discussion, we first model the fast CNOT operation that is driven with a single-step pulse in the recently reported DQD platform [10], and quantify fluctuations in fidelity under charge noises by incorporating random noisy potential profiles to device simulations. Then, as an alternative way, we implement a CNOT operation with a multi-step control that does not employ AC microwave pulses for generation of entanglement. In spite of the loss in fidelity that happens during the real-time transition of control signals, we find a general pattern that the resulting CNOT operation has remarkably increased robustness to charge noises whilst its operating speed can be maintained in a same order compared to the case of a single-step control. Additional in-depth discussion is presented via rigorous modeling to study the optimal control of multi-step CNOT operations in realistic conditions with a trade-off between the speed and the noise-robustness of operations. Being carried as an extension of our preliminary study that focused on the noise-free addressing of individual qubits [26], this work can make a meaningful contribution for Si-based designs of entangling logic blocks that are essential for development of programmable quantum processors.

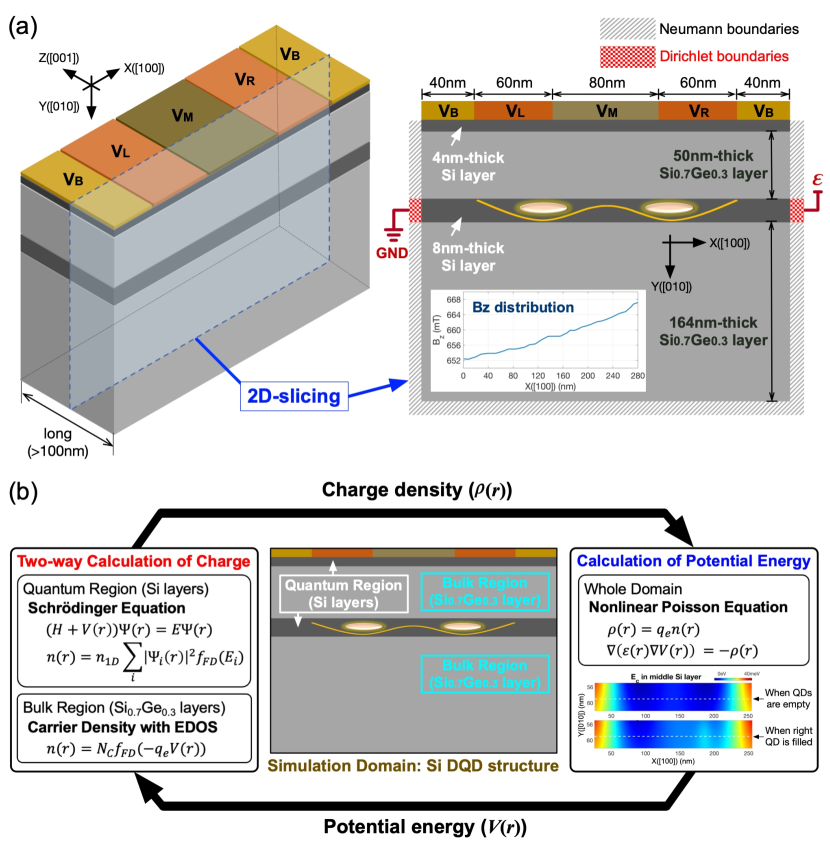
Figure 1(a) shows the DQD structure that is adopted as a target of modeling in this work. Mimicking the reported physical system [10], the target platform is based on a heterostructure that consists of 2 Si and 2 silicon-germanium (SiGe) layers where the fraction of Ge in SiGe layers is 30%. Due to the Si$/$SiGe band offset, the structure has a natural quantum well along the vertical ([010]) direction and electrons can be confined in the 8 nanometer(nm)-thick Si layer. The lateral ([100]) confinement in the 8nm-thick Si layer is controlled with DC biases imposed on top Ti$/$Au electrodes (2 barrier gate biases ($V_{B}$), 1 left$/$middle$/$right gate bias ($V_{L}$$/$$V_{M}$$/$$V_{R}$)), so the system can have up to 2 potential valleys. As the DQD system is quite long ($>$100nm) along the [001] direction, we use its 2D-slice as a simulation domain assuming the structure is infinitely long along that direction. The top electrodes are considered in device simulations by imposing a Dirichlet boundary condition on a 2D Poisson equation with applied biases and Schottky barrier heights ($\Phi_{B}$) that are calculated using the work-function reported for Ti/Au metal layers. [27] The source and drain electron reservoirs, which are secured with 2D electron gas (2DEGs) in reality, are also described with Dirichlet boundaries (the two red boundaries in Figure 1(a)) where we set $\Phi_{B}$ to zero assuming that 2DEGs are formed well and are therefore perfectly ohmic. For simulations, we grounded the source and imposed an extremely small bias ($\varepsilon$ $\simeq$ 0.1mV) on the drain, and a low temperature of 1.5K is assumed.

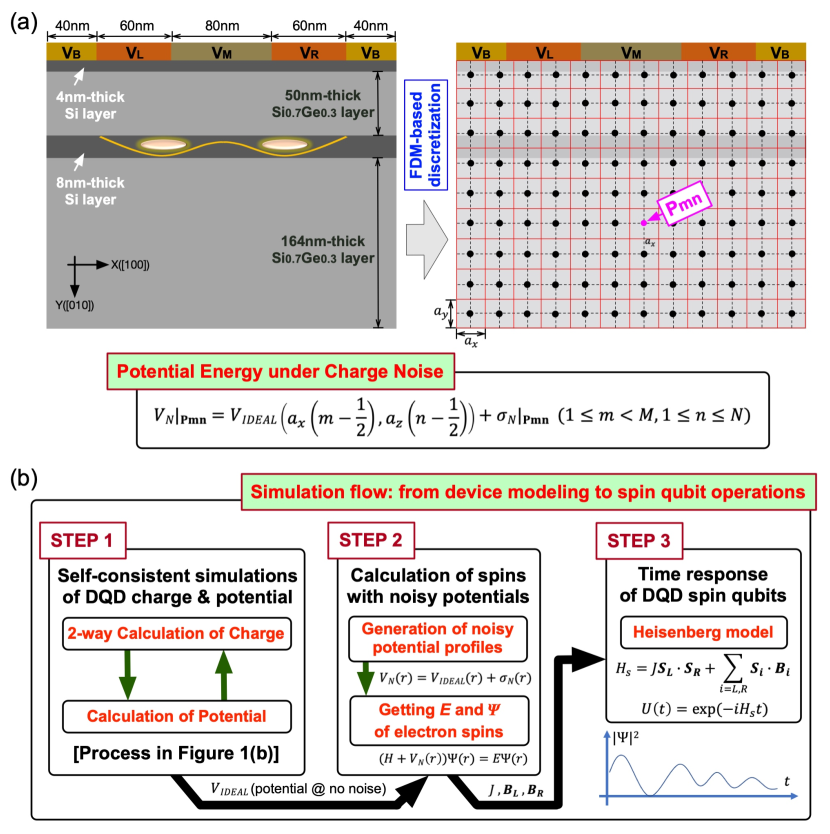
The spatial distribution of potential energy and electron density in the DQD system, which is the outcome of device simulations, is determined with a self-consistent process described in Figure 1(b). While the potential profile is calculated with a normal Poisson solver, the charge profile is evaluated in two ways with regional dependence so the region of thin Si layers (labeled as Quantum Region), which has most of electrons and must be solved quantum mechanically, is treated with electronic structure simulations coupled to a parabolic effective mass model [28], and the region of SiGe layers (labeled as Bulk Region) is solved with the physics of bulk semi-conductors. For precise modeling of spin states, the electronic structure is calculated with a lateral distribution of the static magnetic field along the [001] direction ($B_{Z}$) that is reported by Neumann $et$ $al.$ [29] with simulations of the horseshoe-shaped micromagnet employed in the real experiments [10, 30, 31] (see the inset of Figure 1(a)). Once the potential distribution at a certain set of biases is determined, we disturb this “clean” solution with a noisy potential profile, which is obtained with values that are randomly generated per each real-space grid of the simulation domain as described in Figure 2(a). All the random values here are generated under a zero-mean gaussian distribution, and its standard deviation $\sigma$, which represents the strength of charge noises, is considered up to 5$\mu$eV that is normal in Si-based devices these days [32, 33, 34, 35]. Once the ground states of two QDs are known from device simulations, we can construct the Heisenberg 2-spin Hamiltonian with their Zeeman-spitting energies and exchange interaction [36], and 2-qubit time responses of the DQD system can be then calculated as described in Figure 2(b) that shows the scheme of our full-stack modeling.

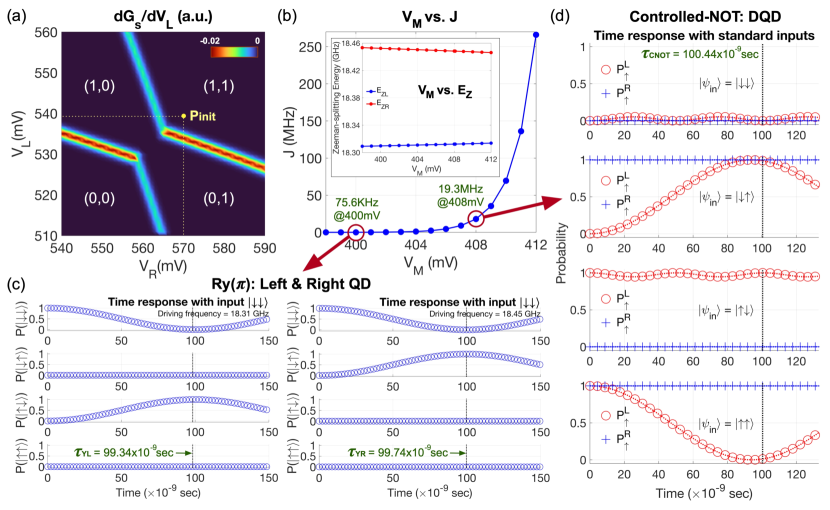
In any physical platforms, the first step for gating operations is to initialize qubits so the system can be prepared for upcoming control pulses. In the target DQD platform where a qubit state 0 and 1 are encoded to the down-spin ($|$$\downarrow$$\rangle$) and the up-spin ($|$$\uparrow$$\rangle$) ground state of a QD, respectively, initialization is done by manipulating biases imposed on top electrodes such that the $|$$\downarrow$$\rangle$ state in each QD is occupied with an electron. To quantify the range of biases that can place the target system in the ($|$$\downarrow$$\rangle_{L}$, $|$$\downarrow$$\rangle_{R}$) state (= $|$$\downarrow$$\downarrow$$\rangle$) where the subscription $L$ and $R$ represent for the left and right QD, respectively, we model the charge stability with device simulations, and present the result in Figure 3(a) as a function of $V_{L}$ and $V_{R}$ at $V_{M}$ = 400mV, where $V_{B}$ is fixed to 200mV. The stability diagram is split to 4 regimes, and each one is identified with two numbers that represent the electron population of each QD. With increasing $V_{L(R)}$, the ground state of the left(right) QD shifts down in energy and is occupied with an electron when the state touches the Fermi-level of the source electron reservoir. Establishing a strong connection to data measured for the physical DQD system [10], our result reveals that ($V_{L}$, $V_{R}$) = (540mV, 570mV) (the yellow point labeled as Pinit) can be an initialization point that is beneficial for noise-robust qubit interactions since two QDs can be symmetrically biased [25].

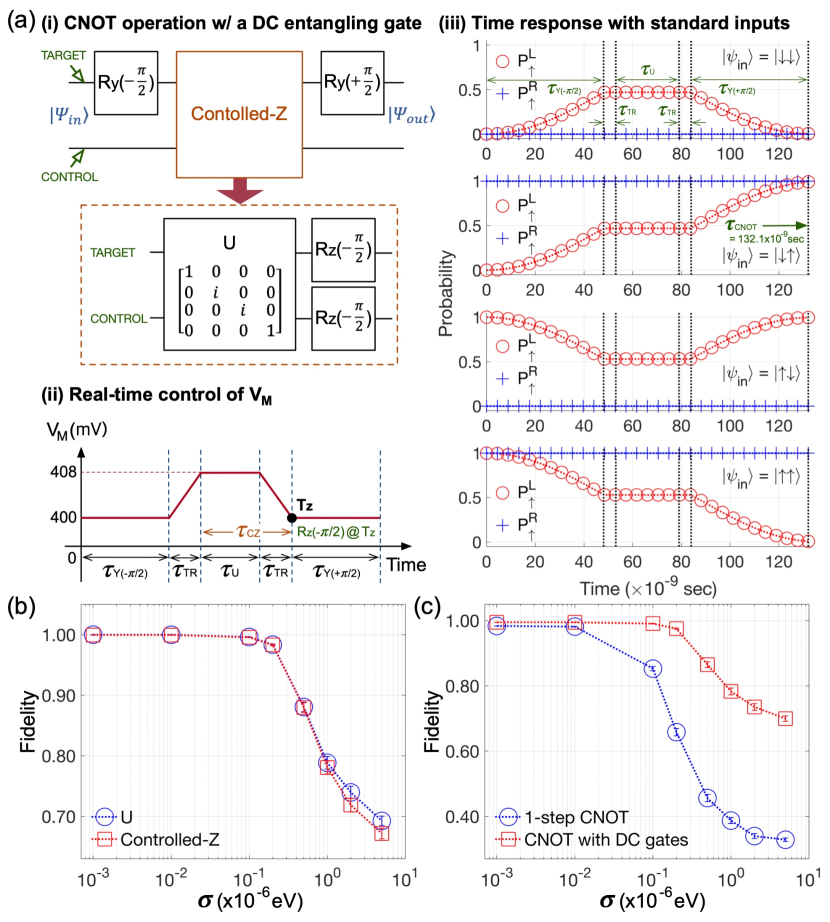
Representing the strength of inter-QD qubit interaction, the exchange energy ($J$) between two ground states serves as a source of 2-qubit entanglement in the DQD platform and can be controlled with the middle gate bias that affects the potential barrier between two QDs. In our simulations, $J$ becomes 75.6KHz at $V_{M}$ = 400mV (at Pinit) and, as shown in Figure 3(b), sharply reaches 19.3MHz when $V_{M}$ is increased by 8mV. Changes in $V_{M}$ also affect Zeeman-splitting energies of the left ($E_{ZL}$) and the right ground state ($E_{ZR}$) that determine the resonance frequency of each spin qubit, but their dependence on $V_{M}$ is not quite noticeable such that ($E_{ZL}$, $E_{ZR}$) is (18.309GHz, 18.453GHz) at $V_{M}$ = 400mV and changes to (18.312GHz, 18.448GHz) when $V_{M}$ is 408mV. Due to the laterally inhomogeneous $B_{Z}$ (the inset of Figure 1(a)), $E_{ZL}$ and $E_{ZR}$ are distinguishable and qubits can be addressed independently if their interaction is weak, and one of such cases is shown in Figure 3(c), where we simulated 2-qubit responses at $V_{M}$ = 400mV with a [010]-oriented time-varying magnetic field $B_{Y}$${(t)}$ = $B_{o}$${cos(\omega_{D}t+\theta)}$ that is generated from a microwave pulse and is incorporated in modeling as elements of the Heisenberg Hamiltonian. In particular, the two subfigures here show that a $R_{Y}(\pi)$ operation (1-qubit rotation by $\pi$ radian around the Y-axis) can be selectively implemented with each qubit by setting $\omega_{D}$ to $E_{ZL}$ or $E_{ZR}$, and gating is completed in 99.34 & 99.47nsec (left & right) when $B_{o}$ = 5.0MHz and $\theta$ = 0. If the interaction is not weak enough to ignore, the resonance frequency of one qubit starts to depend on the spin state ($|$$\downarrow$$\rangle$ or $|$$\uparrow$$\rangle$) of the other qubit, and a CNOT operation can be then realized with a single control pulse [10, 36]. To mimic this 1-step implementation with modeling, we simulate the DQD structure at $V_{M}$ = 408mV with $B_{Y}$${(t)}$ of $\omega_{D}$ (= 1.832GHz), $B_{o}$ (= 4.977MHz) and $\theta$ (= 1.5$\pi$ radian) that are determined with the analytical solution driven by Russ $et$ $al.$ [36]. Simulated 2-qubit responses in Figure 3(d) clearly show the CNOT gating is completed in 100.4nsec, being fairly connected to the experiment [10].

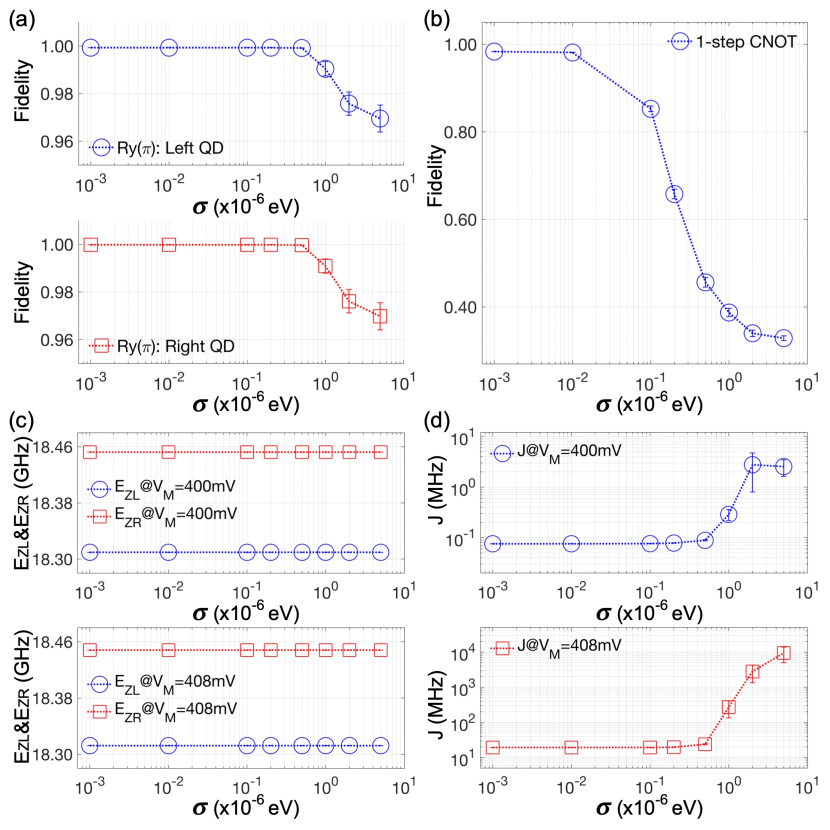
In a noise-free condition, modeling results show that the $R_{Y}(\pi)$ operation is conducted for the left and the right spin with a fidelity of 99.93% and 99.98%, respectively, and the 1-step CNOT operation has a fidelity of 98.34%. To investigate how they are affected by charge noises, we simulate the system with the conditions described in the previous paragraph but disturb the clean potential profiles with random noisy values that are generated under a zero-mean gaussian distribution of a standard deviation $\sigma$. Figure 4(a) and 4(b) show the fidelity of the $R_{Y}(\pi)$ and the 1-step CNOT operation as a function of $\sigma$, respectively, where each case is modeled by conducting 1,000 simulations per a single value of $\sigma$ that is varied from 10^-3 to 5$\mu$eV. Results clearly indicate that both operations continue to lose accuracy as the DQD system experiences more severe noises, but their patterns of the noise-driven degradation in fidelity are different. In the case of $R_{Y}(\pi)$ gating, the fidelity turns out to be 99.93$\pm$10^-6% (left) and 99.98$\pm$10^-6% (right) at $\sigma$ = $10^{-3}$$\mu$eV, and starts to decrease noticeably when $\sigma$ reaches 1$\mu$eV or larger such that it drops to 96.95$\pm$0.5664% (left) and 96.97$\pm$0.5687% (right) at $\sigma$ = 5$\mu$eV, Similarly to the $R_{Y}(\pi)$ case, the 1-step CNOT operation has a nice fidelity (98.34$\pm$0.003%) when $\sigma$ is $10^{-3}$$\mu$eV. Its robustness to noises however is much worse than what $R_{Y}(\pi)$ shows, and the average fidelity plummets more than 60% (32.84$\pm$0.5361%) when $\sigma$ is 5$\mu$eV.

In the extreme case where the left and right qubit never interact ($i.e.$, $J$ = 0), the Heisenberg 2-spin Hamiltonian can be completely described with Zeeman-splitting energies of spin states and external magnetic fields, and so are 2-qubit responses of the DQD system. Accordingly, in the regime of a weak interactions that can be represented with the case of $V_{M}$ = 400mV, the quality of single qubit addressing under charge noises should be determined by how $E_{ZL}$ and $E_{ZR}$ behave. The origin of noise-robust $R_{Y}(\pi)$ rotations (Figure 4(a)) can be therefore clarified with simulation results presented in the upper subfigure of Figure 4(c), which indicate that the noise-driven fluctuation in two Zeeman-splitting energies at $V_{M}$ = 400mV becomes smaller than 100Hz (10^-5% of their clean values) regardless of $\sigma$. If the 2-qubit interaction is not ignorable as it is when $V_{M}$ = 408mV, $J$ also starts to affect the noise-robustness of gating. As Figure 4(d) shows, the noise-driven fluctuation in $J$ is generally much stronger than the $E_{ZL}$ & $E_{ZR}$ case, and, particularly at $V_{M}$ = 408mV, it acts as the major factor that determines the noise-robustness of 2-qubit states because our results reveal that the fluctuation in $E_{ZL}$ and $E_{ZR}$ is still negligible as shown in the lower subfigure of Figure 4(c). In consequence, we can say that the huge reduction in fidelity observed in noisy 1-step CNOT operations (Figure 4(b)) is mainly due to the noise-driven instability of $J$.

Given that the material-inherent charge noise itself would not be easy to be eliminated or hugely suppressed, the next action for implementation of reliable CNOT operations may be to seek for engineering approaches that can make the gate more robust to “existing” noises. For this purpose, here we computationally explore one idea whose main focus is to control qubit interactions such that the “noise-sensitive” interval in time responses can be reduced as much as possible. In Figure 5(a)-(i), we show a simple 2-qubit circuit which also conducts a CNOT operation and will be used as a testbed of the noise-robustness. Here, the desired gating can be implemented with a time-sequential conduction of a $R_{Y}(-\pi/2)$, a controlled-Z (CZ), and a $R_{Y}(\pi/2)$ operation where $R_{Y}$ rotations are applied to the upper (target) qubit. Taking the right QD spin as a control qubit, we can implement the two $R_{Y}$ gates in the DQD platform at $V_{M}$ = 400mV by setting $B_{Y}$${(t)}$ similarly to the $R_{Y}(\pi)$ case except that $\theta$ is $\pi$ (instead of 0) when the rotation angle is negative. The CZ gate in the second step serves as an entangling block and can be obtained without time-varying microwave pulses. Technically, a CZ gate can be further decomposed into 2 steps as illustrated in the bottom subfigure of Figure 5(a)-(i). Here, the 2-qubit controlled-phase gate $U$ is $device$-$native$ [36], which means the unitary can be completely described with only DQD-native spin parameters ($i.e.$, Zeeman-splitting energies and exchange interaction). The Z-rotation ($R_{Z}$) is also device-native but must be carried in the regime of a weak interaction ($e.g.$, $V_{M}$ = 400mV in our case). In real experiments, the $R_{Z}$ is conducted by changing the reference phase for individual spins instead of directly rotating them, which can be done conveniently with software at negligible cost in speed and accuracy [7, 9, 10]. In Figure 5(a)-(ii), we show the real-time pattern of $V_{M}$ that drives this multi-step CNOT gate, where $\tau_{Y}$’s and $\tau_{U}$ on the X-axis are the gating time of $R_{Y}(\pm\pi/2)$ and $U$, respectively. We assume that the $R_{Z}$ gating is performed instantaneously (at the time point labeled as $\bf{T_{Z}}$), adopting a bias-transition time ($\tau_{TR}$) of 5nsec for simulations similarly to the experiment [10]. The resulting responses in Figure 5(a)-(iii) reveal that the entire process takes 132.1nsec, where $\tau_{Y}(\pm\pi/2)$ and $\tau_{U}$ become 48.1nsec and 25.9nsec, respectively.

The focal characteristic of the above-mentioned multi-step CNOT operation is that the 2-qubit entanglement is solely generated by the CZ block, and eventually by the controlled-phase unitary $U$, as all the remaining logics ($R_{Y}$’s and $R_{Z}$’s) handle 1-qubit addressing in the regime of a weak interaction. As the sensitivity of $E_{ZL}$ and $E_{ZR}$ to charge noises is not quite noticeable (Figure 4(c)), the fairly nice noise-robustness of $R_{Y}$ shown in Figure 4(a) also becomes valid for 1-qubit rotations about arbitrary axes. We can thus expect that the noise-driven fidelity of the CZ operation may strongly depend on that of $U$, and this can be confirmed with Figure 5(b) that shows the simulated pattern in fidelity of CZ and $U$ gating. Due to the negligible role of $R_{Y}$ blocks, the overall fidelity of the multi-step CNOT logic, shown with a red dotted line of square marks in Figure 5(c), also closely follows the fidelity of $U$. When $V_{M}$ is 408mV, the multi-step CNOT logic generates 2-qubit entanglement in $\sim$4x less time (25.9nsec) than the 1-step gating (100.4nsec). This “reduced time-period of a strong interaction” can contribute to making the operation more robust to charge noises, so the simulated fidelity of the multi-step operation at $\sigma$ = 5$\mu$eV becomes 69.81$\pm$0.8208% while the 1-step CNOT gate shows 32.84$\pm$0.5361% in the same conduction. Our result in Figure 5(c) also confirms the core message remains effective in the entire range of $\sigma$ that is considered for simulations.

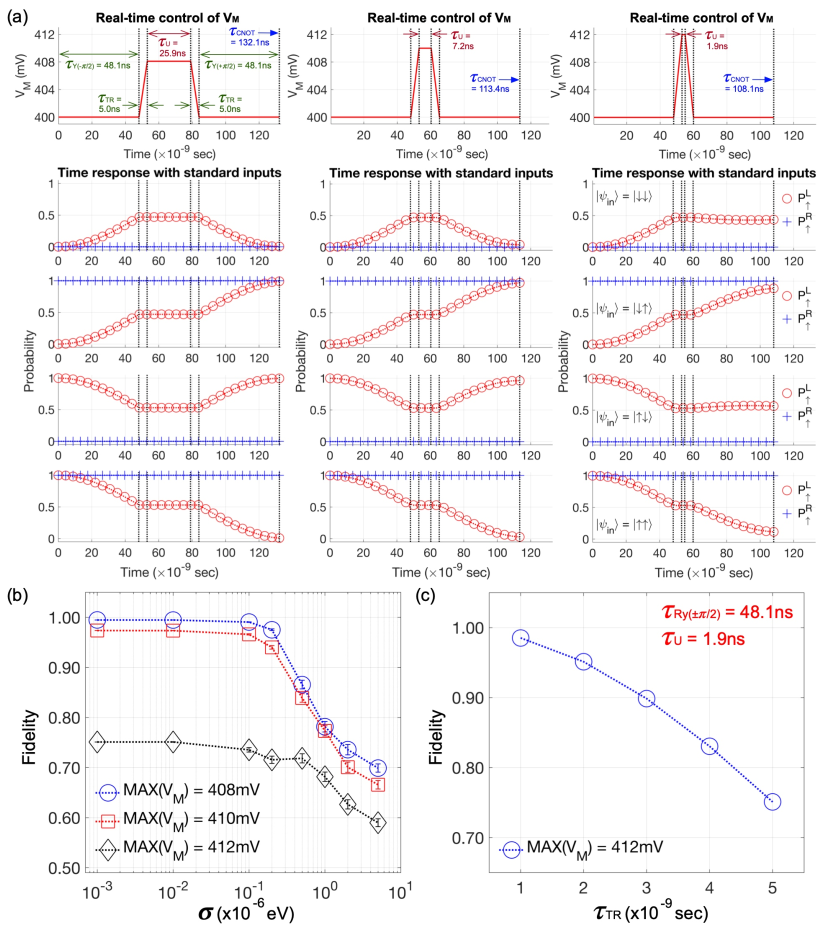
In Figure 3(b), we showed that the interaction energy between QDs has little effects on the resonance frequency of each spin qubit, so the gating time of $U$ can be safely controlled with $J$ (and thus $V_{M}$) with no worries for unintentional variations in any $E_{ZL}$- and $E_{ZR}$-related elements of the 4$\times$4 Heisenberg Hamiltonian [36]. With this background, we investigate what happens on the noise-robustness of the multi-step CNOT operation if the gating time of $U$ is further reduced. For this purpose, the multi-step CNOT gate is simulated at $V_{M}$ = 410mV and 412mV, where other control parameters are kept the same as the previously used ones. The time responses in Figure 6(a) clearly show that the entanglement is generated in 7.2nsec and 1.9nsec when $V_{M}$ is 410mV and 412mV, respectively, and thus the CNOT gating time is reduced to 113.4nsec and 108.1nsec. Figure 6(b), which shows the fidelity of each noisy CNOT operation, indicates that the noise-robustness at $V_{M}$ = 410mV does not quite change compared to the case of $V_{M}$ = 408mV though entanglement is generated must faster (25.9nsec $\rightarrow$ 7.2nsec). This result, being different from the one obtained through a comparison between the single-step and the multi-step CNOT gate at $V_{M}$ = 408mV, can be explained with the fact that the time-integration of $J$ ($i.e.$, $\int_{0}^{\tau_{U}}J(t)\,dt$) remains the same in the two cases (19.3MHz$\times$25.9nsec and 69.5MHz$\times$7.2nsec when $V_{M}$ is 408mV and 410mV, respectively), while, in the previous two cases where $V_{M}$ is kept the same, the time-integration becomes smaller in the multi-step operation (19.3MHz$\times$25.9nsec) than in the single-step one (19.3MHz$\times$100.4nsec). If $V_{M}$ is increased to 412mV, the time-integration still remains similar (266.1MHz$\times$1.9ns), showing $<$1% deviation from the values at $V_{M}$ = 408mV and 410mV. In this case, however, the average fidelity gets worse even under weak noises (75.1% at $\sigma$ = 10^-3$\mu$eV), and this is due to the transition of $V_{M}$ that is essential to switch the interaction strength of QDs. Figure 6(c), which shows the loss in fidelity of the multi-step CNOT operation at $V_{M}$ = 412mV as a function of $\tau_{TR}$, indicates that the loss can be reduced with a faster bias-transition, and we observe that the fidelity is recovered back to 98.52% if the transition can be conducted in 1nsec. Overall, it is fair to say that increasing the speed of U gating has little effects on the fidelity under charge noises, but still contributes to saving the gating time, so, at $V_{M}$ = 410mV where the fidelity is not yet quite affected by a 5nsec-transition of $V_{M}$, the multi-step CNOT gate can be completed with just 10% larger time-cost (113.4nsec) than the single-step gate (100.4nsec).

Entangling logic operations under charge noises are computationally investigated in a silicon double quantum dot (DQD) system where quantum bits (qubits) are encoded to the confined electron spins. Using a realistic DQD platform based on a silicon$/$silicon-germanium (Si$/$SiGe) heterostructure, we make a solid connection to the recent experimental work [10] where a fast controlled-X (CNOT) gate has been implemented with a single-step control, but also extend the modeling scope into noise-driven behaviors of the single-step CNOT operation and 1-qubit rotations by incorporating random noisy potential energies into device simulations. Though the 1-step implementation of a CNOT gate in the Si DQD platform has opened the fundamental pathway for securing a fast CNOT gate with simple controls, it severely suffers from charge noises due to unintended fluctuations in the interaction energy between QDs, so its fidelity reaches lower than 35% when the standard deviation of noisy potential energies ($\sigma$) is 5$\mu$eV. In contrast, 1-qubit rotations are generally quite robust to charge noises since the noisy fluctuation in potential distributions hardly affects the resonance frequency of individual spins. Employing a DQD-native controlled-phase operation can be remarkably helpful for noise-robust implementation of a CNOT gate, because, at the same strength of 2-qubit interaction, it generates quantum entanglement much faster than the single-step CNOT operation. Although additional 1-qubit rotations need to be conducted sequentially in time to complete the CNOT operation, they have little effects on the noise-robustness, so the overall fidelity reaches $\sim$70% at $\sigma$= 5$\mu$eV in spite of the increased complexity in device controls associated with additional 1-qubit rotations. Another benefit of the controlled-phase operation implemented in the DQD platform is that its speed can be enhanced by increasing the strength of 2-qubit interaction with almost no degradation in noise-robustness. In consequence, the associated CNOT gating can be conducted as fast as the single-step operation. Being supported with rigorous simulations, the engineering details discussed in this work can contribute to elevating the current status of a Si QD platform for robust designs of scalable quantum processors.

This work has been supported by the Korea Institute of Science and Technology Information (KISTI) institutional R&D program (K-22-L02-C09) and by the grant from the Institute for Information & Communications Technology Promotion (2019-0-00003) funded by the Korea government (MSIP). The NURION high performance computing resource has been extensively utilized for simulations.