DFAC Framework: Factorizing the Value Function via
Quantile Mixture for Multi-Agent Distributional Q-Learning
Abstract
In fully cooperative multi-agent reinforcement learning (MARL) settings, the environments are highly stochastic due to the partial observability of each agent and the continuously changing policies of the other agents. To address the above issues, we integrate distributional RL and value function factorization methods by proposing a Distributional Value Function Factorization (DFAC) framework to generalize expected value function factorization methods to their DFAC variants. DFAC extends the individual utility functions from deterministic variables to random variables, and models the quantile function of the total return as a quantile mixture. To validate DFAC, we demonstrate DFAC’s ability to factorize a simple two-step matrix game with stochastic rewards and perform experiments on all Super Hard tasks of StarCraft Multi-Agent Challenge, showing that DFAC is able to outperform expected value function factorization baselines.
1 Introduction
In multi-agent reinforcement learning (MARL), one of the popular research directions is to enhance the training procedure of fully cooperative and decentralized agents. Examples of such agents include a fleet of unmanned aerial vehicles (UAVs), a group of autonomous cars, etc. This research direction aims to develop a decentralized and cooperative behavior policy for each agent, and is especially difficult for MARL settings without an explicit communication channel. The most straightforward approach is independent Q-learning (IQL) (Tan, 1993), where each agent is trained independently, with their behavior policies aimed to optimize the overall rewards in each episode. Nevertheless, each agent’s policy may not converge owing to two main difficulties: (1) non-stationary environments caused by the changing behaviors of the agents, and (2) spurious reward signals originated from the actions of the other agents. The agent’s partial observability of the environment further exacerbates the above issues. Therefore, in the past few years, a number of MARL researchers turned their attention to centralized training with decentralized execution (CTDE) approaches, with an objective to stabilize the training procedure while maintaining the agents’ abilities for decentralized execution (Oliehoek et al., 2016). Among these CTDE approaches, value function factorization methods (Sunehag et al., 2018; Rashid et al., 2018; Son et al., 2019) are especially promising in terms of their superior performances and data efficiency (Samvelyan et al., 2019).
Value function factorization methods introduce the assumption of individual-global-max (IGM) (Son et al., 2019), which assumes that each agent’s optimal actions result in the optimal joint actions of the entire group. Based on IGM, the total return of a group of agents can be factorized into separate utility functions (Guestrin et al., 2001) (or simply ‘utility’ hereafter) for each agent. The utilities allow the agents to independently derive their own optimal actions during execution, and deliver promising performance in StarCraft Multi-Agent Challenge (SMAC) (Samvelyan et al., 2019). Unfortunately, current value function factorization methods only concentrate on estimating the expectations of the utilities, overlooking the additional information contained in the full return distributions. Such information, nevertheless, has been demonstrated beneficial for policy learning in the recent literature (Lyle et al., 2019).
In the past few years, distributional RL has been empirically shown to enhance value function estimation in various single-agent RL (SARL) domains (Bellemare et al., 2017; Dabney et al., 2018b, a; Rowland et al., 2019; Yang et al., 2019). Instead of estimating a single scalar Q-value, it approximates the probability distribution of the return by either a categorical distribution (Bellemare et al., 2017) or a quantile function (Dabney et al., 2018b, a). Even though the above methods may be beneficial to the MARL domain due to the ability to capture uncertainty, it is inherently incompatible to expected value function factorization methods (e.g., value decomposition network (VDN) (Sunehag et al., 2018) and QMIX (Rashid et al., 2018)). The incompatibility arises from two aspects: (1) maintaining IGM in a distributional form, and (2) factorizing the probability distribution of the total return into individual utilities. As a result, an effective and efficient approach that is able to solve the incompatibility is crucial and necessary for bridging the gap between value function factorization methods and distributional RL.
In this paper, we propose a Distributional Value Function Factorization (DFAC) framework, to efficiently integrate value function factorization methods with distributional RL. DFAC solves the incompatibility by two techniques: (1) Mean-Shape Decomposition and (2) Quantile Mixture. The former allows the generalization of expected value function factorization methods (e.g., VDN and QMIX) to their DFAC variants without violating IGM. The latter allows the total return distribution to be factorized into individual utility distributions in a computationally efficient manner. To validate the effectiveness of DFAC, we first demonstrate the ability of distribution factorization on a two-step matrix game with stochastic rewards. Then, we perform experiments on all Super Hard maps in SMAC. The experimental results show that DFAC offers beneficial impacts on the baseline methods in all Super Hard maps. In summary, the primary contribution is the introduction of DFAC for bridging the gap between distributional RL and value function factorization methods efficiently by mean-shape decomposition and quantile mixture.
2 Background and Related Works
In this section, we introduce the essential background material for understanding the contents of this paper. We first define the problem formulation of cooperative MARL and CTDE. Next, we describe the conventional formulation of IGM and the value function factorization methods. Then, we walk through the concepts of distributional RL, quantile function, as well as quantile regression, which are the fundamental concepts frequently mentioned in this paper. After that, we explain the implicit quantile network, a key approach adopted in this paper for approximating quantiles. Finally, we bring out the concept of quantile mixture, which is leveraged by DFAC for factorizing the return distribution.
2.1 Cooperative MARL and CTDE
In this work, we consider a fully cooperative MARL environment modeled as a decentralized and partially observable Markov Decision Process (Dec-POMDP) (Oliehoek & Amato, 2016) with stocastic rewards, which is described as a tuple and is defined as follows:
-
•
is the finite set of global states in the environment, where denotes the next state of the current state . The state information is optionally available during training, but not available to the agents during execution.
-
•
is the set of agents. We use to denote the index of the agent.
-
•
is the set of joint observations. At each timestep, a joint observation is received. Each agent is only able to observe its individual observation .
-
•
is the set of joint action-observation histories. The joint history concatenates all received observations and performed actions before a certain timestep, where represents the action-observation history from agent .
-
•
is the set of joint actions. At each timestep, the entire group of the agents take a joint action , where . The individual action of each agent is determined based on its stochastic policy , expressed as . Similarly, in single agent scenarios, we use and to denote the actions of the agent at state and under policy , respectively.
-
•
represents the set of timesteps with horizon , where the index of the current timestep is denoted as . , , , and correspond to the environment information at timestep .
-
•
The transition function specifies the state transition probabilities. Given and , the next state is denoted as .
-
•
The observation function specifies the joint observation probabilities. Given , the joint observation is represented as .
-
•
is the joint reward function shared among all agents. Given , the team reward is expressed as .
-
•
is the discount factor with value within .
Under such an MARL formulation, this work concentrates on CTDE value function factorization methods, where the agents are trained in a centralized fashion and executed in a decentralized manner. In other words, the joint observation history is available during the learning processes of individual policies . During execution, each agent’s policy only conditions on its observation history .
2.2 IGM and Factorizable Tasks
IGM is necessary for value function factorization (Son et al., 2019). For a joint action-value function , if there exist individual utility functions such that the following condition holds:
| (1) |
then are said to satisfy IGM for under . In this case, we also say that is factorized by (Son et al., 2019). If in a given task is factorizable under all , we say that the task is factorizable. Intuitively, factorizable tasks indicate that there exists a factorization such that each agent can select the greedy action according to their individual utilities independently in a decentralized fashion. This enables the optimal individual actions to implicitly achieve the optimal joint action across the agents. Since there is no individual reward, the factorized utilities do not estimate expected returns on their own (Guestrin et al., 2001) and are different from the value function definition commonly used in SARL.
2.3 Value Function Factorization Methods
Based on IGM, value function factorization methods enable centralized training for factorizable tasks, while maintaining the ability for decentralized execution. In this work, we consider two such methods, VDN and QMIX, which can solve a subset of factorizable tasks that satisfies Additivity (Eq. (2)) and Monotonicity (Eq. (3)), respectively, given by:
| (2) |
| (3) |
where is a monotonic function that satisfies , and conditions on the state if the information is available during training. Either of these two equation is a sufficient condition for IGM (Son et al., 2019).
2.4 Distributional RL
For notational simplicity, we consider a degenerated case with only a single agent, and the environment is fully observable until the end of Section 2.6. Distributional RL generalizes classic expected RL methods by capturing the full return distribution instead of the expected return , and outperforms expected RL methods in various single-agent RL domains (Bellemare et al., 2017, 2019; Dabney et al., 2018b, a; Rowland et al., 2019; Yang et al., 2019). Moreover, distributional RL enables improvements (Nikolov et al., 2019; Zhang & Yao, 2019; Mavrin et al., 2019) that require the information of the full return distribution. We define the distributional Bellman operator as follows:
| (4) |
and the distributional Bellman optimality operator as:
| (5) |
where is the optimal action at state , and the expression denotes that random variable and follow the same distribution. Given some initial distribution , converges to the return distribution under , contracting in terms of -Wasserstein distance for all by applying repeatedly; while alternates between the optimal return distributions in the set , under the set of optimal policies by repeatedly applying (Bellemare et al., 2017). The -Wasserstein distance between the probability distributions of random variables , is given by:
| (6) |
where are quantile functions of .
2.5 Quantile Function and Quantile Regression
The relationship between the cumulative distribution function (CDF) and the quantile function (the generalized inverse CDF) of random variable is formulated as:
| (7) |
The expectation of expressed in terms of is:
| (8) |
In (Dabney et al., 2018b), the authors model the value function as a quantile function . During optimization, a pair-wise sampled temporal difference (TD) error for two quantile samples is defined as:
| (9) |
The pair-wise loss is then defined based on the Huber quantile regression loss (Dabney et al., 2018b) with threshold , and is formulated as follows:
| (10) |
| (11) |
Given quantile samples to be optimized with regard to target quantile samples , the total loss is defined as the sum of the pair-wise losses, and is expressed as the following:
| (12) |
2.6 Implicit Quantile Network
Implicit quantile network (IQN) (Dabney et al., 2018a) is relatively light-weight when it is compared to other distributional RL methods. It approximates the return distribution by an implicit quantile function for some differentiable functions , , and . Such an architecture is a type of universal value function approximator (UVFA) (Schaul et al., 2015), which generalizes its predictions across states and goals , with the goals defined as different quantiles of the return distribution. In practice, first expands the scalar to an -dimensional vector by , followed by a single hidden layer with weights and biases to produce a quantile embedding . The expression of can be represented as the following:
| (13) |
where and . Then, is combined with the state embedding by the element-wise (Hadamard) product (), expressed as . The loss of IQN is defined as Eq. (12) by sampling a batch of and quantiles from the policy network and the target network respectively. During execution, the action with the largest expected return is chosen. Since IQN does not model the expected return explicitly, is approximated by calculating the mean of the sampled return through quantile samples based on Eq. (8), expressed as follows:
| (14) |
2.7 Quantile Mixture
Multiple quantile functions (e.g., IQNs) sharing the same quantile may be combined into a single quantile function , in a form of quantile mixture expressed as follows:
| (15) |
where are quantile functions, and are model parameters (Karvanen, 2006). The condition for is that must satisfy the properties of a quantile function. The concept of quantile mixture is analogous to the mixture of multiple probability density functions (PDFs), expressed as follows:
| (16) |
where are PDFs, , and .
3 Methodology
In this section, we walk through the proposed DFAC framework and its derivation procedure. We first discuss a naive distributional factorization and its limitation in Section 3.1. Then, we introduce the DFAC framework to address the limitation, and show that DFAC is able to generalize distributional RL to all factorizable tasks in Section 3.2. After that, DDN and DMIX are introduced as the DFAC variants of VDN and QMIX, respectively, in Section 3.4. Finally, a practical implementation of DFAC based on quantile mixture is presented in Section 3.3. All proofs of the theorems in this section are provided in the supplementary material.
3.1 Distributional IGM
Since IGM is necessary for value function factorization, a distributional factorization that satisfies IGM is required for factorizing stochastic value functions. We first discuss a naive distributional factorization that simply replaces deterministic utilities with stochastic utilities . Then, we provide a theorem to show that the naive distributional factorization is insufficient to guarantee the IGM condition.
Definition 1 (Distributional IGM).
A finite number of individual stochastic utilities , are said to satisfy Distributional IGM (DIGM) for a stochastic joint action-value function under , if satisfy IGM for under , represented as:
Theorem 1.
Given a deterministic joint action-value function , a stochastic joint action-value function , and a factorization function for deterministic utilities:
such that satisfy IGM for under , the following distributional factorization:
is insufficient to guarantee that satisfy DIGM for under .
In order to satisfy DIGM for stochastic utilities, an alternative factorization strategy is necessary.
3.2 The Proposed DFAC Framework
We propose Mean-Shape Decomposition and the DFAC framework to ensure that DIGM is satisfied for stochastic utilities.
Definition 2 (Mean-Shape Decomposition).
A given random variable can be decomposed as follows:
where and .
We propose DFAC to decompose a joint return distribution into its deterministic part (i.e., expected value) and stochastic part (i.e., higher moments), which are approximated by two different functions and , respectively. The factorization function is required to precisely factorize the expectation of in order to satisfy DIGM. On the other hand, the shape function is allowed to roughly factorize the shape of , since the main objective of modeling the return distribution is to assist non-linear approximation of the expectation of (Lyle et al., 2019), rather than accurately model the shape of .
Theorem 2 (DFAC Theorem).
Given a deterministic joint action-value function , a stochastic joint action-value function , and a factorization function for deterministic utilities:
such that satisfy IGM for under , by Mean-Shape Decomposition, the following distributional factorization:
is sufficient to guarantee that satisfy DIGM for under , where and .
Theorem. 2 reveals that the choice of determines whether IGM holds, regardless of the choice of , as long as . Under this setting, any differentiable factorization function of deterministic variables can be extended to a factorization function of random variables. Such a decomposition enables approximation of joint distributions for all factorizable tasks under appropriate choices of and .
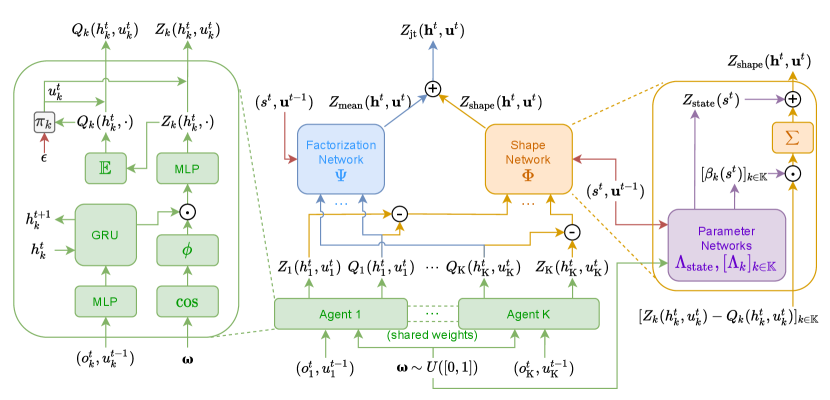
3.3 A Practical Implementation of DFAC
In this section, we provide a practical implementation of the shape function in DFAC, effectively extending any differentiable factorization function (e.g., the additive function of VDN, the monotonic mixing network of QMIX, etc.) that satisfies the IGM condition into its DFAC variant.
Theoretically, the sum of random variables appeared in DDN and DMIX can be described precisely by a joint CDF. However, the exact derivation of this joint CDF is usually computationally expensive and impractical (Lin et al., 2019). As a result, DFAC utilizes the property of quantile mixture to approximate the shape function in time.
Theorem 3.
Given a quantile mixture:
with components and non-negative model parameters . There exist a set of random variables and corresponding to the quantile functions and , respectively, with the following relationship:
Based on Theorem 3, the quantile function of in DFAC can be approximated by the following:
| (17) |
where and are respectively generated by function approximators and , satisfying constraints and . The term models the shape of an additional state-dependent utility (introduced by QMIX at the last layer of the mixing network), which extends the state-dependent bias in QMIX to a full distribution. The full network architecture of DFAC is illustrated in Fig. 1.
This transformation enables DFAC to decompose the quantile representation of a joint distribution into the quantile representations of individual utilities. In this work, is implemented by a large IQN composed of multiple IQNs, optimized through the loss function defined in Eq. (12).
3.4 DFAC Variant of VDN and QMIX
In order to validate the proposed DFAC framework, we next discuss the DFAC variants of two representative factorization methods: VDN and QMIX. DDN extends VDN to its DFAC variant, expressed as:
| (18) |
, ; while DMIX extends QMIX to its DFAC variant, expressed as:
| (19) |
, .
Both DDN and DMIX choose and for simplicity. Automatically learning the values of and is proposed as future work.
4 A Stochastic Two-Step Game
In the previous expected value function factorization methods (e.g., VDN, QMIX, etc.), the factorization is achieved by modeling and as deterministic variables, overlooking the information of higher moments in the full return distributions and . In order to demonstrate DFAC’s ability of factorization, we begin with a toy example modified from (Rashid et al., 2018) to show that DFAC is able to approximate the true return distributions, and factorize the mean and variance of the approximated total return into utilities . Table 2 illustrates the flow of a two-step game consisting of two agents and three states 1, 2A, and 2B, where State 1 serves as the initial state, and each agent is able to perform an action from in each step. In the first step (i.e., State 1), the action of agent (i.e., actions or ) determines which of the two matrix games (State 2A or State 2B) to play in the next step, regardless of the action performed by agent (i.e., actions or ). For all joint actions performed in the first step, no reward is provided to the agents. In the second step, both agents choose an action and receive a global reward according to the payoff matrices depicted in Table 2, where the global rewards are sampled from a normal distribution with mean and standard deviation . The hyperparameters of the two-step game are offered in the supplementary material in detail.
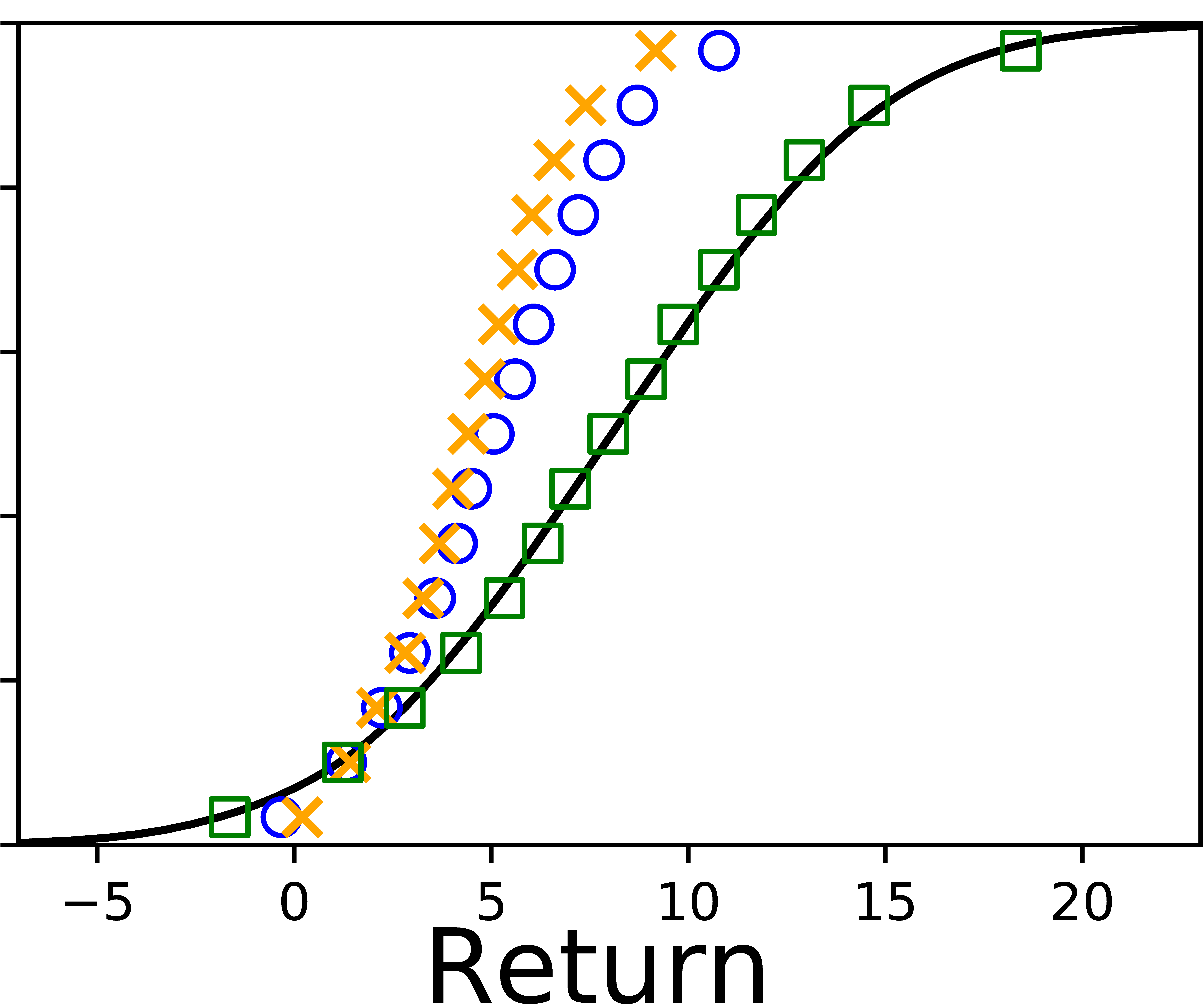
Table 2 presents the learned factorization of DMIX for each state after convergence, where the first rows and the first columns of the tables correspond to the factorized distributions of the individual utilities (i.e., and ), and the main content cells of them correspond to the joint return distributions (i.e., ). From Tables 2(b) and 2(c), it is observed that no matter the true returns are deterministic (i.e., State 2A) or stochastic (i.e., State 2B), DMIX is able to approximate the true returns in Table 2 properly, which are not achievable by expected value function factorization methods. The results demonstrate DFAC’s ability to factorize the joint return distribution rather than expected returns. DMIX’s ability to reconstruct the optimal joint policy in the two-step game further shows that DMIX can represent the same set of tasks as QMIX.
To further illustrate DFAC’s capability of factorization, Figs. 2(a)-2(b) visualize the factorization of the joint action in State A and in State B, respectively. As IQN approximates the utilities and implicitly, , , and can only be plotted in terms of samples. in Fig. 2(a) shows that DMIX degenerates to QMIX when approximating deterministic returns (i.e., ), while in Fig. 2(b) exhibits DMIX’s ability to capture the uncertainty in stochastic returns (i.e., ).
Table 1:
An illustration of the flow of the stochastic two-step game. Each agent is able to perform an action from in each step, with a subscript denoting the agent index. In the first step, action takes the agents from the initial State 1 to State 2A, while action takes them to State 2B instead. The transitions from State 1 to State 2A or State 2B yield zero reward. In the second step, the global rewards are sampled from the normal distributions defined in the payoff matrices.
Agent
Agent
State A
Agent
State B
|
| State | |||
| State A | ||
| State B | ||
5 Experiment Results on SMAC
In this section, we present the experimental results and discuss their implications. We start with a brief introduction to our experimental setup in Section 5.1. Then, we demonstrate that modeling a full distribution is beneficial to the performance of independent learners in Section 5.2. Finally, we compare the performances of the CTDE baseline methods and their DFAC variants in Section 5.3.
|
|
|
| Map | IQL | VDN | QMIX | DIQL | DDN | DMIX |
| (a) | 0.00 | 0.00 | 12.78 | 0.00 | 83.92 | 49.43 |
| (b) | 29.83 | 89.20 | 67.22 | 62.22 | 94.03 | 91.08 |
| (c) | 68.92 | 89.20 | 92.44 | 85.23 | 97.22 | 95.11 |
| (d) | 2.27 | 63.12 | 84.77 | 6.02 | 91.48 | 85.45 |
| (e) | 84.87 | 85.34 | 37.61 | 91.62 | 95.40 | 90.45 |
* Maps (a)-(e) correspond to the maps in Fig. 3.
| Map | IQL | VDN | QMIX | DIQL | DDN | DMIX |
| (a) | 13.78 | 15.41 | 14.37 | 14.94 | 19.40 | 17.14 |
| (b) | 16.54 | 19.75 | 20.16 | 17.52 | 20.94 | 19.70 |
| (c) | 17.50 | 19.36 | 19.42 | 19.21 | 20.90 | 19.87 |
| (d) | 14.01 | 18.45 | 19.41 | 14.45 | 19.71 | 19.43 |
| (e) | 19.42 | 19.47 | 15.07 | 19.68 | 20.00 | 19.66 |
* Maps (a)-(e) correspond to the maps in Fig. 3.
5.1 Experimental Setup
Environment. We verify the DFAC framework in the SMAC benchmark environments (Samvelyan et al., 2019) built on the popular real-time strategy game StarCraft II. Instead of playing the full game, SMAC is developed for evaluating the effectiveness of MARL micro-management algorithms. Each environment in SMAC contains two teams. One team is controlled by a decentralized MARL algorithm, with the policies of the agents conditioned on their local observation histories. The other team consists of enemy units controlled by the built-in game artificial intelligence based on carefully handcrafted heuristics, which is set to its highest difficulty equal to seven. The overall objective is to maximize the win rate for each battle scenario, where the rewards employed in our experiments follow the default settings of SMAC. The default settings use shaped rewards based on the damage dealt, enemy units killed, and whether the RL agents win the battle. If there is no healing unit in the enemy team, the maximum return of an episode (i.e., the score) is ; otherwise, it may exceed , since enemies may receive more damages after healing or being healed.
The environments in SMAC are categorized into three different levels of difficulties: Easy, Hard, and Super Hard scenarios (Samvelyan et al., 2019). In this paper, we focus on all Super Hard scenarios including (a) 6h_vs_8z, (b) 3s5z_vs_3s6z, (c) MMM2, (d) 27m_vs_30m, and (e) corridor, since these scenarios have not been properly addressed in the previous literature without the use of additional assumptions such as intrinsic reward signals (Du et al., 2019), explicit communication channels (Zhang et al., 2019; Wang et al., 2019), common knowledge shared among the agents (de Witt et al., 2019; Wang et al., 2020), and so on. Three of these scenarios have their maximum scores higher than . In 3s5z_vs_3s6z, the enemy Stalkers have the ability to regenerate shields; in MMM2, the enemy Medivacs can heal other units; in corridor, the enemy Zerglings slowly regenerate their own health.
Hyperparameters. For all of our experimental results, the training length is set to 8M timesteps, where the agents are evaluated every 40k timesteps with 32 independent runs. The curves presented in this section are generated based on five different random seeds. The solid lines represent the median win rate, while the shaded areas correspond to the to percentiles. For a better visualization, the presented curves are smoothed by a moving average filter with its window size set to 11. The detailed hyperparameter setups are provided in the supplementary material.
Baselines. We select IQL, VDN, and QMIX as our baseline methods, and compare them with their distributional variants in our experiments. The configurations are optimized so as to provide the best performance for each of the methods considered. Since we tuned the hyperparameters of the baselines, their performances are better than those reported in (Samvelyan et al., 2019). The hyperparameter searching process is detailed in the supplementary material.
5.2 Independent Learners
In order to validate our assumption that distributional RL is beneficial to the MARL domain, we first employ the simplest training algorithm, IQL, and extend it to its distributional variant, called DIQL. DIQL is simply a modified IQL that uses IQN as its underlying RL algorithm without any additional modification or enhancements (Matignon et al., 2007; Lyu & Amato, 2020).
5.3 Value Function Factorization Methods
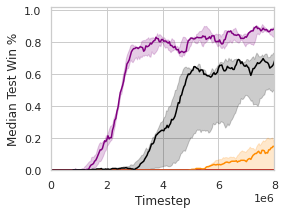
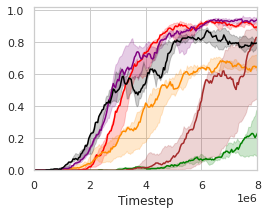
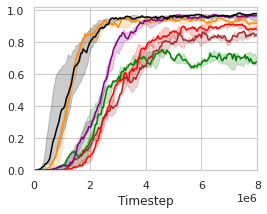
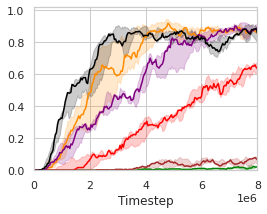
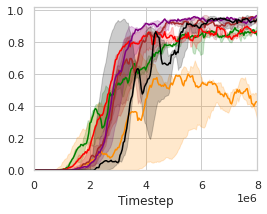
In order to inspect the effectiveness and impacts of DFAC on learning curves, win rates, and scores, we next summarize the results of the baselines as well as their DFAC variants on the Super Hard scenarios in Fig. 3(a)-(e) and Table 4-4.
Fig. 3(a)-(e) plot the learning curves of the baselines and their DFAC variants, with the final win rates presented in Table 4, and their final scores reported in Table 4. The win rates indicate how often do the player’s team wins, while the scores represent how well do the player’s team performs. Despite the fact that SMAC’s objective is to maximize the win rate, the true optimization goal of MARL algorithms is the averaged score. In fact, these two metrics are not always positively correlated (e.g., VDN and QMIX in 6h_vs_8z and 3s5z_vs_3s6z, and QMIX and DMIX in 3s5z_vs_3s6z).
It can be observed that the learning curves of DDN and DMIX grow faster and achieve higher final win rates than their corresponding baselines. In the most difficult map: 6h_vs_8z, most of the methods fail to learn an effective policy except for DDN and DMIX. The evaluation results also show that DDN and DMIX are capable of performing consistently well across all Super Hard maps with high win rates. In addition to the win rates, Table 4 further presents the final averaged scores achieved by each method, and provides deeper insights into the advantages of the DFAC framework by quantifying the performances of the learned policies of different methods.
The improvements in win rates and scores are due to the benefits offered by distributional RL (Lyle et al., 2019), which enables the distributional variants to work more effectively in MARL environments. Moreover, the evaluation results reveal that DDN performs especially well in most environments despite its simplicity. Further validations of DDN and DMIX on our self-designed Ultra Hard scenarios that are more difficult than Super Hard scenarios can be found in our GitHub repository (https://github.com/j3soon/dfac), along with the gameplay recording videos.
6 Conclusion
In this paper, we provided a distributional perspective on value function factorization methods, and introduced a framework, called DFAC, for integrating distributional RL with MARL domains. We first proposed DFAC based on a mean-shape decomposition procedure to ensure the Distributional IGM condition holds for all factorizable tasks. Then, we proposed the use of quantile mixture to implement the mean-shape decomposition in a computationally friendly manner. DFAC’s ability to factorize the joint return distribution into individual utility distributions was demonstrated by a toy example. In order to validate the effectiveness of DFAC, we presented experimental results performed on all Super Hard scenarios in SMAC for a number of MARL baseline methods as well as their DFAC variants. The results show that DDN and DMIX outperform VDN and QMIX. DFAC can be extended to more value function factorization methods and offers an interesting research direction for future endeavors.
7 Acknowledgements
The authors acknowledge the support from NVIDIA Corporation and NVIDIA AI Technology Center (NVAITC). The authors thank Kuan-Yu Chang for his helpful critiques of this research work. The last author would like to thank the funding support from Ministry of Science and Technology (MOST) in Taiwan under grant nos. MOST 110-2636-E-007-010 and MOST 110-2634-F-007-019.
References
- Bellemare et al. (2017) Bellemare, M. G., Dabney, W., and Munos, R. A distributional perspective on reinforcement learning. In Proc. Int. Conf. on Machine Learning (ICML), pp. 449–458, Jul. 2017.
- Bellemare et al. (2019) Bellemare, M. G., Roux, N. L., Castro, P. S., and Moitra, S. Distributional reinforcement learning with linear function approximation. arXiv preprint arXiv:1902.03149, 2019.
- Dabney et al. (2018a) Dabney, W., Ostrovski, G., Silver, D., and Munos, R. Implicit quantile networks for distributional reinforcement learning. In Proc. Int. Conf. on Machine Learning (ICML), pp. 1096–1105, Jul. 2018a.
- Dabney et al. (2018b) Dabney, W., Rowland, M., Bellemare, M. G., and Munos, R. Distributional reinforcement learning with quantile regression. In Proc. AAAI Conf. on Artificial Intelligence (AAAI), pp. 2892–2901, Feb. 2018b.
- de Witt et al. (2019) de Witt, C. S., Foerster, J., Farquhar, G., Torr, P., Böhmer, W., and Whiteson, S. Multi-agent common knowledge reinforcement learning. In Advances in Neural Information Processing Systems, pp. 9924–9935, 2019.
- Du et al. (2019) Du, Y., Han, L., Fang, M., Liu, J., Dai, T., and Tao, D. Liir: Learning individual intrinsic reward in multi-agent reinforcement learning. In Advances in Neural Information Processing Systems, pp. 4405–4416, 2019.
- Guestrin et al. (2001) Guestrin, C., Koller, D., and Parr, R. Multiagent planning with factored mdps. In NIPS, 2001.
- Karvanen (2006) Karvanen, J. Estimation of quantile mixtures via l-moments and trimmed l-moments. Computational Statistics & Data Analysis, 51:947–959, 11 2006. doi: 10.1016/j.csda.2005.09.014.
- Lin et al. (2019) Lin, Z., Zhao, L., Yang, D., Qin, T., Liu, T.-Y., and Yang, G. Distributional reward decomposition for reinforcement learning. In Advances in Neural Information Processing Systems, pp. 6212–6221, 2019.
- Lyle et al. (2019) Lyle, C., Bellemare, M. G., and Castro, P. S. A comparative analysis of expected and distributional reinforcement learning. In Proc. AAAI Conf. on Artificial Intelligence (AAAI), pp. 4504–4511, Feb. 2019.
- Lyu & Amato (2020) Lyu, X. and Amato, C. Likelihood quantile networks for coordinating multi-agent reinforcement learning. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems, pp. 798–806, 2020.
- Matignon et al. (2007) Matignon, L., Laurent, G., and Fort-Piat, N. Hysteretic q-learning : an algorithm for decentralized reinforcement learning in cooperative multi-agent teams. pp. 64 – 69, 12 2007. doi: 10.1109/IROS.2007.4399095.
- Mavrin et al. (2019) Mavrin, B., Yao, H., Kong, L., Wu, K., and Yu, Y. Distributional reinforcement learning for efficient exploration. In Proc. Int. Conf. on Machine Learning (ICML), pp. 4424–4434, Jul. 2019.
- Nikolov et al. (2019) Nikolov, N., Kirschner, J., Berkenkamp, F., and Krause, A. Information-directed exploration for deep reinforcement learning. In Proc. Int. Conf. on Learning Representations (ICLR), May 2019. URL https://openreview.net/forum?id=Byx83s09Km.
- Oliehoek & Amato (2016) Oliehoek, F. A. and Amato, C. A Concise Introduction to Decentralized POMDPs. Springer, 2016. ISBN 3319289276.
- Oliehoek et al. (2016) Oliehoek, F. A., Amato, C., et al. A concise introduction to decentralized POMDPs, volume 1. Springer, 2016.
- Rashid et al. (2018) Rashid, T. et al. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proc. Int. Conf. on Machine Learning (ICML), pp. 4295–4304, Jul. 2018.
- Rowland et al. (2019) Rowland, M. et al. Statistics and samples in distributional reinforcement learning. In Proc. Int. Conf. on Machine Learning (ICML), pp. 5528–5536, Jul. 2019.
- Samvelyan et al. (2019) Samvelyan, M. et al. The starcraft multi-agent challenge. In Proc. Int. Conf. on Autonomous Agents and MultiAgent Systems (AAMAS), pp. 2186–2188, May 2019.
- Schaul et al. (2015) Schaul, T., Horgan, D., Gregor, K., and Silver, D. Universal value function approximators. In International conference on machine learning, pp. 1312–1320, 2015.
- Son et al. (2019) Son, K., Kim, D., Kang, W. J., Hostallero, D. E., and Yi, Y. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. In Proc. Int. Conf. on Machine Learning (ICML), pp. 5887–5896, Jul. 2019.
- Sunehag et al. (2018) Sunehag, P. et al. Value-decomposition networks for cooperative multi-agent learning based on team reward. In Proc. Int. Conf. on Autonomous Agents and MultiAgent Systems (AAMAS), pp. 2085–2087, May 2018.
- Tan (1993) Tan, M. Multi-agent reinforcement learning: Independent versus cooperative agents. In Proc. Int. Conf. on Machine Learning (ICML), pp. 330–337, Jun. 1993. ISBN 1558603077.
- Wang et al. (2019) Wang, T., Wang, J., Zheng, C., and Zhang, C. Learning nearly decomposable value functions via communication minimization. arXiv preprint arXiv:1910.05366, 2019.
- Wang et al. (2020) Wang, T., Dong, H., Lesser, V., and Zhang, C. Multi-agent reinforcement learning with emergent roles. arXiv preprint arXiv:2003.08039, 2020.
- Yang et al. (2019) Yang, D. et al. Fully parameterized quantile function for distributional reinforcement learning. In Proc. Conf. Advances in Neural Information Processing Systems (NeurIPS), pp. 6190–6199, Dec. 2019.
- Zhang & Yao (2019) Zhang, S. and Yao, H. Quota: The quantile option architecture for reinforcement learning. In Proc. AAAI Conf. on Artificial Intelligence (AAAI), pp. 5797–5804, Feb. 2019.
- Zhang et al. (2019) Zhang, S. Q., Zhang, Q., and Lin, J. Efficient communication in multi-agent reinforcement learning via variance based control. In Advances in Neural Information Processing Systems, pp. 3230–3239, 2019.
See pages - of supp.pdf
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6f3e7824-a73c-44dd-8c24-e0157d4702ff/legend-toy.png)