Differential algebra of polytopes and inversion formulas
Abstract.
We use the differential algebra of polytopes to explain the known remarkable relation of the combinatorics of the associahedra and permutohedra with the universal compositional and multiplicative inversion formulas for the formal power series. This approach allows to single out the associahedra and permutohedra among all graph-associahedra and emphasizes the significance of the differential equations for special sequences of simple polytopes derived earlier by one of the authors. We discuss also the link with the geometry of Deligne-Mumford moduli spaces and permutohedral varieties, as well as the interpretation of the combinatorics of cyclohedra in relation with the classical Faà di Bruno’s formula.
1. Introduction
The following natural question goes back at least to Lagrange. For a given power series find the inversion under the substitution: The coefficients of such series are known to be certain polynomials with integer coefficients:
Remarkably these coefficients can be interpreted in terms of the combinatorics of the associahedra (or, Stasheff polytopes), see [5, 41] for the details. For example, the formula for says that associahedron has 6 pentagonal and 3 quadrilateral faces, 21 edges and 14 vertices (see Fig. 1, where we show also its realisation as a truncated cube following [14]).
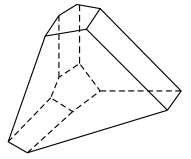
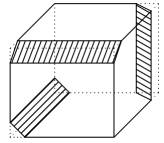
It is difficult to trace who was the first to observe this remarkable fact. The first combinatorial description of the coefficients seems to belong to Raney [53]. Stanley [56] provided 3 proofs in terms of tree combinatorics, known to be closely related to the associahedron. Loday [41] described this explicitly in terms of the associahedra, see also recent book by Aguiar and Ardila [5], who used the theory of Hopf monoids to derive this connection.
The aim of this paper is to provide one more derivation of this link using the differential equations for the generating function of the associahedra derived by one of the authors [11]. This allows us also to prove another known remarkable formula, expressing the multiplicative inversion of a formal power series in terms of combinatorics of permutohedra (see [5]) and to provide an interpretation of the combinatorics of cyclohedra in relation with the classical Faà di Bruno’s formula, which was first discovered by Aguiar and Bastidas [4]. In the case of the stellohedra we derive the relation with permutohedra, which seems to be new.
2. Differential algebra of simple polytopes
We start with a brief description of the differential algebra of simple polytopes following [11, 15]. For the general theory of convex polyhedra we refer to Ziegler [61].
Let be the free abelian group generated by all convex polytopes, considered up to combinatorial equivalence and naturally graded by the dimension of the polytopes. The product of polytopes turns into a graded commutative ring with the unit given by the point, considered as -dimensional polytope. Simple polytopes form a graded subring Note that the ring is different both from the polytope algebra [46] of convex polytopes in with product given by the Minkowski sum and from the Grothendieck ring of -rational polytopes considered in [48].
A polytope is called indecomposable if it cannot be represented as a product of polytopes of positive dimension.
Theorem 2.1 ([13]).
The ring is a polynomial ring generated by indecomposable combinatorial polytopes, so any combinatorial polytope can be uniquely represented as a product of the indecomposable polytopes.
The proof can be found in [13] (see also Prop.1.7.2 in [15]). Note that if we introduce the second grading in by the number of the facets of polytopes, then the number of generators in any bi-graded component of will be finite [15].
Following [11] introduce the derivation in by defining the boundary of a given polytope simply as the sum of all facets of considered as elements in . It is easy to check that preserves the subring and satisfies the Leibnitz identity in
This supplies with a structure of the differential ring, with being its differential subring. Note that in our case in contrast with the differential introduced in [29].
We will be interested in the special class of simple polytopes known as graph-associahedra. They were introduced and studied in the work of Carr and Devadoss [20] and independently by Toledano Laredo [59] under the name De Concini–Procesi associahedra (see also Postnikov [51]). This class contains the classical series of permutohedra and associahedra.
Let be a connected simple (no loops or multiple edges) graph with the set of vertices, which we identify with The corresponding graph-associahedron is a particular case of the nestohedron [27] with the building set consisting of the connected induced subgraphs of , or equivalently as the subsets such that the restriction is connected. Explicitly can be realised as the following -dimensional convex polytope
| (1) |
where is the number of elements in (see [59]).
The boundary of the graph-associahedra can be given by the following formula (see e.g. [15], Prop. 1.7.16). For any connected induced subgraph of with vertex set define the graph with the vertex set having an edge between two vertices and whenever they are path-connected in the restriction Then the boundary of the graph-associahedron can be given combinatorially as
| (2) |
Proposition 2.2.
For any connected graph the corresponding graph-assiciahedron is indecomposable.
Proof.
We can prove this by induction in the number of the vertices of . For this is obvious. Let this be true for all and consider for with vertices. Assume that is decomposable, so that the boundary
On the other hand the boundary can be given by formula (2), so
By induction in the right-hand side we have the products of the indecomposable polytopes, containing for any one-vertex . From the uniqueness part of Theorem 2.1 it follows that either or must be a segment, which easily leads to a contradiction. ∎
There are two famous particular cases of graph-associahedra: associahedra (or Stasheff polytopes, traditionally denoted as ) and permutohedra , corresponding to path and complete graphs with vertices respectively.
For the associahedron the corresponding graph is a path with edges . The connected subgraphs are strings , which can be naturally labelled by the brackets in the product , linking this with the original Stasheff’s description (see [49, 61] for the history of this remarkable polytope and its role in combinatorics and algebra). The number of vertices of is the Catalan number One can also describe also as the Newton polytope of the polynomial For we have pentagon, for 3D associahedron, which is shown on Fig. 1 together with its realisation as 2-truncated cube found in [14].
Permutohedron corresponds to the complete graph with vertices and can be described as the convex hull of the points with or as the Newton polytope of the Vandermonde polynomial For we have hexagon, for - the truncated octahedron shown on Fig. 2.
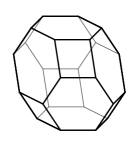
Our first observation is that these two sequences of combinatorial polytopes can be characterised in terms of the differential algebra of polytopes as follows.
Let be a sequence of simple polytopes with the dimension of equal to Consider the following question: when the corresponding subring of generated by these polytopes is closed under differentiation (and thus is a differential subring of )?
Assuming that are graph-associahedra of the connected graphs with vertices, we can give the following answer.
Theorem 2.3.
A sequence of graph-associahedra generates a subring of closed under differentiation only in two cases: associahedra and permutohedra
Proof.
Let be the sequence of connected graphs, such that the corresponding graph-associahedra (which are indecomposable by Proposition 2.2) freely generate a polynomial subring of , which is closed under differentiation
We need the following result from graph theory.
Lemma 2.4.
Let be a sequence of connected graphs with vertices, such that any connected induced subgraph of and the corresponding graph are equivalent to some of with Then this must be the sequence of paths or complete graphs.
Proof.
We will prove this by induction in For the claim is obvious since is either a path or complete graph with 3 vertices. Assume now that the claim is true for and prove it for
Assume first that all induced subgraphs of are paths. Then must be either a tree, or a cycle. Indeed, if is not a tree, it must contain a cycle so the corresponding induced subgraph is not a path. The only exception is when so is a cycle.
Let be a tree. If has a vertex of index then contains a complete graph , which is impossible. So all vertices of have index 1 or 2 and is a path. If is a cycle with vertices, then for its subpath with vertices the graph , which contradicts the assumption. Thus must be a path in this case.
Assume now that all induced subgraphs of are complete graphs. If has two vertices and which are not connected by an edge, then the shortest path connecting them is an induced subgraph, which is not complete. Thus must be a complete graph in this case. ∎
The theorem now follows from Lemma and the boundary formula (2) since the paths and complete graphs correspond to the associahedra and permutohedra respectively. ∎
Remark 2.5.
Note that there are other sequences of the simple polytopes generating a subring in invariant under differentiation (e.g. simplices , cubes ), but the general problem of description of all such sequences seems to be open. We conjecture that in the indecomposable case the answer is given by the sequences of simplices, associahedra and permutohedra.
3. PDEs for graph-associahedra and inversion formulas
We start with the differential equations for the generating functions of some special polytopes, derived by one of the authors [11] (see also [10] and [15], section 1.8).
Let be a convex polytope of dimension and be the set of all faces of of codimension considered as elements of . Consider the corresponding generating function defined by
| (3) |
One can check that the valuation map sending to is a ring-homomorphism for all .
Define now the motivic interior of a polytope as the alternating sum of all the faces of
| (4) |
At the level of the set-theoretical characteristic functions this formula agrees with a well-known result in the theory of finitely additive measures of convex polytopes [45, 52] with being the standard relative interior [61] of the polytope . Note that the polytope can be represented simply as
where denotes the disjoint union of sets (see [61]). More justification for the terminology is given by the theory of toric varieties, see Section 5 below.
For simple polytopes we have the following formula, which will be important for us.
Lemma 3.1.
For any simple convex polytope we have
| (5) |
which can be used to characterise the simple polytopes among all polytopes.
The proof easily follows from the simplicity of the polytope. In particular, for simple polytope the motivic interior can be written as
Following [11], consider now the generating functions of for the families of associahedra and permutohedra
| (6) | |||
Here both and are points and thus are units in the polytopal ring, but for our purposes we will keep track of them considering them as independent variables. In particular, we define the corresponding weighted motivic interiors as
| (7) | |||
For example, for we have The corresponding motivic interiors (4) can be found from the weighted motivic interiors by setting
Denote by
the corresponding partial derivatives of the function
Indeed, the boundary formula (2) in this particular case gives
| (10) |
which together with Lemma leads to the differential equations (8), (9).
The partial differential equation
| (11) |
is called Hopf equation (or inviscid Burgers’ equation) and used as the simplest model to describe the breaking of waves phenomenon.
It is well-known that its solution with initial value can be given implicitly by the formula
| (12) |
which can be easily checked directly. Applying this now for the equation (8), we have the identity
| (13) |
Substituting here we see that the generating function
| (14) |
satisfies the relation
| (15) |
Consider the series , then
Thus we have proved the following theorem, which is an interpretation of the result of Loday [41] (see also [5]).
Theorem 3.3.
The generating power series of associahedra and their weighted motivic interiors
| (16) |
are compositionally inverse to each other in the polytopal ring :
Note that since by Theorem 2.1 and Proposition 2.2 the associahedra are algebraically independent in , this implies the following universal inversion formulae: the coefficients of the formal series and its compositional inverse are related by the following formulae, expressing each other as certain polynomials with integer coefficients:
in agreement with the formulas for the weighted motivic interiors of the associahedra
Note that the faces of of codimension are in one-to-one correspondence with dissections of a based -gon by non-intersecting diagonals (see [30, 25]). Alternatively, the faces of can be labelled by non-isomorphic planar rooted trees with leaves [23], which can be used to rewrite the inversion formulas in these terms (see [56]).
The corresponding polynomials can also be expressed in terms of the partial Bell polynomials (see e.g. [21], Section 3.8) or, more explicitly, as
| (17) |
where (see e.g. [31]).
Similarly, the corresponding permutohedral differential equation (9) has the explicit solution
| (18) |
Substituting here we have the relation This implies that and the following result, which is an interpretation of the known result from [5].
Theorem 3.4.
The exponential generating series of permutohedra and their weighted motivic interiors
| (19) |
is multiplicatively inverse to each other in the polytopal ring :
Again since permotohedra are algebraically independent in this implies the universal multiplicative inversion formulae for the formal power series. Namely, the coefficients of the series and its multiplicative inverse are related by the polynomial formulas with integer coefficients:
in agreement with the fact that is hexagon and has 8 hexagonal and 6 quadrilateral faces, 36 edges and 24 vertices (see Fig. 2). This is also in a good agreement with the formulas for the weighted motivic interiors of the permutohedra:
| (20) |
4. Inversion formula and the Deligne-Mumford moduli spaces
There is an interesting link with the moduli space of stable genus zero curves with ordered marked points. Its real version is known to be tessellated by copies of associahedron (see [36, 23]). This explains the result of McMullen, who interpreted the compositional inversion formulas in terms of the corresponding real strata [44].
It is interesting that the geometry of the complex version allows also to describe the compositional inversion of the exponential power series. More precisely, McMullen proved that the compositional inverse of the formal series is given by
| (21) |
where is the number of strata isomorphic to
(see Theorem 1 in [44]). The proof is based on the well-known bijection between the strata and the marked stable rooted trees, known also as modular graphs [40].
One can combine this with our result [16] claiming that the generating functions of the cobordism classes of the complex projective spaces and the theta-divisors
are compositionally inverse to each other, to express the cobordism class in terms of the cobordism classes as follows
| (22) |
One more remarkable fact here is due to Getzler [32]. Recall that is a special (Deligne-Mumford) compactification of the moduli space of ordered distinct points on complex projective line considered up to projective equivalence. Using the framework of the operads, Getzler proved that the exponential generating functions of the corresponding (in case of , motivic) Poincare polynomials
are inverse to each other: Since the motivic Poincare polynomial
| (23) |
is known explicitly (see e.g. [37]), this determines Substituting here we have the same relation between exponential generating functions of the Euler characteristics
Since we see that is the compositional inverse of the series which allows to compute giving OEIS sequence A074059:
It is interesting that for the real version of Deligne-Mumford spaces McMullen proved that the same relation
describes the functional inversion of the usual power series (see Corollary 5 in [44]).
Over finite fields one can interpret these results within the approach of Weil and Deligne as follows.
Let with prime be the finite field with elements and be the corresponding varieties over Let and be the number of points in these varieties respectively.
Theorem 4.1.
The generating power series of the number of points in and
| (24) |
are compositionally inverse to each other for all primes
Proof.
The number of points in is easy to compute directly:
with
The number of points in was computed by Amburg, Kreines and Shabat in [3], who proved, in particular, that this number coincides with the value of the Poincare polynomial when :
Since motivic Poincare polynomial of is given by (23), we have the same relation for : Now the proof follows from Getzler’s result. ∎
5. Inversion formula and permutohedral varieties
The permutohedral variety is the toric variety [22], corresponding to the -dimensional permutohedron . In particular, , is the degree 6 del Pezzo surface.
Every toric variety is a closure of the algebraic torus , which can be defined as the motivic interior of .
To justify this consider the Grothendieck ring of complex quasi-projective varieties generated by the isomorphism classes of complex quasi-projective varieties modulo the relations
where is a Zariski locally closed subset of , with multiplication given by the formula (see e.g. [33]).
Let be the smooth toric variety corresponding to a Delzant polytope and be the toric subvariety corresponding to the face
The following result provides more justification for our definition of the motivic interior. In analogy with (4) define the motivic interior of as
| (25) |
Proposition 5.1.
In the Grothendieck ring we have the relation
| (26) |
In other words, the motivic interior of toric variety is
The proof follows from the Proposition-definition 6 in [52] reformulated in terms of toric geometry [22] (see also Theorem 3.2.4 in [48]).
Note that similar relation holds for all convex polytopes if we extend it to the framework of the toric topology [15].
This implies that Theorem 3.5 can be reformulated as follows.
Theorem 5.2.
The exponential generating series of permutohedral varieties and algebraic tori
| (27) |
are multiplicatively inverse to each other in the ring
Motivic Poincare polynomial defines the ring homomorphism where for the projective varieties by definition
where is the usual Poincare polynomial. In particular, since is the complement of two points in , the motivic Poincare polynomial and thus
As a corollary we have the following well-known fact (see e.g. [50]) relating permutohedral varieties with the classical Eulerian polynomials [19]. These polynomials were introduced by Euler in 1755 by the relation
They have the generating function
| (28) |
and can be computed recursively by
Their coefficients are known as Eulerian numbers and have natural combinatorial interpretations (see [56]).
Corollary 5.3.
The Poincare polynomial of permutohedral varieties is
| (29) |
where are the Eulerian polynomials.
Proof.
The generating function of the motivic Poincare polynomials of the algebraic tori can be computed explicitly as
This means that
so from Theorem 5.1 we have
Comparing this with (28), we have the claim. ∎
6. Cyclohedra and Faà di Bruno’s formula
There is another remarkable family of the graph-polyhedra: cyclohedra (or Bott-Taubes polytopes) , corresponding to the -cycle graph. In particular, is hexagon and is polyhedron shown on Fig. 3.
These polytopes first appeared in Bott and Taubes [9] in connection with the link invariants, although implicitly they were already in the earlier work by Kontsevich [38] (see more detail in [24]).
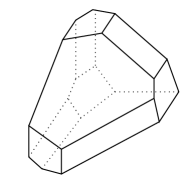
Its combinatorics was studied by Simion [55], who had shown, in particular, that the number of faces of dimension of equals
In particular, has vertices and facets. The corresponding boundary formula implies that the generating function satisfies the following non-autonomous linear differential equation
where are the corresponding function for the associahedra (6) and we set for simplicity . It is best to combine these two functions together as the solution of the following system of PDEs
| (30) |
The solution of this system with the prescribed initial values is given by (15) and
Substituting here we have the following result. Let be the motivic interior (4) of the cyclohedron
Theorem 6.1.
The generating function of the motivic interiors of the cyclohedra
| (31) |
is the result of the substitution into the series , which is the compositional inverse of the associahedral series given by (16).
The result of the substitution of formal series can be given by the following combinatorial formula attributed to Faà di Bruno (see the history in [35]). It has several important interpretations within the theory of Lie and Hopf algebras and operads [28], as well as relations with integrable systems [54].
For the formal power series Faà di Bruno formula has the following form. Let then the coefficients of the composition can be written as
| (32) |
where and the summation is taken over all integer such that In particular, we have
Combining this with the inversion formula (17), one can compute the coefficients of the function
assuming for convenience that :
The combinatorial formulas for the corresponding modification of the Bell polynomials in terms of the so-called pointed non-crossing partitions can be found in [4] (see Theorem 5.8).
As a corollary we have the following polytopal interpretation of the corresponding polynomials, which was first discovered by Aguiar and Bastidas in relation with the Faà di Bruno Hopf monoid [4] (see Theorem 5.6). Note that both composition and inversion of formal series are naturally embedded into the so-called Faà di Bruno Hopf algebra, playing important role in various problems of mathematics and physics, see [47] and references therein.
Corollary 6.2.
The motivic interior of the cyclohedron can be written in the algebra of polytopes as
| (33) |
In particular, we have the formulas
This is in agreement with the fact that is a hexagon and has 4 hexagonal, 4 pentagonal and 4 quadrilateral faces, 30 edges and 20 vertices (see Fig. 3). Again since cyclohedra are algebraically independent, these formulae are universal.
7. Equation and formulas for the stellohedra
There is another interesting graph-associahedron called stellohedron , corresponding to the star-graph with vertices (see Fig.4). In particular, is a pentagon and is the polyhedron shown on Fig.4. For more details about combinatorics of stellohedra we refer to [11, 50].
The corresponding boundary formula
implies that the corresponding exponential generating functions of stellohedra and permutohedra
satisfy the following system of equations
| (34) |
For given initial data this system can be easily solved explicitly as
(see [11, 15]). Substituting here and using theorem 3.5 we have
Theorem 7.1.
The exponential generating function of the motivic interiors of the stellohedra can be expressed via permutohedral generating functions (19) by the formula
| (35) |
In particular, using formulas (20) we have
in agreement with the fact that 3D stellohedron has 1 hexagonal, 6 pentagonal and 3 quadrilateral faces, 24 edges and 16 vertices (see Fig. 4).
Corollary 7.2.
The exponential generating function of the numbers of vertices of the stellohedra has the form
| (36) |
In particular, this implies that the number of vertices is
More general formulas, expressing the number of faces of stellohedra of any dimension, can be found in [11] (Section 9) and [50] (Section 10.4).
For completeness consider also the families of simplices with vertices and -dimensional cubes and define
The corresponding exponential generating functions
satisfy the differential equations [15]
Solving them explicitly with initial data :
we come to the binomial formulas for the interiors
It is interesting to note that the polynomials form the universal Appell sequence [6], satisfying the characteristic relation (see [7], Ch. 19.3).
8. Concluding remarks
We have seen that associahedra and permutohedra play a special role in the differential algebra of graph-associahedra, generating subalgebras of the polytopal algebra , which are invariant under the differentiation. This explains their relation with the differential equations and ultimately with the inversion formulas.
The families of cyclohedra and stellohedra generate the subalgebras of , which can be viewed as the modules over the differential subalgebras generated by associahedra and permutohedra respectively. In the language of operads this was pointed out in [43] (see also [24, 58]). The description of all such subalgebras and modules over them within the differential algebra of polytopes seems to be a very interesting open problem.
The equations which appeared here are easily solvable, which hints the link with the theory of integrable systems. At the combinatorial level this link was already discussed in the literature, see e.g. [26, 39, 47, 54] and references therein. However, a general picture of the relations between combinatorics and integrable systems seems to be quite rich and needs better understanding (see [1, 2] for some very interesting thoughts in this direction).
In this relation it is worthy to mention that the Hopf equation , which appeared in our paper in relation with associahedra, is the dispersionless limit of the celebrated KdV equation
well-known in soliton theory and enumerative algebraic geometry. In particular, according to Witten [60] the KdV hierarchy determines a certain generating function of the characteristic numbers of (see [40] for the detail), which makes the appearance of the inversion formula in the theory of the moduli spaces (discussed in Section 4) a bit less mysterious.
We would like to comment on the choice of the coefficients in the generating functions Most common cases are and , corresponding to the usual and exponential generating functions. However, we have seen that in the case of cyclohedra the most appropriate choice is , related to the usual choice by integration. The role of different choices of in Boas-Buck’s approach [8] to the generating functions was emphasized in [12]. Note that both composition and multiplication of power series play the central role in this approach, going back to Appell [6] and providing umbrella for many classical polynomials.
Since the graph-associahedra are indecomposable, it is natural to ask if the corresponding -polynomials are irreducible over . For example, for the permutohedra the corresponding -polynomials are the Eulerian polynomials . It is known that is divisible by (which is -polynomial of the segment), but there is a conjecture that and are irreducible over (see [34]). It would be interesting to study similar question for other graph-assiciahedra from our paper.
9. Acknowledgements.
We are very grateful to Vsevolod Adler, Alexander Braverman, Nikolai Erokhovets, Alexander Gaifullin and Georgy Shabat for the useful discussions, to Jose Bastidas, who attracted our attention to the preprint [4] and to Jim Stasheff for the encouraging comments.
References
- [1] V.E. Adler On the combinatorics of several integrable hierarchies. J. Phys. A 48 (26) (2015), 265203.
- [2] V.E. Adler Set partitions and integrable hierarchies. Theor. Math.Physics 187:3 (2016), 842-870.
- [3] N. Amburg, E. Kreines, G. Shabat Poincare polynomial for the moduli space and the number of points in Moscow Univ. Math. Bull., 72 (2017),154-160.
- [4] M. Aguiar, J. Bastidas Associahedra, cyclohedra and inversion of power series. arXiv:2010.14283 (2020).
- [5] M. Aguiar, F. Ardila Hopf Monoids and Generalized Permutahedra. Memoirs of the AMS. Vol. 289, N.1437. AMS, 2023. arXiv:1709.07504 (2017).
- [6] P. Appell Sur une classe de polynômes. Annales Sci. École Norm. Supér. 2e Sèrie. 9 (1880), 119-144.
- [7] H. Bateman and A. Erdélyi Higher Transcendental Functions. Vol.III. McGraw-Hill Book Company, 1955.
- [8] R.P. Boas, R.C. Buck Polynomial expansion of analytic functions. Springer, 1958.
- [9] R. Bott and C. Taubes On the self-linking of knots. Journal of Math. Physics 35(10) (1994), 5247-5287.
- [10] V. M. Buchstaber, E. V. Koritskaya The quasi-linear Burgers-Hopf equation and the Stasheff polytopes. Funct. Anal. Appl. 41:3 (2007), 196-207.
- [11] V.M. Buchstaber Ring of simple polyhedra and differential equations. Trudy MIAN 263 (2008), 18-43.
- [12] V.M. Buchstaber, A.N. Kholodov Boas-Buck structures on sequences of polynomials. Funct. Anal. Appl. 23:4 (1989), 266-276.
- [13] V.M. Buchstaber, N. Erokhovets. Polytopes, Fibonacci numbers, Hopf algebras, and quasi-symmetric functions. Russian Math. Surveys 66 (2011), no. 2, 271-367.
- [14] V. M. Buchstaber, V. D. Volodin Combinatorial 2-truncated cubes and applications. Progress in Mathematics, 299 (2012), Birkhäuser, Basel, 161-186.
- [15] V.M. Buchstaber, T.E. Panov Toric Topology. Mathematical Surveys and Monographs, 204, AMS, 2015.
- [16] V.M. Buchstaber, A.P. Veselov Chern-Dold character in complex cobordisms and theta divisors. Advances in Math. 449 (2024), 109720, 1-35.
- [17] V.M. Buchstaber, A.P. Veselov Theta divisors and permutohedra. arXiv:2211.16042.
- [18] V.M. Buchstaber, S. Tersic̀ Moduli space of weighted pointed stable curves and toric topology of Grassmann manifolds. arXiv:2410.01059.
- [19] L. Carlitz Eulerian numbers and polynomials. Mathematics Magazine 32:5 (1959), 247-260.
- [20] M.P. Carr and S.L. Devadoss Coxeter complexes and graph-associahedra. Topology Appl. 153 (2006), no. 12, 2155-2168.
- [21] L. Comtet Advanced Combinatorics. D. Reidel Publ. Comp., Dordrecht, 1974.
- [22] D.A. Cox, J.B. Little, and H.K. Schenck Toric Varieties. Graduate Studies in Mathematics, vol. 124, American Mathematical Society, Providence, RI, 2011.
- [23] S.L. Devadoss Tesselations of moduli spaces and the mosaic operad. Contemp. Math. 239 (1999), 91–114.
- [24] S.L. Devadoss Space of cyclohedra. Discrete and Comput. Geometry 29 (2002), 61-75.
- [25] S.L. Devadoss and R.C. Read Cellular structures determined by polygons and trees. Annals of Combinatorics, 5 (2001), 71–98.
- [26] G. Falqui, C. Reina and A. Zampa Krichever maps, Faà di Bruno polynomials, and cohomology in KP theory. Lett. Math. Phys. 42 (1997), 349-361.
- [27] E.M. Feichtner and B. Sturmfels Matroid polytopes, nested sets and Bergman fans. Port. Math. (N.S.) 62 (2005), no. 4, 437-468.
- [28] A. Frabetti, D. Manchon Five interpretations of Faà di Bruno’s formula. arXiv:1402.5551 (2014).
- [29] A.A. Gaifullin Local formulae for combinatorial Pontrjagin classes. Izvestiya: Mathematics 68:5 (2004), 861-910.
- [30] I. M. Gelfand, M. M. Kapranov, and A. V. Zelevinsky Discriminants, Resultants, and Multidimensional Determinants. Birkhäuser Boston Inc., Boston, MA, 1994.
- [31] I.M. Gessel Lagrange inversion. J. Comb. Theory, Series A 144 (2016), 212-249.
- [32] E. Getzler Operads and moduli spaces of genus 0 Riemann surfaces. Progress in Math. 129 (1995), Birkhäuser Boston, Boston, MA,199-230.
- [33] S. M. Gusein-Zade, I. Luengo and A. Melle-Hernández A power structure over the Grothendieck ring of varieties. Math. Res. Lett. 11 (2004), 49-57.
- [34] A.J.J. Heidrich On the Factorization of Eulerian Polynomials. J. Number Theory 18 (1984), 157-168.
- [35] W.P. Johnson The curious history of Faà di Bruno’s formula. Amer. Math. Monthly 109:3 (2002), 217-234.
- [36] M.M. Kapranov The permutoassociahedron, Mac Lane’s coherence theorem and asymptotic zones for the KZ equation. J. Pure Appl. Algebra 85 (1993), no. 2, 119–142.
- [37] M.E. Kazaryan, S.K. Lando and V.V. Prasolov Algebraic Curves: Towards Moduli Spaces. Springer, 2019.
- [38] M. Kontsevich Feynman diagrams and low-dimensional topology. Progr. Math. 120 (1994), 97-121.
- [39] F. Lambert, J. Springael Soliton equations and simple combinatorics. Acta Appl. Math. 102 (2008), 147-178.
- [40] S.K. Lando, A.K. Zvonkin Graphs on Surfaces and Their Applications. Encyclopaedia of Mathematical Sciences, 141, Berlin, New York: Springer-Verlag, 2004.
- [41] J.-L. Loday The multiple faces of the associahedron. Clay Mathematics Institute Publication, 2005.
- [42] A. Losev and Y. Manin New moduli spaces of pointed curves and pencils of flat connec- tions. Michigan Math. J. 48 (2000), 443-472.
- [43] M. Markl Simplex, associahedron, and cyclohedron. Contemp. Math. 227, Amer. Math. Soc., Providence, RI, 1999.
- [44] C.T. McMullen Moduli spaces in genus zero and inversion of power series. L’Enseign. Math. (2) 60 (2014), 25–30.
- [45] P. McMullen Valuations and Euler-type relations on certain classes of convex polytopes. Proc. London Math. Soc. 35 (1977), 113-130.
- [46] P. McMullen The polytope algebra. Adv. Math. 78 (1989), 76-130.
- [47] Y. Mvondo-She From Hurwitz numbers to Feynman diagrams: Counting rooted trees in log gravity. Nuclear Physics B 995 (2023), 116350.
- [48] J. Nicaise Grothendieck rings of polytopes and non-archimedean semi-algebraic sets. arXiv:2402.11699.
- [49] V. Pilaud, F. Santos, G.M. Ziegler Celebrating Loday’s associahedron. Arch. Math. 121 (2023), 559–601.
- [50] A. Postnikov, V. Reiner, L. Williams Faces of generalized permutohedra. Doc. Math. 13 (2008), 207-273.
- [51] A. Postnikov Permutohedra, associahedra, and beyond. IMRN, 2009 (6), 1026-1106.
- [52] A.V. Pukhlikov, A.G. Khovanski Finitely additive measures of virtual polytopes. St. Petersburg Math. J. 4 (1993), no. 2, 337-356.
- [53] G.N. Raney Functional composition patterns and power series reversion. Trans. Amer. Math. Soc. 94 (1960), 441-451.
- [54] A.B. Shabat, M.Kh. Efendiev On applications of Faà-di-Bruno formula. Ufa Math. Journal 9:3 (2017), 131-136.
- [55] R. Simion A type-B associahedron. Advances in Applied Math. 30 (2003), 2-25.
- [56] R.P. Stanley Enumerative Combinatorics. Vol. 2. Cambridge University Press, 1999.
- [57] J. Stasheff Homotopy associativity of -spaces. I, II. Trans. Amer. Math. Soc. 108 (1963), 275–312.
- [58] J. D. Stasheff The pre-history of operads. Contemp. Math. 202 (1997), 53-81.
- [59] V. Toledano Laredo Quasi-Coxeter algebras, Dynkin diagram cohomology, and quantum Weyl groups. Int. Math. Res. Pap. IMRP 2008, Article ID rpn009, 167 pp.
- [60] E. Witten Two-dimensional gravity and intersection theory on moduli space. Surveys Diff.Geom. 1 (1991), 243-310.
- [61] G.M. Ziegler Lectures on Polytopes. Springer-Verlag, New York, 1995.