Differential cumulants, hierarchical models and monomial ideals
Abstract
For a joint probability density function of a random vector the mixed partial derivatives of can be interpreted as limiting cumulants in an infinitesimally small open neighborhood around . Moreover, setting them to zero everywhere gives independence and conditional independence conditions. The latter conditions can be mapped, using an algebraic differential duality, into monomial ideal conditions. This provides an isomorphism between hierarchical models and monomial ideals. It is thus shown that certain monomial ideals are associated with particular classes of hierarchical models.
Keywords: Differential cumulants, conditional independence, hierarchical models, monomial ideals.
1 Introduction
This paper draws together three areas: a new concept of differential cumulants, hierarchical models and the theory of monomial ideals in algebra. The central idea is that for a strictly positive density of a -dimensional random vector , the mixed partial derivative of the log density can be used to express independence and conditional independence statements. Thus, for random variables , the condition
| (1) |
is equivalent to the conditional independence statement
In the next section we show how such mixed partial derivatives can be interpreted as differential cumulants. Then, in section 3, we show how collections of differential equations like (1) can be used to express independence and conditional independence models. Section 4 shows that, more generally, these collections can be used to define hierarchical statistical models of exponential form.
Section 5 maps the hierarchical model conditions to monomial ideals, which are increasingly being used within algebraic statistics. This isomorphism maps, for example, the mixed partial derivative condition (1) to the monomial ideal within the polynomial ring . The equivalence allows ideal properties to be interpreted as hierarchical model properties, opening up an algebraic-statistical interface with some potential.
2 Local and differential cumulants
This section can be considered as a development from a body of work on local correlation. Good examples are the papers of Holland & Wang (1987), Jones (1996) and Bairamov et al. (2003). We draw particularly on Mueller & Yan (2001).
Let be a random vector. We assume has a times continuously differentiable density . Once we introduce the concept of differential cumulants, we further require be strictly positive.
For we set and Let and denote the moment and cumulant generating functions of respectively. For a vector we set
where is the Manhattan norm. By convention .
The cumulant can be found by evaluating at zero. We use the multivariate chain rule (given e.g. in Hardy, 2006) stated in Theorem 1. At the heart of the chain rule is an identification of differential operators with multisets:
Definition 1 (Multiset, multiplicity, size).
A multiset is a set which may hold multiple copies of its elements. The number of occurrences of an element is its multiplicity. The multiplicity of a multiset is the vector of multiplicities of its elements, denoted by . The total number of elements in is the size. A multiset which is a set is called degenerate.
Example 1 (Partial derivative and multiset).
The partial derivative has associated multiset with multiplicity and size four.
Definition 2 (Partition of a multiset).
Let be some index set and be a family of multisets with associated family of multiplicities . A partition of a multiset is a multiset of multisets such that . Being a multiset itself, a partition can hold multiple copies of one or more multisets.
Example 2 (Partition of a multiset).
The multiset is a partition of , since . In the following, we will use the shorthand .
Associated with a partition of a multiset is a combinatorial quantity to which we refer as the collapse number . It is defined as
See Hardy (2006) for a combinatorial interpretation of .
Theorem 1 (Higher order derivative of chain functions).
where is the set of all partitions of a multiset with multiplicity and is the j-th multiset in the partition .
Proof.
See Hardy (2006). ∎
Corollary 1 (Cumulants as functions of moments).
Let be the k-th cumulant. Then
| (2) |
Proof.
Set , and evaluate at . ∎
Example 3 (Partial derivative).
Consider the partial derivative . The associated multiset is with partitions , , , . The multivariate chain rule tells us that
where function arguments have been suppressed on the right hand side for better readability. In particular we may conclude that
The expression for cumulants in terms of moments is particularly simple in what we shall call the square-free case, that is for cumulants , whose index vector is binary. In that case, the multiset associated with is degenerate and . Equation (2) simplifies to
In this form it is often stated and derived via the classical Faa Di Bruno formula applied to an exponential function followed by a Moebius inversion (see e.g. Barndorff-Nielsen & Cox, 1989).
Local analogues to moments and cumulants can be derived as one considers their limiting counterparts in the neighborhood of a fixed point , an idea proposed by Mueller & Yan (2001). This section derives formulae for local moments and cumulants and local moment generating functions provided its global counterpart exists.
For a strictly positive edge length , let denote the hyper cube centralized at . Let denote its volume. The density of the random variable conditional on being in is given by
where is the indicator function which returns unity if is in and zero otherwise. The conditional moments about are denoted by
Let and denote the set of positive even and odd integers respectively. For symmetry reasons, even and odd orders of individual components have different effects on local moments, which motivates the following definition:
increments the total sum of the components of a vector by one additional unit for each odd component (it is not to be interpreted as a norm).
Theorem 2 (Local moments).
Let be an absolutely continuous random vector with density which is times differentiable in . Let determine the order of moment. Then, for sufficiently small, has local moment
| (3) |
where and .
Proof.
Consider
| (4) |
Approximate through its -th order Taylor expansion, integrate (4) term by term and exploit the point symmetry of odd order terms about the origin. ∎
Example 4 (Local moment ).
Consider a tri-variate random variable with local moment Then and we obtain
A natural way to extend the concept of a local moment is to consider the limiting case when . This leads to our definition of differential moments.
Definition 3 (Differential moment).
The differential moment of an absolutely continuous random vector in is defined as:
Corollary 2 (Differential moment).
For a differential moment of order in it holds that
Proof.
This follows from Theorem 2 upon taking the limit as . ∎
From (3) it is clear that the choice of in the derivative depends only on the pattern of odd and even components of the moment. To be precise, holds a unity corresponding to odd components and a zero corresponding to even component entries. Consequently, the differential moment depends on only via the pattern of odd and even values.
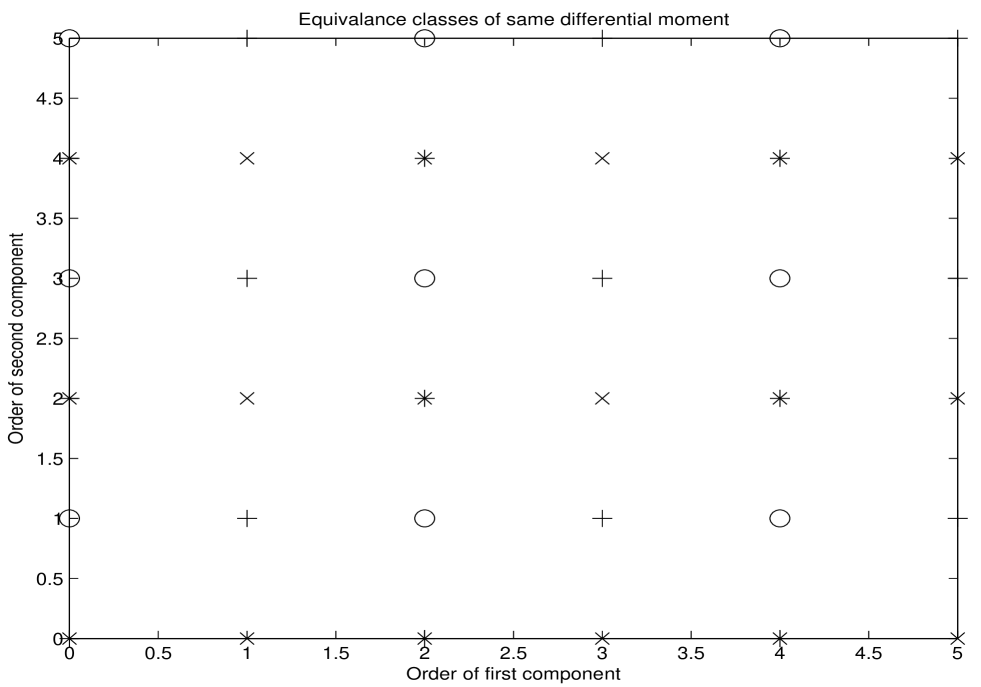
This suggests defining an equivalence relation on : For set . The relation partitions the product space into equivalence classes of same differential moments. The graph corresponding to is depicted in Figure 1 for the bivariate case. The axes give the order of the moment for the two components. Different symbols represent different equivalence classes. For instance, , since . Note that .
Similarly to local moments, for any measurable set we can define a local moment generating function:
Being a conditional expectation, it exists if exists. We have the following expansion:
The local moments can be computed from the local moment generating function via differentiation to appropriate order and evaluation at . The natural logarithm of the local moment generating function defines the local cumulant generating function :
Corollary 3 (Local cumulants).
Under the conditions of Theorem 2 it holds for the local cumulants that
where is a function of the partition and defined as
that is, is binary and holds ones corresponding to odd elements of . Furthermore,
Proof.
Combine the chain rule and Theorem 2. ∎
Similarly to differential moments we can define differential cumulants at . Two different ways of doing so are natural. First, taking the limiting quantity of the local cumulants as or, second, taking the series of differential moments and requiring that the mapping between moments and cumulants is preserved which is induced through the ex-log relation of the associated generating functions, see also the discussion in (McCullagh, 1987, page 62).
As demonstrated below, the two quantities just described differ in general and coincide only in the square-free case. In order to retain the intuitive and familiar relation between cumulants and moments, we define differential cumulants in terms of differential moments.
Definition 4 (Differential cumulant).
For an index vector , the differential cumulant in is defined as
We are now in a position to state the main result of this section, namely that mixed partial derivatives of the log density can be interpreted as differential cumulants.
Lemma 1 (Differential cumulant).
For a differential cumulant in of order it holds that
where projects odd elements of onto one and even elements of onto zero.
Proof.
Apply the chain rule to . ∎
This is a multivariate generalization of the local dependence function introduced by Holland & Wang (1987). The next theorem relates differential cumulants to the limit of local cumulants.
Theorem 3 (Differential and limiting local cumulant).
A differential cumulant equals the limit of the local cumulant if and only if is binary, i.e. is a square-free cumulant.
Proof.
First, let be binary and be a partition of the lattice corresponding to . One can show that . With that
| (5) |
Now take limits as to obtain
Conversely, suppose is not binary. Express as a linear combination of local moments. Consider the degenerate partition , which holds only one multiset with multiplicity . The quantity associated with converges to for some constant . not being binary, this cannot be a differential moment, which are proportional to for some binary . Differential cumulants are linear combinations of differential moment products only. Hence does not converge to a differential cumulant. ∎
Of particular interest to us are differential cumulants which vanish everywhere. We refer to them as zero-cumulants. Writing , we shall usually write to denote the zero-cumulant associated with in the understanding that this holds for all .
The next section shows that sets of zero cumulants are isomorphic to conditional independence statements. As a consequence of lemma 1 zero-cumulants are invariant under diagonal transformations of the random vector . In particular, they are not affected by the probability integral transformation and hence any result below holds also true for the copula density of .
3 Independence and conditional independence
From now on, we shall assume that is strictly positive everywhere. Sets of zero-cumulants are equivalent to conditional and unconditional dependency structures.
Proposition 1 (Independence in the bivariate case).
Let . Then .
Proof.
for some functions . ∎
In the multivariate case, we can express conditional independence of any pair given the remaining variables through square free differential cumulants.
Proposition 2 (Conditional independence of two random variables).
Let . Then
where
and .
Proof.
By analogy with the bivariate case. ∎
Setting several square-free differential cumulants to zero simultaneously allows us to express conditional independence statements.
Proposition 3 (Multivariate conditional independence).
Given three index sets which partition , let . Then
Proof.
From proposition 2 it is clear, that this is equivalent to the conditional independence statement
Sufficiency () and necessity () are semi-graphoid and graphoid axioms referred to as decomposition and intersection respectively. Both hold true for strictly positive conditional densities (see for instance Cozman & Walley, 2005). ∎
Pairwise conditional independence of all pairs is equivalent to independence.
Theorem 4 (Pairwise conditional independence if and only if independence).
The random variables are independent if and only if .
Proof.
Sufficiency follows from differentiation of the log-density. Necessity can be proved by induction on the number of variables . The statement is true for by proposition 1. Let the statement be true for and let the differential cumulants vanish, where and are unit vectors in . Consider . Integration with respect to and yields
| (6) |
for some functions and . Now integrate again with respect to to obtain
The left hand side is an n-dimensional marginal density which factorises into marginals by induction assumption: This allows us to conclude that can be split into a sum of two functions, and , where the latter is a function of only, i.e. Considering (6) again we see that the density factorises
Hence and the density of factorises by induction assumption. ∎
4 Hierarchical models
The analysis of the last section makes clear that setting certain mixed two-way partial derivatives of equal to zero, is equivalent to independence or conditional independence statements. We can go further and define a generalized hierarchical model using the same process.
The basic structure of a hierarchical model can be define via a simplicial complex. Thus let be the vertex set representing the random variables . A collection of index sets is a simplicial complex if it is closed under taking subsets, i.e. if and then .
Definition 5.
Given a simplicial complex over an index set and an absolutely continuous random vector a hierarchical model for the joint distribution function takes the form:
where and is the canonical projection of onto the subspace associated with the index set .
This is equivalent to a quasi-additive model for and we also refer to this model for as being hierarchical. It is clear that we may write the model over the maximal cliques only, namely simplexes which are not contained in a larger simplex. In the terminology of Lauritzen (1996) we require be positive and factorise according to for it to be a hierarchical model with respect to .
Associated to an index set is a differential operator , where holds ones for every member of and zeros otherwise. In the following, we overload the differential operator by allowing it to be superscripted by a set or by a vector. Thus, for an index set we set and similarly . returns the differential cumulant , when applied to .
Example 5.
Let . We obtain and
We collect the results of the last section into a comprehensive statement. First, we define the complementary complex to a simplicial complex on .
Definition 6.
Given a simplicial complex on an index set we define the complementary complex as the collection of every index set which is not a member of .
Note immediately that is closed under unions, i.e. . It is a main point of this paper that there is a duality between setting collections of mixed differential cumulants equal to zero and a general hierarchical model:
Theorem 5.
Given a simplicial complex on an index set , a model is hierarchical, based on if and only if all differential cumulants on the complementary complex vanish everywhere, that is
Proof.
First, let be hierarchical with respect to , that is is a log-density with representation . Then, for , the associated differential operator annihilates any term in , since .
5 The duality with monomial ideals
The growing area of algebraic statistics makes use of computational commutative algebra particularly for discrete probability model, notably Poisson and multinomial log-linear models. Work connecting the algebraic methods to continuous probability models is sparser although considerable process has been made in the Gaussian case. For an overview see Drton et al. (2009). Our link to the algebra is via monomial ideals.
A monomial in is a product of the form , where . A monomial ideal is a subset of a polynomial ring such that any can be written as a finite polynomial combination , where and for all . We write to express that is generated by the family of monomials .
The full set of monomials contained in monomial ideal has the hierarchical structure:
| (7) |
for any index set . A monomial ideal is square-free if its generators are square free, i.e. .
The following discussion shows that there is complete duality between the structure of square-free monomial ideals and hierarchical models. Associated with a simplicial complex is its Stanley-Reisner ideal . This is the ideal generated by all square-free monomial in the complementary complex . For a face let denote the associated square-free monomial. Then
The second step, which is a main point of the paper, is to associate the differential operator with the monomial . We need only confirm that the hierarchical structure implied by (7) is consistent with differential conditions of Theorem 5.
Without loss of generality include all differential operators which are obtained by continued differentiation. Then, (7) is mapped exactly to
simply by continued differentiation. This bijective mapping from monomial ideals into differential operators, is sometimes referred to as a “polarity” and within differential ideal theory has its origins in “Seidenberg’s differential nullstellensatz” (Seidenberg, 1956). It allows us to map properties of hierarchical models in statistics to monomial ideal properties and vice versa.
One of the main conditions discussed in the theory of hierarchical models in statistics is the decomposability of a joint density function into a product of certain marginal probabilities. Simple conditional probability is a canonical case. Thus with the conditional independence is represented by the graph . In this case the graph has the model simplicial complex: , where, again, we write in terms of its maximal cliques. The Stanley-Reisner ideal is .
There is a factorization:
Decomposable graphical models, discussed below, are a generalization of this simple case. There are other cases, however, where one or more factorizations are associated with the same simplicial complex. An example is the -cycle: with The Stanley-Reisner ideal . Although this ideal is rather simple from an algebraic point of view the 4-cycle from a statistical point of view is rather complex. By considering special ideals we obtain general classes of models, in a subsection 5.2.
Another issue is that the structure of may suggest factorizations even when they are problematical. Perhaps the first such case is the 3-cycle: . The Stanley-Reisner ideal is . The maximal clique log-density representation has no three-way interaction:
This might suggest the factorization
| (8) |
A factorization of this kind is the continuous analogue to a perfect three-dimensional table in the discrete case (Darroch, 1962). However, except when are independent we have not been able to provide a standard density for which (8) holds.
5.1 Decomposability and marginality
Our use of the index set notation makes its straightforward to define decomposability.
Definition 7.
Let be the vertex set of a graph and vertex sets such that . Then is decomposable if and only if is complete and forms a maximal clique or the subgraph based on is decomposable and similarly for .
Under this condition the corresponding hierarchical model has a factorization
where the numerator on the right hand side corresponds to cliques and the denominator to separators which arise in the continued factorization under the definition.
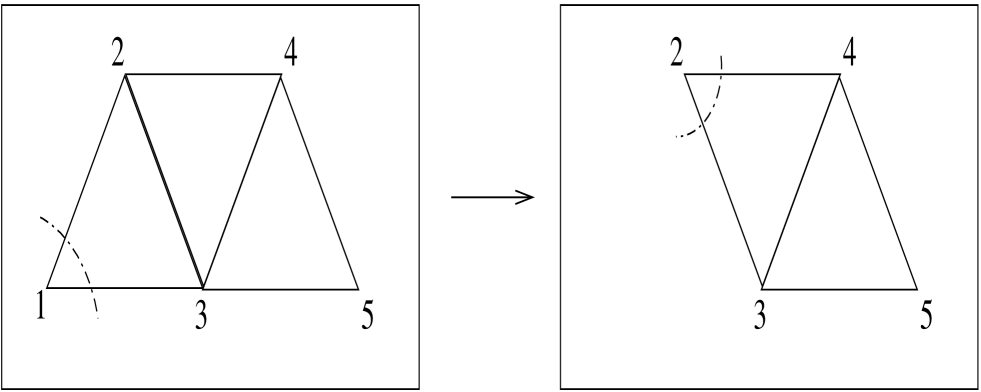
It is important to realize that in order to proceed with the factorization at each stage a marginalisation step is required. Consider the simple case based on the simplicial complex . One choice of factorization at first stage is (with simplified notation):
and we continue the factorization to give
The process of marginalisation is shown in Figure 2. At any stage, we may choose to marginalise with respect to any variable that is member of just a single clique. In the first step these are and and suppose we chose to single out . Once has been integrated with respect to , the marginal model for is obtained. The removal of a the clique leads to being exposed and we may continue with or etc.
The Stanley-Reisner ideal is an ideal in . The factorization of is, however, mapped into the monomial ideal which is an ideal in . A marginalisation has allowed us to drop from five dimensions to four. This is clear from the exponential expression of the model:
Integrating with respect to we obtain a hierarchical model for the marginal joint distribution of . This marginalisation is possible because appears only in the single clique .
We have exposed an interesting relationship between the statistical and algebra formulation: in order to reduce the dimensionality and obtain the Stanley-Reisner ideal for a reduced set of variables, we must first perform a marginalisation, which is a non-algebraic operation, at least, not in general a finite dimensional operation. We capture this in the following Lemma:
Lemma 2.
Whenever a simplicial complex of hierarchical model has a subset of vertexes which form a facet of a unique maximal clique (simplex) then the marginal model obtained by deleting this facet (and its connections) is valid. Moreover the monomial ideal representation is obtained by deleting any generators containing the corresponding variables and is in the ring without these variables.
Proof.
This follows the lines of the example. If is the subset of vertexes and , with , is the unique maximal clique, then in the exponential expression for the density there will be a unique term in which appears. Integrating with respect to to obtain the marginal distribution for gives the reduced model. The monomial ideal representation follows accordingly. ∎
5.2 Artinian closure and polynomial exponential models
The terms which appear in the hierarchical models have not been given any special form. In fact it is a main point of this paper that this is not required to give the monomial ideal equivalence. We note, again, that we always use square-free monomial ideals.
Certain classes of hierarchical models can, however, be obtained by imposing further differential conditions. The following lemma shows that the log-density is polynomial if we impose univariate derivative restriction.
Lemma 3.
If in addition to the differential conditions in Theorem 5 we impose conditions of the form
| (9) |
the -functions in the corresponding hierarchical model are polynomials, in which the degree of does not exceed .
Proof.
Repeated integration with respect to shows that is indeed a polynomial in of degree less than , when the other variable are fixed. Since this holds for all the result follows. ∎
The simultaneous inclusions of derivative operators with respect to one indeterminate in (9) constitutes an Artinian closure of the differential version of the Stanley-Reisner ideal .
Example 6 (BEC density).
Suppose is bivariate and we impose the symmetric Artinian closure conditions
Then integration yields
| and | |||
A comparison of these functionals identifies for some for all , so that can be written as
| (10) |
It can be shown that is distributed exponentially conditional on for all and vice versa. A distributions with that property is called bivariate exponential conditionals (BEC) distribution. BEC distributions are completely described by in the sense that any BEC density is of the form (10) (Arnold & Strauss, 1988). In particular, the independence case is included, if we force by imposing the additional restriction
This confirms Proposition 1 for this particular example.
The previous example extends readily into higher dimension. We call a distribution multivariate exponential conditionals (MEC) distribution, if is distributed exponentially conditional on for all . We capture the extension to the -dimensional case in the following lemma:
Lemma 4 (MEC distributions and Artinian closure).
The following statements are equivalent:
-
1.
A distribution belongs to the class of MEC distributions
-
2.
is multi-linear, i.e there exist indices such that , where denotes the set of dimensional binary vectors
-
3.
Proof.
For a proof of see Arnold & Strauss (1988). The proof of follows the lines of the example. ∎
Another case of considerable importance is the Gaussian distribution. Here
and the maximal cliques are of degree two. The latter condition is partly obtained with an Artinian closure with . However, more is required. We can guess, from the fact that for a normal distribution all (ordinary) cumulants of degree three and above are zero, that if we impose all degree-three differential cumulant to be zero we obtain polynomial terms of maximum degree 2. This is, in fact the correct set of conditions to make the models terms of degree at most two. In the -notation the conditions are
which includes the Artinian closure conditions. The corresponding ideal is generated by all polynomials of degree three. For a non-singular multivariate Gaussian, we, of course, require non-negative definiteness of the degree-two part of the model, considered as a quadratic form.
The hierarchical model is given by additional restrictions which are equivalent to removing certain terms of the form . This is the same as setting the corresponding -th entry in the inverse covariance matrix (influence matrix) equal to zero. The removed generate the Stanley-Reisner ideal so that the zero structure of the influence matrix completely determines the ideal.
5.3 Ideal-generated models
The duality between monomial ideals and hierarchical models encourages the investigation of the properties of hierarchical models for different types of ideals. There are some important properties and features of monomial ideals which may be linked to the corresponding hierarchical models and we mention just a few here in an attempt to introduce a larger research programme.
We begin with the sub-class of decomposable models. It is well know from the statistical literature (see Lauritzen, 1996) that the decomposability property of the model based on a simplicial complex is equivalent to the chordal property: there is no chord-less 4-cycle. Remarkably, the latter is equivalent to a property of the Stanley-Reisner ideal , namely: that the minimal free resolution of be linear(see below for a brief explanation). This is a result of Fröberg (1988), see also Dochtermann & Engström (2009). Petrovic & Stokes (2010) adapt a result of Geiger et al. (2006) to show that , in this case, is generated in degree 2, that is all its generators have degree 2.
Theorem 6.
A decomposable graphical model has a “2-linear” resolution.
The term linear refers to the structure of the minimal free resolution of . In this resolution there are monomial maps between the stages of the resolution sequence. Linear means that these maps are linear. As a simple example consider again the simplicial complex with Stanley-Reisner ideal The minimal free resolution of is given by:
and one sees that the map is linear. By contrast, the 4-cycle is generated in degree 2, but is not linear:
giving a non-linear map.
A special case of 2-linear resolutions are Ferrer ideals. A Ferrer ideal is one in which the degree-two linear generators can be placed in a table with an inverse stair-case. Such staircases arose historically in the study of integer partitions. As an example take the Stanley-Reisner ideal
The Ferrer table is:
Considering the non-empty cells as given by edges this corresponds to a special type of bi-partite graph between nodes and . Corso & Nagel (2009) show that, among the class of bi-partite graphs, Ferrer ideals are indeed uniquely characterized as having a 2-linear minimal free resolution.
It is straightforward to show that the corresponding hierarchical model is decomposable by exhibiting the decomposition given by Lemma 2. First take two simplices based on the variables defining, respectively, the rows and columns. In the example these are . Then join all nodes corresponding to the complement of the Ferrer diagram to give:
The maximal cliques are easily seen to be given by a simple rule on this complementary table. For each non-empty row take the variable which defines that row together with every other variables for nonempty columns in that row and all the variables for the rows below that row. In this example we find, working down the rows, that the maximal cliques are:
Note how to this example we can apply Lemma 2, by successively stripping off variables in the order: . The separators are . The rule provides a proof of the following.
Theorem 7.
Hierarchical models generated by Ferrer ideals are decomposable.
As another illustration of the duality between monomial ideals and conditional independence structures, we next consider two terminal networks. In Sáenz de Cabezón & Wynn (2010) the authors apply the theory and construction of minimal free resolutions to the theory of reliability. One sub-class of these is to networks, in the classical sense of network reliability. Consider a connected graph , with two identified nodes called input and output, respectively. A cut is a set of edges, which if removed from the graph disconnects input and output. A path is connected set of edges from input to output. A minimal cut is a cut for which no proper subset is a cut and minimal path is a path for which no proper subset is a path.
As a simple example consider the network depicted in Figure 3 with input and output and edges:
The minimal cuts are . If we associate a variable with each edge then the minimal cuts generate an ideal. In this example we write
The maximal cliques of for the corresponding model simplicial complex are
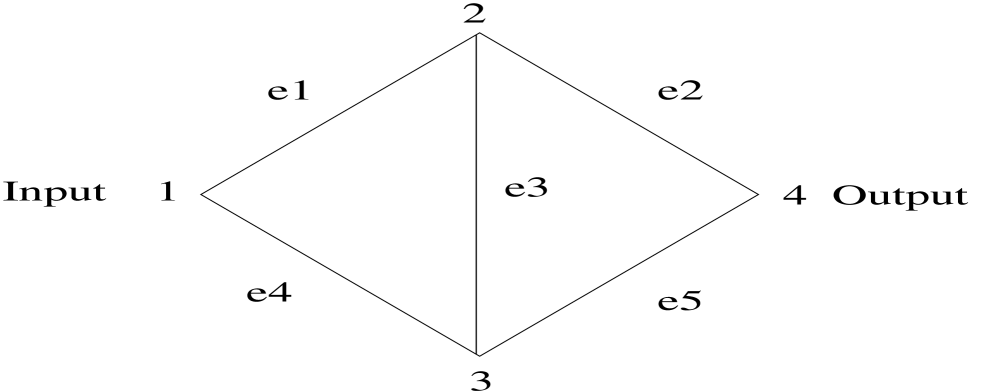
We could, on the other hand define as being the collection of all paths on the network. In this case the is generated by the minimal paths giving:
and consists of the complements of the cuts and has maximal cliques .
There is a duality between cuts and path models for two-terminal networks:
Lemma 5.
The model simplicial complex based on the cut ideal of a two terminal network is formed from the complement of all paths on the network. Conversely, the model simplicial complex based on the path ideal , is formed from the complement of all cuts. Moreover: .
For example, the term of is the complement of the (non-minimal) path and the term in is the complement the (non-minimal) cut .
This duality is a special example of Alexander duality and we omit the proof, see Miller & Sturmfels (2005), Proposition 1.37. The general result says that for a square-free , if we define as the complement of all non-faces of , then .
It will have been noticed that for this network and are self-dual in the sense that the two simplicial complexes have the same structure and only differ in the labelling of the vertexes. Both models have two separate conditional independence properties. Thus for we have and .
5.4 Geometric constructions
Simplicial complexes are at the heart of algebraic topology and it is natural to look in that field for classes of simplicial complexes whose abstract version may be used to support hierarchical models. We mention briefly one class here arising from the fast-growing area of persistent homology, see Edelsbrunner & Harer (2010). This class has already been used by Lunagómez et al. (2009) to construct graphical models using so-called Alpha complexes. We give the construction now. It is to based on the cover provided by a union of balls in , a construction used by Edelsbrunner (1995) in the context of computational geometry and in Naiman & Wynn (1992) and Naiman & Wynn (1997) to study Bonferroni bounds in statistics.
Thus, let be points in and define the solid balls with radius centered at the points:
The nerve of the cover represented by the union of balls is the simplicial complex derived form the intersections of the balls, and is called the Alpha complex. It consists of exactly all index sets for which .
When the radius, , is small consists of unconnected vertexes and the hierarchical model gives independence of the . As there is a value of at and beyond which and consists of a single complete clique. In that case we have a full hierarchical model. Between these two cases, and depending on the position of the and the value of we obtain a rich classes of simplicial complexes and hence hierarchical models. Some of these will be decomposable and we refer to the discussion in Lunagómez et al. (2009).
It is the study of the topology of the nerve as changes, and in particular the behavior of its Betti numbers, which drives the area of persistent homology. A important theoretical and computational result is that this topology is also that of the reduced simplicial complex based on the Delauney complex associated with their Voronoi diagram. That is to say, for fixed it is enough, from a topological (homotopy) viewpoint, to use the sub-complex of the Delauney complex contained in . The theory derives from classical results of Borsuk (1948) and Leray (1945). One beautiful fact is that the Delauney dual complex based on the furthest point Voronoi diagram (Okabe et al., 2000), is obtained by the Alexander duality mentioned in the last subsection.
In this paper we have concentrated on the correspondence between and its Stanley-Reisner ideal . The use of is not always explicit in persistent homology but is implicit in the underlying homology theory: see Sáenz de Cabezón (2008) for a thorough investigation, including algorithms. Also, although the topology of and its reduced Delaunay version is the same, if their actual structure is different they lead to different hierarchical models. One can also use non-Euclidean metrics to define the cover and, indeed, work in different spaces and with other kinds of cover. Notwithstanding these many interesting technical issues the use of geometric constructions to define interesting classes of hierarchical model promises to be very fruitful.
6 Conclusion
There are many features and properties of monomial ideals which remain to be exploited in statistics via the isomorphism discussed in the last section. We should mention minimal free resolutions, the closely related Hilbert series, Betti numbers (including graded and multi-graded versions) and Alexander duality. It is pleasing that in the general case the development of the last section only requires consideration of square-free ideals, whose theory is a little easier than the full polynomial case. Fast algorithms are available for symbolic operations covering all these areas so that as further links are made they can be implemented. We have not covered statistical analysis in this paper. Further work is in progress to fit and test the zero-cumulant conditions using, for example, kernel methods.
References
- Arnold & Strauss (1988) Arnold, B. & Strauss, D. (1988). Bivariate distributions with exponential conditionals. Journal of the American Statistical Association 83, 522–527.
- Bairamov et al. (2003) Bairamov, I., Kotz, S. & Kozubowski, T. (2003). A new measure of linear local dependence. Statistics 37, 243–258.
- Barndorff-Nielsen & Cox (1989) Barndorff-Nielsen, O. & Cox, D. (1989). Asymptotic techniques for use in statistics .
- Borsuk (1948) Borsuk, K. (1948). On the imbedding of systems of compacta in simplicial complexes. Fund. Math 35, 217–234.
- Corso & Nagel (2009) Corso, A. & Nagel, U. (2009). Monomial and toric ideals associated to Ferrers graphs. Transactions of The American Mathematical Society 361, 1371–1395.
- Cozman & Walley (2005) Cozman, F. & Walley, P. (2005). Graphoid properties of epistemic irrelevance and independence. Annals of Mathematics and Artificial Intelligence 45, 173–195.
- Darroch (1962) Darroch, J. (1962). Interactions in multi-factor contingency tables. Journal of the Royal Statistical Society. Series B (Methodological) 24, 251–263.
- Dochtermann & Engström (2009) Dochtermann, A. & Engström, A. (2009). Algebraic properties of edge ideals via combinatorial topology. the electronic journal of combinatorics 16, R2.
- Drton et al. (2009) Drton, M., Sturmfels, B. & Sullivant, S. (2009). Lectures on algebraic statistics. Birkhauser.
- Edelsbrunner (1995) Edelsbrunner, H. (1995). The union of balls and its dual shape. Discrete and Computational Geometry 13, 415–440.
- Edelsbrunner & Harer (2010) Edelsbrunner, H. & Harer, J. (2010). Computational topology: an introduction. American Mathematical Society.
- Fröberg (1988) Fröberg, R. (1988). On Stanley-Reisner rings, in “Topics in Algebra”. Banach Center Public 26, 57–69.
- Geiger et al. (2006) Geiger, D., Meek, C. & Sturmfels, B. (2006). On the toric algebra of graphical models. The Annals of Statistics 34, 1463–1492.
- Hardy (2006) Hardy, M. (2006). Combinatorics of partial derivatives. The Electronic Journal of Combinatorics 13.
- Holland & Wang (1987) Holland, P. & Wang, Y. (1987). Dependence function for continuous bivariate densities. Communications in Statistics-Theory and Methods 16, 863–876.
- Jones (1996) Jones, M. (1996). The local dependence function. Biometrika 83, 899.
- Lauritzen (1996) Lauritzen, S. (1996). Graphical models. Oxford University Press, USA.
- Leray (1945) Leray, J. (1945). Sur la forme des espaces topologiques et sur les points fixes des représentations. J. Math. Pures Appl., IX. Sér. 24, 95–167.
- Lunagómez et al. (2009) Lunagómez, S., Mukherjee, S. & Wolpert, R. (2009). Geometric representations of hypergraphs for prior specification and posterior sampling. Duke University Department of Statistical Science Discussion Paper .
- McCullagh (1987) McCullagh, P. (1987). Tensor methods in statistics. Chapman and Hall London.
- Miller & Sturmfels (2005) Miller, E. & Sturmfels, B. (2005). Combinatorial Commutative Algebra. Springer Verlag.
- Mueller & Yan (2001) Mueller, H. & Yan, X. (2001). On local moments. Journal of Multivariate Analysis 76, 90–109.
- Naiman & Wynn (1992) Naiman, D. & Wynn, H. (1992). Inclusion-exclusion-Bonferroni identities and inequalities for discrete tube-like problems via Euler characteristics. The Annals of Statistics 20, 43–76.
- Naiman & Wynn (1997) Naiman, D. & Wynn, H. (1997). Abstract tubes, improved inclusion-exclusion identities and inequalities and importance sampling. The Annals of Statistics 25, 1954–1983.
- Okabe et al. (2000) Okabe, A., Boots, B., Sugihara, K. & Chiu, S. (2000). Spatial tessellations: Concepts and applications of Voronoi diagrams (POD). New York: John Wiley & Sons.
- Petrovic & Stokes (2010) Petrovic, S. & Stokes, E. (2010). Markov degrees of hierarchical models determined by betti numbers of stanley-reisner ideals ArXiv:0910.1610v2.
- Sáenz de Cabezón (2008) Sáenz de Cabezón, E. (2008). Combinatorial Koszul Homology: Computations and Applications. Ph.D. thesis, Universidad de La Rioja.
- Sáenz de Cabezón & Wynn (2010) Sáenz de Cabezón, E. & Wynn, H. (2010). Mincut ideals of two-terminal networks. Applicable Algebra in Engineering, Communication and Computing 21, 443–457.
- Seidenberg (1956) Seidenberg, A. (1956). Some remarks on Hilbert’s Nullstellensatz. Archiv der Mathematik 7, 235–240.