DiffTAD: Temporal Action Detection with Proposal Denoising Diffusion

Sauradip Nag^1,2 This work was done during internship with Jiankang Deng. Xiatian Zhu^1,3 Jiankang Deng⁴ Yi-Zhe Song^1,2 Tao Xiang^1,2
¹ CVSSP, University of Surrey, UK ² iFlyTek-Surrey Joint Research Center on Artificial Intelligence, UK
³ Surrey Institute for People-Centred Artificial Intelligence, UK ⁴ Imperial College London, UK

Abstract

We propose a new formulation of temporal action detection (TAD) with denoising diffusion, DiffTAD in short. Taking as input random temporal proposals, it can yield action proposals accurately given an untrimmed long video. This presents a generative modeling perspective, against previous discriminative learning manners. This capability is achieved by first diffusing the ground-truth proposals to random ones (i.e., the forward/noising process) and then learning to reverse the noising process (i.e., the backward/denoising process). Concretely, we establish the denoising process in the Transformer decoder (e.g., DETR) by introducing a temporal location query design with faster convergence in training. We further propose a cross-step selective conditioning algorithm for inference acceleration. Extensive evaluations on ActivityNet and THUMOS show that our DiffTAD achieves top performance compared to previous art alternatives. The code will be made available at https://github.com/sauradip/DiffusionTAD.

1 Introduction

Temporal action detection (TAD) aims to predict the temporal duration (i.e., start and end time) and the class label of each action instance in an untrimmed video [32, 9]. Existing methods rely on proposal prediction by regressing anchor proposals [83, 13, 21, 47] or predicting the start/end times of proposals [41, 8, 42, 87, 49, 84, 85]. These models are all discriminative learning based.

In the generative learning perspective, diffusion model [63] has been recently exploited in image based object detection [15]. This represents a new direction for designing detection models in general. Although conceptually similar to object detection, the TAD problem presents more complexity due to the presence of temporal dynamics. Besides, there are several limitations with the detection diffusion formulation in [15]. First, a two-stage pipeline (e.g., RCNN [13]) is adopted, suffering localization-error propagation from proposal generation to proposal classification [48]. Second, as each proposal is processed individually, their relationship modeling is overlooked, potentially hurting the learning efficacy. To avoid these issues, we adopt the one-stage detection pipelines [72, 77] that have already shown excellent performance with a relatively simpler design, in particular, DETR [11].

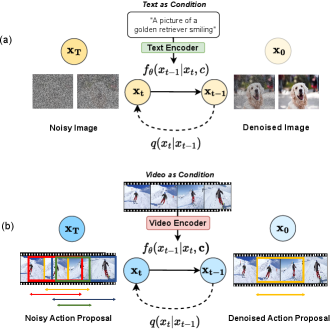
Refer to caption — Figure 1: Diffusion for temporal action detection (TAD). (a) A diffusion model for text-to-image generation where text embeddings are passed as the condition in the denoising (reverse) process. We draw an analogy by exploiting (b) a diffusion model for TAD: To generate action temporal boundaries from noisy proposals with the condition of video embedding.

Nonetheless, it is non-trivial to integrate denoising diffusion with existing detection models, due to several reasons. (1) Whilst efficient at handling high-dimension data simultaneously, diffusion models [18, 39] typically work with continuous input data. But temporal locations in TAD are discrete. (2) Denoising diffusion and action detection both suffer low efficiency, and their combination would make it even worse. Both of the problems have not been investigated systematically thus far.

To address the aforementioned challenges, a novel Conditioned Location Diffusion method is proposed for efficiently tackling the TAD task in a diffusion formulation, abbreviated as DiffTAD. It takes a set of random temporal proposals (i.e., the start and end time pairs) following Gaussian distribution, and outputs the action proposals of a given untrimmed video. At training time, Gaussian noises are first added to the ground truth proposals to make noisy proposals. These discrete noisy proposals are then projected into a continuous vector space using sinusoidal projection [44] to form noisy queries in which the decoder (e.g., DETR) will conduct the denoising diffusion process. Our denoising space choice facilitates the adoption of existing diffusion models, as discussed above. As a byproduct, the denoising queries strategy itself can accelerate the training convergence of DETR type models [38]. At inference time, conditioned on a test video, DiffTAD can generate action temporal boundaries by reversing the learned diffusion process from Gaussian random proposals. For improving inference efficiency, we further introduce a cross-timestep selective conditioning mechanism with two key functions: (1) minimizing the redundancy of intermediate predictions at each sampling step by filtering out the proposals far away from the distribution of corrupted proposals generated in training, and (2) conditioning the next sampling step by selected proposals to regulate the diffusion direction for more accurate inference.

Our contributions are summarized as follows. (1) For the first time we formulate the temporal action detection problem through denoising diffusion in the elegant transformer decoder framework. Additionally, integrating denoising diffusion with this decoder design solves the typical slow-convergence limitation. (2) We further enhance the diffusion sampling efficiency and accuracy by introducing a novel selective conditioning mechanism during inference. (3) Extensive experiments on ActivityNet and THUMOS benchmarks show that our DiffTAD achieves favorable performance against prior art alternatives.

2 Related Works

Temporal action detection. Inspired by object detection in static images [55], R-C3D [83] uses anchor proposals by following the design of proposal generation and classification. With a similar model design, TURN [21] aggregates local features to represent snippet-level features for temporal boundary regression and classification. SSN [93] decomposes an action instance into three stages (starting, course, and ending) and employs structured temporal pyramid pooling to generate proposals. BSN [42] predicts the start, end, and actionness at each temporal location and generates proposals with high start and end probabilities. The actionness was further improved in BMN [41] via additionally generating a boundary-matching confidence map for improved proposal generation. GTAN [47] improves the proposal feature pooling procedure with a learnable Gaussian kernel for weighted averaging. G-TAD [87] learns semantic and temporal context via graph convolutional networks for more accurate proposal generation. BSN++ [68] further extends BMN with a complementary boundary generator to capture rich context. CSA [67] enriches the proposal temporal context via attention transfer. VSGN [92] improves short-action localization using a cross-scale multi-level pyramidal architecture. Recently, Actionformer [90] and React [60] proposed a purely DETR based design for temporal action localization at multiple scales. Our DiffTAD is the very first TAD model which proposes action detection as a generative task.

Diffusion models. As a class of deep generative models, diffusion models [28, 64, 66] start from the sample in random distribution and recover the data sample via a gradual denoising process. Diffusion models have recently demonstrated remarkable results in fields including computer vision [5, 54, 58, 51, 26, 20, 57, 61, 27, 91, 29, 89], nature language processing [4, 39, 24], audio processing [52, 88, 82, 37, 70, 31, 35], interdisciplinary applications[33, 30, 3, 86, 73, 81, 59], etc. More applications of diffusion models can be found in recent surveys [89, 10].

Diffusion model for perception tasks. While Diffusion models have achieved great success in image generation [28, 66, 18], their potential for other perception tasks has yet to be fully explored. Some pioneer works tried to adopt the diffusion model for image segmentation tasks [79, 6, 25, 34, 7, 2, 16]. For example, Chen et al. [16] adopted Bit Diffusion model [17] for panoptic segmentation [36] of images and videos. However, despite significant interest in this idea, there is no previous solution that successfully adapts generative diffusion models for object detection, the progress of which remarkably lags behind that of segmentation. This might be because the segmentation task can be processed in an image-to-image style, which is more similar to image generation in formulation [14]. While object detection is a set prediction problem [11] with a need for assigning object candidates [56, 43, 11] to ground truth objects. However, Chen et al. [15] managed to apply a diffusion model to object detection for the first time. Similarly, we make the first attempt at formulating TAD in the diffusion framework by integrating the denoising process with the single-stage DETR architecture.

3 Methodology

3.1 Preliminaries

Temporal action detection. Our DiffTAD model takes as input an untrimmed video $V$ with a variable number of frames. Video frames are first pre-processed by a feature encoder (e.g., a Kinetics pre-trained I3D network [12]) into a sequence of localized snippets following the standard practice [41]. To train the model, we collect a set of labeled video training set $\mathcal{D}^{train}=\{V_{i},\Psi_{i}\}$ . Each video $V_{i}$ is labeled with temporal annotation $\Psi_{i}=\{(\psi_{j},\xi_{j},y_{j})\}_{j=1}^{M_{i}}$ where $\psi_{j}$ / $\xi_{j}$ denote the start/end time, $y_{j}$ is the action category, and $M_{i}$ is the number of action instances.

Diffusion models [62, 28, 64, 63] are a class of likelihood-based models inspired by nonequilibrium thermodynamics [64, 65]. These models define a Markovian chain of diffusion forward process by gradually adding noises to the sample data. The forward noising process is defined as

q(\bm{z}_{t}|\bm{z}_{0})=\mathcal{N}(\bm{z}_{t}|\sqrt{\bar{\alpha}_{t}}\bm{z}_{0},(1-\bar{\alpha}_{t})\bm{I}),

(1)

which transforms a sample $\bm{z}_{0}$ to a latent noisy sample $\bm{z}_{t}$ ( $t\in\{0,1,...,T\}$ ) by adding noises to $\bm{z}_{0}$ . $\bar{\alpha}_{t}\coloneqq\prod_{s=0}^{t}\alpha_{s}=\prod_{s=0}^{t}(1-\beta_{s})$ and $\beta_{s}$ represents the noise variance schedule [28]. During training, a neural network $f_{\theta}(\bm{z}_{t},t)$ is trained to predict $\bm{z}_{0}$ from $\bm{z}_{t}$ by minimizing the training objective with $\ell_{2}$ loss [28]:

\mathcal{L}_{\text{train}}=\frac{1}{2}||f_{\theta}(\bm{z}_{t},t)-\bm{z}_{0}||^{2}.

(2)

At inference, a sample $\bm{z}_{0}$ is reconstructed from noise $\bm{z}_{T}$ with the model $f_{\theta}$ and an updating rule [28, 63] in an iterative way, i.e., $\bm{z}_{T}\rightarrow\bm{z}_{T-\Delta}\rightarrow...\rightarrow\bm{z}_{0}$ . More details of diffusion models can be found in Supplementary.

3.2 DiffTAD

Diffusion-based TAD formulation.

In this work, we formulate the temporal action detection task in a conditional denoising diffusion framework. In our setting, data samples are a set of action temporal boundaries $\bm{z}_{0}=\bm{b}$ , where $\bm{b}\in\mathbb{R}^{N\times 2}$ denotes $N$ temporal proposals. A neural network $f_{\theta}(\bm{z}_{t},t,\bm{x})$ is trained to predict $\bm{z}_{0}$ from noisy proposals $\bm{z}_{t}$ , conditioned on the corresponding video $\bm{V}$ . The corresponding category label $\bm{\hat{y}}$ is produced accordingly.

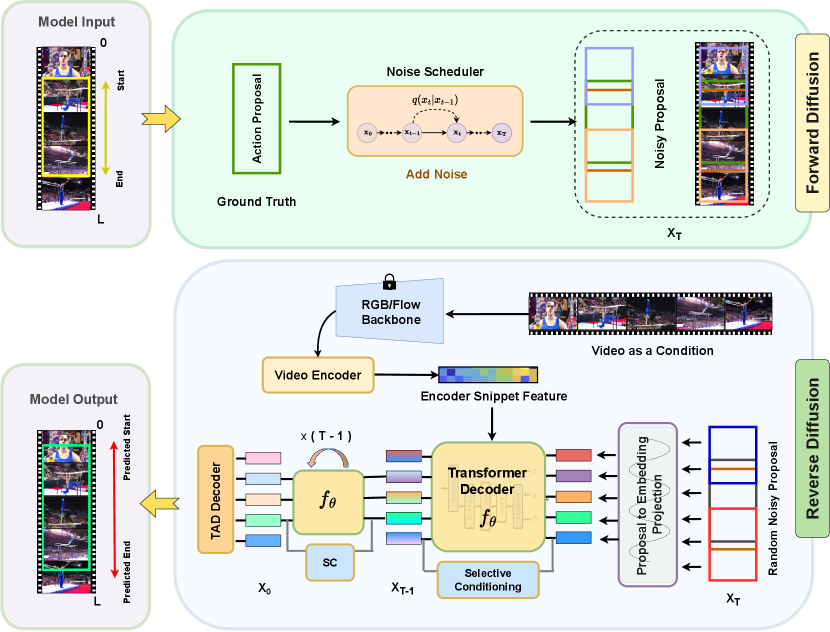
Since the diffusion model generates a data sample iteratively, it needs to run the model $f_{\theta}$ multiple times in inference. However, it would be computationally intractable to directly apply $f_{\theta}$ on the raw video at every iterative step. For efficiency, we propose to separate the whole model into two parts, video encoder and detection decoder, where the former runs only once to extract a feature representation of the input video $\bm{V_{i}}$ , and the latter takes this feature as a condition to progressively refine the noisy proposals $\bm{z}_{t}$ .

Video encoder. The video encoder takes as input the pre-extracted video features and extracts high-level features for the following detection decoder. In general, any video encoder can be used. We use a video encoder same as [90]. More specifically, the raw video $V$ is first encoded by a convolution encoder to obtain multiscale feature $H_{i}\in\mathbb{R}^{T\times D}$ for RGB and optical flow separately. This is followed by a multi-scale temporal transformer [74] $\mathcal{T}$ that performs global attention across the time dimension to obtain the global feature as:

\displaystyle F^{i}_{g}=\mathcal{T}(H_{i}),i\in[1,\cdots,L]

(3)

where query/key/value of the transformer is set to $H_{i}$ and $L$ is the number of scales. We estimate the shared global representations $F^{i}_{g}\in\mathbb{R}^{T\times D}$ across all the scales and concatenate them as $F_{g}=\{F^{0}_{g},F^{1}_{g},...,F^{L}_{g}\}$ .

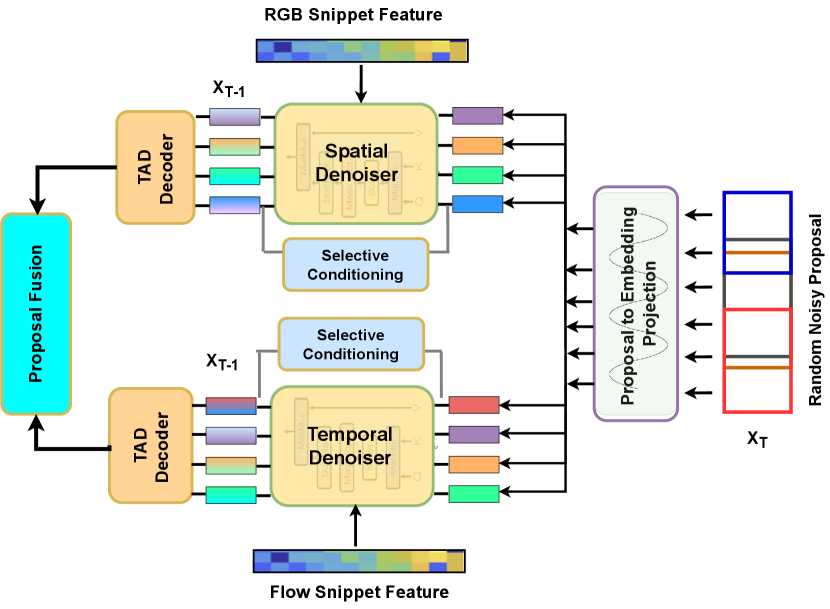
Previous TAD works [41, 87] typically use fused RGB and flow features (i.e., early fusion) for modeling. Considering the feature specificity (RGB for appearance, and optical flow for motion), we instead exploit a late fusion strategy (Fig. 3). Specifically, we extract the video features $F^{rgb}_{g}$ and $F^{flow}_{g}$ for RGB and optical flow separately. The proposal denoising is then conducted in each space individually. The forward/noising process is random (i.e., feature agnostic) and thus shared by both features. We will compare the two fusion strategies empirically (see Table 6).

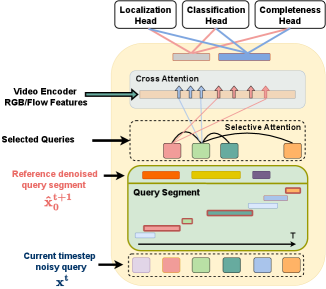
Detection decoder. Similar to DETR [40], we use a transformer decoder [74] (denoted by $f_{\theta}$ ) for detection. Functionally it serves as a denoiser. In traditional DETR, the queries are learnable continuous embeddings with random initialization. In DiffTAD, however, we exploit the queries as the denoising targets.

Specifically, we first project discrete proposals $\psi\in\mathbb{R}^{N\times 2}$ to continuous query embeddings [78]:

\displaystyle Q=g(\psi)\in\mathbb{R}^{N\times D}

(4)

where $g$ is MLP-based learnable projection. Taking $Q$ as input, the decoder then predicts $N$ outputs:

\displaystyle F_{d}=f_{\theta}(Q;F_{g})\in\mathbb{R}^{N\times D}

(5)

where $F_{g}$ is the global encoder feature and the $F_{d}$ is the final embedding. $F_{d}$ is finally decoded using three parallel heads namely (1) action classification head, (2) action localization head, and (3) completeness head, respectively. The first estimates the probability of a particular action within the action proposal. The second estimates the start, end and IOU overlap between the proposals. The third estimates the quality of predicted action proposals.

Cross-timestep selective conditioning.

In DiffTAD, the denoising decoder $f_{\theta}$ takes $N$ action queries and then denoises each of them iteratively. Processing a large number of queries is thus inefficient. An intuitive way for better efficiency is to use static thresholds to suppress unimportant candidates [15], which however is ad-hoc and ineffective.

Here, we propose a more principled cross-timestep selective conditioning mechanism (Fig. 4). More specifically, we calculate a similarity matrix $A\in\mathbb{R}^{N\times N}$ between the $N$ queries $x_{t}$ of current timestep and $N$ queries $x_{t+1}$ of conditioned/previous timestep $x_{t+1}$ . Each element of $A$ represents the similarity of the same queries across two successive timesteps. We select a set of queries according to:

\displaystyle\hat{P}_{sim}=\{(i,j)|A[i,j]-\gamma>0\}

(6)

where $\gamma\in[-1,1]$ is a preset similarity threshold. We consider higher IoU with the desired (approximated by the estimate of the last step) proposals, more effective for the queries to be denoised. Thus, we construct an IoU based matrix $B\in\mathbb{R}^{N\times N}$ between two successive timesteps:

\displaystyle\hat{P}_{iou}=\{(i,j)|B[i,j]-\gamma>0\}

(7)

where $i$ / $j$ indexes the queries. This allows for the most useful queries to be selected (see Fig. 1 in Supplementary).

We obtain the final query set as $Q_{c}=(\hat{P}_{iou}/\hat{P}_{sim})\bigcup Q$ with $/$ denotes the set divide operation. For a selected query $q_{i}$ , its key and value features can be obtained by fusion as $K_{i}/V_{i}=cat(\{k_{j}/v_{j}|(i,j)\in Q_{c}\})$ . Each query feature is then updated as

\displaystyle\hat{q}_{i}=softmax(q_{i}K^{\top}_{i}).V^{\top}_{i}

(8)

These selected queries $\{\hat{q}_{i}\}$ will be passed through the cross-attention with video embeddings for denoising. This selective conditioning is applied on a random proportion (e.g., 70%) of proposals per mini-batch during training, and on all the proposals during inference.

Our selective conditioning strategy shares the spirit of self-conditioning [17] in the sense that the output of the last step is used for accelerating the subsequent denoising. However, our design and problem setup both are different. For example, self-conditioning can be simply realized by per-sample feature concatenation, whilst our objective is to select a subset of queries based on the pairwise similarity and IoU measurement in an attention manner. We validate the conditioning design in the experiments (Table 2).

3.3 Training

During training, we first construct the diffusion process that corrupts the ground-truth proposals to noisy proposals. We then train the model to reverse this noising process. Please refer to Algorithm 1 for more details.

Algorithm 1 DiffTAD Training

⬇

def train(video_feat, gt_proposals):

# Encode image features

feats = video_encoder(video_feat)

# Signal scaling

pb = (pb * 2 - 1) * scale

# Corrupt gt_proposals

t = randint(0, T) # time step

eps = normal(mean=0, std=1) # noise: [B, N, 2]

pb_crpt = sqrt( alpha_cumprod(t)) * pb +

sqrt(1 - alpha_cumprod(t)) * eps

# Project to continuous embedding

pb_crpt = project(pb_crpt) # query : [B, N, D]

# Calculate Self-condition estimate

pb_pred = zeros_like(pb_crpt)

if self_cond and uniform(0,1) > 0.7:

pb_pred = decoder(pb_crpt, pb_pred, feats, t)

pb_pred = stop_gradient(pb_pred)

# Predict

pb_pred = decoder(pb_crpt, pb_pred, feats, t)

# Set prediction loss

loss = set_prediction_loss(pb_pred, gt_proposals)

return loss

alpha_cumprod(t): cumulative product of $\alpha_{i}$ , i.e., $\prod_{i=1}^{t}\alpha_{i}$

Proposal corruption.

We add Gaussian noises to the ground truth action proposals. The noise scale is controlled by $\alpha_{t}$ (in Eq. (1)), which adopts the monotonically decreasing cosine schedule in different timestep $t$ , following [50]. Notably, the ground truth proposal coordinates need to be scaled as well since the signal-to-noise ratio has a significant effect on the performance of diffusion model [16]. We observe that TAD favors a relatively lower signal scaling value than object detection [15] (see Table 4). More discussions are given in Supplementary.

Training losses.

The detection detector takes as input $N_{train}$ corrupted proposals and predicts $N_{train}$ predictions each including the category classification, proposal coordinates, and IOU regression. We apply the set prediction loss [11, 69, 94] on the set of $N_{train}$ predictions. We assign multiple predictions to each ground truth by selecting the top $k$ predictions with the least cost by an optimal transport assignment method [22, 23, 80, 19].

3.4 Inference

In inference, starting from noisy proposals sampled in Gaussian distribution, the model progressively refines the predictions as illustrated in Algorithm 2.

Algorithm 2 DiffTAD Sampling

⬇

def infer(video_feat, steps, T):

# Encode video features

feats = video_encoder(video_feat)

# noisy proposals: [B, N, 2]

pb_t = normal(mean=0, std=1)

# noisy embeddings: [B, N, D]

pb_t = project(pb_t)

pb_pred = zeros_like(pb_t)

# uniform sample step size

times = reversed(linespace(-1, T, steps))

# [(T-1, T-2), (T-2, T-3), ..., (1, 0), (0, -1)]

time_pairs = list(zip(times[:-1], times[1:])

for t_now, t_next in zip(time_pairs):

# Predict pb_0 from pb_t

if not self_cond:

pb_pred = zeros_like(pb_t)

pb_pred = decoder(pb_t, pb_pred, feats, t_now)

# Estimate pb_t at t_next

pb_t = ddim_step(pb_t, pb_pred, t_now, t_next)

return pb_pred

linespace: generate evenly spaced values

Sampling step.

At each sampling step, the random or estimated proposals from the last sampling step are first projected into the continuous query embeddings and sent into the detection decoder to predict the category, proposal IOU and proposal coordinates. After obtaining the proposals of the current step, DDIM [63] is adopted to estimate the proposals for the next step.

Proposal prediction.

DiffTAD has a simple proposal generation pipeline without post-processing (e.g., non-maximum suppression). To make a reliable confidence estimation for each proposal, we fuse the action classification score $p_{bc}$ and completeness score $p_{c}$ for each proposal with a simple average to obtain the final proposal score $p_{sc}$ .

3.5 Remarks

One model multiple trade-offs.

Once trained, DiffTAD works under multiple settings with a varying number of proposals and sampling steps during inference (Fig. 5(b)). In general, better accuracy can be obtained using more proposals and more steps. Thus, a single DiffTAD can realize a number of trade-off needs between speed and accuracy.

Faster convergence.

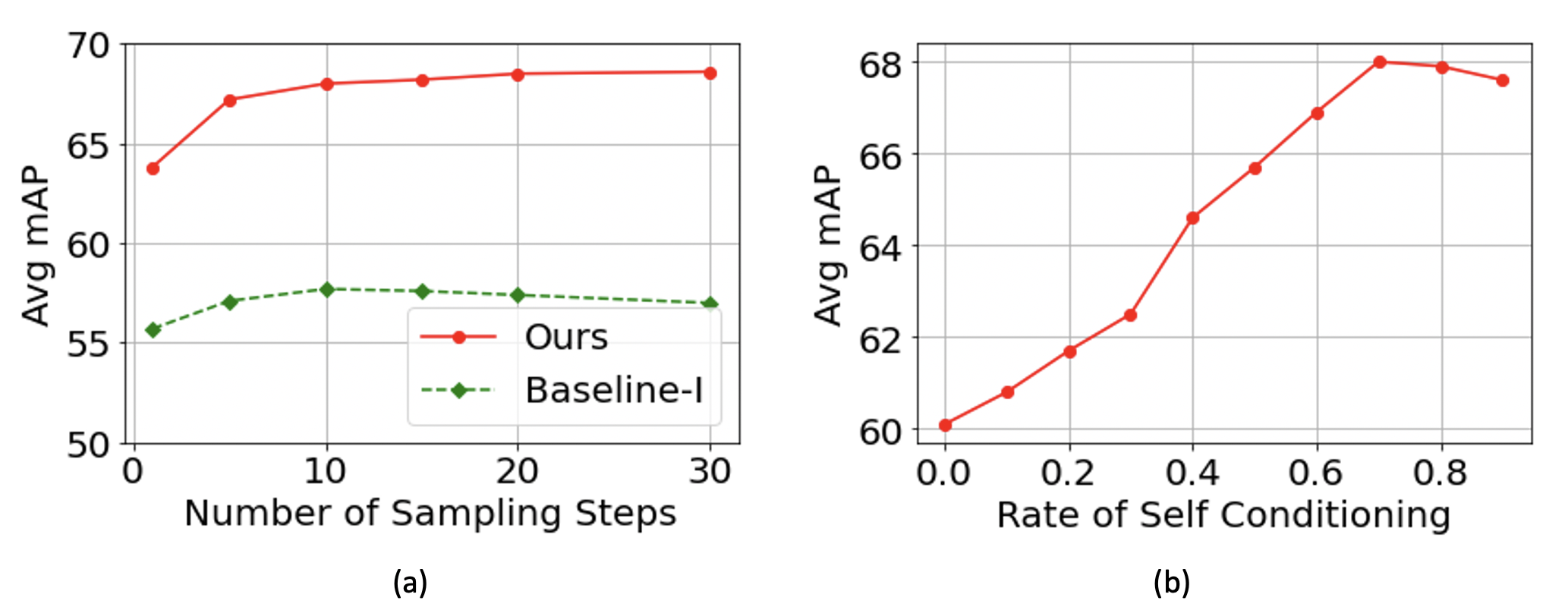
DETR variants suffer generally slow convergence [45] due to two reasons. First, inconsistent updates of the anchors, the objective for the object queries to learn, would make the optimization of target boundaries difficult. Second, the ground truth assignment using a dynamic process (e.g., Hungarian matching) is unstable due to both the nature of discrete bipartite matching and the stochastic training process. For instance, a small perturbation with the cost matrix might cause enormous matching and inconsistent optimization. Our DiffTAD takes a denoising strategy that makes learning easier. More specifically, each query is designed as a proposal proxy, a noised query, that can be regarded as a good anchor due to being close to a ground truth. With the ground truth proposal as a definite optimization objective, the ambiguity brought by Hungarian matching can be well suppressed. We validate that our query denoising based DiffTAD converges more stably than DiffusionDet [15] based Baseline-I (Fig. 5(a)), whilst achieving superior performance (Table 1).

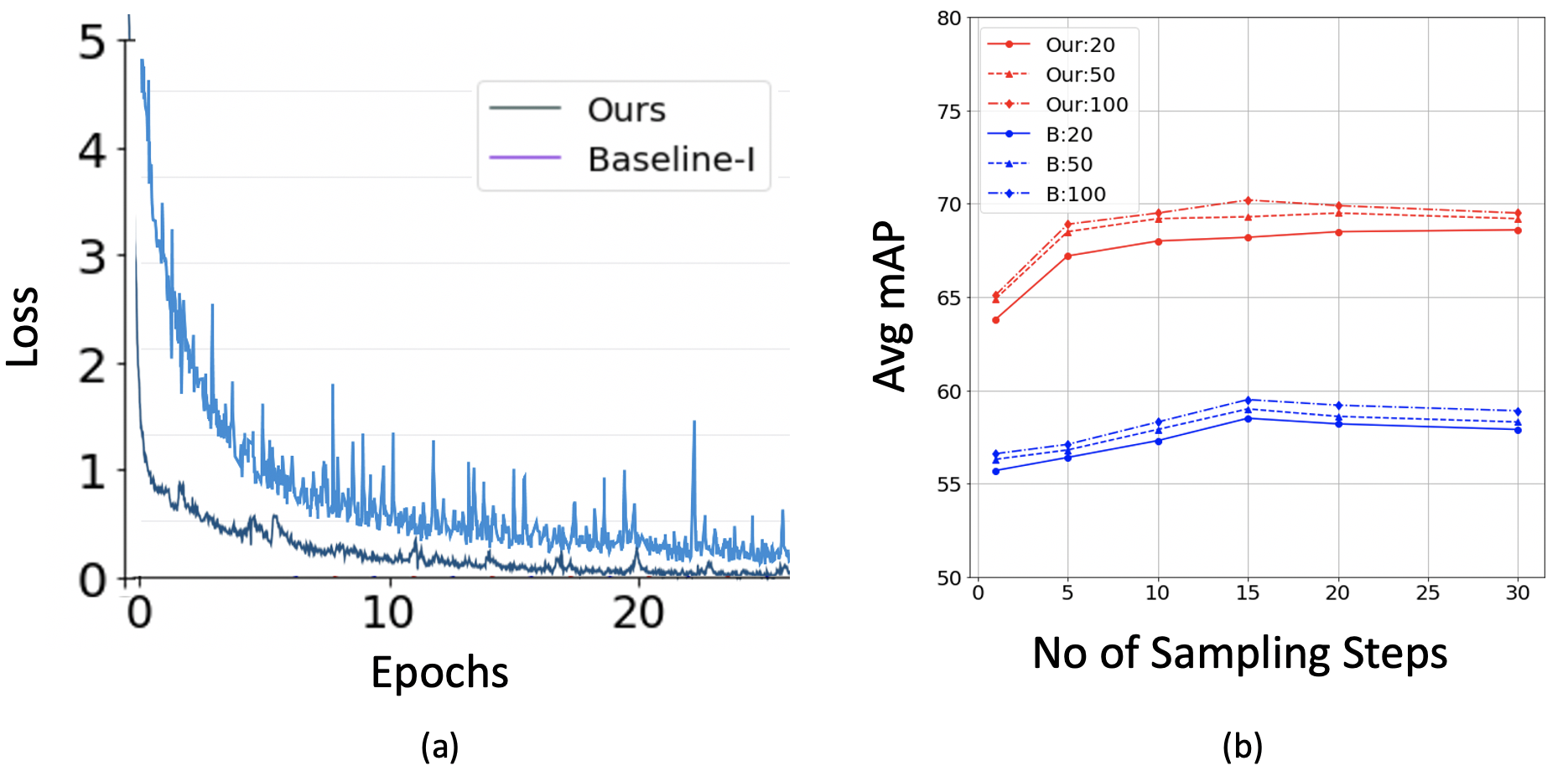
Better sampling.

We evaluate DiffTAD under a varying number of (10/50/100) random proposals by increasing the sampling steps from 1 to 30. As shown in Table 1, under all three settings, DiffTAD yields steady performance gains from more steps consumed. In particular, in the case of fewer random proposals, often DiffTAD can achieve larger gains than DiffusionDet [15]. For example, in the case of 50 proposals, the mAP of DiffTAD boosts the avg mAP from 64.9% (1 step) to 68.5% (5 steps), i.e., an absolute gain of 3.6% avg mAP. Unlike object detection, we find TAD benefits little from increasing the number of proposals. One intuitive reason is that positive samples are less in TAD than in object detection. Compared to the previous two-stage refinement of discriminative learning based TAD models [71], our gain is also more decent (0.8% vs. 4.2% (10 steps)). This is because it lacks a principled iterative inference ability as in diffusion models.

Table 1: Performance comparison with the state-of-the-art methods. Metrics: mAP at different IoU thresholds, and average mAP in [0.3 : 0.1 : 0.7] on THUMOS14 and [0.5 : 0.05 : 0.95] on ActivityNet-v1.3.

			THUMOS						ActivityNet
Models	Design	Feature	0.3	0.4	0.5	0.6	0.7	Avg	0.5	0.75	0.95	Avg
Discriminative learning based models
TAL-Net [13]	2-stage	I3D	53.2	48.5	42.8	33.8	20.8	-	38.2	18.3	1.3	20.2
BMN [41]	2-stage	TSN	56.0	47.4	38.8	29.7	20.5	38.5	50.1	34.8	8.3	33.9
GTAD [87]	2-stage	TSN	54.5	47.6	40.3	30.8	23.4	39.3	50.4	34.6	9.0	34.1
RTD-Net [71]	2-stage	I3D	68.3	62.3	51.9	38.8	23.7	-	47.2	30.7	8.6	30.8
TCANet [53]	2-stage	I3D	60.6	53.2	44.6	36.8	26.7	44.3	52.3	36.7	6.9	35.5
MUSES [46]	2-stage	I3D	68.9	64.0	56.9	46.3	31.0	—	50.0	35.0	6.6	34.0
ContextLoc [95]	2-stage	I3D	68.3	63.8	54.3	41.8	26.2	50.9	56.0	35.2	3.6	34.2
RCL [76]	2-stage	I3D	70.1	62.3	52.9	42.7	30.7	57.1	51.7	35.2	8.0	34.4
React [60]	1-stage	I3D	69.2	65.0	57.1	47.8	35.6	55.0	49.6	33.0	8.6	32.6
TAGS [48]	1-stage	I3D	68.6	63.8	57.0	46.3	31.8	52.8	56.3	36.8	9.6	36.5
ActionFormer [90]	1-stage	I3D	82.1	77.8	71.0	59.4	43.9	66.8	53.5	36.2	8.2	35.6
Generative learning based models
Baseline(1-step)	2-stage	I3D	65.2	61.3	55.4	44.6	35.5	52.4	48.5	31.4	8.6	31.5
Baseline(5-step)	2-stage	I3D	69.1	65.7	60.2	47.1	36.4	55.7	50.2	32.3	8.9	32.2
Baseline(10-step)	2-stage	I3D	70.0	66.5	60.6	47.5	36.9	56.3	51.0	32.9	9.0	32.4
\cellcolor[HTML]CBCEFB DiffTAD(1-step)	\cellcolor[HTML]CBCEFB 1-stage	\cellcolor[HTML]CBCEFBI3D	\cellcolor[HTML]CBCEFB68.7	\cellcolor[HTML]CBCEFB66.8	\cellcolor[HTML]CBCEFB64.7	\cellcolor[HTML]CBCEFB61.2	\cellcolor[HTML]CBCEFB57.3	\cellcolor[HTML]CBCEFB63.8	\cellcolor[HTML]CBCEFB52.4	\cellcolor[HTML]CBCEFB35.6	\cellcolor[HTML]CBCEFB8.8	\cellcolor[HTML]CBCEFB34.8
\cellcolor[HTML]CBCEFBDiffTAD(5-step)	\cellcolor[HTML]CBCEFB 1-stage	\cellcolor[HTML]CBCEFBI3D	\cellcolor[HTML]CBCEFB73.4	\cellcolor[HTML]CBCEFB71.5	\cellcolor[HTML]CBCEFB69.9	\cellcolor[HTML]CBCEFB62.8	\cellcolor[HTML]CBCEFB58.4	\cellcolor[HTML]CBCEFB67.2	\cellcolor[HTML]CBCEFB55.2	\cellcolor[HTML]CBCEFB36.8	\cellcolor[HTML]CBCEFB8.9	\cellcolor[HTML]CBCEFB36.0
\cellcolor[HTML]CBCEFBDiffTAD(10-step)	\cellcolor[HTML]CBCEFB 1-stage	\cellcolor[HTML]CBCEFBI3D	\cellcolor[HTML]CBCEFB74.9	\cellcolor[HTML]CBCEFB72.8	\cellcolor[HTML]CBCEFB71.2	\cellcolor[HTML]CBCEFB62.9	\cellcolor[HTML]CBCEFB58.5	\cellcolor[HTML]CBCEFB68.0	\cellcolor[HTML]CBCEFB56.1	\cellcolor[HTML]CBCEFB36.9	\cellcolor[HTML]CBCEFB9.0	\cellcolor[HTML]CBCEFB36.1

4 Experiments

Datasets. We conduct extensive experiments on two popular TAD benchmarks. (1) ActivityNet-v1.3 [9] has 19,994 videos from 200 action classes. We follow the standard setting to split all videos into training, validation and testing subsets in ratio of 2:1:1. (2) THUMOS14 [32] has 200 validation videos and 213 testing videos from 20 categories with labeled temporal boundary and action class.

4.1 Implementation details

Training schedule. For video feature extraction, we use Kinetics pre-trained I3D model [12, 90] with a downsampling ratio of 4 and R(2+1)D model [1, 90] with a downsampling ratio of 2. Our model is trained for 50 epochs using Adam optimizer with a learning rate of $10^{-4}/10^{-5}$ for AcitivityNet/THUMOS respectively. The batch size is set to 40 for ActivityNet and 32 for THUMOS. For selective conditioning, we apply the rate of 70% during training. All models are trained with 4 NVIDIA-V100 GPUs.

Testing schedule. At the inference stage, the detection decoder iteratively refines the predictions from Gaussian random proposals. By default, we set the total sampling time steps as 10.

4.2 Main results

Competitors.

We compare our DiffTAD with the state-of-the-art non-generative approaches including BMN [41], GTAD [87], React [60] and ActionFormer [90]. Further, we adapt the object detection counterpart DiffusionDet [15] to a two-stage generative TAD method, termed as Baseline.

Results on THUMOS.

We make several observations from Table 1: (1) Our DiffTAD achieves the best result, surpassing strong discriminative learning based competitors like TCANet [75] and ActionFormer [90] by a clear margin. This suggests the overall performance advantage of our model design and generative formulation idea. (2) Importantly, DiffTAD excels on the alternative generative learning design (i.e., Baseline), validating the superiority of our diffusion-based detection formulation. For both generative models, more sampling steps lead to higher performance. This concurs with the general property of diffusion models. (3) In particular, our model achieves significantly stronger results in stricter IOU metrics (e.g., IOU@0.5/0.6/0.7), as compared to all the other alternatives. This demonstrates the potential of generative learning in tackling the action boundary often with high ambiguity, and the significance of proper diffusion design.

Results on ActivityNet.

Similar observations can be drawn in general on ActivityNet from Table 1. We further highlight several differences: (1) Indeed, overall our DiffTAD is not the best performer, with a slight edge underneath TAGS [48]. However, we note that all other DETR style methods (e.g., RTD-Net) are significantly inferior. This means that our method has already successfully filled up the most performance disadvantage of the DETR family. We attribute this result to our design choice of denoising in the query space and cross-timestep selective conditioning. That being said, our formulation in exploiting the DETR architecture for TAD is superior than all prior attempts. (2) Compared to the generative competitor (i.e., Baseline), our model is not only more stable to converge (Fig. 5(a)), but also yields a margin of 3.7% (smaller than that on THUMOS as this is a more challenging test for the DETR family in general).

4.3 Ablation study

We conduct ablation experiments on THUMOS to study DiffTAD in detail. In all experiments, we use 30 proposals for training and inference, unless specified otherwise.

Cross-timestep selective conditioning.

We examine the effect of the proposed selective conditioning for proposal refinement (Section 3.2). To that end, we vary the rate/portion of proposals per batch at which selective conditioning is applied during training. The case of 0% training rate means no conditioning. Note, during inference selective conditioning is always applied to all the proposals (i.e., 100% test rate). As demonstrated in Fig. 6(b), we observe a clear correlation between conditioning rate and sampling quality (i.e., mAP), validating the importance of our selective conditioning in refining proposals for enhanced denoising.

Additionally, we compare with two different refinement designs: (1) Feature concatenation as in self-conditioning [17], and (2) Proposal renewal as in DiffusionDet [15]. We observe from Table 2 that our selective conditioning is superior to both alternatives, verifying our design idea.

Table 2: Proposal refinement design. Dataset: THUMOS.

	mAP
Design	0.3	0.5	0.7	Avg
Feature Concatenation [17]	71.1	66.3	56.5	65.9
Proposal Renewal [15]	71.2	65.4	54.2	65.1
\rowcolor[HTML]EFEFEF Selective Condition (Ours)	74.9	71.2	\cellcolor[HTML]EFEFEF58.5	68.0

Sampling decomposition.

We decompose the sampling strategy with DiffTAD by testing four variants: (1) No denoising: No DDIM [63] is applied, which means the output prediction of the current step is used directly as the input of the next step (i.e., a naive baseline). (2) Vanilla denoising: DDIM is applied in the original form. (3) Selective conditioning: Only selective conditioning is used but no vanilla denoising. (4) Both vanilla denoising and selective conditioning: Our full model. We observe from Table 3 that (1) Without proper denoising, applying more steps will cause more degradation, as expected, because there is no optimized Markovian chain. (2) Applying vanilla denoising can address the above problem and improve the performance from multiple sampling accordingly. However, the performance increase saturates quickly. (3) Interestingly, our proposed selective conditioning even turns out to be more effective than vanilla denoising. (4) When both vanilla denoising and selective conditioning are applied (i.e., our full model), the best performances can be achieved, with a clear gain over the either and even improved saturation phenomenon. This suggests that the two ingredients are largely complementary, which is not surprising given their distinctive design nature.

Table 3: Sampling decomposition in terms of iterative denoising (ID) and selective conditioning (SC). Dataset: THUMOS.

ID	SC	step 1	step 5	step 10
✗	✗	62.7	62.9	61.3
✓	✗	62.7	65.0	64.9
✗	✓	62.7	65.7	65.6
\rowcolor[HTML]EFEFEF ✓	✓	62.7	67.2	68.0

Signal scaling.

The signal scaling factor (Eq. (1)) controls the signal-to-noise ratio (SNR) of the denoising process. We study the influence of this facet in DiffTAD. As shown in Table 4, the scaling factor of 0.5 achieves the optimal performance. This means this setting is task-specific at large (e.g., the best choice is 2.0 for object detection [15]).

Table 4: Signal-noise ratio under a variety of different scaling factors. Dataset: THUMOS.

	mAP
Scale	0.3	0.5	0.7	Avg
0.1	70.5	67.5	57.2	66.6
\rowcolor[HTML]EFEFEF 0.5	74.9	71.2	\cellcolor[HTML]EFEFEF58.5	68.0
1.0	73.2	70.6	58.0	67.3
2.0	69.9	67.3	56.8	64.2

Accuracy vs. speed.

We evaluate the trade-off between the accuracy and memory cost with DiffTAD. In this test, we experiment with three choices $\{10,50,100\}$ in the number of proposals. For each choice, the same is applied to both model training and evaluation consistently. We observe in Table 5 that: (1) Increasing the number of proposals/queries from 30 to 50 brings about 0.5% in mAP with extra 0.46 GFLOPs, thanks to the proposed selective conditioning. (2) However, further increasing the proposals is detrimental to the model performance. This is because the number of action instances per video is much fewer than that of objects per image on average. (3) With 50 proposals, increasing the sampling steps from 1 to 5 provides an mAP gain of $3.6\%$ with an additional cost of 1.9 GFLOPs. A similar observation is with the case of 100 proposals.

Table 5: Accuracy vs. speed under a variety of different proposal numbers and sampling steps. Dataset: THUMOS.

		mAP
Proposals	Step	0.3	0.5	0.7	Avg	GFLOPs
\cellcolor[HTML]EFEFEF30	\cellcolor[HTML]EFEFEF5	\cellcolor[HTML]EFEFEF74.9	\cellcolor[HTML]EFEFEF71.2	\cellcolor[HTML]EFEFEF58.5	\cellcolor[HTML]EFEFEF68.0	\cellcolor[HTML]EFEFEF0.81
50	1	69.2	65.2	53.0	64.9	1.27
50	5	77.2	73.5	59.1	68.5	3.17
100	1	70.4	66.1	53.8	65.1	2.18
100	5	77.1	73.8	58.7	68.4	6.32

Decoupled diffusion strategy.

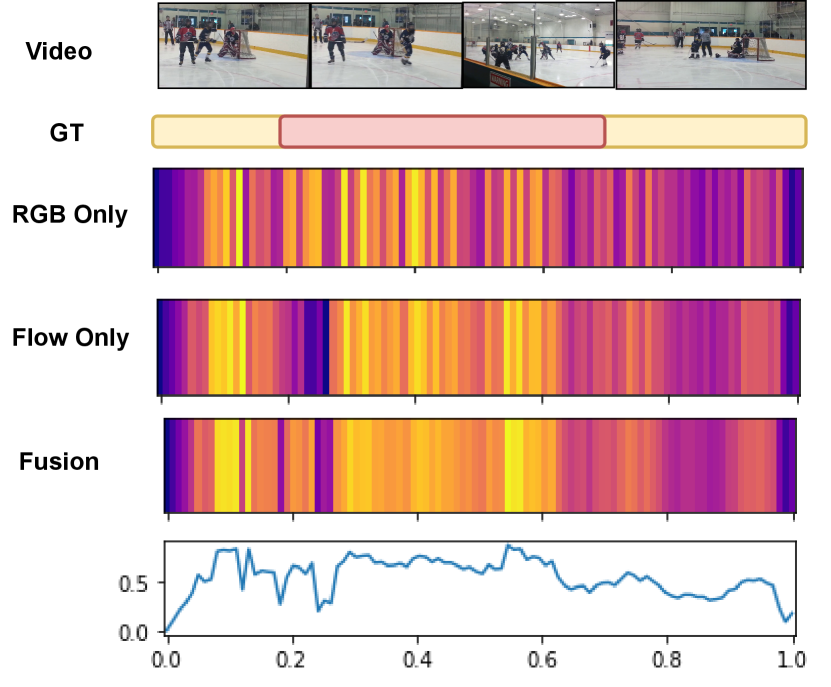
We evaluate the impact of feature decoupling (video encoder in Sec. 3.2). Typically, existing TAD methods [87, 41] use fused RGB and optical flow video features (i.e., early fusion). However, we take a late fusion strategy where the RGB and flow features are processed separately before their proposals are fused (Fig. 3). We contrast the two fusion strategies. It is evident in Table 6 that with the typical early fusion (i.e., passing early fused features as a condition to our detection decoder), a drop of $2\%$ in average mAP is resulted. This indicates that due to modal specificity there is a need for specific conditional inference, validating our design consideration. For visual understanding, an example is given in Fig. 7 to show how the two features can contribute to TAD in a cooperative manner.

Table 6: Decoupling the denoising. RGB and optical flow video features are decoupled for individual denoising (i.e., late fusion), in contrast to typical early fusion strategy where the two features are first fused in prior to being processed. Dataset: THUMOS.

Decoupling	0.5	0.75	0.95	Avg
✗	71.8	67.4	57.1	66.0
\rowcolor[HTML]C0C0C0 ✓	74.9	71.2	58.5	68.0

NMS-free design.

As shown in Table 7, when comparing DiffTAD with and without non-maximum suppression (NMS), we observe similar results. NMS is not necessary in DiffTAD because the predictions are relatively sparse and minor overlapped with our cross-step conditional strategy (Sec. 3.2). In contrast, existing non-generative TAD works like BMN [41] and GTAD [87] generate highly overlapped proposals with similar confidence. Thus, NMS becomes necessary to suppress redundant proposals.

Table 7: Ablation study on non-maximum suppression (NMS) on THUMOS14, measured by AR@AN.

Model	AR@50	AR@100	AR@500
BMN [41]	29.04	37.72	56.07
BMN [41] + NMS	32.73	40.68	56.42
DiffTAD	63.6	69.6	73.1
DiffTAD + NMS	64.3	69.9	72.8

Ablation of denoising strategy.

Due to the inherent query based design with the detection decoder, (1) we can corrupt discrete action proposals and project them as queries, and (2) we can also corrupt the action label and project it as label queries. Both can be taken as the input to the decoder. For corrupting the label queries, we use random shuffle as the noise in the forward diffusion step. To validate this design choice experimentally, we test three variants: (1) only labels are corrupted, (2) only proposals are corrupted, and (3) both proposals and labels are corrupted. For the non-corrupted quantity, we add noise to the randomly initialized embedding. For the last variant, we stack all the corrupted proposals and labels and pass them into the decoder. It can be observed in Table 4.3 that corrupting labels alone observes the most drop in performance, and corrupting both labels and proposals is inferior to only corrupting the proposals.

DiffTAD: Temporal Action Detection with Proposal Denoising Diffusion

Abstract

1 Introduction

2 Related Works

3 Methodology

3.1 Preliminaries

3.2 DiffTAD

Diffusion-based TAD formulation.

Cross-timestep selective conditioning.

3.3 Training

Proposal corruption.

Training losses.

3.4 Inference

Sampling step.

Proposal prediction.

3.5 Remarks

One model multiple trade-offs.

Faster convergence.

Better sampling.

4 Experiments

4.1 Implementation details

4.2 Main results

Competitors.

Results on THUMOS.

Results on ActivityNet.

4.3 Ablation study

Cross-timestep selective conditioning.

Sampling decomposition.

Signal scaling.

Accuracy vs. speed.

Decoupled diffusion strategy.

NMS-free design.

Ablation of denoising strategy.

5 Visualization of proposal denoising

6 Conclusion

References

Denoising Strategy		mAP
Proposal	Label	0.3	0.5	0.7	Avg
✗	✓	70.1	65.9	52.7	62.4
\rowcolor[HTML]EFEFEF \cellcolor[HTML]EFEFEF✓			✗	74.9	71.2	\cellcolor[HTML]EFEFEF58.5	68.0
✓	✓	73.8	70.4	58.0	67.3