Direct and Semi-Direct Approaches to Lepton Mixing with a Massless Neutrino

The main question around which the framework of residual symmetries in the fermion mass matrices [11, 12, 13, 14, 15, 16, 17, 3, 5] has been constructed is the question: When do symmetries of a $3\times 3$-matrix (partly) fix the matrix which diagonalises it?

The answer to this question is fairly simple. Consider unitary matrices $S_{i}$ and $T_{j}$ which leave a complex symmetric matrix $M$ or a Hermitian matrix $H$ invariant,³³3For application to the fermion mass problem the study of Hermitian and complex symmetric matrices is sufficient. For the lepton sector we will later have $M=M_{\nu}$ and $H=M_{\ell}M_{\ell}^{\dagger}$. i.e.

The set of all matrices $S_{i}$ forms a group $G_{M}$ of unitary $3\times 3$-matrices. In the same way, also the matrices $T_{j}$ form a unitary group $G_{H}$. If the matrices $M$ and $H$ have non-degenerate singular values⁴⁴4 The singular values are the elements of the diagonalised matrix. This condition is necessarily fulfilled in all relevant applications, because the singular values of $H$ will be identified with the charged-lepton masses squared and the singular values of $M$ will be identified with the three light-neutrino masses. the groups $G_{M}$ and $G_{H}$ must be Abelian. For this case one can show that the matrices $U_{M}$ and $U_{H}$ which (simultaneously) bring all $S_{i}$ and $T_{j}$ to diagonal form, i.e.

also diagonalise $H$ and $M$ via⁵⁵5Let us, as an illustration, give the derivation of this fact for a complex symmetric matrix $M$. From equation (6a) we have $Mu_{k}=m_{k}u_{k}^{\ast}$ (no summation over $k$) for the columns $u_{k}$ of $U_{M}$, i.e. the $u_{k}$ are singular vectors of $M$ with singular values $m_{k}$. From equation (3a) we then have $$S_{i}^{T}MS_{i}u_{k}=m_{k}u_{k}^{\ast}\Rightarrow M(S_{i}u_{k})=m_{k}(S_{i}u_{k})^{\ast}.$$ (5) Since the singular values $m_{i}$ are assumed to be non-degenerate, the corresponding singular vectors are unique up to multiplication with a constant, i.e. $S_{i}u_{k}=s_{i}u_{k}$. Therefore, the $u_{k}$ are simultaneous eigenvectors to all $S_{i}$, which implies equation (4a). [12]

where hatted matrices are diagonal matrices. In other words the set of symmetries $S_{i}$ of a matrix $M$ fixes its diagonalising matrix $U_{M}$. The same statement holds for $T_{j}$ and $H$.

Let us now apply these mathematical considerations to the case of residual symmetries in the lepton sector. The assumption of residual symmetries is that there is a flavour symmetry group $G_{f}$ (acting on the lepton fields) which is spontaneously broken to a symmetry group $G_{\nu}$ in the neutrino sector,

and a symmetry group $G_{\ell}$ in the charged-lepton sector,

Identifying $M=M_{\nu}$ and $H=M_{\ell}M_{\ell}^{\dagger}$ in the above discussion, we immediately find $G_{\nu}\subset G_{M}$ and $G_{\ell}\subset G_{H}$. Therefore, the symmetry groups $G_{\ell}$ and $G_{\nu}$ potentially (but not necessarily) impose constraints on the matrices $U_{\nu}$ and $U_{\ell}$, which diagonalise $M_{\nu}$ and $M_{\ell}M_{\ell}^{\dagger}$ via

and consequently also on the mixing matrix $U_{\mathrm{PMNS}}=U_{\ell}^{\dagger}U_{\nu}$.

In order to know how $G_{\nu}$ and $G_{\ell}$ constrain $U_{\nu}$ and $U_{\ell}$ we have to understand to which degree an Abelian unitary $3\times 3-$matrix group $A$ determines the unitary matrix $U$ which simultaneously diagonalises all elements of $A$. There are only three possibilities:

• •

  None of the common eigenvectors of the elements of $A$ is unique.⁶⁶6For eigenvectors unique here means unique up to multiplication with a complex number. $\Rightarrow A=\{\mathbbm{1}_{3}\}$ and $U$ is an arbitrary unitary matrix.

• •

  One of the common eigenvectors of the elements of $A$ is unique. $\Rightarrow$ One column of $U$ is proportional to this eigenvector. $\Rightarrow$ One column of $U$ is fixed by $A$ up to a rephasing.

• •

  All three of the common eigenvectors of the elements of $A$ are unique. $\Rightarrow$ Each column of $U$ is proportional to one of these eigenvectors. $\Rightarrow$ $U$ is fixed by $A$ up to rephasing and reordering of its columns.

According to this finding, one classifies models based on residual symmetries into two categories:

• (A)

  Direct models: $G_{\nu}$ fixes $U_{\nu}$ and $G_{\ell}$ fixes $U_{\ell}$ (up to reordering and rephasing of the columns). $\Rightarrow$ $U_{\mathrm{PMNS}}$ is fixed (up to reordering and rephasing of rows and columns).

• (B)

  Semidirect models: In one sector the full diagonalising matrix is fixed, in the other sector only a column is fixed.

  • (B1)

    $G_{\ell}$ fixes $U_{\ell}$, $G_{\nu}$ fixes a column of $U_{\nu}$. $\Rightarrow$ One column of $U_{\mathrm{PMNS}}$ is fixed up to permutation of its elements. One may choose (if not determined by a concrete model) which column of $U_{\mathrm{PMNS}}$ is fixed.

  • (B2)

    $G_{\ell}$ fixes one column of $U_{\ell}$, $G_{\nu}$ fixes $U_{\nu}$. $\Rightarrow$ One row of $U_{\mathrm{PMNS}}$ is fixed up to permutation of its elements. One may choose (if not determined by a concrete model) which row of $U_{\mathrm{PMNS}}$ is fixed.

In this work we will only study the cases A and B1. Case B2 has for example been studied in [18]. One could in principle also consider a third very weakly restrictive case C for which in each sector only one column is fixed (up to rephasing). In this case only one element of $U_{\mathrm{PMNS}}$ would be fixed. Due to its low predictive power, this scenario is usually not studied, and also we will not study it here.

The residual symmetry groups $G_{\nu}$ and $G_{\ell}$ are Abelian groups of unitary $3\times 3$-matrices. Therefore, they are subgroups of $U(1)\times U(1)\times U(1)$. For the charged lepton sector, this is also the maximal symmetry group, i.e. $G_{H}=U(1)\times U(1)\times U(1)$. For Majorana neutrinos the situation is different. If all neutrinos are massive, the maximal symmetry group is $G_{M}=\mathbbm{Z}_{2}\times\mathbbm{Z}_{2}\times\mathbbm{Z}_{2}$, while, if one neutrino is massless, also $G_{M}=U(1)\times\mathbbm{Z}_{2}\times\mathbbm{Z}_{2}$ is allowed. The case of one massless neutrino has been studied in [8, 9].

Here we will further elaborate on the case of a massless neutrino within the framework of residual symmetries. The case of direct models has been studied in [9] for all suitable finite groups up to order 511. In the present paper we extend this analysis to order 1535. Moreover, we discuss semidirect models (of type B1) with a massless neutrino, also up to order 1535. Before we discuss the details of the group searches we have performed, we want to have a look on the generic requirements potential flavour groups $G_{f}$ with a massless neutrino have to fulfill. As outlined in detail in appendix A, viable groups $G_{f}$

• •

  must possess a faithful three-dimensional irreducible representation,

• •

  must not be of the form $G_{f}\simeq G_{f}^{\prime}\times\mathbbm{Z}_{n}$ $(n>1)$ and

• •

  must not be of the form of the following theorem by Joshipura and Patel [9]: Let $G$ be a group of $3\times 3$ matrices which contains only elements of the form “diagonal matrix of phases times permutation matrix”, where the six permutation matrices are given by

  $$\begin{split}&P_{1}=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix},\quad P_{2}=\begin{pmatrix}0&1&0\\ 1&0&0\\ 0&0&1\end{pmatrix},\quad P_{3}=\begin{pmatrix}0&0&1\\ 0&1&0\\ 1&0&0\end{pmatrix},\\ &P_{4}=\begin{pmatrix}1&0&0\\ 0&0&1\\ 0&1&0\end{pmatrix},\quad P_{5}=\begin{pmatrix}0&0&1\\ 1&0&0\\ 0&1&0\end{pmatrix},\quad P_{6}=\begin{pmatrix}0&1&0\\ 0&0&1\\ 1&0&0\end{pmatrix}.\end{split}$$

  (11)

  Then, if such a group $G$ is used to build models enforcing a massless neutrino, the column vector of the mixing matrix associated to the massless neutrino must be

  $$\begin{pmatrix}1\\ 0\\ 0\end{pmatrix},\;\frac{1}{\sqrt{3}}\begin{pmatrix}1\\ 1\\ 1\end{pmatrix},\;\frac{1}{\sqrt{2}}\begin{pmatrix}0\\ 1\\ 1\end{pmatrix}$$

  (12)

  or permutations thereof (i.e. permutations of the elements of an individual column.)

As a starting point for our analysis, we need a list of groups fulfilling these criteria. We used the library SmallGroups⁷⁷7Throughout the paper we will use the SmallGroups ID to identify groups. This ID consists of two numbers in square brackets, i.e. $[g,n]$, $g$ being the group order and $n$ being a label. Two groups with different SmallGroups IDs are non-isomorphic. [19, 20] and the computer algebra system GAP [21] to find all groups of order smaller than 1536 which fulfill these minimal criteria.⁸⁸8Since we require groups which have a three-dimensional irreducible representation, the group order must be divisible by 3. Up to order 1535 there are 1342632 groups whose order is divisible by three. For the group order 1536 alone there are 408641062 groups. Therefore, we had to stop our searches at order 1535. As a result of this scan we have found 22 groups of order smaller than 1536 fulfilling the minimal criteria.⁹⁹9In this paper we follow the approach of scanning over a set of eligible groups, in the end discarding which are incompatible with experiment. The opposite approach of constructing eligible groups directly from experimental data on the mixing matrices has e.g. been used in [22, 23]. They are shown in equation (LABEL:groups-massless) in appendix A.

In order to test the seven candidate groups for direct models with a massless neutrino, we computed all faithful three-dimensional irreducible representations of the groups, computed all Abelian subgroups and listed all possible combinations $(G_{\ell},G_{\nu})$. For each of these combinations, the possible mixing matrices have been computed—see [3] for a detailed description of this procedure. In order to compare the predictions for the mixing matrix with experiment we fitted the three mixing angles to the global fit data of [24]. As $\chi^{2}$-function we used

which has three degrees of freedom. For the errors $\sigma(\mathrm{sin}^{2}\theta_{ij})$ we used the values given in [24] (in case of an asymmetric error distribution we used the larger error). The resulting minimal values of $\chi^{2}$ are listed in table 1.

Evidently, none of the candidate groups is compatible with the experimental data. For groups up to order 511 this result has been found earlier in [9].

For the semidirect models, there is a unique candidate group $[648,533]$. It has six faithful three-dimensional irreducible representations, each of which can predict (the same) 19 different patterns for a column of the mixing matrix. It is therefore sufficient to study only one of the faithful three-dimensional irreducible representations constructed with GAP, i.e. we pick one of them and use it to define the group $[648,533]$ as a matrix group. In this representation the group is generated by the two matrices

and

where

i.e.

$Q_{8}$ here denotes the quaternion group of order 8. This group corresponds to $[648,533]$ which we denote as $Q(648)$.

The two only columns predictable by $Q(648)$ being compatible with experiment emerge from the choice

We are already in a basis where all elements of $G_{\ell}$ are diagonal. Therefore, the eigenvector of $S$ with eigenvalue $\neq\pm 1$ is the predicted column of $U_{\mathrm{PMNS}}$. Indeed, $S$ has two eigenvalues $+1$ and an eigenvalue $\omega\equiv\exp(2\pi i/3)=\epsilon^{3}$ with the corresponding eigenvector

The absolute values of the entries of this vector are

This leads to two patterns compatible with the first column¹¹¹¹11Since the neutrino mass associated with the predicted column vanishes, we have $m_{1}=0$ which requires a normal neutrino mass spectrum. of $U_{\mathrm{PMNS}}$, namely:

Note that we here have used the permutation freedom of the elements of the predicted column, which comes from the fact that the residual symmetries cannot fix any mass orderings. The equations

where $s_{ij}\equiv\mathrm{sin}\,\theta_{ij}$ and $c_{ij}\equiv\mathrm{cos}\,\theta_{ij}$, give relations between the mixing angles and the Dirac phase $\delta$. These relations can be used to predict $\theta_{12}$ as a function of $\theta_{13}$ and $\mathrm{cos}\,\delta$ as a function of $\theta_{13}$ and $\theta_{23}$:

Here $t_{ij}\equiv\mathrm{tan}\,\theta_{ij}$. Using the values of the global fit of ref. [24],

we find (best-fit)

for $|U_{e1}|=|u_{1}|$, $|U_{\mu 1}|=|u_{2}|$. The other possibility with $|U_{e1}|=|u_{1}|$, $|U_{\mu 1}|=|u_{3}|$ turns out to be incompatible with the best-fit values of equation (31),

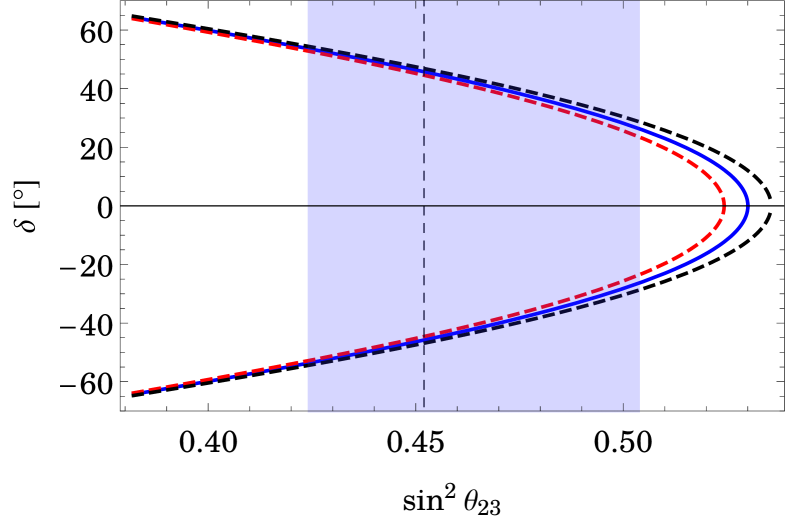
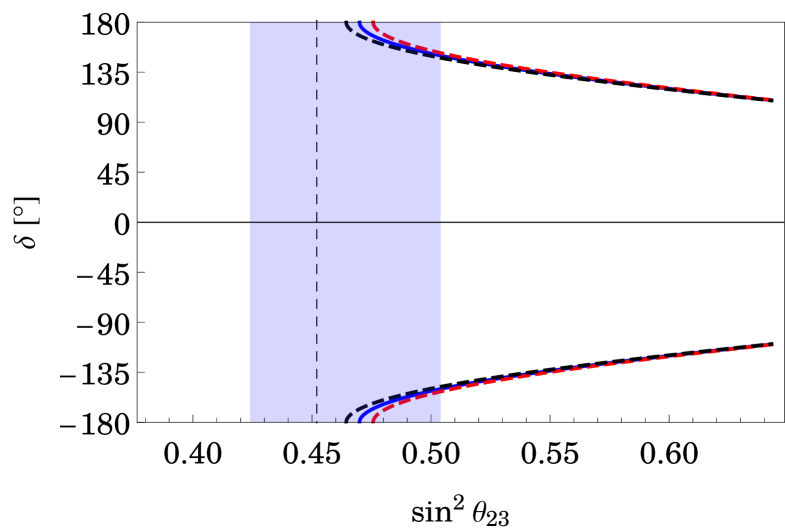
but remains consistent with experiment for $s_{23}^{2}\gtrsim 0.47$. Using the best-fit values of the mass-squared differences and $\mathrm{sin}^{2}\theta_{13}$ from [24] as input parameters, the predicted range for $m_{\beta\beta}$ is $(1.22\div 3.38)\,\mathrm{meV}$, i.e. several meV (as for every model with a normal neutrino mass spectrum and vanishing $m_{1}$). Since $m_{\beta\beta}$ depends only on the sum of $\delta$ and one of the (unconstrained) Majorana phases, our model puts no stronger constraint on $m_{\beta\beta}$.

In total, the two discussed column patterns are compatible with the global fit values of [24] at about $2-3$ sigma. The reason for tension is the too small value of the solar mixing angle predicted by the group using the reactor angle as an input. The global-fit result for the solar mixing angle is

The main prediction of the model is a value of $\delta$ of about $\pm 45^{\circ}$ or $\pm\pi$ (for the best-fit values). The value of $\delta$ for different values of $s_{23}^{2}$ and $s_{13}^{2}$ is shown in figure 1.