Direct determination of zero-field splitting for single Co2+ ion
embedded in a CdTe/ZnTe quantum dot
Abstract
When Co2+ impurity is embedded in semiconductor structure, crystal strain strongly influences zero-filed splitting between Co2+ states with spin projection and . Experimental evidences of this effect have been given in previous studies, however direct measurement of the strain induced zero-field splitting has been inaccessible so far. Here this splitting is determined thanks to magneto-optical studies of individual Co2+ ion in epitaxial CdTe quantum dot in ZnTe barrier. Using partially allowed optical transitions we measure strain induced zero-field splitting of Co2+ ion directly on excitonic photoluminescence spectrum. Moreover, by observation of anticrossing of and Co2+ spin states in magnetic field, we determine axial and in-plane components of crystal field acting on Co2+. Proposed technique can be applied for optical determination of zero-field splitting of other transition metal ions in quantum dots.
I Introduction
The first observation of excitonic emission from quantum dot (QD) with a single Co2+ ionKobak et al. (2014) led to the discovery that the quantum dot containing single magnetic ion exhibits efficient radiative excitonic recombination, even in case when recombination energy is higher than intraionic transition of magnetic ion. Therefore optical manipulation of single magnetic ion spin is possible not only in classical systems with single Mn2+ in QDs with relatively low energy gap CdTe/ZnTeBesombes et al. (2004, 2005); Le Gall et al. (2009); Goryca et al. (2009, 2010) and InAs/GaAsKudelski et al. (2007); Krebs et al. (2009); Baudin et al. (2011), but also in QDs with higher energy gap such as CdSe/ZnSeKobak et al. (2014); Smoleński et al. (2015); Fainblat et al. (2016) or in QD systems doped with impurities considered previously as killers of photoluminescence: Co2+,Kobak et al. (2014) Fe2+,Smolenski et al. (2016) Cr2+.Lafuente-Sampietro et al. (2016a, b) For all the systems studied so far it has been found that ground state of the magnetic ion is significantly influenced by the local strain present in a quantum dot. Such effect is of particular importance for the future applications in solotronics (optoelectronics based on single dopantsKoenraad and Flatte (2011)) and spintronics based on magnetic QDs.Beaulac et al. (2009); Whitaker et al. (2011); Pandey et al. (2012); Qu et al. (2015); Barman et al. (2015); Loureço et al. (2015); Rice et al. (2016); Nistor et al. (2016); Moldoveanu et al. (2016); Balanta et al. (2016); Muckel et al. (2016) Effect of strain may be demonstrated as the beating in coherent precession of single magnetic ion spin,Goryca et al. (2014) as changes of occupation and energy of levels corresponding to various projection of ion spin,Kudelski et al. (2007); Kobak et al. (2014); Lafuente-Sampietro et al. (2016a), or even as the change of the character of Fe2+ ion ground state, from nonmagnetic in bulk, to the magnetic in QD.Smolenski et al. (2016) However so far only indirect method were used for estimation of strain induced zero-field splitting of single magnetic ions in QDs: from depolarization efficiency of optically oriented ion,Le Gall et al. (2009) from PL peaks line-shapeBesombes and Boukari (2014), from variation of coherent oscillation amplitude,Goryca et al. (2014); Lafuente-Sampietro et al. (2015) and from relative PL peaks intensity of lines corresponding to various spin-projection.Kudelski et al. (2007); Kobak et al. (2014); Lafuente-Sampietro et al. (2016a); Smolenski et al. (2016) Here we present a method for measurement of strain induced zero-field splitting of magnetic ion directly by observation of corresponding splitting in exciton photoluminescence spectrum. We apply this method for precise determination of zero-field splitting of Co2+ in CdTe/ZnTe QD.
The paper is organized in the following way: first we give experimental details and we recall typical spectrum of the neutral exciton in a QD with a single Co2+ ion. Next we introduce partially allowed transitions which are used to determine zero-field splitting of a single Co2+ ion in a QD. Finally we present magneto-optical effects of anticrossing of Co2+ spin states. From this anticrossing we determine Hamiltonian parameters and representing axial and in-plane components of the crystal field.
II Samples and experimental setup
We have studied similar structures with ZnTe barriers and CdTe QDs doped with Co2+ ions. The growth of investigated structures was performed by molecular beam epitaxy on GaAs (100) oriented substrate. Formation of the QDs was induced by amorphous Te desorption method.Tinjod et al. (2003) During the CdTe deposition process we introduced low level delta–doping with Co2+ ions using high temperature effusion cell working at C. Since molecular fluxes of cobalt used during the growth of QDs are smaller than the accuracy of the vacuum gauge, for both investigated structures we fabricated the reference Zn1-xCoxTe layers grown under the same Co2+ flux. Such layers of diluted magnetic semiconductor allowed us to determine precisely Co2+ concentration by measuring the giant Zeeman effect (more details in Papaj et al., 2014, 2012). The final Co2+ concentration in reference samples was found to be equal about %. The same concentration was therefore expected in thin Cd1-xCoxTe layer before transformation into QDs.
Maximal compressive strain in our QDs is related to lattice mismatch of about 6% defined by lattice constance of CdTe (a = 6.48 Å) and ZnTe (a = 6.10 Å). In practice, strain can be lower due to intermixing of Zn and Cd between QDs and barrier or due to partial relaxation of 2 monolayer thick CdTe layer during formation of QDs.
For microphotoluminesce experiments the samples were immersed in liquid helium inside a magneto-optical bath cryostat with magnetic field of up to 10 T. The measurements were performed at the temperature of about 1.5 K using a high resolution reflective microscope, which results in about 0.5 m diameter of laser spot. Such experimental setup allowed us to study optical properties of well-separated emission lines in magnetic fields with a polarization resolution. Complementary studies requiring a high magnetic field were performed in Grenoble High Magnetic Field Laboratory, where samples were immersed in helium gas at T = 10 K inside a 20 MW resistive magnet producing magnetic field of up to 28 T.
III Results
III.1 Typical photoluminescence spectrum of a QD with a single Co2+ ion
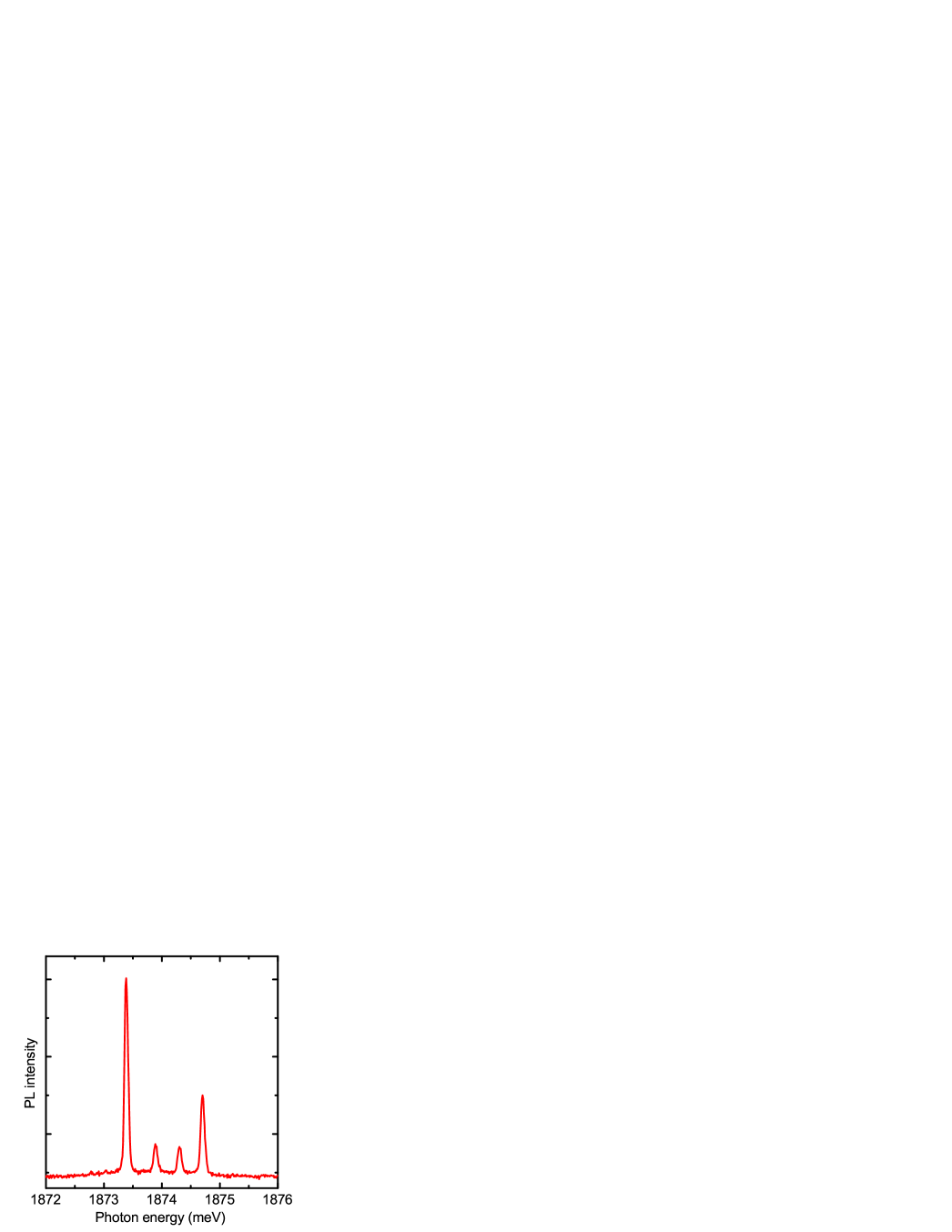
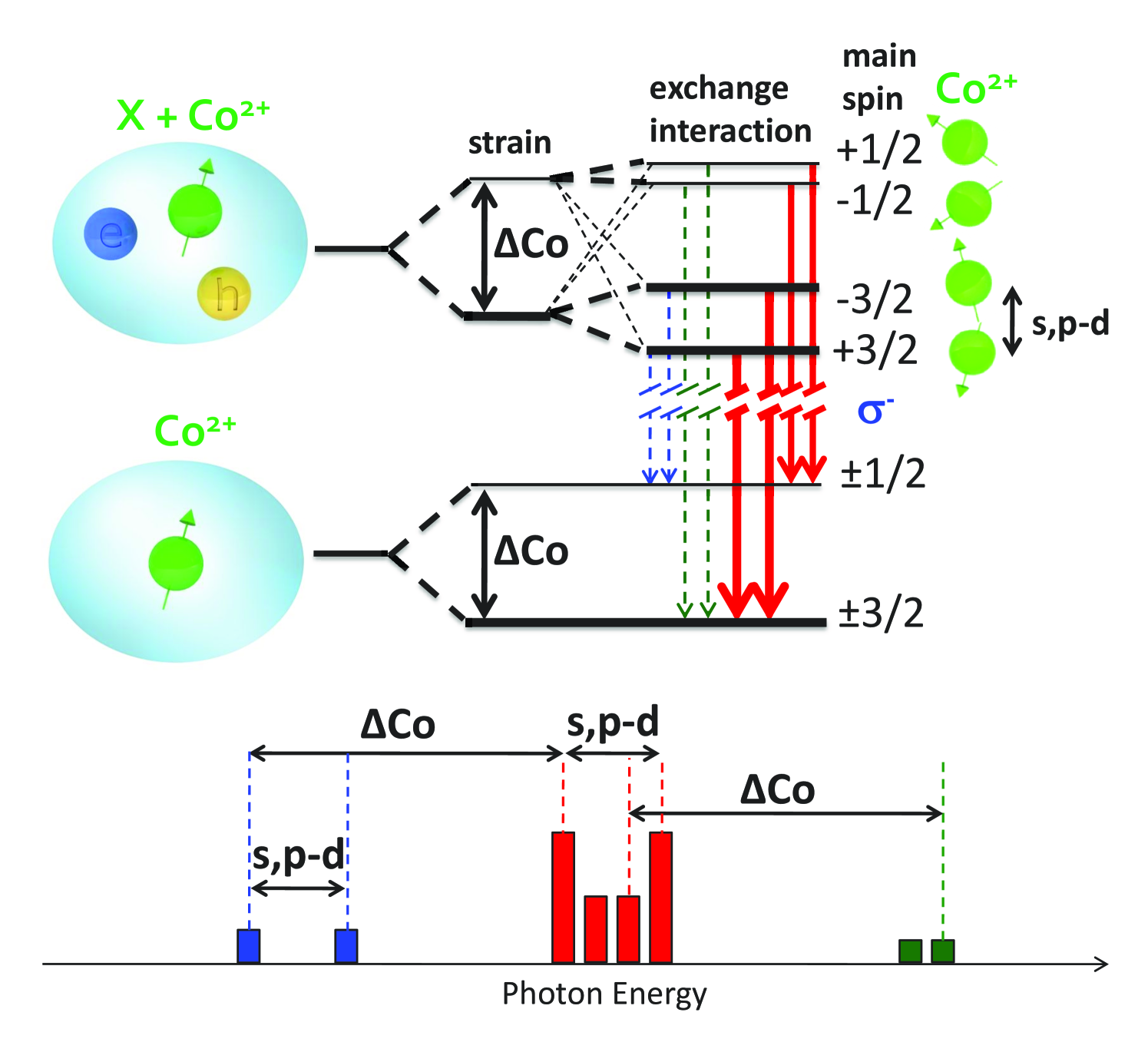
Fig. 1 presents photoluminescence spectrum of a bright neutral exciton in a CdTe/ZnTe QD with a single Co2+ ion in zero magnetic field. Emission is split due to - exchange interaction between exciton and magnetic ion. Four observed lines result from four possible spin projection of Co2+ ion with spin onto the quantization axis given by heavy-hole exciton in QD.Kobak et al. (2014) More precisely, in excited state formed by exciton and Co2+ ion, for each projection of excitonic spin (, corresponding to , circular polarisations) there are four energy levels and in the final state after exciton recombination there are four quantum states (two doubly degenerate levels at zero field) of Co2+. In each circular polarization there are 16 possible transitions but only 4 are optically allowed due to requirement of Co2+ spin conservation for electric dipole transition (solid arrows on Fig. 2). In zero magnetic field the 4 lines for polarization coincide with those for .
Intensity of two inner and two outer lines reflects differences in occupancy of various Co2+ states. Fig. 1 shows a typical case, when cobalt has a fundamental state with spin projection and consequently outer lines related to such a spin states are more pronounced than lines related to states (inner lines). However we argue that apart from Co2+ level ordering, such four main lines do not carry sufficient information about absolute value of Co2+ zero-field splitting. It is because line separation energy is determined by - exchange interaction not by splitting of Co2+ states. Moreover, occupancy of various states of Co2+ under optical excitation is not simply governed by temperature and Boltzmann distribution. One could try to describe it by an effective temperature, but there is no good method of determination of such a parameter, which could be order of magnitude larger than actual experimental temperature (e.g. 10 or 30 K instead of 1.7 K in Supplementary Information of Ref. Kobak et al., 2014). Moreover, Fig. 1 shows that two outer lines of a QD with a single Co2+ ion exhibit not-equal intensity which is a fingerprint of efficient relaxation of Co2+ - exciton system during lifetime of a single exciton introduced to the QD. This makes measurement of occupancy distribution of Co2+ states in empty dot even more complex. Therefore we conclude that precise determination of Co2+ zero-field splitting from analysis of four main photoemission lines of a QD with a single Co2+ is not feasible.

III.2 Partially allowed transitions and determination of Co2+ zero-field splitting
In previous section we discussed four main optical transitions with conserved spin of Co2+ ion. In this section we report about additional bright neutral exciton transitions, which can be observed only if in–plane strain mixes Co2+ spin states. Since such mixing is influenced by ,- exchange interaction between carriers and magnetic ion, Co2+ spin mixing is slightly different for a QD with and without exciton. When spin wavefunction of Co2+ is not identical in initial and final state of optical transition, part of oscillator strength is distributed between transitions where main spin component is different in initial and final state, but both states are not fully orthogonal. This effect opens possibility of studying partially allowed optical transitions shown by blue and green dashed arrows in Fig. 2. The intensity of such emission lines is strongly sensitive on parameters describing Co2+ ion. For values of parameters determined in this work, intensity ratio between main emission lines (red colour in Fig. 2) and partially allowed lines (blue and green color in Fig. 2) is 3 orders of magnitude. Measurements of such weak PL lines is experimentally challenging but it is worth of effort because partially allowed lines carry information about parameters describing spin structure of Co2+ ion. In particular, energy difference between the strongest emission lines in spectra (red outer lines) and weak, partially allowed lines at lower energy (blue lines) are equal exactly to cobalt spin state splitting () since such transitions have the same initial states ( with admixture of ) but different final states ( with admixture of and with admixture of , respectively). The same energy distance () is between inner main lines (red color) and partially allowed emission lines at higher energy (green color). The energy splitting of low energy weak emission lines (blue) is related to ,- exchange interaction in initial state, so it is the same as splitting of outer main emission lines (red). Similarly, high energy weak emission lines (green) exhibit splitting equal to splitting of inner main lines (red).
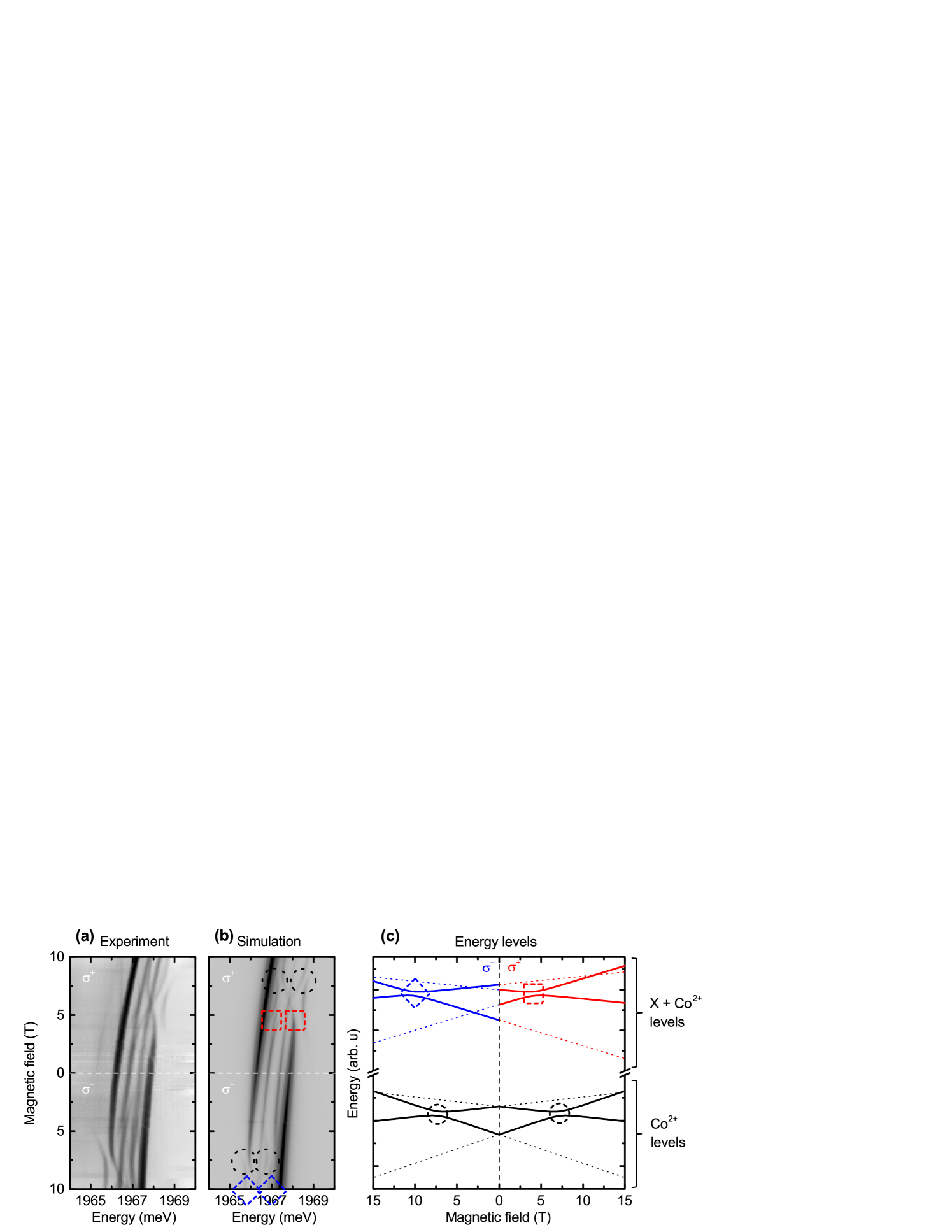
Experimental observation of partially allowed transitions is shown in Fig. 3(a) which presents typical low temperature magnetophotoluminescence of bright exciton in a QD with a single Co2+ ion in Faraday configuration, measured in two circular polarizations of detection. Line identification on the spectra is in agreement with simulation shown in Fig. 3(b). In both figures (a) and (b) we observe strong main emission lines (red lines on panel (b) or scheme of Fig. 2) corresponding to transitions with conserved spin of Co2+. Additionally we observe also three weak emission lines. The first one is associated with the dark exciton recombination (black line on panel (b)) which involves change of Co2+ spin from mainly +3/2 to mainly -3/2, so it exhibit the largest g-factor and it is a fingerprint of Co2+ spin states mixing, but it does not carry information about zero-field splitting of Co2+. Two more weak lines are related to bright exciton transitions partially allowed by cobalt and spin states mixing (blue lines on panel (b) and scheme of Fig. 2). We determine zero-field splitting of cobalt ( meV for Co2+ shown in Fig. 3) by subtraction of emission energies of lines related to the the transitions for which initial state is the same (mainly ) but final state is different (mainly and for weak and strong lines respectively). Note that values of parameter estimated from two pairs of emission lines are the same.

Simulation presented in Fig. 3 (b) is based on simple model of exciton - Co2+ - ion system described in details in Methods of Ref. Kobak et al., 2014. The most important part of our theoretical description is given by the standard Hamiltonian of Co2+ ion, which is also the Hamiltonian of the final state of the system after the exciton recombination:
| (1) |
where the first term represents the Zeeman effect described by magnetic ion -factor, Bohr magneton , magnetic field and total magnetic momentum (). The second and the third term describe magnetic anisotropy of a magnetic impurity with and representing axial and in-plane components of crystal field. Both parameters and can be determined basing on anticrossings discussed in detail in the next section.
III.3 Anticrossing of Co2+ ion spin states and determination of crystal field parameters
Since g-factors are different for main and partially allowed transitions (see Fig. 3), approaching of various lines in magnetic field is inevitable. Series of anticrossigs between main and partially allowed transitions are observed in magnetophotoluminescence experiment shown in Fig. 4(a). Additionally, Fig. 4(b) presents corresponding simulation of the optical spectra and Fig. 4(c) presents simulated energy levels of neutral exciton in a CdTe QD with Co2+ (initial states of photoluminescence) and empty dot with single cobalt (final states). All panels of Fig. 4 show important spectral features closely related to the spin structure of Co2+ ion. Anticrossing between and cobalt spin states in the absence of exciton appears four times in excitonic spectra (due to final state of recombination), all appearances are at the same magnetic field (about 7 T for QD from Fig. 4a). They are denoted on panel (b) and (c) by black circles. Red and blue squares on panel (b) and (c) represent anticrossings of cobalt spin states modified by the presence of carriers forming neutral exciton, which acts on Co2+ as effective magnetic field of about 3 T for QD from Fig. 4a. As a consequence such anticrossings are shifted and are visible at about T and T for and polarization of detection respectively. Observed shift is analogical to the shift of the magnetic ion levels anticrossing from zero field to field of about 2 T which has been already reported for Mn2++h complex in InAs/GaAs QDs,Kudelski et al. (2007); Krebs et al. (2009); Baudin et al. (2011) and for Fe2+ in CdSe/ZnSe QDsSmolenski et al. (2016) where ,- exchange interaction with exciton was also acting on magnetic ion as an effective magnetic field.
Particularly important for this work are anticrossings in the final state which are marked in Fig. 4 by black circles. They give additional information about Co2+ properties in absence of carriers. In such an anticrossing separation energy of spectral lines corresponds directly to separation energy between Co2+ states close to the anticrossing of spin states +3/2 and -1/2. In Fig. 5 we plot the dependence of such Co2+ spin states splitting as a function of the magnetic field for QDs shown in Fig. 3 (violet points), Fig. 4 (green points), and for three other QDs with a single Co2+ ion.
Solving of Hamiltonian (1) leads us to analytical formula describing magnetic field evolution of energy distance between mixed and spin states of Co2+:
| (2) |
where parameters and (axial and in-plane components of crystal field) can be extracted directly from the experimental data. Parameter can be determined from the value of for magnetic field at which anticrossing between and spin states appears (). Knowing parameter one can obtain parameter from the zero-field spin states splitting given by formula: . Finally -factor is equal to . Parameters , , and the -factor of Co2+ ion can be also determined by fit of Eq. 2 to experimental data, as shown by solid lines in Fig. 5.
| (meV) | (meV) | ||
|---|---|---|---|
| (meV) | |||
The values of the parameters describing Co2+ ions in all studied QDs are summarized in Table 1. The data are sorted in increasing order with respect to the zero-field splitting , which varies from about meV to almost meV. The value of parameter is in the range between meV and meV. For all discussed QDs parameter is negative which favours states of spin equal . Parameter , which causes the mixing of Co2+ spin states, varies from meV to meV. The values of Co2+ -factor strongly differ from each other starting from and ending with the value . Analysis of the Table 1 shows that there is an anti-correlation between and . The smaller Co2+ zero-field splitting the larger value of Co2+ -factor. Surprisingly, for the declining value of Co2+ zero-field splitting we do not observe the convergence of Landé factor of Co2+ to the limit defined by unstrained CdTe crystal,Ham et al. (1960) which is equal . This shows that there are other important factors affecting the structure of the energy states of cobalt ion. One of possible explanations of g-facotor lower than 2.31 is that larger g-factor would be observed for other axis than growth axis tested in our experiment.
We note that distribution of measured values of zero-field splitting is probably not governed by distribution in the studied samples, but it is rather affected by preselection of studied Co2+ ions caused by our experimental limitations. At zero field or at magnetic field in range of a few Tesla, only relatively small zero-field splitting of Co2+ can be determined. For large zero-field splitting partially allowed transitions are too weak to be observed. Therefore we expect that real distribution Co2+ zero-field splitting in the samples is even wider than observed and that typical value is larger than about 3 meV observed a few times in our first experiments. This expectation is supported by high magnetic field experiment (black data of Fig. 5), where anticrossing of +3/2 and -1/2 is expected at about 35 T for Co2+ ion with equal to almost 8 meV and parameter meV.
Absolute values of parameter obtained in this work are significantly larger than values reported for semiconductor systems without strain. For Co2+ in zinc blende semiconductors like CdTe, ZnTe or ZnSe parameter is neglectedHam et al. (1960); Wu and Dong (2004); Grzybowski et al. (2015). In wurtzite structure diluted magnetic semicondutors with Co2+ parameter was found to be positive with absolute value much smaller than in our experminets on QDs: +0.06 meV for CdSe,Lewicki et al. (1991); Isber et al. (1995) +0.08 meV for CdS,Lewicki et al. (1991); Bindilatti et al. (1994) and +0.34 meV for ZnO.Estle and De Wit (1961); Macfarlane (1970); Koidl (1977); Jedrecy et al. (2004); Ferrand et al. (2005); Sati et al. (2006); Pacuski et al. (2006)
In strained semiconductor systems, parameter obtained in this work for Co2+ can be compared to values obtained for transition metal ions. For Mn2+ QDs CdTe/ZnTe, parameter meV was determined from depolarization efficiency of optically oriented ionLe Gall et al. (2009) and from variation of coherent oscillation amplitude,Goryca et al. (2014) which were also used for determination of parameter eV.Lafuente-Sampietro et al. (2016a) Much larger values, in range of meV, are expected from magneto-photoluminescence of main emission lines in QDs with transition metal ions exhibiting non-zero orbital momentum, meVSmolenski et al. (2016) for Fe2+, meVLafuente-Sampietro et al. (2016a) for Cr2+. Finally, in our first report on main emission lines of a QD CdTe/ZnTe with a single Co2+, using multi parameter fit we obtained value meV,Kobak et al. (2014) in the same range as directly determined values presented in this work.
IV Conclusions
We presented optical studies of individual Co2+ ions in epitaxial QDs. Using partially allowed optical transitions we describe strain induced zero-field splitting of Co2+ ions and anticrossing of Co2+ spin states. From this anticrossing we determine Hamiltonian parameters and representing axial and in-plane components of crystal field. Our technique, can be applied for optical measurements of zero-field splitting of other transition metal ions (e.g. Cr2+, Fe2+) in QDs, providing that very low noise spectra or high enough magnetic fields are available.
Acknowledgements.
This work was partially supported by the Polish National Science Centre under decision DEC-2015/18/E/ST3/00559, DEC-2011/02/A/ST3/00131, DEC-2013/09/B/ST3/02603, DEC-2012/05/N/ST3/03209, by Polish Ministry of Science and Higher Education programme „Iuventus Plus” in years 2015-2017 project number IP2014 034573, and in years 20132017 as research grant ”Diamentowy Grant”. The two of us (JK and TS) were supported by the Foundation for Polish Science through the START programme. Project was carried out with the use of CePT, CeZaMat, and NLTK infrastructures financed by the European Union - the European Regional Development Fund within the Operational Programme ”Innovative economy”.References
- Kobak et al. (2014) J. Kobak, T. Smoleński, M. Goryca, M. Papaj, K. Gietka, A. Bogucki, M. Koperski, J.-G. Rousset, J. Suffczyński, E. Janik, M. Nawrocki, A. Golnik, P. Kossacki, and W. Pacuski, Designing quantum dots for solotronics, Nat. Commun. 5, 3191 (2014).
- Besombes et al. (2004) L. Besombes, Y. Léger, L. Maingault, D. Ferrand, H. Mariette, and J. Cibert, Probing the Spin State of a Single Magnetic Ion in an Individual Quantum Dot, Phys. Rev. Lett. 93, 207403 (2004).
- Besombes et al. (2005) L. Besombes, Y. Leger, L. Maingault, D. Ferrand, H. Mariette, and J. Cibert, Carrier-induced spin splitting of an individual magnetic atom embedded in a quantum dot, Phys. Rev. B 71, 161307 (2005).
- Le Gall et al. (2009) C. Le Gall, L. Besombes, H. Boukari, R. Kolodka, J. Cibert, and H. Mariette, Optical Spin Orientation of a Single Manganese Atom in a Semiconductor Quantum Dot Using Quasiresonant Photoexcitation, Phys. Rev. Lett. 102, 127402 (2009).
- Goryca et al. (2009) M. Goryca, T. Kazimierczuk, M. Nawrocki, A. Golnik, J. A. Gaj, P. Kossacki, P. Wojnar, and G. Karczewski, Optical Manipulation of a Single Mn Spin in a CdTe-Based Quantum Dot, Phys. Rev. Lett. 103, 087401 (2009).
- Goryca et al. (2010) M. Goryca, P. Plochocka, T. Kazimierczuk, P. Wojnar, G. Karczewski, J. A. Gaj, M. Potemski, and P. Kossacki, Brightening of dark excitons in a single CdTe quantum dot containing a single ion, Phys. Rev. B 82, 165323 (2010).
- Kudelski et al. (2007) A. Kudelski, A. Lemaître, A. Miard, P. Voisin, T. C. M. Graham, R. J. Warburton, and O. Krebs, Optically Probing the Fine Structure of a Single Mn Atom in an InAs Quantum Dot, Phys. Rev. Lett. 99, 247209 (2007).
- Krebs et al. (2009) O. Krebs, E. Benjamin, and A. Lemaître, Magnetic anisotropy of singly Mn-doped InAs/GaAs quantum dots, Phys. Rev. B 80, 165315 (2009).
- Baudin et al. (2011) E. Baudin, E. Benjamin, A. Lemaître, and O. Krebs, Optical Pumping and a Nondestructive Readout of a Single Magnetic Impurity Spin in an InAs/GaAs Quantum Dot, Phys. Rev. Lett. 107, 197402 (2011).
- Smoleński et al. (2015) T. Smoleński, W. Pacuski, M. Goryca, M. Nawrocki, A. Golnik, and P. Kossacki, Optical spin orientation of an individual ion in a CdSe/ZnSe quantum dot, Phys. Rev. B 91, 045306 (2015).
- Fainblat et al. (2016) R. Fainblat, C. J. Barrows, E. Hopmann, S. Siebeneicher, V. A. Vlaskin, D. R. Gamelin, and G. Bacher, Giant Excitonic Exchange Splittings at Zero Field in Single Colloidal CdSe Quantum Dots Doped with Individual Mn2+ Impurities, Nano Lett. Article ASAP x, x (2016).
- Smolenski et al. (2016) T. Smolenski, T. Kazimierczuk, J. Kobak, M. Goryca, A. Golnik, P. Kossacki, and W. Pacuski, Magnetic ground state of an individual Fe2+ ion in strained semiconductor nanostructure, Nat. Commun. 7, 10484 (2016).
- Lafuente-Sampietro et al. (2016a) A. Lafuente-Sampietro, H. Utsumi, H. Boukari, S. Kuroda, and L. Besombes, Individual Cr atom in a semiconductor quantum dot: Optical addressability and spin-strain coupling, Phys. Rev. B 93 (2016a).
- Lafuente-Sampietro et al. (2016b) A. Lafuente-Sampietro, H. Utsumi, H. Boukari, S. Kuroda, and L. Besombes, Spin dynamics of an individual Cr atom in a semiconductor quantum dot under optical excitation, Appl. Phys. Lett. 109, 053103 (2016b).
- Koenraad and Flatte (2011) P. M. Koenraad and M. E. Flatte, Single dopants in semiconductors, Nat. Mater 10, 91 (2011).
- Beaulac et al. (2009) R. Beaulac, L. Schneider, P. I. Archer, G. Bacher, and D. R. Gamelin, Light-Induced Spontaneous Magnetization in Doped Colloidal Quantum Dots, Science 325, 973 (2009).
- Whitaker et al. (2011) K. M. Whitaker, M. Raskin, G. Kiliani, K. Beha, S. T. Ochsenbein, N. Janssen, M. Fonin, U. Rüdiger, A. Leitenstorfer, D. R. Gamelin, and R. Bratschitsch, Spin-on Spintronics: Ultrafast Electron Spin Dynamics in ZnO and Zn1–xCoxO Sol–Gel Films, Nano Lett. 11, 3355 (2011).
- Pandey et al. (2012) A. Pandey, S. Brovelli, R. Viswanatha, L. Li, J. Pietryga, V. I. Klimov, and S. Crooker, Long-lived photoinduced magnetization in copper-doped ZnSe-CdSe core-shell nanocrystals, Nat. Nanotechnol. 7, 792 (2012).
- Qu et al. (2015) F. Qu, L. Villegas-Lelovsky, and P. C. Morais, Spin-split antibonding molecular ground state in manganese-doped quantum dot molecules, Phys. Rev. B 92, 115445 (2015).
- Barman et al. (2015) B. Barman, R. Oszwałdowski, L. Schweidenback, A. H. Russ, J. M. Pientka, Y. Tsai, W.-C. Chou, W. C. Fan, J. R. Murphy, A. N. Cartwright, I. R. Sellers, A. G. Petukhov, I. Žutić, B. D. McCombe, and A. Petrou, Time-resolved magnetophotoluminescence studies of magnetic polaron dynamics in type-II quantum dots, Phys. Rev. B 92, 035430 (2015).
- Loureço et al. (2015) S. A. Loureço, R. S. Silva, A. C. A. Silva, and N. O. Dantas, Structural and Optical Properties of Co2+-Doped PbSe Nanocrystals in Chalcogeneide Glass Matrix, J. Phys. Chem. C 119, 13277 (2015).
- Rice et al. (2016) W. D. Rice, W. Liu, T. A. Baker, N. A. Sinitsyn, V. I. Klimov, and S. A. Crooker, Revealing giant internal magnetic fields due to spin fluctuations in magnetically doped colloidal nanocrystals, Nat. Nanotechnol. 11, 137 (2016).
- Nistor et al. (2016) S. Nistor, M. Stefan, L. Nistor, D. Ghica, and I. Vlaicu, Distribution and interaction of Mn2+ ions incorporated in cubic ZnS quantum dots over a broad concentration range, J. Alloy. Comp. 662, 193 (2016).
- Moldoveanu et al. (2016) V. Moldoveanu, I. V. Dinu, R. Dragomir, and B. Tanatar, Light-hole exciton mixing and dynamics in Mn-doped quantum dots, Phys. Rev. B 93, 165421 (2016).
- Balanta et al. (2016) M. Balanta, M. Brasil, F. Iikawa, U. C. Mendes, J. Brum, Y. A. Danilov, M. Dorokhin, O. Vikhrova, and B. Zvonkov, Optically controlled spin-polarization memory effect on Mn delta-doped heterostructures, Sci. Rep. 6, 24537 (2016).
- Muckel et al. (2016) F. Muckel, J. Yang, S. Lorenz, W. Baek, H. Chang, T. Hyeon, G. Bacher, and R. Fainblat, Digital Doping in Magic-Sized CdSe Clusters, ACS Nano 10, 7135 (2016).
- Goryca et al. (2014) M. Goryca, M. Koperski, P. Wojnar, T. Smoleński, T. Kazimierczuk, A. Golnik, and P. Kossacki, Coherent precession of an individual 5/2 spin, Phys. Rev. Lett. 113, 227202 (2014).
- Besombes and Boukari (2014) L. Besombes and H. Boukari, Resonant optical pumping of a Mn spin in a strain-free quantum dot, Phys. Rev. B 89, 085315 (2014).
- Lafuente-Sampietro et al. (2015) A. Lafuente-Sampietro, H. Boukari, and L. Besombes, Strain-induced coherent dynamics of coupled carriers and Mn spins in a quantum dot, Phys. Rev. B 92, 081305 (2015).
- Tinjod et al. (2003) F. Tinjod, B. Gilles, S. Moehl, K. Kheng, and H. Mariette, II–VI quantum dot formation induced by surface energy change of a strained layer, Appl. Phys. Lett. 82, 4340 (2003).
- Papaj et al. (2014) M. Papaj, J. Kobak, J.-G. Rousset, E. Janik, M. Nawrocki, P. Kossacki, A. Golnik, and W. Pacuski, Photoluminescence studies of giant Zeeman effect in MBE-grown cobalt-based dilute magnetic semiconductors, J. Cryst. Growth 401, 644 (2014).
- Papaj et al. (2012) M. Papaj, J. Kobak, J.-G. Rousset, E. Janik, A. Golnik, P. Kossacki, and W. Pacuski, MBE Growth and Magnetooptical Properties of (Zn,Co)Te Layers, Acta Phys. Pol. A 122, 1010 (2012).
- Ham et al. (1960) F. S. Ham, G. W. Ludwig, G. D. Watkins, and H. H. Woodbury, Spin Hamiltonian of , Phys. Rev. Lett. 5, 468 (1960).
- Wu and Dong (2004) S.-Y. Wu and H.-N. Dong, On the EPR parameters of divalent cobalt in ZnX (X= S, Se, Te) and CdTe, Z. Naturforsch. 59, 938 (2004).
- Grzybowski et al. (2015) M. Grzybowski, A. Golnik, M. Sawicki, and W. Pacuski, Effect of magnetic field on intraionic photoluminescence of (Zn,Co)Se, Solid State Commun. 208, 7 (2015).
- Lewicki et al. (1991) A. Lewicki, A. I. Schindler, I. Miotkowski, B. C. Crooker, and J. K. Furdyna, Specific heat of Cd1-xCoxS and Cd1-xCoxSe at low temperatures, Phys. Rev. B 43, 5713 (1991).
- Isber et al. (1995) S. Isber, M. Averous, Y. Shapira, V. Bindilatti, A. N. Anisimov, N. F. Oliveira, V. M. Orera, and M. Demianiuk, Axial anisotropy of in CdSe from the magnetization step and EPR, Phys. Rev. B 51, 15211 (1995).
- Bindilatti et al. (1994) V. Bindilatti, A. N. Anisimov, N. F. Oliveira, Y. Shapira, M. Goiran, F. Yang, S. Isber, M. Averous, and M. Demianiuk, Axial anisotropy of in CdS from magnetization-step and high-frequency EPR, Phys. Rev. B 50, 16464 (1994).
- Estle and De Wit (1961) T. Estle and M. De Wit, Paramagnetic Resonance of Co2+ and V2+ in ZnO, Bull. Am. Phys. Soc 6, 445 (1961).
- Macfarlane (1970) R. M. Macfarlane, Perturbation Methods in the Calculation of Zeeman Interactions and Magnetic Dipole Line Strengths for Trigonal-Crystal Spectra, Phys. Rev. B 1, 989 (1970).
- Koidl (1977) P. Koidl, Optical absorption of Co2+ in ZnO, Phys. Rev. B 15, 2493 (1977).
- Jedrecy et al. (2004) N. Jedrecy, H. J. V. Bardeleben, Y. Zheng, and J. L. Cantin, Electron paramagnetic resonance study of Zn1-xCoxO: A predicted high-temperature ferromagnetic semiconductor, Phys. Rev. B 69, R041308 (2004).
- Ferrand et al. (2005) D. Ferrand, S. Marcet, W. Pacuski, E. Gheeraert, P. Kossacki, J. A. Gaj, J. Cibert, C. Deparis, H. Mariette, and C. Morhain, Spin Carrier Exchange Interactions in (Ga,Mn)N and (Zn,Co)O Wide Band Gap Diluted Magnetic Semiconductor Epilayers, J. Superconductivity 18, 15 (2005).
- Sati et al. (2006) P. Sati, R. Hayn, R. Kuzian, S. Régnier, S. Schäfer, A. Stepanov, C. Morhain, C. Deparis, M. Laügt, M. Goiran, and Z. Golacki, Magnetic Anisotropy of Co2+ as Signature of Intrinsic Ferromagnetism in ZnO:Co, Phys. Rev. Lett. 96, 017203 (2006).
- Pacuski et al. (2006) W. Pacuski, D. Ferrand, J. Cibert, C. Deparis, J. A. Gaj, P. Kossacki, and C. Morhain, Effect of the ,- exchange interaction on the excitons in (Zn,Co)O epilayers, Phys. Rev. B 73, 035214 (2006).