Discovery and Identification of Extra Neutral Gauge Bosons at the LHC
Abstract
We present the discovery prospects for a resonance and some expected results for diagnostic measurements at the LHC. The discovery reach is highly dependent on the energy and luminosities that may be attained at the LHC, and a number of energy and integrated luminosity scenarios are presented. In addition, the use of third generation quark final states for distinguishing between models and for measuring a forward-backward asymmetry is explored.
I Introduction
There is a general consensus that the Standard Model (SM) is a low energy effective theory and that some sort of new physics exists at higher energies than we can currently explore. Many models have been developed to describe potential new physics and explain electroweak symmetry breaking (EWSB), among which are extended gauge sectors, including models with extra factors Hewett:1988xc ; Langacker:2008yv ; Rizzo:2006nw ; Leike:1998wr ; Cvetic:1995zs . Grand Unified Theories with breaking to Hewett:1988xc are one example, while the Left-Right Symmetric model Mohapatra:uf , , is another. Other approaches to describing EWSB include the Little Higgs model and variants ArkaniHamed:2002qy ; Schmaltz:2004de , theories with extra dimensions Randall:1999ee , Supersymmetry, and Technicolor and Topcolor models.
New TeV scale -channel structures are common to many of these models of new physics. If an -channel resonance were discovered, the immediate task would be to try to identify the underlying theory. In this report, we describe some approaches to distinguish between the different extra neutral gauge bosons () that appear in models of new physics. We start with an update on discovery limits of ’s at the LHC for the low centre-of-mass energy and low luminosity scenarios in the early years of the LHC program Godfrey:1994qk ; Erler:2009jh ; Salvioni:2009mt . We then describe the use of top and bottom quark final states to distinguish between models Godfrey:2008vf ; Rizzo:1998ut ; Barger:2006hm ; Frederix:2007gi ; Mohapatra:1992tc , and give a preliminary account of more recent studies of forward-backward asymmetries () Langacker:1984dc ; Petriello:2008zr including the use of top and bottom quarks.
The models analyzed in this contribution are the E6 set of models (E6 , , ) Hewett:1988xc , the Left-Right Symmetric (LR, ) Mohapatra:uf and Alternate Left-Right Symmetric models (ALR, ) Ma:1986we , the Ununified Model (UUM, ) Georgi:1989xz , the Sequential Standard model (SSM), a Topcolor Assisted Technicolor model (TC2, ) Harris:1999ya ; Hill:1991at , the Littlest Higgs model (LH, ) ArkaniHamed:2001nc ; ArkaniHamed:2002qy , the Simplest Little Higgs model (SLH) Schmaltz:2004de ; ArkaniHamed:2001nc , the Anomaly Free Simple Little Higgs model (AFSLH) Han:2005ru ; Kong:2003vm , a 331 model Barreto:2007mt ; Dias:2005xj , and generic models with group structures of () Chivukula:1994mn ; Chivukula:1995gu ; Simmons:1996ws ; Malkawi:1996fs ; Muller:1996qs ; He:1999vp and () Hill:1994hp ; Lane:1995gw ; Lane:1996ua ; Lane:1998qi ; Popovic:1998vb .
II Discovery Limits of Extra Neutral Gauge Bosons at the LHC
An extra neutral gauge boson would be produced by a hadron collider via the Drell-Yan process and would show up as a resonant peak of events in the invariant mass distribution of the fermion-anti-fermion final stateGodfrey:1994qk . For non-leptophobic ’s, the cleanest search channel uses dilepton final states ( or ) Hewett:1988xc ; Langacker:2008yv ; Rizzo:2006nw ; Leike:1998wr ; Cvetic:1995zs due to the small irreducible backgrounds and a clear, distinguishable signal in the ATLAS :2008zzm ; :1999fq and CMS Ball:2007zza detectors. A small number of dilepton events clustered in an isolated invariant mass bin would be strong evidence for the existence of an -channel resonance.
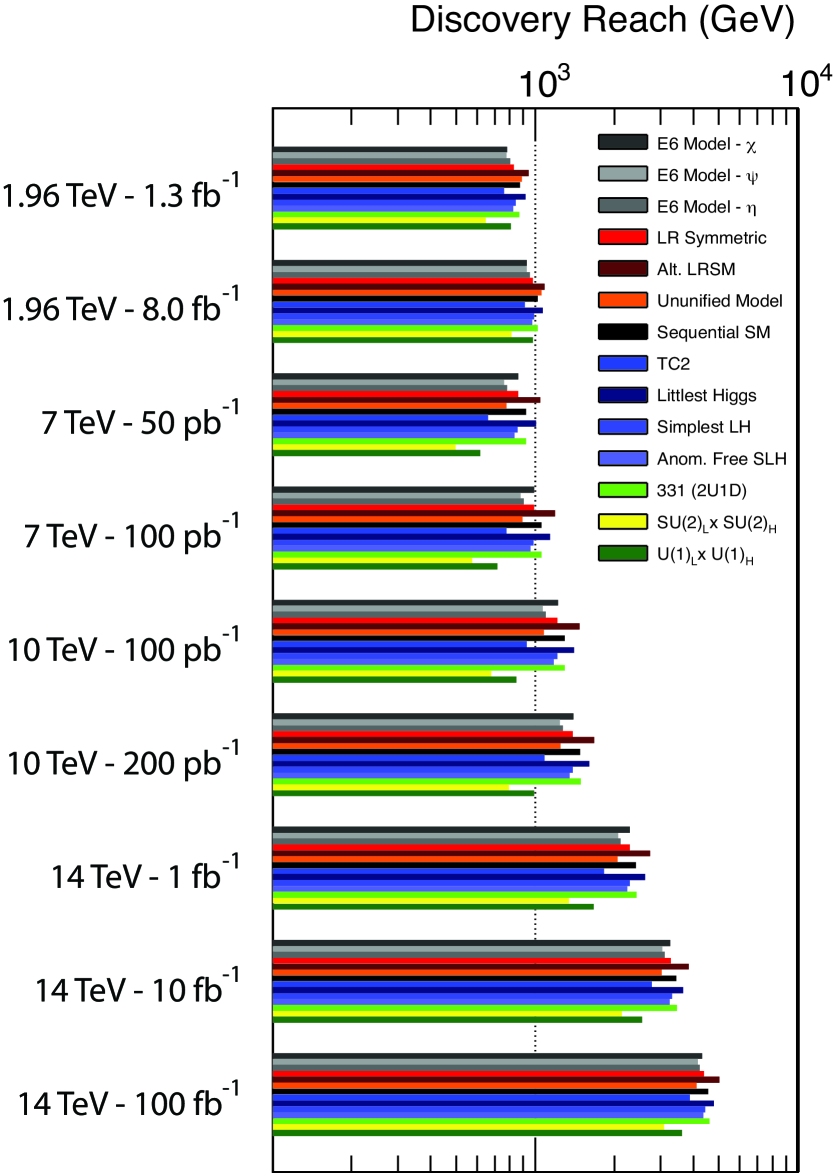
To predict the discovery potential of the LHC for various models, we calculate the cross section to dimuon final states for a given mass and impose the following kinematic cuts to reflect detector acceptances: GeV and :2008zzm ; :1999fq . In addition, we consider only contributions from events within an invariant mass bin around the resonance mass peak, as defined by the ATLAS TDR :1999fq . We define the discovery reach as the largest resonance mass, , that would result in the observation of 5 events per dilepton channel, based on the luminosity provided. The discovery reach for various LHC energy and luminosity scenarios are shown in Fig. 1.
Also included are estimates of the discovery reach for the same models at the Tevatron assuming both 1.3 fb-1 of integrated luminosity, as in Ref. Aaltonen:2008vx , and 8 fb-1 to estimate the reach from the full expected luminosity. In our analysis, we use similar detector acceptance and cuts as in Ref. Aaltonen:2008vx : we impose a kinematic cut of GeV and consider events within two regions of pseudorapidity - where both leptons satisfy , and where one lepton satisfies and the other satisfies . As well, we consider only events within an invariant mass window of . We use the discovery criteria of 5 observed dilepton events as with the LHC study. We note that our approach differs from that used by the CDF collaboration to obtain the current direct limits in Refs. Aaltonen:2008vx and Aaltonen:2008ah .
III Identification Using and Quarks
The discovery of a TeV scale -channel resonance would be a first step in a particle physics revolution. But to determine the underlying physics will require the determination of the properties of the resonance. For dilepton final states, the observables that have been studied so far include: the cross section and width Langacker:1984dc , the angular distribution and centre-edge asymmetry delAguila:1993ym ; Dvergsnes:2004tw , and various analyses of the rapidity distributions through asymmetries and matrix analysis delAguila:1993ym ; Dittmar:2003ir ; Petriello:2008zr ; Li:2009xh .
Quark final states were considered to have limited usefullness due to the inability to identify individual quark flavours in the final state. However, and quarks can be uniquely identified :2008zzm ; :1999fq from other jets in the final state, as can a small percentage of quarks. We have shown that this ability to identify and quarks in the final state can be used to discriminate between models. The primary challenges of this analysis will be the identification efficiency and rejection rates against reducible QCD backgrounds.
The recent ATLAS detector paper :2008zzm suggests quark tagging efficiencies of are possible for high events at high luminosities, with a 100 to 1 rejection against light and jets. Requiring the tag for both the and events reduces the efficiency, but improves the rejection by another factor of 100 to 1. Depending on the expected light jet backgrounds, the tradeoff between efficiency and rejection can be adjusted to improve signal significance - a higher rejection rate corresponds to a lower identification efficiency.
Top quarks decay rapidly to , where the boson subsequently decays either to lepton (, , ) or light quark (, ) final states. The single lepton plus jets decay mode, , accounts for approximately of events, and is often considered to have the best signal to background ratio. The CMS and ATLAS collaborations estimate an efficiency of Khramov:2007ev ; :2008zzm ; :1999fq ; D'hondt:2007aj , but more recent studies suggest may be possible. A number of recent studies have considered purely hadronic modes, where both bosons from the pair decay to light jets, and suggest rejection rates of may be possible Baur:2007ck ; Kaplan:2008ie ; Thaler:2008ju ; Baur:2008uv . If these can be utilized, the total number of events that could be used would be increased significantly.
Light jet rejection is not the only concern with measurements of electroweak processes involving hadronic final states. Even if large rejection rates are achieved, the irreducible SM QCD backgrounds are large Baur:2007ck ; Kaplan:2008ie ; Thaler:2008ju ; Baur:2008uv . Figure 2(a) shows the the expected invariant mass distributions for a representative set of models with TeV decaying to final states, including the expected SM backgrounds (), without kinematic cuts. We found that this background can be significantly reduced by imposing a cut on the of the reconstructed or jet Godfrey:2008vf . We found that a value of provided a good balance between improving the signal to background ratio while maintaining good total statistics. The invariant mass distribution with this cut is shown in Fig. 2(b), where we can see an improvement in the visibility of the peak over the backgrounds.
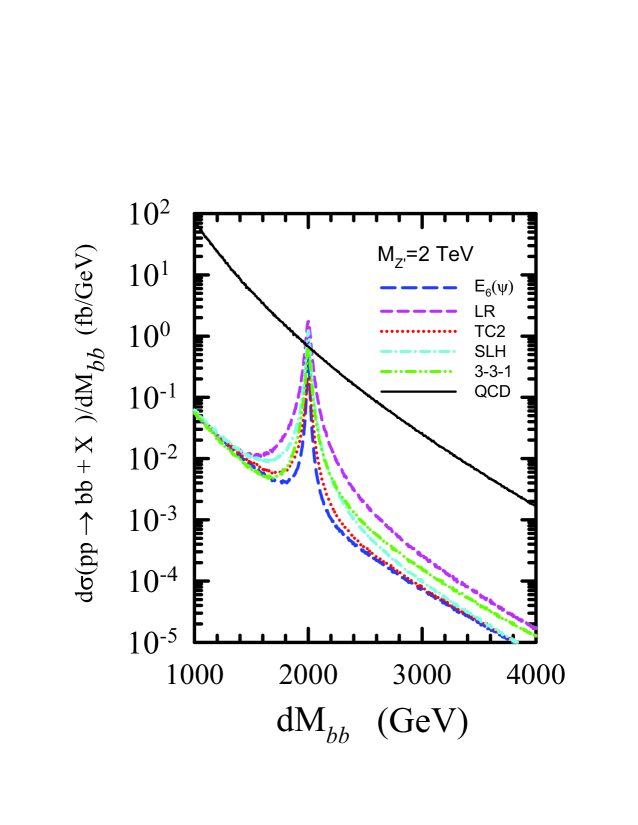
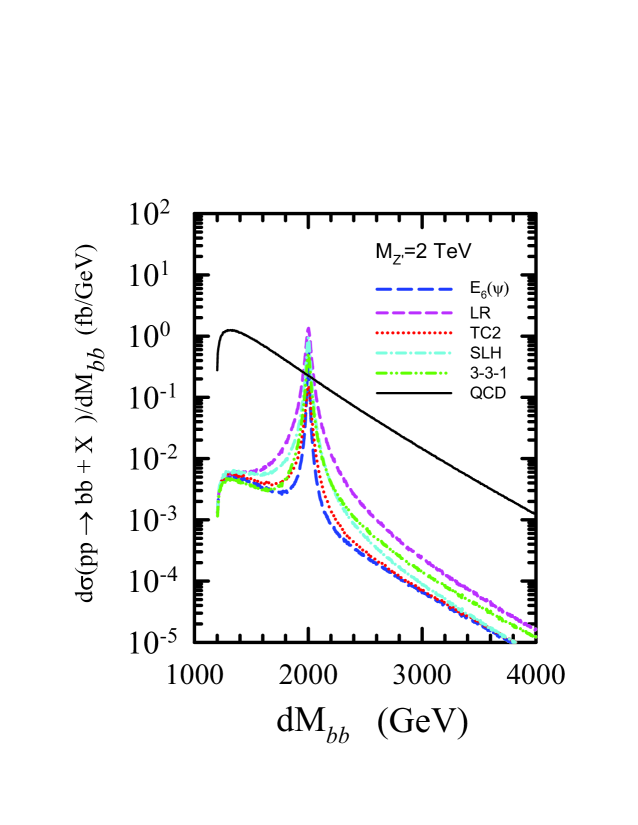
Other important issues not considered in this study include non-QCD SM backgrounds, such as , , , and others. These backgrounds can be controlled by constraints on the cluster transverse mass and invariant mass of the jets.
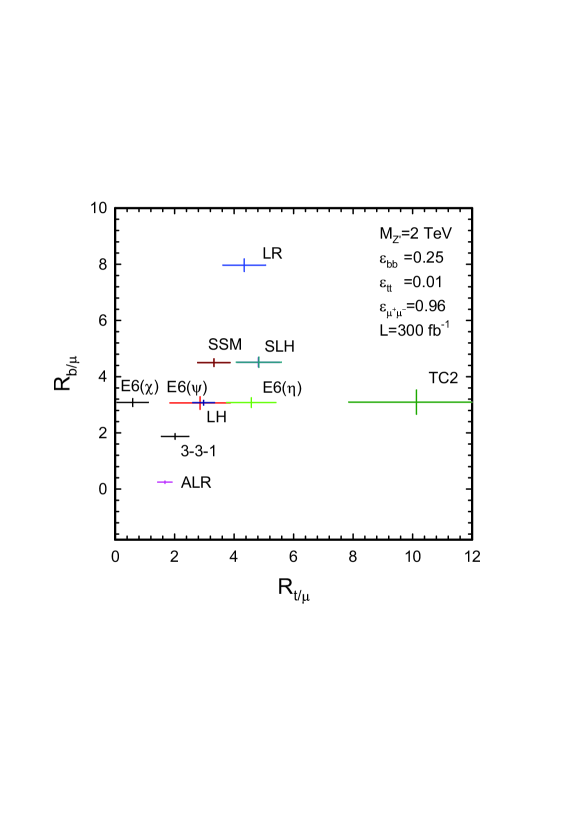
In our analysis, we did not consider contributions to uncertainties from the parton distribution functions and from higher order loop corrections, though the effect of PDF uncertainties can be reduced by taking the ratio of cross sections to different final states. To distinguish between models, we define:
| (1) | |||||
| (2) | |||||
where depends on QCD and electroweak corrections. These ratios depend on model dependent couplings that will produce distinctive results based on the model.
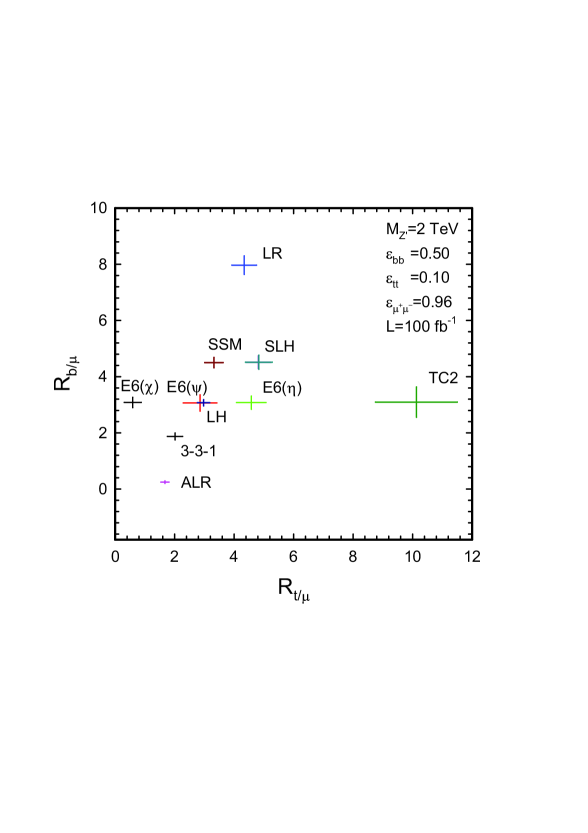
In Fig. 3, we plot the ratios vs Godfrey:2008vf for a selection of models for two scenarios representing optimistic and pessimistic views of the identification efficiency and background rejection capabilities of the detectors at the LHC. We assume that a has been discovered and a measurement of the mass and width has been found from the dilepton channel. The errors shown represent purely statistical uncertainties resulting from subtracting the background signal from the total backgroundsignal that would be observed.
It should be noted that the unique position of each model in these plots is due to the specific choice of the mixing parameter value in each case. In some cases, the mixing parameter is free to vary depending on the nature of the symmetry, resulting in overlapping regions in the plane so that one could not uniquely distinguish the precise model using this measurement alone. In this case, although it might not be possible to uniquely identify the underlying model, some models could be ruled out and the mixing parameter for others could be constrained in conjunction with other measurements.
IV Forward-Backward Asymmetry
It is possible to take advantage of heavy flavour identification to measure forward-backward asymmetries () in production. The forward-backward asymmetry is defined as:
| (3) | |||||
| (4) |
where are the left and right handed couplings of the to fermions, and are the integrated symmetric and antisymmetric combinations of the parton distribution functions. The differential cross sections, , are even and odd contributions to the rapidity distribution, found via:
| (5) |
where the centre-of-mass scattering angle, , is measured from the outgoing fermion relative to the incoming quark.
For collisions at the LHC, there is an ambiguity in determining the direction of the quark where it is impossible to tell on an event-by-event basis whether the was boosted in the direction of the quark or anti-quark. Because the momentum distributions are harder for the valence quarks than for the sea anti-quarks, this ambiguity can be resolved to a certain extent by assuming that the boost direction is the same as the quark direction Dittmar:1996my . For small values of the rapidity of the , the quark and anti-quark momenta are more evenly balanced and this procedure is less likely to correctly identify the quark direction.
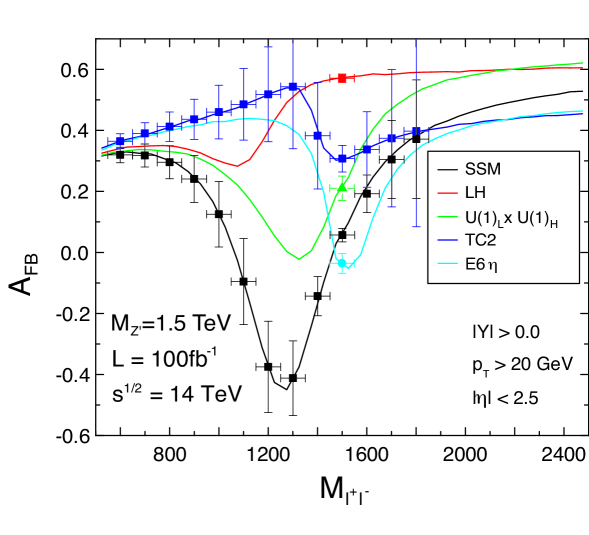
In a recent paper, we suggested that a simpler method of performing the forward-backward asymmetry measurement is possible by using the direct pseudorapidity measurements of the final state particles Diener:2009ee . It can be shown that a “forward” event is one in which in the lab frame, and vice-versa for a “backward” event, assuming that the initial state quark has a greater momentum than the initial state anti-quark. This method of finding the has the advantage of being very straightforward and clean, as it relies only on counting events depending on the pseudorapidity. No calculation of the centre-of-mass scattering angle or rapidity is required. In Fig. 4, we show the distribution in invariant mass bins of the final state for a with mass TeV.
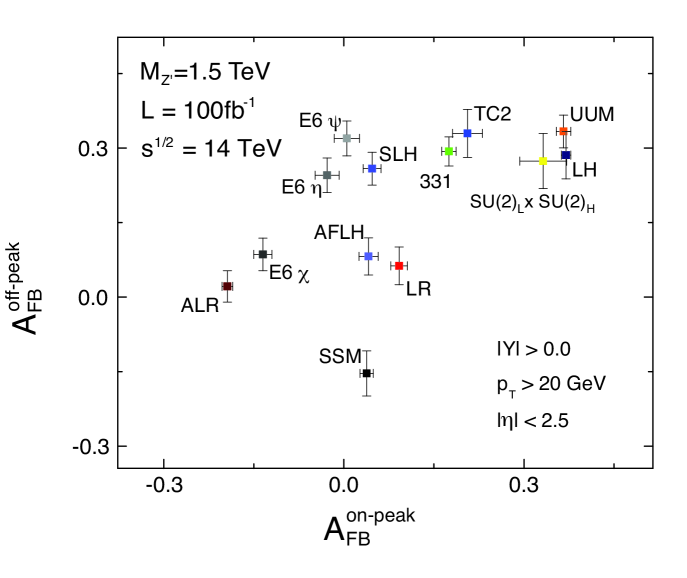
Typically the on-peak has been studied to determine the couplings, where the statistical uncertainty is smallest due to the resonance enhanced cross section. However, it is clear that information can still be obtained from an off-peak measurement Petriello:2008zr . In Fig. 5 we show the results of an analysis of the on-peak versus off-peak for the final state for a number of models with TeV. In this case, the on-peak measurement includes all events within and off-peak includes all events within the range .
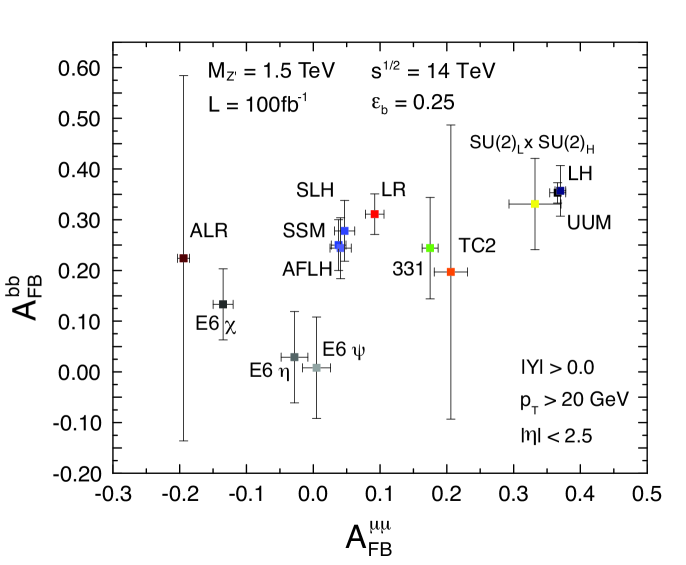
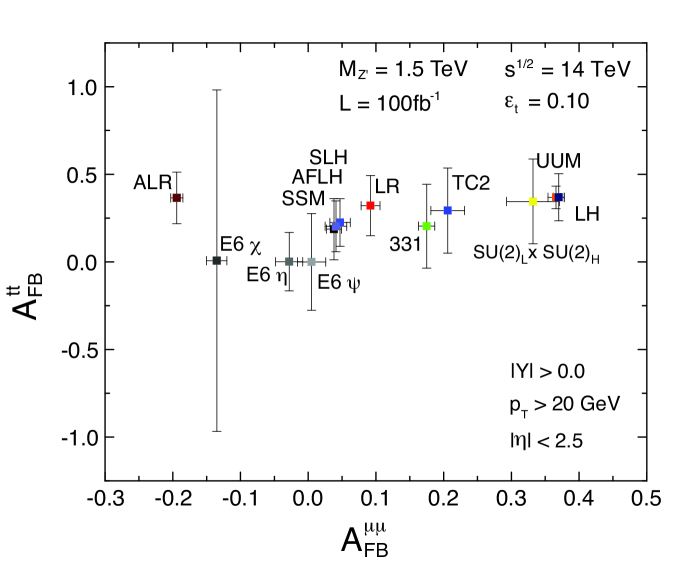
In addition to using third generation final states for ratios of cross sections, it may also be possible to measure the forward-backward asymmetry measurement in the and channels. Using pseudorapidity information to make a measurement of an may reduce potentially large systematic errors resulting from determining and for hadronic final states. The large QCD backgrounds will make this measurement difficult, but an measurement would provide additional information about the couplings to and quarks that cannot be obtained from other measurements. From Eq. (4), it is clear that the term in the second set of brackets does not depend on the final state. Measurements of to other final states can therefore, potentially, give information about the coupling of a to the final state heavy quarks and will be useful in a global fit of couplings. Figure 6 shows for the and channels versus for the the muon channel. While large uncertainties are apparent for some models, a reasonable measurement can still be expected for a number of models including the Left-Right Symmetric Model and variants of the Little Higgs that are included.
V Summary
Many models of new physics predict new -channel resonances. It is possible that a may be discovered early in the LHC program, especially a state decaying to muons or electrons. Numerous observables have been proposed to distinguish between the different possibilities of models. In this contribution, we showed that flavour tagging of 3rd generation quarks can be used to distinguish between models and measure individual quark couplings to a . We also described a new method for measuring the forward-backward asymmetry, which is of particular use in measuring the to third generation quark final states. Values of were shown for , and final states.
Acknowledgements.
This work was supported in part by the Natural Sciences and Engineering Research Council of Canada.References
- (1) J. L. Hewett and T. G. Rizzo, Phys. Rept. 183, 193 (1989).
- (2) P. Langacker, arXiv:0801.1345 [hep-ph].
- (3) T. G. Rizzo, arXiv:hep-ph/0610104.
- (4) A. Leike, Phys. Rept. 317, 143 (1999).
- (5) M. Cvetic and S. Godfrey, arXiv:hep-ph/9504216.
- (6) R. N. Mohapatra, Unification And Supersymmetry. The Frontiers Of Quark - Lepton Physics (Springer, Berlin, 1986).
- (7) N. Arkani-Hamed, A. G. Cohen, E. Katz and A. E. Nelson, JHEP 0207, 034 (2002).
- (8) M. Schmaltz, JHEP 0408, 056 (2004).
- (9) L. Randall and R. Sundrum, Phys. Rev. Lett. 83, 3370 (1999).
- (10) S. Godfrey, Phys. Rev. D 51, 1402 (1995); [arXiv:hep-ph/0201093].
- (11) J. Erler, P. Langacker, S. Munir and E. R. Pena, arXiv:0906.2435 [hep-ph].
- (12) E. Salvioni, G. Villadoro and F. Zwirner, arXiv:0909.1320 [hep-ph].
- (13) S. Godfrey and T. A. W. Martin, Phys. Rev. Lett. 101, 151803 (2008).
- (14) V. Barger, T. Han and D. G. E. Walker, Phys. Rev. Lett. 100, 031801 (2008).
- (15) R. Frederix and F. Maltoni, arXiv:0712.2355 [hep-ph].
- (16) P. K. Mohapatra, Mod. Phys. Lett. A 8, 771 (1993).
- (17) T. G. Rizzo, Phys. Rev. D 59, 015020 (1999).
- (18) P. Langacker, R. W. Robinett and J. L. Rosner, Phys. Rev. D 30, 1470 (1984).
- (19) F. Petriello and S. Quackenbush, Phys. Rev. D 77, 115004 (2008).
- (20) E. Ma, Phys. Rev. D 36, 274 (1987); T. G. Rizzo, Phys. Lett. B 206, 133 (1988); J. F. Gunion, A. Mendez and F. I. Olness, Int. J. Mod. Phys. A 2, 1085 (1987).
- (21) H. Georgi, E. E. Jenkins and E. H. Simmons, Nucl. Phys. B 331, 541 (1990).
- (22) R. M. Harris, C. T. Hill and S. J. Parke, arXiv:hep-ph/9911288.
- (23) C. T. Hill, Phys. Lett. B 266, 419 (1991); C. T. Hill, Phys. Lett. B 345, 483 (1995).
- (24) N. Arkani-Hamed, A. G. Cohen and H. Georgi, Phys. Lett. B 513, 232 (2001).
- (25) T. Han, H. E. Logan and L. T. Wang, JHEP 0601, 099 (2006).
- (26) O. C. W. Kong, J. Korean Phys. Soc. 45, S404 (2004) [arXiv:hep-ph/0312060].
- (27) E. Ramirez Barreto, Y. D. A. Coutinho and J. Sa Borges, Eur. Phys. J. C 50, 909 (2007) [arXiv:hep-ph/0703099].
- (28) A. G. Dias, J. C. Montero and V. Pleitez, Phys. Lett. B 637, 85 (2006).
- (29) R. S. Chivukula, E. H. Simmons and J. Terning, Phys. Lett. B 331, 383 (1994).
- (30) R. S. Chivukula, E. H. Simmons and J. Terning, Phys. Rev. D 53, 5258 (1996).
- (31) E. H. Simmons, Phys. Rev. D 55, 5494 (1997).
- (32) E. Malkawi, T. Tait and C. P. Yuan, Phys. Lett. B 385, 304 (1996).
- (33) D. J. Muller and S. Nandi, arXiv:hep-ph/9610404.
- (34) H. J. He, T. Tait and C. P. Yuan, Phys. Rev. D 62, 011702 (2000).
- (35) C. T. Hill, Phys. Lett. B 345, 483 (1995).
- (36) K. D. Lane and E. Eichten, Phys. Lett. B 352, 382 (1995) [arXiv:hep-ph/9503433].
- (37) K. D. Lane, Phys. Rev. D 54, 2204 (1996).
- (38) K. D. Lane, Phys. Lett. B 433, 96 (1998).
- (39) M. B. Popovic and E. H. Simmons, Phys. Rev. D 58, 095007 (1998).
- (40) G. Aad et al. [ATLAS Collaboration], JINST 3, S08003 (2008).
- (41) “ATLAS: Detector and physics performance technical design report. Volume 1,” CERN-LHCC-99-14 “ATLAS: Detector and physics performance technical design report. Volume 2,” CERN-LHCC-99-15
- (42) G. L. Bayatian et al. [CMS Collaboration], J. Phys. G 34 (2007) 995.
- (43) T. Aaltonen et al. [CDF Collaboration], Phys. Rev. Lett. 102, 031801 (2009).
- (44) T. Aaltonen et al. [CDF Collaboration], Phys. Rev. Lett. 102, 091805 (2009).
- (45) F. del Aguila, M. Cvetic and P. Langacker, Phys. Rev. D 48, 969 (1993).
- (46) E. W. Dvergsnes, P. Osland, A. A. Pankov and N. Paver, Phys. Rev. D 69, 115001 (2004); P. Osland, A. A. Pankov, N. Paver and A. V. Tsytrinov, Phys. Rev. D 78, 035008 (2008); Phys. Rev. D 79, 115021 (2009).
- (47) M. Dittmar, A. S. Nicollerat and A. Djouadi, Phys. Lett. B 583, 111 (2004).
- (48) Y. Li, F. Petriello and S. Quackenbush, arXiv:0906.4132 [hep-ph].
- (49) E. V. Khramov, A. Tonoyan, V. A. Bednyakov and N. A. Rusakovich, arXiv:0705.2001 [hep-ex].
- (50) J. D’hondt, arXiv:0707.1247 [hep-ph].
- (51) U. Baur and L. H. Orr, Phys. Rev. D 76, 094012 (2007).
- (52) D. E. Kaplan, K. Rehermann, M. D. Schwartz and B. Tweedie, arXiv:0806.0848 [hep-ph].
- (53) J. Thaler and L. T. Wang, arXiv:0806.0023 [hep-ph].
- (54) U. Baur and L. H. Orr, Phys. Rev. D 77, 114001 (2008). [arXiv:0803.1160 [hep-ph]].
- (55) M. Dittmar, Phys. Rev. D 55, 161 (1997).
- (56) R. Diener, S. Godfrey and T. A. W. Martin, Phys. Rev. D (2009; in press) arXiv:0909.2022 [hep-ph].