Discovery of Eclipses from the Accreting Millisecond X-ray Pulsar SWIFT J1749.42807
Abstract
We report the discovery of X-ray eclipses in the recently discovered accreting millisecond X-ray pulsar Swift J1749.42807. This is the first detection of X-ray eclipses in a system of this type and should enable a precise neutron star mass measurement once the companion star is identified and studied. We present a combined pulse and eclipse timing solution that enables tight constraints on the orbital parameters and inclination and shows that the companion mass is in the range for a likely range of neutron star masses, and that it is larger than a main sequence star of the same mass. We observed two individual eclipse egresses and a single ingress. Our timing model shows that the eclipse features are symmetric about the time of longitude from the ascending node, as expected. Our eclipse timing solution gives an eclipse duration (from the mid-points of ingress to egress) of s. This represents 6.85% of the 8.82 hr orbital period. This system also presents a potential measurement of “Shapiro” delay due to General Relativity; through this technique alone, we set an upper limit to the companion mass of 2.2 .
1 Introduction
The neutron star mass (and radius) distribution has important implications for our understanding of the equation of state (EOS) of ultra-dense matter. The EOS sets directly a number of potentially observable quantities, including the maximum mass and spin frequency of a neutron star (Lattimer & Prakash 2001). Moreover, measurements of neutron star radii would strongly constrain the nuclear symmetry energy (Steiner et al. 2010). At present there remain serious gaps in our understanding of the mass distribution of neutron stars, particularly as regards their upper mass limit. Where neutron star masses are known with precision it is in most cases for relatively young, binary radio pulsars in which one or more relativistic, Post Keplerian (PK) parameters can be directly measured (Thorsett & Chakrabarty 1999). Two famous examples of such systems include the original Hulse - Taylor binary pulsar PSR 1913+16 (Taylor & Weisberg 1989), and the double pulsar PSR J07373039 (Kramer et al. 2006). These neutron stars have masses that appear to cluster near or below the “canonical” value of 1.4 , and hence do not strongly constrain the maximum mass nor the EOS.
Studies of older, accreting neutron star systems hold significant promise for directly probing the high end of the mass distribution because it is likely these objects have accreted significant mass during their evolutionary history. Pulsar timing studies of binary millisecond radio pulsars have recently led to strong indications for higher mass neutron stars. For example, Freire et al. (2009) present timing measurements of PSR J1903+0327 that indicate its neutron star has a mass of (also Champion et al. 2008). A related population of sources which could provide important mass constraints are accreting millisecond X-ray pulsars (AMXPs). Additionally, these systems also produce X-ray emission directly from the neutron star surface in the form of thermonuclear X-ray bursts, and in principle can also be used to constrain neutron star radii, something that cannot be done for the radio pulsar systems unless spin orbit coupling can be directly observed (Lattimer & Schutz 2005). Currently twelve of these systems are known, with the first, SAX J1808.43658 (catalog SAX J1808.4-3658), having been discovered in 1998 (Wijnands & van der Klis 1998). A subset of the AMXPs are ultracompact binaries, with orbital periods less than an hour and have very low mass (), degenerate dwarf companions. An example of a system of this type is XTE J1751305 (catalog XTE J1751-305) (Markwardt et al. 2002). The remainder appear to more closely resemble the “classical” accreting, neutron star low mass X-ray binaries (LMXBs), with orbital periods of hours and low mass main sequence companions (such as SAX J1808.43658).
Several factors currently limit the use of these systems to obtain precise neutron star mass estimates. First, the population is largely associated with the Galactic bulge. Therefore the resulting high optical extinction makes detection of companions challenging. Second, their binary inclinations have, to date, not been strongly constrained, as would be possible, for example, with the detection and timing of X-ray eclipses. Indeed, observations of eclipsing AMXPs would enable the binary inclination to be tightly constrained and, combined with precision X-ray pulse timing and spectroscopic measurements of the companion, could lead to precise mass constraints for their neutron stars. Finally, it has not yet been possible to measure any PK parameters (such as the Shapiro delay) in these systems.
In this Letter we report the first detection of X-ray eclipses from an AMXP, in the system SWIFT J1749.42807 (catalog SWIFT J1749.4-2807) (hereafter J1749). J1749 was first discovered in 2006 based on the detection with Swift/BAT of a thermonuclear X-ray burst (Schady et al. 2006). Follow-up observations with Swift set an upper limit to the source distance of kpc (Wijnands et al. 2009). The source was detected again in 2010 by INTEGRAL, exhibiting both persistent and bursting activity (Pavan et al. 2010; Chenevez et al. 2010). Altamirano et al. (2010a), using RXTE observations during the recent outburst of this object, found that it harbors a 518 Hz accreting millisecond pulsar, with strong power also evident at the 1036 Hz first harmonic (Bozzo et al. 2010). Analysis of additional RXTE observations first by Belloni et al. (2010) and then by Strohmayer & Markwardt (2010) found an 8.82 hr circular orbit, and eclipses centered at the orbital phase of superior conjunction of the neutron star (Markwardt et al. 2010). Here we present a timing analysis of the pulsar and its eclipses, and derive constraints on the properties of the binary components. Our goal in this work is to establish the orbital solution from pulse timing to a sufficient degree of precision to place the eclipse observations in context. We leave a detailed characterization of the pulse profiles and timing noise to other work (Altamirano et al. 2010b; Ferrigno et al. 2010).
2 Observations
The RXTE PCA instrument (Jahoda et al. 2006) observed J1749 between 2010-04-14 and 2010-04-20 (UTC) for a combined total exposure of 45 ks (observation ID 95085-09 (catalog ADS/Sa.RXTE#P/95085-09)). PCA observations were performed with data mode “E_125us_64M_0_1s,” which reports individual photon times with a resolution of 122 s. We corrected event arrival times to the solar system barycenter using the Swift/XRT source position (Yang et al. 2010; Table 1).
Over the course of the RXTE observing campaign, the 2–10 keV flux of the source decayed from a peak of 9 mCrab, to an approximate quiescent level. J1749 is located 0.32∘ from the galactic plane and 1.17∘ from the galactic center. The PCA field of view is approximately 1.1∘ (radius to zero-response), so galactic diffuse emission and point sources in the field of view also contribute to the total count rate. We determined background count rate in the 2–30 keV band to be 17.5 ct/s/PCU for PCUs 2–4 and 21.4 ct/s/PCU for PCUs 0 and 1, based on data taken after 2010-04-20, when the source had reached near-quiescence (also confirmed by Swift/XRT imaging observations; Yang et al. 2010).
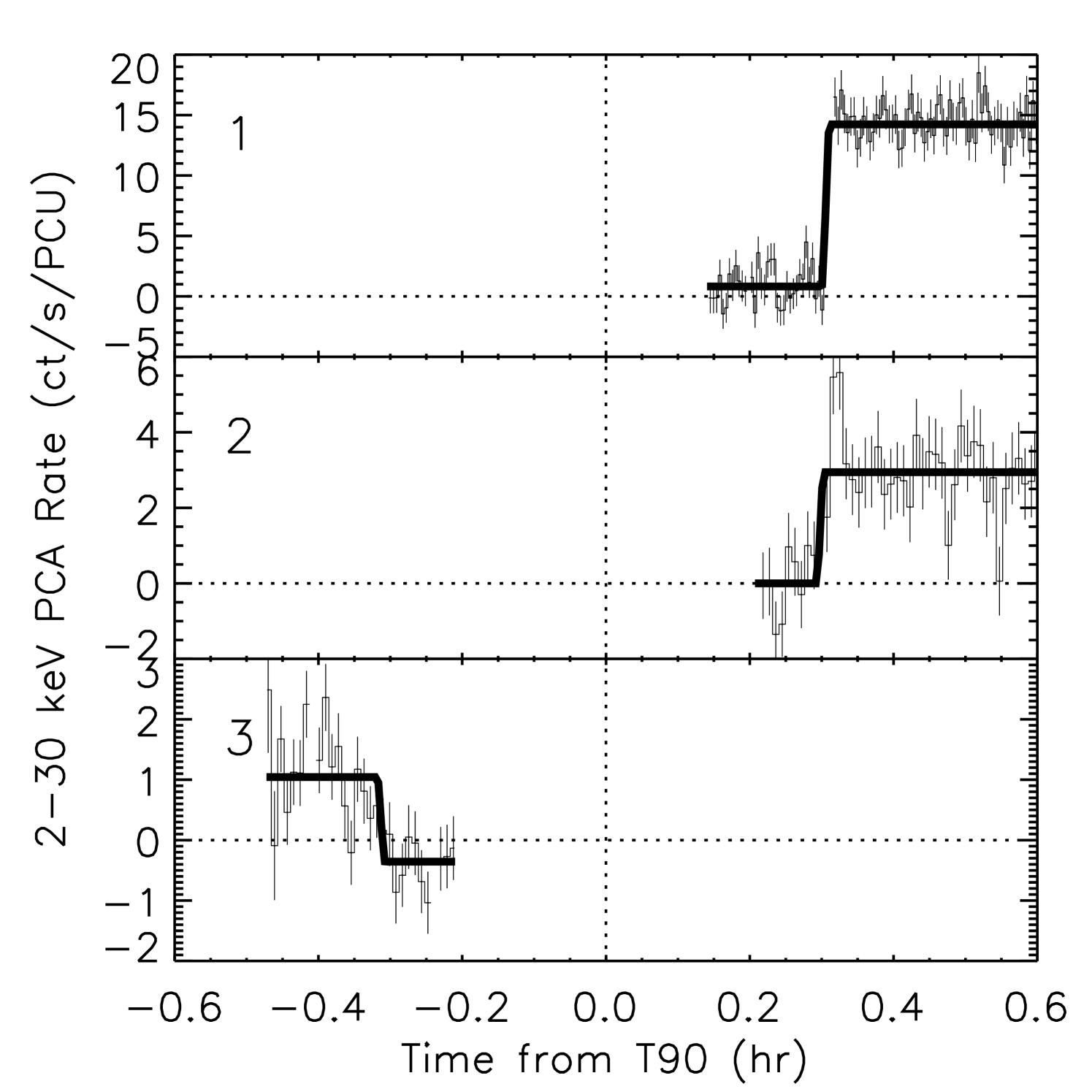
Upon visual inspection, there are sharp “dip-like” features in the X-ray light curve (Fig. 1. Here, we based our analysis on data taken by the PCA in “Standard2” mode, which has 16 second time bins and 129 bins of energy resolution. It was verified that the dips were not due to satellite or PCA instrumental effects such as earth occultations or instrument turn-ons or -offs. Furthermore, the dips coincided with the time when eclipses would be expected from the timing solution (see below). Therefore we concluded that it was likely we were seeing X-ray eclipse features produced by the companion star. We did not detect any other orbit-related modulations.
3 Data Reduction
As reported previously (Altamirano et al. 2010a; Bozzo et al. 2010),
the pulsed signal is detectable at both the fundamental frequency of
518 Hz and the first harmonic at 1036 Hz. The pulsed signal of the
fundamental was intermittent, whereas we have found the first harmonic
to always provide a reasonably strong signal. Therefore, we proceeded
with a pulse timing analysis using the first harmonic. We used the
statistic (or Rayleigh’s statistic; Buccheri et al. 1983; also
described in Markwardt et al. 2002). Signal from each detected count
in the 2–30 keV band (PCA channels 5–80) is added coherently using a
trial pulse and orbital model. The pulse model includes a constant
pulse frequency, , and a frequency derivative term, , if
desired. The orbital model is derived from the ELL1 model
(Wex, unpublished; Lange et al. 2001) of the radio pulsar timing
software “TEMPO 2” (Hobbs et al. 2006). This model is advantageous
for low-eccentricity binary systems where it may be difficult to
disentangle the classical eccentricity and longitude-of-periastron
orbital parameters. The parameters are adjusted until the maximum
signal is obtained. By examining smaller segments of data, it is
possible to construct a timing pseudo-residual using the phases of the
cosine and sine terms in the , which describes effective time of
arrival of the first harmonic pulse compared with the model.
The apparent eclipse features in the 2–30 keV X-ray light curve were fitted by a simple eclipse profile model. The model consists of a constant flux level in-eclipse and out-of-eclipse, and a linear transition between the two flux levels at a specified time. For the purposes of this analysis, we performed an individual analysis of the eclipse features in order to derive their times of arrival independently. Eclipse occurences are expected to be centered at the epoch of pulsar longitude 90∘, , as measured from the ascending node. We also fitted a model to all the data jointly where the ingress/egress time, as measured from , was a single parameter. Such an analysis gives a single weighted estimate of the eclipse duration, assuming that it is centered on . Background subtraction was performed as described above.
4 Results
Using the pulse timing techniques described above, we found a single coherent pulse timing solution. Timing residuals before 2010-04-19 are less than 130 s, equivalent to of the harmonics’s period; after that date, the statistical errors become larger. The best pulse timing solution is shown in Table 1. The harmonic pulse semi-amplitude ranges from about 8% to as high as 30% of the persistent flux during the outburst. The standard deviation of all residuals is 90 s, with evidence of red timing noise in the residuals, so parameter uncertainties have been scaled upward by in order to present a more conservative picture of the uncertainties. We attempted to add a pulse frequency derivative and eccentricity terms to the model. In the case of eccentricity, we report a marginal value, corresponding to 2.8. Given the presence of red noise, it appears likely that this value is not significant. For the frequency derivative term, we set only an upper limit. Both of these terms were set to zero in subsequent analysis. The results presented in the table are slightly different than those reported by Strohmayer & Markwardt (2010), because of the inclusion of more data in this work.
The eclipse features are shown in Figure 1, including the best-fit models. The features plotted in Figure 1 represent all light curve points which pass within 20 min of . The first eclipse egress, labeled “1,” is most strongly constraining, and the other two ingress/egress features are weaker and less constraining. We also verified that the pulsations were effectively eclipsed during those phases. The results of the individual light curve fits are shown in Table 2. Those results are consistent with a single ingress/egress time, approximately 1100 s equidistant from , and thus we are justified in fitting the light curves jointly with a single eclipse-duration parameter. The results of that joint fit are shown in Table 1, as the full eclipse duration from ingress to egress mid-points. We note that the eclipse duration reported here is somewhat different than that reported in Markwardt et al. (2010); that report differed due to a numerical error which was corrected in this work.
The ingress/egress duration is constrained primarily by eclipse number “1.” The reported egress duration of 2814 s is consistent with zero at the significance level. Thus, we consider this solution to be only a 95% confidence upper limit of 55 s.
During eclipse “1,” we find a residual count rate of ct/s/PCU, or of the persistent flux level. The fitted count rates during eclipses “2” and “3” are only 95% confidence upper limits of 20% and 30%, respectively, which are consistent with eclipse “1.”
5 Interpretation
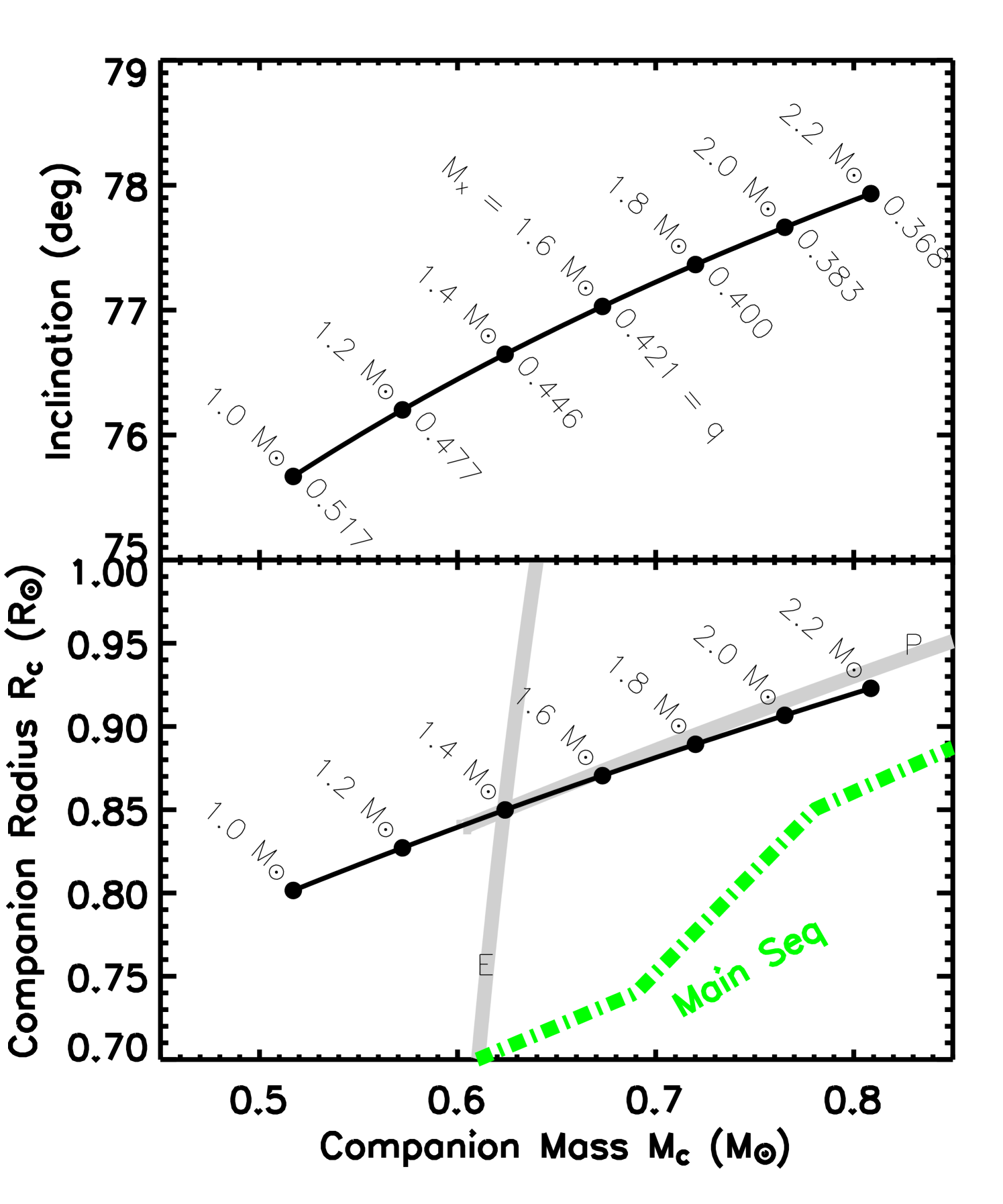
J1749 is the first AMXP to manifest X-ray eclipses. The measured eclipse ingress and egress epochs are symmetric about , as expected based on simple orbital geometry. The presence of eclipses allows us to constrain the orbital parameters much more closely than possible by pulse timing alone. Our combined pulse timing and eclipse solution is shown in Figure 2.
Here we assume that the companion star fills its Roche lobe (which leads to a constraint on the approximate density of the companion star; Eggleton 1983). This assumption is reasonable because the system is similar to other low-mass X-ray binary systems driven by disk accretion. The minimum companion mass is also constrained by the measured mass function, . The mass function for binary systems is defined as,
| (1) |
where is the gravitational constant and other variables are defined in Table 1. For the special case of an edge-on system, , this defines a minimum companion mass for a given neutron star mass . The resulting curve is shown in Figure 2 (“P” line), for an example neutron star mass of 1.4 .
An eclipse duration measurement essentially determines the solid angle subtended by the companion as seen by the neutron star (“E” line in Figure 2). The actual constraint is given by (e.g. Chakrabarty et al. 1993),
| (2) |
where is the angular diameter of the star as seen by the neutron star, , and is the total binary separation. For the same example neutron star mass, this curve is shown in Figure 2 (“E” line).
The constraint lines intersect at a single point for a given neutron star mass. Assuming that the neutron star mass lies somewhere in the range 1.4–2.2 , the joint solution produces a continuous curve shown in Figure 2 (thin black line). These joint constraints on the companion mass, radius and inclination are also shown in Table 1.
For this system’s estimated companion mass and nearly edge-on inclination, the effect of a Shapiro-like delay is appreciable (Shapiro et al. 1971). According to General Relativity, photons from the pulsar will experience an additional delay due to the gravitational potential of the companion star, with magnitude given by,
| (3) |
where is the orbital longitude, and we used . Although the maximum effect is expected to occur at the center of eclipse when pulsations are not visible, of the effect is present near but outside of occultation. In principle, a 21 s delay is within the grasp of RXTE’s absolute timing uncertainty (Jahoda et al. 2006).
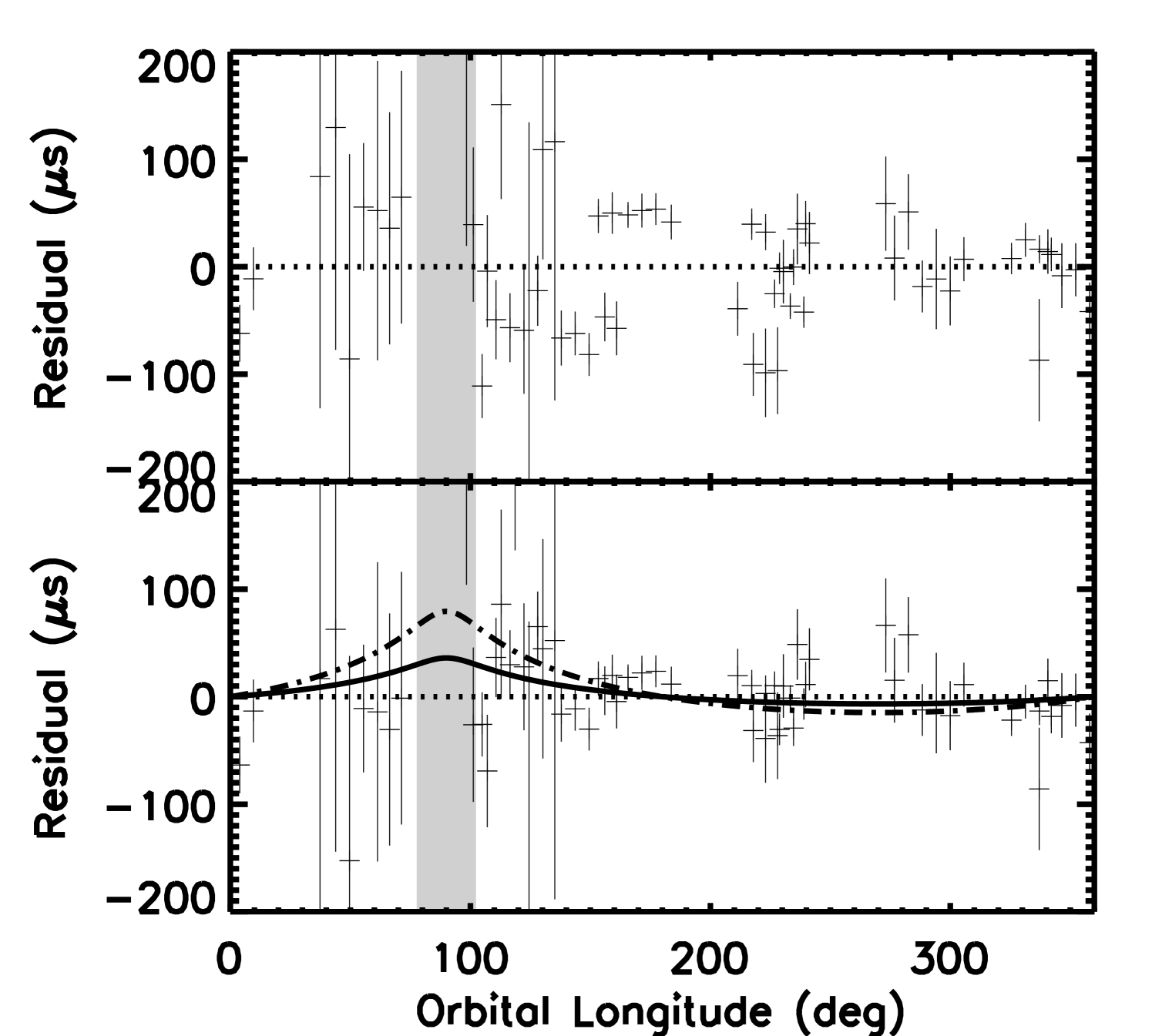
Figure 3 (top) shows the timing residuals folded at the orbital period. There are no strong trends in this representation, but significant red noise in the residuals causes the plot to have a choppy appearance. We attempted to remove this noise by fitting a spline function with control points on days April 15, 16, 17, 18, and 20. The control points were set near midnight on those days, and rounded to the nearest point of longitude = , where the Shapiro effect is expected to be minimum. We argue that by fitting a spline with daily variation, we will remove the long term trends while leaving any more compact signal near undisturbed.
The bottom panel of Figure 3 shows the same residuals after the spline trend has been removed. The improves from 225 to 70.2 (for 59 degrees of freedom), showing the benefit of this procedure. Adding a Shapiro term reduces the to 67.7, which is not significant (an -ratio test would demand a reduction of 10 to achieve 99% confidence). Thus, the data do not demand the presence of the Shapiro effect. However, assuming it is present we set an upper limit to the companion mass of (95% confidence).
6 Conclusions
The simultaneous presence of X-ray pulsations and X-ray eclipses have allowed us to constrain the companion of the system with unprecedented accuracy. The companion mass of 0.7 is rather large compared to most of the other AMXP companions. In contrast to the “ultra-compact” systems such as XTE J1751305, whose companion mass is a reasonable multiple of Jupiter’s mass (Markwardt et al. 2002), J1749 has a mass more comparable to the Sun.
The companion of J1749 appears to be larger than a typical main sequence star, as obtained from Zombeck (1982; see Figure 2), but also from more modern studies (Chabrier et al. 2007). For a neutron star of 1.4 , the companion is about 20% larger than expected from the main sequence track. We can interpret this as “bloating” of the companion due to X-ray irradiation by the neutron star which will cause the outer layers of the star to expand (Bildsten & Chakrabarty 2001).
The eclipse timing presented here places relatively tight constraints on the structure of the mass donor. Theoretical calculations indicate that the donor in a mass transfer binary can be perturbed away from a main sequence spectral type – mass relationship (see Beuermann et al. 1998; Kolb, King & Baraffe 2001). Beuermann et al. (1998) compare observational results for the donors in CVs with results of theoretical calculations, and show that systems with orbital periods longer than about 6 hours span a range of spectral type, whereas short period systems (less than 2 hr) behave more like solar-abundance, main-sequence stars. In related work, Kolb, King & Baraffe (2001) show that for a given measured spectral type a range of masses is possible based on the evolutionary status of the donor and its mass transfer history. The limits from their Table 1, when compared with our companion mass estimates, would suggest a spectral type for the secondary of J1749 from about K1 to K3. This range is also consistent with the results of Beuermann et al. (1998) for an hr binary period (see their Fig. 5).
There is only one orbital variable left in the system to be known. If the orbital inclination or companion mass or radius could be determined, then the neutron star mass could also be determined. In general, spectroscopic measurements of the companion to determine its radial velocity profile would provide the mass ratio and thus fully constrain the system components, including the neutron star mass. As noted in the introduction, systems like J1749 provide a unique opportunity to probe the high mass end of the neutron star mass distribution. Before this can be accomplished, an IR/optical counterpart must be identified. Unfortunately, high resolution imaging Chandra observations performed shortly after the current outburst failed to detect an X-ray source (Chakrabarty et al. 2010), so IR/optical observations will be difficult. Nevertheless, spectroscopy should be a focus of future observations when the source reappears.
We believe this is the first time that realistic limits have been set for the Shapiro delay effect at X-ray wavelengths, for a system outside of our solar system. While our companion mass upper limit was ultimately unconstraining compared to the eclipse mass constraint, the technique does show the power to measure relativistic effects with a mission like RXTE. If J1749 has another outburst (especially a longer duration outburst which allows better coverage near eclipse), it may be possible to place stronger constraints on the system masses.
References
- Altamirano et al. (2010a) Altamirano, D., et al. 2010, The Astronomer’s Telegram, 2565, 1 (2010a)
- Altamirano et al. (2010b) Altamirano, D., et al. 2010, ApJ, submitted (2010b; arXiv:1005.3527)
- Belloni et al. (2010) Belloni, T., Stella, L., Bozzo, E., Israel, G., & Campana, S. 2010, The Astronomer’s Telegram, 2568, 1
- Beuermann et al. (1998) Beuermann, K., Baraffe, I., Kolb, U., & Weichhold, M. 1998, A&A, 339, 518
- Bildsten & Chakrabarty (2001) Bildsten, L. & Chakrabarty, D. 2001, ApJ, 557, 292
- Bozzo et al. (2010) Bozzo, E., Belloni, T., Israel, G., & Stella, L. 2010, The Astronomer’s Telegram, 2567, 1
- Ferrigno et al. (2010) Ferrigno, C., et al. 2010, A&A, submitted (arXiv:1005.4554)
- Buccheri et al. (1983) Buccheri, R., et al. 1983, A&A, 128, 245
- Campana (2009) Campana, S. 2009, ApJ, 699, 1144
- Chabrier et al. (2007) Chabrier, G., Gallardo, J., & Baraffe, I. 2007, A&A, 472, L17
- Chakrabarty et al. (1993) Chakrabarty, D., et al. 1993, ApJ, 403, L33
- Chakrabarty et al. (2010) Chakrabarty, D., Jonker, P. G., & Markwardt, C. B. 2010, The Astronomer’s Telegram, 2585, 1
- Champion et al. (2008) Champion, D. J., et al. 2008, Science, 320, 1309
- Chenevez et al. (2010) Chenevez, J., et al. 2010, The Astronomer’s Telegram, 2561, 1
- Eggleton (1983) Eggleton, P. P. 1983, ApJ, 268, 368
- Freire (2009) Freire, P. C. C. 2009, proc. “Neutron Stars and Gamma Ray Bursts,” Cairo, Egypt, arXiv:0907.3219
- Hobbs et al. (2006) Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655
- Jahoda et al. (2006) Jahoda, K., Markwardt, C. B., Radeva, Y., Rots, A. H., Stark, M. J., Swank, J. H., Strohmayer, T. E., & Zhang, W. 2006, ApJS, 163, 401
- Kolb et al. (2001) Kolb, U., King, A. R., & Baraffe, I. 2001, MNRAS, 321, 544
- Kramer et al. (2006) Kramer, M., et al. 2006, Science, 314, 97
- Lange et al. (2001) Lange, C., Camilo, F., Wex, N., Kramer, M., Backer, D. C., Lyne, A. G., & Doroshenko, O. 2001, MNRAS, 326, 274
- Lattimer & Prakash (2001) Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426
- Lattimer & Schutz (2005) Lattimer, J. M., & Schutz, B. F. 2005, ApJ, 629, 979
- Markwardt et al. (2002) Markwardt, C. B., Swank, J. H., Strohmayer, T. E., in ’t Zand, J. J. M., & Marshall, F. E. 2002, ApJ, 575, L21
- Markwardt et al. (2010) Markwardt, C. B., Strohmayer, T. E., Swank, J. H., Pereira, D., & Smith, E. 2010, The Astronomer’s Telegram, 2576, 1
- Pavan et al. (2010) Pavan, L., et al. 2010, The Astronomer’s Telegram, 2548, 1
- Schady et al. (2006) Schady, P., Beardmore, A. P., Marshall, F. E., Palmer, D. M., Rol, E., & Sato, G. 2006, GRB Coordinates Network, 5200, 1
- Shapiro et al. (1971) Shapiro, I. I., Ash, M. E., Ingalls, R. P., Smith, W. B., Campbell, D. B., Dyce, R. B., Jurgens, R. F., & Pettengill, G. H. 1971, Physical Review Letters, 26, 1132
- Steiner et al. (2010) Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, arXiv:1005.0811
- Strohmayer & Markwardt (2010) Strohmayer, T. E., & Markwardt, C. B. 2010, The Astronomer’s Telegram, 2569, 1
- Taylor & Weisberg (1989) Taylor, J. H., & Weisberg, J. M. 1989, ApJ, 345, 434
- Thorsett & Chakrabarty (1999) Thorsett, S. E., & Chakrabarty, D. 1999, ApJ, 512, 288
- Wijnands & van der Klis (1998) Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344
- Wijnands et al. (2009) Wijnands, R., Rol, E., Cackett, E., Starling, R. L. C., & Remillard, R. A. 2009, MNRAS, 393, 126
- Yang et al. (2010) Yang, Y. J., et al. 2010, The Astronomer’s Telegram, 2579, 1
- Zombeck (1982) Zombeck, M. V. 1982, Handbook of space astronomy and astrophysics, Cambridge, Cambridge University Press, 1982
| Parameter | Value |
|---|---|
| Pulsar Timing | |
| Solution Time Range (UTC) | 2007-04-14 to 2010-04-20 |
| Barycentric pulse frequency, (Hz) | 1035.840027850(65)aaUncertainties are in the last quoted digits, and have been scaled by .bbPulse frequency of the pulsar first harmonic. |
| Pulsar frequency derivative, (Hz s-1) | cc95% upper limit. |
| Projected semimajor axis, (lt-s) | 1.899494(12) |
| Binary orbital period, (s) | 31740.719(8) |
| Time of ascending node, | 2455301.1522542(5) ddJulian days, referred to TDB timescale. |
| Orbital eccentricity, | 4.2(1.5) |
| Pulsar mass function, () | 5.463(8) |
| Maximum Power, | 2362 |
| Timing residuals, (s) | 92 |
| Solution quality, for d.o.f. | 225 / 60 d.o.f. |
| Eclipse Timing | |
| Eclipse duration, (s) | 2172(13) |
| Egress duration, s | 30(12) |
| Solution quality, for d.o.f. | 372 / 372 d.o.f. |
| Joint SolutioneeAssuming neutron star mass, , between 1.4–2.2 . | |
| Companion mass, () | 0.62–0.81 |
| Companion radius, () | 0.85–0.92 |
| Inclination, (degrees) | 76.65–77.93 |
| Right Ascension (J2000)ffPulsar celestial position (Yang et al. 2010). | 17h49m3194 |
| Declination (J2000) | |
| No. | TimeaaJulian day epoch of eclipse ingress/egress, referred to TDB. | Type | OffsetbbOffset in seconds from time of nearest pulsar longitude = 90∘, . |
|---|---|---|---|
| 1 | 2455303.46026 | Egress | 1098 3 |
| 2 | 2455306.39913 | Egress | 1091 10 |
| 3 | 2455307.47573 | Ingres | 1113 12 |