Discovery of Griffiths phase in itinerant magnetic semiconductor Fe_1-xCo_xS₂

The paramagnetic (PM) to ferromagnetic (FM) transition in magnetic semiconductors is a prominent topic in condensed matter physics because of efforts to discover materials useful for spintronicsspintrev . Magnetic semiconducting materials are considered essential for use as spin injectors in this nascent technology, yet single phase materials with Curie temperatures, $T_{C}$, well above 300 K that are compatible with today’s technologies have not been identified. Problems encountered by efforts to increase $T_{C}$ of Mn doped III-V semiconductors suggest that a deeper understanding is neededmatsukura and recent theoretical investigations have provided some progresspriour ; schulthess . However, disorder and strong Coulomb interactions are both central issues in semiconductors with magnetic impurities and this makes modeling difficult. In Mn doped III-V semiconductors, Mn provides localized magnetic moments as well as a smaller number of hole carriers that couple the local moments via the RKKY interaction. Models based on a magnetic-polaron Hamiltonian with random arrangements of RKKY-coupled moments have predicted a zero-temperature, $T$, percolative transition at critical magnetic moment and charge carrier densitiespriour . This critical point is governed by the competition between a nonmagnetic ground state and the magnetically ordered one and because of the doping induced disorder these materials are expected to display Griffiths phase singularities. Other than reports in doped LaMnO₃ and LaCoO₄ suggestive of Griffiths phase physicssalamon , there are no convincing demonstrations of Griffiths phases in magnetic semiconductors. A second class of materials predicted to display the Griffiths phase is the heavy fermion metals tuned by chemical substitution to be near a $T=0$ quantum critical point (QCP)Stewart ; Griffiths ; CastroNeto ; ouyang . In this case, rare clusters of strongly coupled magnetic moments are predicted to tunnel between magnetization states over classically forbidden regions resulting in non-analytic thermodynamic quantities at $T=0$CastroNeto .

In this letter we report on a magnetic and semiconducting system which resembles (GaMn)As with the advantage that single crystals can easily be grown and characterized; Co doped iron pyrite or ’fools gold’. FeS₂ is an insulator with a $\sim 1$ eV band gap. It is isostructural to CoS₂, an itinerant ferromagnet with $T_{C}=120$ KJarrett . FeS₂ and CoS₂ form a continuous solid solution over the entire concentration range, $x$, in Fe_1-xCo_xS₂, where it is fully spin-polarized for $0.25<x<0.9$PyriteHalfMetal . Previous magnetic susceptibility, $\chi$, measurements found FM order at $T>2$ K for $x\geq 0.05$Jarrett . Here, we discover metallic behavior for $x\geq 0.001$ with magnetic order at $x>x_{c}=0.01\pm 0.005$ consistent with earlier work. In addition, we observe an evolution from a partially Kondo screened metal at $x<x_{c}$ to a ferromagnet characterized by a percolative transition for $x>x_{c}$. For $x\approx x_{c}$ we find a divergent Sommerfeld coefficient at low-$T$ indicating non-Fermi liquid behavior along with a magnetic field $H$ and $T$ dependent magnetization $M$ that suggests a critical transition to a Griffiths phase-like state. In metallic Fe_1-xCo_xS₂ we discover evidence for the unusual coexistence of magnetically ordered phases and partial Kondo screening of magnetic moments. In contrast the modelpriour for (GaMn)As predicts a Griffiths phase under the conditions of localized electronic carriers where magnetic-polarons are important. In light of the inferred competition between the RKKY coupling and Kondo screening, as well as the divergent thermodynamic properties at $x_{c}$ and $T\rightarrow 0$, this system may be more closely described by models of $f$-electron materials displaying quantum criticalityCastroNeto .

Single crystals were synthesized by standard I₂ vapor techniques from high purity starting materials. Crystals were etched in HCl to remove any remaining flux and characterized by single crystal X-ray diffraction and energy dispersive X-ray microanalysis. The Co concentration of our crystals is consistent with the saturated $M$ at 5 T and 1.8 K and is about 70% of the nominal concentration of our starting materials. $M$ and $\chi$ were measured in a SQUID magnetometer for $T>1.8$ K and a dilution refrigerator above 50 mK. The resistivity, $\rho$, and Hall effect were measured using four-probe lock-in techniques at 17 or 19Hz, with thin Pt wires attached using silver paste or silver epoxy. The specific heat was measured using a standard thermal relaxation method.

Our $M$ measurements identify magnetically ordered states with $T_{C}$s shown in Fig. 1a by way of a peak in the real part of the AC susceptibility, $\chi^{\prime}$ (Fig. 2a), that is apparent in all of our samples with $x>x_{C}=0.01\pm 0.005$. We have checked that $T_{c}$ signals a FM transition by comparing to a standard Arrott analysis of a dense set of $M(H,T)$ data for a few samples with $x\geq 0.05$Arrott . A comparison is made in Fig. 1a between $T_{C}$ and the Weiss temperature, $\theta_{W}$, determined from the $T$-dependence of $\chi^{\prime}$ at $T$’s well above $T_{C}$, Fig. 2a, b. It is apparent that for $x>x_{c}$ a FM phase emerges and that $T_{C}$ increases systematically with $x$. The scatter in these data is likely due to the variations in simultaneously grown crystals as is evident by the range of $\theta_{W}$ values for crystals of the same or similar $x$. In Fig. 1b the density of magnetic moments, $n$, determined from fits of the Curie-Weiss (CW) form (Fig. 2b) to $\chi(T)$ for $T>>T_{C}$ are displayed. We have assumed an effective moment of $J=1/2$ and found $n$ much larger than the high-$H$ low-$T$ saturated moment for $x>x_{c}$. This could indicate either a large Rhodes-Wohlfarth ratio as in itinerant ferromagnets (between 1.8 and 7 as compared to 3.5 in MnSi), or $J>1/2$ local momentsmoriya . To investigate this we have measured the Hall effect to determine the carrier concentration, $n_{Hall}$, of our samples. $n_{Hall}$ was determined at high-$H$ to eliminate anomalous contributions. Fig. 1b shows that $n_{Hall}$ ranges from 10 to 30% of $x$ indicating that only a fraction of dopants donate electrons to a conducting band. Thus, it is likely that the difference between the Curie and saturated moments results from localized electrons with $J>1/2$.

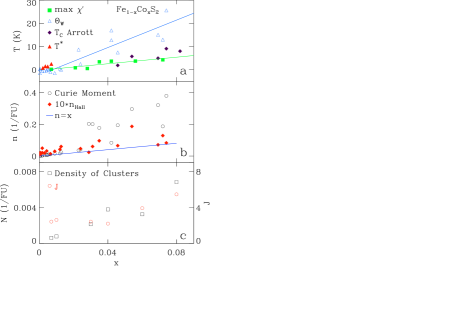
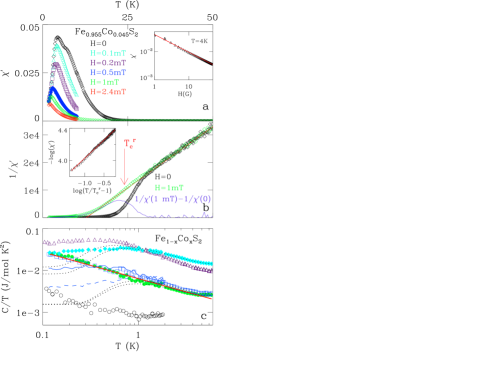
To explore more fully the properties of Fe_1-xCo_xS₂, we have measured the specific heat, $C$, finding nearly identical $C$ for all our crystals above 20 K since this region is dominated by phonons. However, at lower $T$’s we find a contribution that grows with $x$ shown in Fig. 2c. Samples that display a finite-$T$ peak in $\chi$ also display a broad maximum in $C(T)/T$, albeit at a lower $T$. The idea of spin clusters suggested by $M(H,T)$ and $\chi^{\prime}(T)$ was probed by comparing $C(T)$ and $\chi^{\prime}(T)$ to determine $J$, the fluctuating moment above $T_{C}$. At $T>2K$ we fit $C(T)$ by the sum of $\gamma T$, a phonon term $\beta T^{3}$ ($\beta=2.17\times 10^{-5}$ J/mol K⁴), and a Schottky term due to localized magnetic moments with $nJ(J+1)$ determined by fits of the CW form to $\chi^{\prime}(T)$ (Fig. 2c). The best fit $n$ and $J$ are shown in Fig. 1c where we observe that $J>1/2$, $n<x$, and that both grow with $x$. Thus, spin clusters are consistent with both $C(T)$ above 2 K and $\chi^{\prime}(T)$.

The magnetic transitions were explored in detail by measuring the low-$H$ $\chi^{\prime}(H,T)$ as in Fig. 2a, b. What is interesting is that both the $T$ and magnitude of the $\chi^{\prime}$ maxima are significantly suppressed by very small $H$. $\chi^{\prime}(H)$ at 4 K is displayed in the inset to Fig. 2a where a power law form $\chi^{\prime}(H)=bH^{-\beta}$ with $\beta=0.62\pm 0.03$ describes the data well. In addition to this extreme field sensitivity we have observed deviations from CW behavior. In Fig. 2b we plot $1/\chi^{\prime}$ at DC fields of 0 and 1 mT with dramatic changes evident below 30 K. The 1 mT data follow a CW form, $\chi^{\prime}\propto(T-\theta_{W})^{-1}$ with $\theta_{W}=13$ K for $T>\theta_{W}$. In contrast, the $H=0$ data cannot be described by a CW form to much higher $T$s and the deviation is in the direction of smaller $1/\chi^{\prime}$. The growth of $\chi^{\prime}$ beyond the CW form is an indication of short range FM correlations [See e.g.ouyang ] as spin clusters imply larger $\chi^{\prime}$. In the inset of Fig. 2b we display a fit of the form $1/\chi^{\prime}=(T-T_{C}^{r})^{\delta}$ to the data, $T_{C}^{r}=24$ $\pm 0.5$ K $\approx 2\Theta_{W}$ the critical $T$ for the largest clusters and $\delta=0.45\pm 0.04$, suggestive of Griffiths phase formation.

Samples that remain PM down to our lowest $T$ have a $C(T)/T$ that decreases with $T$ and that can be accurately described by a $aT^{-\alpha}$ form with $\alpha<1$. The red line in Fig. 2c represents this form with $\alpha=0.69\pm 0.03$. Application of $H>0$ suppresses the low-$T$ $C(T)/T$ of all of our samples and the PM samples display a $C(T)/T$ that resembles our FM samples. If we make the assumption that the conduction electron gas acts independently from a set of weakly interacting local moments, then $C(T)$ would be well fit by the sum of $\gamma T$, $\beta T^{3}$ and a Schottky-like anomaly down to zero-$T$. At finite field, the anomaly would evolve into a Schottky peak. Although this description works well above 1 K, our low-$T$ data does not conform to this simple picture. Interestingly, materials in proximity to metal-insulator transitions have a diverging $C(T)/T$ also described by a $T^{-\alpha}$ form. This is ascribed to the random position of local moments that are interacting antiferromagnetically leading to a singlet ground stateBhattandLee . However, since our samples are either FM or nearly FM, we do not consider this to be a likely explanation of our data. Instead, we suggest that the divergence of $C(T)/T$ for $x\sim x_{c}$ is indicative of Griffiths phase physics and/or to the proximity to a FM QCP. Magnetic fields or ordering return $C(T)/T$ to a Fermi liquid form at $T$’s proportional to $H$ or $T_{C}$.

The charge carrier transport properties of our crystals are presented in Fig. 3. While nominally pure FeS₂ displays insulating behavior, Co doping at a level of $x=0.001$ is sufficient to create a metal (Fig. 3a). Larger $x$ tends to increase $n_{Hall}$ and decrease the resistivity, $\rho$. One interesting feature is that the $T$-dependence of $\rho$ for $x\approx x_{c}$ closely follows a $T^{\xi}$ form with $\xi=1.6\pm 0.1$ over a wide $T$-range similar to that found in MnSi near the critical pressure for suppression of ferromagnetism. It is also consistent with the spin fluctuation model of nearly FM metals where a $T^{5/3}$ dependence is predicted for itinerant magnets. However, as noted above, the magnetic moments are likely to result from localized electrons so it is not clear that this model is appropriate. Evidence for the importance of magnetic fluctuationsmoriya ; millis1 ; nicklas in determining $\rho(T)$ can be seen in Fig. 3b where the $T$-derivative of $\rho$ normalized by $\rho_{0}=\rho(4K)$, $d\rho/dT/\rho_{0}$, is displayed. The normalization removes error in crystal geometry determination as well as changes due to variations in $n_{Hall}$. This quantity is strongly peaked near $x_{c}$. Thus, we observe a reduced power-law behavior of $\rho(T)$ along with an increased scattering rate over a wide $T$-range in proximity to the zero-$T$ critical point for magnetism.

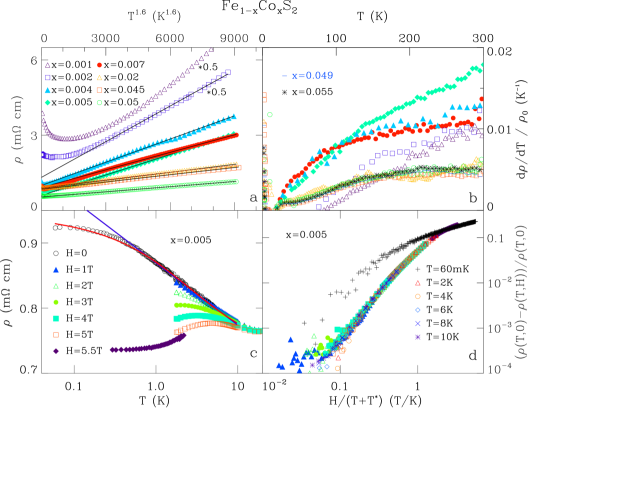
In addition, a second contribution to $\rho$ is apparent at $T<20$ K as demonstrated for a PM sample in Fig. 3c. Here $\rho$ increases with decreasing $T$ in a manner that is well described by a logarithm over more than a decade in $T$ with Kondo temperatures $T^{*}=$ 0.8, 1.5, 1.4, and 2.5 K for $x=$0.002, 0.004, 0.005, and 0.007, Fig. 1aHamann . We have also measured a large negative magnetoresistance (MR) (Fig. 3c, d) that is identical in the transverse and longitudinal current directions. This indicates a spin, rather than orbital, mechanism for the MR consistent with a Kondo effect dominating $\rho(T,H)$. Furthermore, all of our $T$- and $H$-dependent data can be scaled by a single ion Kondo form; $\rho(T,H)-\rho(T,0)/\rho(T,0)$ scales as $H/(T+T^{*})$ for $T\geq T^{*}$ as shown in Fig. 3dSchlottmann . We conclude that a single energy scale, likely a Kondo coupling of conduction electrons with the local moments associated with the Co ions, determines the low-$T$ $\rho$ of Fe_1-xCo_xS₂.

The observation of power-law divergent $C$ and $\chi^{\prime}$ for $x\sim x_{c}$ with similar exponents suggests that a single physical mechanism describes both. The sensitivity to magnetic fields indicates that there is weak coupling between clusters creating a fragile magnetic order for small $x$. In Fig. 4 we summarize the evolution of Fe_1-xCo_xS₂ from a strongly PM low-carrier-density metal to a FM with increasing $x$. In Fig. 4a, for $x<x_{c}$ and $T=0$, the system consists of a small density of magnetic moments localized on the Co impurity sites. The electron carriers screen only a portion of these moments via the Kondo coupling evident in the carrier transport. As $x$ increases to $x_{c}$ in Fig. 4b there is a percolative transition at $T=0$ and we observe a divergent $C(T)/T$ at low-$T$. Clearly for a magnetic transition to occur at $x\sim 0.01$ long range interactions between moments is necessary. Thus, a percolative transition occurs at $x_{c}<<0.2$ required for a face-centered-cubic lattice with short range interactionslorenz . At still larger $x$, Figs. 4c and d, the FM state is complete at low-$T$. For $T$s above the critical point the system is dominated by super-paramagnetic regions where magnetic moments are correlated, but long range ordering is not apparent. The system consists of weakly coupled clusters that are easily modified by small $H$. In addition, the clusters have a finite probability to tunnel to nearly degenerate $M$ states.

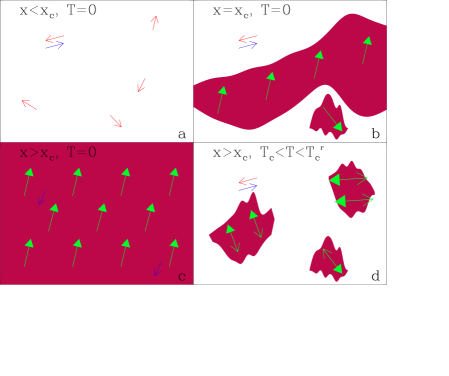
These features are described by Griffiths phase models Griffiths ; CastroNeto where disorder is sufficient to cause clusters of localized short lived magnetic order at $T$’s above the global ordering temperature. As the system is cooled toward $T_{C}$, these clusters grow and display switching of $M$ via tunneling. The consequence of this model is a power-law form, $1/(T-T_{C}^{r})^{1-\lambda}$, with $\lambda<1$, of the thermodynamic quantities above $T_{C}$ that can be suppressed with small to moderate magnetic fields. For Fe_1-xCo_xS₂ $0.30<\lambda<0.55$. Griffiths phase physics has been suggested to explain the non-Fermi liquid behavior of heavy fermion antiferromagnets with Néel temperatures driven to zero by chemical substitution. However, Millis et al.millis2 point out that the coupling of magnetic clusters to conduction electrons will suppress tunneling, removing the non-Fermi liquid response in the model. In contrast to well developed conductors, our materials are nascent metals with poor electrical screening formed by doping an insulator. Although Fe_1-xCo_xS₂ does not appear to be described by a magnetic-polaron Hamiltonian as in Ref. [3], our data suggest that Griffiths phase anomalies, likely influenced by Kondo screening, are in fact observable in magnetic semiconductors. The result is singular behavior at $T=0$ similar to models of Griffiths phases in $f$-electron antiferromagnets.

We thank I. Vekhter and C. Capan for discussions. JFD, DPY, and JYC acknowledge support of the NSF under DMR0406140, DMR0449022, and DMR0237664.