Discovery of the Type-II Superconductor Ta4Rh2C1-δ with a High Upper Critical Field
Abstract
We report on the discovery of superconductivity in the previously unknown compound Ta4Rh2C1-δ. Ta4Rh2C1-δ crystallizes in the -carbide structure type, in the cubic space group (No.227) with a unit cell parameter of 11.7947 Å. Temperature-dependent magnetic susceptibility, resistivity, and specific heat capacity measurements reveal that Ta4Rh2C1-δ is a type-II bulk superconductor with a critical temperature of = 6.4 K, and a normalized specific heat jump = 1.56. Notably, we find Ta4Rh2C1-δ has a high upper critical field of = 17.4 T, which is exceeding the BCS weak coupling Pauli limit of = 11.9 T.
I Introduction
The discovery of new superconductors with enhanced properties for diverse applications remains a significant challenge in condensed matter physics [1, 2, 3, 4]. A crucial property for these applications is the upper critical field , which is essential for technological applications [5]. When an external magnetic field is applied to a superconductor, Cooper pairs may break due to two effects: the orbital-limiting effect, which induces a momentum leading to a supercurrent that exceeds the superconducting gap, and the Pauli paramagnetic effect (Zeeman effect), where the Zeeman energy surpasses the superconducting condensation energy [6]. Near the critical temperature , the orbital-limiting effect dominates, while the Pauli paramagnetic effect is more significant at lower temperatures. In BCS theory, the maximum is limited by the Pauli paramagnetic effect, known as the Pauli paramagnetic limit , given as [6]. Several superconductors with the -carbide type crystal structure have recently been found to violate the Pauli paramagnetic limit, exhibiting very high upper critical fields [7, 8, 9].
-carbide type compounds crystallize in the cubic space group , and commonly form with compositions of and where A and B stand for transition metals, and X for carbon, nitrogen, or oxygen [10, 11, 12, 13]. -carbide type compounds consist of more than 100 known members with combinations of different technologically useful properties such as high hardness, high thermal stability, rich variety of magnetic states, exotic electronic properties, and catalytic properties [14, 15, 16]. One of the most striking characteristics of -carbide compounds is that they exist over wide ranges of chemical compositions and allow for a high degree of atomic substitutions [17]. In this structure type, tuning of the chemical composition allows for modifying and controlling of the physical properties in a wide range. Hence, the flexibility and tunability of the -carbide structure provide numerous opportunities to achieve new quantum materials with intriguing physical properties.
Among the systematically investigated -carbide type superconductors, Ti4Co2O, Ti4Ir2O, Nb4Rh2C1-δ, and Zr4Pd2O were found to have larger than the weak coupling Pauli limit, where [7, 8, 9, 18]. These isostructural superconductors share many electronic property features; therefore, it is likely they also share a common origin for the unusually high upper critical fields. Recently, in the high-field region of Ti4Ir2O signatures for a Fulde-Ferrell-Larkin-Ovchinnikov state have been observed, and SR measurements have revealed a small superfluid density in the superconducting state of Ti4Ir2O [19]. Both observations point towards unconventional superconductivity in this family of materials. Therefore, the -carbide family of compounds has become a fertile ground for the discovery of novel superconducting materials.
Here, we report on the discovery of superconductivity in the previously unreported -carbide compound Ta4Rh2C1-δ. We find Ta4Rh2C1-δ to crystallize in the -carbide structure type with a unit cell parameter of 11.7947 Å. Furthermore, we show that this compound is a type-II bulk superconductor with a critical temperature of = 6.4 K, and a specific heat jump of 1.56. Moreover, we find that Ta4Rh2C1-δ – like some other -carbide superconductors – has a very high upper critical field of of 17.4 T, which exceeds the weak coupling Pauli paramagnetic limit of 11.9 T.
II EXPERIMENTAL DETAILS
Synthesis: Polycrystalline Ta4Rh2C1-δ was synthesized from nearly stoichiometric amounts of the elements using tantalum powder (99.99 %, Alfa Aesar), rhodium powder (99.95 %, Strem Chemicals), and carbon rod (99.999 %, Sigma-Aldrich). A total mass of 150 mg of starting material was used. The reactants were thoroughly mixed in an agate mortar and pressed into a pellet. The pellet was first melted in an arc furnace in a purified argon atmosphere on a water-cooled copper plate. The sample was flipped over and molten five times to ensure an optimal homogeneity. After arc-melting, only a small mass loss of approximately 1 % was observed. The very hard solidified melt ingot was crushed into small particles in a tungsten carbide mortar and ground to fine powders in an agate mortar and pressed into a pellet. The pellet was wrapped with thin Ta foil, sealed in a quartz tube under a 1/3 partial argon, and annealed in a furnace for 4 days at 1200 ∘C. After reaction, the quartz tube was cooled down to room temperature by quenching in water.
Structure and Composition: The crystal structure and phase purity of the sample were checked using powder X-ray diffraction (PXRD) measurements on a Rigaku SmartLab diffractometer with Cu Kα radiation in Bragg-Brentano reflection geometry. The PXRD patterns were collected in the 2 range of 5 -120∘ with a scan rate of 0.25∘/min. Rietveld refinements were performed using the FULLPROF program package [20]. The chemical composition of the polycrystalline samples were examined under a scanning electron microscope (SEM) (JEOL JSM-IT800 operated at 15 keV) equipped with an energy-dispersive X-ray (EDX) spectrometer.
Physical Property Measurements: Temperature- and field-dependent magnetization measurements were performed on a Quantum Design magnetic properties measurement system (MPMS3) with a 7 T magnet equipped with a vibrating sample magnetometry (VSM) option. The measured pellet was placed parallel to the external magnetic field to minimize the demagnetization effects in the superconducting state. The electrical resistivity and specific heat capacity measurements were conducted in a Quantum Design physical property measurement system (PPMS) with a 9 T magnet. For the resistivity measurements, the four-probe technique was employed with gold wires connected to the sample with silver paint. Specific heat measurements were performed with the Quantum Design heat-capacity option, using a relaxation technique.
Electronic Structure Calculations: We performed density functional theory (DFT) calculations based on the full potential local orbital (FPLO) basis set [21] to understand the electronic structure of Ta4Rh2C1-δ . Due to heavy elements Ta and to some extent Rh, spin-orbit coupling is expected to be strong in Ta4Rh2C1-δ , and we use fully relativistic calculations with the generalized gradient approximation exchange correlation functional [22] to account for the spin-orbit coupling effects in the electronic structure. We converge the calculations on meshes.
III RESULTS and DISCUSSION
IV Synthesis
To the best of our knowledge, no compound in the ternary Ta-Rh-C phase space has been previously reported. Here, we report the -carbide compound Ta4Rh2C1-δ in this system. We have obtained polycrystalline Ta4Rh2C1-δ as a silver colored pellet. Achieving a phase-pure Ta4Rh2C1-δ sample proved to be challenging. Direct high-temperature reactions of mechanically mixed elements pressed into a pellet produced low-quality samples with multiple phases. This is likely due to the difficulty in homogeneously mixing the grains of the reactants. We found that arc-melting the reactants was crucial, even though the -carbide phase was not present in the ingot immediately after arc-melting, but seems to allow for optimal mixing of the elements (see supporting information S-Fig.1) [23]. In preparative chemistry, the synthesis of phase pure ternary -carbides is generally known to be challenging [11, 24]. In a series of synthesis experiments, the highest purity final samples were obtained with a starting ratio of Ta:Rh:C as 3.85:2.15:0.85. Deviation from this compositional ratio or from the annealing temperature (1200 ∘C) resulted in the formation of significant impurity phases.
IV.1 Crystal Structure
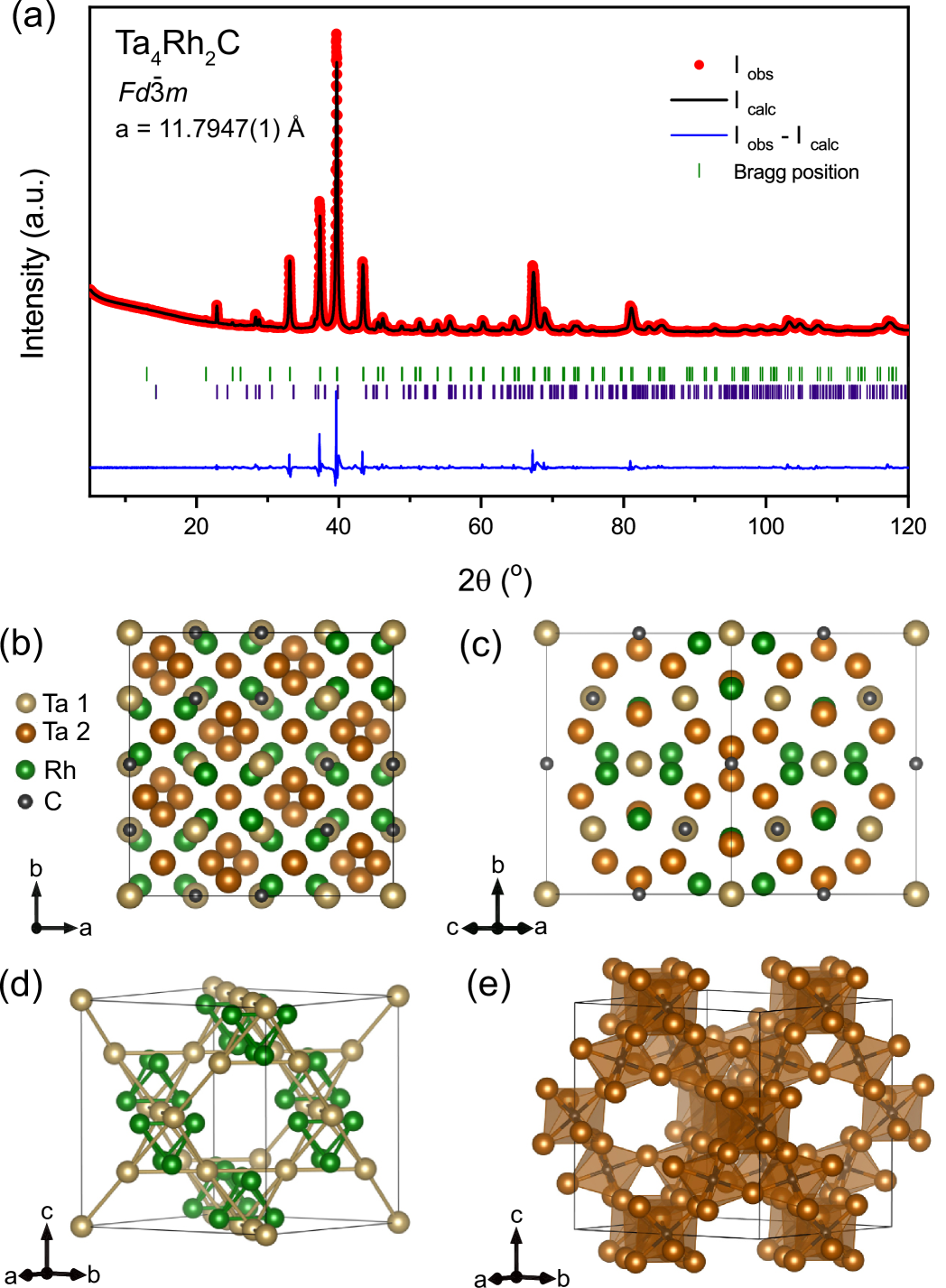
We find Ta4Rh2C1-δ to crystallize in the -carbide type structure, with the cubic space group (no.227) with the cell parameter of 11.7947(1) Å. This structure can be rationalized as related compounds, e.g. Nb4Rh2C1-δ ( 11.8527(2) Å) crystallize also in it. Here, the powder X-ray diffraction technique was employed to identify the phase purity and cell parameters of the obtained samples.
The powder X-ray diffraction (PXRD) pattern and the corresponding Rietveld refinement of the obtained Ta4Rh2C1-δ sample are presented in Figure 1(a). Energy-dispersive X-ray spectroscopy (EDS) analysis reveals a Ta:Rh ratio of 1.9(5):1 for the sample, which is close to the ideally stoichiometric value of 2:1. Reliable quantification of the carbon content by EDS is not possible and is challenging by X-ray diffraction as well [23]. Assuming only a negligible carbon loss during the arc-melting process, the carbon content in Ta4Rh2C1-δ should be close to 0.85, i.e. the nominal composition, for the amount of carbon used for the purest obtained sample. Rietveld refinement analysis determined that the main phase, Ta4Rh2C1-δ, constitutes 96.5 % of the sample, with a minor impurity phase of Ta2O5 at 3.5 %. Notably, the formation of TaC as an impurity phase was not observed for these synthesis conditions. Details on the Rietveld refinements of Ta4Rh2C are summarized in Table 1, assuming a model -carbide structure type, with the cubic space group and Ta4Rh2C stoichiometry.
| Atom | Site | |||||
| Ta1 | 0 | 0 | 0 | 1.13(1) | 1 | |
| Rh | 0.21185(7) | 0.21185(7) | 0.21185(7) | 0.77(3) | 1 | |
| Ta2 | 0.44067(7) | 0.125 | 0.125 | 1.13(1) | 1 | |
| C | 0.5 | 0.5 | 0.5 | 1.1* | 1 | |
| (no.227); = 11.7947(1) Å | ||||||
| (%) = 5.97: (%) = 9.56; (%) = 5.43 | ||||||
| Note : Here, * is fixed to the refined overall value | ||||||
In Figure 1(b)-(e), we show the crystal structure of Ta4Rh2C1-δ in an ideal chemical stoichiometric general formula of Ta4Rh2C. In this -carbide structure, Ta atoms occupy the and the Wyckoff positions, Rh atoms occupy the Wyckoff positions, and C atoms occupy the Wyckoff positions. Even though there are only 4 Wyckoff positions required to describe the crystal structure, the unit contains nevertheless results in a total of 112 atoms and a formula of Ta64Rh32C16 for one unit cell. In Figure 1(b)&(c) the unit cell with all atoms are shown in two orientations. In 1(d), the connectivity of the Ta1 and Rh atoms are shown: the Ta1 atoms form a network of tetrahedra resulting in a stella quadrangla structure, while the Rh atoms arrange in isolated tetrahedra. The Ta 2 atoms form a network of octahedra in which every second one is slightly distorted, as shown in figure 1(e), with the C atoms filling the octahedral voids.
IV.2 Physical Properties
To understand the physical properties of -carbide compound Ta4Rh2C1-δ, we performed temperature dependent magnetic susceptibility, resistivity, and specific heat capacity measurements.
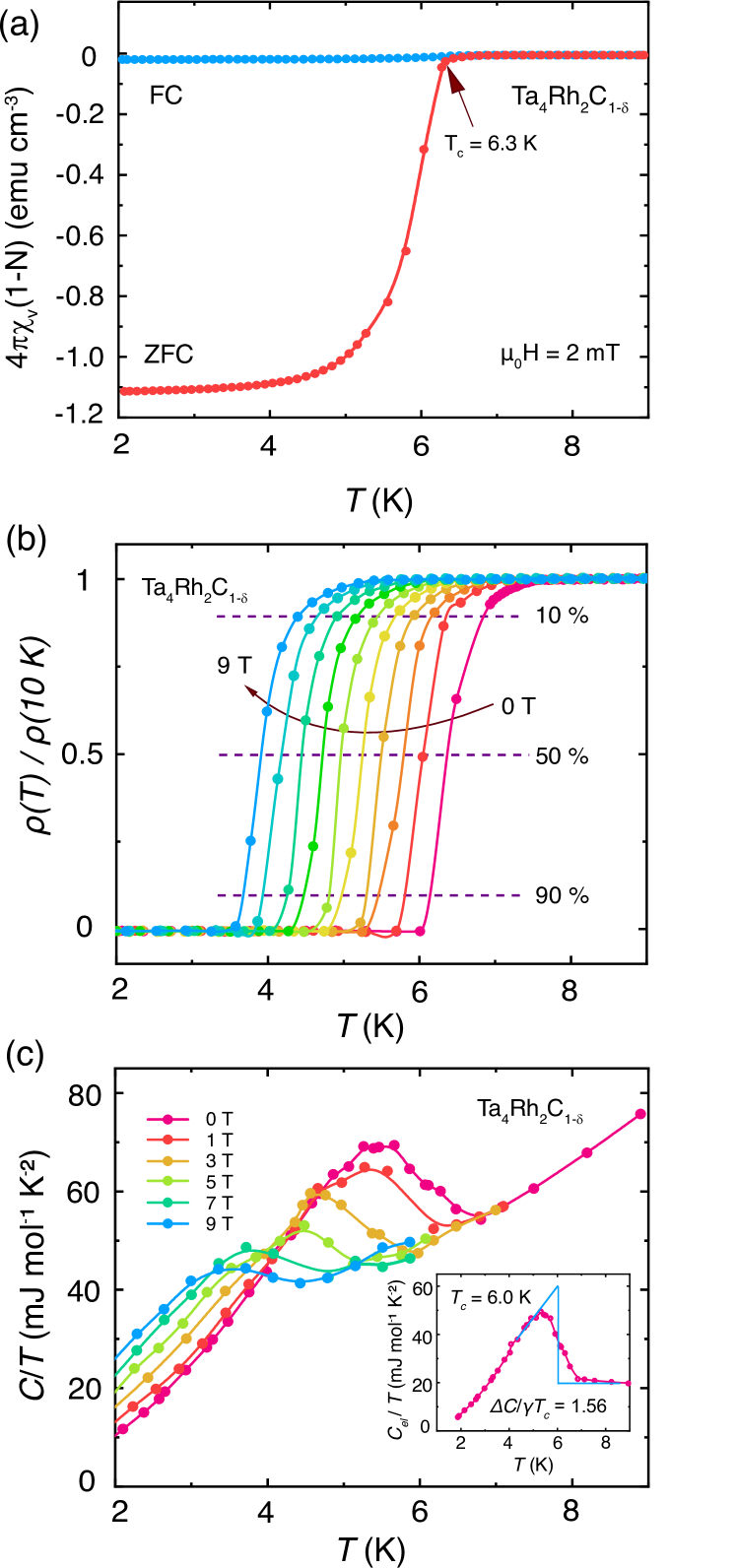
In Figure 2(a), we observe a superconducting transition at a critical temperature of = 6.3 K in the temperature dependence of the magnetic susceptibility in zero-field cooled (ZFC) and field-cooled (FC) modes under an external field of 2 mT, respectively. The difference between the FC and ZFC measurements in the superconducting state are prototypical for a type-II superconductor. When dealing with the magnetic susceptibility data, a demagnetization factor N was estimated using the relationship -b = 1/[4 (1-N)] [25]. Here, we obtain a value of N = 0.53 for our sample by fitting the field-dependent measurements of the magnetization to a line ( = b + a) in the low-field region [25].
In the normal state, Ta4Rh2C1-δ shows a Pauli paramagnetic behavior, as confirmed by magnetization measurement between 10 K to 300 K in an external field of 1 T (see supporting information S-Fig.3) [23]. To estimate the lower critical field , we performed a series of field-dependent measurements of the magnetization in low fields below the critical temperature , as shown in S-Fig 4.(a) of the supporting information [23]. Here, we used the magnetic-field point where the () curve first deviates from linearity as the measure for [26]. With this approximation, the obtained values are fitted using the semi-empirical formula:
| (1) |
The lower critical field at 0 K is determined to be = 9.4 mT as shown in the S-Fig 4 (b) (see supporting information) [23]. After taking the demagnetization factor N = 0.53 into account, the lower critical field is corrected to be = 20 mT.
We find the resistivity of Ta4Rh2C1-δ to decrease with decreasing temperature, showing a metallic behavior. The temperature dependent electrical resistivity measurement of the polycrystalline Ta4Rh2C1-δ sample from 300 to 1.8 K is shown in the supporting information (see S-Fig. 5) [23]. At a critical temperature of 7.2 K, Ta4Rh2C1-δ starts to undergo a transition to a superconducting state and the resistivity completely drops to zero at 6.0 K. Here, the residual resistivity ratio (RRR) value of the annealed polycrystalline sample is defined as (300 K)/(10 K) 1.22, corresponding to a poor metal behavior. This small RRR value may arise from the polycrystalline nature of the sample. In Figure 2(b), we show the temperature- and field-dependent resistivity (,) in a temperature range from = 2 to 9 K and magnetic fields between 0 T and 9 T. We show that the resistivity drops to zero at the transition to the superconducting state for all applied fields. In zero field, we determine the critical temperature to be = 6.4 K with a 50 % criterion. As expected, the critical temperature decreases steadily as the applied magnetic field increases. However, the critical temperature is only suppressed to 3.9 K in the maximal applied field of 9 T, which is already evidence of the remarkably high upper critical field of this superconductor.
In Figure 2(c), we present the temperature- and field-dependent specific heat (,) in the vicinity of the superconducting transitions, where the data are plotted as versus in magnetic fields between 0 T and 9 T. The specific heat jumps corresponding to the superconducting transitions are well-pronounced in all measured fields, and shift to lower temperatures, which are in good agreement with the results from the resistivity measurements. At zero field, the specific heat jump temperature corresponding to the superconducting transition is determined to be = 6.0 K based on an entropy-conserving construction, as shown in the inset of Figure 2(c).
In the normal state – close to the superconducting transition – the specific heat can be fitted according to the expression:
| (2) |
where is the Sommerfeld coefficient, corresponding to the electronic contribution to (), and is the phonon contribution to the specific heat. Here, we obtain the to be 20.9 mJ mol-1 K-2, and the to be 0.707 mJ mol-1 K-4 for Ta4Rh2C1-δ (see supporting information S-Fig.6) [23]. With above obtained and values, the normalized specific heat jump is found to be = 1.56 in zero field, which is slightly larger than the weak-coupling BCS value of 1.43 and evidence for the bulk nature of the superconducting state in Ta4Rh2C1-δ.
We determined the Debye temperature to be 268 K, using the following relationship:
| (3) |
Here n = 7 is the number of atoms per formula unit, and R = 8.314 J mol-1 K-1 is the ideal gas constant.
The electron-phonon coupling constant can be estimated from the Debye temperature, using the semi-empirical McMillan approximation [27]:
| (4) |
Here, the Coulomb repulsion parameter is set to be 0.13 according to an empirical approximation that was widely used in superconductors with similar elements (e.g. NbRh2B2 and TaRh2B2) [28, 25, 29, 30, 31]. Based on these values, the value for Ta4Rh2C1-δ is calculated to be 0.71, which is smaller than the 0.83 for Nb4Rh2C1-δ.
The measured value corresponds to a density of states at the Fermi-level of of 5.23 states eV-1 per formula unit (f.u.) in Ta4Rh2C1-δ, when using the following relationship:
| (5) |
IV.3 High upper critical field in Ta4Rh2C1-δ
In Figure 3(a), we present the field-dependence of the critical temperatures determined from the resistivity measurements using the common 10 %-, 50 %-, and 90 %-criteria , as well as the specific heat capacity as shown in Figures 2(b) and (c), (compare, e.g., references [7, 28, 32]). When using the Ginzburg-Landau (GL) formalism, the zero-temperature upper-critical field (0) for Ta4Rh2C1-δ is determined to be 23.5 T, 20.7 T, 20.1 T, and 21.3 T for the 10 %-, 50 %-, and 90 %-criteria of resistivity and the specific heat capacity, respectively (see supporting information S-Fig.7) [23]. Usually, a Ginzburg-Landau (GL) model fitting will give higher estimated upper-critical field values for the -carbide structure type superconductors [7, 8, 19].
Here, we make a conservative estimation of the upper-critical field for Ta4Rh2C1-δ using the Werthamer-Helfand-Hohenberg (WHH) formalism in the dirty limit according to [33, 7, 34]:
| (6) |
with being
| (7) |
where = ( is the transition temperature at zero field), while = 0.153 and = 0.152 are two parameters [34]. The zero-temperature upper-critical field (0) is determined to be 19.3 T, 17.4 T, 16.9 T, and 17.7 T for the 10 %-, 50 %-, and 90 %-criteria of resistivity and the specific heat capacity, respectively. All of these values exceed the corresponding weak-coupling BCS Pauli paramagnetic limits of 12.5 T, 11.9 T, 11.1 T, and 11.2 T, respectively.
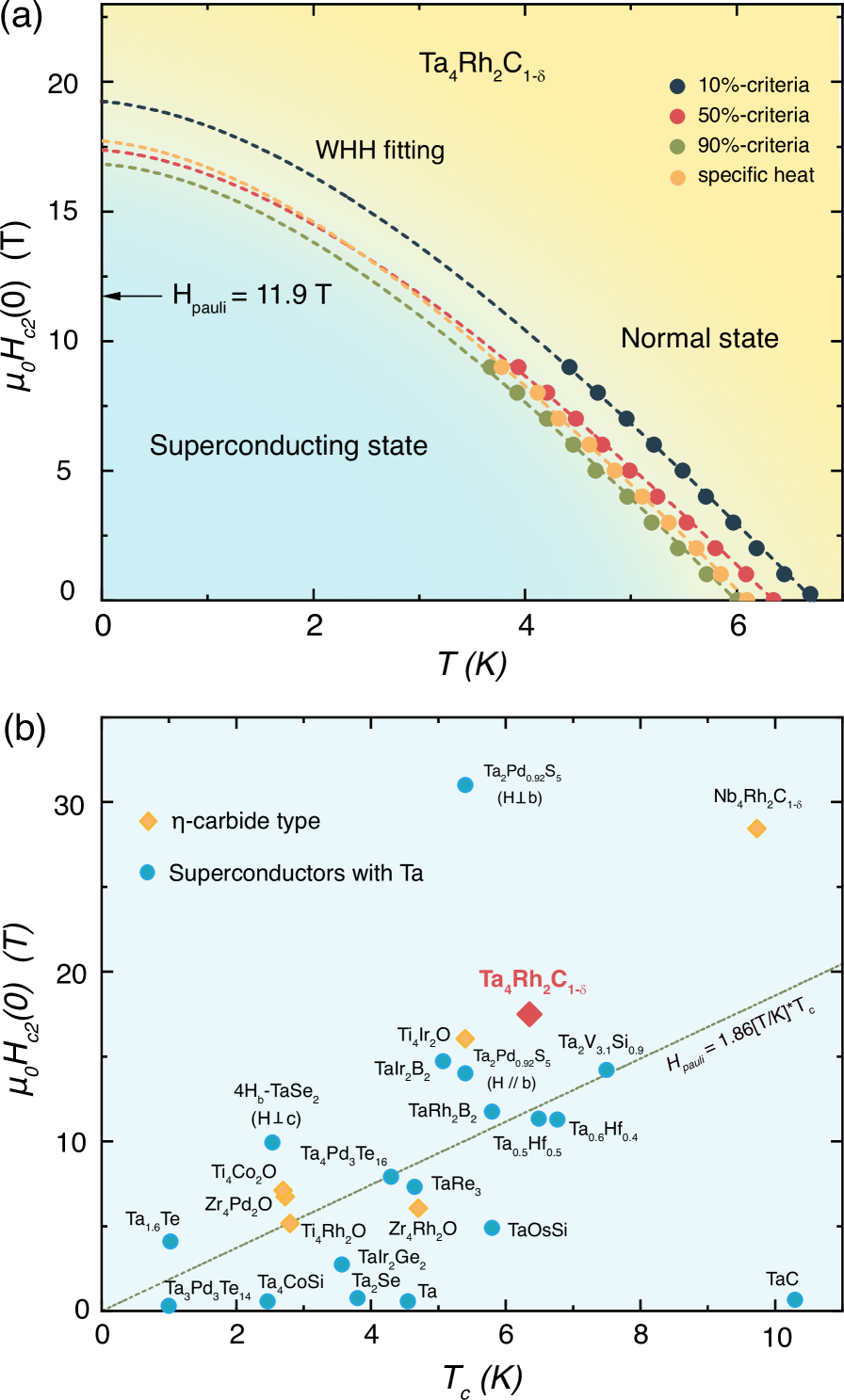
In Figure 3(b), we present a comparison of Ta4Rh2C1-δ with previously reported superconductors containing Ta in and evaluation [25, 35, 36, 37, 38, 31, 39, 40, 41, 42, 29, 43, 44, 45, 46]. The critical temperature of Ta4Rh2C1-δ is higher than most of the reported Ta-based superconductors and its value is higher than all the listed known superconductors except the highly anisotropic Ta2Pd0.92S6, when this material is measured with the applied field being vertical to the -axis [43]. Until now, reported Ta-based superconductors with value higher than the weak coupling Pauli limit are limited to: TaRh2B2, TaIr2B2, Ta2Pd0.92S6, 4-TaSe2, Ta2V3.1Si0.9, and the quasi-crystal superconductor Ta1.6Te [25, 29, 43, 44, 45, 46]. All these superconductors have highly anisotropic crystal structures. In contrary to this, the crystal structure of Ta4Rh2C1-δ is cubic and centrosymmetric, which strongly reflects the unusual nature of the Pauli limit violation in this material. It should be noted that Ta4Rh2C1-δ has the second highest critical temperature and upper critical field values among all reported -carbide structure type superconductors, to date [7, 8, 9, 47].
| Parameters | Units | Ta4Rh2C1-δ | Nb4Rh2C1-δ |
|---|---|---|---|
| K | 6.3 | 9.7 | |
| K | 6.4 | 9.8 | |
| K | 6.0 | 9.5 | |
| RRR | - | 1.22 | 1.16 |
| mT | 20 | 13.6 | |
| T | 17.4 | 28.5 | |
| mJ mol-1 K-4 | 0.7 | 0.6 | |
| mJ mol-1 K-2 | 21 | 40 | |
| - | 0.71 | 0.83 | |
| K | 268 | 283 | |
| Å | 44 | 34 | |
| Å | 1743 | 2252 | |
| - | 40 | 66.2 | |
| - | 1.56 | 1.64 | |
| () | states eV-1/f.u. | 5.23 | 9.32 |
| () | states eV-1/f.u. | 5.45 | 9.63 |
| / | T/K | 2.85 | 2.92 |
Note : value for Ta4Rh2C1-δ is corrected with demagnetization factor.
IV.4 Parameters in the superconducting state of Ta4Rh2C1-δ
The obtained upper critical field value, together with the lower critical field value can be used to calculate other relevant superconducting parameters for Ta4Rh2C1-δ. Here, the value from the 50%-criterion is 17.4 T, and it corresponds to a superconducting Ginzburg-Landau coherence length of 43.5 Å according to the following equation:
| (8) |
where Wb is the quantum flux. The superconducting penetration depth can be estimated from the values of and obtained above by using the relation:
| (9) |
We obtained a value of 1743 Å for Ta4Rh2C1-δ. The value of is calculated to be 40. These values demonstrate that Ta4Rh2C1-δ is a type-II superconductor with a short superconducting coherence length and a large superconducting penetration depth .
In Table 2, we list all the parameters that we have obtained for Ta4Rh2C1-δ and compare them with its isostructural superconductor Nb4Rh2C1-δ. We find the superconducting properties of Ta4Rh2C1-δ are similar to those of Nb4Rh2C1-δ, especially the high upper critical field exceeding the weak coupling Pauli limit. Therefore, Ta4Rh2C1-δ is both isostructural and isoelectronic to its sister compound Nb4Rh2C1-δ. Previously, the isostructural and isoelectronic Nb/Ta superconducting sister compounds pairs NbC - TaC [39], NbRh2B2 - TaRh2B2 [25], and NbIr2B2 - TaIr2B2 [29] have been explored and compared. Here, Ta4Rh2C1-δ and Nb4Rh2C1-δ represent a new pair of isostructural and isoelectronic Nb/Ta superconducting compounds.
IV.5 Electronic structure of Ta4Rh2C1-δ
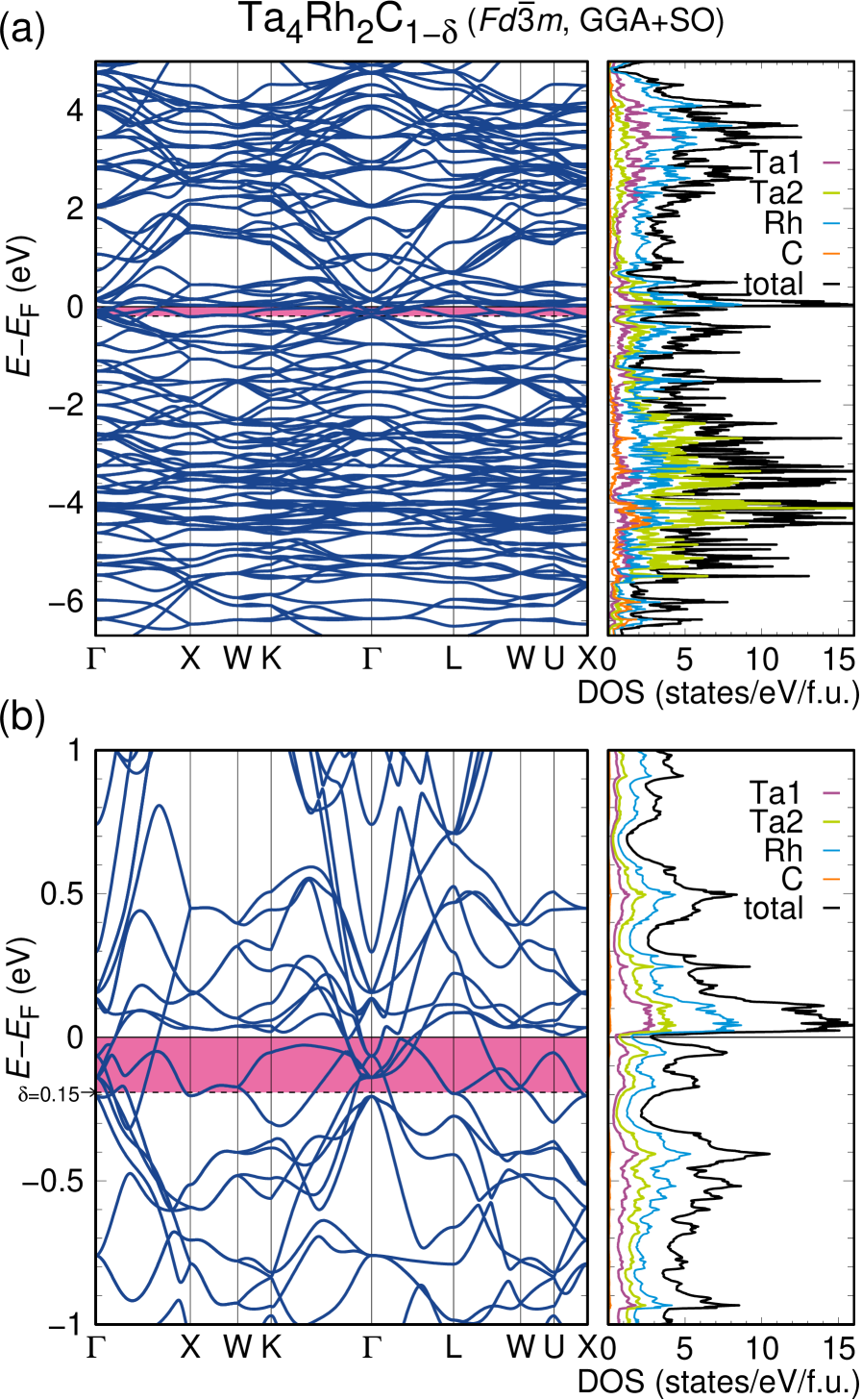
We performed density functional theory calculations for Ta4Rh2C1-δ based on the structure determined in this work and given in Table 1. Figure 4 shows the band structure and density of states (DOS) of Ta4Rh2C1-δ. We perform the calculation for , but we determine the amount of hole doping a carbon deficiency of would entail; it is marked by a pink region in Figure 4. As Ta is chemically similar to Nb, it is not surprising that the electronic structure of Ta4Rh2C1-δ does resemble the electronic structure of Nb4Rh2C1-δ (see Ref. [7]). From the calculated DOS shown in Figure 4 (b), the DOS at with gives a theoretical value of 5.45 states eV-1/f.u., which is comparable with the value of 5.23 states eV-1/f.u. calculated from heat capacity measurement (see Table 2). Similarly, in the previous study on Nb4Rh2C1-δ, the DOS at with provided a theoretical value of 9.63 states eV-1/f.u., which is close to the experimentally derived value of 9.32 states eV-1/f.u. from heat capacity measurement(see Ref. [7]).
We have also compared the effect of spin-orbit coupling on the band structures of Nb4Rh2C and Ta4Rh2C, respectively. We find significantly stronger splitting of bands in Ta4Rh2C, indicating stronger effects of spin-orbit coupling due to the replacement of the transition metal Ta for the transition metal Nb (see supplementary information S-Figure 8) [23]. In the supporting information (S-Figure (9) and (10)), we present the calculated Fermi surface of Nb4Rh2C1-δ with , and , respectively [23].
V Conclusion
In summary, we have successfully synthesized a new -carbide superconductor Ta4Rh2C1-δ by arc-melting followed by the high-temperature annealing method. Our X-ray diffraction measurements show that Ta4Rh2C1-δ crystallizes in the -carbide structure type, and is isostructural to the known superconductor Nb4Rh2C1-δ. Our systematic temperature dependent magnetic susceptibility, resistivity, and specific heat capacity measurements show Ta4Rh2C1-δ is a bulk superconductor with a critical temperature of of 6.4 K, and a specific heat jump value of 1.56, close to the weak-coupling BCS value of 1.43.
It is indeed an extreme type-II superconductor with a to be 40. The upper critical field of 17.4 T is exceeding the weak-coupling BCS Pauli paramagnetic limit of 11.9 T. All these intriguing properties make Ta4Rh2C1-δ an exotic superconductor similar to its sister compound Nb4Rh2C1-δ. In the future, the development of improved preparation techniques to obtain single phase or even single crystal samples of these -carbide type superconductors for the development of superconducting wires, but also for an improved understanding of the underlying superconducting mechanism, is highly desired.
Acknowledgements.
This work was supported by the Swiss National Science Foundation under Grant No. PCEFP2_194183. Research performed at Gdansk Tech. was supported by the National Science Center (Poland), Project No. 2022/45/B/ST5/03916References
- Larbalestier and Canfield [2011] D. Larbalestier and P. C. Canfield, Superconductivity at 100—where we’ve been and where we’re going, Mrs Bulletin 36, 590 (2011).
- von Rohr [2023] F. O. von Rohr, Chemical principles of intrinsic topological superconductors, Chemistry of Materials 35, 9455 (2023).
- Simon [1997] A. Simon, Superconductivity and chemistry, Angewandte Chemie International Edition in English 36, 1788 (1997).
- Santoro et al. [1988] A. Santoro, F. Beech, M. Marezio, and R. Cava, Crystal chemistry of superconductors: A guide to the tailoring of new compounds, Physica C: Superconductivity 156, 693 (1988).
- Hahn et al. [2019] S. Hahn, K. Kim, K. Kim, X. Hu, T. Painter, I. Dixon, S. Kim, K. R. Bhattarai, S. Noguchi, J. Jaroszynski, et al., 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet, Nature 570, 496 (2019).
- Tinkham [2004] M. Tinkham, Introduction to superconductivity (Courier Corporation, 2004).
- Ma et al. [2021a] K. Ma, K. Gornicka, R. Lefèvre, Y. Yang, H. M. Rønnow, H. O. Jeschke, T. Klimczuk, and F. O. von Rohr, Superconductivity with high upper critical field in the cubic centrosymmetric -carbide \ceNb4Rh2C_1-δ, ACS Materials Au 1, 55 (2021a).
- Ma et al. [2021b] K. Ma, R. Lefèvre, K. Gornicka, H. O. Jeschke, X. Zhang, Z. Guguchia, T. Klimczuk, and F. O. von Rohr, Group-9 transition-metal suboxides adopting the filled-\ceTi2Ni structure: A class of superconductors exhibiting exceptionally high upper critical fields, Chemistry of Materials 33, 8722 (2021b).
- Watanabe et al. [2023] Y. Watanabe, A. Miura, C. Moriyoshi, A. Yamashita, and Y. Mizuguchi, Observation of superconductivity and enhanced upper critical field of -carbide-type oxide \ceZr4Pd2O, Scientific Reports 13, 22458 (2023).
- Kuo [1953] K. Kuo, The formation of carbides, Acta metallurgica 1, 301 (1953).
- Ku and Johnston [1984] H. Ku and D. Johnston, New superconducting ternary transition metal compounds with the E93-type structure, Chinese Journal of Physics 22, 59 (1984).
- Gupta et al. [2009] S. Gupta, D. J. Sordelet, and J. D. Corbett, Structural and compositional investigations of \ceZr4Pt2O: A filled-cubic \ceTi2Ni-type phase, Journal of Solid State Chemistry 182, 1708 (2009).
- Mackay et al. [1994] R. Mackay, G. J. Miller, and H. F. Franzen, New oxides of the filled-\ceTi2Ni type structure, Journal of alloys and compounds 204, 109 (1994).
- Waki et al. [2010] T. Waki, Y. Umemoto, S. Terazawa, Y. Tabata, A. Kondo, K. Sato, K. Kindo, S. Alconchel, F. Sapina, Y. Takahashi, et al., Itinerant electron metamagnetism in -carbide-type compound \ceCo3Mo3C, Journal of the Physical Society of Japan 79, 093703 (2010).
- Prior and Battle [2004] T. J. Prior and P. D. Battle, Superparamagnetism and metal-site ordering in quaternary nitrides with the -carbide structure, Journal of Materials Chemistry 14, 3001 (2004).
- Cui et al. [2020] S. Cui, A. C. Mtukula, X. Bo, and L. Guo, High-efficiency \ceCo6W6C catalyst with three-dimensional ginger-like morphology for promoting the hydrogen and oxygen evolution reactions, International Journal of Hydrogen Energy 45, 6404 (2020).
- Taylor and Sachs [1952] A. Taylor and K. Sachs, A new complex eta-carbide, Nature 169, 411 (1952).
- Ruan et al. [2022] B.-B. Ruan, M.-H. Zhou, Q.-S. Yang, Y.-D. Gu, M.-W. Ma, G.-F. Chen, and Z.-A. Ren, Superconductivity with a violation of pauli limit and evidences for multigap in -carbide type \ceTi4Ir2O, Chinese Physics Letters 39, 027401 (2022).
- Das et al. [2024] D. Das, K. Ma, J. Jaroszynski, V. Sazgari, T. Klimczuk, F. O. von Rohr, and Z. Guguchia, \ceTi4Ir2O: A time reversal invariant fully gapped unconventional superconductor, Physical Review B 110, 174507 (2024).
- Rodriguez-Cavajal [2001] J. Rodriguez-Cavajal, Recent developments of the program fullprof, Comm. Powder Diffract. Newsl. 26, 12 (2001).
- Koepernik and Eschrig [1999] K. Koepernik and H. Eschrig, Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme, Phys. Rev. B 59, 1743 (1999).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- sup [2024] See supplemental material for discovery of the type-II superconductor \ceTa4Rh2C_1-δ with a high upper critical field at xxxxx, url-will-be-inserted-by-publisher (2024).
- Ku [1985] H. Ku, Effect of composition on the superconductivity of the E93 phase in the ternary nb-rh-c system, Physica B+ C 135, 417 (1985).
- Carnicom et al. [2018] E. M. Carnicom, W. Xie, T. Klimczuk, J. Lin, K. Górnicka, Z. Sobczak, N. P. Ong, and R. J. Cava, \ceTaRh2B2 and \ceNbRh2B2: Superconductors with a chiral noncentrosymmetric crystal structure, Science advances 4, eaar7969 (2018).
- Naito et al. [1990] M. Naito, A. Matsuda, K. Kitazawa, S. Kambe, I. Tanaka, and H. Kojima, Temperature dependence of anisotropic lower critical fields in \ce(La_1-xSr_x)2 CuO4, Physical Review B 41, 4823 (1990).
- McMillan [1968] W. McMillan, Transition temperature of strong-coupled superconductors, Physical Review 167, 331 (1968).
- von Rohr et al. [2016] F. von Rohr, M. J. Winiarski, J. Tao, T. Klimczuk, and R. J. Cava, Effect of electron count and chemical complexity in the \ceTa-Nb-Hf-Zr-Ti high-entropy alloy superconductor, Proceedings of the National Academy of Sciences 113, E7144 (2016).
- Górnicka et al. [2021] K. Górnicka, X. Gui, B. Wiendlocha, L. T. Nguyen, W. Xie, R. J. Cava, and T. Klimczuk, \ceNbIr2B2 and \ceTaIr2B2–new low symmetry noncentrosymmetric superconductors with strong spin–orbit coupling, Advanced Functional Materials 31, 2007960 (2021).
- Gui and Cava [2022] X. Gui and R. J. Cava, \ceLaIr3Ga2: A superconductor based on a kagome lattice of Ir, Chemistry of Materials 34, 2824 (2022).
- Zeng et al. [2022] L. Zeng, X. Hu, S. Guo, G. Lin, J. Song, K. Li, Y. He, Y. Huang, C. Zhang, P. Yu, et al., \ceTa4CoSi: A tantalum-rich superconductor with a honeycomb network structure, Physical Review B 106, 134501 (2022).
- Stolze et al. [2018] K. Stolze, J. Tao, F. O. von Rohr, T. Kong, and R. J. Cava, \ceSc-Zr-Nb-Rh-Pd and \ceSc-Zr-Nb-Ta-Rh-Pd high-entropy alloy superconductors on a \ceCsCl-type lattice, Chemistry of Materials 30, 906 (2018).
- Helfand and Werthamer [1966] E. Helfand and N. Werthamer, Temperature and purity dependence of the superconducting critical field, H. II, Physical Review 147, 288 (1966).
- Baumgartner et al. [2013] T. Baumgartner, M. Eisterer, H. Weber, R. Flükiger, C. Scheuerlein, and L. Bottura, Effects of neutron irradiation on pinning force scaling in state-of-the-art \ceNb3Sn wires, Superconductor Science and Technology 27, 015005 (2013).
- Srivichitranond et al. [2017] L. C. Srivichitranond, E. M. Seibel, W. Xie, Z. Sobczak, T. Klimczuk, and R. J. Cava, Superconductivity in a new intermetallic structure type based on endohedral \ceTa@\ceIr7Ge4 clusters, Physical Review B 95, 174521 (2017).
- Jiao et al. [2016] W.-H. Jiao, L.-P. He, Y. Liu, X.-F. Xu, Y.-K. Li, C.-H. Zhang, N. Zhou, Z.-A. Xu, S.-Y. Li, and G.-H. Cao, Superconductivity in \ceTa3Pd3Te14 with quasi-one-dimensional \cePdTe2 chains, Scientific Reports 6, 21628 (2016).
- Xu et al. [2019] C. Xu, B. Li, J. Feng, W. Jiao, Y. Li, S. Liu, Y. Zhou, R. Sankar, N. D. Zhigadlo, H. Wang, et al., Two-gap superconductivity and topological surface states in \ceTaOsSi, Physical Review B 100, 134503 (2019).
- Shi et al. [2020] Z. Shi, S. Kuhn, F. Flicker, T. Helm, J. Lee, W. Steinhardt, S. Dissanayake, D. Graf, J. Ruff, G. Fabbris, et al., Incommensurate two-dimensional checkerboard charge density wave in the low-dimensional superconductor \ceTa4Pd3Te16, Physical Review Research 2, 042042 (2020).
- Shang et al. [2020] T. Shang, J. Zhao, D. J. Gawryluk, M. Shi, M. Medarde, E. Pomjakushina, and T. Shiroka, Superconductivity and topological aspects of the rocksalt carbides \ceNbC and \ceTaC, Physical Review B 101, 214518 (2020).
- Klimczuk et al. [2023] T. Klimczuk, S. Królak, and R. J. Cava, Superconductivity of \ceTa-Hf and \ceTa-Zr alloys: Potential alloys for use in superconducting devices, Physical Review Materials 7, 064802 (2023).
- Barker et al. [2018] J. Barker, B. Breen, R. Hanson, A. Hillier, M. R. Lees, G. Balakrishnan, D. M. Paul, and R. Singh, Superconducting and normal-state properties of the noncentrosymmetric superconductor \ceRe3Ta, Physical Review B 98, 104506 (2018).
- Gui et al. [2020] X. Gui, K. Górnicka, Q. Chen, H. Zhou, T. Klimczuk, and W. Xie, Superconductivity in metal-rich chalcogenide \ceTa2Se, Inorganic Chemistry 59, 5798 (2020).
- Lu et al. [2014] Y. Lu, T. Takayama, A. F. Bangura, Y. Katsura, D. Hashizume, and H. Takagi, Superconductivity at 6 K and the violation of pauli limit in \ceTa2Pd_xS5, Journal of the Physical Society of Japan 83, 023702 (2014).
- Yan et al. [2023] L. Yan, C. Ding, M. Li, R. Tang, W. Chen, B. Liu, K. Bu, T. Huang, D. Dai, X. Jin, et al., Modulating charge-density wave order and superconductivity from two alternative stacked monolayers in a bulk 4\ceHb-\ceTaSe2 heterostructure via pressure, Nano Letters 23, 2121 (2023).
- Liu et al. [2023] H. Liu, J. Yao, J. Shi, Z. Yang, D. Yan, Y. Li, D. Chen, H. L. Feng, S. Li, Z. Wang, et al., Vanadium-based superconductivity in the breathing kagome compound \ceTa2V_3.1Si_0.9, Physical Review B 108, 104504 (2023).
- Terashima et al. [2024] T. Terashima, Y. Tokumoto, K. Hamano, T. Konoike, N. Kikugawa, and K. Edagawa, Anomalous upper critical field in the quasicrystal superconductor \ceTa_1.6Te, npj Quantum Materials 9, 56 (2024).
- Ma et al. [2019] K. Ma, J. Lago, and F. O. von Rohr, Superconductivity in the -carbide-type oxides \ceZr4Rh2O_x, Journal of Alloys and Compounds 796, 287 (2019).