Discovery of topological metamaterials by symmetry relaxation
and smooth topological indicators
Abstract
Robustness against small perturbations is a crucial feature of topological properties. This robustness is both a source of theoretical interest and a drive for technological applications, but presents a challenge when looking for new topological systems: Small perturbations cannot be used to identify the global direction of change in the topological indices. Here, we overcome this limitation by breaking the symmetries protecting the topology. The introduction of symmetry-breaking terms causes the topological indices to become non-quantized variables, which are amenable to efficient design algorithms based on gradient methods. We demonstrate this capability by designing discrete and continuous phononic systems realizing conventional and higher-order topological insulators.
The key idea in topological physics has remained largely unchanged since its beginnings in the explanation of the Quantum Hall Effect v. Klitzing et al. (1980) by means of the Chern number Thouless et al. (1982): We can associate integer-valued topological invariants to the bulk band properties of a material, and these topological invariants in turn predict the material’s boundary physics Zhu et al. (2011). A crucial property of topological invariants is that they are insensitive to smooth deformations, as long as these respect the protecting symmetries of the topological invariant. This equips topological materials with their characteristic robustness, but presents a challenge from a design point of view, as one cannot systematically discover new topological systems by smoothly-modifying a non-topological model in the direction of growth of the topological index. Proof of this challenge is that discovering new topological models is still as much of an art as a science, as exemplified by the diversity of approaches to the design problem. These include engineering the symmetries of the system Mousavi et al. (2015), exhaustive search of crystal structure databases Bradlyn et al. (2017), identifying geometries that mimic known topological tight-binding models over a range of frequencies Matlack et al. (2018); Serra-Garcia et al. (2018), using artificial-intelligence constructs such as neural networks Pilozzi et al. (2018); Peano et al. (2019), or optimizing for proxy quantities such as boundary modes He et al. (2016) or energy transfer Christiansen et al. (2019a, b) that, while not topological themselves, are frequently associated with nontrivial topology.
In this paper, we approach the realization of topological phases by breaking the protecting symmetries and therefore challenging the discreteness of topological invariants. The approach can be understood in the SSH Su et al. (1979) model (Fig. 1a), which consists of a 1-dimensional chain with dimerized hoppings of strength and . Such a system is described by the Bloch Hamiltonian
| (1) |
When the hoppings follow the inequality , the system will be in a topological phase, and finite samples will present boundary-localized states in the gap. When , the system will be in a trivial phase, and finite samples will not present in-gap states at the boundary. This topology can be characterized by a Berry phase invariant of the form
| (2) |
Where is the eigenfunction of Eq. (1) with energy below the gap.
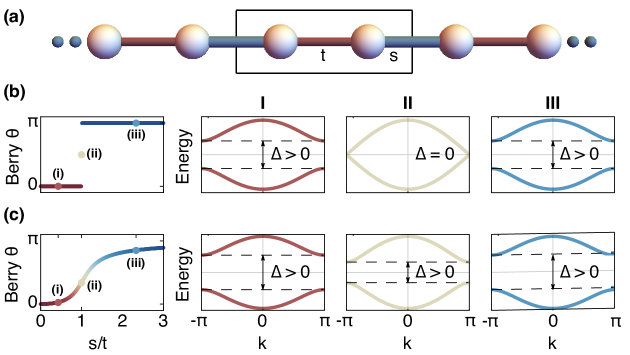
Smoothly deforming the system by altering the couplings or (Fig. 1b) does not affect the topological invariant in Eq. (1), unless the system goes through the configuration where . In this configuration, the lattice is not dimerized, the gap closes and the topological invariant is not defined. This picture is, however, only true when the symmetry that protects the topological invariant is preserved – which in this case corresponds to inversion symmetry. If we eliminate the inversion symmetry, by adding a local potential,
| (3) |
we observe two effects (Fig. 1c): First, the Berry phase changes smoothly when we vary the hoppings and , and second, the gap does not close in the configuration where , meaning that Eq. (1) can be evaluated for all hoppings. While this quantity can no longer be interpreted as a topological invariant, we will show that it can be used in the search process to discover novel topological systems. We refer to these quantities as smooth topological indicators.
We will now demonstrate this method by designing a continuous phononic system with non-trivial band gaps, and demonstrate the existence of boundary modes. Classical systems presenting topological wave phenomena Wang et al. (2009); Hafezi et al. (2013); Khanikaev et al. (2013); Süsstrunk and Huber (2015); Ningyuan et al. (2015); Albert et al. (2015) are an established platform for the demonstration of novel condensed matter physics. Examples include the demonstrations of fragile topological phases Peri et al. (2020), higher-order topological insulators Peterson et al. (2018); Serra-Garcia et al. (2018), and Weyl semi-metal effects such as axial fields Peri et al. (2019) and surface physics He et al. (2018), which were all first observed in classical models.
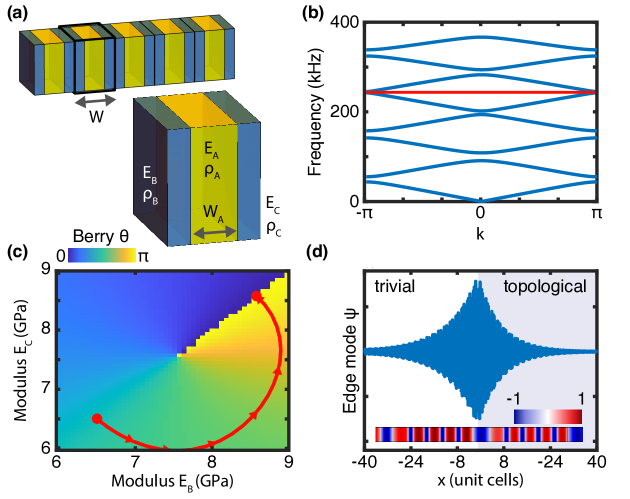
The continuous phononic metamaterial considered here is a one-dimensional slab of elastic material, satisfying the elastic wave equation,
| (4) |
where is the displacement along the longitudinal direction () of the slab, is the density and is the modulus of elasticity. The metamaterial is made by periodically repeating a unit cell consisting of a three-material sandwich Xiao et al. (2014); Tsai et al. (2019) with constant density and moduli , and , respectively (Fig. 2a). This system has multiple band gaps (Fig. 2b) We will consider a Berry-phase like topological invariant, generalized to multi-band systems Vanderbilt (2018), defined by:
| (5) |
where is obtained by parallel-transport of the Bloch wavefunctions from to .
Figure 2c shows the multi-band Berry phase associated to the fifth band gap, for different values of the parameters and . Along the line where the , inversion symmetry quantizes the Berry phase to the values of or . However, allowing symmetry violations results in a path through parameter space where the Berry phase transitions smoothly between trivial and topological values, without going through a gap closing. Using a gradient-ascent algorithm, it is therefore possible to identify topological configurations of the phononic system in a direct manner. We demonstrate this ability by identifying parameter values for and resulting in topological and trivial configurations (Fig. 2c) and observing the presence of localized interface modes at the selected band gap in a Finite Element Method simulation of the designed phononic material (Fig. 2d). Two aspects of this result deserve special mention: By having selected realistic initial conditions, we obtain a system geometry and material properties that can be easily realized experimentally. Second, the system ends up naturally in a symmetry-respecting configuration. Symmetry in the final configuration cannot be always guaranteed to appear automatically, but can be restored by penalizing symmetry-breaking terms towards the end of the optimization.
Topological insulators with time-reversal and inversion symmetries can also be characterized through the eigenvalues of the parity operator evaluated at the Time-Reversal Invariant Momenta (TRIM) points in reciprocal space Fu and Kane (2007). This type of invariant can also be smoothed out by symmetry relaxation, as we demonstrate in the double-SSH model. The double-SSH model consists of two parallel coupled SSH chains (Fig. 3a), and cannot be characterized with a conventional Berry phase, which is zero for both topological and trivial configurations. The system is described by the Hamiltonian
| (6) |
where is a local potential ensuring postive-definiteness of the classical model, , , and are the real-valued hopping parameters for the two chains, and are the real-valued chain coupling strengths and and are real-valued symmetry-breaking terms introduced to obtain a smooth topological indicator.
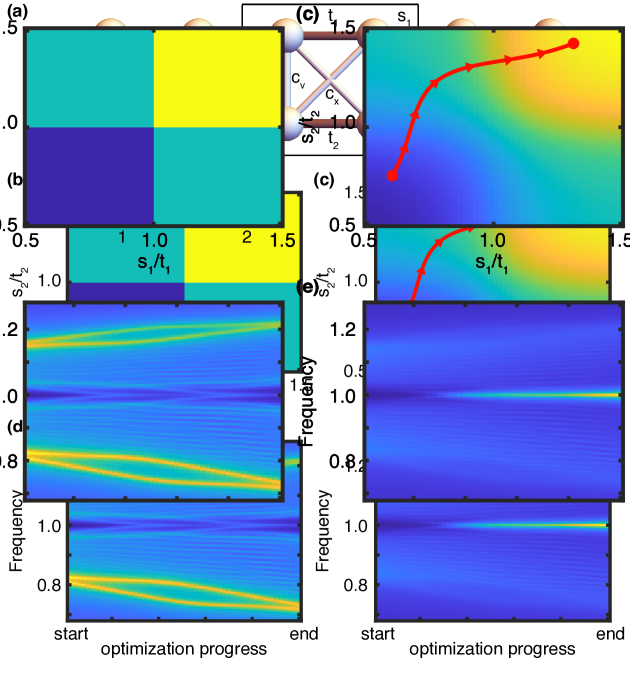
The topological invariant is defined as Alexandradinata et al. (2014) where is the number of Bloch eigenfunctions with parity eigenvalue, evaluated at the point . For inversion-symmetric systems at TRIMs, the parity eigenfunctions can only take values or , and the invariant reduces to the form
| (7) |
where is the identity operator, is a parity transformation and is a matrix whose columns are the Bloch eigenfunctions below the band gap of interest, evaluated at the momentum point . The function in Eq. (7) is gauge-invariant and becomes quantized when the inversion symmetry () is respected (Fig. 3b).
If we lift the inversion symmetry by setting and , the value of Eq. (7) becomes smooth (Fig. 3c). Under these conditions, cannot be interpreted as a topological quantity. However, since is smooth and equals the topological invariant when symmetry is respected, it can be used to guide a search algorithm towards a topological configuration. This process is illustrated in Fig. 3c and Fig. 3d for a 20-site, classical implementation of the tight-binding model in Fig. 3a, where each site is implemented as a mass with local damping . As the gradient-ascent algorithm increases the smooth topological indicator, the frequency response of the finite, symmetry-preserving system nucleates boundary modes. Two distinct transitions can be observed in Fig. 3d, corresponding to the points where and .
Design by symmetry relaxation can also be applied to Higher-Order Topological Insulators (HOTIs), systems where the non-trivial bulk topology gives rise to boundary modes that are more than one dimension below that of the bulk Schindler et al. (2018); Benalcazar et al. (2017). Two-dimensional HOTIs can be protected by mirror symmetries and . For such systems, we introduce a topological characterization Sup based on four mirror-graded invariants Alexandradinata et al. (2014); Alexandradinata and Bernevig (2016); Schindler et al. (2019) of the form and , with the topological phase characterized by . The quantities are multiband Berry phases calculated on a sub-set of the bands below the gap of interest, selected according to the band symmetry characteristics, with () being the multiband Berry phase calculated using the bands with positive (negative) eigenvalue according to the classifying symmetry. When calculating the invariants (), the classifying symmetry will be (). The multiband Berry phases that appear in the expression of () are quantized by a different mirror symmetry, (), as the one used for classification. Therefore, by lifting one of the symmetries while respecting the other, a pair of invariants becomes a well-defined smooth topological indicator.
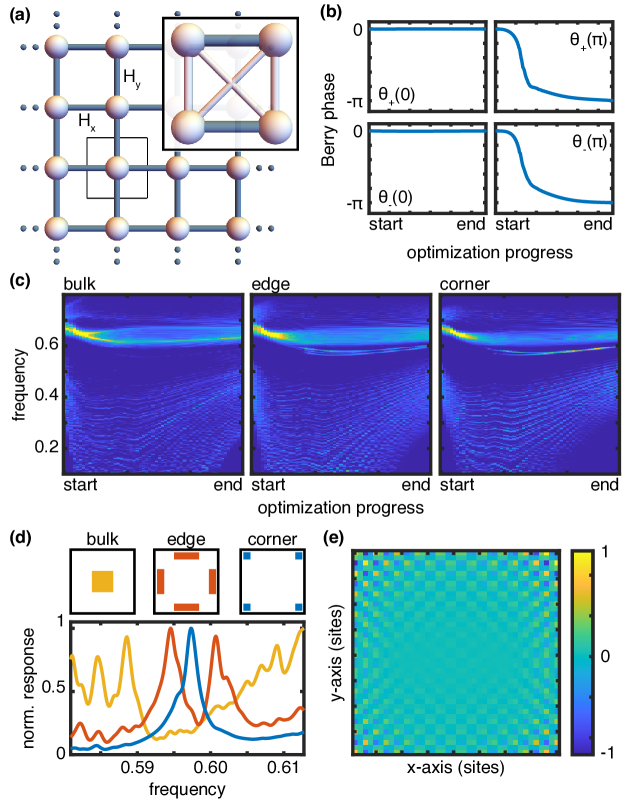
Smoothed mirror-graded invariants can be used to design HOTIs in a straightforward way. We will demonstrate this in a square lattice with four sites per unit cell (Fig. 4a). Interactions are restricted to nearest-neighbor unit cells, but not to nearest-neighbor sites. The system is described by a Hamiltonian of the form
| (8) |
with representing the potentials and interactions inside the unit cell, and , the hoppings between unit cells in the and direction, respectively. It should be noted that the model does not require any prior knowledge of higher-order topological models. It must only respect the appropriate symmetries and provide a large enough search space so that a topological solution can be identified.
The optimization process for the invariants starts from a highly symmetric configuration that respects , and . During optimization, the classifying symmetry is respected, while the quantizing symmetry is allowed to relax. The matrices of the system are optimized following a gradient-ascent algorithm, with two additional requirements: First, the direction of change is required to be orthogonal to the gradient of the band gap size –meaning that changes in the system parameters are not allowed to alter the gap size. This is done to prevent the system from undergoing a gap closing during optimization, which could result in an exchange of classifying symmetry eigenvalues. Second, as the optimization progresses, violations of the symmetry are increasingly penalized, to compensate for the fact that the system does not naturally converge to a symmetric configuration as it was the case in previous examples. As shown in the Supplemental Material Sup , the presence of the and symmetries causes the topological invariants along to be equal to those along , and therefore the system ends up in a fully topological configuration. In this example, the optimization process can get trapped in local-minima. Here, we escape them by re-starting the optimization from a different random configuration (see supplementary materials for source code implementing the exact algorithms and parameters Sup ), but for more complex metamaterials, advanced stochastic algorithms such as Hamiltonian Monte Carlo will be more performant Gebraad et al. (2020).
The optimization process is illustrated in Fig. 4b-c. The four multiband Berry phases converge to quantized values of or (Fig. 4b) while the gap remains open (Fig. 4c), although not fully constant, as one would expect from the imposed orthogonality condition. We attribute this to inaccuracies in the gap gradient estimation due to degeneracies and finite differentiation. As the optimization progresses, edge and corner modes nucleate in the gap (Fig. 4c). The system ends up presenting the hallmarks of higher-order topology Serra-Garcia et al. (2018), namely gapped edge states in the the bulk band gap, and corner states in the edge gap (Fig. 4d) The eigenfunction corresponding to one of such eigenstates is presented in Fig. 4e.
In conclusion, we have demonstrated that it is possible to derive smooth topological indicators by relaxing a topological system’s protecting symmetries, and that these indicators can be used to guide a search process towards topological configurations. The approach is very generic, as shown by the fact that it was successfully applied to discrete and continuous systems, indices based on geometric phases and symmetry eigenvalues, as well as on conventional and higher-order topological insulators. The approach should provide a novel route towards the realization of topological phases in diverse platforms such as photonic and phononic metamaterials or ultracold atoms. In fact, we expect the approach to be applicable to all symmetry-protected topological systems, including crystalline topological insulators Fu (2011) or those protected by chiral, time-reversal or parity symmetries Ryu et al. (2010).
I Acknowledgements
The authors would like to thank Valerio Peri, Eliška Greplova and Sebastian Huber for helpful discussions.
This work was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (Grant Agreements No. 694407 and 714069). T.D. acknowledges funding from the ETH Zurich Postdoctoral Fellowship program. F.S. was supported by the Swiss National Science Foundation (Grant No. 200021_169061).
References
- v. Klitzing et al. (1980) K. v. Klitzing, G. Dorda, and M. Pepper, New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance, Phys. Rev. Lett. 45, 494 (1980), URL.
- Thouless et al. (1982) D. J. Thouless, M. Kohmoto, M. Nightingale, and M. den Nijs, Quantized Hall Conductance in a Two-Dimensional Periodic Potential, Phys. Rev. Lett. 49, 405 (1982), URL.
- Zhu et al. (2011) Z.-H. Zhu, G. Levy, B. Ludbrook, C. N. Veenstra, J. A. Rosen, R. Comin, D. Wong, P. Dosanjh, A. Ubaldini, P. Syers, et al., Rashba Spin-Splitting Control at the Surface of the Topological Insulator , Phys. Rev. Lett. 107, 186405 (2011), URL.
- Mousavi et al. (2015) S. H. Mousavi, A. B. Khanikaev, and Z. Wang, Topologically protected elastic waves in phononic metamaterials, Nature Communications 6, 8682 EP (2015), article, URL.
- Bradlyn et al. (2017) B. Bradlyn, L. Elcoro, J. Cano, M. G. Vergniory, Z. Wang, C. Felser, M. I. Aroyo, and B. A. Bernevig, Topological quantum chemistry, Nature 547, 298 (2017), ISSN 1476-4687, URL.
- Matlack et al. (2018) K. H. Matlack, M. Serra-Garcia, A. Palermo, S. D. Huber, and C. Daraio, Designing perturbative metamaterials from discrete models, Nature Materials (2018), URL.
- Serra-Garcia et al. (2018) M. Serra-Garcia, V. Peri, R. Süsstrunk, O. R. Bilal, T. Larsen, L. G. Villanueva, and S. D. Huber, Observation of a phononic quadrupole topological insulator, Nature 555, 342 EP (2018), URL.
- Pilozzi et al. (2018) L. Pilozzi, F. A. Farrelly, G. Marcucci, and C. Conti, Machine learning inverse problem for topological photonics, Communications Physics 1, 57 (2018), ISSN 2399-3650, URL.
- Peano et al. (2019) V. Peano, F. Sapper, and F. Marquardt, Rapid Exploration of Topological Band Structures using Deep Learning (2019), eprint 1912.03296.
- He et al. (2016) C. He, X. Ni, H. Ge, X.-C. Sun, Y.-B. Chen, M.-H. Lu, X.-P. Liu, and Y.-F. Chen, Acoustic topological insulator and robust one-way sound transport, Nature Physics 12, 1124 (2016), ISSN 1745-2481, URL.
- Christiansen et al. (2019a) R. E. Christiansen, F. Wang, and O. Sigmund, Topological Insulators by Topology Optimization, Phys. Rev. Lett. 122, 234502 (2019a), URL.
- Christiansen et al. (2019b) R. E. Christiansen, F. Wang, S. Stobbe, and O. Sigmund, in Metamaterials, Metadevices, and Metasystems 2019, edited by N. Engheta, M. A. Noginov, and N. I. Zheludev, International Society for Optics and Photonics (SPIE, 2019b), vol. 11080, pp. 1 – 6, URL.
- Su et al. (1979) W. P. Su, J. R. Schrieffer, and A. J. Heeger, Solitons in Polyacetylene, Phys. Rev. Lett. 42, 1698 (1979), URL.
- Wang et al. (2009) Z. Wang, Y. Chong, J. D. Joannopoulos, and M. Soljačić, Observation of unidirectional backscattering-immune topological electromagnetic states, Nature 461, 772 (2009), ISSN 1476-4687, URL.
- Hafezi et al. (2013) M. Hafezi, S. Mittal, J. Fan, A. Migdall, and J. M. Taylor, Imaging topological edge states in silicon photonics, Nature Photonics 7, 1001 (2013), ISSN 1749-4893, URL.
- Khanikaev et al. (2013) A. B. Khanikaev, S. Hossein Mousavi, W.-K. Tse, M. Kargarian, A. H. MacDonald, and G. Shvets, Photonic topological insulators, Nature Materials 12, 233 (2013), ISSN 1476-4660, URL.
- Süsstrunk and Huber (2015) R. Süsstrunk and S. D. Huber, Observation of phononic helical edge states in a mechanical topological insulator, Science 349, 47 (2015), URL.
- Ningyuan et al. (2015) J. Ningyuan, C. Owens, A. Sommer, D. Schuster, and J. Simon, Time- and Site-Resolved Dynamics in a Topological Circuit, Phys. Rev. X 5, 021031 (2015), URL.
- Albert et al. (2015) V. V. Albert, L. I. Glazman, and L. Jiang, Topological Properties of Linear Circuit Lattices, Phys. Rev. Lett. 114, 173902 (2015), URL.
- Peri et al. (2020) V. Peri, Z.-D. Song, M. Serra-Garcia, P. Engeler, R. Queiroz, X. Huang, W. Deng, Z. Liu, B. A. Bernevig, and S. D. Huber, Experimental characterization of fragile topology in an acoustic metamaterial, Science 367, 797 (2020).
- Peterson et al. (2018) C. W. Peterson, W. A. Benalcazar, T. L. Hughes, and G. Bahl, A quantized microwave quadrupole insulator with topologically protected corner states, Nature 555, 346 EP (2018), URL.
- Peri et al. (2019) V. Peri, M. Serra-Garcia, R. Ilan, and S. D. Huber, Axial-field-induced chiral channels in an acoustic Weyl system, Nature Physics 15, 357 (2019).
- He et al. (2018) H. He, C. Qiu, L. Ye, X. Cai, X. Fan, M. Ke, F. Zhang, and Z. Liu, Topological negative refraction of surface acoustic waves in a Weyl phononic crystal, Nature 560, 61 (2018), ISSN 1476-4687, URL.
- (24) See supplemental material for a discussion of the higher-order topological invariant, source codes and finite element simulations.
- Xiao et al. (2014) M. Xiao, Z. Q. Zhang, and C. T. Chan, Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems, Phys. Rev. X 4, 021017 (2014), URL.
- Tsai et al. (2019) Y.-W. Tsai, Y.-T. Wang, P.-G. Luan, and T.-J. Yen, Topological Phase Transition in a One-Dimensional Elastic String System, Crystals 9 (2019), ISSN 2073-4352, URL.
- Vanderbilt (2018) D. Vanderbilt, Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators (Cambridge University Press, 2018).
- Fu and Kane (2007) L. Fu and C. L. Kane, Topological insulators with inversion symmetry, Phys. Rev. B 76, 045302 (2007), URL.
- Alexandradinata et al. (2014) A. Alexandradinata, X. Dai, and B. A. Bernevig, Wilson-loop characterization of inversion-symmetric topological insulators, Phys. Rev. B 89, 155114 (2014), URL.
- Schindler et al. (2018) F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Higher-order topological insulators, Science Advances 4 (2018), eprint https://advances.sciencemag.org/content/4/6/eaat0346.full.pdf, URL.
- Benalcazar et al. (2017) W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Quantized electric multipole insulators, Science 357, 61 (2017), ISSN 0036-8075, eprint https://science.sciencemag.org/content/357/6346/61.full.pdf, URL.
- Alexandradinata and Bernevig (2016) A. Alexandradinata and B. A. Bernevig, Berry-phase description of topological crystalline insulators, Phys. Rev. B 93, 205104 (2016), URL.
- Schindler et al. (2019) F. Schindler, M. Brzezińska, W. A. Benalcazar, M. Iraola, A. Bouhon, S. S. Tsirkin, M. G. Vergniory, and T. Neupert, Fractional corner charges in spin-orbit coupled crystals, Phys. Rev. Research 1, 033074 (2019), URL.
- Gebraad et al. (2020) L. Gebraad, C. Boehm, and A. Fichtner, Bayesian Elastic Full-Waveform Inversion Using Hamiltonian Monte Carlo, Journal of Geophysical Research: Solid Earth 125, e2019JB018428 (2020), e2019JB018428 10.1029/2019JB018428.
- Fu (2011) L. Fu, Topological Crystalline Insulators, Phys. Rev. Lett. 106, 106802 (2011), URL.
- Ryu et al. (2010) S. Ryu, A. P. Schnyder, A. Furusaki, and A. W. Ludwig, Topological insulators and superconductors: tenfold way and dimensional hierarchy, New Journal of Physics 12, 065010 (2010).