Dispersion by pulsars, magnetars, fast radio bursts and massive electromagnetism at very low radio frequencies

Mark J. Bentum^a,b¹¹1m.j.bentum@utwente.nl, Luca Bonetti^c,d²²2luca.bonetti@cnrs-orleans.fr, Alessandro D.A.M. Spallicci^c,d³³3Corresponding author, spallicci@cnrs-orleans.fr, http://lpc2e.cnrs-orleans.fr/

\sim

spallicci/ ^aUniversiteit van Twente
Faculteit van Elektrotechniek, Wiskunde en Informatica, Telecommunication Engineering
Postbus 217, 7500 AE Enschede, Nederland
^bASTRON
Postbus 2, 7900 AA Dwingeloo, Nederland
^cUniversité d’Orléans
Observatoire des Sciences de l’Univers en région Centre
1A rue de la Férollerie, 45071 Orléans, France
Collegium Sciences et Techniques, Pôle de Physique
Rue de Chartres, 45100 Orléans, France
^dCentre Nationale de la Recherche Scientifique
Laboratoire de Physique et Chimie de l’Environnement et de l’Espace
3A Av. de la Recherche Scientifique, 45071 Orléans, France

(17 October 2016)

Abstract

Our understanding of the universe relies mostly on electromagnetism. As photons are the messengers, fundamental physics is concerned in testing their properties. Photon mass upper limits have been earlier set through pulsar observations, but new investigations are offered by the excess of dispersion measure (DM) sometimes observed with pulsar and magnetar data at low frequencies, or with the fast radio bursts (FRBs), of yet unknown origin. Arguments for the excess of DM do not reach a consensus, but are not mutually exclusive. Thus, we remind that for massive electromagnetism, dispersion goes as the inverse of the frequency squared. Thereby, new avenues are offered also by the recently operating ground observatories in 10-80 MHz domain and by the proposed Orbiting Low Frequency Antennas for Radio astronomy (OLFAR ). The latter acts as a large aperture dish by employing a swarm of nano-satellites observing the sky for the first time in the 0.1 - 15 MHz spectrum. The swarm must be deployed sufficiently away from the ionosphere to avoid distortions especially during the solar maxima, terrestrial interference and offer stable conditions for calibration during observations.

Photons, Radioastronomy, Satellites, Pulsars, Magnetars, Fast Radio Bursts, Dispersion
MSC 2010: 70S05

pacs:

14.70.Bh, 95.30.-k, 95.55.Jz, 95.85.Bh, 97.60.Gb, 95.40.+s

I Motivations

For many years, many of us have worked, see e.g., Spallicci et al. (2005), for the opening of one of the gravitational wave windows on the universe, that has finally occurred Abbott and et al. (2016), while for other windows we still have to wait Spallicci (2013). Nevertheless, we can genuinely state that even when gravitational wave information will be exploited by ground or space laser interferometers, or by the pulsar timing array, our understanding of the large scale universe will be largely (exception made for neutrinos and cosmic rays) based on electromagnetic observations of the four interactions that rule the physical world. As photons are the messengers, fundamental physics has the concern of testing the foundations of electromagnetism, while astrophysics the task of interpreting the universe accordingly.

Furthermore, while alternative theories to general relativity, including those based on massive gravitons, are also conceived for solving the questions raised by the dark universe or to couple gravity with the other interactions, less effort is deployed for studying alternative electromagnetism. But electromagnetism at large scales may differ from the Maxwellian conception of the nineteenth century and thereby contribute to solve some of the riddles in contemporary physics and cosmology. Since neutrinos have been declared massive, while waiting for the elusive graviton, and leaving aside gluons that are not observed as free particles, the photon is the sole particle of the standard model to be massless.

Finally, massive photons would manifest themselves through delays of low frequency electromagnetic signals, being the sub-MHz part of the spectrum yet unexplored Lacki (2010). Thus, this work addresses the potential of the low frequency region to test the foundations of physics.

We shall use SI units throughout the paper.

II Massive electromagnetism

Non-Maxwellian theories can be grouped into two main classes: non-linear massless theories and linear massive photon theories. The former were initiated by Born and Infeld Born and Infeld (1934) who remove the divergence of the electron self-energy by introducing an upper bound of the electric field at the origin, and by Heisenberg and Euler Heisenberg and Euler (1936) who describe the non-linear dynamics of electromagnetic fields in vacuum and predict the rates of quantum electrodynamics light interaction processes. The analysis of the propagation of photons in vacuum within theories of non-linear electrodynamics is carried by supposing the photon to propagate in an effective metric. The latter represents the underlying dynamics that modifies the structure of the geometry in such a way that the geometry on which the photons move is no longer the background geometry. In the linear Maxwell theory, there is no influence of a background field on the propagation of light. In the non-linear theories, however, the phase velocity of light depends on the strength of the background field and on the propagation direction relative to the background field. Photon-photon scattering Breit and Wheeler (1934); Halpern (1934); Euler (1936); Heisenberg and Euler (1936); Achieser (1937); Karplus and Neuman (1950, 1951) has been tested Burke et al. (1997), while for other experiments aiming to verify other features of non-linear theories see Schellstede et al. (2015) and references therein.

The latter class assume or predict the photon being massive. Massive photons have been evoked in different realms: dark matter and dark energy, inflation, charge conservation, magnetic monopoles, Higgs boson, non-cosmological redshifts; in applied physics, superconductors and ”light shining through walls” experiments. The mass can be considered effective, when supposed depending on given parameters.

The concept of a massive photon was pursued by de Broglie de Broglie (1922, 1923, 1940), also thanks to the work of his doctorate student Proca, originally aimed at the description of electrons and positrons Proca (1936a, b, c, d, 1937, 1938).

How much the theory of relativity would be affected by the massive photon assumption, is not straightforward to assess: due partly to the variety of the theories, and partly to the removal of our ordinary landmarks and the rising of interwoven implications. For instance, the de Broglie-Proca, henceforth dBP, equations follow special relativity laws for reference frames moving at constant velocities (they obey Lorentz-Poincaré’s transformations and hence the Lagrangian can be written covariantly); instead, a change of potential implies a change in the field (the equations are not Lorenz gauge invariant).

Massive electromagnetic theories, possibly gauge invariant, have been later proposed by several authors, see Bopp (1940); Podolsky (1942); Podolsky and Kikuchi (1944); Podolsky and Schwed (1948); Stueckelberg (1957); Chern and Simons (1974) to mention the earliest contributors. Also the works Landé (1941); Landé and Thomas (1941, 1944) can also be interpreted as dealing with a massive photon Gratus et al. (2015).

We spell out the Lagrangian density in SI base units. In the 4-vector potential $A^{\alpha}=(\phi/c,\vec{A})$ , to the scalar component $\phi$ , measured in Volt, correspond [kg m² s^-3 A^-1], to the vectorial component $\vec{A}$ , measured in Volt/c, [kg m s^-2 A^-1]; to the electromagnetic field tensor $F_{\alpha\beta}=\partial_{\alpha}A_{\beta}-\partial_{\beta}A_{\alpha}$ , measured in Volt/metre, correspond [kg m s^-3 A^-1]; to the permeability $\mu$ , measured in Henry/metre, [kg m s^-2 A^-2] (in vacuum $\mu_{0}$ = 1.26 H m^-1); in the 4-vector current $j\!~^{\beta}=\left(\rho c,\vec{j}\right)$ , to the charge density $\rho$ , measured in Coulomb/metre³, correspond [m^-3 s A], to the current density, measured already in base units Ampère/metre² [m^-2 A]. The additional dBP term contains ${\cal M}=m_{\gamma}c/{\hbar}=1/\lambdabar$ [m^-1], where $m_{\gamma}$ is the photon mass [kg], $\hbar=1.05\times 10^{-34}$ Joule $\cdot$ second, that is [kg m² s^-1], and $\lambdabar$ the reduced Compton wavelength. Finally, the speed of light $c=2.99\times 10^{8}$ m s^-1 is meant as the limiting - Maxwellian - velocity of the theory., The dBP Lagrangian density $\cal L$ reads, e.g., Greiner and Reinhardt (1996); Tu et al. (2005); Accioly et al. (2010); Goldhaber and Nieto (2010); Spavieri et al. (2011), turned into energy density SI units

{\cal L}=-\frac{1}{4\mu}F_{\alpha\beta}F^{\alpha\beta}+{j^{\alpha}}A_{\alpha}-\frac{{\cal M}^{2}}{2\mu}A_{\alpha}A^{\alpha}~.

(1)

Of the four Maxwell’s equations, the dBP formalism modifies two by letting appear a mass dependent term: the divergence of the electric field (Coulomb-Gauss’ law), and the curl of the magnetic field (Ampère-Maxwell’s law).

The test of the former in a ground laboratory determined the mass upper limit of $2\times 10^{-50}$ kg Williams et al. (1971). For the latter, analysis in the solar wind and Parker modelling led first to $m_{\gamma}<10^{-52}$ kg at 1 AU Ryutov (1997), and later $m_{\gamma}<1.5\times 10^{-54}$ kg at $40$ AU Ryutov (2007), limit accepted by the Particle Data Group Olive and the Particle Data Group (2014). Nevertheless, such solar wind limits are far from being unquestionable Retinò et al. (2016).

A supposedly more stringent limit has been achieved through modelling of the hydromagnetic waves in the Crab Nebula Barnes and Scargle (1975), namely $3\times 10^{-56}$ kg; therein the authors state that their arguments are not rigorous and open to doubt. A re-analysis has led to a mass upper value of $3\times 10^{-63}$ kg Chibisov (1976). The difference of seven orders of magnitude for the same analysis is indicative of the scarce reliability of these approaches. Lower limits, as $10^{-62}$ kg, have been claimed also when modelling the galactic magnetic field Yamaguchi (1959); Adelberger et al. (2007).

The lowest theoretical limit on the measurement of any mass is prescribed by the Heisenberg uncertainty principle $m\geq\hbar/2\Delta t~c^{2}$ , and gives $1.2\times 10^{-69}$ kg, where $\Delta t$ is the currently supposed age of the Universe ( $1.37\times 10^{10}$ years). Photon mass upper limits are not quantum mechanics direct limits, but indirect ones. They are deduced from the modifications to classic laws that an ensemble of massive photons would produce.

The examination of the literature inspires a critical attitude and prompt to question whether the limits are nothing more than the outcome of idealised models: ”Quoted photon-mass limits have at times been overly optimistic in the strengths of their characterizations. This is perhaps due to the temptation to assert too strongly something one knows to be true” Goldhaber and Nieto (2010). We share this concern also for the actual solar wind limits, and feel safer if values larger than $m_{\gamma}=10^{-54}$ kg are still considered partially under investigation.

For $m_{\gamma}=0$ , Eq. (1) reduces to the usual Maxwell Lagrangian. The Euler-Lagrange equation leads to the dBP wave equation

\left[\square+{\cal M}^{2}\right]A^{\alpha}=\mu_{0}j^{\alpha}~,

(2)

where the permeability $\mu_{0}=1.23\times 10^{-6}$ H m^-1. Equation (2) also holds for Stueckelberg’s theory Stueckelberg (1957), where the auxiliary (real) scalar field is a ghost in the sense that it does not interact with any of the observable particles. Its purpose is to make the theory manifestly gauge invariant.

For $m_{\gamma}\neq 0$ , the speed of propagation ⁴⁴4Photons can indeed be interpreted as quanta of harmonic waves. However, it must be noted that the concept of photon has its own independence. The nature of light is considered to be double, according to the scale, with respect to the wavelength, at which we are observing it. Not only wave packets are composed of photons, but also plane waves. Further, if we refer to a quantum theory, its Hamiltonian will be given in terms of annihilation and creation operators. This means that photons with a defined wave numbers are destroyed or destroyed. These are supposed to be diffused wavefunctions, which, in the classical limit that is of interest here translate into to plane wave with a well defined wavelength. For such a wave, the local effects are negligible. $v_{g}$ depends upon the frequency $f$ and is smaller than the Maxwellian speed of light $c$

v_{g}=c\left[1-\left(\frac{c{\cal M}}{2\pi f}\right)^{2}\right]^{1/2}~.

(3)

At sufficiently high frequencies, for which the photon rest energy is small with respect to the total energy (in practice $f\gg 1$ Hz), the positive difference in velocity for two different frequencies ( $f_{2}>f_{1}$ ) is at first order de Broglie (1940)

\Delta v_{g}=v_{{\rm g}2}-v_{{\rm g}1}=\frac{c^{3}{\cal M}^{2}}{8\pi^{2}}\left(\frac{1}{f_{1}^{2}}-\frac{1}{f_{2}^{2}}\right)~,

(4)

being $v_{g}$ the group velocity. For a single source at distance d, the difference in the time of arrival of the two photons is

\Delta t=\frac{d}{v_{{\rm g}1}}-\frac{d}{v_{{\rm g}2}}\simeq\frac{\Delta v_{g}d}{c^{2}}=\frac{d{c\cal M}^{2}}{8\pi^{2}}\left(\frac{1}{f_{1}^{2}}-\frac{1}{f_{2}^{2}}\right)=\frac{dc^{3}m_{\gamma}^{2}}{8\hbar^{2}\pi^{2}}\left(\frac{1}{f_{1}^{2}}-\frac{1}{f_{2}^{2}}\right)~.

(5)

Inserting all values in SI units, we get

\Delta t~[{\rm s}]\simeq\frac{d~[{\rm m}]}{c~[{\rm ms}^{-1}]}\left(\frac{1}{f_{1}[{\rm s}^{-1}]^{2}}-\frac{1}{f_{2}[{\rm s}^{-1}]^{2}}\right)\left(10^{100}~{\rm s}^{-2}{\rm kg}^{-2}\right)m_{\gamma}[{\rm kg}]^{2}~.

(6)

Equations (5,6) imply that low frequency photons arrive later than high frequency photons. In Eq. (6), we have multiplied and divided by c to get a mnemonic expression. Modern approaches to gravity quantisation, e.g., Amelino-Camelia et al. (1998); Amelino-Camelia (2002); Kowalski-Glikman and Nowak (2002); Magueijo and Smolin (2003); Abdo and et al. (2009); Amelino-Camelia (2009); Mavromatos (2010); Bolmont and Jacholkowska (2011); Amelino-Camelia (2013); Ellis and Mavromatos (2013), lead also to variation of light speed versus the wavelength. Conversely to Eq. (5), they manifest themselves at high frequencies, thereby the interest for Gamma-Ray Bursts.

III Pulsars, magnetars, fast radio bursts and dispersion

III.1 Pulsars and magnetars

Pulsar and magnetars are neutron stars characterised by a high magnetic field $10^{4}-10^{11}$ T, fast rotation $10^{-1}-10^{3}$ Hz, and the emission of a beam of electromagnetic radiation, from radio to gamma rays, including bursts Coti Zelati et al. (2015). Few magnetars, though, are known to be active in the radio spectrum and above, such as the magnetar in the Galactic centre Kaspi et al. (2014); Torne et al. (2015); Pennucci et al. (2015). While the rotation slow down of pulsars is used for timing, the variability of the rotation of magnetars induces a larger timing noise.

The pulsar radiation passes through the interstellar medium (ISM), which temperature of ranges from $10$ to $10^{7}$ K. Free electrons in the ISM affect the radiation. Due to the dispersive nature of plasma, or the ionised part of the atoms, lower frequency radio waves travel through the ISM slower than higher frequency ones ⁵⁵5For a more detailed description of dispersion and waves in plasmas, see Bekefi (1966); Melrose (1980); Nicholson (1983); Bastian (2005). Nevertheless, the literature on massive photons, e.g., Feinberg (1969); Goldhaber and Nieto (1971); Tu et al. (2005, 2005) deals with plasmas as we deal with in this paper. Feinberg Feinberg (1969) pointed out that pulse arrival times show no sign of any dispersion, except that implied by the simple quadratic, over the whole range of frequency from radio to optical. We invite observers to analyse any departure from this law.. The delay in the arrival of the pulses is directly measurable as the dispersion measure (DM) of the pulsar. The DM is the total column density of free electrons $n$ between the observer and the pulsar, and it is used to construct models of the free electron distribution. It is computed through the integral along the propagation path from the source to the observer

DM=\int ndl~.

(7)

Purging the raw measurements of the flux vis á vis the frequency through the DM is the first step in signal processing. The DM conveys valuable information about the location of a burst or pulsed source. It gives an estimate of the path length and hence the source distance. In pulsar timing, different arrival times of the incoming photons are routinely measured, but lacking any other independent measurement of the electron density of the ISM, the delays are solely attributed to plasma, or the ionised part of the atoms. The group velocity is given by Lorimer and Kramer (2005)

v_{g}=c\left[1-\left(\frac{f_{P}}{f}\right)^{2}\right]^{1/2}~,

(8)

being $f_{\rm P}=e/(2\pi)[n/(\epsilon_{0}m_{\rm e})]^{1/2}$ the plasma frequency and $n$ the average electron density along the line of sight.

Indeed, Eq. (8) resembles Eq. (3). Again at first order, we have that the delay in pulse arrival times across a finite bandwidth due to the frequency dependence of the group velocity of the pulse on the ionised components of the ISM, is given by

\Delta t=\frac{d}{c}\frac{f_{\rm P}^{2}}{2}\left(\frac{1}{f_{1}^{2}}-\frac{1}{f_{2}^{2}}\right)~.

(9)

Inserting all values in SI units, we get

\Delta t~[{\rm s}]\simeq\frac{d~[{\rm m}]}{c~[{\rm ms}^{-1}]}\left(\frac{1}{f_{1}[{\rm s}^{-1}]^{2}}-\frac{1}{f_{2}[{\rm s}^{-1}]^{2}}\right)\left(4.03\times 10^{1}{\rm m}^{3}{\rm s}^{-2}\right)n~[{\rm m}^{-3}]~.

(10)

Incidentally using the Dispersion Measure (DM) in units pc cm^-3, that is $3.0857\times 10^{22}$ m^-2, Eq. (10) may be cast as

\Delta t~[{\rm s}]\simeq\left(\frac{1}{f_{1}[{\rm s}^{-1}]^{2}}-\frac{1}{f_{2}[{\rm s}^{-1}]^{2}}\right)\left(4.17\times 10^{15}{\rm pc}^{-1}{\rm cm}^{3}{\rm s}^{-1}\right)~{\rm DM}~[{\rm pc}~{\rm cm}^{-3}]~.

(11)

The numerical values in Eq. (11) are arranged to let the reader use DM in pc cm^-3 units. Comparing Eqs. (6,10), we get

\frac{m_{\gamma}}{\sqrt{n}}\left[{\rm kg}~{\rm m}^{3/2}\right]={6.62\times 10^{-50}}~,

(12)

which implies that for this ratio - in different units in Feinberg (1969); Goldhaber and Nieto (1971); Tu et al. (2005, 2005) - a massive photon and the average electron density along the line of sight determine the same dispersion.

Anisotropy, inhomogeneity, and time variability of the electron density (and thereby turbulence, scintillations, multipaths) are the main constraints in establishing an upper limit to the photon mass.

Pulsar observations Bay and White (1972) indicated that the speed of light was constant to within $10^{-20}$ throughout the visible, near infrared and ultraviolet regions of the spectrum, corresponding to a rough upper limit to the photon mass of $3\times 10^{-49}$ kg Bay and White (1972); Tu et al. (2005); Accioly et al. (2010). It is evident that exploring lower frequencies provides more stringent upper limits to the photon mass.

We remark in passing that also millisecond pulsars Schaefer (1999); Tu et al. (2005) have been considered in the context of testing photon mass.

III.1.1 Superdispersion

Pulsars

The LOw Frequency ARray (LOFAR) van Haarlem and et al. (2013) is now operating and getting data at 15 MHz. LOFAR, Westerbork and Lovell Telescope frequencies $15-1400$ MHz, are used Pilia et al. (2016) also to analyse superdispersion, i.e. an excess of dispersion at lower frequencies.

Superdispersion has been detected by some Shitov and Malofeev (1985); Kuz’min (1986); Shitov et al. (1988); Hankins et al. (1991); Pennucci et al. (2015); Cordes et al. (2016), while others have not found evidence Hassall et al. (2012); Pilia et al. (2016). In Phillips and Wolcszan (1992); Ahuja et al. (2005, 2007) the larger dispersion is at higher frequencies, but for a limited number of sampling frequencies.

One possible explanation of superdispersion is based on the inhomogeneous properties of the ISM that, by causing multi-path propagation of radio waves where the path depends on the frequency, determines the sampled column density of free electrons being also a function of frequency. Thereby, the DM inconsistencies might be the consequence of imposing a $1/f^{2}$ simple law onto a frequency-dependent and more complex dispersion due to an inhomogeneous ISM Pennucci et al. (2015).

Magnetars

In Pennucci et al. (2015), for the magnetar SGR J1745-2900, the authors find superdispersion between the L and S bands. They exclude causes as low quality data, profile misalignments, modelling and systematic errors, time variability. On the other hand, the authors observe that frequency dependencies other than $1/f^{2}$ appear to produce DM inconsistencies. We complement their conclusions by commenting that it is not evident to assume that the medium inhomogeneities, and thereby the multipaths, determine always the same behaviour versus frequency. Whether, this is due to an extra-dispersion $1/f^{2}$ caused by a massive photon cannot be claimed, even theoretically at this stage.

Indeed, for magnetars we are compelled to consider the presence of the overcritical magnetic field. The latter demands the analysis of alternative electromagnetism Heisenberg and Euler (1936) to see if delays can be caused by the large magnetic field. In Bonetti et al. (2016), there is the description of how photons red or blue shift exiting the magnetar and travelling towards the observer at infinity.

III.2 Fast radio bursts

Fast Radio Bursts (FRB) are millisecond bursts of radio radiation, not yet consensually identified with an astronomical object or phenomenon, and discovered in pulsar surveys. The bursts are strongly dispersed, possibly hinting that FRBs are at cosmological distances with redshifts in the range 0.3-1.3 Dennison (2014); Tuntsov (2014); Keane et al. (2016); Katz (2016).

They are characterised by the fluence (dimensions of action per surface area), time integral of the flux (dimension of energy per surface area)

{\cal F}=\int F(t)dt~.

(13)

The fluence is measured in Jy ms (Jansky millisecond, where a Jansky is 10^-26 W m^-2 Hz ^-1). Seventeen FRBs have been catalogued so far Petroff et al. (2016).

FRB have large values of DM, though they are observed at high galactic latitude. After subtraction of the (small) estimated Galactic component, the remaining DM must have another origin. Leaving aside massive photons, there are two conventional explanations. One is the close plasma environment of the galactic source, the other is the intergalactic plasma.

FRBs have been used recently to set photon mass upper limits Bonetti et al. (2016); Wu et al. (2016) in the GHz region. Meanwhile, FRB are also targeted Trott et al. (2013); Karastergiou et al. (2015); Obrocka et al. (2015); Thyagarajan et al. (2015); Tingay et al. (2015); Rowlinson et al. (2016) at lower frequencies by numerous radio telescopes like LOFAR van Haarlem and et al. (2013), the Long Wavelength Array (LWA) Ellingson et al. (2013), and the Murchison Widefield Array (MWA) Bowman et al. (2013).

In the future, the different redshift dependences of the plasma and photon mass contributions to DM can be used to improve the sensitivity to the photon mass if more FRB redshifts are measured. For a fixed fractional uncertainty in the extra-galactic contribution to the DM of an FRB, one with a lower redshift would provide greater sensitivity to the photon mass Bonetti et al. (2016).

IV Discussion

This research note addresses massive electromagnetism ⁶⁶6Instead, we have not addressed nor the classic or quantum frequency shifts Ginzburg (1961); Wolf and Foley (1989); Foley and Wolf (1989); Laio et al. (1997) nor Doppler shifts nor the cosmological redshift.. We have four areas of investigations in front of us. We spell them out in form of questions

•

Is usual pulsar dispersion hiding a massive photon?. There is abundant literature showing that the upper limits to the photon mass from traditional analysis of pulsars are not competitive with other estimates. The latter, though, often are product of theoretical models, and not real experiments.
•

Is pulsar superdispersion (also) a manifestation of a massive photon? This is a new line of investigation, but we feel that the question will be unanswered as long as a mathematical model of superdispersion does not exist.
•

Is magnetar superdispersion (also) a manifestation of a massive photon? The results from the study Pennucci et al. (2015), for the magnetar SGR J1745-2900 need to be confirmed. Further, the effects of the overcritical magnetic field must be separated out.
•

Is the extra dispersion from FRBs (also) a manifestation of a massive photon? This question will be unanswered as long as the distance of the FRB sources remains uncertain.

Disentangling the distance to sources objects from dispersion appears one main obstacle. Lacking the ability of estimating distances independently from dispersion, the similarity of massive photon and electron density dispersions obliges to set only upper limit to the photon mass. Possibly, double pulsars Kramer et al. (2006) might provide a mean to disentangle distance from both dispersions, but unlikely to assign the nature of such dispersion.

Another hope for disentanglement might be to study signals around the cusp of the plasma frequency $f_{P}$ . Around and below such frequency, the group velocity would differ from the $1/f^{2}$ behaviour, while massive photon dispersion would keep its mathematical profile.

When referring also to gravitational wave detection studies with pulsar timing arrays, dispersion emerges as a crucial issue. Time variable delays due to radio wave propagation in the ionised interstellar medium are a substantial source of error Stinebring (2013); Lam et al. (2015); Levin (2015); Palliyaguru et al. (2015). We further remark that setting upper limits to the photon mass may be mandatory to set limits to the graviton mass, or testing general relativity and the equivalence principle, when the two travel speeds are compared, e.g., Cutler et al. (2003); Deffayet and Menou (2007); Kocsis et al. (2008); Nishizawa and Nakamura (2014); Branchina and De Domenico (2016); Liu et al. (2016); Wu et al. (2016). While for general relativity, the graviton mass is null, it is not the case for the numerous alternative theories Goldhaber and Nieto (2010); Will (2014) ⁷⁷7 In Abbott and et al. (2016), there is an upper limit to the graviton mass of $2\times 10^{-58}$ kg, based on a similar expressions to Eq. (3), going as $1/f^{2}$ . For clarity, this upper limit does not rely on a comparison with photon times of arrival but solely on the gravitational waveforms. Obviously, such limit is not to be intended as on a single graviton, but on the dispersion that an ensemble of massive gravitons would produce macroscopically. Otherwise, for the Heisenberg principle the strict measurement of the mass upper limit as $2\times 10^{-58}$ kg on a single graviton would demand an observation time of approximately a month. For a review on photon and graviton mass upper limits, see Goldhaber and Nieto (2010)..

What studies should target? 1) an analysis of the frequency scaling as $af^{-1}+bf^{-2}+cf^{-3}+df^{-4}$ ; 2) an improvement of data quality in terms of timing at low frequencies; 3) an analysis of time, space, and frequency variability of the electron density; 4) extensive studies at very low frequencies, possibly of sources at large distances, towards sky directions where electron density dispersion is supposedly not large.

A contribution to the answers to these queries might be provided by opening a new window in the sub-MHz region.

V OLFAR

Opening a new window in the sub-MHz region consists of a few challenges. First of all the wavelength of the signals is in the order of tens of meters, meaning that usually large antennas are needed (or synthetic apertures in the case of array antennas). Usually this is done by creating large arrays instead of single dish antennas. Secondly for very low frequencies, the Earth’s ionosphere blocks frequencies below 30 MHz. To overcome this problem, initiatives based on satellite systems have been proposed. Because of the large baselines needed for low frequencies, array antennas are the only feasible option in space. One of the first initiatives is the DARIS project Rajan et al. (2016). DARIS is a scenario with eight slave spacecraft and a central spacecraft, in which the nodes will do the sensing part while the mothership will have additional processing and communication tasks. One of the conclusions of the study was that technology has reached a level where this type of scenario is realistic and can be implemented with commercial off-the-shelf components. However, having a central spacecraft will increase the risk of failure of the system.

The following up project for radioastronomy is the Orbiting Low Frequency Antennas for Radio astronomy (OLFAR) Verhoeven et al. (2011); Dekens et al. (2014); Budianu et al. (2015); Rajan et al. (2016) intends to map the celestial sources in the 0.1-10 MHz range and be a tool for navigation Tartaglia et al. (2011). OLFAR plans to place a swarm of satellites into a Moon orbit. The purpose of these satellites is to function as a distributed low frequency array far away from man-made Radio Frequency Interference (RFI) and away from the blocking ionosphere. A swarm of 50 or more nano-satellites orbiting faraway from terrestrial interference will be used to sense and sample the cosmic signals, process the information by means of distributed correlation, and send the processed data to a base station on Earth. Thus, each member of the swarm will have to fulfil three main tasks: radio observation, data distribution and processing, and down-linking. From the hardware point of view separate subsystems will have to be designed and integrated on a miniaturised spacecraft platform. Multiple antenna systems will have to be hosted by the nano-satellites to be able to support the data flow into, within, and out of the swarm.

To prevent terrestrial radio frequency interference (RFI), a Moon orbit or the Earth-Moon Lagrangian point behind the Moon (L2 point) is considered. When the swarm is behind the Moon, the latter can act as a shield against the RFI produced by the Earth. This will reduce the amount of RFI coming from Earth. However, due to diffraction, the RFI might bend around the Moon, and still have significant presence at locations where there is no direct line of sight to Earth, especially at the lowest frequencies. The amount of RFI presence behind the Moon due to diffraction is not known, but can be predicted.

Interference produced at the surface of the Earth, artificial radio transmissions and lighting, are effectively blocked by the Moon. Below 3 MHz, these signals are already attenuated a lot by the ionosphere of the Earth, and above 3 MHz the attenuation during ground wave propagation around the Moon is so high that the surface produced RFI will not be observed behind the Moon. The Auroral Kilometric Radiation (AKR) is more troublesome because it is not produced at the surface, but at an altitude of 1-3 times the radius of the Earth. This means that it does not have to propagate through the ionosphere to reach the Moon. The AKR has a frequency range of 100 kHz to 1 MHz. These low frequencies are less attenuated by ground wave propagation. However, due to the very low conductivity of the Moon surface and the very rough terrain, the RFI produced by AKR will still be much weaker than the Galactic background radio noise when there is no direct Line Of Sight (LOS). However, due to the high altitude of the AKR, there will be a smaller area behind the Moon where there is no direct LOS to the source, which reduces the amount of time where observations can be executed during a Moon orbit. For a satellite at the Earth-Moon L2 point it is even worse. This point is located outside the LOS-free area, and therefore satellites located there will be directly exposed to RFI produced by the AKR. Because the interference will be very significant, this location is not suitable for OLFAR. Another issue is the reflection of the AKR at an altitude of 20-40 times the radius of the Earth. During these reflections that occur approximately 10% of the time, RFI produced by AKR will directly travel to the backside of the Moon and OLFAR will not be able to do observations in orbits higher than approximately 1000 km. During the other 90% of the time, observations will be possible.

V.1 OLFAR contribution to fundamental physics

OLFAR will open the unexplored frequency range of 0.1-10 MHz. By doing so, new astrophysical sources or new signal from know sources will emerge Lacki (2010). Meanwhile, it will contribute to answer to the queries posed in Section IV.

Figure 1 shows four dispersion curves due to photon mass and the average electron density along the line of sight in frequency band of OLFAR.

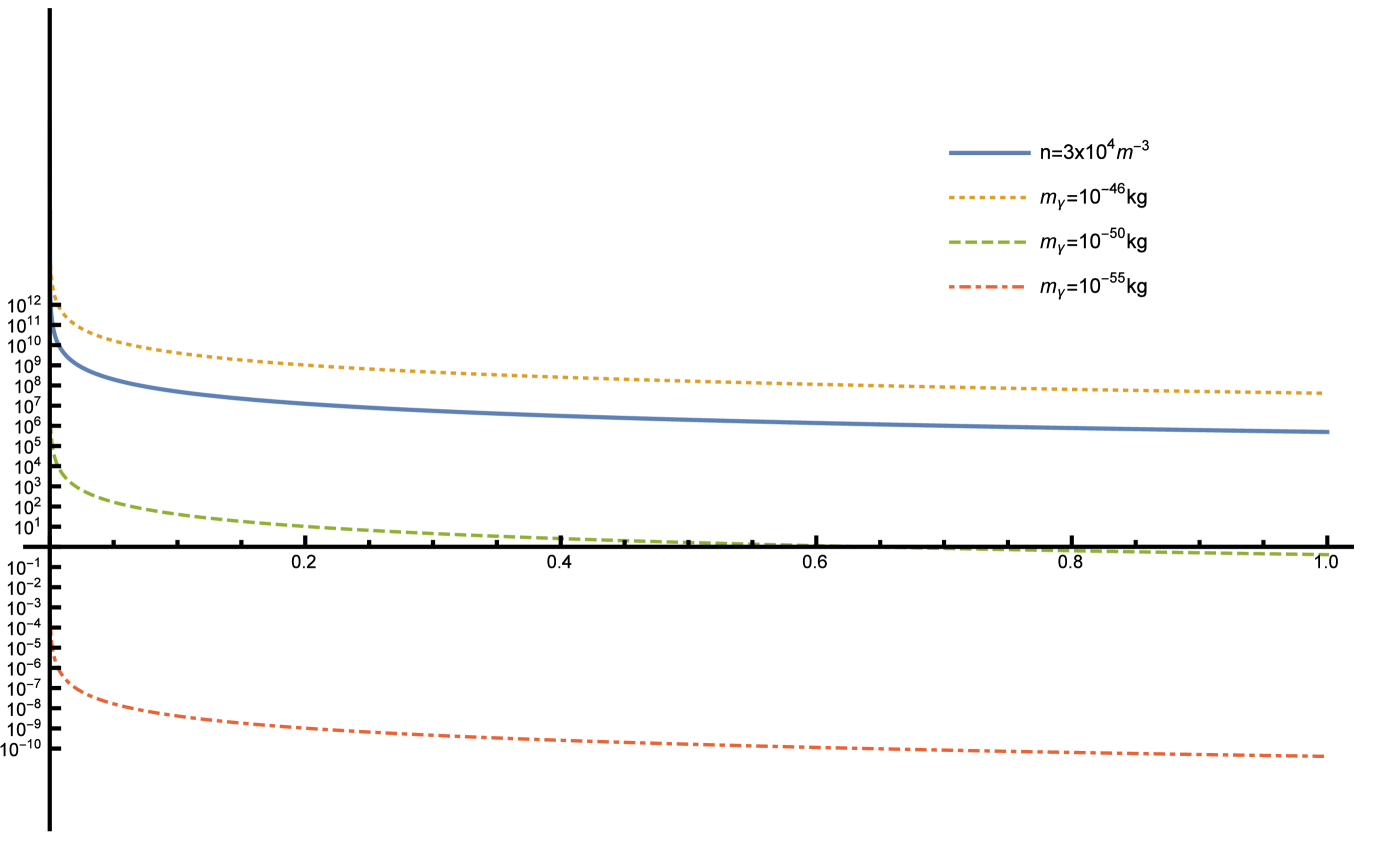
Refer to caption — Figure 1: For illustration, electron density and dBP dispersions are plotted versus the horizontal and vertical axis, indicating the frequency [MHz] and the delay [s], respectively. Equations (5,9) are applied to a distance $d=4$ kpc (representative pulsar distance), an average electron density along the line of sight $n=3\times 10^{4}$ m^-3 (thick blue line), photon mass $m_{\gamma}=10^{-46}$ kg (dotted orange line), $10^{-50}$ kg (dashed green line) and $10^{-55}$ kg (dotted-dashed red line). The frequency range is $0.1-1$ MHz and the delays are computed with respect to the time of arrival at high frequencies. For these values, the dispersion of the massive photon is either larger or smaller than the contribution of the average electron density along the line of sight. The dispersion value at $1$ MHz for $m_{\gamma}=10^{-46}$ kg is $4.11\times 10^{7}$ s (around 1.3 years), for $10^{-50}$ kg is 0.411 s, for $10^{-55}$ kg is 4.11 $\times 10^{-11}$ s. The dispersion for the electron density is $4.96\times 10^{5}$ s (about 6 days).

Applying Eqs. (5-12) at $1$ MHz, we get for a typical distance $d=4$ kpc (representative pulsar distance), the values in Tab. 1. They show that a given delay might be attributed to the electron density in the line of sight or else to a supposed massive photon, Eq. 12. More subtly, a delay discrepancy at low frequencies, may hide something more fundamental than the variation of dispersion.

Table 1: The equivalent theoretical delays at

1

MHz due to the electron content or massive photon dispersions, Eqs. (5-12), and for a typical distance

d=4

kpc (representative pulsar distance), computed with respect to the time of arrival at high frequencies.

$\Delta t$ [s]	$m_{\gamma}$ [kg]	$n$ [m^-3]
$10^{-10}$	$1.6\times 10^{-55}$	$6\times 10^{-12}$
$10^{-8}$	$1.6\times 10^{-54}$	$6\times 10^{-10}$
$10^{-6}$	$1.6\times 10^{-53}$	$6\times 10^{-8}$
$10^{-4}$	$1.6\times 10^{-52}$	$6\times 10^{-6}$
$10^{-2}$	$1.6\times 10^{-51}$	$6\times 10^{-4}$
$1$	$1.6\times 10^{-50}$	$6\times 10^{-2}$
$10^{2}$	$1.6\times 10^{-49}$	$6$
$10^{4}$	$1.6\times 10^{-48}$	$6\times 10^{2}$
$10^{6}$	$1.6\times 10^{-47}$	$6\times 10^{4}$
$10^{8}$	$1.6\times 10^{-46}$	$6\times 10^{6}$

V.2 Expected signals and processing

The availability of this extended frequency range makes it possible to study pulsars and pulsar timing in a frequency range in which most pulsars are intrinsically brightest. However, despite of this, the vast majority of pulsars have been discovered and studied at higher frequencies, in the range 300-2000 MHz. There are three main reasons for this: the deleterious effects of the ISM on pulsed signals; the effective background sky temperature of the Galactic synchrotron emission; and ionospheric effects. All of the effects become worse towards lower frequencies. With OLFAR the ionospheric effects are eliminated, leaving the ISM effects and the high background sky temperature. Measuring dispersion measure variations and modelling the scattering of pulse profiles at the OLFAR frequencies has the potential to help improve pulse shapes and thus enhance high precision timing. At the same time, this means we can study the ISM.

Timing in the OLFAR swarm has been studied as part of the synchronisation for the swarm Rajan et al. (2013). The requirements of the clock in each of the satellites can be briefly summarised as:

1.
Sampling jitter $\Delta t_{jitter}$
1. (a)
  
  $\Delta t_{jitter}<10$ ps for 8 bit sampling
2. (b)
  
  $\Delta t_{jitter}<1$ ps for 12 bit sampling
2.
Allan deviation $\sigma_{\zeta}(\tau_{c})$
1. (a)
  
  Short term $\sigma_{\zeta}(\tau_{c})\leq 10^{-8}$ for $\tau_{c}$ = 1 second
2. (b)
  
  Long term $\sigma_{\zeta}(\tau_{c})\leq 10^{-11}$ for $\tau_{c}$ = 1000 seconds

To achieve Allan deviations of order $10^{-8}$ and $10^{-11}$ the usual solutions are Rubidium standards and Oven controlled Crystal oscillators (OCXO). Although cesium and maser families can offer orders of magnitude lower Allan deviations, they are also very expensive, in terms of mass and power for an OLFAR satellite and hence not considered. There has been consistent research in developing chip scale atomic clocks, especially on rubidium clocks, Knappe et al. (2006)) based on Vertical Cavity Surface Emitting Lasers (VCSELs), which enable orders of magnitude reduction in size and power. The Quantum SA.45s is a Rubidium CSAC, Chip Scale Atomic Clock, which is based on VCSEL and meets the Allan deviation requirements of OLFAR up to 1000 seconds. This CSAC weighs less than 35 grams and has a steady power consumption of 125 mW. This suits the requirements on an OLFAR node.

V.3 Other opportunities

Ground observatories at low radio frequencies include the already mentioned LOFAR van Haarlem and et al. (2013) and NenuFAR Zarka et al. (2016).

Naturally, we recall the potential offered by the Square Kilometre Array (SKA) Lazio (2013); Salzano et al. (2016) operating at ns level.

Supposing an ambitious sub-picosecond precision and ideal conditions, a low Earth Orbit satellite as the Atomic Clocks Ensemble in Space (ACES) Lounis et al. (1993); European Space Agency (1994) (ESA) would determine an $m_{\gamma}$ upper limit around $10^{-46}$ kg; instead the Space-Time Explorer and Quantum Equivalence Principle Space Test (STE-QUEST) Altschul et al. (2015) could use the highly elliptic orbit to get around $10^{-47}$ kg; a large space mission as LISA Decher et al. (1980); Bertotti (1984) with million kilometer interferometric arms around $10^{-48}$ kg; finally, a mission to the frontiers of the Solar System as Neptun, Pluto and the Kuiper belt around around $10^{-51}$ kg. All the estimates refer to the S band.

VI Conclusions and perspectives

We have focused on the interest raised by the newly operating and future ground and space detectors at very low radio frequencies. The foundations of electromagnetism could be tested, confirming our beliefs or else contributing to establish new physics. Studies on dispersion appear crucial to unveil the causes of the excess of DM, and disentangle the measure of DM from distance. Low frequency observatories placed faraway from the Earth will be an essential aid to such studies, and will possibly set competitive limits to the photon mass.

Meanwhile, theoretical investigations on the plausibility and implications of massive photons is to be pursued. In the context of Standard Model Extensions (SMEs), four general classes of Super Symmetry (SuSy) and Lorentz Symmetry (LoSy) breaking were analysed, leading to observable imprints at our energy scales Bonetti et al. (2016). The photon dispersion relations show a non-Maxwellian behaviour for the CPT (Charge-Parity-Time reversal symmetry) odd and even sectors. The group velocities exhibit also a directional dependence with respect to the breaking background vector (odd CPT) or tensor (even CPT). In the former sector, the group velocity may decay following an inverse squared frequency behaviour. Thus, a massive and gauge invariant Carroll-Field-Jackiw photon term in the Lagrangian has been extracted and the induced mass shown to be proportional to the breaking vector. The latter is estimated by ground measurements and leads to a photon mass upper limit of $10^{-19}$ eV or $2\times 10^{-55}$ kg.

Implications for cosmology by non-linear and massive photon theories, and generally non-Maxwellian behaviour have not yet been evaluated adequately. Finally, laboratory experiments should be pursued, investigating in all directions, including the search of frequency shifts, incidentally using the same equipment to set upper limit to the Hubble parameter at small scale Shamir and Fox (1967); Bonnor (1999); Dumin (2012); Price and Romano (2012); Kopeikin (2015).

Acknowledgements

This work was partly carried during a visit of LB and ADAMS to the Centro Brasileiro de Pesquisas Físicas in Rio de Janeiro. The latter also acknowledges discussions with J.-C. Pecker (Collège de France), C. Salomon (Ecole Normale Supérieure, Paris), A. Possenti and M. Pilia (Osservatorio Astronomico di Cagliari), L. Iess (Università di Roma, La Sapienza).

References

Spallicci et al. (2005) A. Spallicci, S. Aoudia, J. de Freitas Pacheco, T. Regimbau, G. Frossati, Virgo detector optimization for gravitational waves by inspiralling binaries, Class. Q. Grav. 22 (2005) S461.
Abbott and et al. (2016) B. P. Abbott, et al., Observation of gravitational waves from a binary black hole merger, Phys. Rev. Lett. 116 (2016) 061102.
Spallicci (2013) A. D. A. M. Spallicci, On the complementarity of pulsar timing and space laser interferometry for the individual detection of supermassive black hole binaries, Astrophys. J. 764 (2013) 187.
Lacki (2010) B. C. Lacki, The end of the rainbow: what can we say about the extragalactic sub-MegaHertz radio sky?, Mon. Not. Roy. Astron. Soc. 406 (2010) 863.
Born and Infeld (1934) M. Born, L. Infeld, Foundations of the new field theory, Proc. R. Soc. Lond. A 144 (1934) 425.
Heisenberg and Euler (1936) W. Heisenberg, H. Euler, Folgerungen aus der Diracschen theorie des positron, Zeitschr. Phys. 98 (1936) 714.
Breit and Wheeler (1934) G. Breit, J. A. Wheeler, Positron production in multiphoton light-by-light scattering, Phys. Rev. 46 (1934) 1087.
Halpern (1934) O. Halpern, Scattering processes produced by electrons in negative energy states, Phys. Rev. 44 (1934) 855.
Euler (1936) H. Euler, Über die streuung von licht an licht nach der Diracschen theorie, Ann. Phys. (Leipzig) 26 (1936) 398.
Achieser (1937) A. Achieser, Über die streuung von licht an licht, Physik Zeits. Sowjetunion 11 (1937) 263.
Karplus and Neuman (1950) R. Karplus, M. Neuman, Non-linear interactions between electromagnetic fields, Phys. Rev. 80 (1950) 380.
Karplus and Neuman (1951) R. Karplus, M. Neuman, The scattering of light by light, Phys. Rev. 83 (1951) 776.
Burke et al. (1997) D. L. Burke, R. C. Field, G. Horton-Smith, J. E. Spencer, D. Walz, S. C. Berridge, W. M. Bugg, K. Shmakov, A. W. Weidemann, C. Bula, K. T. McDonald, E. J. Prebys, C. Bamber, S. J. Boege, T. Koffas, T. Kotseroglou, A. C. Melissinos, D. D. Meyerhofer, D. A. Reis, W. Ragg, Positron production in multiphoton light-by-light scattering, Phys. Rev. Lett. 79 (1997) 1626.
Schellstede et al. (2015) G. O. Schellstede, V. Perlick, C. Lämmerzahl, Testing non-linear vacuum electrodynamics with Michelson interferometry, Phys. Rev. D 92 (2015) 025039.
de Broglie (1922) L. de Broglie, Rayonnement noir et quanta de lumière, J. Phys. et Radium VI 3 (1922) 422.
de Broglie (1923) L. de Broglie, Ondes et quanta, Comptes Rendus Hebd. Séances Acad. Sc. Paris 177 (1923) 507.
de Broglie (1940) L. de Broglie, La méchanique ondulatoire du photon, Une novelle théorie de la lumiére, Hermann, Paris, 1940.
Proca (1936a) A. Proca, Sur la théorie du positon, Comptes Rendus Hebd. Séances Acad. Sc. Paris 202 (1936a) 1366.
Proca (1936b) A. Proca, Sur les équations fondamentales des particules élementaires, Comptes Rendus Hebd. Séances Acad. Sc. Paris 202 (1936b) 1490.
Proca (1936c) A. Proca, Sur les photons et les particules charge pure, Comptes Rendus Hebd. Séances Acad. Sc. Paris 203 (1936c) 709.
Proca (1936d) A. Proca, Sur la théorie ondulatoire des électrons positifs et négatifs, J. Phys. et Radium VII (1936d) 347.
Proca (1937) A. Proca, Particules libres photons et particules charge pure, J. Phys. et Radium VIII (1937) 23.
Proca (1938) A. Proca, Théorie non relativiste des particules à spin entier, J. Phys. et Radium IX (1938) 61.
Bopp (1940) F. Bopp, Eine lineare theorie des elektrons, Ann. Phys. (Leipzig) 430 (1940) 345.
Podolsky (1942) B. Podolsky, A generalized electrodynamics. Part I - non-quantum, Phys. Rev. 62 (1942) 68.
Podolsky and Kikuchi (1944) B. Podolsky, C. Kikuchi, A generalized electrodynamics. Part II - quantum, Phys. Rev. 65 (1944) 228.
Podolsky and Schwed (1948) B. Podolsky, P. Schwed, Review of a generalized electrodynamics, Rev. Mod. Phys. 20 (1948) 40.
Stueckelberg (1957) E. C. G. Stueckelberg, Théorie de la radiation de photons de masse arbitrairement petite, Helv. Phys. Acta 30 (1957) 209.
Chern and Simons (1974) S. Chern, J. Simons, Characteristic forms and geometric invariants, Ann. Math. 99 (1974) 48.
Landé (1941) A. Landé, Finite self-energies in radiation theory. Part I, Phys. Rev. 60 (1941) 121.
Landé and Thomas (1941) A. Landé, L. H. Thomas, Finite self-energies in radiation theory. Part II, Phys. Rev. 60 (1941) 514.
Landé and Thomas (1944) A. Landé, L. H. Thomas, Finite self-energies in radiation theory. Part III, Phys. Rev. 65 (1944) 175.
Gratus et al. (2015) J. Gratus, V. Perlick, R. W. Tucker, On the self-force in Bopp-Podolsky electrodynamics, J. Phys. A: Math. Theor. 48 (2015) 435401.
Greiner and Reinhardt (1996) W. Greiner, J. Reinhardt, Field quantization, Springer, Berlin, 1996.
Tu et al. (2005) L.-C. Tu, J. Luo, G. T. Gillies, The mass of the photon, Rep. Progr. Phys. 68 (2005) 77.
Accioly et al. (2010) A. Accioly, J. Helayël-Neto, E. Scatena, Upper bounds on the photon mass, Phys. Rev. D 82 (2010) 065026.
Goldhaber and Nieto (2010) A. S. Goldhaber, M. M. Nieto, Photon and graviton mass limits, Rev. Mod. Phys. 82 (2010) 939.
Spavieri et al. (2011) G. Spavieri, J. Quintero, G. T. Gillies, M. Rodriguez, A survey of existing and proposed classical and quantum approaches to the photon mass, Eur. Phys. J. D 61 (2011) 531.
Williams et al. (1971) E. R. Williams, J. E. Faller, H. A. Hill, New experimental test of Coulomb’s law: A laboratory upper limit on the photon rest mass, Phys. Rev. Lett. 26 (1971) 721.
Ryutov (1997) D. D. Ryutov, The role of finite photon mass in magnetohydrodynamics of space plasmas, Plasma Phys. Contr. Fus. 39 (1997) A73.
Ryutov (2007) D. D. Ryutov, Using plasma physics to weigh the photon, Plasma Phys. Contr. Fus. 49 (2007) B429.
Olive and the Particle Data Group (2014) K. A. Olive, the Particle Data Group, Review of particle physics, Chin. Phys. C 38 (2014) 090001.
Retinò et al. (2016) A. Retinò, A. D. A. M. Spallicci, A. Vaivads, Solar wind test of the de Broglie-Proca’s massive photon with Cluster multi-spacecraft data, Astropart. Phys. 82 (2016) 49.
Barnes and Scargle (1975) A. Barnes, J. D. Scargle, Improved upper limit on the photon rest mass, Phys. Rev. Lett. 35 (1975) 1117.
Chibisov (1976) G. V. Chibisov, Astrophysical upper limits on the photon rest mass, Sov. Phys. Usp. 19 (1976) 624. [Usp. Fiz. Nauk, 119 (1976) 591].
Yamaguchi (1959) Y. Yamaguchi, A composite theory of elementary particles, Progr. Theor. Phys. Suppl. 11 (1959) 1.
Adelberger et al. (2007) E. Adelberger, G. Dvali, A. Gruzinov, Photon-mass bound destroyed by vortices, Phys. Rev. Lett. 98 (2007) 010402.
Amelino-Camelia et al. (1998) G. Amelino-Camelia, J. Ellis, N. E. Mavromatos, D. V. Nanopoulos, S. Sarkar, Tests of quantum gravity from observations of $\gamma$ -ray bursts, Nat. 393 (1998) 763. Correction, 1998, Nat., 395, 525.
Amelino-Camelia (2002) G. Amelino-Camelia, Relativity in space-times with short-distance structure governed by an observer-independent (Planckian) length scale, Int. J. Mod. Phys. D 11 (2002) 35.
Kowalski-Glikman and Nowak (2002) J. Kowalski-Glikman, S. Nowak, Doubly special relativity theories as different bases of k-Poincaré algebra, Phys. Lett. B 539 (2002) 126.
Magueijo and Smolin (2003) J. Magueijo, L. Smolin, Generalized Lorentz invariance with an invariant energy scale, Phys. Rev. D 67 (2003) 044017.
Abdo and et al. (2009) A. A. Abdo, et al., A limit on the variation of the speed of light arising from quantum gravity effects, Nat. 462 (2009) 331.
Amelino-Camelia (2009) G. Amelino-Camelia, Burst of support for relativity, Nat. 462 (2009) 291.
Mavromatos (2010) N. E. Mavromatos, String quantum gravity, Lorentz-invariance violation and gamma ray astronomy, Int. J. Mod. Phys. A 25 (2010) 5409.
Bolmont and Jacholkowska (2011) J. Bolmont, A. Jacholkowska, Lorentz symmetry breaking studies with photons from astrophysical observations, Adv. Sp. Res. 47 (2011) 380.
Amelino-Camelia (2013) G. Amelino-Camelia, Quantum spacetime phenomenology, Liv. Rev. Rel. 16 (2013).
Ellis and Mavromatos (2013) J. Ellis, N. E. Mavromatos, Probes of Lorentz violation, Astropart. Physics 43 (2013) 50.
Coti Zelati et al. (2015) F. Coti Zelati, N. Rea, A. Papitto, D. Viganò, J. A. Pons, R. Turolla, P. Esposito, D. Haggard, F. K. Baganoff, G. Ponti, G. L. Israel, S. Campana, D. F. Torres, A. Tiengo, S. Mereghetti, R. Perna, S. Zane, R. P. Mignani, A. Possenti, L. Stella, The x-ray outburst of the galactic centre magnetar SGR J1745-2900 during the first 1.5 year, Mon. Not. R. Astroc. Soc. 449 (2015) 2685.
Kaspi et al. (2014) V. M. Kaspi, R. F. Archibald, V. Bhalerao, F. Dufour, E. V. Gotthelf, H. An, M. Bachetti, A. M. Beloborodov, S. E. Boggs, F. E. Christensen, W. W. Craig, B. W. Grefenstette, C. J. Hailey, F. A. Harrison, J. A. Kennea, C. Kouveliotou, K. K. Madsen, K. Mori, C. B. Markwardt, D. Stern, J. K. Vogel, W. W. Zhang, Timing and flux evolution of the galactic center magnetar SGR J1745-2900, Astrophys. J. 786 (2014) 84.
Torne et al. (2015) P. Torne, R. P. Eatough, R. Karuppusamy, M. Kramer, G. Paubert, B. Klein, G. Desvignes, D. J. Champion, H. Wiesemeyer, C. Kramer, L. G. Spitler, C. Thum, R. Güsten, K. F. Schuster, I. Cognard, Simultaneous multifrequency radio observations of the galactic centre magnetar SGR J1745-2900, Mon. Not. Roy. Astron. Soc. 451 (2015) L50.
Pennucci et al. (2015) T. T. Pennucci, A. Possenti, P. Esposito, N. Rea, D. Haggard, F. K. Baganoff, M. Burgay, F. Coti Zelati, G. L. Israel, A. Minter, Simultaneous multi-band radio and x-ray observations of the galactic center magnetar SGR 1745-2900, Astrophys. J. 808 (2015) 81.
Lorimer and Kramer (2005) D. R. Lorimer, M. Kramer, Handbook of pulsar astronomy, Cambridge University Press, Cambrige, 2005.
Feinberg (1969) G. Feinberg, Pulsar test of a variation of the speed of light with frequency, Science 166 (1969) 879.
Goldhaber and Nieto (1971) A. S. Goldhaber, M. M. Nieto, Terrestrial and extraterrestrial limits on the photon mass, Rev. Mod. Phys. 43 (1971) 277.
Tu et al. (2005) L.-C. Tu, H.-L. Ye, J. Luo, Variations of the speed of light with frequency and implied photon mass, Chin. Phys. Lett. 22 (2005) 3057.
Bay and White (1972) Z. Bay, J. A. White, Frequency dependence of the speed of light in space, Phys. Rev. D 5 (1972) 796.
Schaefer (1999) B. E. Schaefer, Severe limits on variations of speed of light with frequency, Phys. Rev. Lett. 82 (1999) 4964.
van Haarlem and et al. (2013) M. P. van Haarlem, et al., LOFAR: the low frequency array, Astron. Astrophys. 556 (2013) A2.
Pilia et al. (2016) M. Pilia, J. W. T. Hessels, B. W. Stappers, V. I. Kondratiev, M. Kramer, J. van Leeuwen, P. Weltevrede, A. G. Lyne, K. Zagkouris, T. E. Hassall, A. V. Bilous, R. P. Breton, H. Falcke, J. Grießmeier, E. Keane, A. Karastergiou, M. Kuniyoshi, A. Noutsos, S. Osłowski, M. Serylak, C. Sobey, S. ter Veen, A. Alexov, J. Anderson, A. Asgekar, I. M. Avruch, M. E. Bell, M. J. Bentum, G. Bernardi, L. Bîrzan, A. Bonafede, F. Breitling, J. W. Broderick, M. Brüggen, B. Ciardi, S. Corbel, E. de Geus, A. de Jong, A. Deller, S. Duscha, J. Eislöffel, R. A. Fallows, R. Fender, C. Ferrari, W. Frieswijk, M. A. Garrett, A. W. Gunst, J. P. Hamaker, G. Heald, A. Horneffer, P. Jonker, E. Juette, G. Kuper, P. Maat, G. Mann, S. Markoff, R. McFadden, D. McKay-Bukowski, J. C. A. Miller-Jones, A. Nelles, H. Paas, M. Pandey-Pommier, M. Pietka, R. Pizzo, A. G. Polatidis, W. Reich, H. Röttgering, A. Rowlinson, D. Schwarz, O. Smirnov, M. Steinmetz, A. Stewart, J. D. Swinbank, M. Tagger, Y. Tang, C. Tasse, D. Thoudam, M. C. Toribio, A. J. van der Horst, R. Vermeulen, C. Vocks, R. J. van Weeren, R. A. M. J. Wijers, R. Wijnands, S. J. Wijnholds, O. Wucknitz, P. Zarka, W. B. Belayev, Wide-band, low-frequency pulse profiles of 100 radio pulsars with LOFAR, Astron. Astrophys. 586 (2016) A92.
Shitov and Malofeev (1985) Y. P. Shitov, V. M. Malofeev, A superdispersion of the meter wave pulses of PSR 0809+74, Sov. Astron. Lett. 11 (1985) 39. [Pis’ma Astron. Zh., 11 (1985) 94].
Kuz’min (1986) A. D. Kuz’min, Pulsar radio pulses: the frequency-dependent dispersion measure and the extra arrival-time delay, Sov. Astron. Lett. 12 (1986) 325. [Pis’ma Astron. Zh., 12 (1986) 778].
Shitov et al. (1988) Y. P. Shitov, V. M. Malofeev, V. A. Izvekova, Superdispersion delay of low-frequency pulsar pulses, Sov. Astron. Lett. 14 (1988) 181. [Pis’ma Astron. Zh., 14 (1988) 429].
Hankins et al. (1991) T. H. Hankins, V. A. Izvekova, V. M. Malofeev, J. M. Rankin, Y. P. Shitov, D. R. Stinebring, Microstructure-determined pulsar dispersion measures and the problem of profile alignment, Astrophys. J. Lett. 373 (1991) L17.
Cordes et al. (2016) J. M. Cordes, R. M. Shannon, D. R. Stinebring, Frequency dependent dispersion measures and implications for pulsar timing, Astrophys. J. 817 (2016) 16.
Hassall et al. (2012) T. E. Hassall, B. W. Stappers, J. W. T. Hessels, M. Kramer, A. Alexov, K. Anderson, T. Coenen, A. Karastergiou, E. F. Keane, V. I. Kondratiev, K. Lazaridis, J. van Leeuwen, A. Noutsos, M. Serylak, C. Sobey, J. P. W. Verbiest, P. Weltevrede, K. Zagkouris, R. Fender, R. A. M. J. Wijers, L. Bähren, M. E. Bell, J. W. Broderick, S. Corbel, E. J. Daw, V. S. Dhillon, J. Eislöffel, H. Falcke, J. M. Grießmeier, P. Jonker, C. Law, S. Markoff, J. C. A. Miller-Jones, R. Osten, E. Rol, A. M. M. Scaife, B. Scheers, P. Schellart, H. Spreeuw, J. Swinbank, S. ter Veen, M. W. Wise, R. Wijnands, O. Wucknitz, P. Zarka, A. Asgekar, M. R. Bell, M. J. Bentum, G. Bernardi, P. Best, A. Bonafede, A. J. Boonstra, M. Brentjens, W. N. Brouw, M. Brüggen, H. R. Butcher, B. Ciardi, M. A. Garrett, M. Gerbers, A. W. Gunst, M. P. van Haarlem, G. Heald, M. Hoeft, H. Holties, A. de Jong, L. V. E. Koopmans, M. Kuniyoshi, G. Kuper, G. M. Loose, P. Maat, J. Masters, J. P. McKean, H. Meulman, M. Mevius, H. Munk, J. E. Noordam, E. Orrú, H. Paas, M. Pandey-Pommier, V. N. Pandey, R. Pizzo, A. Polatidis, W. Reich, H. Röttgering, J. Sluman, M. Steinmetz, C. G. M. Sterks, M. Tagger, Y. Tang, C. Tasse, R. Vermeulen, R. J. van Weeren, S. J. Wijnholds, S. Yatawatta, Wide-band simultaneous observations of pulsars: disentangling dispersion measure and profile variations, Astron. Astrophys. 543 (2012) A66.
Phillips and Wolcszan (1992) J. A. Phillips, A. Wolcszan, Precision measurements of pulsar dispersion, Astrophys. J. 385 (1992) 273.
Ahuja et al. (2005) A. L. Ahuja, Y. Gupta, D. Mitra, A. K. Kembhavi, Tracking pulsar dispersion measures using the giant metrewave radio telescope, Mon. Not. Roy. Astron. Soc. 357 (2005) 1013.
Ahuja et al. (2007) A. L. Ahuja, D. Mitra, Y. Gupta, The effect of pulse profile evolution on pulsar dispersion measure, Mon. Not. Roy. Astron. Soc. 377 (2007) 677.
Bonetti et al. (2016) L. Bonetti, S. Perez Bergliaffa, A. D. A. M. Spallicci, Electromagnetic shift arising from Heisenberg–Euler dipole, in: M. Bianchi, R. T. Jantzen, R. Ruffini (Eds.), 14^th Marcel Grossmann Meeting, World Scientific, Singapore, 2016. To appear.
Dennison (2014) B. Dennison, Fast radio bursts: constraints on the dispersing medium, Mon. Not. Roy. Astron. Soc. 443 (2014) L11.
Tuntsov (2014) A. V. Tuntsov, Dense plasma dispersion of fast radio bursts, Mon. Not. Roy. Astron. Soc. 441 (2014) L26.
Keane et al. (2016) E. F. Keane, S. Johnston, S. Bhandari, E. Barr, N. D. R. Bhat, M. Burgay, M. Caleb, C. Flynn, A. Jameson, M. Kramer, E. Petroff, A. Possenti, W. van Straten, M. Bailes, S. Burke-Spolaor, R. P. Eatough, B. W. Stappers, T. Totani, M. Honma, H. Furusawa, T. Hattori, T. Morokuma, Y. Niino, H. Sugai, T. Terai, N. Tominaga, S. Yamasaki, N. Yasuda, R. Allen, J. Cooke, J. Jencson, M. M. Kasliwal, D. L. Kaplan, S. J. Tingay, A. Williams, R. Wayth, P. Chandra, D. Perrodin, M. Berezina, M. Mickaliger, C. Bassa, A fast radio burst host galaxy, Nat. 530 (2016) 453.
Katz (2016) J. I. Katz, Fast radio bursts - a brief review: some questions, fewer answers, Mod. Phys. Lett. A 31 (2016) 1630013.
Petroff et al. (2016) E. Petroff, E. D. Barr, A. Jameson, E. F. Keane, M. Bailes, M. Kramer, V. Morello, D. Tabbara, W. van Straten, FRBCAT: The Fast Radio Burst catalogue, Publ. Astron. Soc. Australia 33 (2016) e045.
Bonetti et al. (2016) L. Bonetti, J. Ellis, N. E. Mavromatos, A. S. Sakharov, E. K. Sarkisian-Grinbaum, A. D. A. M. Spallicci, Photon mass limits from fast radio bursts, Phys. Lett. B 757 (2016) 548.
Wu et al. (2016) X. Wu, S. Zhang, H. Gao, J. Wei, Y. Zou, W. Lei, B. Zhang, Z. Dai, P. Mészáros, Constraints on the photon mass with fast radio bursts, Astophys. J. Lett. 822 (2016) L15.
Trott et al. (2013) C. M. Trott, S. J. Tingay, R. B. Wayth, Prospects for the detection of fast radio bursts with the Murchison widefield array, Astrophys. J. Lett. 776 (2013) L16.
Karastergiou et al. (2015) A. Karastergiou, J. Chennamangalam, W. Armour, C. Williams, B. Mort, F. Dulwich, S. Salvini, A. Magro, S. Roberts, M. Serylak, A. Doo, A. V. Bilous, R. P. Breton, H. Falcke, J. Grießmeier, J. W. T. Hessels, E. F. Keane, V. I. Kondratiev, M. Kramer, J. van Leeuwen, A. Noutsos, S. Oslowski, C. Sobey, B. W. Stappers, P. Weltevrede, Limits on fast radio bursts at 145 MHz with ARTEMIS, a real-time software backend, Mon. Not. Roy. Astron. Soc. 452 (2015) 1254.
Obrocka et al. (2015) M. Obrocka, B. Stappers, P. Wilkinson, Localising fast radio bursts and other transients using interferometric arrays, Astron. Astrophys. 579 (2015) A69.
Thyagarajan et al. (2015) N. Thyagarajan, A. P. Beardsley, J. D. Bowman, M. F. Morales, A generic and efficient E-field parallel imaging correlator for next-generation radio telescopes, 2015. ArXiv:1510.08318 [astro-ph.IM].
Tingay et al. (2015) S. J. Tingay, C. M. Trott, R. B. Wayth, G. Bernardi, J. D. Bowman, F. Briggs, R. J. Cappallo, A. A. Deshpande, L. Feng, B. M. Gaensler, L. J. Greenhill, P. J. Hancock, B. J. Hazelton, M. Johnston-Hollitt, D. L. Kaplan, C. J. Lonsdale, S. R. McWhirter, D. A. Mitchell, M. F. Morales, E. Morgan, T. Murphy, D. Oberoi, T. Prabu, N. Udaya Shankar, K. S. Srivani, R. Subrahmanyan, R. L. Webster, A. Williams, C. L. Williams, G. Tifft, A search for fast radio bursts at low frequencies with Murchison widefield array high time resolution imaging, Astron. J. 150 (2015) 199.
Rowlinson et al. (2016) A. Rowlinson, M. E. Bell, T. Murphy, C. M. Trott, N. Hurley-Walker, S. Johnston, S. J. Tingay, D. L. Kaplan, D. Carbone, P. J. Hancock, L. Feng, A. R. Offringa, G. Bernardi, J. D. Bowman, F. Briggs, R. J. Cappallo, A. A. Deshpande, B. M. Gaensler, L. J. Greenhill, B. J. Hazelton, M. Johnston-Hollitt, C. J. Lonsdale, S. R. McWhirter, D. A. Mitchell, M. F. Morales, E. Morgan, D. Oberoi, S. M. Ord, T. Prabu, N. Udaya Shankar, K. S. Srivani, R. Subrahmanyan, R. B. Wayth, R. L. Webster, A. Williams, C. L. Williams, Limits on fast radio bursts and other transient sources at 182 MHz using the Murchison widefield array, Mon. Not. Roy. Astron. Soc. 458 (2016) 3506.
Ellingson et al. (2013) S. W. Ellingson, G. B. Taylor, J. Craig, J. Hartman, J. Dowell, C. N. Wolfe, T. E. Clarke, B. C. Hicks, N. E. Kassim, P. S. Ray, L. J. Rickard, F. K. Schinzel, K. W. Weiler, The LWA1 radio telescope, IEEE Trans. Ant. Prop. 61 (2013) 2540.
Bowman et al. (2013) J. D. Bowman, I. Cairns, D. L. Kaplan, T. Murphy, D. Oberoi, L. Staveley-Smith, W. Arcus, D. G. Barnes, G. Bernardi, F. H. Briggs, S. Brown, J. D. Bunton, A. J. Burgasser, R. J. Cappallo, S. Chatterjee, B. E. Corey, A. Coster, A. Deshpande, L. de Souza, D. Emrich, P. Erickson, R. F. Goeke, B. M. Gaensler, L. J. Greenhill, L. Harvey-Smith, B. J. Hazelton, D. Herne, J. N. Hewitt, M. Johnston-Hollitt, J. C. Kasper, B. B. Kincaid, R. Koenig, E. Kratzenberg, C. J. Lonsdale, M. J. Lynch, L. D. Matthews, S. Russell McWhirter, D. A. Mitchell, M. F. Morales, E. H. Morgan, S. M. Ord, J. Pathikulangara, P. Thiagaraj, R. A. Remillard, T. Robishaw, A. E. E. Rogers, A. A. Roshi, J. E. Salah, R. J. Sault, N. Udaya Shankar, K. S. Srivani, J. B. Stevens, R. Subrahmanyan, S. J. Tingay, R. B. Wayth, M. Waterson, R. Webster, A. R. Whitney, A. J. Williams, C. L. Williams, J. S. B. Wyithe, Science with the Murchison widefield array, Publ. Astron. Soc. Australia 30 (2013) e031.
Kramer et al. (2006) M. Kramer, I. H. Stairs, R. N. Manchester, M. A. McLaughlin, A. G. Lyne, R. D. Ferdman, M. Burgay, D. R. Lorimer, A. Possenti, N. D’Amico, J. M. Sarkissian, G. B. Hobbs, J. E. Reynolds, P. C. C. Freire, F. Camilo, Tests of general relativity from timing the double pulsar, Sc. 314 (2006) 97.
Stinebring (2013) D. Stinebring, Effects of the interstellar medium on detection of low-frequency gravitational waves, Class. Q. Grav. 30 (2013) 224006.
Lam et al. (2015) M. Lam, J. Cordes, S. Chatterjee, T. Dolch, Pulsar timing errors from asynchronous multi-frequency sampling of dispersion measure variations, Astrophys J. 801 (2015) 130.
Levin (2015) L. Levin, Interstellar medium mitigation techniques in pulsar timing arrays, J. Phys. Conf. Ser. 610 (2015) 012020.
Palliyaguru et al. (2015) N. Palliyaguru, D. Stinebring, M. McLaughlin, P. Demorest, G. Jones, Correcting for interstellar scattering delay in high-precision pulsar timing: simulation results, Astrophys. J. 815 (2015) 89.
Cutler et al. (2003) C. Cutler, W. A. Hiscock, S. L. Larson, Lisa, binary stars, and the mass of the graviton, Phys. Rev. D 67 (2003) 024015.
Deffayet and Menou (2007) C. Deffayet, K. Menou, Probing gravity with spacetime sirens, Astrophys. J. Lett. 668 (2007) L143.
Kocsis et al. (2008) B. Kocsis, Z. Haiman, K. Menou, Premerger localization of gravitational wave standard sirens with LISA: triggered search for an electromagnetic counterpart, Astrophys. J. 684 (2008) 870.
Nishizawa and Nakamura (2014) A. Nishizawa, T. Nakamura, Measuring speed of gravitational waves by observations of photons and neutrinos from compact binary mergers and supernovae, Phys. Rev. D 90 (2014) 044048.
Branchina and De Domenico (2016) V. Branchina, M. De Domenico, Simultaneous observation of gravitational and electromagnetic waves, 2016. ArXiv:1604.08530 [gr-qc].
Liu et al. (2016) M. Liu, Z. Zhao, X. You, J. Lu, L. Xu, Violation of Einstein’s equivalence principle on gravitational wave event GW150914 associated with GBM transient GW150914-GBM, 2016. ArXiv:1604.06668 [gr-qc].
Wu et al. (2016) X. Wu, H. Gao, J. Wei, X. Fan, P. Mészáros, B. Zhang, Z. Dai, S. Zhang, Z. Zhu, Testing Einstein’s equivalence principle with gravitational waves, Phys. Rev. D 94 (2016) 024061.
Will (2014) C. M. Will, The confrontation between general relativity and experiment, Living Rev. Relativity 17 (2014) 4.
Rajan et al. (2016) R. T. Rajan, A. Boonstra, M. J. Bentum, M. Klein Wolt, F. Belien, M. Arts, N. Saks, A. van der Veen, Space-based aperture array for ultra-long wavelength radio astronomy, Exp. Astron. 41 (2016) 271.
Verhoeven et al. (2011) C. J. M. Verhoeven, M. J. Bentum, G. L. E. Monna, J. Rotteveel, J. Guo, On the origin of satellite swarms, Acta Astronaut. 68 (2011) 1392.
Dekens et al. (2014) E. Dekens, S. Engelen, R. Noomen, A satellite swarm for radio astronomy, Acta Astronaut. 102 (2014) 321.
Budianu et al. (2015) A. Budianu, A. Meijerink, M. J. Bentum, Swarm-to-Earth communication in OLFAR, Acta Astronaut. 107 (2015) 14.
Tartaglia et al. (2011) A. Tartaglia, M. L. Ruggiero, E. Capolongo, A null frame for spacetime positioning by means of pulsating sources, Adv. Sp. Res. 47 (2011) 645.
Rajan et al. (2013) R. T. Rajan, M. J. Bentum, A. J. Boonstra, Synchronization for space based ultra low frequency interferometry, in: IEEE Aerospace Conference, 2013. 2-9 March 2013 Big Sky Montana.
Knappe et al. (2006) S. Knappe, P. D. D. Schwindt, V. Gerginov, V. Shah, L. Liew, J. Moreland, H. G. Robinson, L. Hollberg, J. Kitching, Microfabricated atomic clocks and magnetometers, J. Optics A: Pure Appl. Optics 8 (2006).
Zarka et al. (2016) P. Zarka, M. Tagger, L. Denis, J. N. Girard, A. Konovalenko, M. Atemkeng, M. Arnaud, S. Azarian, M. Barsuglia, A. Bonafede, F. Boone, A. Bosma, R. Boyer, M. Branchesi, C. Briand, B. Cecconi, S. Célestin, D. Charrier, E. Chassande-Mottin, A. Coffre, I. Cognard, F. Combes, S. Corbel, C. Courte, A. Dabbech, S. Daiboo, R. Dallier, C. Dumez-Viou, M. N. El Korso, E. Falgarone, I. Falkovych, A. Ferrari, C. Ferrari, K. Ferrière, C. Fevotte, A. Fialkov, M. Fullekrug, E. Gérard, J. Grießmeier, B. Guiderdoni, L. Guillemot, J. Hessels, L. Koopmans, V. Kondratiev, L. Lamy, T. Lanz, P. Larzabal, M. Lehnert, F. Levrier, A. Loh, G. Macario, J. Maintoux, L. Martin, D. Mary, S. Masson, M. Miville-Deschenes, D. Oberoi, M. Panchenko, M. Pandey-Pommier, A. Petiteau, J. Pinçon, B. Revenu, F. Rible, C. Richard, H. O. Rucker, P. Salomé, B. Semelin, M. Serylak, O. Smirnov, B. Stappers, C. Taffoureau, C. Tasse, G. Theureau, P. Tokarsky, S. Torchinsky, O. Ulyanov, W. van Driel, I. Vasylieva, J. Vaubaillon, F. Vazza, S. Vergani, M. Was, R. Weber, V. Zakharenko, NenuFAR: instrument description and science case, in: Int. Conf. Antenna Theory and Techniques (ICATT) 2015, 2016, p. 8. 21-24 April 2015 Kharkiv.
Lazio (2013) T. J. W. Lazio, The Square Kilometre Array pulsar timing array, Class. Q. Grav. 30 (2013) 224011.
Salzano et al. (2016) V. Salzano, M. P. Dabrowski, R. Lazkoz, Probing the constancy of the speed of light with future galaxy survey: the case of SKA, Euclid, and WFIRST-2.4, Phys. Rev. D 93 (2016) 063521.
Lounis et al. (1993) B. Lounis, J. Reichel, C. Salomon, Laser cooling of atoms in micro-gravity, Comptes Rendus Acad. Sc. Paris II 316 (1993) 739.
European Space Agency (1994) (ESA) European Space Agency (ESA), Time & Frequency science utilization and Space Station study, Technical Report Contract 11287/94/NL/VK, CERGA Grasse, DLR, ENS Paris, Un. Dresden, Un. München, Un. Stuttgart, Un. Tübingen, Prime contractor: DASA-RI, 1994. C. Salomon, C. Veillet and A. Spallicci, ESA Study scientist, conceived the Atomic Clock Ensemble in Space (ACES) in this study.
Altschul et al. (2015) B. Altschul, Q. G. Bailey, L. Blanchet, K. Bongs, P. Bouyer, L. Cacciapuoti, S. Capozziello, N. Gaaloul, D. Giulini, J. Hartwig, L. Iess, P. Jetzer, A. Landragin, E. Rasel, S. Reynaud, S. Schiller, C. Schubert, F. Sorrentino, U. Sterr, J. D. Tasson, G. M. Tino, P. Tuckey, P. Wolf, Quantum tests of the Einstein equivalence principle with the STE-QUEST space mission, Adv. Sp. Res. 55 (2015) 501.
Decher et al. (1980) R. Decher, J. L. Randall, P. L. Bender, J.-E. Faller, Design aspects of a laser gravitational wave detector in space, in: W. Cuneo Jr. (Ed.), Proc. SPIE on Active optical devices and applications, volume 228, Society of Photo-Optical Instrumentation Engineers, Bellingham, 1980, p. 149. 10-11 April 1980 Washington.
Bertotti (1984) B. Bertotti, Future of laser interferometry in space, in: B. Battrick, E. Rolfe (Eds.), SPLAT: Space and Laser Applications and Technology, volume ESA SP-202, ESA, Noordwijk, 1984, p. 147. 25-30 March 1984 Les Diablerets.
Bonetti et al. (2016) L. Bonetti, L. R. dos Santos Filho, J. A. Helayël-Neto, A. D. A. M. Spallicci, Massive photons from Super and Lorentz symmetry breaking, 2016. ArXiv:1607.08786 [hep-ph].
Shamir and Fox (1967) J. Shamir, R. Fox, Is the cosmological red-shift an aging of photons?, N. Cim. B 50 (1967) 371.
Bonnor (1999) W. B. Bonnor, Size of a hydrogen atom in the expanding universe, Class. Q. Grav. 16 (1999) 1313.
Dumin (2012) Y. V. Dumin, A new application of the Lunar Laser Retroreflectors: searching for the ’local’ Hubble expansion, Adv. Space Res. 31 (2012) 2461.
Price and Romano (2012) R. H. Price, J. D. Romano, In an expanding universe, what doesn’t expand?, Am. J. Phys. 80 (2012).
Kopeikin (2015) S. M. Kopeikin, Optical cavity resonator in an expanding universe, Gen. Rel. Grav. 47 (2015) 5.
Bekefi (1966) G. Bekefi, Radiation processes, John Wiley & Sons, New York, 1966.
Melrose (1980) D. B. Melrose, Plasma astrophysics. Nonthermal processes in diffuse magnetized plasmas. Vol. 1: the emission, absorption and transfer of waves in plasmas, Gordon and Breach, Science Publishers, New York, 1980.
Nicholson (1983) D. R. Nicholson, Introduction to plasma theory, John Wiley & Sons, New York, 1983.
Bastian (2005) T. S. Bastian, Notes on electromagnetic waves in a plasma, Technical Report, National Radio Astronomy Observatory, 2005. http://hesperia.gsfc.nasa.gov/summerschool/lectures/bastian/Notes_on_Waves.pdf.
Ginzburg (1961) V. L. Ginzburg, Propagation of electromagnetic waves in plasma, Gordon and Breach, New York, 1961.
Wolf and Foley (1989) E. Wolf, J. T. Foley, Scattering of electromagnetic fields of any state of coherence from space-time fluctuations, Phys. Rev. A 40 (1989) 579.
Foley and Wolf (1989) J. T. Foley, E. Wolf, Frequency shifts of spectral lines generated by scattering from space-time fluctuations, Phys. Rev. A 40 (1989) 588.
Laio et al. (1997) A. Laio, G. Rizzi, A. Tartaglia, Quantum theory of frequency shifts of an electromagnetic wave interacting with a plasma, Phys. Rev. E 55 (1997) 747.