Dissecting nucleon transition electromagnetic form factors

The same picture has also been employed in the description of nucleon-to-resonance transition form factors, where the final state is either the $\Delta$-baryon [$\Delta(1232)(3/2)^{+}$] or Roper resonance [$N(1440)(1/2)^{+}$] Eichmann:2011aa ; Segovia:2013rca ; Segovia:2014aza ; Segovia:2015hra . This suggests the absence of environment sensitivity for DCSB in the nucleon, $\Delta$ and Roper, i.e. DCSB in these systems is expressed in ways that can readily be predicted once its manifestation is understood in the pion, and this includes the generation of diquark correlations with the same character in each of these baryons Roberts:2016dnb . In order to aid the empirical validation of these ideas, herein we follow Refs. Segovia:2014aza ; Segovia:2015hra and present a comprehensive analysis of the transition form factors via their separation into contributions from different correlation sectors and subsequently, where appropriate, a flavour separation for each of these.

Electromagnetically induced $N\to\Delta$, $N\to R$ transitions proceed via the current introduced in Ref. Oettel:1999gc and refined in Ref. Segovia:2014aza (see Appendix C therein). In two separate ways, this current can be considered as a sum of three distinct terms, viz.

T1 = diquark dissection

T1A – scalar diquark in both the initial- and final-state baryon, T1B – pseudovector diquark in both the initial- and final-state baryon, and T1C – a different diquark in the initial- and final-state baryon; and

T2 = scatterer dissection

T2A – photon strikes a bystander dressed-quark, T2B – photon interacts with a diquark, elastically or causing a transition scalar $\leftrightarrow$ pseudovector, and T2C – photon strikes a dressed-quark in-flight, as one diquark breaks up and another is formed, or appears in one of the two associated “seagull” terms.

The anatomy of a given transition process is revealed by combining the information provided by the T1 and T2 dissections.

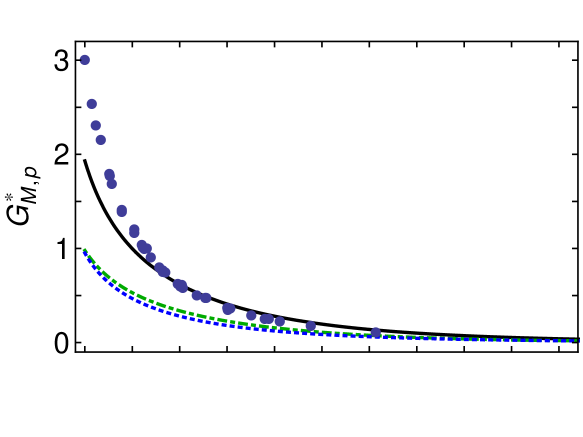
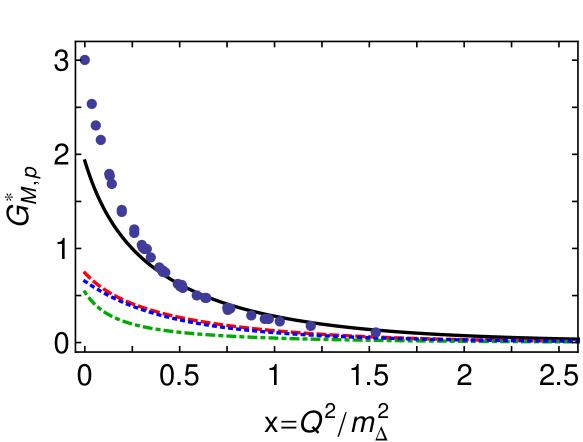
The anatomy of $G_{M}^{\ast}$ is revealed in Fig. 1. The upper panel shows that T1B and T1C diagrams contribute equally, but, since the scalar diquark, $[ud]$, is a larger part of the nucleon’s Faddeev amplitude, this means that contributions with a pseudovector diquark, $\{qq\}$, in both $p$ and $\Delta^{+}$ contribute more strongly to the transition. The lower panel shows that the dominant contributions are those in which the photon strikes a dressed-quark. Hence, the magnetic component of the transition proceeds predominantly via spin-flip of an uncorrelated quark, T2C for $[ud]$ in the proton and T2A for $\{qq\}$, with slightly greater transition strength in the latter configuration.

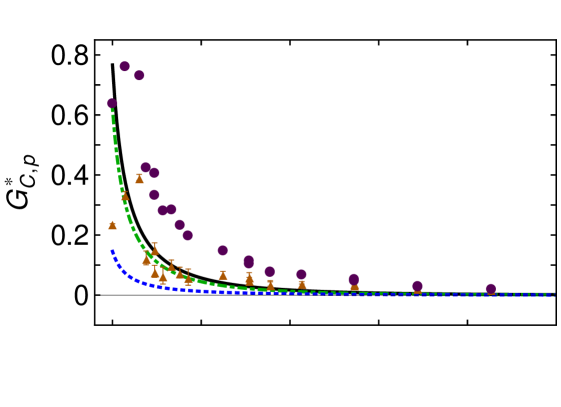
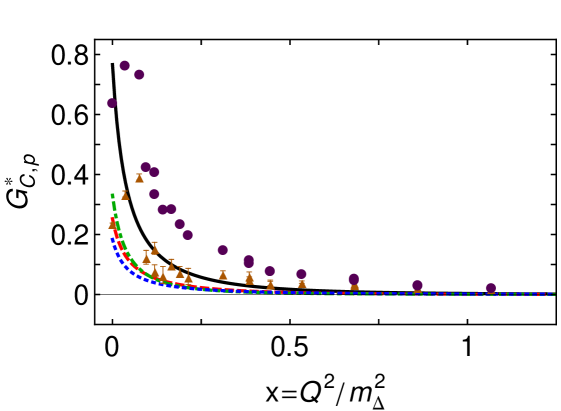
The electric quadrupole transition form factor, $G_{E}^{\ast}$, is dissected in Fig. 2. The upper panel shows that this component of the transition is dominated by diagrams involving a scalar diquark in the proton and a pseudovector diquark in the $\Delta^{+}$ (T1C); and the lower panel indicates that photon-diquark interactions control the transition away from $x_{\Delta}\simeq 0$. It follows that, within the dressed-quark core, the electric quadrupole transition proceeds primarily by a photon transforming the $0^{+}$-diquark into a $1^{+}$-diquark ($\delta J=1$) with the overlap of what may be said to be quark-diquark components in the rest-frame Faddeev wave functions of the proton and $\Delta^{+}$ that differ by one unit of angular momentum.

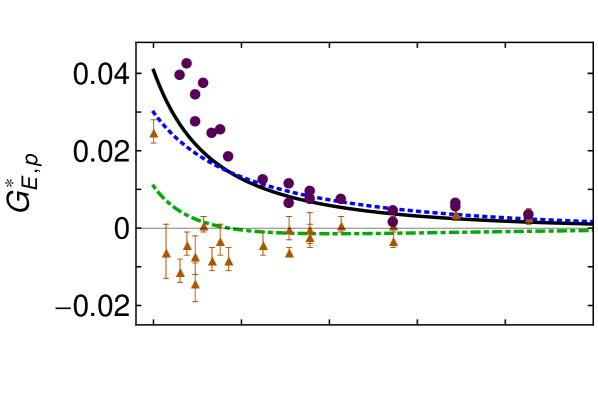
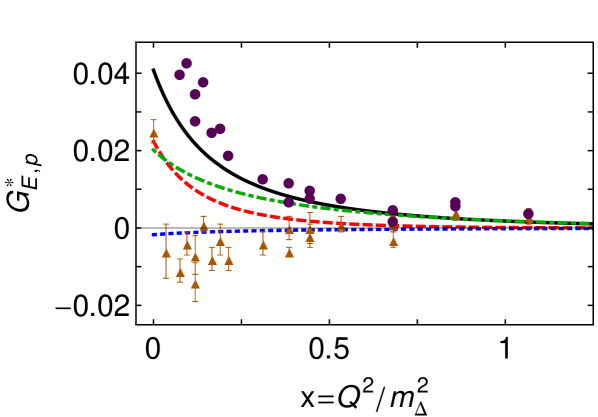
Whilst not apparent in Fig. 2, $G_{E}^{\ast}$ possesses a zero at $x_{\Delta}\approx 3$ (see Fig. 11 in Ref. Segovia:2014aza ). Its origin lies in the existence of a zero at $x_{\Delta}\approx 3$ in the (T1C) $[ud]\to\{ud\}$ diquark transition contribution. However, its position is also influenced by the size of the dressed-quark anomalous magnetic moment ($\kappa_{Q}$) Singh:1985sg ; Bicudo:1998qb ; Kochelev:1996pv ; Chang:2010hb , shifting to larger values of $x_{\Delta}$ as this moment increases. Our analysis reveals the cause, viz. greater values of $\kappa_{Q}$ increase the domain of positive support for the T2A contribution, and this pushes the zero to larger values of $x_{\Delta}$. The impact of $\kappa_{Q}$ is also a signal that meson-cloud effects are important to the behaviour of $G_{E}^{\ast}$ because they act, inter alia, to increase the magnitude of $\kappa_{Q}$ Horikawa:2005dh ; Cloet:2012cy ; Cloet:2014rja .

It is worth recalling here that helicity conservation at large momentum scales requires $R_{\rm EM}(x_{\Delta})=-G_{E}^{\ast}/G_{M}^{\ast}\to 1$ as $x_{\Delta}\to\infty$ Carlson:1985mm ; Segovia:2013rca , so $G_{E}^{\ast}$ must exhibit a zero once the dressed-quark core becomes the dominant contribution. Apparently, however, this is not the case on the measured domain, within which many factors compete in producing $G_{E}^{\ast}$. The analysis in Ref. Segovia:2014aza suggests that the zero occurs on $x_{\Delta}\gtrsim 6$.

Figure 2 also compares our calculation with the dynamical coupled-channels (DCC) analysis of $G_{E}^{\ast}$ in Ref. JuliaDiaz:2006xt . In contrast to $G_{M}^{\ast}$ in Fig. 1, here the DCC-inferred bare contribution (triangles) is zero, within errors, and hence differs markedly from our prediction for the dressed-quark core contribution. Instead, the complete DCC result (circles) is aligned with our curve. Given that Poincaré-covariance entails the presence of rest-frame quark-diquark orbital angular momentum in bound-state Faddeev amplitudes, we judge that our result is the better estimate of the dressed-quark core contribution in this case, with the analysis in Ref. JuliaDiaz:2006xt failing here owing to the very small size of $G_{E}^{\ast}$ on the measured domain.

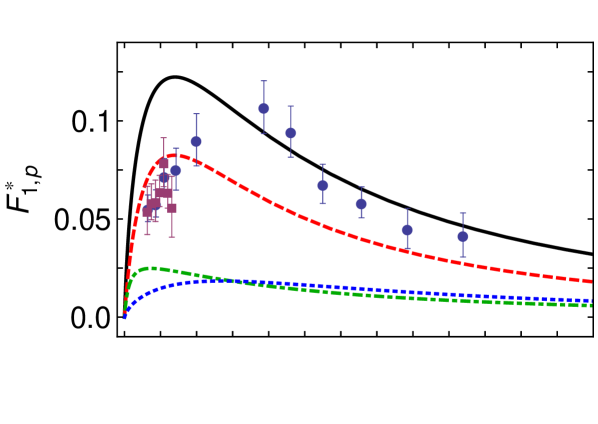
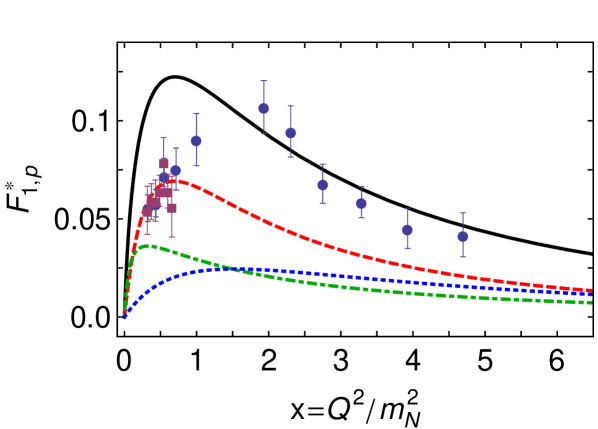
The anatomy of $G_{C}^{\ast}$ is revealed in Fig. 3. The upper panel indicates that T1B contributions dominate, i.e. transition processes with a pseudovector diquark in both the proton and $\Delta^{+}$. The lower panel shows that photon-diquark interactions control the transition at small $x_{\Delta}$, but photon-quark scattering dominates on $x_{\Delta}\gtrsim 1/8$. Regarding the dressed-quark core, these observations suggest that on $x_{\Delta}\simeq 0$ this $C2$ transition is influenced a little by the strength of the pseudovector diquark’s own quadrupole moment, but otherwise it is a measure of an overlap between what may be called $S$- and $D$-wave quark-diquark angular momentum components in the rest-frame proton and $\Delta^{+}$ Faddeev wave functions.

It is worth remarking that $G_{C}^{\ast}$ is an order-of-magnitude larger than $G_{E}^{\ast}$; and in this case, as with $G_{M}^{\ast}$, the DCC-inferred bare contribution to $G_{C}^{\ast}$, computed in Ref. JuliaDiaz:2006xt and depicted in Fig. 3, agrees well with our prediction for the dressed-quark core component.

The anatomy of the $\gamma\,p\to R^{+}$ Dirac transition form factor is revealed in Fig. 4. Plainly, this component of the transition proceeds primarily through a photon striking a bystander dressed quark that is partnered by $[ud]$, with lesser but non-negligible contributions from all other processes. In exhibiting these features, $F_{1,p}^{\ast}$ shows marked qualitative similarities to the proton’s elastic Dirac form factor (cf.  Fig. 3 in Ref. Cloet:2008re ).

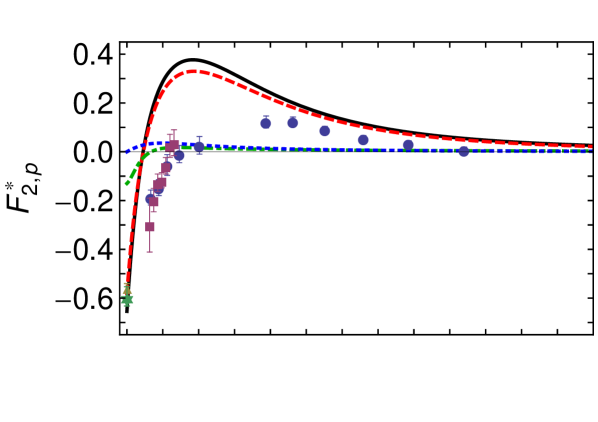
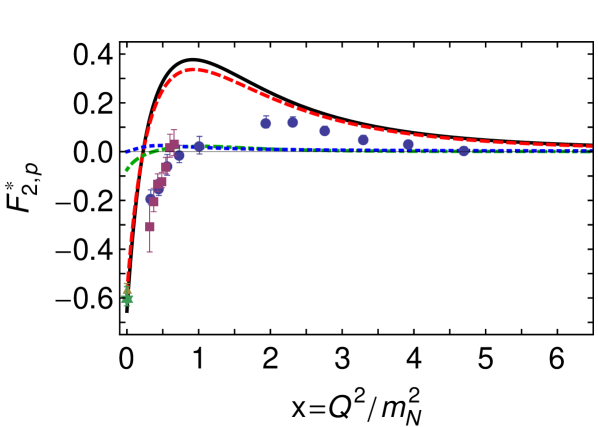
The $\gamma\,p\to R^{+}$ Pauli transition form factor is dissected in Fig. 5. In this case, a single contribution is overwhelmingly important, viz. photon strikes a bystander dressed-quark in association with $[ud]$ in the proton and $R^{+}$. No other diagram makes a significant contribution. A comparison with Fig. 4 in Ref. Cloet:2008re reveals that the same may be said for the dressed-quark core component of the proton’s elastic Pauli form factor.

In hindsight, given that the diquark content of the proton and $R^{+}$ are almost identical, with the $\psi_{0}\sim u[ud]$ component contributing roughly 60% of the charge of both systems, the qualitative similarity between the proton elastic and proton-Roper transition form factors is not surprising. This observation immediately raises the issue of whether and how that similarity is transmitted into the flavour separated form factors.

If one supposes that $s$-quark contributions to the nucleon-Roper transitions are negligible, as is the case for nucleon elastic form factors, and assumes isospin symmetry, then a flavour separation of the transition form factors is accomplished by combining results for the $\gamma\,p\to\,R^{+}$ and $\gamma\,n\to R^{0}$ transitions:

where $p$ and $n$ are superscripts that indicate, respectively, the charged and neutral nucleon-Roper reactions. Our conventions are that $F_{1(2),u}^{\ast}$ and $F_{1(2),d}^{\ast}$ refer to the $u$- and $d$-quark contributions to the equivalent Dirac (Pauli) form factors of the $\gamma p\to R^{+}$ reaction, and the results are normalised such that the elastic Dirac form factors of the proton and charged-Roper yield $F_{1u}(Q^{2}=0)=2$, $F_{1d}(Q^{2}=0)=1$, thereby ensuring that these functions count $u$- and $d$-quark content in the bound-states.

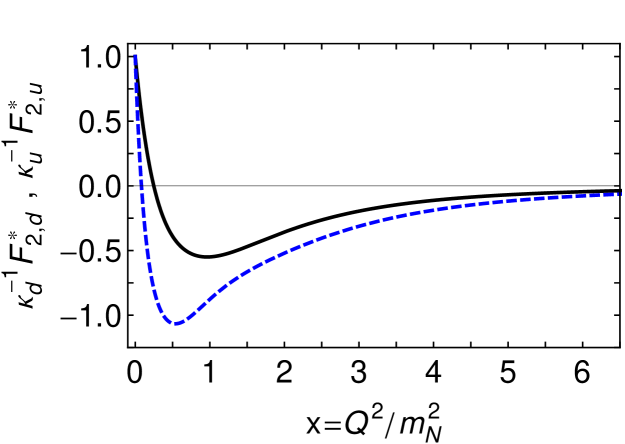
We computed the $\gamma\,n\to R^{0}$ transition form factors, using the framework in Ref. Segovia:2015hra , and employed Eqs. (1) to determine the flavour separation of the nucleon-Roper transition. The results are depicted in Figs. 6, 7.

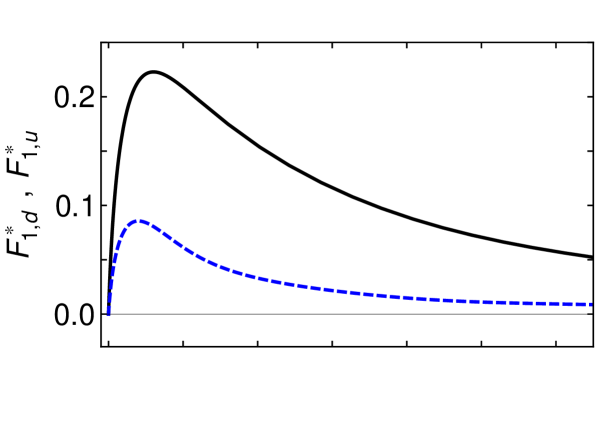
The upper panels of Figs. 6, 7, depicting the flavour-separated Dirac transition form factor, show an obvious similarity to the analogous form factor determined in elastic scattering: the $d$-quark contribution is less-than half the $u$-quark contribution for momenta sufficiently far outside the neighbourhood of $x_{N}=0$ within which they both vanish; and the $d$-quark contribution falls more rapidly after their almost coincident maxima. The noticeable difference, however, is the absence of a zero in $F_{1,d}^{\ast}$, which is a salient feature of the analogous proton elastic form factor.

The lower panels of Figs. 6, 7 depict the flavour-separated Pauli transition form factor. In this instance the similarities are less obvious, but they are revealed once one recognises that the rescaling factors satisfy $|\kappa_{d}^{\ast}/\kappa_{u}^{\ast}|<\tfrac{1}{6}$ cf. a value of $\sim\tfrac{2}{5}$ in the elastic case Cloet:2008re . Accounting for this, the behaviour of the $u$- and $d$-quark contributions to the charged-Roper Pauli transition form factor are comparable with the kindred contributions to the elastic form factor, especially insofar as the $d$-quark contribution falls dramatically on $x\gtrsim 4$ whereas the $u$-quark contribution evolves more slowly.

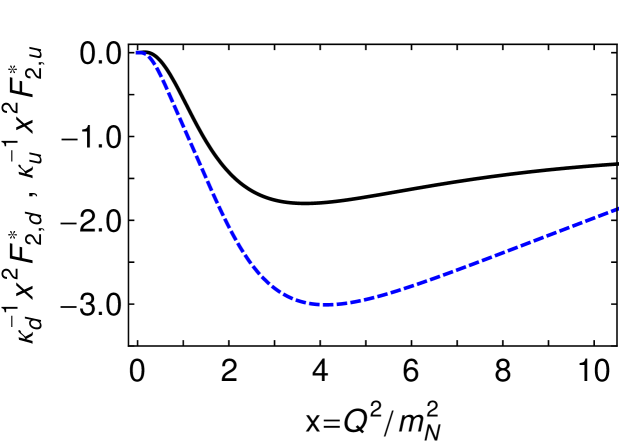
An explanation for the pattern of behaviour in Figs. 6, 7 is much the same as that for the analogous proton elastic form factors Segovia:2015ufa because the diquark content of the proton and its first radial excitation are almost identical. In both systems, the dominant piece of the associated Faddeev wave functions is $\psi_{0}$, namely a $u$-quark in tandem with a $[ud]$ (scalar diquark) correlation, which produces 62% of each bound-state’s normalisation Segovia:2015hra . If $\psi_{0}$ were the sole component in both the proton and charged-Roper, then $\gamma$–$d$-quark interactions would receive a $1/x_{N}$ suppression on $x_{N}>1$, because the $d$-quark is sequestered in a soft correlation, whereas a spectator $u$-quark is always available to participate in a hard interaction. At large $x_{N}$, therefore, scalar diquark dominance leads one to expect $F^{\ast}_{d}\sim F^{\ast}_{u}/x_{N}$. Naturally, precise details of this $x_{N}$-dependence are influenced by the presence of pseudovector diquark correlations in the initial and final states, which guarantees that the singly-represented quark, too, can participate in a hard scattering event, but to a lesser extent.

The infrared behaviour of the flavour-separated $\gamma p\to R^{+}$ transition form factors owes to a complicated interference between the influences of orthogonality, which forces $F^{\ast}_{1,u}(x_{N}=0)=0=F^{\ast}_{1,d}(0)$, and quark-core and MB FSI contributions. However, whilst the latter pair act in similar ways for both elastic and transition form factors, orthogonality is a fundamental difference between the two processes and it is therefore likely to be the dominant effect at infrared momenta.

The information contained in Figs. 4 – 7 provides clear evidence in support of the notion that many features in the measured behaviour of $\gamma N\to R$ electromagnetic transition form factors are primarily driven by the presence of strong diquark correlations in the nucleon and its first radial excitation. In our view, inclusion of a “meson cloud” cannot qualitatively affect the salient features of these transition form factors, any more than it does the analogous nucleon elastic form factors Cloet:2012cy ; Cloet:2014rja .