Distinguishing features of longitudinal magnetoconductivity for a Rarita-Schwinger-Weyl node
Abstract
The band-degeneracy points in the Brillouin zones of chiral crystals exist in multiple avatars, with the high-symmetry points being able to host multifold nodes of distinct characters. A class of such crystals, assisted by the spin-orbit coupling, harbours fourfold degeneracy in the form of Rarita-Schwinger-Weyl node (RSWN) at the -point. Our aim is to explore the nature of longitudinal magnetoconductivity, arising from applying collinear electric and magnetic fields, for such systems. Adjusting the chemical potential to lie near the intrinsic energy-location of the RSWN, the multifold nature of the RSWN is revealed by an interplay of intraband and interband scatterings, which would not arise in twofold degeneracies like the conventional Weyl nodes. The current study fills up the much-needed gap in obtaining the linear response from an exact computation, rather than the insufficient relaxation-time approximation employed earlier.
I Introduction
The unprecedented advancement on the experimental fronts, coupled with the DFT studies of materials, have put forward numerous generalisations of the archetypal Weyl semimetal (WSM) of the three-dimensional (3d) variety[1, 2, 3]. The excitement surrounding these so-called semimetallic systems mainly stems form the fact that their Brillouin zones (BZs) harbour nodal points, which, in turn, furnish the momentum space with the mathematical properties of topology [4, 5, 6, 7], when viewed as closed manifolds. Physical properties like the Berry curvature (BC) and the orbital magnetic moment (OMM) quantify the topological properties lurking beneath, which are detectable in transport experiments [8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]. Generalising the simplest prototype of an isotropic and linear-in-momentum twofold band-crossing, a pseudospin-3/2 Rarita-Schwinger-Weyl node (RWSN) [19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30] represents a fourfold band-crossing at a high-symmetry point of the BZ of a chiral crystal [19, 31, 32]. Adding to the cornucopia of transport properties that can reflect the exquisite character of RSWNs [28, 26, 29, 30, 33, 15, 34], we investigate here the longitudinal magnetoconductivity arising from an isolated node [35].
The perks of invoking the analogy of the BC (existing in the momentum space) to a magnetic field (existing in the momentum space) is that we conjure up the intuitive picture of nonzero BC monopoles sitting at the nodal points [36, 37], acting as the sources and sinks of the vector field of the BC-flux. Utilising the mathematical machinery of algebraic topology, the monopoles’ charges also represent the so-called Chern numbers about the nodal points. The sign of is pictured as the chirality () of the node, conferring a notion of handedness or chirality on the quasiparticles populating the bands converging there. Appropriately, they are termed as right-handed or left-handed quasipartcles, depending on whether or .
The appearance of chirally-charged nodes in 3d crystal-lattices is governed by the Nielsen-Ninomiya theorem [38], which is physically reflected by the fact that the sum of the Chern numbers over the entire BZ must yield zero. For nodes arising in achiral crystals (e.g., TaAs family [39]), such conjugate partners are typically (almost) degenerate in energy, due to the presence of mirror or other roto-inversion symmetries. Therein, charge-pumping is an important internode phenomenon in the presence of collinear external electric () and magnetic () fields. The phenomenon in question is an embodiment of the chiral anomaly in the arena of condensed matter physics [40, 41, 14, 34], where the analog of the well-known concept of spacetime chirality (of relativistic fermions) is realised in the momentum space. It provides a sharp contrast with the oppositely-charged chiral nodes in chiral crystals, where they need not be degenerate in energy, because the conjugate nodes are not related by crystal symmetries. In fact, they are observed to have discernible separations in energy and momenta, with a isolated nodes sitting at their intrinsic chemical potentials [42, 31, 43]. The inevitable outcome is that the internode-scattering induced charge pumping gets irrelevant. However, at the same time, the energy-offset between the nodes of opposite chiralities fulfills the requisite conditions for observing other important phenomena like quantised circular photogalvanic effect [19, 31, 44, 45, 46, 47, 48] and circular dichroism [26, 49].
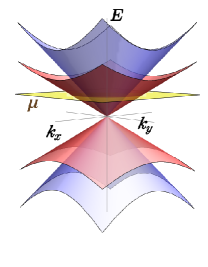
In our recent works, we have addressed the pertinent problem of computing longitudinal magnetoconductivity in systems where multiple bands contribute to transport at a particular node, encompassing the cases of chirally-conjugate nodes [17] and isolated Kramers-Weyl nodes [35] (the latter arising exclusively in chiral crystals [50, 51]). In this paper, we take up a similar problem where an isotropic RSWN (sitting at the -point) is the system under consideration. As pointed out earlier, only the isolated RWSN will be relevant here for computing the linear response, since we will consider tuning the external chemical potential to lie near the intrinsic energy of the concerned nodal point, safely assuming that the chirally-conjugate node is sufficiently separated in energy and momenta. For example, in RhSi, there exist fourfold- and sixfold-degenrate nodes at the - and -points of the BZ, carrying Chern numbers of , and featuring the largest possible momentum-separation between the nodal-points’ locations [52, 43]. While the former represents an RSWN, the bands at the latter are doubly-degenerate, featuring a pair of pseudospin-1 triple-point fermions (TPFs). The energy-offset between these nodes is eV. All these make it possible to observe really long Fermi arcs, spanning the distance constrained by the separation of the multiply-degenerate bulk-nodes, and topologically protected by their bulk chiral charges. Other examples of chiral crystals include AlPt [53], RhGe (with the energy-separatation between RSWN and the TPFs being eV) [54], sanchez [52] Li2Pd3B [55], Li2Pt3B [55], and CoSi [52, 24].
A typical RSWN is depicted schematically in Fig. 1, with the four bands visualised near the degeneracy point. Exploiting the universal applicability of the Boltzmann equations as the kinetic theory for transport [56, 57], we will carry out the exercise of computing the longitudinal conductivity exactly, arising from applying collinear electromagnetic fields (). The framework will be limited to the realm of weak (implying nonquantising) magnetic fields, so that the splitting of the dispersion into discrete Landau-levels can be ignored. Improving on our earlier ventures along similar lines [33, 34], we will go beyond the relaxation-time approximation, thereby solving the semimeclassical Boltzmann equations exactly. To elaborate on the context further, we would like to point out that the nature of in-plane and out-of-plane components of conductivity in planar-Hall set-ups have been derived in Refs. [33, 34], within the simplifying framework of the relaxation-time approximation, considered the aspects of intranode [33] and internode [34] scatterings. The current calculations will help us fix the shortcomings arising from the assumption of a momentum-independent relaxation-time.
The paper is organised as follows: In Sec. II, we describe the explicit form of the low-energy effective Hamiltonian in the vicinity of an RSWN node, and the emerging topological properties. Sec. III is devoted to deriving the equations leading to the final values of the longitudinal magnetoconductivity. The results are discussed in Sec. III.3 therein, illustrated by representative plots. Finally, we end with a summary and some future perspectives in Sec. IV. In all our expressions, we will adopt the natural units, which involves setting the reduced Planck’s constant (), the speed of light (), and the Boltzmann constant () to unity. Additionally, the electric charge has no units. Despite the fact that the magnitude () of a single unit of electrons’ charge is unity, we will retain it in our expressions solely for the purpose of book-keeping.
II Model
The widely used method of linearising the Hamiltonian about a fourfold degeneracy at the -point of a chiral crystal leads us to the generic forms of the RWSN nodes [43, 58]. Adopting the isotropic version for the sake of simplicity, we use the model Hamiltonian captured by
| (1) |
where represents the vector operator whose three components comprise the the angular momentum operators in the spin- representation of the SU(2) group. We choose the commonly-used representation with
| (2) |
The energy eigenvalues are found to be
| (3) |
where . Thus, each of the four bands demonstrates an isotropic linear-in-momentum dispersion like a Weyl cone [cf. Fig. 1(a)]. The signs of “” and “” give us the dispersion relations for the conduction and valence bands, respectively, with respect to the nodal point. The corresponding group velocities of the quasiparticles are given by
| (4) |
The isotropy of indicates that the required calculations can be simplified by adopting the spherical-polar coordinates. Hence, we will be the employing the transformations involving
| (5) |
where , , and .
II.1 Eigenvectors
For an orthonormal set of eigenvectors, , the explicit forms of the positive-energy bands are given by
| (6) |
This will be used to determine the strength of the scattering cross-sections and, also, an ansatz for the nonequilibirum quasiparticle-distributions.
II.2 Topological quantities
Due to a nontrivial topology of the bandstructure, we need to compute the BC and the OMM, using the starting expressions of [5, 59]
| (7) |
respectively. Evaluating these expressions for the RSW node described by , we get [60, 33]
| (8) |
Since and are the intrinsic properties of the bandstructure, they depend only on the wavefunctions.
A nonzero BC manifests itself primarily via modifying the phase-space volume element, incorporated through the factor of [56, 6, 61, 57, 33, 15]
| (9) |
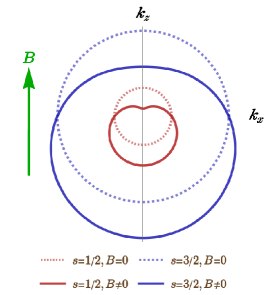
This, in turn, it affects the explicit forms of the Hamilton’s equations, which we will discuss In Sec. III. On the other hand, the OMM distorts the Fermi surfaces along the direction of , by adding the term
| (10) |
as schematically depicted in Fig. 1(b). Consequently, in addition to affecting the Fermi-Dirac distributions functions, it causes modifications of the group-velocities via adding
| (11) |
to .
III Conductivity
In this section, we will review the step-by-step procedure to compute the electric conductivity, applying the machinery of semiclassical Boltzmann equations [56, 6, 61, 57, 33, 15, 12, 17]. Although this has been demonstrated multiple times in our earlier works [17, 35], it is primarily needed here to set the notations. The main line of arguments for obtaining the final equations was developed in Ref. [12], which we adapt and generalise for our system under study. For the sake of simplicity, we will perform our calculations by setting , and an application of a positive chemical potential, , to the node. Consequently, the bands with and will contribute to transport.
III.1 Kinetic equations driven by electromagnetic fields
In thermal equilibrium, the distribution of the quasiparticles follows the Fermi-Dirac distribution,
| (12) |
where is the temperature and is the effective energy (containing the OMM contribution). The quantity will appear in the equations that follow, where we will suppress showing its - and -dependence explicitly, just for the sake of uncluttering of notations. We note that, as , , which serves to reduce the momentum-space integrals over a Fermi pocket to the respective Fermi surface.
The Hamilton’s equations of motion for the quasiparticles, occupying a given Bloch band, are described by [56, 6, 61, 57, 33, 15]
| (13) |
where
| (14) |
The presence of various terms involving the BC and the OMM reflect the nontrivial role played by the topological properties, as compared to systems where such topology does not exist. For comparison, one can look at the structure of the phase-space equations in Refs. [62, 63], for example. We notice that the term appearing as represents an anomalous velocity, with the BC (existing in the momentum space) playing the counterpart of the magnetic field (existing in the real space).
The semiclassical Boltzmann’s transport formalism is implemented by starting with the basic kinetic equations, embodied by
| (15) |
The function represents the nonequilibrium quasipaticle-distribution for the fermions populating band , caused by a small deviation from , as soon as probe fields (like electric field, temperature gradient [11, 33, 16], or chemical potential gradient [15]) are applied externally. On the right-hand side of Eq. (15), we have the collision integral, . Obviously, its role is to account for the appropriate scattering processes relaxing towards the equilibrium value of . As seen from the equation itself, the probe field here is just an electric field (), and the deviation, , is assumed to be of the same order of smallness (say, ) as . Since we restrict ourselves to spatially-uniform and time-independent electromagnetic fields, must must also be independent of position and time, so that . Observing that , we expand the terms on both sides upto a given order in . When we are interested in the linear response, we just retain the leading-order corrections, meaning terms which are linear-in-.
In this paper, we will be focussing on the simple case of elastic point-scattering mechanisms, for which the collision integral takes the form of
| (16) |
is the compact symbol for indicating a 3d momentum-space integral. Needless to say, it includes the modified phase-space factor caused by a nonzero BC. The scatterings being elastic, they do not involve any dissipation of energy. Using the Fermi’s golden rule, they can be expressed as
| (17) |
where, denotes the impurity-concentration, stands for the system’s spatial volume, and represents the matrix-elements of the effective scattering-potential. The consideration of elastic and spinless scattering-centres reduces the potential to an identity matrix in the spinor space, i.e., . Thus, we can now use the version of
| (18) |
which can be easily computed by using the spinorial forms shown in Eq. (II.1). Assuming a reciprocal interband-scattering function between the and bands, we set . For this system, altogether we need three parameters for the scattering strengths, leading to
| (19) |
We have added the self-explanatory subscripts, “intra” and “inter”, to clearly indicate the intraband- and interband-parts, respectively.
III.2 Linearised Boltzmann equation and its solutions
Gathering all the ingredients of the preceding subsections, we are now ready to solve the linearised Boltzmann equation, embodied by
| (20) |
Specifically, we choose the collinear electromagnetic fields to act along the -axis, such that and . To proceed further, we rewrite the deviation in the particles’ distribution-functions as
| (21) |
where is the vectorial mean-free path. Because of our specific choice of coordinates, only the -component of [i.e., ] emerges as the nontrivial component as a result of the probe electric field. Consequently, the only equation that needs to be solved turns out to be
| (22) |
Looking at the structure of the terms on both the sides, we infer that at an energy , which is independent of . The fact that can depend only and follows from the constraints imposed by the delta functions, reducing an integral over the full momentum space to one over the Fermi-surface contour with energy-profile . Essentially, the dependence on the azimuthal angle drops out because of the residual rotational symmetry of the system about the -axis. The equations of the Fermi surfaces are derived by solving , with the -dependent radii of parametrising the local Fermi momenta. Overall, the justification of assuming the -independent forms of is evident from the self-consistency — is -independent and reduces to zero.
Making use of the above arguments, we can now compute the spinor overlaps, , with the help of Eq. (II.1). Knowing that the dependence of the azimuthal angles, and , will disappear once we perform the azimuthal-angle integrations, we list the overlap-functions as
| (23) |
Here, the answer contains the results obtained after already performing the trivial -integrals. We are now ready to solve Eq. (22), starting from its simplified version of
| (24) |
where
| (25) |
Incorporating the energy-conservation restrictions, which reduce the integrals to the respective Fermi surfaces at energy , we simply it even further to
| (26) |
We note that the factor arises as the Jacobian for switching to the spherical polar coordinates. Tackling the factors of , arising from Eq. (18), needs re-expressing them in the language of , which sources the appearance of the other multiplicative factor of
As a final step, observing the powers of in (III.2)], we set forth an ansatz of
| (27) |
In total we have 8 undetermined coefficients so determine, denoted as the set . We have 8 linear equations at our disposal, extracted from Eq. (26) by equating the coefficients of , , , and on both the sides for each value of . This system of linear equations can be expressed compactly as a matrix equation, captured by
| (28) |
The explicit forms of the square and row matrices, and , are demonstrated in the appendix. Now there is a catch —- the eight equations represented above are not linearly independent. This is because ’s rank is lower than 8. It is actually well and good since it prevents from the system from becoming overdetermined, as we must also employ the constraint of the electron-number conservation, embodied by
| (29) |
Plugging in the solutions obtained, the charge-current density along the -direction is computed as
| (30) |
finally leading to the desired longitudinal magnetoconductivity,
| (31) |
III.3 Results and discussions
The solutions of Eq. (26) are obtained numerically for a given set of parameter-values. In our illustrations, we resort to plotting
where the residual conductivity at (i.e., the Drude part) is subtracted off. The parameter values have been taken from Ref. [58]. There, eV Å, which translates into
where is the speed of light. Therefore, in natural units, we set the value of to .
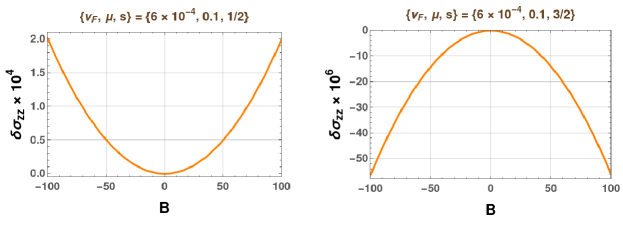
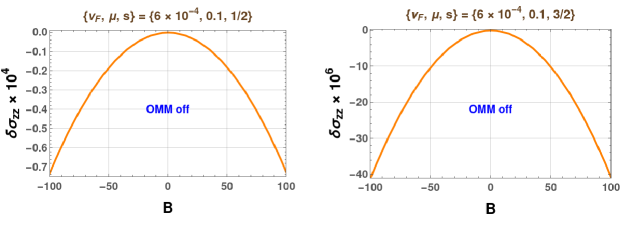
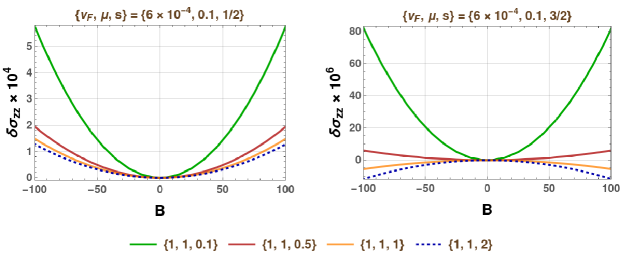
To start with, we attempt to make sense of the response-characteristics for the scenarios when there is no interband scattering, i.e., is set to zero. This leads to the reduction of into the direct sum of the two matrices, and , each of them being a matrix. In every case, we find that they have rank (instead of ), with providing the necessary extra equation. Fig. 2 captures such a scenario. Curiously, the parabolic-shaped response-profiles curve in opposite ways for and . In order to gauge the nature of the OMM-contributions, the lower panel represent the behaviour bbtained by switching off the OMM. It leads to the conclusion that (I) the OMM-parts come with a positive sign and are strong enough to flip the BC-only response into the positive domain for ; (II) the OMM-contributions have a negative sign which assist in increasing the magnitude of the already negative-valued response (from the BC-only parts) for .
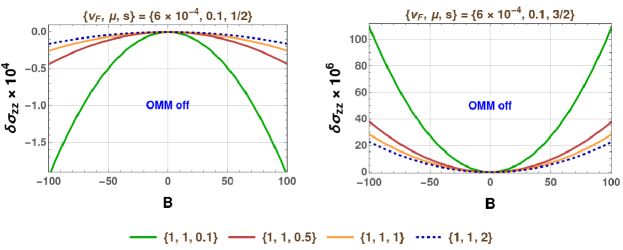
Next, we consider the generic situations when the quasiparticles populating both the bands can scatter with each other. The matrix is found to have rank , ensuring the internal consistency of the available equations. As discussed earlier, this means that the charge-conservation provides the remaining linearly independent equation [viz., Eq. (29)]. Fig. 3 provides some representative curves. From the data presented here, as well as our scans of the parameter space (not shown here), we find that for greater than some small threshold value, the curves for are turned upside down (into the negative domain), while the continuing to curve upwards (remaining positive). To probe into the role of the OMM-sourced parts, we plot the nature of the curves by switching off the OMM (lower panel of Fig. 3). Intriguingly, the curves for and behave in an opposite nature, the former always remaining negatve and curving downward, irrespective of the values of . Overall, comparing the upper and the lower panels, we conclude that, while the OMM-parts have a positive sign and are strong enough to flip the BC-only response into the positive domain for , the OMM-contributions have a negative sign and try to pull the positive-valued response (from the BC-only parts) towards lower values for .
Overall, comprises only even powers of , which is in agreement with the Onsager-Casimir reciprocity relation, [64, 65, 66]. From analysing the generic features, we conclude that there is little wisdom to be gained from the to infer anything regarding the case. The only thing that matches between the two separate analyses is regarding the signs and strengths of the OMM-sourced parts. Albeit, the rationale behind not to try to extract similarities between the two cases is that the charge conservation equation(s) that come into picture are distinctly different — (I) for a single band with , the charge conservation must be satisfied individually for that particular band; (II) a nonzero interband-coupling demands that the net charge, from summing over the two bands, must be conserved. The observations serve to reinforce the recurrent phenomenon that the response from a single isolated band is fundamentally different from the case when the quasiparticles are free to scatter with those populating other bands. In fact, the same thing has been onserved for the two bands of an isolated Kramers-Weyl node [35], where downward-curved parabolas morph into upward-curved ones for each of the bands, as soon as is turned on.
IV Summary and outlook
In the current piece of work, we have ventured into determining the nature of the linear response in the form of longitudinal magnetoconductivity, focussing on on isolated RSWN. We have attempted to include both the BC and the OMM in a cohesive manner, as the necessary topological ingredients in the semiclassical Boltzmann equations. A major stride forward has been to solve the linearised (in the strength of the probe field) equations exactly, not limiting to the relaxation-time approximation with a constant phenomenological time (). Needless to say, our results quantify the serious drawbacks of using momentum-independent relaxation times and neglecting the angle-dependent spinor-overlaps in the collision integrals (see Refs. [33, 34] for the analytical expressions). By comparing the nontrivial results with those obtained in our earlier works [33, 34], we do identify the inadequacies of dropping the angular-dependence in and the ramifications of the nontrivial spinor-structures, as the exact answers turn out to be fundamentally different. Of course, in Ref. [33], we did not account for interband scatterings, and neither shall we attempt to do so anymore, because we have already successfully implemented the generic formalism without resorting to any approximation. Another point is that, a linear-in-momentum term accompanying the identity matrix (in the operator space for the four-component spinors), is not allowed in the most generic Hamiltonian for the RSWNs [58] derived from group-theoretical arguments. Consequently, tilting is completely irrelevant for the RSWNs, preventing the possibility of having odd powers of . We note that tilting is a ubiquitous feature of the WSMs [67, 68, 9, 11, 13], because the conventional Weyl nodes generically appear at the low-symmetry points of the BZs (not limited to those of chiral crystals).
In the future, it will be a rewarding enterprise to redo the calculations of linear response at finite temperatures [8, 9, 11, 15, 33, 63, 16, 69], which will also enable us to compute the temperature-dependent linear-response coefficients like the thermoelectric and thermal-conductivity tensors. Another avenue worth exploring is to investigate the effects of strain [70, 8, 11, 33], which breaks the rotational symmetry and can lead to pseudomagnetic fields (). A nonzero makes it possible for odd powers of to show up in the response.
Data availability
All data generated or analysed during this study are available within the article article.
Appendix: Explicit forms of the matrices
The two matrices, and , shown in Eq. (28), take the explicit forms of
and
respectively. The various notations used above represent the following integrals:
| (32) |
References
- Burkov and Balents [2011] A. A. Burkov and L. Balents, Weyl semimetal in a topological insulator multilayer, Phys. Rev. Lett. 107, 127205 (2011).
- Armitage et al. [2018] N. P. Armitage, E. J. Mele, and A. Vishwanath, Weyl and Dirac semimetals in three-dimensional solids, Rev. Mod. Phys. 90, 015001 (2018).
- Yan and Felser [2017] B. Yan and C. Felser, Topological materials: Weyl semimetals, Annual Rev. of Condensed Matter Phys. 8, 337 (2017).
- Berry [1984] M. V. Berry, Quantal phase factors accompanying adiabatic changes, Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 392, 45 (1984).
- Xiao et al. [2010] D. Xiao, M.-C. Chang, and Q. Niu, Berry phase effects on electronic properties, Rev. Mod. Phys. 82, 1959 (2010).
- Sundaram and Niu [1999] G. Sundaram and Q. Niu, Wave-packet dynamics in slowly perturbed crystals: Gradient corrections and Berry-phase effects, Phys. Rev. B 59, 14915 (1999).
- Graf and Piéchon [2021] A. Graf and F. Piéchon, Berry curvature and quantum metric in -band systems: An eigenprojector approach, Phys. Rev. B 104, 085114 (2021).
- Ghosh and Mandal [2024a] R. Ghosh and I. Mandal, Electric and thermoelectric response for Weyl and multi-Weyl semimetals in planar Hall configurations including the effects of strain, Physica E: Low-dimensional Systems and Nanostructures 159, 115914 (2024a).
- Ghosh and Mandal [2024b] R. Ghosh and I. Mandal, Direction-dependent conductivity in planar Hall set-ups with tilted Weyl/multi-Weyl semimetals, Journal of Physics: Condensed Matter 36, 275501 (2024b).
- Balduini et al. [2024] F. Balduini, A. Molinari, L. Rocchino, V. Hasse, C. Felser, M. Sousa, C. Zota, H. Schmid, A. G. Grushin, and B. Gotsmann, Intrinsic negative magnetoresistance from the chiral anomaly of multifold fermions, Nature Communications 15, 6526 (2024).
- Medel et al. [2024] L. Medel, R. Ghosh, A. Martín-Ruiz, and I. Mandal, Electric, thermal, and thermoelectric magnetoconductivity for Weyl/multi-Weyl semimetals in planar Hall set-ups induced by the combined effects of topology and strain, Scientific Reports 14, 21390 (2024).
- Knoll et al. [2020] A. Knoll, C. Timm, and T. Meng, Negative longitudinal magnetoconductance at weak fields in Weyl semimetals, Phys. Rev. B 101, 201402 (2020).
- Mandal [2024a] I. Mandal, Anisotropic conductivity for the type-I and type-II phases of Weyl/multi-Weyl semimetals in planar Hall set-ups, arXiv e-prints (2024a), arXiv:2410.05028 [cond-mat.mes-hall] .
- Li et al. [2017] Y. Li, Z. Wang, P. Li, X. Yang, Z. Shen, F. Sheng, X. Li, Y. Lu, Y. Zheng, and Z.-A. Xu, Negative magnetoresistance in Weyl semimetals NbAs and NbP: Intrinsic chiral anomaly and extrinsic effects, Frontiers of Phys. 12, 127205 (2017).
- Mandal et al. [2025] I. Mandal, S. Saha, and R. Ghosh, Signatures of topology in generic transport measurements for Rarita-Schwinger-Weyl semimetals, Solid State Communications 397, 115799 (2025).
- Haidar and Mandal [2025] F. Haidar and I. Mandal, Reflections of topological properties in the planar-Hall response for semimetals carrying pseudospin-1 quantum numbers, Annals of Physics 478, 170010 (2025).
- Mandal [2025] I. Mandal, Longitudinal magnetoconductivity in chiral multifold semimetals exemplified by pseudospin-1 nodal points, arXiv e-prints (2025), arXiv:2505.19636 [cond-mat.mes-hall] .
- Hussain Rather et al. [2025] F. Hussain Rather, M. Jaffar A., and I. Mandal, Direction-dependent linear response for gapped nodal-line semimetals in planar-Hall configurations, arXiv e-prints (2025), arXiv:2503.10712 [cond-mat.mes-hall] .
- Bradlyn et al. [2016] B. Bradlyn, J. Cano, Z. Wang, M. G. Vergniory, C. Felser, R. J. Cava, and B. A. Bernevig, Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals, Science 353 (2016).
- Liang and Yu [2016] L. Liang and Y. Yu, Semimetal with both Rarita-Schwinger-Weyl and Weyl excitations, Phys. Rev. B 93, 045113 (2016).
- Boettcher [2020] I. Boettcher, Interplay of topology and electron-electron interactions in Rarita-Schwinger-Weyl semimetals, Phys. Rev. Lett. 124, 127602 (2020).
- Link et al. [2020] J. M. Link, I. Boettcher, and I. F. Herbut, -wave superconductivity and Bogoliubov-Fermi surfaces in Rarita-Schwinger-Weyl semimetals, Phys. Rev. B 101, 184503 (2020).
- Isobe and Fu [2016] H. Isobe and L. Fu, Quantum critical points of Dirac electrons in antiperovskite topological crystalline insulators, Phys. Rev. B 93, 241113 (2016).
- Tang et al. [2017] P. Tang, Q. Zhou, and S.-C. Zhang, Multiple types of topological fermions in transition metal silicides, Phys. Rev. Lett. 119, 206402 (2017).
- Mandal [2020] I. Mandal, Transmission in pseudospin-1 and pseudospin-3/2 semimetals with linear dispersion through scalar and vector potential barriers, Phys. Lett. A 384, 126666 (2020).
- Sekh and Mandal [2022a] S. Sekh and I. Mandal, Circular dichroism as a probe for topology in three-dimensional semimetals, Phys. Rev. B 105, 235403 (2022a).
- Ma et al. [2021] J.-Z. Ma, Q.-S. Wu, M. Song, S.-N. Zhang, E. Guedes, S. Ekahana, M. Krivenkov, M. Yao, S.-Y. Gao, W.-H. Fan, et al., Observation of a singular Weyl point surrounded by charged nodal walls in ptga, Nature Communications 12, 3994 (2021).
- Sekh and Mandal [2022b] S. Sekh and I. Mandal, Magnus Hall effect in three-dimensional topological semimetals, Eur. Phys. J. Plus 137, 736 (2022b).
- Mandal [2023] I. Mandal, Transmission and conductance across junctions of isotropic and anisotropic three-dimensional semimetals, European Physical Journal Plus 138, 1039 (2023).
- Mandal [2024b] I. Mandal, Andreev bound states in superconductor-barrier-superconductor junctions of Rarita-Schwinger-Weyl semimetals, Phys. Lett. A 503, 129410 (2024b).
- Chang et al. [2018] G. Chang, B. J. Wieder, F. Schindler, D. S. Sanchez, I. Belopolski, S.-M. Huang, B. Singh, D. Wu, T.-R. Chang, T. Neupert, S.-Y. Xu, H. Lin, and M. Z. Hasan, Topological quantum properties of chiral crystals, Nature Materials 17, 978 (2018).
- Flicker et al. [2018] F. Flicker, F. de Juan, B. Bradlyn, T. Morimoto, M. G. Vergniory, and A. G. Grushin, Chiral optical response of multifold fermions, Phys. Rev. B 98, 155145 (2018).
- Ghosh et al. [2024] R. Ghosh, F. Haidar, and I. Mandal, Linear response in planar Hall and thermal Hall setups for Rarita-Schwinger-Weyl semimetals, Phys. Rev. B 110, 245113 (2024).
- Mandal [2025a] I. Mandal, Chiral anomaly and internode scatterings in multifold semimetals, Phys. Rev. B 111, 165116 (2025a).
- Mandal [2025b] I. Mandal, Disentangling contributions to longitudinal magnetoconductivity for Kramers-Weyl nodes, arXiv e-prints (2025b), arXiv:2506.07913 [cond-mat.mes-hall] .
- Cayssol and Fuchs [2021] J. Cayssol and J. N. Fuchs, Topological and geometrical aspects of band theory, Journal of Physics: Materials 4, 034007 (2021).
- Polash et al. [2021] M. M. H. Polash, S. Yalameha, H. Zhou, K. Ahadi, Z. Nourbakhsh, and D. Vashaee, Topological quantum matter to topological phase conversion: Fundamentals, materials, physical systems for phase conversions, and device applications, Materials Science and Engineering: R: Reports 145, 100620 (2021).
- Nielsen and Ninomiya [1981] H. Nielsen and M. Ninomiya, A no-go theorem for regularizing chiral fermions, Phys. Lett. B 105, 219 (1981).
- Lv et al. [2015] B. Q. Lv, H. M. Weng, B. B. Fu, X. P. Wang, H. Miao, J. Ma, P. Richard, X. C. Huang, L. X. Zhao, G. F. Chen, Z. Fang, X. Dai, T. Qian, and H. Ding, Experimental discovery of Weyl semimetal TaAs, Phys. Rev. X 5, 031013 (2015).
- Nielsen and Ninomiya [1983] H. Nielsen and M. Ninomiya, The Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal, Physics Letters B 130, 389 (1983).
- Son and Spivak [2013] D. T. Son and B. Z. Spivak, Chiral anomaly and classical negative magnetoresistance of Weyl metals, Phys. Rev. B 88, 104412 (2013).
- He et al. [2021] W.-Y. He, X. Y. Xu, and K. T. Law, Kramers Weyl semimetals as quantum solenoids and their applications in spin-orbit torque devices, Communications Physics 4, 66 (2021).
- Chang et al. [2017] G. Chang, S.-Y. Xu, B. J. Wieder, D. S. Sanchez, S.-M. Huang, I. Belopolski, T.-R. Chang, S. Zhang, A. Bansil, H. Lin, and M. Z. Hasan, Unconventional chiral fermions and large topological Fermi arcs in RhSi, Phys. Rev. Lett. 119, 206401 (2017).
- Ni et al. [2021] Z. Ni, K. Wang, Y. Zhang, O. Pozo, B. Xu, X. Han, K. Manna, J. Paglione, C. Felser, A. G. Grushin, F. de Juan, E. J. Mele, and L. Wu, Giant topological longitudinal circular photo-galvanic effect in the chiral multifold semimetal CoSi, Nature Communications 12, 154 (2021).
- Moore [2018] J. E. Moore, Optical properties of Weyl semimetals, National Science Rev. 6, 206 (2018).
- Guo et al. [2023] C. Guo, V. S. Asadchy, B. Zhao, and S. Fan, Light control with Weyl semimetals, eLight 3, 2 (2023).
- Avdoshkin et al. [2020] A. Avdoshkin, V. Kozii, and J. E. Moore, Interactions remove the quantization of the chiral photocurrent at Weyl points, Phys. Rev. Lett. 124, 196603 (2020).
- Mandal [2020] I. Mandal, Effect of interactions on the quantization of the chiral photocurrent for double-Weyl semimetals, Symmetry 12 (2020).
- Mandal [2024c] I. Mandal, Signatures of two- and three-dimensional semimetals from circular dichroism, International Journal of Modern Physics B 38, 2450216 (2024c).
- Zahid Hasan et al. [2021] M. Zahid Hasan, G. Chang, I. Belopolski, G. Bian, S.-Y. Xu, and J.-X. Yin, Weyl, Dirac and high-fold chiral fermions in topological quantum materials, arXiv e-prints , arXiv:2103.01714 (2021), arXiv:2103.01714 [cond-mat.mtrl-sci] .
- Zhang et al. [2017] C.-L. Zhang, F. Schindler, H. Liu, T.-R. Chang, S.-Y. Xu, G. Chang, W. Hua, H. Jiang, Z. Yuan, J. Sun, H.-T. Jeng, H.-Z. Lu, H. Lin, M. Z. Hasan, X. C. Xie, T. Neupert, and S. Jia, Ultraquantum magnetoresistance in the Kramers-Weyl semimetal candidate -Ag2Se, Phys. Rev. B 96, 165148 (2017).
- Sanchez et al. [2019] D. S. Sanchez, I. Belopolski, T. A. Cochran, X. Xu, J.-X. Yin, G. Chang, W. Xie, K. Manna, V. Süß, C.-Y. Huang, N. Alidoust, D. Multer, S. S. Zhang, N. Shumiya, X. Wang, G.-Q. Wang, T.-R. Chang, C. Felser, S.-Y. Xu, S. Jia, H. Lin, and M. Zahid Hasan, Topological chiral crystals with helicoid-arc quantum states, Nature 567, 500–505 (2019).
- Schröter et al. [2019] N. B. M. Schröter, D. Pei, M. G. Vergniory, Y. Sun, K. Manna, F. de Juan, J. A. Krieger, V. Süss, M. Schmidt, P. Dudin, B. Bradlyn, T. K. Kim, T. Schmitt, C. Cacho, C. Felser, V. N. Strocov, and Y. Chen, Chiral topological semimetal with multifold band crossings and long Fermi arcs, Nature Physics 15, 759 (2019).
- Mardanya et al. [2024] S. Mardanya, M. Kargarian, R. Verma, T.-R. Chang, S. Chowdhury, H. Lin, A. Bansil, A. Agarwal, and B. Singh, Unconventional superconducting pairing in a B20 multifold Weyl fermion semimetal, Phys. Rev. Mater. 8, L091801 (2024).
- Gao et al. [2022] Z. S. Gao, X.-J. Gao, W.-Y. He, X. Y. Xu, T. K. Ng, and K. T. Law, Topological superconductivity in multifold fermion metals, Quantum Frontiers 1, 3 (2022).
- Ashcroft and Mermin [2011] N. Ashcroft and N. Mermin, Solid State Physics (Cengage Learning, 2011).
- Mandal and Saha [2024] I. Mandal and K. Saha, Thermoelectric response in nodal-point semimetals, Ann. Phys. (Berlin) 536, 2400016 (2024).
- Xu et al. [2020] B. Xu, Z. Fang, M.-Á. Sánchez-Martínez, J. W. F. Venderbos, Z. Ni, T. Qiu, K. Manna, K. Wang, J. Paglione, C. Bernhard, C. Felser, E. J. Mele, A. G. Grushin, A. M. Rappe, and L. Wu, Optical signatures of multifold fermions in the chiral topological semimetal CoSi, Proceedings of the National Academy of Science 117, 27104 (2020).
- Xiao et al. [2007] D. Xiao, W. Yao, and Q. Niu, Valley-contrasting physics in graphene: Magnetic moment and topological transport, Phys. Rev. Lett. 99, 236809 (2007).
- Graf [2022] A. Graf, Aspects of multiband systems: Quantum geometry, flat bands, and multifold fermions, Theses, Université Paris-Saclay (2022).
- Li et al. [2023] L. Li, J. Cao, C. Cui, Z.-M. Yu, and Y. Yao, Planar hall effect in topological Weyl and nodal-line semimetals, Phys. Rev. B 108, 085120 (2023).
- Mandal and Saha [2020] I. Mandal and K. Saha, Thermopower in an anisotropic two-dimensional Weyl semimetal, Phys. Rev. B 101, 045101 (2020).
- Mandal [2025c] I. Mandal, Linear response of tilted anisotropic two-dimensional Dirac cones, The European Physical Journal B 98, 123 (2025c).
- Onsager [1931] L. Onsager, Reciprocal Relations in Irreversible Processes. I., Phys. Rev. 37, 405 (1931).
- Casimir [1945] H. B. G. Casimir, On Onsager’s principle of microscopic reversibility, Rev. Mod. Phys. 17, 343 (1945).
- Jacquod et al. [2012] P. Jacquod, R. S. Whitney, J. Meair, and M. Büttiker, Onsager relations in coupled electric, thermoelectric, and spin transport: The tenfold way, Phys. Rev. B 86, 155118 (2012).
- Stålhammar et al. [2020] M. Stålhammar, J. Larana-Aragon, J. Knolle, and E. J. Bergholtz, Magneto-optical conductivity in generic Weyl semimetals, Phys. Rev. B 102, 235134 (2020).
- Yadav et al. [2023] S. Yadav, S. Sekh, and I. Mandal, Magneto-optical conductivity in the type-I and type-II phases of Weyl/multi-Weyl semimetals, Physica B: Condensed Matter 656, 414765 (2023).
- Mandal and Freire [2024] I. Mandal and H. Freire, Transport properties in non-Fermi liquid phases of nodal-point semimetals, Journal of Physics: Condensed Matter 36, 443002 (2024).
- Bose and Narayan [2021] A. Bose and A. Narayan, Strain-induced topological charge control in multifold fermion systems, Journal of Physics: Condensed Matter 33, 375002 (2021).