Distributed Mirror Descent Algorithm with Bregman Damping for Nonsmooth Constrained Optimization
Abstract
To solve distributed optimization efficiently with various constraints and nonsmooth functions, we propose a distributed mirror descent algorithm with embedded Bregman damping, as a generalization of conventional distributed projection-based algorithms. In fact, our continuous-time algorithm well inherits good capabilities of mirror descent approaches to rapidly compute explicit solutions to the problems with some specific constraint structures. Moreover, we rigorously prove the convergence of our algorithm, along with the boundedness of the trajectory and the accuracy of the solution.
I INTRODUCTION
Distributed optimization has served as a hot topic in recent years for its broad applications in various fields such as sensor networks and smart grids [1, 2, 3, 4, 5, 6, 7]. Under multi-agent frameworks, the global cost function consists of agents’ local ones, and each agent shares limited information with its neighbors through a network to achieve an optimal solution. Meanwhile, distributed continuous-time algorithms have been well developed thanks to system dynamics and control theory [8, 9, 10, 11, 12].
Up to now, various approaches have been employed for distributed design of constrained optimization. Intuitively, implementing projection operations on local constraints is a most popular method, such as projected proportional-integral protocol [8] and projected dynamics with constraints based on KKT conditions [9]. In addition, other approaches such as distributed primal-dual dynamics and penalty-based algorithms [10, 11, 12] also perform well provided that constraints are endowed with specific expressions. However, time complexity in finding optimal solutions with complex or high-dimensional constraints forces researchers to exploit efficient approaches for special constraint structures, such as the unit simplex and the Euclidean sphere.
In fact, the mirror descent (MD) method serves as a powerful tool for solving constrained optimization. As we know, first introduced in [13], MD is regarded as a generalization of (sub)gradient methods. With mapping the variables into a conjugate space, MD employs the Bregman divergence and performs well in handling local constraints with specific structures [14, 15, 16]. This process results in a faster convergence rate than that of projected (sub)gradient descent algorithms, especially for large-scale optimization problems. Undoubtedly, as such an important tool, MD has played a crucial role in various distributed algorithm designs, as given in [17, 18, 19, 20].
In recent years, continuous-time MD-based algorithms have also attracted much attention. For example, [14] proposed the acceleration of a continuous-time MD algorithm, and afterward, [21] showed continuous-time stochastic MD for strongly convex functions, while [22] proposed a discounted continuous-time MD dynamics to approximate the exact solution. In the distributed design, although [19] presented a distributed MD dynamics with integral feedback, the result merely achieved optimal consensus and part variables turn to be unbounded. Due to the booming development and extensive demand of distributed design, distributed continuous-time MD-based methods need more exploration and development actually.
Therefore, we study continuous-time MD-based algorithms to solve distributed nonsmooth optimization with local and coupled constraints. The main contributions of this note can be summarized as follows. We propose a distributed continuous-time mirror descent algorithm by introducing the Bregman damping, which can be regarded as a generalization of classic distributed projection-based dynamics [8, 23] by taking the Bregman damping in a quadratic form. Moreover, our algorithm well inherits the good capabilities of MD-based approaches to rapidly compute explicit solutions to the problems with some concrete constraint structures like the unit simplex or the Euclidean sphere. With the designed Bregman damping, our MD-based algorithm makes all the variables’ trajectories bounded, which could not be ensured in [14, 19], and avoids the inaccuracy of the convergent point occurred in [22].
The remaining part is organized as follows. Section II gives related preliminary knowledge. Next, Section III formulates the distributed optimization and provides our algorithm, while Section IV presents the main results. Then, Section V provides illustrative numerical examples. Finally, Section VI gives the conclusion.
II Preliminaries
In this section, we give necessary notations and related preliminary knowledge.
II-A Notations
Denote (or ) as the set of -dimensional (or -by-) real column vectors (or real matrices), and as the identity matrix. Let (or ) be the -dimensional column vector with all entries of (or ). Denote as the Kronecker product of matrices and . Take , as the Euclidean norm, and as the relative interior of the set [24].
An undirected graph can be defined by , where is the set of nodes and is the set of edges. Let be the adjacency matrix of such that if , and , otherwise. The Laplacian matrix is , where with . If the graph is connected, then .
II-B Convex analysis
For a closed convex set , the projection map is defined as . Especially, denote for convenience. For , denote the normal cone to at by
A continuous function is -strongly convex on if
where , , and .
The Bregman divergence based on the differentiable generating function is defined as
The convex conjugate function of is defined as
The following lemma reveals a classical conclusion about convex conjugate functions, of which readers can find more details in [13, 15].
Lemma 1
Suppose that a function is differentiable and strongly convex on a closed convex set . Then is convex and differentiable, and . Moreover, , where
| (1) |
II-C Differential inclusion
A differential inclusion is given by
| (2) |
where is a set-valued map. is upper semi-continuous at if there exists for all such that
and it is upper semi-continuous if it is so for all . A Caratheodory solution to (2) defined on is an absolutely continuous function satisfying (2) for almost all in Lebesgue measure [25]. The solution is right maximal if it has no extension in time. A set is said to be weakly (strongly) invariant with respect to (2) if contains a (all) maximal solution to (2) for any . If , then is an equilibrium point of (2). The existence of a solution to (2) is guaranteed by the following lemma [25].
Lemma 2
If is locally bounded, upper semicontinuous, and takes nonempty, compact and convex values, then there exists a Caratheodory solution to (2) for any initial value.
Let be a locally Lipschitz continuous function, and be the Clarke generalized gradient of at . The set-valued Lie derivative for is defined by . Let be the largest element of . Referring to [25], we have the following invariance principle for (2).
Lemma 3
Suppose that is upper semi-continuous and locally bounded, and takes nonempty, compact, and convex values. Let be a locally Lipschitz and regular function, be compact and strongly invariant for (2), and be a solution to (2). Take
and as the largest weakly invariant subset of , where is the closure of . If for all , then .
III Formulation and algorithm
In this paper, we consider a nonsmooth optimization problem with both local and coupled constraints. There are agents indexed by in a network . For agent , the decision variable is , the local feasible set is , and the local cost function is . Define and . All agents cooperate to solve the following distributed optimization:
| s.t. | (3) |
where , and , for . Except for the local constraint , other constraints in (III) are said to be coupled ones since the solutions rely on global information. In the multi-agent network, agent only has the local decision variable , and moreover, the local information , , and . Thus, agents need communication with neighbors through the network .
Actually, MD replaces the Euclidean regularization in (sub)gradient descent algorithms with Bregman divergence. In return, different generating functions of Bregman divergence may efficiently bring explicit solutions on different special feasible sets. For example, if and is convex and closed, then
| (4) |
which actually turns into the classical Euclidean regularization with projection operations. Furthermore, if and with the convention , then
| (5) |
which is the well-known KL-divergence on the unit simplex.
Assign a generating function of the Bregman divergence to each agent . Then we consider the following assumptions for (III).
Assumption 1
-
(i)
For , is closed and convex, and are convex on , and moreover, is differentiable and strongly convex on .
-
(ii)
There exists at least one such that and .
-
(iii)
The undirected graph is connected.
Remark 1
Clearly, (III) can be regarded as a generalization for both distributed optimal consensus problems [26, 12, 19] and distributed resource allocation problems [27, 23]. Moreover, in the coupled constraints may not required to be affine, which is more general than the constraints in previous works [10, 28]. Also, the problem setting does not require strongly or strictly convexity for either cost functions or constraint functions [27, 10], and the selection qualification for generating function has also been widely used [19, 14, 22].
For designing a distributed algorithm, we introduce auxiliary variables , , , , and for each agent . Moreover, we employ the gradient of generating functions as the Bregman damping in the algorithm, which ensures the trajectories’ boundedness [14, 19] and avoids the convergence inaccuracy [22]. Recall that is the -th entry of the adjacency matrix and is defined in (1). Then we propose a distributed mirror descent algorithm with Bregman damping (MDBD) for (III).
Initialization:
, , , ,
, , ;
take a proper generating function according to .
Flows renewal:
In Algorithm 1, for each agent , information like , , and serves as private knowledge, and values like , , and should be exchanged with neighbors through the network . Moreover, generating function and Bregman damping can be determined privately and individually, not necessarily identical. It follows from Lemma 2 that the existence of a Caratheodory solution to Algorithm 1 can be guaranteed.
For simplicity, define
Let , and moreover,
Take the Lagrangian function as
| (6) |
For such a distributed convex optimization (III) with a zero dual gap, is an optimal solution to problem (III) if and only if there exist auxiliary variables , such that is a saddle point of [23], that is, for arbitrary ,
Define
| (7) |
where and . In fact, is a saddle point of if and only if , which was obtained in [27, 23, 10].
Remark 2
In fact, if , then and , and therefore, (8) can be rewritten as
| (10) |
which is actually a widely-investigated dynamics such as the proportional-integral protocol in [8] and projected output feedback in [23]. Thus, MDBD generalizes the conventional distributed projection-based design for constrained optimization. Obviously, in (10) is replaced with the Bregman damping in (8).
IV Main results
In this section, we investigate the convergence of MDBD. Though Bregman damping improves the convergence of MDBD, the process also brings challenges for the convergence analysis. The following lemma shows the relationship between MDBD and the saddle points of the Lagrangian function .
Lemma 4
Proof. For , the first-order condition is
| (11) |
We firstly show the sufficiency. Given , suppose that there exists such that . Thus, (11) holds with , and , which means that is a saddle point of .
Secondly, we show the necessity. Suppose and take . Recall that (11) holds with , which implies that is a solution to . Furthermore, since and are strongly convex, the solution to is unique. Therefore, .
The following theorem shows the correctness and the convergence of Algorithm 1.
Theorem 1
Proof. (i) Firstly, we show that the output is bounded. By Lemma 4, take as a saddle point of and thus, there exists such that . Take as the convex conjugate of , and construct a Lyapunov candidate function as
| (12) |
Since , it follows from Lemma 1 that
| (13a) | ||||
| (13b) | ||||
Thus, by substituting (13), the Bregman divergence becomes
Since is strongly convex for , there exists a positive constant such that
In fact, , which leads to
Thus, . In addition,
Therefore,
| (14) |
where . This means , that is, is radially unbounded in . Clearly, the function along (20) satisfies
Combining the convexity of and with the property for saddle point ,
| (15) | ||||
Thus,
| (16) | ||||
On the one hand, for , we consider a differentiable function
with a constant . Correspondingly, we have
Recalling , , , because of the convexity of . This yields , that is,
On the other hand,
Therefore, , which implies that the output is bounded.
Secondly, we show that is bounded. Actually, it follows from (IV) and the statement above that is bounded. Thereby, we merely need to consider . Take another Lyapunov candidate function as
| (17) |
which is radially unbounded in . Along the trajectories of Algorithm 1, the derivative of satisfies
It is clear that for a positive constant , since , and have been proved to be bounded. On this basis, it can be easily verified that is bounded, so is . Together, is bounded.
(ii) Set . Clearly, by (15), . Let be the largest invariant subset of . By Lemma 3, as . Take any . Let , and clearly as well. Similar to (IV), we take another Lyapunov function by replacing with . Based on similar arguments, is Lyapunov stable, so is . By Proposition 4.7 in [29], there exists such that as , which yields that in Algorithm 1 converges to an optimal solution to problem (III).
Remark 3
It is worth mentioning that the Bregman damping in (8) is fundamental to make the trajectory of variable avoid going to infinity [14, 19], or converging to an inexact optimal point [22]. Clearly, in the first ODE in (10) derives actually not from the variable itself, but from the gradient of the quadratic function instead. This is exactly the crucial point in designing the distributed MD-based dynamics (8). Correspondingly, the properties in conjugate spaces, referring to (13), play an important role in the analysis.
V Numerical examples
In this section, we examine the correctness and effectiveness of Algorithm 1 on the classical simplex-constrained problems (see, e.g., [22, 18]), where the local constraint set is an -simplex, e.g.,
First, we consider the following nonsmooth optimization problem with and ,
| (19) | ||||
| s.t. |
where is a positive semi-definite matrix, , and . The coupled inequality constraint is
while and are random matrices ensuring the Slater’s constraint condition. Here, , , , and are private to agent , and all agents communicate through an undirected cycle network :
To implement the MD method, we employ the negative entropy function as the generating function on in Algorithm 1. In Fig. 1, we show the trajectories of one dimension of each and , respectively. Clearly, the trajectories of both and in MDBD are bounded, while the boundedness of may not be guaranteed in [14, 19].
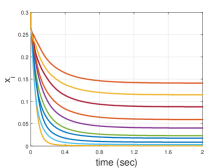
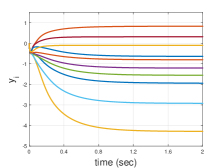
Next, we show the effectiveness of MDBD by comparisons. As is investigated in [16, 14], when the generating function satisfies on the unit simplex, can be explicitly expressed as (5). In this circumstance, the MD-based method works better than projection-based algorithms, since it can be regarded as projection-free and effectively saves the time for projection operation, especially with high-dimensional variables.
To this end, we investigate different dimensions of decision variable and compare MDBD with two distributed continuous-time projection-based algorithms — the proportional-integral protocol (PIP-Yang) in [8] and the projected output feedback (POF-Zeng) in [23], still for the cost functions and the coupled constraints given in (19).
| MDBD | 0.47 | 2.42 | 6.76 | 12.98 | 27.99 | 146.62 | 466.60 |
| PIP-YANG | 2.51 | 19.63 | 48.51 | 195.67 | 892.74 | ||
| POF-ZENG | 3.92 | 21.78 | 39.73 | 207.03 | 1136.85 |
In Fig. 2, the -axis is for the real running time of the GPU, while the -axis is for the optimal error . As the dimension increases, the real running time of the two projection-based dynamics is obviously longer than that of MDBD, because obtaining (5) is much faster than calculating a projection on high-dimensional constraint sets via solving a general quadratic optimization problem.
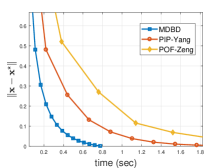
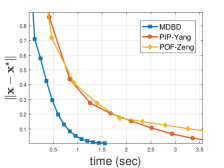
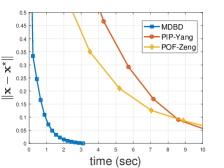
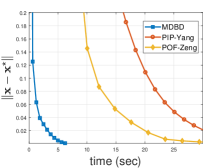
Furthermore, Table I lists the real running time for three algorithms with different dimensions of decision variables. As the dimension increases, finding the projection points in large-scale circumstances becomes more and more difficult. But remarkably, MDBD still maintains good performance, due to the advantage of MD.
VI CONCLUSIONS
We investigated distributed nonsmooth optimization with both local set constraints and coupled constraints. Based on the mirror descent method, we proposed a continuous-time algorithm with introducing the Bregman damping to guarantee the algorithm’s boundedness and accuracy. Furthermore, we utilized nonsmooth techniques, conjugate functions, and the Lyapunov stability to prove the convergence. Finally, we implemented comparative experiments to illustrate the effectiveness of our algorithm.
References
- [1] T. Yang, X. Yi, J. Wu, Y. Yuan, D. Wu, Z. Meng, Y. Hong, H. Wang, Z. Lin, and K. H. Johansson, “A survey of distributed optimization,” Annual Reviews in Control, vol. 47, pp. 278–305, 2019.
- [2] M. Zhu and S. Martínez, “On distributed convex optimization under inequality and equality constraints,” IEEE Transactions on Automatic Control, vol. 57, no. 1, pp. 151–164, 2011.
- [3] D. Yuan, D. W. Ho, and S. Xu, “Regularized primal–dual subgradient method for distributed constrained optimization,” IEEE Transactions on Cybernetics, vol. 46, no. 9, pp. 2109–2118, 2015.
- [4] A. Cherukuri and J. Cortes, “Initialization-free distributed coordination for economic dispatch under varying loads and generator commitment,” Automatica, vol. 74, pp. 183–193, 2016.
- [5] J.-M. Xu and Y. C. Soh, “A distributed simultaneous perturbation approach for large-scale dynamic optimization problems,” Automatica, vol. 72, pp. 194–204, 2016.
- [6] K. You, R. Tempo, and P. Xie, “Distributed algorithms for robust convex optimization via the scenario approach,” IEEE Transactions on Automatic Control, vol. 64, no. 3, pp. 880–895, 2018.
- [7] K. Lu, G. Jing, and L. Wang, “Online distributed optimization with strongly pseudoconvex-sum cost functions,” IEEE Transactions on Automatic Control, vol. 65, no. 1, pp. 426–433, 2019.
- [8] S. Yang, Q. Liu, and J. Wang, “A multi-agent system with a proportional-integral protocol for distributed constrained optimization,” IEEE Transactions on Automatic Control, vol. 62, no. 7, pp. 3461–3467, 2016.
- [9] Y. Zhu, W. Yu, G. Wen, G. Chen, and W. Ren, “Continuous-time distributed subgradient algorithm for convex optimization with general constraints,” IEEE Transactions on Automatic Control, vol. 64, no. 4, pp. 1694–1701, 2018.
- [10] S. Liang, X. Zeng, and Y. Hong, “Distributed nonsmooth optimization with coupled inequality constraints via modified Lagrangian function,” IEEE Transactions on Automatic Control, vol. 63, no. 6, pp. 1753–1759, 2017.
- [11] X. Li, L. Xie, and Y. Hong, “Distributed continuous-time nonsmooth convex optimization with coupled inequality constraints,” IEEE Transactions on Control of Network Systems, vol. 7, no. 1, pp. 74–84, 2019.
- [12] W. Li, X. Zeng, S. Liang, and Y. Hong, “Exponentially convergent algorithm design for constrained distributed optimization via non-smooth approach,” IEEE Transactions on Automatic Control, 2021, doi: 10.1109/TAC.2021.3075666.
- [13] A. S. Nemirovskij and D. B. Yudin, Problem Complexity and Method Efficiency in Optimization. Wiley-Interscience, 1983.
- [14] W. Krichene, A. Bayen, and P. Bartlett, “Accelerated mirror descent in continuous and discrete time,” in Advances in Neural Information Processing Systems, vol. 28, 2015, pp. 2845–2853.
- [15] J. Diakonikolas and L. Orecchia, “The approximate duality gap technique: A unified theory of first-order methods,” SIAM Journal on Optimization, vol. 29, no. 1, pp. 660–689, 2019.
- [16] A. Ben-Tal, T. Margalit, and A. Nemirovski, “The ordered subsets mirror descent optimization method with applications to tomography,” SIAM Journal on Optimization, vol. 12, no. 1, pp. 79–108, 2001.
- [17] S. Shahrampour and A. Jadbabaie, “Distributed online optimization in dynamic environments using mirror descent,” IEEE Transactions on Automatic Control, vol. 63, no. 3, pp. 714–725, 2017.
- [18] D. Yuan, Y. Hong, D. W. Ho, and G. Jiang, “Optimal distributed stochastic mirror descent for strongly convex optimization,” Automatica, vol. 90, pp. 196–203, 2018.
- [19] Y. Sun and S. Shahrampour, “Distributed mirror descent with integral feedback: Asymptotic convergence analysis of continuous-time dynamics,” IEEE Control Systems Letters, vol. 5, no. 5, pp. 1507–1512, 2020.
- [20] Y. Wang, Z. Tu, and H. Qin, “Distributed stochastic mirror descent algorithm for resource allocation problem,” Control Theory and Technology, vol. 18, no. 4, pp. 339–347, 2020.
- [21] P. Xu, T. Wang, and Q. Gu, “Continuous and discrete-time accelerated stochastic mirror descent for strongly convex functions,” in International Conference on Machine Learning, 2018, pp. 5492–5501.
- [22] B. Gao and L. Pavel, “Continuous-time discounted mirror-descent dynamics in monotone concave games,” IEEE Transactions on Automatic Control, 2020, doi: 10.1109/TAC.2020.3045094.
- [23] X. Zeng, P. Yi, Y. Hong, and L. Xie, “Distributed continuous-time algorithms for nonsmooth extended monotropic optimization problems,” SIAM Journal on Control and Optimization, vol. 56, no. 6, pp. 3973–3993, 2018.
- [24] S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004.
- [25] J. Cortés, “Discontinuous dynamical systems,” IEEE Control Systems Magazine, vol. 28, no. 3, pp. 36–73, 2008.
- [26] G. Shi and K. H. Johansson, “Randomized optimal consensus of multi-agent systems,” Automatica, vol. 48, no. 12, pp. 3018–3030, 2012.
- [27] P. Yi, Y. Hong, and F. Liu, “Initialization-free distributed algorithms for optimal resource allocation with feasibility constraints and application to economic dispatch of power systems,” Automatica, vol. 74, pp. 259–269, 2016.
- [28] G. Chen, Y. Ming, Y. Hong, and P. Yi, “Distributed algorithm for -generalized nash equilibria with uncertain coupled constraints,” Automatica, vol. 123, p. 109313, 2021.
- [29] W. M. Haddad and V. Chellaboina, Nonlinear Dynamical Systems and Control: A Lyapunov-based Approach. Princeton University Press, 2011.