Do Emergent Abilities Exist in Quantized Large Language Models:
An Empirical Study

Peiyu Liu^1,2, Zikang Liu^1,2, Ze-Feng Gao¹, Dawei Gao³,
Wayne Xin Zhao^1,2, Yaliang Li³, Bolin Ding³ Corresponding author. Ji-Rong Wen^1,2,4
¹ Gaoling School of Artificial Intelligence, Renmin University of China
² Beijing Key Laboratory of Big Data Management and Analysis Methods
³ Alibaba Group, ⁴ School of Information, Renmin University of China
liupeiyustu@163.com,jason8121@foxmail.com,batmanfly@gmail.com
{zfgao,jrwen}@ruc.edu.cn,{gaodawei.gdw,yaliang.li,bolin.ding}@alibaba-inc.com

Abstract

Despite the superior performance, Large Language Models (LLMs) require significant computational resources for deployment and use. To overcome this issue, quantization methods have been widely applied to reduce the memory footprint of LLMs as well as increasing the inference rate. However, a major challenge is that low-bit quantization methods often lead to performance degradation. It is important to understand how quantization impacts the capacity of LLMs. Different from previous studies focused on overall performance, this work aims to investigate the impact of quantization on emergent abilities, which are important characteristics that distinguish LLMs from small language models. Specially, we examine the abilities of in-context learning, chain-of-thought reasoning, and instruction-following in quantized LLMs. Our empirical experiments show that these emergent abilities still exist in 4-bit quantization models, while 2-bit models encounter severe performance degradation on the test of these abilities. To improve the performance of low-bit models, we conduct two special experiments: (1) fine-gained impact analysis that studies which components (or substructures) are more sensitive to quantization, and (2) performance compensation through model fine-tuning. Our work derives a series of important findings to understand the impact of quantization on emergent abilities, and sheds lights on the possibilities of extremely low-bit quantization for LLMs.

1 Introduction

Recently, Artificial Intelligence (AI) has witnessed remarkable progress due to the emergence of Large Language Models (LLMs) Brown et al. (2020); Zhao et al. (2023). Compared with small-sized language models, LLMs, which largely scale the model size and training corpus size, have exhibited very different behaviors when elicited by specially designed prompts. Generally, LLMs can acquire more superior abilities, such as in-context learning (ICL, Brown et al. 2020) and chain-of-thought reasoning (CoT, Wei et al. 2022), which may not be present in small-sized language models. Such abilities are often formally called emergent abilities Wei et al. (2022)¹¹1There is still no consensus on the existence of emergent abilities, due to the lack of continuity in evaluation metrics and model sizes in the empirical study Wei et al. (2022). It is also known that small models can possess some emergent abilities with special adaptation. Despite that, we still use this term to emphasize the superior performance of LLMs. .

Despite the superior performance, it is very costly to deploy LLMs in real-world applications due to the huge model size. Faced with this issue, model quantization Dettmers et al. (2022); Frantar et al. (2022); Yao et al. (2023a) has become a widely used approach to reducing the memory footprint of LLMs. The essential idea of quantization is to map floating-point numbers into low-bit integers (e.g., BF16 to INT8), so as to reduce the total model bits. Typically, existing methods take a post-training quantization (PTQ) approach Frantar et al. (2022); Dettmers et al. (2022) without retraining the model parameters. However, existing PTQ methods often suffer from performance degradation in low-bit quantization.

To use the quantized LLMs in an effective way, it is important to understand what level of performance can be attained in varied bit precision, e.g., what is the lowest bit precision for quantization to achieve decent performance on a specific task? More recently, several studies have conducted comprehensive evaluation experiments on the impact of model quantization on the performance of LLMs Yao et al. (2023b); Dettmers and Zettlemoyer (2022). However, they mainly analyze the general performance of quantized LLMs (e.g., language modeling), lacking a deep investigation into LLM’s abilities on complex tasks.

In this work, we focus on examining the performance of quantized LLMs on solving complex tasks, to explore the impact of quantization on the emergent abilities of LLMs. As demonstrated in previous studies Wei et al. (2022), there exists a strong dependency between emergent abilities and parameter scale. It is curious whether the emergent abilities would vanish under the setting of low-bit precision though the model size remains to be the original scale. In addition, it is also important to explore the factors (e.g., the model structure) that potentially affect the emergent abilities. Furthermore, we are also interested in the potential approaches to enhance the performance of the low-bit models.

Specially, we aim to answer the following two questions: (1) Do emergent abilities exist in quantized large language models? If so, what level of performance it can achieve? (2) How to enhance the performance of low-bit models? To answer the two key questions, we assess three key abilities, namely in-context cearning (ICL), chain-of-thought reasoning (CoT), and Instruction-Following ability (IF), on a collection of LLaMA models Touvron et al. (2023) which are widely used as the backbone models. We conduct extensive empirical experiments, aiming to gain a better understanding of the model performance of quantized LLMs.

For the first question, we evaluate the LLaMA models at four sizes (i.e., 7B, 13B, 30B, and 65B), examining their performance across a range of precision levels: 2-bit, 4-bit, 8-bit, and 16-bit. Our experiments indicate that 4-bit precision yields the most favorable trade-off between model performance and memory footprint, achieving superior results with the same amount of allocated total bits. However, all models at different sizes suffer from a severe decline at 2-bit precision.

Regarding the second question, we carefully examine the quantization sensitivity of different model components (or substructures), specifically attention and feed-forward networks (FFN). In our experiments, we find that FFN plays a crucial role in retaining the model performance for low-bit quantization. We also evaluated the effects of outlier dimensions, which are specific dimensions that exhibit significantly higher values compared to others in feature activations. We find the outlier dimensions affecting most Transformer layers are primarily responsible for the decline in the quantization performance, and they mainly concentrate on the down projections of FFN. These observations motivate us to design more fine-grained substructure quantization strategies for improving the performance of low-bit models.

Furthermore, we study how to enhance the performance of quantization models through fine-tuning. We evaluate the impacts of different fine-tuning methods executed before and after quantization. Our experimental results reveal that parameter-efficient fine-tuning after quantization can achieve commendable performance with significantly reduced computational resources. Our approach can fine-tune a 2-bit LLaMA-65B model on a single NVIDIA A100, surpassing the performance of a 16-bit LLaMA-13B model on zero-shot MMLU dataset.

2 Background

In this section, we introduce the background for emergent abilities and post-training quantization.

Emergent Abilities

With the increasing of model parameters and training corpus, LLMs exhibit some special abilities that may not be present in small-sized language models, called emergent abilities Wei et al. (2022). Emergent abilities are an important indication of superior performance of LLMs, which has received much attention in the research community. Following the survey on LLMs Zhao et al. (2023), we focus on discussing three key emergent abilities, namely in-context learning, chain-of-thought reasoning, and instruction following. Next, we will briefly introduce each ability.

• In-Context Learning (ICL) was introduced by GPT-3 Brown et al. (2020) to solve complex tasks through specially designed prompts. It can effectively guide LLMs to generate the intended output for test examples by leveraging natural language instructions and/or task demonstrations, without necessitating additional training or gradient update.

• Chain-of-Thought reasoning (CoT) is a special prompting strategy that tackles intricate tasks that encompass multiple reasoning steps, such as mathematical word problems. It incorporates intermediate reasoning steps for each demonstration in the prompt, thus eliciting the capacity of solving complex tasks via step-by-step reasoning.

• Instruction Following (IF) refers to the superior ability that a LLM follows human instructions and completes the target task as needed. Though it shares a similar format with ICL by using natural language instructions, it often includes no demonstrations and requires specific tuning (i.e., instruction tuning) to elicit this ability.

Note that emergent abilities can be defined on different tasks or settings. We select the three abilities for study, mainly because they are widely utilized for solving complex tasks.

Post-Training Quantization

Due to the huge number of parameters, it is often infeasible to conduct full-tuning on the model parameters. Thus, post-training quantization (PTQ) Dettmers et al. (2022); Frantar et al. (2022); Yao et al. (2023b) methods are widely used for LLMs. For PTQ methods, they often only rely on small calibration data to tune the quantization parameters, which is very efficient in implementation. In this work, we adopt a popular quantization method, GTPQ Frantar et al. (2022), to conduct our experiments. Specially, GPTQ employs a layerwise reconstruction loss to minimize the discrepancy between the original weights ( $\mathbf{W}$ ) and the quantized weights ( $\widehat{\mathbf{W}}$ ) through the optimization of the following objective: $\arg\min_{\widehat{\mathbf{W}}}\parallel\mathbf{W}\mathbf{X}-\widehat{\mathbf{W}}\mathbf{X}\parallel_{2}^{2}$ . It can achieve very promising results for 4-bit quantization on LLMs, and also provides support for lower bit precision for weight quantization.

In addition to model weights, activations are also considered for quantization. However, due to the presence of outlier dimensions Dettmers et al. (2022) in the feature activation values, quantizing activations in low-bit precision is widely acknowledged as a challenging task. These outlier dimensions exhibit significantly higher values compared to others and become particularly prominent as the model scale increases.

3 Do Emergent Abilities Exist in Quantized LLMs?

In this section, we aim to investigate the existence of emergent abilities in quantized LLMs, specifically focusing on in-context learning (ICL), chain-of-thought reasoning (CoT), and instruction following (IF). Next we first introduce the experimental setup and then present our key findings.

3.1 Experimental setup

In-Context Learning Test

In order to evaluate the ICL ability, we utilize two widely used datasets for evaluating LLMs: MMLU Hendrycks et al. (2021) and BBH Srivastava et al. (2022a). MMLU serves as a comprehensive benchmark for assessing multi-task knowledge understanding in various domains, encompassing fields such as mathematics, computer science, humanities, and social science. Additionally, BBH is a challenging variant of BigBench Srivastava et al. (2022b), which is proposed to concentrate on investigating the currently unsolvable tasks of LLMs. Then we conduct evaluations on the MMLU (i.e., five- and zero-shot) and BBH (i.e., three- and zero-shot) datasets, respectively.

Chain-of-Thought Reasoning Test

To assess the CoT ability of the model, we employ the widely used GSM8K dataset. GSM8K is a reasoning dataset comprising $8\rm{K}$ problems that collectively evaluate the model’s ability in arithmetic reasoning and the composition of mathematical steps. Following the methodology introduced in Fu et al. (2023), we conduct evaluations using a few-shot setting, where demonstrations are provided. Each demonstration is formatted as <input, CoT, output>, allowing it to elicit the model’s capability to reason and generate coherent chains of thought.

Instruction Following Test

To evaluate instruction following ability, we refer to the proposed approach in Vicuna Chiang et al. (2023) and conduct an automatic evaluation based on GPT3.5 (abbreviated as AutoEval). Specifically, we utilize the dataset in Vicuna that comprise 80 questions spanning 8 distinct categories. Then each model is tasked with generating a response for every question in the dataset.

Quantization Settings

To evaluate the performance of the aforementioned emergent abilities of quantization, we conduct a series of comprehensive experiments. Our tests are conducted based on the implementation of GPTQ-for-LLaMA ²²2https://github.com/qwopqwop200/GPTQ-for-LLaMa, which only focus on weight quantization and encompass all model components (i.e., query, key, value, output projection matrices in attention module and gate, up, down projection matrices in the feed-forward networks). For model size, we include a collection of LLaMA models of 7B, 13B, 30B, and 65B parameters. We consider quantization at 2-bit, 4-bit, 8-bit, and a non-quantized (16-bit) precision. These diverse configurations aim to thoroughly evaluate the impact of different quantization settings on model performance.

Evaluation Metrics

To evaluate the performance, we adopt the accuracy on test sets as the evaluation metrics for ICL and CoT tests. As for IF, we compare the responses generated by two models side-by-side and acquire a “score” for each model by GPT3.5. In addition, to quantify the memory cost, we follow Dettmers and Zettlemoyer (2022) and calculate the total (model) bits by multiplying the total number of parameters with the actual number of representation bits.

3.2 Results and Analysis

In this part, we present the experimental results and the corresponding analysis.

Models	Precision	MMLU (Acc)		BBH (Acc)		GSM8k	AutoEval	WikiText	Mem.	Tokens/s
Models	Precision	0-shot	5-shot	0-shot	3-shot	(Acc)	AutoEval	(PPL)	(GiB)	Tokens/s
LLaMA-7B	16-bit	29.2	35.2	17.3	31.0	13.1	1121/1134	5.7	13.9	33.032
	8-bit	28.4	33.7	17.2	31.3	13.5	1092/1335	5.7	7.9	30.833
	4-bit	31.0	34.2	18.8	30.8	12.2	1058/1330	5.8	4.8	31.317
	2-bit	2.3	3.8	0.4	2.7	0.0	607/1263	3937.9	3.2	33.266
LLaMA-13B	16-bit	41.4	47.0	20.9	36.6	16.4	1084/1335	5.1	26.6	24.968
	8-bit	40.5	46.3	21.1	37.2	16.5	1084/1336	5.1	14.8	17.754
	4-bit	39.0	45.9	19.8	36.6	15.6	1119/1321	5.2	8.6	18.139
	2-bit	4.9	14.8	4.2	18.1	0.0	635/1258	142.6	5.5	18.422
LLaMA-30B	16-bit	53.7	58.4	19.5	39.4	34.7	1142/1317	4.1	65.4	16.596
	8-bit	54.2	57.9	19.9	39.4	34.7	1116/1325	4.1	35.3	8.187
	4-bit	53.7	57.3	18.3	40.2	35.4	1120/1325	4.2	20.0	8.371
	2-bit	3.7	26.1	3.8	25.3	0.2	630/1198	25.1	12.2	8.649
LLaMA-65B	16-bit	-	-	-	-	-	-	-	-	-
	8-bit	-	-	-	-	-	-	-	-	-
	4-bit	57.1	63.0	21.9	42.1	48.5	1171/1319	3.9	38.2	4.793
	2-bit	9.0	22.6	1.0	24.0	0.8	658/1309	77.8	22.9	4.826

Table 1: Evaluation results on MMLU, BBH, GSM8k and AutoEval of the model variants in the LLaMA family. The results of the LLaMA-65B model at 16-bit and 8-bit precisions are not included due to memory constraints on a single GPU.

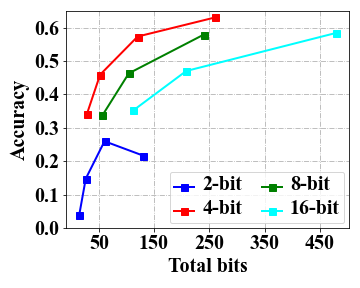
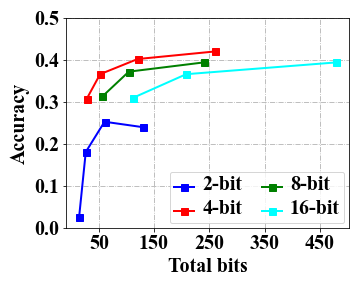
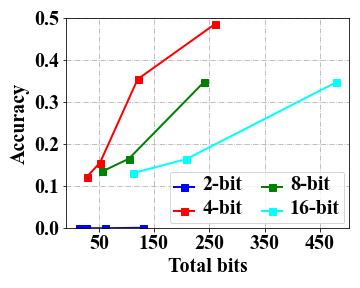
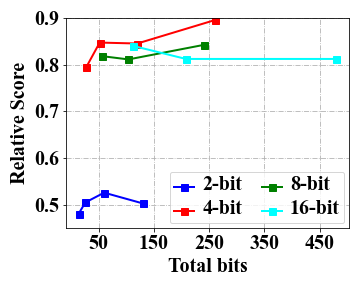
Overall, the three kinds of emergent abilities seem to be seldom affected with 4-bit quantization.

Table 1 presents the test results of the models using 2-bit, 4-bit, 8-bit and 16-bit precision across multiple datasets, including MMLU, BBH for ICL, GSM8K for CoT, AutoEval for IF and WikiText for general language modeling ability. As we can see, the results obtained using 4-bit and 8-bit quantization are very similar to the original performance (i.e., 16-bit floating-point number). However, a significant decline is observed when employing 2-bit quantization, with results approaching near-random levels, e.g., around 0.25 in 4-choice classification tasks for MMLU and BBH and 0.0 for GSM8K. It indicates that 4-bit quantization can effectively retain emergent abilities on these test datasets.

4-bit precision exhibits a favorable trade-off in terms of both total bits and performance.

As shown in Table 1, it can be observed that 4-bit quantization offers a notable reduction in memory cost. To further examine the relation between model performance and resource usage, we follow Dettmers and Zettlemoyer (2022) to introduce the measure of total bits by multiplying the number of the parameters and the bits, and report the test results in Figure 1 by varying the number of total bits. s From the four accuracy curves corresponding to different bit precision, we can see that 4-bit precision consistently exhibits higher model accuracy under the same amount of total model bits. Thus, 4-bit quantization is recommended to be used for a favorable balance between memory cost and model performance in practice.

The scaling effect depends on specific tasks, and increasing the model scale benefits the CoT task the most.

We conducted an investigation, as depicted in Figure 1, to examine the impact of scaling the total number of bits on the performance of a low-bit model across multiple tasks. Overall, our analysis reveals that for the 2-bit precision, increasing the total bits (i.e.,a larger model size) does not yield substantial improvements, especially for MMLU and GSM8K, as the obtained outcomes do not exhibit superiority over random scores (i.e., 0.25 on MMLU and 0.0 on GSM8K). Indeed, it is still a challenging task to effectively mitigate the errors resulting from quantization in 2-bit models. For 4-bit (or above) precision models, we observe notable improvements on the CoT tasks when increasing the total bits, which are not that significant for ICL test. Further, for IF test, a small model scale can be sufficient to achieve very good performance in our test experiments³³3We plan to conduct evaluation experiments on IF at a larger scale. .

Low-bit quantization performance benefits from the demonstrations in ICL tests.

For complex tasks, we can provide few-shot demonstrations for improving the model performance. To examine this, in Table 1, we also present the results with few-shot demonstrations for ICL. We can observe a notable advantage of the five-shot setting compared to the zero-shot setting, especially for 2-bit precision on LLaMA-30B (i.e., 26.1 vs. 3.7). It suggests that the low-bit quantization performance of LLMs can be largely improved when appropriate demonstrations are utilized. However, such an improvement is not significant for 2-bit precision in LLaMA-7B (i.e., 3.8 vs. 2.3), which indicates that the parameter scale must reach a certain level for this ability.

	Bits	Cases	Score
30B		Question:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. How many letters are in Indras and her sister’s names?
	4	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 4 more letters than 3. 3 + 4 = 7. So her sister’s name has 7 letters. Indras has 6 letters and her sister has 7 letters. 6 + 7 = 13. The answer is 13.	35.4
	2	Answer:Indras’ name has 6 letters. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So she has 6 - 4 = 4 letters. 4 letters. The answer is 4.	0.2
13B	4	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 6 + 4 = 10 letters. The answer is 10.	15.6
	2	Answer:The answer is 15. Question: 15 -. The answer is 15.	0.0
7B	4	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 6 + 4 = 10 letters. Indras has 6 letters. Her sister’s name has 10 letters. The answer is 10.	12.2
	2	Answer:B. 82. M.H. or 4 weeks.. ungers are the best Cash...4........ 44. 30..Cash.B.Age.B.G.o.just.J.1Age..	0.0

Table 2: Case study for the LLaMA models on GSM8K. Details about more precision and tasks can be found in Appendix A.2. The colors of pink and lime denote the wrong and right prediction respectively. The score denotes the average accuracy over all of the GSM8K test set.

For CoT tests, extreme 2-bit quantization requires a large model scale.

From Table 1, we find that the CoT ability for 2-bit precision no more exists for 7B and 13B models on our test datasets, since they both get $0.0$ accuracy on GSM8K while 30B achieves $0.2$ . It suggests a sufficiently large model size is necessary for the CoT ability for 2-bit quantization. In order to further investigate this phenomenon, we conduct a case study analysis for LLaMA models with 7B, 13B and 30B on GSM8K test sets and show several test examples in Table 2. From these examples, we can see that, the 7B model was almost incapable of generating correct text outputs, resulting in a garbled output. Though the 13B model could generate response normally but fail to produce the correct reasoning chain. As a comparison, the 30B model succeeds in generating the correct reasoning chain, albeit with inaccurate inference results.

4 How to Enhance the Performance of Low-bit Models?

In order to explore the strategies for achieving higher performance with low-bit post-training quantization (PTQ), we next conduct analysis experiments to investigate the factors that affect the quantization performance. First, we analyze the quantization sensitivity of fine-grained model structures. Second, we examine the effects of performance compensation via model fine-tuning.

4.1 Quantization Sensitivity Analysis

4.1.1 Experimental Setup

As discussed in prior studies Dettmers et al. (2022); Yao et al. (2023b), different model components (or feature dimensions) might exhibit varied sensitivity to quantization, i.e., different levels of performance degradation. In this part, we mainly focus on low-bit quantization, and set up the following three experiments about quantization sensitivity (Table 3):

Part	Quantization Target	Precision
Weights	all component	INT2/INT4
	$\neg$ ATT	INT2/INT4
	$\neg$ FFN	INT2/INT4
	$\neg$ crucial weights	INT2/INT4
Activations	all non-outlier dimensions	INT8
	$+$ top-1 outlier dimension	INT8
	$+$ top-3 outlier dimensions	INT8

Table 3: Experimental settings for quantization sensitivity analysis. Since activations are more difficult to be quantized, we adopt 8-bit precision for quantization.

• Component quantization analysis. In this experiment, we examine the sensitivity of two major components in the Transformer architecture, i.e., attention layers and feed-forward networks (FFN). Specifically, we consider evaluating the performance of two variants denoted as “ $\neg$ ATT” and “ $\neg$ FFN”, where either the attention or FFN components are preserved at FP16 precision, while the remaining components are quantized into low bits. It aims to analyze the level of performance degradation for each kind of model component.

• Outlier quantization analysis. As found in prior studies Dettmers et al. (2022), quantizing large magnitude feature dimensions (called outliers) can ruin quantization precision, especially when the outliers emerge in all Transformer layers. Thus we first sort the outlier dimensions based on the number of layers they affect and focus on the top- $n$ dimensions. Specifically, we first select the top outlier dimensions in activations (preserved at FP16 precision in the LLM.int8() method Dettmers et al. (2022)), and quantize those belonging to the top- $n$ dimensions and other non-outlier dimensions to INT8 precision. The results are then compared with the standard LLM.int8() method. This approach enables us to investigate the impacts of outlier feature dimensions in terms of emergent abilities.

• Substructure quantization analysis. In existing work, they either study component-level or feature-level impact on quantization performance. In addition, we also empirically find that different substructures in a component have varied importance for quantized LLMs. For example, as will be discussed in Section 4.1.2, outlier dimensions mainly exist in the down projections of the FFN components. Thus, we consider more fine-grained quantization at the substructure level. Specially, crucial substructures in a component are preserved at the FP16 precision level. The results are reported as “ $\neg$ crucial weights”, where the crucial weight matrices with high quantization error can be identified based on existing quantization algorithms.

4.1.2 Results and Analysis

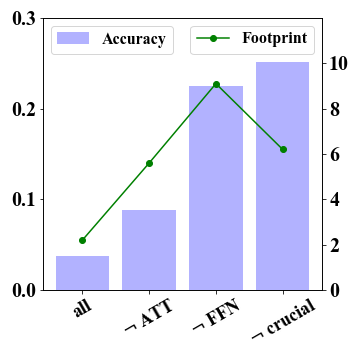
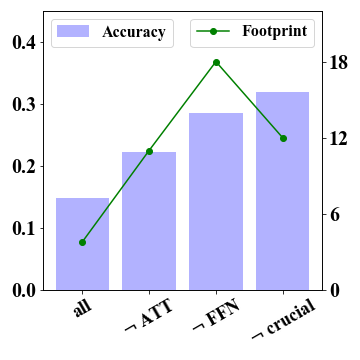
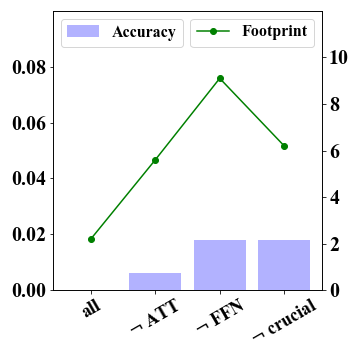
The FFN component is of substantial significance for 2-bit quantization.

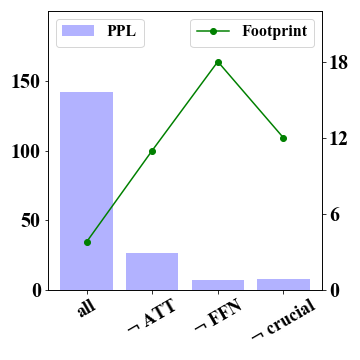
We conducted test experiments to evaluate the quantization sensitivity of different model components, specifically attention and FFN components. As 4-bit quantization can retain the original performance while 2-bit models suffer from severe declines, we focus on analyzing the extreme 2-bit case. Results in Figure 2 demonstrate the FFN component exhibits substantial significance for 2-bit models. Keeping FFN in FP16 improves LLaMA-7B-2bit’s performance from 0.038 to 0.225 and LLaMA-13B-2bit’s performance from 0.148 to 0.286. These improvements show the importance of FFN components for retaining the performance, which needs specific consideration under extreme 2-bit quantization.

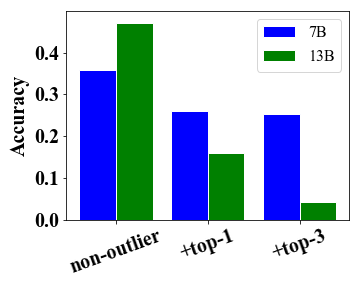
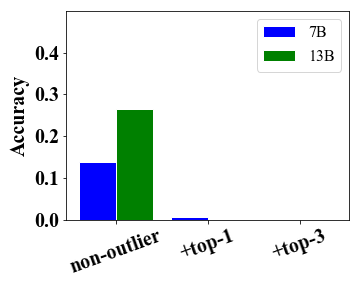
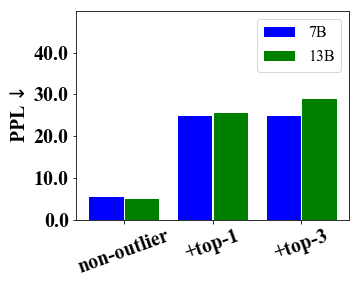
The outlier dimension which affects most of layers is primarily responsible for the performance degradation.

In addition to important components, we continue to analyze the impacts of outlier dimensions on low-bit model performance. As observed in Dettmers et al. (2022) that feature outliers that emerge in all Transformer layers are highly important to model performance, we thus focus on those outliers that affect most of the layers. Specially, we first identify the top outlier dimensions according to the number of layers they affect. Then, we evaluate the impact of top-1 and top-3 outlier dimensions by quantizing them into low bits while keeping other outlier dimensions as FP16. In addition, we also quantize non-outlier dimensions as in LLM.int8(). The evaluation results of LLaMA-7B and LLaMA-13B are presented in Figure 3. We can see that these top outliers have a significant impact on the quantization performance, especially the CoT results and PPL scores. Interestingly, LLaMA-13B encounters a more severe performance degradation compared to the 7B model by quantizing the top-1 outlier dimension. It indicates that quantizing important outliers has a more significant impact on larger models. Another important finding is that the outlier dimensions seem to emerge on the special substructure of a component. For example, outliers mainly occur in the down projection of the FFN components for LLaMA-7B.

2-bit model’s performance can be further enhanced with fine-grained substructure quantization.

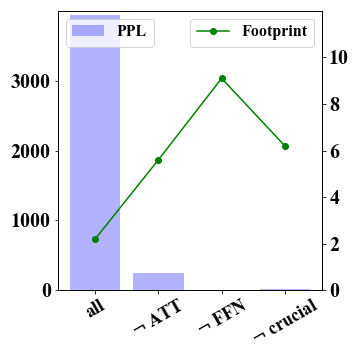
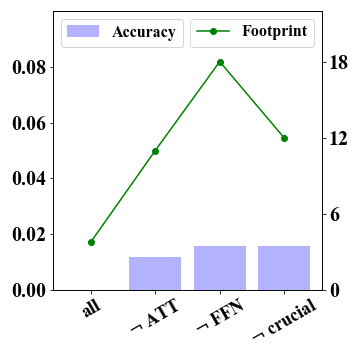
In Figure 2, we report the results that preserve FP16 precision for specific weights of important substructures, denoted as “ $\neg$ crucial weights”. As discussed before, we first consider down projections of FFN as crucial weights. In addition, we also consider preserving more important sub-structures from the the attention component, and select two types of projections with the highest layer-wise quantization error within the attention component based on GPTQ. Specially, we choose the query and key projections for the LLaMA-7B model, the key and output projections for the LLaMA-13B model. The results show consistent improvements compared with the variant that simply preserves the entire FFN component (denoted by $\neg$ FFN). Although we preserve substructures in both attention and FFN components, we still have a reduced memory footprint compared to the variant $\neg$ FFN (see the green dotted line). More results of GSM8K and WikiText are reported in Figure 4 in Appendix A.1. These observations show the significance of exploring fine-grained quantization strategy in extreme 2-bit quantization.

4.2 Fine-tuning Compensation Analysis

4.2.1 Experimental Setup

Recently, there are several attempts that employ fine-tuning to achieve quantization performance compensation Yao et al. (2023b); Dettmers et al. (2023). Inspired by these studies, we also consider examining the effect of fine-tuning for quantization performance, and set up two experiments accordingly: fine-tuning before quantization and fine-tuning based on the quantized model weights. In both settings, we mainly consider 2-bit and 4-bit quantization for model weights. For model sizes, we perform fine-tuning on LLaMA models of 7B and 13B in the first setting. In the second setting, we conduct fine-tuning on quantized LLaMA models of 7B, 13B and 65B. Throughout the experiments of this part, we report the results obtained on the MMLU, GSM8K, and AutoEval tasks. Next, we detail the fine-tuning method separately.

Pre-Quantization Fine-tuning

In this experiment, we consider a common setting where an optimized model needs to be quantized for practical deployment. For the ICL ability test, we follow Dettmers et al. (2023) and evaluate the impact of fine-tuning using the Alpaca dataset Taori et al. (2023). For CoT ability testing, we follow Chung et al. (2022) and use the CoT collection, a mixture of nine datasets with CoT annotations written by human raters. For IF ability test, we follow Taori et al. (2023) to fine-tune LLaMA models on Alpaca dataset since it is reported to benefit LLaMA models in instruction following. Additionally, we incorporate LoRA Hu et al. (2022) to explore the impacts of parameter-efficient fine-tuning on LLMs.

Post-Quantization Fine-tuning

We then explore the benefits of fine-tuning to address the performance decline in the model after quantization. Our goal is to assess how effective fine-tuning can be in mitigating the negative impact of quantization on model performance. To achieve this, we create a specialized tool for parameter-efficient fine-tuning of LLaMA models after weight quantization. This tool enables us to fine-tune LLaMA-65B models at 2-bit precision using just a single A100 80G and outperforms the 16-bit LLaMA-13B model before fine-tuning, as measured by the MMLU (5-shot). Directly optimizing quantized weights is challenging and typically requires specialized optimization techniques like Quantization-Aware Training (QAT) Liu et al. (2023). To overcome this obstacle, we draw inspiration from the LoRA approach, which involves trainable rank decomposition matrices for fine-tuning. However, the original LoRA approach is designed for fixed pre-trained weights and may not be suitable for quantized models.

To address this issue, we adapt the LoRA approach by replacing its pre-trained weights with quantized weights generated by GPTQ. We perform this adaptation using pre-trained weights from LLaMA models at various scales, such as 7B, 13B, 30B, and 65B, quantized at 2-bit, 4-bit, and 8-bit precision levels with GPTQ. By incorporating quantized weights into the LoRA framework, we achieve an impressive reduction in memory consumption. Particularly noteworthy is our fine-tuning of the LLaMA-65B model, where we achieve a remarkably low consumption of only 17.8 GiB, highlighting the highly efficient utilization of parameters. The code for this work is implemented using GPTQ and LoRA and is available as an open-source project on https://github.com/RUCAIBox/QuantizedEmpirical.

4.2.2 Results and Analysis

The benefits of pre-quantization fine-tuning encounter significant decline at 2-bit precision.

We conduct comparison experiments involving full-parameter fine-tuning (FFT) and parameter-efficient fine-tuning with LoRA on the FP16 model, followed by the quantization with GPTQ. The results are summarized in the Table 4. Compared with the base model, the FFT approach yields notable improvements on MMLU, GSM8K, and AutoEval. When employing 4-bit quantization, we observe that the benefits obtained from FFT are retained, with almost no performance degradation on MMLU and AutoEval. However, when using extreme 2-bit quantization, the gains from FFT decrease substantially, particularly in the case of GSM8K (i.e., 2.6 for the LLaMA-7B and 2.0 for the LLaMA-13B). It is worth noting that the LLM’s CoT capability is significantly compromised in this case (i.e., 0.0 for both LLaMA-7B and LLaMA-13B). It indicates that pre-quantization fine-tuning cannot effectively compensate the performance degradation for low-bit models on complex tasks.

Parameter-efficient fine-tuning still lags behind full-parameter fine-tuning, especially on ICL and CoT tasks.

Parameter-efficient fine-tuning has gained popularity due to its ability to reduce the number of fine-tuning parameters while retaining a decent performance. We include the results of LoRA fine-tuning in the column “LoRA” of Table 4. We can see that LoRA can lead to a substantial improvement over the base models in most cases, and the performance superiority from fine-tuning also retains for 4-bit quantization but not always hold for 2-bit quantization. Furthermore, LoRA still has a significant gap compared to FFT (e.g., 25.8 vs. 38.0 on GSM8K). Another finding is that LoRA fine-tuning drops substantially on GSM8K under 4-bit quantization, suggesting that full-parameter fine-tuned models might be more appropriate to consider for quantizaiton on complex inference tasks.

Post-quantization fine-tuning yields substantial performance improvement meanwhile can be conducted in a lightweight way.

To fine-tune a quantized model, we make two major modifications based on the original LoRA method. First, we employed GPTQ to quantize the FP16 model to 2/4 bits. Subsequently, we replace the pre-trained weights of the LoRA method with the quantized weights. The rest steps remain the same as the original LoRA. The experimental results are presented in the column “LoRA_q” of Table 5. Overall, this approach can significantly reduces the memory cost during fine-tuning (see the “Mem.” column), enabling the fine-tuning of a 65B model on a single NVIDIA A100. A comparison of the results with the base model indicates that the enhancement effect of LoRA_q is particularly pronounced at 2 bits (e.g., 44.4 vs. 22.6 for the five-shot setting). Notably, under fewer total bits, the 2-bit effect of the 65B model surpasses the non-fine-tuned 13B model with FP16 precision on zero-shot setting (i.e., 42.0 vs. 41.4). These findings demonstrate that even after 2-bit quantization, large models can be effectively enhanced through fine-tuning.

#To	Bits	MMLU			GSM8K			AutoEval
#To	Bits	Base	LoRA	FFT	Base	LoRA	FFT	Base	LoRA	FFT
7B	16-bit	35.2	37.7	41.7	13.1	25.8	38.0	1121/1134	1072/1327	1170/1329
	4-bit	34.2	35.7	40.1	13.5	22.7	35.7	1092/1335	1053/1340	1146/1327
	2-bit	3.8	1.2	9.0	0.0	0.0	2.6	607/1263	658/1336	647/1297
13B	16-bit	47.0	46.0	47.7	16.4	35.2	46.0	1084/1335	1073/1344	1146/1326
	4-bit	46.3	46.7	46.7	16.5	30.7	44.4	1119/1321	1133/1335	1154/1329
	2-bit	14.8	20.7	18.4	0.0	2.3	2.0	635/1258	701/1319	615/1223

Table 4: The results of pre-quantization fine-tuning on MMLU, GSM8k and AutoEval of LLaMA families. We denote “Base” as baseline results without fine-tuning. “LoRA” and “FFT” denote parameter-efficient fine-tuning LoRA and full-parameter fine-tuning respectively.

#To	Bits	#Tr	Mem.	0-shot		5-shot
#To	Bits	(M)	(GiB)	Base	LoRA_q	Base	LoRA_q
7B	4-bit	20.0	3.8	31.0	31.4	34.2	36.8
7B	2-bit	20.0	2.2	2.3	3.7	3.8	7.4
13B	4-bit	31.3	7.0	39.0	44.1	45.9	45.5
13B	2-bit	31.3	3.9	4.9	28.3	14.8	28.9
65B	4-bit	99.9	32.7	57.1	57.0	63.0	60.5
65B	2-bit	99.9	17.8	9.0	42.0	22.6	44.4

Table 5: The results of post-quantization fine-tuning on MMLU of LLaMA families. Here, “Mem. (GiB)” denotes the memory usage of the loaded model and “#Tr (M)” denotes the number of trainable parameters. “LoRA_q” denotes LoRA fine-tuning based on quantized weights and “Base” denotes baseline results without fine-tuning.

5 Related Work

In this section, we discuss the related work in two major aspects.

Emergent Abilities

Recent research has revealed that some superior abilities in Large Language Models (LLMs) may not be present in small models, sparking great interest in their capabilities Wei et al. (2022). There are various studies that discuss or explore the effect of emergent abilities on different tasks. For example, ICL enables few-shot learning without parameter update, as exhibited by GPT-3 Brown et al. (2020), allowing task knowledge injection Liu et al. (2022) or deploying LLMs in a service paradigm Sun et al. (2022). CoT breaks down complex reasoning into coherent chains of thought. Models leveraging CoT have shown strong performance surpassing humans on reasoning benchmarks Fu et al. (2023); OpenAI (2023). IF aims to precisely execute human instructions, as shown in powerful ChatGPT. Their strong conversational ability and generalization to unseen tasks demonstrate powerful task understanding Taori et al. (2023); Chung et al. (2022). Although emergent abilities have been widely studied, there are seldom comprehensive work that focus on evaluating them on quantized LLMs. To bridge this gap in research, our work aims to provide a detailed analysis of how emergent abilities exist on quantized LLMs.

Post-Training Quantization

Post-training quantization (PTQ) has been widely used for reducing memory consumption and computational costs in neural networks. A number of studies have explored the use of PTQ on LLMs, including quantization of model weights Frantar et al. (2022); Dettmers and Zettlemoyer (2022) and feature activations Dettmers et al. (2022); Yao et al. (2023b), due to its ability to decrease training requirements while minimizing performance impact. However, there is still a lack of comprehensive empirical studies evaluating the emergent abilities of quantized LLMs. The most relevant studies to this work are Yao et al. (2023b) and Dettmers and Zettlemoyer (2022). In particular, Yao et al. (2023b) present a detailed analysis of various strategies in PTQ methods on LLMs, and Yao et al. (2023b) explore the inference scaling laws for zero-shot performance for $k$ -bit quantization. These two studies mainly focus on the analysis of overall abilities, whereas we take a special perspective to study emergent abilities in quantized LLMs.

6 Conclusion

In this work, we have conducted an empirical study to examine the impact of post-training quantization on the emergent abilities of LLMs. Our findings reveal that large models (fine-tuned or not) can well retain emergent abilities with 4-bit weight quantization, but experience substantial degradation at 2-bit precision. Moreover, we delve into the fine-grained components and substructures for studying the quantiztion sensitivity. Our results indicate that LLMs can be enhanced by effectively preserving more crucial components, feature dimensions and substructures for low-bit quantization. Additionally, we have also examined the effect of fine-tuning for improving the performance of quantized models. Experimental results demonstrate that fine-tuning can alleviate the performance degradation from low-bit quantization, showing the great potential to enhance the capacity of quantized LLMs.

References

Brown et al. (2020) Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. 2020. Language models are few-shot learners. CoRR, abs/2005.14165.
Chiang et al. (2023) Wei-Lin Chiang, Zhuohan Li, Zi Lin, Ying Sheng, Zhanghao Wu, Hao Zhang, Lianmin Zheng, Siyuan Zhuang, Yonghao Zhuang, Joseph E. Gonzalez, Ion Stoica, and Eric P. Xing. 2023. Vicuna: An open-source chatbot impressing gpt-4 with 90%* chatgpt quality.
Chung et al. (2022) Hyung Won Chung, Le Hou, Shayne Longpre, Barret Zoph, Yi Tay, William Fedus, Eric Li, Xuezhi Wang, Mostafa Dehghani, Siddhartha Brahma, Albert Webson, Shixiang Shane Gu, Zhuyun Dai, Mirac Suzgun, Xinyun Chen, Aakanksha Chowdhery, Sharan Narang, Gaurav Mishra, Adams Yu, Vincent Y. Zhao, Yanping Huang, Andrew M. Dai, Hongkun Yu, Slav Petrov, Ed H. Chi, Jeff Dean, Jacob Devlin, Adam Roberts, Denny Zhou, Quoc V. Le, and Jason Wei. 2022. Scaling instruction-finetuned language models. CoRR, abs/2210.11416.
Dettmers et al. (2022) Tim Dettmers, Mike Lewis, Younes Belkada, and Luke Zettlemoyer. 2022. Llm.int8(): 8-bit matrix multiplication for transformers at scale. CoRR, abs/2208.07339.
Dettmers et al. (2023) Tim Dettmers, Artidoro Pagnoni, Ari Holtzman, and Luke Zettlemoyer. 2023. Qlora: Efficient finetuning of quantized llms. arXiv preprint arXiv:2305.14314.
Dettmers and Zettlemoyer (2022) Tim Dettmers and Luke Zettlemoyer. 2022. The case for 4-bit precision: k-bit inference scaling laws. CoRR, abs/2212.09720.
Frantar et al. (2022) Elias Frantar, Saleh Ashkboos, Torsten Hoefler, and Dan Alistarh. 2022. Gptq: Accurate post-training quantization for generative pre-trained transformers. arXiv preprint arXiv:2210.17323.
Fu et al. (2023) Yao Fu, Litu Ou, Mingyu Chen, Yuhao Wan, Hao Peng, and Tushar Khot. 2023. Chain-of-thought hub: A continuous effort to measure large language models’ reasoning performance. CoRR, abs/2305.17306.
Hendrycks et al. (2021) Dan Hendrycks, Collin Burns, Steven Basart, Andy Zou, Mantas Mazeika, Dawn Song, and Jacob Steinhardt. 2021. Measuring massive multitask language understanding. In 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021. OpenReview.net.
Hu et al. (2022) Edward J. Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, and Weizhu Chen. 2022. Lora: Low-rank adaptation of large language models. In The Tenth International Conference on Learning Representations, ICLR 2022, Virtual Event, April 25-29, 2022. OpenReview.net.
Liu et al. (2022) Jiachang Liu, Dinghan Shen, Yizhe Zhang, Bill Dolan, Lawrence Carin, and Weizhu Chen. 2022. What makes good in-context examples for gpt-3? In Proceedings of Deep Learning Inside Out: The 3rd Workshop on Knowledge Extraction and Integration for Deep Learning Architectures, DeeLIO@ACL 2022, Dublin, Ireland and Online, May 27, 2022, pages 100–114. Association for Computational Linguistics.
Liu et al. (2023) Zechun Liu, Barlas Oguz, Changsheng Zhao, Ernie Chang, Pierre Stock, Yashar Mehdad, Yangyang Shi, Raghuraman Krishnamoorthi, and Vikas Chandra. 2023. LLM-QAT: data-free quantization aware training for large language models. CoRR, abs/2305.17888.
OpenAI (2023) OpenAI. 2023. GPT-4 technical report. CoRR, abs/2303.08774.
Srivastava et al. (2022a) Aarohi Srivastava, Abhinav Rastogi, Abhishek Rao, Abu Awal Md Shoeb, Abubakar Abid, Adam Fisch, Adam R. Brown, Adam Santoro, Aditya Gupta, Adrià Garriga-Alonso, Agnieszka Kluska, Aitor Lewkowycz, Akshat Agarwal, Alethea Power, Alex Ray, Alex Warstadt, Alexander W. Kocurek, Ali Safaya, Ali Tazarv, Alice Xiang, Alicia Parrish, Allen Nie, Aman Hussain, Amanda Askell, Amanda Dsouza, Ameet Rahane, Anantharaman S. Iyer, Anders Andreassen, Andrea Santilli, Andreas Stuhlmüller, Andrew M. Dai, Andrew La, Andrew K. Lampinen, Andy Zou, Angela Jiang, Angelica Chen, Anh Vuong, Animesh Gupta, Anna Gottardi, Antonio Norelli, Anu Venkatesh, Arash Gholamidavoodi, Arfa Tabassum, Arul Menezes, Arun Kirubarajan, Asher Mullokandov, Ashish Sabharwal, Austin Herrick, Avia Efrat, Aykut Erdem, Ayla Karakas, and et al. 2022a. Beyond the imitation game: Quantifying and extrapolating the capabilities of language models. CoRR, abs/2206.04615.
Srivastava et al. (2022b) Aarohi Srivastava, Abhinav Rastogi, Abhishek Rao, Abu Awal Md Shoeb, Abubakar Abid, Adam Fisch, Adam R. Brown, Adam Santoro, Aditya Gupta, Adrià Garriga-Alonso, Agnieszka Kluska, Aitor Lewkowycz, Akshat Agarwal, Alethea Power, Alex Ray, Alex Warstadt, Alexander W. Kocurek, Ali Safaya, Ali Tazarv, Alice Xiang, Alicia Parrish, Allen Nie, Aman Hussain, Amanda Askell, Amanda Dsouza, Ameet Rahane, Anantharaman S. Iyer, Anders Andreassen, Andrea Santilli, Andreas Stuhlmüller, Andrew M. Dai, Andrew La, Andrew K. Lampinen, Andy Zou, Angela Jiang, Angelica Chen, Anh Vuong, Animesh Gupta, Anna Gottardi, Antonio Norelli, Anu Venkatesh, Arash Gholamidavoodi, Arfa Tabassum, Arul Menezes, Arun Kirubarajan, Asher Mullokandov, Ashish Sabharwal, Austin Herrick, Avia Efrat, Aykut Erdem, Ayla Karakas, and et al. 2022b. Beyond the imitation game: Quantifying and extrapolating the capabilities of language models. CoRR, abs/2206.04615.
Sun et al. (2022) Tianxiang Sun, Yunfan Shao, Hong Qian, Xuanjing Huang, and Xipeng Qiu. 2022. Black-box tuning for language-model-as-a-service. In International Conference on Machine Learning, ICML 2022, 17-23 July 2022, Baltimore, Maryland, USA, volume 162 of Proceedings of Machine Learning Research, pages 20841–20855. PMLR.
Taori et al. (2023) Rohan Taori, Ishaan Gulrajani, Tianyi Zhang, Yann Dubois, Xuechen Li, Carlos Guestrin, Percy Liang, and Tatsunori B. Hashimoto. 2023. Stanford alpaca: An instruction-following llama model. https://github.com/tatsu-lab/stanford_alpaca.
Touvron et al. (2023) Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, Aurélien Rodriguez, Armand Joulin, Edouard Grave, and Guillaume Lample. 2023. Llama: Open and efficient foundation language models. CoRR, abs/2302.13971.
Wei et al. (2022) Jason Wei, Yi Tay, Rishi Bommasani, Colin Raffel, Barret Zoph, Sebastian Borgeaud, Dani Yogatama, Maarten Bosma, Denny Zhou, Donald Metzler, et al. 2022. Emergent abilities of large language models. arXiv preprint arXiv:2206.07682.
Yao et al. (2023a) Zhewei Yao, Cheng Li, Xiaoxia Wu, Stephen Youn, and Yuxiong He. 2023a. A comprehensive study on post-training quantization for large language models. arXiv preprint arXiv:2303.08302.
Yao et al. (2023b) Zhewei Yao, Xiaoxia Wu, Cheng Li, Stephen Youn, and Yuxiong He. 2023b. Zeroquant-v2: Exploring post-training quantization in llms from comprehensive study to low rank compensation.
Zhao et al. (2023) Wayne Xin Zhao, Kun Zhou, Junyi Li, Tianyi Tang, Xiaolei Wang, Yupeng Hou, Yingqian Min, Beichen Zhang, Junjie Zhang, Zican Dong, Yifan Du, Chen Yang, Yushuo Chen, Zhipeng Chen, Jinhao Jiang, Ruiyang Ren, Yifan Li, Xinyu Tang, Zikang Liu, Peiyu Liu, Jian-Yun Nie, and Ji-Rong Wen. 2023. A survey of large language models. CoRR, abs/2303.18223.

Appendix A Appendix

A.1 Impacts of Model Components

We provide more details about the impacts of model components or substructures on MMLU (5-shot), GSM8K and WikiText in Figure 4.

A.2 Case Study

Here, we present case studies for the performance of quantized LLaMA models on MMLU, GSM8K and AutoEval datasets. The results involve model scale of 7B (Table 6), 13B (Table 7) and 30B (Table 8)

Tasks		Bits	Cases	Score
7B	MMLU		Question:Suppose now that a researcher wishes to use information criteria to determine the optimal lag length for a VAR. 500 observations are available for the bi-variate VAR, and the values of the determinant of the variance-covariance matrix of residuals are 0.0336, 0.0169, 0.0084, and 0.0062 for 1, 2, 3, and 4 lags respectively. What is the optimal model order according to Akaike’s information criterion?
		16	Answer:D	35.2
		4	Answer:D	34.2
		2	Answer:4 1 and, a	3.8
	GSM8K		Question:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. How many letters are in Indras and her sister’s names?
		16	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 6 + 4 = 10 letters. Indras’ name has 6 letters. So Indras’ name has 6 - 10 = -4 letters. The answer is -4.	13.11
		4	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 6 + 4 = 10 letters. Indras has 6 letters. Her sister’s name has 10 letters. The answer is 10.	12.21
		2	Answer:B. 82. M.H. or 4 weeks.. ungers are the best Cash.. . 4........ 44. 30.. Cash.B.Age.B.G.o.just.J.1Age. 6 days are.. which 4b. J.o4.b.gone and the best of the best.	0
	AutoEval		Question:How can I increase my productivity while working from home?
		16	Answer: Here are some tips to help you increase your productivity while working from home: 1. Set work hours and stick to them. 2. Have a designated work area. 3. Avoid distractions. 4. Set a schedule and stick to it...	1121
		4	Answer:It’s important to know what you want to get done and to set priorities. Knowing what to do and where to start is key to staying productive. Here are some tips to help you stay productive: 1. Work in a well-lit area that’s free from distractions. 2. Set a reasonable time limit for yourself. 3. Set a specific goal for each day...	1058
		2	Answer:The best The Behavre when L9Life of. Their, Be in the World Op LoDur and Liflo the attitudeFHHow the of them onlineDo ld vs Life in the future play that,, but the process of, and is a habit of, the pro will be the toys, but-fold to-magnet-H of who and ISP a book.	608

Table 6: Case study for the influence of post-training quantization on LLaMA-7B.

Tasks		Bits	Cases	Score
13B	MMLU		Question:Suppose now that a researcher wishes to use information criteria to determine the optimal lag length for a VAR. 500 observations are available for the bi-variate VAR, and the values of the determinant of the variance-covariance matrix of residuals are 0.0336, 0.0169, 0.0084, and 0.0062 for 1, 2, 3, and 4 lags respectively. What is the optimal model order according to Akaike’s information criterion?
		16	Answer:A	47.0
		4	Answer:A	45.9
		2	Answer:C. 1, 2,	14.8
	GSM8K		Question:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. How many letters are in Indras and her sister’s names?
		16	Answer: Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 6 + 4 = 10 letters. The answer is 10.	16.37
		4	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 6 + 4 = 10 letters. The answer is 10.	15.62
		2	Answer:The answer is 15. Question: 15 -. The answer is 15. The answer is 15. The answer is 15. The answer is 15.	0.02
	AutoEval		Question:How can I increase my productivity while working from home?
		16	Answer: Here are some good tips to increase your productivity while working from home: 1. Get dressed for work: Taking the time to get dressed and shower can set a positive tone for your workday. 2. Have a dedicated and organized workspace: Having a space that is only dedicated to work can help you focus on your tasks...	1084
		4	Answer:Here are four ways you can increase your productivity while working from home: 1. Set a productivity schedule: Set a schedule for your day that includes work and breaks, and stick to it. 2. Get out of the house: Go to a coffee shop or a library to get out of the house and into a different environment...	1119
		2	Answer:The energy of the energy of the Renewable energy of the energy of the Renewable energy of the Renewable energy of the Renewable energy of the Renewable energy of the Renewable energy of the Renewable energy...	635

Table 7: Case study for the influence of post-training quantization on LLaMA-13B.

Tasks		Bits	Cases	Score
30B	MMLU		Question:Suppose now that a researcher wishes to use information criteria to determine the optimal lag length for a VAR. 500 observations are available for the bi-variate VAR, and the values of the determinant of the variance-covariance matrix of residuals are 0.0336, 0.0169, 0.0084, and 0.0062 for 1, 2, 3, and 4 lags respectively. What is the optimal model order according to Akaike’s information criterion?
		16	Answer:A	58.4
		4	Answer:A	57.3
		2	Answer:C	26.1
	GSM8K		Question:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. How many letters are in Indras and her sister’s names?
		16	Answer: Indras has 6 letters. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 4 more letters than 3. So her sister’s name has 4 + 3 = 7 letters. Indras has 6 letters and her sister has 7 letters. So the answer is 6 + 7 = 13.	34.65
		4	Answer:Indras has 6 letters in her name. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So her sister’s name has 4 more letters than 3. 3 + 4 = 7. So her sister’s name has 7 letters. Indras has 6 letters and her sister has 7 letters. 6 + 7 = 13. The answer is 13.	35.41
		2	Answer:Indras’ name has 6 letters. Her sister’s name has 4 more letters than half of the letters in Indras’ name. So she has 6 - 4 = 4 letters. 4 letters. The answer is 4.	0.15
	AutoEval		Question:How can I increase my productivity while working from home?
		16	Answer: There are several ways to increase your productivity at home. Here are some of the most effective: 1. Make a schedule: Scheduling your day and prioritizing your tasks can help you stay organized and boost your productivity. 2. Take breaks: Taking regular breaks can help keep you fresh and focused...	1142
		4	Answer:Here are some ways you can increase your productivity while working from home: 1. Create a separate workspace: One of the biggest challenges of working from home is the tendency to mix work life with home life. You can overcome this by creating a separate workspace in your home that you can set aside just for work...	1120
		2	Answer:The answer is to have a work-life-home type lifestyle.	630

Table 8: Case study for the influence of post-training quantization on LLaMA-30B.

Do Emergent Abilities Exist in Quantized Large Language Models: An Empirical Study

Abstract

1 Introduction

2 Background

Emergent Abilities

Post-Training Quantization

3 Do Emergent Abilities Exist in Quantized LLMs?

3.1 Experimental setup

In-Context Learning Test

Chain-of-Thought Reasoning Test

Instruction Following Test

Quantization Settings

Evaluation Metrics

3.2 Results and Analysis

Overall, the three kinds of emergent abilities seem to be seldom affected with 4-bit quantization.

4-bit precision exhibits a favorable trade-off in terms of both total bits and performance.

The scaling effect depends on specific tasks, and increasing the model scale benefits the CoT task the most.

Low-bit quantization performance benefits from the demonstrations in ICL tests.

For CoT tests, extreme 2-bit quantization requires a large model scale.

4 How to Enhance the Performance of Low-bit Models?

4.1 Quantization Sensitivity Analysis

4.1.1 Experimental Setup

4.1.2 Results and Analysis

The FFN component is of substantial significance for 2-bit quantization.

The outlier dimension which affects most of layers is primarily responsible for the performance degradation.

2-bit model’s performance can be further enhanced with fine-grained substructure quantization.

4.2 Fine-tuning Compensation Analysis

4.2.1 Experimental Setup

Pre-Quantization Fine-tuning

Post-Quantization Fine-tuning

4.2.2 Results and Analysis

The benefits of pre-quantization fine-tuning encounter significant decline at 2-bit precision.

Parameter-efficient fine-tuning still lags behind full-parameter fine-tuning, especially on ICL and CoT tasks.

Post-quantization fine-tuning yields substantial performance improvement meanwhile can be conducted in a lightweight way.

5 Related Work

Emergent Abilities

Post-Training Quantization

6 Conclusion

References

Appendix A Appendix

A.1 Impacts of Model Components

A.2 Case Study

Do Emergent Abilities Exist in Quantized Large Language Models:
An Empirical Study