Do we expect to find the Super-Earths close to the gas giants?

In this part we investigate the evolution of the Super-Earth on the internal orbit and the Jupiter on the external one. The planets are embedded in the flat part of the surface density profile and their relative separation varies in the range from 0.15 to 0.45. In order to get convergent migration of the planets we have performed the simulations with a constant aspect ratio $h$=0.05, a constant kinematic viscosity $\nu=10^{-5}$, which at the initial interior planet’s radius corresponds to the viscosity parameter $\alpha=4\cdot 10^{-3}$, and $\Sigma=6\cdot 10^{-4}$, which is two Jupiter masses spread out within the mean distance of the Jupiter from the Sun. For this set of disc parameters and masses of the planets the Jupiter migrates faster than the Super-Earth, and thus the planets approach each other. As the evolution proceeds two outcomes are possible, either the Super-Earth is ejected from the disc or it becomes locked in the 3:2 or 4:3 mean motion resonances (Podlewska & Szuszkiewicz, [2008]). The resonances located closer to the Jupiter such as 5:4 or 6:5 are not possible, because for such small separations the system becomes unstable and the Super-Earth is scattered from the disc. All the simulations are summarized in Fig. 1. Moreover, not all planetary pairs initially locked in a mean-motion resonance survived further evolution. In the case of 3:2 commensurability the libration width increases with time. In fact, in the case of relative separations 0.26 and 0.27, the amplitude of the oscillation grows and eventually the Super-Earth is scattered from the disc. The direct reason of this scattering is the excitation of the Super-Earth eccentricity.

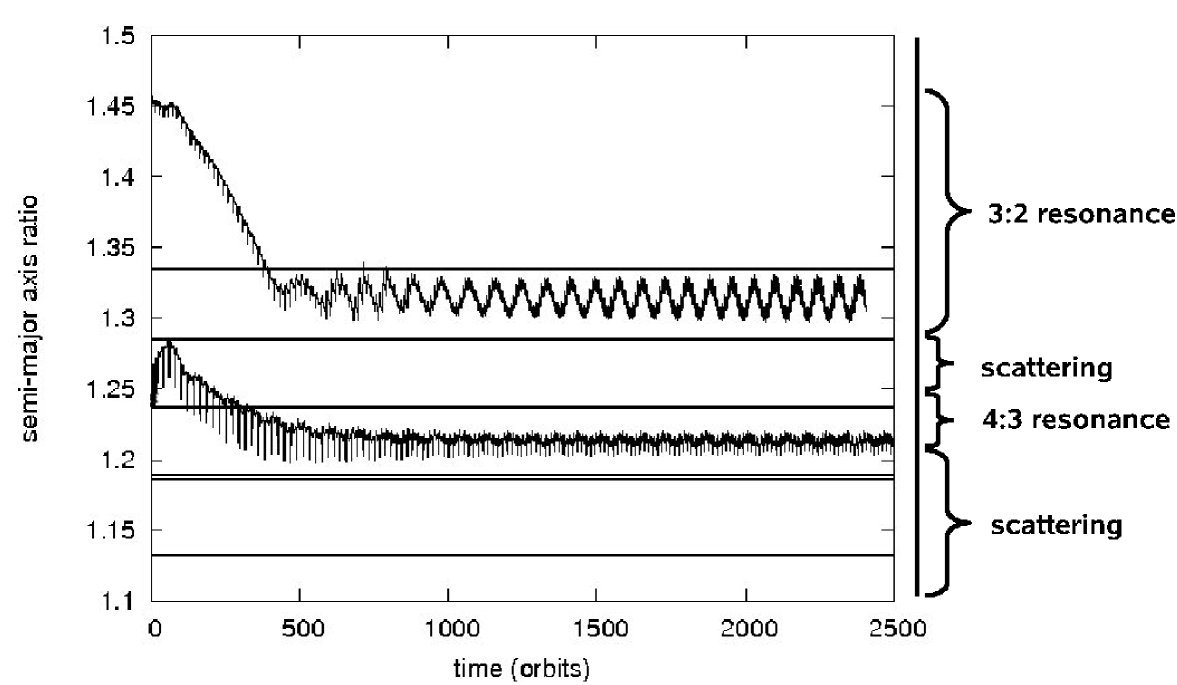
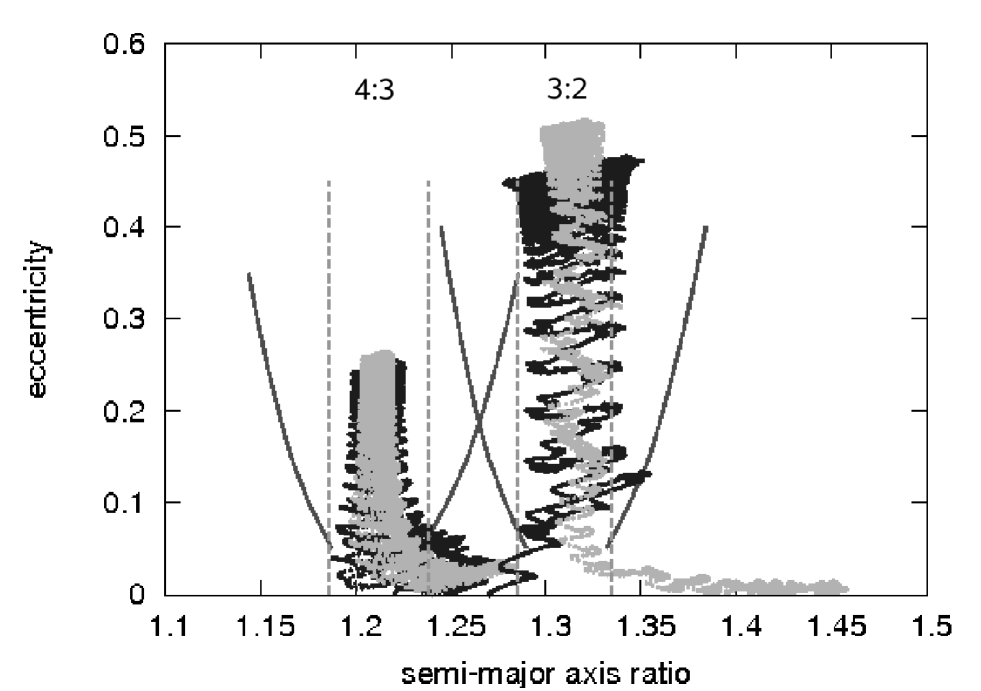
The eccentricity evolution of the terrestrial planets which survived in resonant configurations till the end of our calculations are shown in Fig.2. In this figure, we plot the eccentricity versus the semi-major axis ratio, which was calculated by dividing the semi-major axis of the Jupiter by the semi-major axis of the Super-Earth. For each commensurability the two solid lines show the maximum libration width obtained from the formula given by Winter & Murray ([1997]) in the pendulum approximation of the classical restricted three-body problem. The two dashed vertical lines in Fig. 2 denote the resonance width for the circular case. The eccentricity of the Super-Earth locked in 3:2 commensurability increases and at the end of simulations reaches a value of about 0.5. If the Super-Earth is locked in 4:3 mean motion resonance its eccentricity in all simulations approaches to a value around 0.3.

As we have shown in the previous section it is very likely that the Super-Earth on the internal orbit and the gas giant on the external one form a resonant configuration. Now we ask ourselves if the mean-motion commensurabilities can be established when the terrestrial planet is on the external orbit and the Jupiter is the internal planet. By changing the disc parameters we have succeeded in bringing the planets close to each other. Convergent migration has been achieved for the kinematic viscosity $\nu=2\cdot 10^{-6}$, the surface density $\Sigma=6\cdot 10^{-4}$ and the aspect ratio $h=0.03$. We have located the gas giant initially at distance 1 and the Super-Earth further from the star. In Fig. 3a (left panel) we show the evolution of the semi-major axis ratio of the planets for the initial separation 0.35. The horizontal lines show the width of the 2:3 resonance (Lecar et al., [2001]). However, the resonant configuration lasts just for a few hundred orbits and after that the relative distance between the planets increases. Before revealing the reason for which the 2:3 mean motion resonance cannot be sustained, let us check the possibility of the occurrence of the another first order commensurability, namely 1:2. To this aim, we have placed the Super-Earth further out from the Jupiter, at the relative separation 0.62. The evolution of this configuration is shown in Fig. 3b (right panel). The convergent migration continues for about 2000 orbits and after that, similarly to the previous case, the migration becomes divergent.

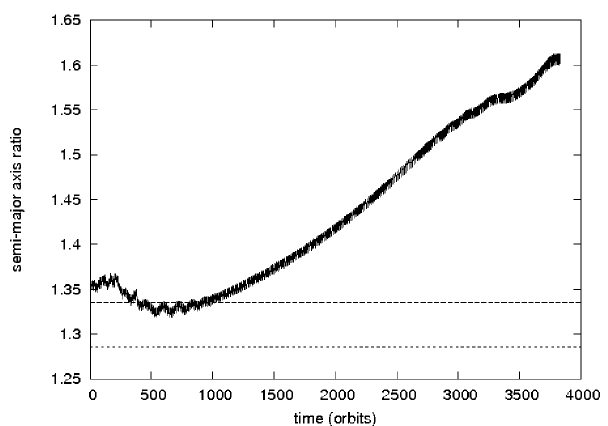
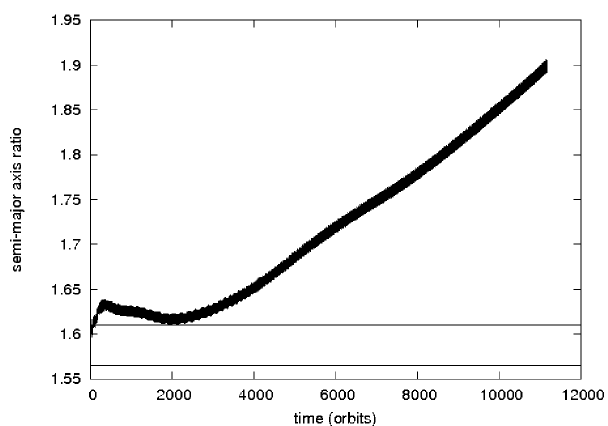
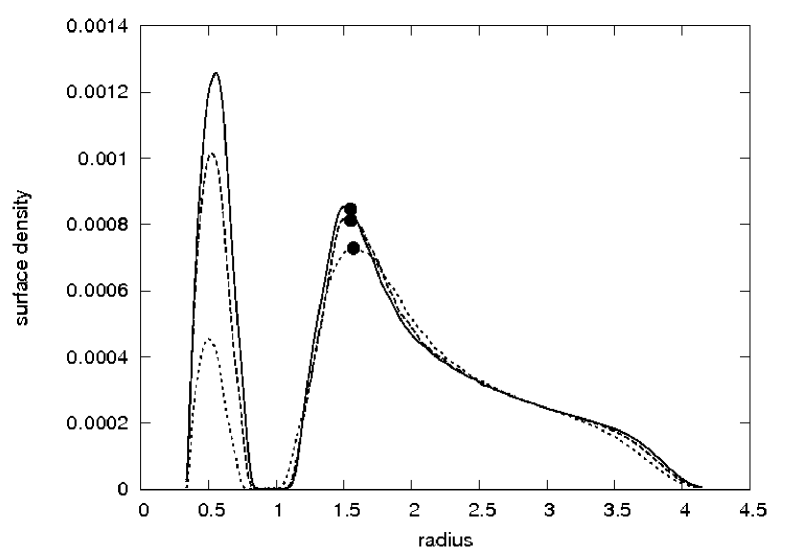
Mean-motion commensurability cannot be attained because the migration of the terrestrial planet is stopped at the outer edge of the gap and this is the reason for which the relative distance between the planets increases. The whole evolution can be described as follows. The Super-Earth embedded in the disc migrates inward toward the Jupiter according to type I migration until it reaches the outer edge of the gap, where it is trapped. This is illustrated in Fig. 4 where we show the surface density profile changes after about 2355, 3925 and 7850 orbits, together with the position of the terrestrial planet marked by the black dot. Once the terrestrial planet reaches the trap it remains captured till the end of the simulation. Such planetary trapping has been already noticed by Masset et al. ([2006]) and Pierens & Nelson ([2008]).

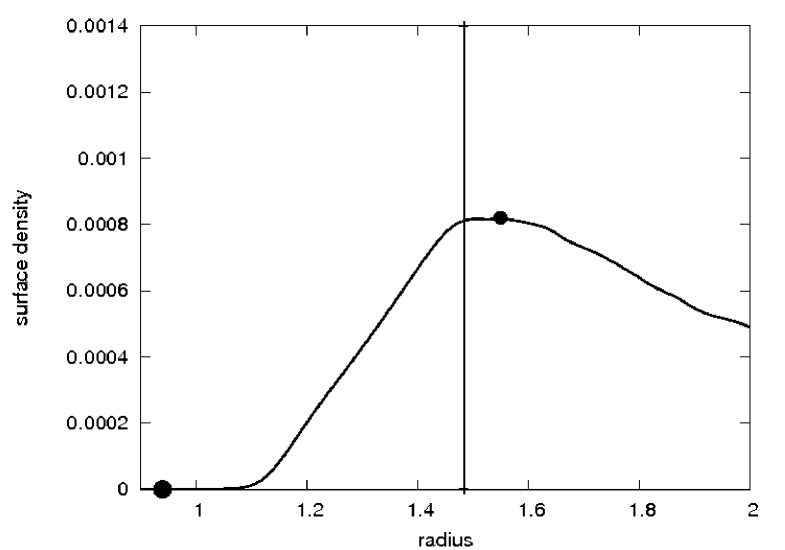
The conclusion is that first-order mean-motion commensurability cannot be achieved because the gap is very wide and the Super-Earth reaches the trap before it is captured in the resonance (Podlewska & Szuszkiewicz, [2009]). We have presented this in Fig. 5 where we plot the gap profile of the disc after 3925 orbits. The dots denote the position of the Super-Earth and the Jupiter. The vertical line shows the location of the 1:2 commensurability.