Does a large quantum Fisher information imply Bell correlations?

The quantum Fisher information (QFI) is an important quantity in the geometry of Hilbert spaces Braunstein and Caves (1994); Uhlmann (1991) and has implications for the foundations of quantum mechanics Tóth and Apellaniz (2014); Taddei et al. (2013); Fröwis and Dür (2012) as well as for quantum metrology Helstrom (1976); Holevo (2011); Pezzè et al. (2018) and quantum computation Shimizu et al. (2013); Demkowicz-Dobrzański and Markiewicz (2015). A well-studied case is $\rho_{t}=\exp(-iAt)\rho_{0}\exp(iAt)$, where $\rho_{0}$ is an $N$-partite qubit state and $A$ is a local operator $A=\sum_{i=1}^{N}A^{(i)}$ (with fixed operator norm $\lVert A^{(i)}\rVert_{\infty}=1/2$ for convenience). Then, the QFI $\mathcal{F}(\rho,A)$ is a function of $\rho_{0}\equiv\rho$ and $A$. This is a typical situation in quantum metrology, where $A$ is the generator of a small perturbation (like a weak external magnetic field) whose strength we would like to measure as precisely as possible. The celebrated quantum Cramér-Rao bound implies that a large QFI is necessary for a high sensitivity Helstrom (1976, 1967). It is well known that certain entangled states allows one to go beyond the so-called standard quantum limit for separable states Caves (1981); Huelga et al. (1997); Giovannetti et al. (2006). More concretely, it was shown Sørensen et al. (2001); Pezzé and Smerzi (2009) that $\mathcal{F}(\rho,A)>N$ implies entanglement between the qubits. The larger the QFI, the larger the entanglement depth of the state Sørensen and Mølmer (2001); Tóth (2012); Hyllus et al. (2012).

Among the nonclassical properties of quantum systems, Bell correlations are of particular importance. On the fundamental side, quantum states exhibiting Bell correlations potentially violate Bell inequalities, thereby proving that nature cannot be modeled with local (hidden) variables Brunner et al. (2014). This insight can be used to design device-independent protocols for quantum applications such as secure communication Acín et al. (2007) or random number generation Pironio et al. (2010); Colbeck . Every quantum state with Bell correlations is entangled, but not every entangled quantum state necessarily has Bell correlations Werner (1989); Barrett (2002); Bowles et al. (2016). Hence, the latter represents a strictly stronger form of quantum correlations.

In the present work we ask whether there exists a connection between large QFI and Bell correlations. Intuitively such a connection can be motivated by the following observation. Both large QFI and Bell correlations are properties of a quantum state associated to specific measurements. That is they cannot be a property of a quantum state (or measurement) alone, but require the judicious combination of states and measurements.

More specifically, we investigate here whether quantum states with a high enough QFI generically exhibit Bell correlations. If this is the case, then are the same measurements that reveal Bell correlations (potentially in a device-dependent manner) useful to show the presence of a large QFI? While we do not provide a fully general answer to these questions, we discuss two examples that hint at affirmative answers. To this end, we linearize a well-known lower bound on the QFI. First, we take its elements to start with an ansatz for a Bell inequality, which turns out to be of the form of multipartite Bell inequalities based on two-body correlators recently introduced by Tura et al. Tura et al. (2014). Considering a multi-setting extension of this Bell inequality Wagner et al. (2017), we show that (i) only quantum states with $\mathcal{F}(\rho,A)>N$ (i.e. beating the standard limit of separable states) can potentially violate the inequality, and (ii) any quantum state with $\mathcal{F}(\rho,A)>3N$ will violate the Bell inequality. Notably, the same measurements that witness the presence of Bell correlations also demonstrate a large QFI.

The second type of linearization is a relaxation of the QFI bound. For a special case which is optimal for the Greenberger-Horne-Zeilinger (GHZ) state, we show that one side of this linear bound becomes the Bell operator for the Mermin inequality Mermin (1990), another multipartite Bell inequality specially suited to detect Bell correlations of GHZ states. Again, a very large QFI is necessary for the violation of the Bell inequality and the same measurements that show large QFI are sufficient choices for a potential Bell inequality violation.

The QFI $\mathcal{F}(\rho,A)$ is a nonlinear quantity that is defined by measuring the infinitesimal change of $\rho$ evolving under $U=\exp(-iAt)$ with the Bures distance $s_{B}$ in state space,

$$ds_{B}=\frac{1}{2}\sqrt{\mathcal{F}(\rho,A)}dt.$$

(1)

While the exact value of $\mathcal{F}(\rho,A)$ is generally only accessible with complete knowledge about $\rho$ and $A$ ¹¹1Given the spectral decomposition $\rho=\sum_{k}p_{k}|\psi_{k}\rangle\langle\psi_{k}|$, the QFI reads $\mathcal{F}(\rho,A)=2\sum_{k,l}(p_{k}-p_{l})^{2}/(p_{k}+p_{l})|\langle\psi_{k}|A|\psi_{l}\rangle|^{2}$., there are powerful lower bounds based on relatively simple measurements. For example, a tighter version of the Heisenberg uncertainty relation holds for all hermitian operators $B$ Hotta and Ozawa (2004); Pezzé and Smerzi (2009); Fröwis et al. (2015)

$$\mathcal{F}(\rho,A)\geq\frac{\langle i[A,B]\rangle_{\rho}^{2}}{\langle(B-\langle B\rangle_{\rho})^{2}\rangle_{\rho}},$$

(2)

where, in the following, we restrict ourselves to $\langle B\rangle_{\rho}=0$ without loss of generality. There is always an operator $B$ that makes inequality (2) tight for given $\rho,A$. Hence, a well-chosen $B$ allows to optimally bound the QFI.

Bell inequalities are bounds on local variable models. Violations of these inequalities are possible in quantum mechanics and imply the presence of Bell correlations. For our purpose, it is sufficient to consider symmetric Bell inequalities of $N$ parties. Following Ref. Tura et al. (2014), we define the symmetrized $k$-body correlators

$$\mathcal{C}_{j_{1},\dots,j_{k}}=\sum_{\begin{subarray}{c}i_{1},\dots,i_{k}=1\\ \text{all $i$ different}\end{subarray}}^{N}\left\langle M_{j_{1}}^{(i_{1})}\dots M_{j_{k}}^{(i_{k})}\right\rangle,$$

(3)

where $M_{j}^{(i)}$ is the measurement operator for setting $j$ at site $i$. Suppose we have $d$ measurement settings per party. Then, general linear, symmetric Bell inequalities are of the form

$$\sum_{k=1}^{N}\sum_{j_{1},\dots,j_{k}=0}^{d-1}a_{j_{1},\dots,j_{k}}\mathcal{C}_{j_{1},\dots,j_{k}}+a_{0}\geq 0,$$

(4)

where $a_{j_{1},\dots,j_{k}},a_{0}\in\mathbb{R}$. They are fulfilled by any local hidden variable model. Here, we are interested in nontrivial Bell inequalities, that is, in those that are violated by some quantum states.

Assuming a connection between large QFI and Bell correlations, one could directly try to turn the right hand side of Eq. (2) into a Bell inequality up to an additional local bound $a_{0}$. Every symmetric, multipartite operator can be expressed in a basis of products of Pauli operators, and its expectation value can be written as a function of correlators (3). However, the nonlinear terms in Eq. (2) render this approach difficult. Therefore, we propose the linear ansatz

$$\alpha+\beta\langle B^{2}\rangle_{\rho}-\gamma\langle C\rangle_{\rho}\geq 0,$$

(5)

with $C=i[A,B]$ and $\alpha,\beta,\gamma>0$. The idea is that if $\langle B^{2}\rangle_{\rho}$ is sufficiently small and $\langle C\rangle$ sufficiently large then inequality (5) can be violated which implies Bell correlations and a large QFI via Eq. (2).

This approach turns out to be successful for spin-squeezed states Kitagawa and Ueda (1993). For concreteness, we choose $A=S_{z}=\frac{1}{2}\sum_{i}\sigma_{z}^{(i)}$ and $B=S_{y}=\frac{1}{2}\sum_{i}\sigma_{y}^{(i)}$, that is, collective spin operators. From the well-known SU(2) commutation relations, one has $C=S_{x}=\frac{1}{2}\sum_{i}\sigma_{x}^{(i)}$. An $N$-partite qubit state is called spin-squeezed if

$$\xi^{2}=\frac{N\langle S_{y}^{2}\rangle}{\langle S_{x}\rangle^{2}}<1,$$

(6)

potentially after a suitable change of collective coordinates. Hence, with our choices for $A$ and $B$, Eq. (5) seems to be a promising candidate for a Bell inequality that can be violated with spin-squeezed states.

However, a direct translation of $S_{x}$ and $S_{y}^{2}$ into measurement settings cannot lead to nontrivial Bell inequalities because then an LHV model can minimize $\langle S_{y}^{2}\rangle$ and maximize $\langle S_{x}\rangle$ independently of each other. To couple the two we introduce new measurement bases for every party $i$

$$\begin{split}M_{0}^{(i)}=&\cos\phi\,\sigma_{y}^{(i)}+\sin\phi\,\sigma_{x}^{(i)}\\ M_{1}^{(i)}=&\cos\phi\,\sigma_{y}^{(i)}-\sin\phi\,\sigma_{x}^{(i)}.\end{split}$$

(7)

We note that $4\sin\phi\langle S_{x}\rangle={\color[rgb]{0,0,1}\mathcal{C}_{0}-\mathcal{C}_{1}}$ and $4\cos^{2}\phi\langle S_{y}^{2}\rangle=N\cos^{2}\phi+\frac{1}{4}(\mathcal{C}_{00}+2\mathcal{C}_{01}+\mathcal{C}_{11})$. Inserting these relations in Eq. (5) we obtain an inequality of the class recently studied by Tura et al. Tura et al. (2014), who show that Eq. (5) constitutes a Bell inequality if $\alpha=2N\sin^{2}\phi,\beta=8\cos^{2}\phi$ and $\gamma=4\sin\phi$. It reads

$$C_{0}-C_{1}+\frac{1}{2}C_{00}+C_{01}+\frac{1}{2}C_{11}+2N\geq 0.$$

(8)

Under the restriction that the measurement settings $M_{j}^{i}$ are identical for all parties, the choice of Eq. (7) turns out to be the most general parametrization. The Bell inequality can then be written as a Bell correlation witness which requires collective spin measurements only Schmied et al. (2016); Wagner et al. (2017). With the definition of the scaled second moment $\zeta^{2}=\langle S_{y}^{2}\rangle/(N/4)$, and of the scaled contrast $\mathcal{C}=\langle S_{x}\rangle/(N/2)$, the inequality becomes

$$\zeta^{2}\geq\dfrac{1}{2}\left(1-\sqrt{1-\mathcal{C}^{2}}\right)\,.$$

(9)

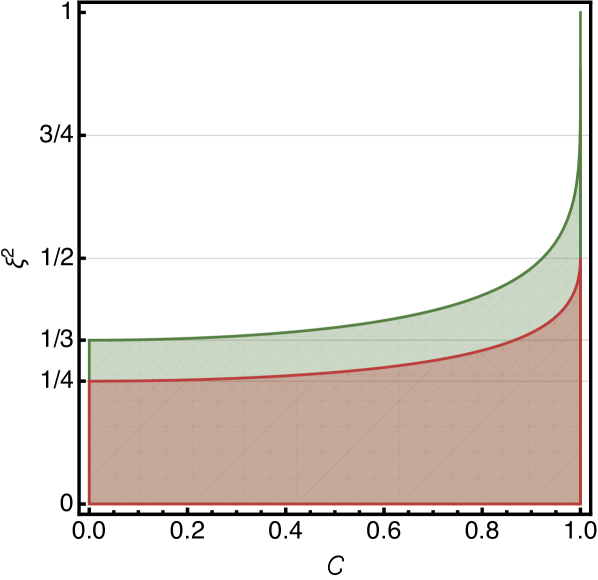
From the fact that $\xi^{2}=\zeta^{2}/\mathcal{C}^{2}$ we can express Eq. (9) as a function of $\xi^{2}$ and $\mathcal{C}$, and observe that (see Fig. 1): i) for $\xi^{2}\leq 1/4$ the inequality is always violated, independently on $\mathcal{C}$, ii) for $1/4<\xi^{2}<1/2$ a minimal $\mathcal{C}$ is needed to violate the inequality, iii) for $\xi^{2}\geq 1/2$ the inequality is never violated. This implies that only states with $\mathcal{F}(\rho,S_{z})>2N$ are able to violate inequality (8). Moreover, all states with $\mathcal{F}(\rho,S_{z})>4N$ will give violation, that is for sufficiently squeezed states, such as the one-axis and the two-axes twisted spin-squeezed state Kitagawa and Ueda (1993).

It turns out that these results can be improved by considering a multi-setting generalization of the Bell inequality (8) presented in Ref. Wagner et al. (2017). Again, this inequality can be written as a Bell correlation witness which requires collective spin measurements only. Specifically, consider the family of $m$-settings inequalities

$$\sum_{k=0}^{m-1}\alpha_{k}C_{k}+\dfrac{1}{2}\sum_{k,l}C_{k,l}+\beta_{c}\geq 0\;,$$

(10)

with $\alpha_{k}=m-2k-1$ and $\beta_{c}=\lfloor m^{2}N/2\rfloor$. This inequality can again be written as a witness which in the limit $m\rightarrow\infty$ takes the form Wagner et al. (2017)

$$\zeta^{2}\geq 1-\dfrac{\mathcal{C}}{\text{arctanh}(\mathcal{C})}\;,$$

(11)

which holds for all states featuring local correlations. Performing the same analysis as above, we observe that (see Fig. 1): i) for $\xi^{2}\leq 1/3$ the inequality is always violated, independently on $\mathcal{C}$, ii) for $1/3<\xi^{2}<1$ a minimal $\mathcal{C}$ is needed to violate the inequality.

To conclude, from Eqs. (2), (6) and (11), we see that $\mathcal{F}(\rho,S_{z})>N$ is a necessary condition for violating the Bell inequality (10). That is, only quantum states that beat the standard limit of separable states can potentially violate the Bell inequality. Moreover, the condition $\mathcal{F}(\rho,S_{z})>3N$ is sufficient for violating the Bell inequality, i.e. all states satisfying it will give violation. Again, here the measurement settings are assumed to be identical for all parties.

In the previous section, we took a rather free inspiration from the Heisenberg uncertainty relation to construct a Bell inequality where only states with a large enough QFI could potentially violate it. Here, we tackle the problem more directly by linearizing the right hand side of Eq. (2). We simply use $\langle B^{2}\rangle_{\rho}\leq\lVert B\rVert^{2}_{{\color[rgb]{0,0,1}\infty}}$, to arrive at a linear lower bound

$$\sqrt{\mathcal{F}(\rho,A)}\geq\langle W\rangle_{\rho}\equiv\frac{1}{\lVert B\rVert_{\infty}}\langle i[A,B]\rangle_{\rho}.$$

(12)

Here, and in the following, we choose the sign of $B$ such that $\langle W\rangle_{\rho}$ is positive.

Interestingly, since $\mathcal{F}(\rho,A)\leq N$ for all separable states, Eq. (12) can be turned into an entanglement witness with operator $\mathcal{W}=\sqrt{N}-W$ for all $B$. In other words, the correctness of the Heisenberg uncertainty relation gives us a constructive tool to derive new entanglement witnesses.

This linearization seems to come at the price that the bound is now much looser, but it turns out that, at least for pure states, there always exists a $B$ to achieve tightness.

We study a specific example for the choice of Eq. (13). We consider the GHZ state,

$$\left|\mathrm{GHZ}\right\rangle=\frac{1}{\sqrt{2}}(\left|0\right\rangle^{\otimes N}+\left|1\right\rangle^{\otimes N}).$$

(14)

This state has the maximal QFI for $A=S_{z}$ with $\mathcal{F}(\mathrm{GHZ},S_{z})=N^{2}$. Again, direct calculation shows that $W=N(\left|\mathrm{GHZ}\right\rangle\!\left\langle\mathrm{GHZ}\right|-|\mathrm{GHZ}^{\perp}\rangle\!\langle\mathrm{GHZ}^{\perp}|)$, where $|\mathrm{GHZ}^{\perp}\rangle=1/\sqrt{2}(\left|0\right\rangle^{\otimes N}-\left|1\right\rangle^{\otimes N})$.

Interestingly, the very same $W$ as in Eq. (12) appears when quantum mechanics is applied to the Bell inequality of Mermin Mermin (1990), up to a constant and an irrelevant phase. With our choice of the normalization, Mermin’s inequality show Bell correlations of $\rho=\left|\mathrm{GHZ}\right\rangle\!\left\langle\mathrm{GHZ}\right|$ whenever

$$\langle W\rangle_{\rho}\leq\begin{cases}N\,2^{-N/2+1}&\text{$N$ is even},\\ N\,2^{-N/2+1/2}&\text{$N$ is odd}.\end{cases}$$

(15)

is violated. We compare this to the witness of large QFI

$$\langle W\rangle_{\rho}\leq\sqrt{\mathcal{F}(\rho,S_{z})}.$$

(16)

We observe a connection between the Bell inequality and the lower bound on the QFI. The GHZ state maximally violates the Bell inequality and makes Eq. (16) being tight. We see that a certain minimal QFI is necessary to potentially violate the Bell inequality. However, the fact that $W$ is tailored to the GHZ state makes both inequalities not very useful for other states. Furthermore, a QFI beyond the shot noise limit $N$ is not necessary in this case. To illustrate this, we consider the quantum state

$$\rho=\frac{1+p}{2}\left|\mathrm{GHZ}\right\rangle\!\left\langle\mathrm{GHZ}\right|+\frac{1-p}{2}|\mathrm{GHZ}^{\perp}\rangle\!\langle\mathrm{GHZ}^{\perp}|$$

(17)

with $p\in[0,1]$. Using the PPT criterion, one easily convince oneself that the state has bipartite entanglement for any $p>0$. It violates the Mermin inequality if $p>2^{-N/2+1}N$. Last, the state has a QFI of $\mathcal{F}(\rho,S_{z})=p^{2}N^{2}$, implying that $p>1/\sqrt{N}$ is necessary to have a QFI that is larger than for any separable state. For large $N$, the latter bound is exponentially more restrictive than the local bound of the Mermin inequality.

We investigated whether Bell correlations and large quantum Fisher information (QFI) are connected. For two examples of Bell inequalities, one instance from a class studied in Tura et al. (2014) and the Mermin inequality Mermin (1990), we showed that a sufficiently large QFI is necessary for a violation. How generic is this connection? Is it possible to find a Bell inequality that is violated for any quantum state with large QFI? Both approaches presented in this paper give hope to find further Bell inequalities designed for such states like the Dicke states. Currently, however, we are not aware of a constructive method to conjecture and prove these inequalities. This is mainly due to the step of finding good measurement basis for a quantum operator like in Eq. (5) for a nontrivial Bell inequality.

Finally, note that a large QFI is generally not necessary for a quantum state to violate a Bell inequality. Indeed, every pure entangled state can violate a Bell inequality Gisin (1991); Popescu and Rohrlich (1992); Gachechiladze and Gühne (2017), but not every pure entangled state has a QFI beyond the standard quantum limit if only collective measurements are performed Hyllus et al. (2010).

Acknowledgements.— We would like to acknowledge discussions with Roman Schmied. Financial support by the European ERC-AG MEC and the Swiss national science foundation (Starting grant DIAQ, NCCR-QSIT, and Grant No. $20020\_169591$) is gratefully acknowledged.